Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Chemistry
versão On-line ISSN 1996-840X
versão impressa ISSN 0379-4350
S.Afr.j.chem. (Online) vol.72 Durban 2019
http://dx.doi.org/10.17159/0379-4350/2019/v72a29
RESEARCH ARTICLE
Control of Electric Dipole Moment using Deformation induced by Functionalization of (5, 0) Zigzag Carbon Nanotubes as Gigahertz Oscillators
Siroos RastaniI, *; Hossein MostaanzadehII
IDepartment of Electrical Engineering, University of Qom, Iran
IIDepartment of Chemistry, University of Qom, Iran
ABSTRACT
Electric dipole moment (EDM) required for the relative motion of carbon nanotube (CNT) walls in nanoelectromechanical systems (NEMS) such as actuators and oscillators is studied by functionalization. Pristine (5,0) zigzag carbon nanotube with little inherent electric dipole moment (ì) were deformed by adding three -OH functional groups to its end rims. The properties of eight yielded isomers are studied. The Gibbs free energy calculations demonstrate that the eight structures are more stable than pristine CNT. The induced deformation resulted in charge imbalances which developed large electric dipole moments for each case. The values of dipole moments produced for all cases are calculated. The bandgap energy, conductivity, density of state (DOS) and IR spectra of these structures are also computed and analyzed. The study revealed that the location of the -OH positioning (site selectivity) which gives rise to different degrees of deformation has a significant impact on all of the above parameters, especially the magnitude and direction of the electric dipole moment. The functionalization produced large ì of about 6.9 D for 60 carbon atoms nanotube which is higher than in the previous study. Applying an external electric field to the isomers causes the CNTs with large dipole moments to either get attracted or repelled and hence physical movement or oscillation of the nanotube occurs. The frequency of this oscillation is in gigahertz scale.
Keywords: Gigahertz oscillator, electric dipole moment, deformation, carbon nanotube, hydroxyl functionalization, site selectivity.
1. Introduction
With the advent of carbon nanotubes (CNTs) special structural, electronic, and optical devices along with many potential applications are being introduced to scientists and engineers.1-5 One-dimensional single-wall carbon nanotubes (SWCNT) for example, are employed in new composites, molecular electronics,6,7 optics,8 sensors,9 nanomechanics10 and catalysts.11 Using nanotubes in the implementation of devices such as actuators,12 nanomotors13,14 and NEMS are also demonstrated.15,16 Even some of the characteristics of nanotubes such as their electric dipole moments (EDM, μ) are identified to have a role in the physical movement of the CNTs in low-friction bearings17,18 and sliders.19 It is reported that in a double-walled nanotube there is a van der Waals interaction between the outer wall with its inner core, so that if the inner core is extracted out, the van der Waals restoring force will quickly and fully, after release, retract the extruded core into the outer shell.20 When the core returns to the fully retracted position, although the van der Waals interaction energy is minimized, the speed of retraction will give the core a kinetic energy that will cause it to pass over this minimum energy point. It is subjected to a repulsive force as soon as it passes the position of minimum potential energy and thus the motion will be reversed, causing the core to extrude again which leads to the oscillation of the core. This makes the basis for a back and forth oscillation. To produce the initial extrusion of the core and to help maintain the oscillation at its natural frequency (giga-hertz),20,21 studies on the gigahertz oscillators have proposed three different displacement mechanisms; 1) use of a metallic nanotube which in an external magnetic field will extrude the inner core, 2) applying metal ions onto a nanotube surface which can be attracted or repelled by an exterior electric field, and 3) employing the pressure of a heating gas. Unfortunately, none of these methods have produced satisfactory results. However, if by functionalization of the inner core one transforms the wall of the nanotube into an electric dipole, then by applying a non-uniform external electric field to this electric dipole, the core would be easily extracted out and oscillation can start.22
In our previous work, it was shown that the dipole moment of CNTs have a direct relationship with their degree of deforma-tion.23 That is, the deformation controls the magnitude and the direction of the dipole moment responsible for the oscillation of nanotubes under the influence of the electric field. Figure 1 shows such a deformed CNT inside a larger one with its EDM (ì) interacting with the applied external non-uniform field, causing it to physically move back and forth in the direction shown.
However, when nanotube deformation is studied by methods such as radial deformation,24 defect formation25 hydrostatic pressure26 and functionalization using groups such as -OH and COOH,27 the details of the induced deformation by an electrical charge imbalance which is responsible for dipole moment is not considered and mostly changes in bandgap, conductivity, and electronic structure are reported. Therefore, to be able to study the effect of electric field on movement of a nanotubes through interaction with its dipole moment, data on the details of deformation and magnitude and direction of the electric dipole moment generated are required; this article addresses this issue.
In this work, zigzag SWCNTs are deformed by end functionali-zation (adding 3 -OH groups to the end rims rather than the body of the nanotube) and the resulting deformation as well as magnitude and direction of electric dipole moment for each case is calculated. This was done to explain more clearly the relation between deformation and dipole moment while achieving higher values for dipole moment than were found previously by adding two -OH groups.23 Furthermore, complete geometry optimizations of the (5, 0) pristine and functionalized SWCNT are implemented by DFT calculations. In addition, properties of each of the yielded isomers such as Gibbs free energies, the density of states, energy bandgap, conductivity and IR spectra are evaluated.
2. Model and Computational Methods
As an SWCNT model, a (5,0) zigzag carbon nanotube containing 60 atoms was used. In the pristine CNT, the ten dangling bonds of the terminal carbon atoms at either end are saturated by hydrogen atoms. In order to obtain the functionalized model, three of these hydrogen atoms were replaced by three -OH groups (Fig. 2). This results in eight structural isomers as follows. From the eight cases, two structures have all three -OH groups located on one end. While the six other possible isomers have only two -OH groups on one rim and the third one on the opposite end.
To find the lowest energy state of the functionalized SWCNTs, these structures were optimized. The ground state calculations are done using DFT and B3LYP (Becke Three Parameter) hybrid functional, where the exchange functional is Becke's three parameter type. The gradient correction is considered and the correlation correction covers the gradient-corrected functional of Lee, Yang and Parr.28 The reason for such choice is the fact that it is less demanding (computationally) than the other methods because it considers the inclusion of electron correlation and it seems to correctly predict a spectrum of molecular properties. The software package Gaussian 03 is used29 along with the basis set 6-31G(d). The calculations did not result in any imaginary frequencies as the solution. Based on the nuclear displacements calculated by visual inspection of the animated normal modes using GaussView 03 software,30, the vibrational mode descriptions were made.
3. Results and Discussion
3.1. Thermodynamic Aspects
The main reaction to form the functionalized CNT's is assumed to be:
Using the B3LYP/6-31G(d) level of theory, the structures of both the functionalized as well as non-functionalized CNT'S are fully optimized. The Gibbs free energy of reaction in the standard conditions (ΔG0) is as follows:
Where, and
and  are the standard
are the standard 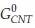 free energies of tri-hydroxylated CNT, O2 and initial CNT, respectively, calculated from the theory level mentioned above.
free energies of tri-hydroxylated CNT, O2 and initial CNT, respectively, calculated from the theory level mentioned above.
Table 1 shows the orbital energies for HOMO, LUMO and the energy gaps ( ΔE) in the first three columns. The next column represents the dipole moments (ì) of each compound. The Gibbs free energy for each case is negative. Thermodynamically that refers to stability and favourable structure and condition of each compound. The ΔG values found and displayed in the last column are all obtained from Equation 1 in the gaseous phase. They represent negative values as well, indicating that the CNT reaction with the O2 molecule is favourable with a high percentage of possibility for production.
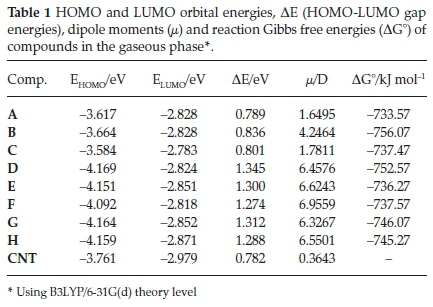
The differences from -733.57 to -756.07 kJ mol-1 indicate the significance of the position of the hydroxyl group in five sites around either end. Considering all the possible hydroxylated isomers, the structure B where all three -OH groups are located at one end of CNT and an empty site in between the two hydroxyl groups show the lowest value for AG (-756.07 kJ mol-1).
However, the structure A, where three -OH groups are next to each other, with AG value of -733.57 kJ mol-1 is the least stable state and therefore, thermodynamically has the lowest possibility to form. This could be due to the electrostatic repulsion between the electron clouds of adjacent hydroxyl groups. Interestingly, the two cases that produce the most and the least stable cases are the ones that all three OH groups are located at one of the ends.
3.2. Structural Deformation and Frontier Orbital Nature
Bonding of -OH groups to the rim Carbon atoms have caused the geometries of the CNTs to be modified so that the cross-sections are not circular anymore but rather elliptical.
Calculated major and minor axes of the ellipses at the inlets of ends as well as their differences (δ1 and δ2) are reported in Table 2. Here, μ1is related to the end which contains three or two hydroxyl groups and μ2 is related to the end that either does not have any or contains only one hydroxyl group. From these values, one can realize the degree of structural deformation.
Addition of the third hydroxyl group at the site F generates an isomer which has the highest level of deformation with respect to the initial CNT (Fig. 3). It is obvious that in structures C-H, the end which contains only one hydroxyl group show more distortion than the other end containing two hydroxyl groups.
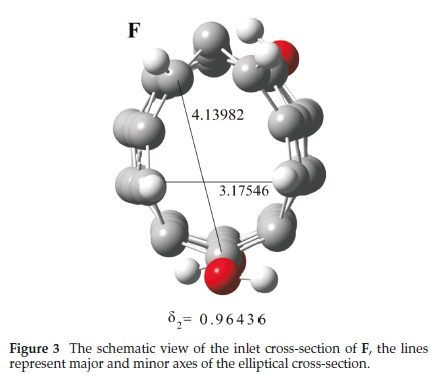
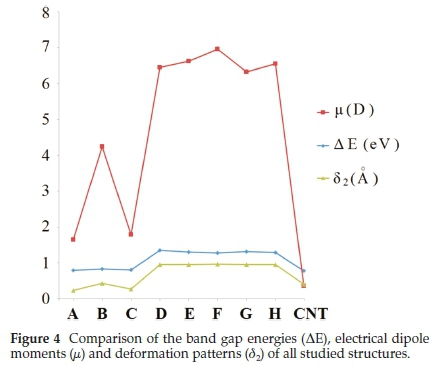
Figure 4 depicts the values of band gap energies (ΔE), electrical dipole moment (μ) and deformation (δ2) of all the structures studied in Tables 1 and 2. From this figure, it is clear that the ΔE and ì are related to δ2. For instance, the structures D-E show higher deformation (δ2), indicating higher values for AE and ì. Interestingly, the structures A and C have similar values for δ2, ΔE and μ..
The shapes and symmetry of HOMO and LUMO orbitals that are related to the location of -OH groups are shown in Fig. 5. In structures A and B where the three -OH groups are at either end or only two of the hydroxyl groups are located on one end (C-H), this dependency becomes more evident. It seems that in structures A-C the frontier orbitals display a vertical symmetry with respect to a sheet normal to the figure along the length of the CNT. This symmetry turns diagonal for the cases E-H.
3.3. Evaluation of Dipole Moment
The direction and the relative magnitude of the electrical dipole moments are tabulated in Table 1 and illustrated in Fig. 5. From these data, dipole moments are clearly dependent on the hydroxyl group positions.
Since the electronegativity of O atoms is higher than C atoms, one expects that the direction of the resultant dipole moment to be toward the end that has a higher number of -OH groups. Here, case A verifies this expectation while the cases B-H, do not follow this line of thought. As it became clear the deformation has a stronger impact on the direction of the dipole moment. From δ1 and δ2 data in Table 2 and Fig. 5, the direction of dipole moment seems to be always from the side that has larger deformation toward the less deformed end. From the magnitude point of view, when the two -OH groups are located at one end, the magnitude of the resultant dipole moment (6.6243-6.9559 D) is larger than the ones that all three are located on one end (1.6495 and 4.2464 D). Only case C is an exception (1.7811 D). It has to be mentioned that in the previous paper,23 the highest dipole moment obtained was μ = 5.6604 D (for 60 carbon atom nanotube). From these data and the values of δ2in Table 2 as well as the diagram of Fig. 4, whenever the deformation of CNT is higher, the magnitude of dipole moment is also larger.
Ershova el aí.22report that by adding 10 fluorine atoms as electron acceptors on one rim and 10 hydrogen atoms as electron donors to the opposite end of a nanotube containing 240 carbon atoms, one can generate a dipole moment of the size 22.4 D (7.4 x 10-29 C m) which can produce oscillation frequencies of up to 388 GHz. Despite the smaller dipole moment in this study, a three -OH functionalized CNT with the molecular mass of 778 g mol-1 has an oscillation frequency higher than what has been reported before. Recall that Ershova el aí.22used a 10-F functionalized CNT with the molecular mass of 3080 g mol-1. It has to be mentioned that the frequency of oscillation is proportional to square root of the inverse mass of a nanotube.22
3.4. IR Spectra of Tri-hydroxylated CNT
The IR-spectra of all the structures A-H along with the pristine CNT is depicted in Fig. 6. From Table 3 and the figure, it is clear that IR vibrational frequencies are dependent on the positions of -OH groups. In Fig. 6 the frequency range of 3000-1000 cm-1, the vibrational frequencies of O-H, as well as C-H, are depicted. Due to the three -OH groups, one expects that three peaks corresponding to the stretching frequency (vO-H) to be observed. This can be seen in Table 3, where values of frequencies are distinctively enumerated. Some of these resulting frequencies are so adjacent to each other that in plotting them, they almost overlap and indistinguishable, except for the cases A and D where the three frequencies are distinct (Fig. 6).
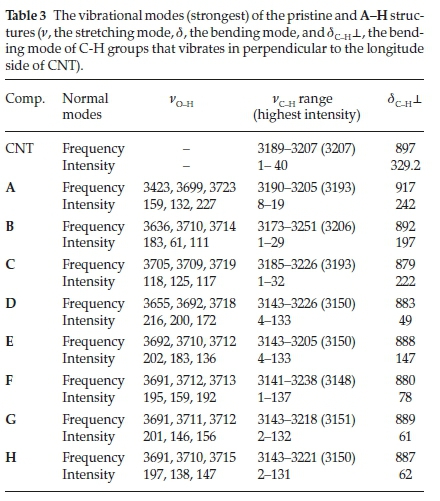
Apparently, in Case A where the three -OH groups are next to each other, the three peaks are not only spaced out but the middle hydroxyl group causes a frequency (3423 cm-1) that is separated from the other two peaks ( 3699 and 3723 cm-1). This is the lowest frequency among all eight structures. Such a low frequency might be due to intra-molecular hydrogen bonding between this hydroxyl group with one of the neighboring -OH groups.
The exact values of the C-H stretching frequencies (vC-H) are shown in Table 3. For the sake of discussion, the values of the highest intensities are put in parentheses. From the study of these values, it seems that the structures which possess two -OH on one end and another one on the other end, show a lower frequency compared to CNT and cases A & B. The only exception is again the case C which shows high vC-H. For the case of bending C-H frequencies (<5C-H), it appears that by adding -OH groups to the nanotube, the resulting áC-H for all structures except for the case A, is always smaller than pristine CNT. Referring to Fig. 6, the breathing frequencies are clearly visible in cases A-C & CNT. However, for D-H the intensity of these frequencies is not as evident.
3.5. The Density of States (DOS)
This parameter is usually used for the evaluation of conductivity and optical properties of materials. In Fig. 7 the DOS of regular CNT, as well as hydroxylated ones, are presented. The values of bandgap reported in Table 1 and DOS diagrams can be used to qualify the electrical conductivity. The conclusion here is that the position of hydroxyl groups strongly influences the electrical properties of structures.
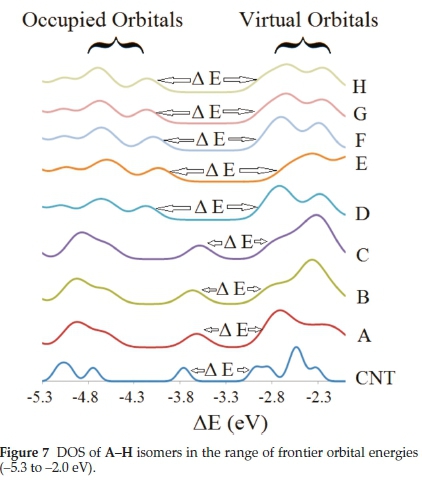
As it is seen, right at the start of virtual orbitals, the height of these peaks in structures A, D, F & G are more pronounced than the rest of the CNT's and therefore it will provide a higher number of virtual orbitals for the electrons to move into. In cases of A, B, C and E due to the fact that the virtual orbitals are more compact, the energy associated with them appears as a continuum and consequently one expects that they have greater conduction in these structures.
Referring to Table 1, for the cases A & B where the three -OH groups are on one end, the bandgaps are smaller than the other structures except the case C. Furthermore, from Fig. 7 the location of HOMO orbitals in cases A, B, and C are around Fermi level of the cases D, G and H. so, the cases A, B and C can function as n-type for the cases D, G and H which can be considered p-type.
4. Conclusions
The electric dipole moment magnitude and direction for eight isomers resulting from end functionalization of CNTs with three -OH groups are calculated. The hydroxylated structures were optimized and analyzed in detail. Calculations show that the molecular properties such as geometry, stability, vibrational frequency and electrical aspects of the resulted hydroxylated CNTs strongly depend on the position of -OH groups. It was found that these structures are thermodynamically more stable than pristine CNT. One of the major conclusions of the addition of -OH groups is that the degree of induced deformation has a direct relationship with the magnitude and direction of dipole moment as well as energy gap of the resulting functionalized CNT's. Moreover, the direction of dipole moment seems to be always from the side that has larger deformation toward the less deformed end. The magnitude of dipole moment obtained is higher than previous study which resulted in a higher oscillation frequency. The concept of tailoring of the CNT structures with functionalization to control their dipole moments through deformation and subsequently to control the frequency of its oscillation is successfully presented.
Acknowledgement
The authors would like to acknowledge the financial support of the University of Qom and the Iranian National Committee of Nanotechnology in the Ministry of Science, Research, and Technology.
§ORCID iD
H. Mostaanzadeh: © orcid.org/0000-0002-9647-9006
References
1 S. Iijima, Helical microtubules of graphitic carbon, Nature, 1991, 354, 56-58. [ Links ]
2 A. Minett, F. Schüth, S.W. Sing, J. Weitkapmp, K. Atkinson andS. Roth, Carbon nanotubes, in Handbook of Porous Solids, Wiley-VCH, Weinheim, Germany, 2002. [ Links ]
3 Z. Yao, H.W.C. Postma, L. Balents and C. Dekker, Carbon nanotube intramolecular junctions, Nature, 1999, 402, 273-276. [ Links ]
4 O. Zhou, H. Shimoda, B. Gao, S. Oh, L. Fleming and G. Yue, Materials science of carbon nanotubes: fabrication, integration, and properties of macroscopic structures of carbon nanotubes, Acc. Chem. Res., 2002, 35, 1045-1053. [ Links ]
5 R.H. Baughman, C. Cui, A.A. Zakhidov, Z. Iqbal, J.N. Barisci, G.M. Spinks, G.G Wallace, A. Mazzoldi, D. De Rossi, A.G. Rinzler, O. Jaschinski, S. Roth and M. Kertesz, Carbon nanotube actuators, Science, 1999, 284, 1340-1344. [ Links ]
6 N. Ferrer-Anglada, V. Gomis, Z. El-Hachemi, U.D. Weglikovska, M. Kaempgen and S. Roth, Carbon nanotube based composites for electronic applications: CNT conducting polymers, CNT-Cu, Phys. Status Soíidi, 2006, 203, 1082-1087. [ Links ]
7 Z. Chen, J. Appenzeller, Y.M. Lin, et al., An integrated logic circuit assembled on a single carbon nanotube, Science, 2006, 311, 1735. [ Links ]
8 Y. Sakakibara, A.G. Rozhin, H. Kataura, Y. Achiba and M. Tokumoto, Carbon nanotube-poly(vinylalcohol) nanocomposite film devices: applications for femtosecond fiber laser mode lockers and optical amplifier noise suppressors, Japan.J.Appl. Phys., 2005,44,1621-1625. [ Links ]
9 M.E. Kose, B.A. Harruff, Y. Lin, L.M. Veca, F. Lu and Y.P. Sun, Efficient quenching of photoluminescence from functionalized single-walled carbon nanotubes by nitroaromatic molecules, J. Phys. Chem. B, 2006, 110, 14032-14034. [ Links ]
10 D.A. Britz and A.N. Khlobystov, Noncovalent interactions of molecules with single-walled carbon nanotubes, Chem. Soc. Rev., 35 (2006) 637-659. [ Links ]
11 P. Serp, M. Corrias and P. Kalck, Carbon nanotubes and nanofibers in catalysis, Appí. Cataíysis A, 2003, 253, 337-358. [ Links ]
12 S.S. Kuznetsov, Y.E. Lozovik and A.M. Popov, The nanoactuator based on a carbon nanotube, Phys. Solid State, 2007,49, 1004-1012. [ Links ]
13 A.M. Fennimore, T.D. Yuzvinsky, W.Q. Han, et al., Rotational actuators based on carbon nanotubes, Nature, 2003, 424, 408-410. [ Links ]
14 B. Bourlon, D.C. Glatti, L. Forro, C. Miko and A. Bachtold, Carbon nanotube based bearing for rotational motions, Nano Lett, 2004,4(4), 709-712. [ Links ]
15 A.M. Popov, E. Bichoutskaia, Y.E. Lozovik and A.S. Kulish. Nanoelectromechanical systems based on multi-walled nanotubes: nanothermometer,nanorelay,andnanoactuator, Phys. Status SolidiA, 2007, 204, 1911-1917. [ Links ]
16 E. Bichoutskaia, A.M. Popov, Y.E. Lozovik, G.S. Ivanchenko and N.G. Lebedev. Electromechanical nanothermometer, Phys. Lett. A, 2007, 366, 480-486. [ Links ]
17 M.F. Yu, O. Lourie,M.J. Dyer, etal., Strengthandbreakingmechanism of multiwalled carbon nanotubes under tensile load, Science, 2000, 287, 637-640. [ Links ]
18 J. Cumings and A. Zettl, Low-friction nanoscale linear bearing realized from multiwall carbon nanotubes, Science, 2000, 289, 602-604. [ Links ]
19 A. Kis, K. Jensen, S. Aloni, W. Mickelson and A. Zettl, Interlayer forces and ultralow sliding friction in multiwalled carbon nanotubes, Phys. Rev. Lett., 2006, 97, 025501. [ Links ]
20 Q. Zheng and Q. Jiang, Multiwalled carbon nanotubes as gigahertz oscillators, Phys. Rev. Lett., 2002, 88, 045503. [ Links ]
21 Q. Zheng, J.Z. Liu and Q. Jiang, Excess van der Waals interaction energy of a multiwalled carbon nanotube with an extruded core and the induced core oscillation, Phys. Rev. B., 2002, 65, 245409. [ Links ]
22 O.V Ershova, Y.E. Lozovick, A.M. Popov, O.N. Bubel, E.F. Kislyakov, N.A. Polokonski, A.A. Knizhnik and I.V. Lebedeva, Control of motion of NEMS based on carbon nanotubes by electric field, J. Exp. Theoret. Phys, 2008,107(4), 653-661. [ Links ]
23 H. Mostaanzadeh, A. Abbasi and E. Honarmand, DFT theoretical calculation of the site selectivity of di-hydroxylated (5, 0) zigzag carbon nanotube, Russian J. Phys. Chem. A, 2017, 91, 148-154. [ Links ]
24 Y.V Shtogun and L.M. Woods, Electronic and magnetic properties of deformed and defective single-wall carbon nanotubes, CARBON, 2009,47, 3252-3262. [ Links ]
25 A.R. Rocha, J.E. Padilha, A. Fazzio and A.J.R. da Silva, Transport properties of single vacancies in nanotubes. Phys. Rev. B., 2008,77,153406. [ Links ]
26 V. Gadagkar, P.K. Maiti, Y. Lansac, A. Jagota and A.K. Sood, Collapse of double-walled carbon nanotube bundles under hydrostatic pressure, Phys. Rev. B., 2006, 73, 085402. [ Links ]
27 P.H. Shah and R.C. Batra, Effect ofCovalent Functionalization on Young's Modulus of a Single-wall Carbon Nanotube, Springer International Publishing, Switzerland, 2014, 111-134. [ Links ]
28 A.D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648-5652. [ Links ]
29 M.J. Frisch, et al., Gaussian 03, Revision E.01, Gaussian, Inc., Walling- ford CT, 2004. [ Links ]
30 GaussView 03, Gaussian, Inc., Wallingford, CT, 2003. [ Links ]
Received 3 March 2019
Revised 19 June 2019
Accepted 16 July 2019
* To whom correspondence should be addressed. E-mail: S.R.: s-rastani@qom.ac.ir / H.M.: h.mostaan@qom.ac.ir














