Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Chemistry
On-line version ISSN 1996-840X
Print version ISSN 0379-4350
S.Afr.j.chem. (Online) vol.72 Durban 2019
http://dx.doi.org/10.17159/0379-4350/2019/v72a10
RESEARCH ARTICLE
A Liquid-Solid Two-phase Flow Computational Fluid Dynamic Modelling of the Operational Characteristics Effects on the Cleaning Time of a Circulating Flow Loop
Mohsen DehvedarI; Parviz MoarefvandII, *; Ali Reza KiyaniI
IDepartment of Petroleum Engineering, Amirkabir University of Technology (Tehran Polytechnic), Tehran, Iran
IIDepartment of Mining & Metallurgical Engineering, Amirkabir University of Technology (Tehran Polytechnic), Tehran, Iran
ABSTRACT
Flow loops and computational fluid dynamics are the main research approaches for resolving the hole-cleaning problems. Cutting transport phenomena can be considered as a Computational Fluid Dynamic (CFD) model by using Eulerian assumptions for the turbulent liquid-solid flow in concentric annuli. The effect of time along with the main operational characteristics on the hole-cleaning phenomena is not negligible but recent studies have had paid little attention to it. Poor near bit cleaning causes many problems such as bit balling, decline in the rate of penetration, pipe sticking, etc. In addition to the effect of inclination, drill pipe rotary speed, cutting size, nozzle velocity and fluid viscosity as well as the effect of the bit nozzle arrangement on the cutting transport process were discussed. The results demonstrate that at a critical inclination angle of 30 degrees the cutting transport is inefficient. For all sections, the effect of drill pipe rotary speed was negligible at high velocities. In the horizontal section, at low flow rates and high drill pipe rotation speeds, Newtonian viscous fluids or water has no effect on the time needed for initial hole-cleaning butby removing the drill pipe rotation speed in similar conditions, a dramatic influence on time is observed. In inclined annuli, increasing the cuttings size and decreasing the nozzle velocity result in having no cutting in the output. Under critical inclination (30 degrees) the effect of the nozzle angle pattern on the hole-cleaning time is negligible. However, for a vertical annulus, the nozzle angle significantly influences the cutting transport. The best performance is obtained when the nozzle angle was perpendicular to the drill pipe axes.
Keywords: Two-phase flow, flow characteristics, CFD, jetting flow.
1. Introduction
The cutting transport phenomenon is one of the main important subjects in drilling of horizontal and extended reach wells. Inadequate cutting transport is associated with many problems such as lowering the drilling performance, grinding of cuttings into fines at bit, difficulties in mud and solid control maintenance, increasing the equivalent circulating density (ECD), increasing the mechanical torque and drag, over pull on drilling string and unnecessary back reaming and fishing operation.1,2,3 Therefore, the bottom hole has been a concern for drilling operations which is resulted in excessive well construction expenditure.4
Bottom Hole Assembly (BHA), drill pipe rotary speed (RPM), flow rate, rate of penetration (ROP) and drilling fluid properties and inclination are the common factors that can be manipulated and controlled to gain a proper hole .5 Since the investigation and study of the effective drilling characteristics on the bottom hole on a drilling rig is costly, researchers have attempted to study this subject with a variety of approaches such as flow loops and Computational Fluid Dynamics (CFD).6,7 Usually the cutting concentration, mean bed height and the length of the bed are the main variables that are traced for hole-cleaning efficiency across the annulus.8,9
Cutting transport phenomenon can be considered as a liquid-solid system in CFD modelling.10 Simulations are validated based on the experimental data from the flow loops.11 Many parameters can be considered in simulations such as collisional mod-els,4,12 drag models,2,13 aggregation,14 restitution coefficient,15 specularity coefficient,16 sphericity,17 and the mesh size effect.18 In this study, cutting transport phenomena is considered as a CFD model using Eulerian assumptions for the turbulent liquidsolid flow in a concentric annulus. In reality, it was not a good assumption for a long annulus but it helps to have a good sense about the cleaning process time. The first step was the validation of a model built based on the dimension of our experimental setup. The effect of the jet velocity and the nozzle angle (with respect to the drill pipe axes), inclination, viscosity, rotary speed and the cutting size are investigated on the particle removal in the annulus. The initial mass of cuttings at the bottom of the annulus was cleaned by the fluid flow. In our previous work,19 the critical cleaning inclination at which the cutting transport was inferior was been found to be 30 degrees.
2. Materials and Methods
This work describes a simulation model built in ANSYS Fluent, together with an experimental setup to study the effect of key parameters such as time, flow rate, cuttings size, etc., on wellbore cleaning in simulated horizontal, vertical and inclined well sections.
2.1. Experimental Flow loop
A flow loop was designed and developed providing a variety of options for controlling test settings, i.e. properties of the annulus, drilling fluid, cuttings, the drill string, temperature and pressure, see Fig. 1a. The annulus was an acrylic tubing with a length and internal diameter of 220.0 cm and 9.0 cm, respectively. Increasing the length of the flow loop not only increased the mesh number and consequently, the simulation time, but also caused some limitation in the inclination range. The inner stainless steel pipe had an outside diameter of 4.3 cm and contained four nozzles with an internal diameter of 0.8 cm. The nozzles were attached on the body of the pipe as shown in Fig. 1b. The inner pipe was connected to an AC motor with a shaft and gear-box and the rotary speed was controlled by an inverter. The cuttings were injected into the annulus at different rates through a designated inlet. The inclination was also adjusted with two arms from a vertical to a horizontal position. A centrifugal pump was used to inject the fluid into the string and the flow rate was controlled with a flow meter and a bypass system which was installed between pump and flow loop. At the output, a screen was used to collect the cuttings. A mixer was used to prepare the drilling fluid and a differential pressure (DP) transducer recorded the pressure drop in the annulus as indicated in Fig. 1c.
The circulating flow loops mechanism was similar to the drilling operation with minor modifications to suite the laboratory conditions. First, the length of the flow loop seemed a bit small for a horizontal or inclined flow. Second, the jet from the four nozzles had a strong effect on the cuttings transport in the present setup. The jetting nozzles were placed at a 7.5 cm distance from the origin. Third, in the drilling operation, the nozzle size was usually optimized based on maximizing the jet impact force or hydraulic horse power, but the pattern of placement was not seen in this setup because of using a centrifuge pump instead of triplex pumps.
2.2. CFD Method
The flow loop model was generated with Gambit software used for CFD modelling. The model materials were sand and water. The solver in ANSYS Fluent was pressure-based for absolute velocity formulation in the transient flow. An Eulerian-Eulerian two-phase flow for granular cuttings was selected with a standard k-e and a standard wall function with mixture multiphase model.
2.2.1. Governing Equations
With merging Eulerian-Eulerian sub-models with the kinetic theory of granular flow,20,21 the governing equations are presented in this section.
The continuity equation for the solid phase can be written as Equation 1:

The momentum equation for the solid phase is:
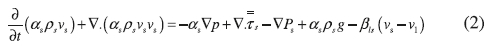
The fluctuation energy of the solid particles (granular temperature) is written as:
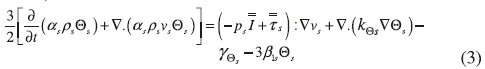
The constitutive equations used for the Euler-Euler model are22,23,24: Liquid phase stress tensor:
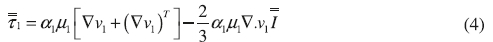
Solid phase stress tensor:
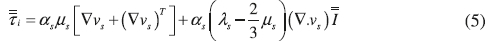
Solid shear viscosity:

where
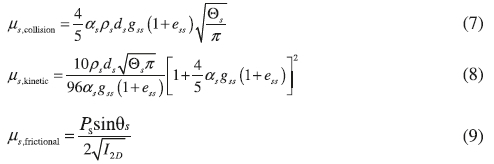
Solid bulk viscosity:

Collision energy dissipation:

Solid pressure:

Radial distribution function:

where as is the solid volume fraction and asmax is the maximum packing limit.25 And the drag coefficient Cd is:
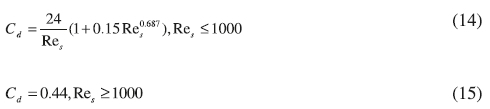
2.2.2. Model Assumptions
The flow loop model was generated with Gambit software to be used in CFD modelling. The model materials are sand and water. The solver in ANSYS Fluent was pressure-based for absolute velocity formulation in the transient flow. An Eulerian-Eulerian two-phase flow for granular cuttings was selected with a standard k-e and a standard wall function with mixture multi-phase model. The plexy wall was stationary with standard roughness and no-slip condition for solids. The roughness constant was 0.5. The drill pipe was a moving wall with 11.5 rad s-1 rotary speed. The k-e turbulent model has some limitations for the near wall condition. In this study, an effort was made to neglect these defects with an attempt to y+ diagram. Table 1 shows the related cutting properties in the model.
Solid phase shear bulk viscosity was obtained through applying the kinetic theory to granular flows. Frictional viscosity for modelling the granular flow was also available. The fluid was water with 998.2 kg m-3 for density and 0.001003 kg m-s-1 for viscosity. The model assumptions for the designated inlet and outlet are given in Table 2.
All simulations were performed on a core (TM) i7-6700K CPU at 4.00 GHz with 32.0 GB RAM.
2.2.3. Mesh Independency and Model Validation
The geometry of the model was meshed by a hybrid of tetrahe-dral and hexagonal elements as shown in Table 3a. A structural mesh has many advantages such as reducing the grids and consequently the simulation run time, but it was difficult to confirm as a single block for this case. Matching and merging the separated meshed volume was a big challenge. If the annulus was assumed symmetric, the structural mesh was perfect. While, due to the complexities in the geometry, it was not possible to mesh it structurally. There were nozzles, cutting inlet and drilling fluid outlet and they made the geometry of the model hard to mesh. Likewise, in this study, there were three main sections and in each of them the turbulent flow regime, fluctuation in the flow parameters and the velocity of the drilling fluid were different especially in the inlet section (cutting inlet and nozzles) there were five velocities inlet surfaces. Unstructured mesh was a better choice due to these constraints and limitations. Each inlet and outlet section had the separated subsections. The mesh generation for each section led to specific errors in Fluent software. With changing the mesh type from structured to unstructured, the ANSYS Fluent errors were resolved within the volume interfaces. The unstructured mesh was more flexible than the structured mesh type.
In this study, three types of mesh with different mesh numbers were applied. The mesh properties such as maximum ortho-skew, minimum orthogonal quality, the existence of boundary layer and aspect ratio were shown in Table 3b . For the investigation of mesh independency, the results of the three mesh types were compared to each other in the ANSYS Fluent software environment (Table 3c). The results of cutting transport experiments were compared to the simulation results. For the validation of the simulation results, the calculated error value between the experience and simulation results was used (Table 3d).
2.2.4. CFD Tests
The effect of the main drilling characteristics such as inclination, drill pipe rotation, cutting size, nozzle velocity, drilling fluid and the jetting angle on the hole-cleaning phenomena were investigated with CFD simulations. Table 4 summarizes the design of experiment parameters including the test ID and the testing parameters. The effect of inclination was studied from test T1 to T7. The effects of cutting size (from T8 to T10), drill pipe rotary speed (from T11 to T13), nozzle velocity (from T14 to T16), the combination of the effective characteristics (from T18 to T19) and the jetting angle (from T20 to T22) were investigated under three configurations.
Table 5 lists the parameters of four experiments designed to evaluate the effect of the nozzle jetting angle (test numbers: T1, T5, T21 and T22).
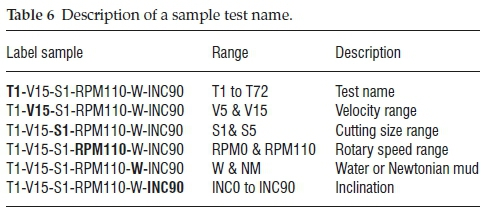
Each test has a specific label. Table 6 gives the details of a typical sample label of /T1V15S1RPM110WINC90'.
3. Results and Discussion
A decline in the nozzle velocity or annular velocity can lead to an increase in the cutting amount. In addition, there is a correlation between the increasing amount of the cuttings and the increasing of the rate of penetration (ROP). In this situation the amount of cuttings, the bed length and the height are increased and also the hole-cleaning problems such as sticking are increased. In the lower rate of penetrations, as the drill pipe rotation speed increases, the ROP increases linearly with the higher penetration rate. With the further increase the ROP rate decreases and it leads to the low hole-cleaning efficiency. Note that removing the drill pipe rotation has no effect on the hole cleaning of the slant wells at the high velocities. The hole cleaning of horizontal sections is one of the hard situations in the cutting transport. As mentioned in the introduction, drill pipe rotation speed, drilling fluid rheological properties, the flow rate or nozzle velocity and the time are the most important characteristic ones.
The main characteristics considered in this study are: inclination, rotary speed, fluid viscosity, cutting size, nozzle velocity and jetting angle.
3.1. Inclination
Directional wells can be categorized into four types, namely S-shaped, slanted, inclined and horizontal types. In each type, if the pump is turned off, the cuttings are slumped in the low side of the borehole bottom due to gravity. The minimum amount of hole cleaning occurs in a critical inclination, at which the cutting transport is more problematic.
In CFD simulation, the critical inclination can be determined with different approaches. In the first method, the volume fraction was calculated at different times. In the second approach, the sand and water velocities are compared across the annulus at different times. Lastly, the critical inclination was determined based on the knowledge of the mass of the remaining cuttings in the annulus. It was found that the remaining cuttings in the annulus were increased by increasing the inclination from 0 to 30 degrees and then it was decreased from 30 to 75 degrees inclination (Fig. 2). In all approaches, it was found that the critical inclination angle was approximately 30 degrees.
3.2. Drill Pipe Rotary Speed and Drilling Fluid Viscosity
The agitation and rotation of drill string improve the cutting transport process by decreasing the pressure drop and cutting bed height across the annulus. The rotation of drill string has no significant effect on the cutting transport process at high flow rates. In other words, the effect of the drill string rotation in assisting cutting transport can be replaced by increasing the flow rate. At high flow rates, during the drilling operation, the rotation of drilling string did not affect the cutting transport a lot. In the presence of water or Newtonian viscous fluids as drilling fluids, at low flow rates but at high speeds of drilling rotation, the initial hole-cleaning time was not affected by these parameters. However, in the state of the drilling string with no rotation, the time for completing the hole cleaning changed for each drilling fluid. In the horizontal sections in similar operational conditions, the hole-cleaning time for water at low flow rates and non-rotating pipe (T52-RPM0-NV) was approximately two times of the hole-cleaning time for a Newtonian viscous fluid (T42-NV 5) (Fig. 3). This can be interpreted as the roles of viscous force in increasing the cutting carrying capacity. In this study, the effect of drilling fluid viscosity was investigated on cutting transport by water with 1 cp and a high viscosity Newtonian fluid with 10 cp of viscosity. Using viscous fluid forms a specific cuttings transport regime across the annulus. Figures 4 and 5 show the effects of viscous drilling fluid in the presence of the drilling string rotation and no rotation of the drilling stringin a horizontal section. Figure 4 is a snapshot of the system with no rotation of the drilling string after 30 seconds in different cross-sections. In this state, the cutting bed extended on the low side of the system as the cross-section views show. As the cutting bed has been moved and extended from the first points of the system, its height was increased gradually toward the middle points of the system. Hence, at the end points of the system, the height of the cutting bed was decreased. This state can demonstrate the effect of viscosity in increasing the shearing forces to pick up and carry the cutting from the cutting bed into the drilling fluid. This caused the cutting bed to gradually creep toward the outlet.
In the state of the drilling string rotating, as is obvious in Fig. 5 after 23 seconds, the cuttings were dispersed in the annulus and there was no concern for forming the cutting bed in the horizontal section. The cuttings were agitated by the rotation of the drilling string and moved spirally toward the outlet. As shown in the cross-section views in Fig. 5, the cuttings were agitated and rotated around the drilling string and they were picked up from the low side to the annulus space and carried by the flow regime.
3.3. Effect of Cutting Size
To investigate the effect of particle size on the cutting transport; two particle sizes (1 mm and 5 mm) were selected. These sizes are normal cutting sizes in drilling operations. Figure 6 shows the results of 1 and 5 mm of particle sizes on the hole-cleaning time. The hole-cleaning time was prolonged as the cutting size increased. In the critical inclination, increasing the particle size had an adverse effect on the hole-cleaning process and almost no cuttings were carried out of the annulus (T13). However, in vertical (T11) and horizontal (T12) conditions, an increase in the particle size results in much more time for an efficient hole cleaning.
3.4. Effect of Nozzle Velocity
In this section, the effects of the nozzle velocity on the cutting transport were investigated for two jetting velocities (5 m s-1 and 15 m s-1). For 15 m s-1 velocity of the nozzle jetting, the cleaning process of the annulus was efficient at all inclinations, whereas, for5ms-1 of jetting velocity of nozzles, the cleaning process took longer for both vertical and horizontal sections. CFD results demonstrated that in the critical inclination, no cutting was carried to the outlet by decreasing the nozzle velocity from 15 m s-1 to 5 m s-1 (see Fig. 7).
Figure 8 shows a streamline contour view of the system after 2.065 seconds from the drilling fluid pumping. The streamlines were started from the nozzle and flown through the system.
3.5. Jetting Angle
In this section, the effects of jetting angle on the hole cleaning were studied for three different patterns of nozzle angles (Fig. 9) due to different types of nozzle arrangement in common bit types (Fig. 10). Initially, a mixed pattern of 75, 60, 45, 30 nozzle angles was used for a vertical annulus and after that due to the poor hole cleaning at the low nozzle velocity (5 m s-1)at 30-degrees of inclination, we investigated the effect of changing the nozzle angles to 45-degree rather than the normal vector of the jetting surface.
3.5.1. INC30-90 Degree Nozzle Angle
In this case, the cutting transport process was investigated by the system in 30 degrees inclination with 90 degrees nozzle angles. The cuttings were deposited on the low side of the annu-lus. A narrow tail of the cuttings was formed on the low side and traced toward the output of the annulus. The cuttings were carried to the upper part of the annulus space, but according to this inclination as the critical inclination (30 degrees), the cuttings slumped down on the low side of the annulus space. Eventually, they were deposited over each other, massively on the lower side of the annulus (Fig. 11).
In this situation, after 40 seconds about less than 1 gram of cuttings had exited from the annulus space which is very small compared to the elapsed time of the drilling fluid pumping.
3.5.2. Mixed Pattern (75, 60, 45, 30 Degrees)
In this case, a mixed pattern of nozzle jetting angles was studied. 750 grams of the cuttings was injected into the annulus space after that the drilling fluid (water) was pumped after 500 seconds all of the cuttings were evacuated from the annulus space. After 70 seconds of pumping water, the cuttings were dispersed in the annulus space, but some separated bulks of the cuttings were formed around the drilling string. It can be illustrated that the rotation of the drilling string agitated the whole mass of the cuttings and cut them into smaller bulks that can be carried by drilling fluid. This simulation demonstrated that the mixed pattern of nozzle angles was not as effective as the 90-degree nozzle angle pattern on the cutting transport process. Even after about 500 seconds of the simulation, there was still about 50 grams of the cuttings in the annulus space. Changing the nozzle angle into the mixed pattern resulted in an improper hole cleaning and the hole-cleaning time was sharply increased.
In practice, the nozzle angle design has a strong effect on the near bit cleaning as the first point of hole-cleaning process. Improper design of the nozzle angles can cause poor near bit cleaning, bit ball, bit burning and consequently increasing drilling time and cost.
In this case, as Fig. 12 shows after about 500 seconds almost 750 g of cuttings were evacuated from the annulus space.
3.5.3. INC30 - Nozzle Angle 45 Degrees
In this simulation, the nozzle angles were changed to 45-degrees (Fig. 9). For 30-degree inclination as the critical inclination, in practice, almost no cutting was transported out of the annulus (less than 1 g). This amount of cuttings was very negligible rather than the elapsed time of the simulation (Fig. 13).
Similar to the previous case, the cuttings were deposited on the low side of the annulus over each other and due to the rotation of the drill string, a snake tail of cuttings was extended on the low side of the annulus space toward the output. The tail was not as thick as the pattern with 90 degrees jetting angles. Similarly, due to the previous case, the cuttings were carried up by the flow regime to the upper parts of the annulus; however, they were slumped down and deposited at the bottom of the annulus. Maybe an increase in the flow rate can carry the cuttings out of the annulus space.
In these two cases, the nozzle angle pattern affected the bottom hole cleaning in a deviated drilling system. If two systems are considered for a certain elapsed time of 40 seconds, almost no cuttings have been exited from the system in 45-degree nozzle angles; however, when the nozzle angle pattern was 90 degrees, it was slightly more effective than the case of 45-degree nozzle angles. The 90-degree nozzle pattern generally had a better performance than the 45-degree nozzle angle pattern. It can be demonstrated that the nozzle angle pattern did not influence the cutting transport near the bit and the system inclination was a dominant factor in this situation (Fig. 13).
4. Conclusion
In this study, the cutting removal was studied by using a three-dimensional model based on the kinetic theory for the granular flows. The model was further validated with the experimental data. In both experimental and CFD ANSYS modelling, an attempt was made to remove the initial sand by the means of the water jetting. The following are the main conclusions:
1. At low flow rates but at high speeds of the drilling string rotation, for Newtonian viscous fluids or water, the viscosity had no effect on the initial hole-cleaning times; however, by setting the speed to zero, the required time for each fluid changed.
2. As the particle size of the cuttings increased, the time of the hole cleaning increases. In the critical inclination, increasing the size had an adverse impact on the hole-cleaning progress and in practice no cuttings exited from the annulus space. However, for vertical and horizontal cases, by increasing the cutting size, the time of the hole cleaning increased.
3. In the critical inclined section, the cutting transport was stopped by lowering the nozzle velocity from 15 m s-1 to 5 ms-1. The 90-degree nozzle pattern generally had the better performance than the 45-degree arrangement. Downward jetting angle pattern was not suitable for the hole-cleaning process.
4. Adding viscosifiers into the low viscous dense fluids can lead to an increase in bed length that reduces the mechanical sticking probability.
5. All conditions that lead to a decrease in cutting size can be efficient for the cutting transport process.
6. The 90-degree nozzle pattern generally has better performance than the 45-degree arrangement at the critical inclination.
7. In the critical inclination, downward jetting angle pattern is not profitable for the hole-cleaning process.
Nomenclature
Cd Drag coefficient
d Diameter (m)
e Restitution coefficient
g Gravity (m s-2)
go Radial distribution function
kQ Diffusion coefficient for granular energy (kg msJ) Unit tensor
12D Second invariant of deviatoric stress tensor
p Pressure (Pa)
v Velocity vector (m s-1)
Re Reynolds number
t Time (s)
x Particle concentration
M0 Initial patched mass (gram)
Mt (Min) Current mass in the annulus (gram)
Mout Exited mass from the annulus (gram)
t1/2 The time of exiting semi amount of initial patched mass
Greek letters
a Volume fraction
ñ Density (kg m-1)
t Stress tensor (Pa)
b Inter-phase momentum exchange coefficient (kg m3 s-1)
g Collisional energy dissipation (kg ms-3)
ë Bulk viscosity (kg ms-1)
ì Shear viscosity (kg ms-1)
as,max Maximum solid volume fraction
Q Granular temperature (m2 s-2)
0 Internal friction angle (°)
Subscripts
1 Liquid phase s Solid phase
ORCID iDs
Ì. Dehvedar: orcid.org/0000-0003-2620-3028
P. Moarefvand: orcid.org/0000-0002-2117-4937
References
1 J. Li and S. Walker, Sensitivity analysis of hole cleaning parameters in directional wells, SPE J., 2001, 6, 356-363. [ Links ]
2 O. Ayeni, C.L. Nandakumar and J.B. Joshi, Development and validation of a new drag law using mechanical energy balance approach for DEM-CFD simulation of gas-solid fluidized bed, Chem. Eng. J., 2016, 302, 395-05. [ Links ]
3 A. Bush, A. Islam, D.W. Martins, F.P. Iversen, M. Khatibi, S.T. Johansen ... and E.A. Meese, Cuttings-transport modeling - Part 1: specification of benchmark parameters with a Norwegian-continental-shelf perspective, SPE Drill Completion, 2018, 33, 130-148. [ Links ]
4 E.V.P.J. Manjula, W.H. Ariyaratne, C. Ratnayake and M.C. Melaaen, A review of CFD modelling studies on pneumatic conveying and challenges in modelling offshore drill cuttings transport, Powder Technol., 2017, 305, 782-793. [ Links ]
5 X. Song, Z. Xu, M. Wang, G. Li, S.N. Shah and Z. Pang, Experimental study on the wellbore-cleaning efficiency of microhole-horizontal-well drilling, SPE J., 2017, 22, 189-200. [ Links ]
6 B. Amanna and M.R.K. Movaghar, Cuttings transport behavior in directional drilling using computational fluid dynamics (CFD), J. Nat. Gas. Sci. Eng., 2016, 34, 670-679. [ Links ]
7 M. Kamyab and V. Rasouli, Experimental and numerical simulation of cuttings transportation in coiled tubing drilling, J. Nat. Gas. Sci. Eng., 2016, 29, 284-302. [ Links ]
8 P. Allahvirdizadeh, E. Kuru and M. Parlaktuna, Experimental investigation of solids transport in horizontal concentric annuli using water and drag reducing polymer-based fluids, J. Nat. Gas. Sci. Eng., 2016, 35, 1070-1078. [ Links ]
9 A. Tripathy, S. Bagchi, S.K. Biswal and B.C. Meikap, Study of particle hydrodynamics and misplacement in liquid-solid fluidized bed separator, Chem. Eng. Res. Des., 2017,117, 520-532. [ Links ]
10 S.M. Han, Y.K. Hwang, N.S. Woo and Y.J. Kim, Solid-liquid hydrodynamics in a slim hole drilling annulus, J. Petrol. Sci. Eng., 2010, 70, 308-319. [ Links ]
11 S. Sayindla, B. Lund, J.D. Ytrehus and A. Saasen, CFD Modelling of observed cuttings transport in oil-based and water-based drilling fluids. SPE/IADC Drilling Conference and Exhibition, March 2017. [ Links ]
12 M.T. Shah, R.P. Utikar, VK. Pareek, M.O. Tade and G.M. Evans, Effect of closure models on Eulerian-Eulerian gas-solid flow predictions in riser, Powder Technol, 2015, 269, 247-258. [ Links ]
13 J. Gan, H. Zhao, A.S. Berrouk, C. Yang and H. Shan, Impact of the drag law formulation on the predicted binary-particle segregation patterns in a gas-solid fluidized bed, Powder Technol., 2012,218,69-75. [ Links ]
14 L. Liu, Effects of aggregation on the kinetic properties of particles in fluidised bed granulation, Powder Technol., 2015, 271, 278-291. [ Links ]
15 C. Loha, H. Chattopadhyay and P.K. Chatterjee, Effect of coefficient of restitution in Euler-Euler CFD simulation of fluidized-bed hydrodynamics, Particuology, 2014, 15, 170-177. [ Links ]
16 X. Lan, C. Xu, J. Gao and M. Al-Dahhan, Influence of solid-phase wall boundary condition on CFD simulation of spouted beds, Chem. Eng. Sci., 2012, 69, 419-430. [ Links ]
17 R. Escudie, N. Epstein, J.R. Grace and H.T. Bi, Layer inversion and bed contraction in down-flow binary-solid liquid-fluidized beds, Can. J. Chem. Eng., 2007, 85, 25-35. [ Links ]
18 P.C. Sande and S. Ray, Mesh size effect on CFD simulation of gas-fluidized Geldart A particles, Powder Technol., 2014, 264, 43-53. [ Links ]
19 M. Dehvedar and P. Moarefvand, Detecting and drilling in critical inclination window in slant wells by means of a two phase liquidsolid CFD model and experimental study, Kuwait J. Sci., 2019,46,6-11. [ Links ]
20 Schaeffer, D.G. Instability in the evolution-equations describing incompressible antigranulocytes flow, J. Differ. Equations, 1987, 66, 19-50. [ Links ]
21 D. Gidaspow, Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions, Academic Press, London, United Kingdom, 1994. [ Links ]
22 C.K.K. Lun, S.B. Savage, D.J. Jeffrey and N. Chepurniy, Kinetic theories for granular flow: inelastic particles in Couette flow and slightly inelastic particles in a general flow field, J Fluid Mech., 1984, 140, 223-256. [ Links ]
23 D. Gidaspow, R. Bezburuah and J. Ding, Hydrodynamics ofCirculating Fluidized Beds: Kinetic Theory Approach, Illinois Inst. of Tech., Chicago, IL (United States). Department of Chemical Engineering. 1991. [ Links ]
24 M. Syamlal, W. Rogers and T.J. O'Brien, MFIX Documentation: Theory Guide, National Energy Technology Laboratory, Department of Energy, Technical Note, 1993. [ Links ]
25 ANSYS Fluent 14.5 Theory Guide, Canonsburg, PA, ANSYS Inc., USA, 2012. [ Links ]
26 J.T. Cornelissen, F. Taghipour, R. Escudie, N. Ellis and J.R. Grace, CFD modelling of a liquid-solid fluidized bed, Chem. Eng. Sci, 2007, 62, 6334-6348. [ Links ]
27 X. Huang, CFD modeling of liquid-solid fluidization: effect of drag correlation and added mass force, Particuology, 2011, 9, 441-445. [ Links ]
28 J. Riera, S. Zeppieri and S. Derjani-Bayeh, Hydrodynamic study of a multiphase spouted column, Fuel, 2014,138, 183-192. [ Links ]
29 K. Zhang, G. Wu, S. Brandani, H. Chen and Y. Yang, CFD simulation of dynamic characteristics in liquid-solid fluidized beds, Powder Technol, 2012, 227, 104-110. [ Links ]
30 X. Sun, K. Wang, T. Yan, S. Shao and J. Jiao. Effect of drill pipe rotation on cuttings transport using computational fluid dynamics (CFD) in complex structure wells, J. Petrol. Explor. Prod. Technol., 2014, 4, 255-261. [ Links ]
Received 15 July 2018
Revised 27 December 2018
Accepted 28 January 2019
* To whom correspondence should be addressed. E-mail: parvizz@aut.ac.ir














