RESEARCH ARTICLE

 

Lyapunov exponents and the Belousov-Zhabotinsky oscillator: an interactive computational approach

 

 

Matthew W. Eskew^I; Reuben H. Simoyi^{I, II, *}

^IDepartment of Chemistry, Portland State University, Portland, OR 97207-0751, USA
^IISchool of Chemistry and Physics, University of KwaZulu-Natal, Westville Campus, Durban 4014. South Africa

 

 

---

ABSTRACT

The Belousov-Zhabotinsky (BZ) chemical oscillator is the most studied oscillator. It has been modelled on the basis of single-step mechanisms which have been continuously refined since the seminal manuscript by Field, Koros and Noyes in 1972. This manuscript reports on a unique way of modelling the global dynamics of the oscillator by assuming that the BZ oscillator has shown chaotic behaviour. The unique mathematical definition of chaos is very stringent, and, in this manuscript, we attempt to trace this unique exotic behaviour by the use of 'onto' maps of the interval onto itself which are known to exhaustively show a universal sequence of states that has all the hallmarks of chaotic behaviour. A series of one-humped maps of the interval display, through iterations and subsequent symbolic dynamics, a universal sequence of steps that commence with period-doubling, culminating in chaotic behaviour at some accumulation point of an appropriate bifurcation parameter. We put this theory to the test for the BZ oscillator in this manuscript by selecting a unique continuous map of the interval. This was then decomposed by an iterative treatment. Metric entropy and subsequent arbiter of chaotic behaviour was determined by evaluation of Lyapunov exponents which were then compared to observed BZ oscillator states. Our proposed map satisfactorily modelled the global dynamics of the BZ oscillator; predicted period-doubling, and a regime after a critical bifurcation parameter, where chaotic sequences were dense. We also produce, in the Addendum, an iterative MatLab procedure that any reader can utilize to reveal the type of states and behaviour reported here.

Keywords: BZ Oscillator, chemical chaos, one-dimensional maps, maps of the interval, symbolic dynamics, Lyapunov characteristic exponent.

---

 

 

1. Introduction

The idea of an oscillating reaction in a batch reaction system without inflow and outflow violates the very basic tenet of the most inviolable law of thermodynamics: the second law, which deals with entropy and disorder. Thus there was healthy skepticism when the Belousov-Zhabotinsky (BZ) reaction was discovered serendipitously, in 1958, by two Russian scientists, Pavlovich Belousov and Anatol Zhabotinsky.¹ With the advent of mathematical modelling, it has since been proved that oscillatory behaviour is acceptable and possible in reaction systems with sufficient nonlinearity in the form of feedback loops to unambiguously produce oscillatory behaviour while in the process of attaining equilibrium. If a flow term is added to a batch system in which reactants are continuously fed into a reactor and products flown out, it is possible to maintain oscillatory behaviour indefinitely.² This setup is commonly known as a continuously-stirred tank reactor (CSTR). The traditional BZ reaction involves the metal-ion catalyzed oxidation of malonic acid by acidic bromate.³ If allowed to go to completion, the stoichiometry of the reaction is:

4BrO3^– + 3CH2(COOH)2 → 4Br^– + 9CO₂(g) + 6H₂O R1

It has a very favorable free energy of reaction, ∆G_r = -4.797 x 10³ kJ mol^-1. The first metal ion used as a catalyst was the Ce⁴⁺/Ce³⁺couple.⁴ For production of vivid colour changes, the Fe(o-phen)₃³⁺/Fe(o-phen)₃²⁺ couple is used. However, overall, it is a very slow reaction. For the production of exotic oscillatory behaviour, the reaction is never allowed to go to completion. There are crucial active intermediates that oscillate. These are Br^-, Br₂, HOBr, HBrO₂ and the radical species BrO₂* .^3,5

This article details a new method of modelling the BZ reaction. This modelling technique involves the use of symbolic dynamics and 'onto' maps of the interval onto itself.^6-8 We detail, initially, a listing and description of the three known models of the BZ known so far. This will allow the reader to appreciate the level of sophistication derived from our model which does not utilize any of the relevant chemistry of the BZ. The model, instead, utilizes the global oscillatory dynamics of the BZ system and fits bifurcation sequences to a universal sequence generated by the iterations of one-humped tent-like maps of the interval. This modelling runs counter to the established method of modelling chemical kinetics in which the generated ordinary differential equations are solved through eigenvalues and eigenvectors.^9-12 A model of the chemical system which does not utilize kinetics constants may appear to have no relationship with the system under study.

1.1. The Field-Koros-Noyes Mechanism (FKN)

The first successful kinetics description of the BZ was derived by John Field, Endre Koros and Richard Noyes at the University of Oregon in 1972.⁵ They published the seminal paper on the first plausible mechanism of the dynamics of oscillatory reactions. Though the proposed mechanism was long and convoluted, the major aspect of the mechanism was the suggestion of a new species, a bromine dioxide radical, which was the crucial species in a suggested autocatalytic route in which the bromous acid, HBrO₂ was tagged as the autocatalytic species. The mathematical modelling of this system gave relaxation-type oscillations in which slow processes were linked to fast processes; the switch between the two was controlled by bromide concentrations. When bromide concentrations reached a certain critical concentration, a switch occurred and a new set of reactions became relevant.^9,13,14 The three relevant processes could be condensed into nine reactions which could be separated into three specific set of events.

Process A

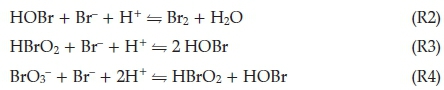
In the classical BZ system, bromate is in such high excess that we assume it is buffered and remains constant in concentration throughout the reaction progress. This process, Process A, is slow and dominates in the presence of sufficient Br^-. The sequence of reactions R2, R3 and R4 reduces bromide concentrations but leaves the concentrations of the catalyst, Ce(III) invari_ant.

Process B

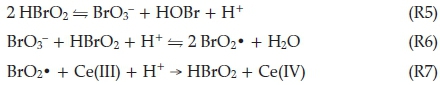
Process B dominates when bromide concentrations decay below a critical level and the autocatalytic Process B cycle commences. In this process, hypobromous acid, HBrO₂, can compete as a reducing agent for bromate, reaction R6. This produces two molecules of the radical BrO₂ ·, through the prior formation and subsequent dissociation of Br₂O₄. This Br(IV) species can be reduced by Ce(III) in a single electron transfer step to produce HBrO₂ in reaction R7. These two steps, R6 + 2(R7), together, constitute an autocatalytic sequence in HBrO₂ since reaction R6 is the rate-determining step. This, then implies that rate of reaction is dependent on rate of formation of HBrO₂. The rate of R6 + 2(R7) accelerates and the cerium catalyst is rapidly converted to its oxidized form as a result of the autocatalysis. There is a sharp colour change from colourless to yellow (or red to blue with ferroin indicator). Process A does not completely shut down, but becomes less dominant and is dwarfed by the rapid autocatalytic Process B. Process B is turned on when bromide concentrations have decreased to low enough concentrations for reaction R6 to compete with reaction R3 for bromous acid. From the known rate constants of reactions R3 and R6, the rates of these two reactions will be equal when

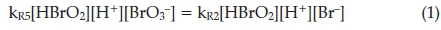
This implies that the critical bromide concentration is given by:

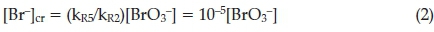
Thus when [Br^-] > [Br^-]_cr, Process A dominates, leading to a reduction in the concentration of bromide ion.¹⁵ When bromide concentrations are lower than the critical concentration, Process B dominates via the autocatalysis route, leading, indirectly, to an increase in bromide ion concentrations. If one recognizes that Process B is still competitive at bromide concentrations higher than the critical concentration limit, then the critical can be recalculated as:

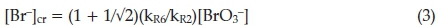
Thus the BZ system switches from A to B even when the rate of reaction R3 exceeds that of R6. Process B, in order to avoid an -uncontrolled build-up of HBrO_2; has an built-in disproportio-nation reaction of HBrO₂; reaction R5. The overall stoichiometry of Process B is obtained from 2(R6) + 4(R7) + (R5):

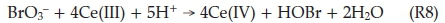
So far, Process A and Process B involve the removal of bromide ions, with each process dominant based on the prevailing instantaneous bromide ion concentration. The BZ reaction oscillates because in Process C, bromide ions are regenerated. Bromomalonic acid and Ce(IV) can react together to regenerate Br^-:

Process C

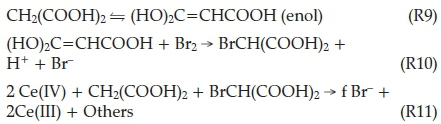
The exact stoichiometry of reaction R11 is not known for certain, since it never occurs quantitatively, and the factor 'f' is refined through modelling studies. The best value for f is derived from the best fit with experimental data. Thus the BZ reaction is bromide-controlled, with Processes A and B alternating relevancy on the basis of whether bromide concentrations are above a critical concentration (Process A) or below (Process B). Process C also regenerates the catalyst. This produces relaxation-type oscillations because Process B, when switched on, is much faster than Process A.

1.2. The Oregonator Model¹⁶

The whole FKN mechanism was very complicated, and has been, in successive manuscripts, been simplified to fewer variables without any loss in accuracy of the modelling dynam-ics.^17-19 The fewer variable models were also computationally simpler. Several of the chemical species are not completely independent and can be linked to others through several equilibria that exist in the reaction system. Earlier, a theoretical model, developed by Ilya Prigogine called the Brusselator had generated limit cycle oscillations in two crucial intermediates of the mechanism.^20-25 Its biggest flaw was a reliance on a termolecular step which involved cubic autocatalysis. This is an unrealistic kinetics model. Hence, though it oscillates, it does not represent a chemical oscillatory system. The reduced FKN mechanism was used to generate the now widely used Oregonator Model.¹⁵ It became the first realistic model of an oscillating reaction mechanism with kinetics terms no larger than bimolecular. The oscillatory dynamics as well as the pattern-forming symmetry-breaking bifurcations were also modelled successfully by this model. Briefly, it can be described as follows. They determined that the whole BZ oscillator could be modelled sufficiently by using four important chemical species: HBrO₂,Br^-, Ce(IV) and HOBr. There is a strong link between HBrO₂ and HOBr through reaction R3 such that HOBr does not appear in the ODE's generated from the model.

Key: [HBrOJ=X; [Br^-] = Y; [Ce(IV] = Z; [HOBr] = P (P will not appear in the reduced model).

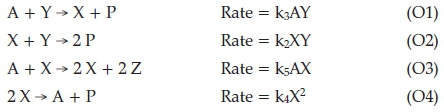
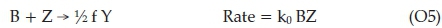
01 is equivalent to R3

02 is equivalent to R2

O4 is equivalent to R4

Autocatalysis is R5 + 2(R6); with R5 as the rate-determining step.

The rates for determination of X, Y and Z are:

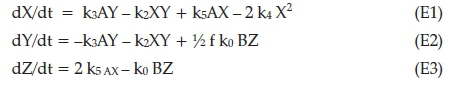
Equations 1-3 need to be reduced to their dimensionless forms:

where Xo = k5A/2k4; Yo = k5A/k2; Zo = (k5A)²/k4koB; To = (koB)^v1 x, y, z are dimensionless concentrations of HBrO₂,Br^- and Ce(IV) respectively The chemical time scale, t, is based on the pseudo-first order rate constant for the regeneration of Br^-. The dimensionless rate equations become:

The new dimensionless parameters are:

ε depends on the ratio of the initial concentrations of the organic species and bromate ion; B/Ä.

q is independent of all the concentrations.

Using this modified Oregonator model, the BZ reaction could be modelled not only with respect to its oscillatory dynamics, but also with respect to its symmetry-breaking bifurcations. It was, however, heavily dependent on the fudge factor 'f' in step O5.

 

2. Theory: Use of Topological Mappings and Symbolic Dynamics

A priori, it is difficult to make the connection between surjective 'onto' maps with the dynamics of a chemical oscillator. However, the iterative properties of 1-1 transformations of the unit interval onto itself have received considerable study, and we feel the symbolic dynamics derived from these transformations are well-understood. It is known that there is some coherence to these transformations, in that they exhibit an infinite sequence of finite limit sets whose structure is common to a broad class of non 1-1 transformations of interval [o,1] onto itself. Metropolis, Stein and Stein showed that unimodal maps:²⁶

where Xi+1 is an iterate of X, based on the function f(X), display a universal (U) sequence ofstates thatare independentofthe map as long as f(X) satisfies some general and not very stringent preconditions. λ is the bifurcation parameter. For the BZ reaction, λ is related to the residence time of reactants in the reactor. This is experimentally related to the inverse of the flow rate of reactants in the reactor. f(X) should be continuous, single-valued and can even be piece-wise C⁽¹⁾ on [o,1], strictly positive in this interval, and anchored at both ends; i.e. f(o) = f(1) = o. f(X) should have a single maximum, fmax < 1, assumed either at a point or in an interval. Effectively these are tent-like maps. These unimodal maps display this U-sequence which mimics ourstringent mathematical definition of chaos. Specifically, if a system that displays this U-sequence were to display an initial period-doubling sequence, then the dynamics of the system would be similar to that of a 1-dimensional (1-D) map. The 1-D map is a next-return map in which a plot is made of successive returns of positively-disposed (or negatively) trajectories across a set hypersurface. If any coherence is obtained in such a plot, then the function describing this parameterized curve, f(X), can be determined using standard cubic spline fits. Experimental data from the BZ reaction have displayed a period-doubling sequence as the residence time of reactants in the reactor is increased (inverse of flow rate), culminating with an accumulation point where the chaotic or aperiodic states are dense with periodic windows. Further decrease in flow rate after the chaotic region displays a reverse bifurcation sequence as predicted by Lorenz. Several other physical, unrelated systems have shown period-doubling. Before discovery of the BZ reaction, only the experiments involving an electrical oscillator with three degrees of freedom by Testa et al showed extensive period-doubling followed by a chaotic region.^27,28 The adherence of a system to 1-D maps as determined by Equation (1) shows determinism even in the chaotic region.

2.1. Map Decomposition/Iteration

For a given value of λ, one picks any initial condition (except for a set of measure zero) and iterates the map until transient behaviour disappears. Further behaviour of the sequence,²⁹ can be either periodic or aperiodic. The simplest way to decompose the map is to utilize the super-cycle; one that involves the extremum of the map where the derivative, f'(X) = o and X = X_o. The standard one-humped tent-map utilized for most derivations of the U-sequence is the quadratic map:

This can be normalized between [o,1] for f(X) as well. It is symmetric and has its maximum atX=o.5.Fromthe super-cycle, if the nth iterate of x_o fall to the right of the extremum, then that character string is set to 'R', otherwise it is labelled as 'L'. Figure 1 shows a 4-cycle sequence, described by the string 'RLR'. The extremum is omitted from the label. Thus each periodic state is described by a symbol sequence of Ls and Rs where the nth symbol specifies the location (to the right or left of X_o) on the nth iterate of X_o.

 

 

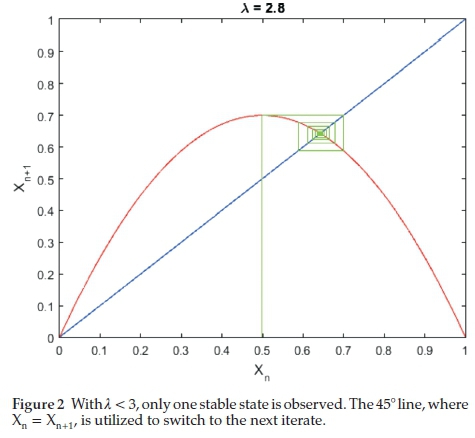
In the seminal paper by Metropolis, Stein and Stein²⁶, with Equation (2) as their map of choice, they used symbolic dynamics to deduce, from the single extremum property of the map, the symbol sequences for the periodic states and the order in which they occur as a function of bifurcation parameter, l. For small l, < 3.0, the map has a single fixed point (1-cycle). This is shown in Fig. 2.

 

 

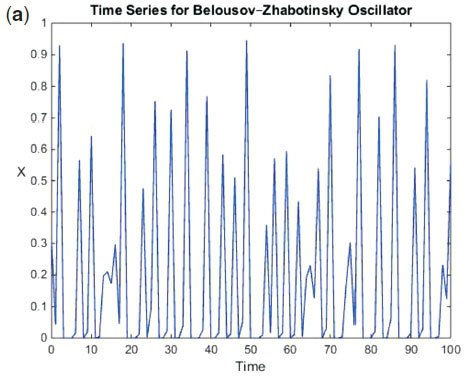
The BZ oscillatory reaction data, however, did not produce a symmetric one-humped 1-D map. Figure 3 shows the type of map obtained in this case. The fact that the next-return 1-D map shows data on a parameterized curve indicates that the BZ reaction in the chaotic region, is deterministic.

This map is not symmetric, according the model map use by Metropolis, Stein and Stein. However, if we could decipher its functionalform,we couldsubjectitto thesame mapdecomposi-tions and symbolic dynamics used on map in Equation (2) and determine ifthe BZoscillatoryglobaldynamics canbe modelled by the iterations of this map.

Using cubic spline fits, functional form of the parameterized curve obtained for the 1-D map in Fig. 3b was initially fitted to:

deriving the recursive equation of:

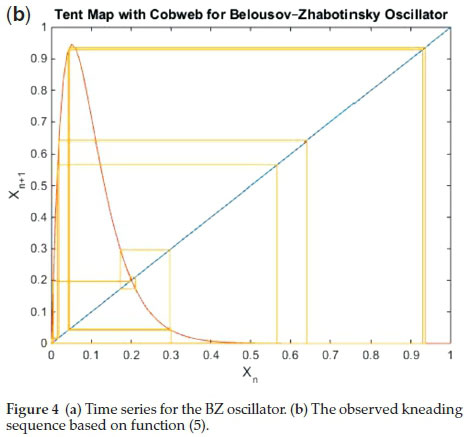
On taking the derivative of the function to seek the turning point and normalizing f(X) between the interval [0, 1], the value of 'b' adopted was a/e. Bifurcation parameter was the residence time of reagents in the reactor, 'a'. This is also interpreted as the inverse of the flow rate. The standard kneeding mechanisms were used on function (4). Though it went through the expected period-doubling sequence up to the accumulation point where chaotic dynamics were observed, the ordering of the states was slightly off from the observed sequences from BZ experimental data. Further refinement of function (4) noted that this function did not close at f(X = 1), even though its value was small at this point, especially with a = 150, which was the parameter at which periodic traces were observed. To ensure closure and anchoring in the interval; f(X = 0) = f(X = 1) = 0; the following function was utilized:

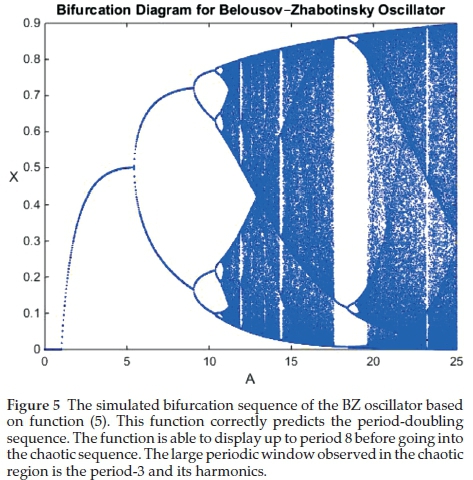
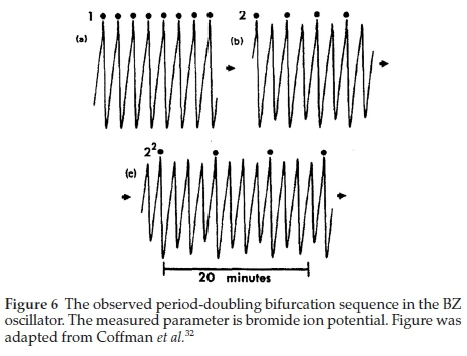
With 'b' maintained at the same a/e value to normalize the function. Using this refinement, we were better able to predict the sequences experimentally-observed in the BZ system (see Figure 4(a) and (b). The most remarkable aspect of function (5) is its ability to predict, accurately, the bifurcation sequence of the BZ oscillator, commencing with the expected period-doubling sequence (see Fig. 5). The resolution is able to show 3 series of period-doubling events, up to 2³. The theory predicts infinite period-doubling sequences. According the work of Mitchell Feigenbaum, each successive sequence exists over a range of bifurcation parameter at 4.669^-1 the value of the preceding state.³¹ Hence we expect a very rapid convergence and subsequent entry into the chaotic region at the accumulation point of the bifurcation parameter. Experimentally, the BZ has, unequivocally, displayed period 8 as well. Figure 6 shows the experimentally-observed BZ bifurcation sequence up to period 4.

 

 

 

 

 

 

2.2. Lyapunov Exponents

Lyapunov exponents estimate the rate of divergence of nearby trajectories, a key component of chaotic dynamics.³³ A quantitative measure of chaotic, nonperiodic behaviour is provided by the value of the largest Lyapunov exponent which characterizes the average rate of separation of nearby trajectories.³⁴ The exponent is positive for a chaotic state and zero or negative for a periodic state. A state with a positive Lyapunov exponent exhibits sensitive dependence on initial conditions.³⁵ This means that, trajectories initially very close together will, on the average, diverge, such that after a time dependent on the size of the exponent there will be no relationship between them. The larger the exponent the faster the rate of divergence and information about the initial conditions is rapidly lost, and any uncertainty in the initial values will be magnified until it becomes as large as the attractor dimension, e.g. Fig. 3a.

The novel aspect of this article is the use of the Lyapunov characteristic exponent, LCE, to derive and simulate the bifurcation sequence of the BZ oscillator. This is largely dependent on the correct determination of the functional form of the 1-D map. In this case we are utilizing function (4) as our parameterized curve of the 1-D map. The largest LCE can be computed from the functional form of the 1-D map as:

Where f '(X_i) is the derivative of the map at X_i. The optimum value of n is determined by the highest value above which further increase in n does not deliver varying values of the LCE, l. The remarkable aspect of our treatment was a mimicry of the bifurcation sequence of the BZ oscillator by displaying the period-doubling cascade with a resolution that went up to the 2⁴ cycle.

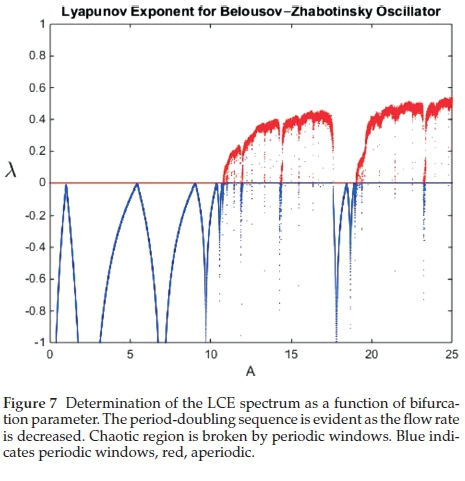
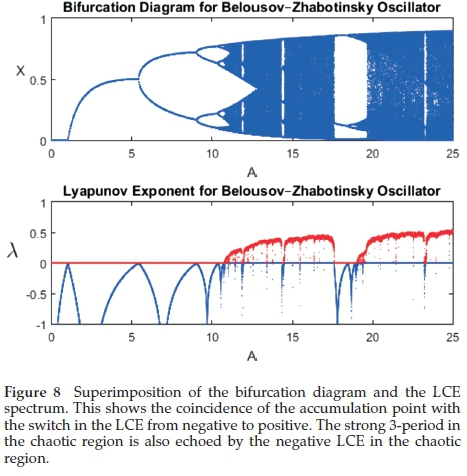
The chaotic region, with l > 0 is observed just after the accumulation point as each successive period-doubling exists over a much narrower bifurcation parameter than its predecessor according to the Feigenbaum number.³¹ The special congruence with experimental data is the observation of a very strong and visible 3-cycle in the chaotic region as well as its harmonics: 2⁰ x3-cycle → 2¹ x 3-cycle → 2² x 3-cycle......until this sequence

attains its own accumulation point. Figure 8 shows a superimpo-sition of the bifurcation diagram and the LCE spectrum. It shows the coincidence of the accumulation point with the chaotic region as evidenced by the positive LCE.

 

 

 

 

3. Conclusion

This article shows that there is another way of modelling the BZ oscillator using the global dynamics of the oscillator. Despite the BZ oscillator consisting of over 30 chemical species, the system is coherent enough to be modelled solely on its dynamics by assuming that it displays chemical chaos.³⁰ From this premise, we can assume such chaotic features such as an initial cascade of period-doubling, culminating in an accumulation point beyond which chaotic states are dense. The periodic windows could also be modelled by the use of the Lyapunov characteristic exponent.

The derived function for the 1-D map of the BZ oscillator correctly predicts the global dynamics of the whole oscillator, including the appearance and ordering of periodic windows in the chaotic region.

 

Addendum

For the Matlab source code for the kneading sequences and calculation of Lyapunov Exponents, the reader is directed to this site: http://www.mathworks.cormmatlabcentraVfileexchange/54936-interactive-bz-oscillator

 

Acknowledgements

This work was supported by Grant Number CHE 1056366 from the National Science Foundation and a Research Professorship vote from the University of KwaZulu-Natal.

 

References

1 T. Bansagi, Jr., M. Leda, M. Toiya, A.M. Zhabotinsky and I.R. Epstein, High-frequency oscillations in the Belousov-Zhabotinsky reaction, J. Phys. Chem. A, 2009,113, 5644-5648.         [ Links ]

2 K.M. Kovacs and G. Rabai, Mechanism of the oscillatory decomposition of the dithionite ion in a flow reactor, Chem. Commun., 2002, 790-791.         [ Links ]

3 R.J. Field, R.M. Noyes and E. Koros, Oscillations in chemical systems. 2. Thorough analysis of temporal oscillation in bromate-cerium-malonic acid system, J. Am. Chem. Soc., 1972, 94, 8649-8664.         [ Links ]

4 H. Onuma, A. Okubo, M. Yokokawa, M. Endo, A. Kurihashi and H. Sawahata, Rebirth of a dead Belousov-Zhabotinsky oscillator, J. Phy.s Chem. A, 2011, 115, 14137-14142.         [ Links ]

5 R.M. Noyes, R.J. Field and E. Koros, Oscillations in chemical systems. I. Detailed mechanism in a system showing temporal oscillations, J. Am. Chem. Soc., 1972, 94, 1394-1395.         [ Links ]

6 A.S. Balankin, Dynamic scaling approach to study time series fluctuations, Phys. Rev. E Stat. Nonlin. Soft. Matter. Phys., 2007, 76, 056120.         [ Links ]

7 N. Metropol, M.L. Stein and P.R. Stein, Stable states of a non-linear transformation, Numer. Math., 1967,10, 1-19.         [ Links ]

8 O.W Rechard, Invariant measures for many-one transformations, Duke Math. J., 1956, 23, 477-488.         [ Links ]

9 H.M. Hastings, S.G. Sobel, R.J. Field, D. Bongiovi, B. Burke, D. Richford, K. Finzel and M. Garuthara, Bromide control, bifurcation and activation inthe Belousov-Zhabotinsky reaction,J. Phys. Chem. A, 2008,112, 4715-4718.         [ Links ]

10 L. Hegedus, M. Wittmann, Z. Noszticzius, S.H. Yan, A. Sirimungkala, H.D. Forsterling and R.J. Field, HPLC analysis of complete BZ systems. Evolution of the chemical composition in cerium and ferroin catalysed batch oscillators: experiments and model calculations, Faraday Discuss., 2001,120, 21-38.         [ Links ]

11 B.R. Johnson, S.K. Scott and B.W. Thompson, Modelling complex transient oscillations for the BZ reaction in a batch reactor, Chaos, 1997, 7, 350-358.         [ Links ]

12 L. Sciascia, F. Rossi, C. Sbriziolo, M.L.T. Liveriand R. Varsalona, Oscillatory dynamics of the Belousov-Zhabotinsky system in the presence of a self-assembling nonionic polymer. Role of the reactants concentration, Phys. Chem. Chem. Phys., 2010,12, 11674-11682.         [ Links ]

13 S.M. Blagojevic, S.R. Anic, Z.D. Cupic, N.D. Pejic and L.Z. Kolar-Anic, Malonic acid concentration as a control parameter in the kinetic analysis of the Belousov-Zhabotinsky reaction under batch conditions, Phys. Chem. Chem. Phys., 2008, 10, 6658-6664.         [ Links ]

14 M. Seipel, F.W Schneider and A.F. Munster, Control and coupling of spiral waves in excitable media, Faraday Discuss., 2001,120, 395-405.         [ Links ]

15 J.L. Liu and S.K. Scott, Reduced models for the uncatalyzed Belousov- Zhabotinskii reaction, J. Phys. Chem-Us, 1992, 96, 9870-9875.         [ Links ]

16 R.J. Field, Limit cycle oscillations in reversible Oregonator, J. Chem. Phys, 1975, 63, 2289-2296.         [ Links ]

17 I.Z. Kiss, J.H. Merkin, S.K. Scott and P.L. Simon, Travelling waves in the Oregonator model for the BZ reaction, Phys. Chem. Chem. Phys., 2003, 5, 5448-5453.         [ Links ]

18 S.R. Pullela, D. Cristancho, P. He, D.W Luo, K.R. Hall and Z.D. Cheng, Temperature dependence of the Oregonator model for the Belousov-Zhabotinsky reaction, Phys. Chem. Chem. Phys., 2009,11, 4236-4243.         [ Links ]

19 R. Toth, A. Papp, V Gaspar, J.H. Merkin, S.K. Scott and A.F. Taylor, Flow-driven instabilities in the Belousov-Zhabotinsky reaction: modelling and experiments, Phys. Chem. Chem. Phys., 2001,3,957-964.         [ Links ]

20 P. Gray, S.K. Scott and J.H. Merkin, The Brusselator model of oscillatory reactions - Relationships between 2-variable and 4-variable models with rigorous application of mass conservation and detailed balance, J. Chem. Soc. Farad. T. 1, 1988, 84, 993-1012.         [ Links ]

21 P.N. Jha and R.K. Prasad. Stability and phase plane analysis of the Brusselator, J. Indian Chem. Soc., 1981, 58, 377-381.         [ Links ]

22 R. Larter,H. Rabitz and M. Kramer, Sensitivity analysis oflimit-cycles with application to the Brusselator, J. Chem. Phys., 1984,80,4120-4128.         [ Links ]

23 R. Lefever, G. Nicolis and P. Borckmans, The Brusselator - It does oscillate all the same, J. Chem. Soc. Farad. T. 1, 1988, 84, 1013-1023.         [ Links ]

24 R.S. Li, Extended Brusselator - Multiple attractors, J. Chem. Phys., 1986, 85, 4752-4753.         [ Links ]

25 R. Schranner, S. Grossmann and P.H. Richter, Dynamic correlation-functions in the Brusselator, Z. Phys. B Con. Mat., 1979, 35, 363-381.         [ Links ]

26 N. Metropolis, M.L. Stein and P.R. Stein, On finite limit sets for transformations on the unit interval, J. Comb. Theory, Ser. A, 1973,15, 25-4.         [ Links ]

27 J. Testa, J. Perez and C. Jeffries, Evidence for universal chaotic behavior of a driven non-linear oscillator, Phys. Rev. Lett., 1982, 48, 714-717.         [ Links ]

28 J. Testa, J. Perez and C. Jeffries, A driven non-linear oscillator - Reply, Phys. Rev. Lett., 1982, 49, 1055-1055.         [ Links ]

29 M. Meixner, S.M. Zoldi, S. Bose and E. Scholl, Karhunen-Loeve local characterization of spatiotemporal chaos in a reaction-diffusion system, Phys. Rev. E, 2000, 61, 1382-1385.         [ Links ]

30 R.H. Simoyi, A. Wolf and H.L. Swinney, One-dimensional dynamics in a multicomponent chemical-reaction, Phys. Rev. Lett., 1982, 49, 245-248.         [ Links ]

31 M.J. Feigenbaum, The transition to aperiodic behavior in turbulent systems, Commun. Math. Phys., 1980, 77, 65-86.         [ Links ]

32 K.G. Coffman, W.D. McCormick, Z. Noszticzius, R.H. Simoyi and H.L. Swinney, Universality, multiplicity, and the effect of iron impurities in the Belousov-Zhabotinskii reaction, J. Chem. Phys., 1987, 86, 119-129.         [ Links ]

33 T. Akimoto, M. Nakagawa, S. Shinkai and Y. Aizawa, Generalized Lyapunov exponent as a unified characterization of dynamical instabilities, Phys. Rev. E, 2015, 91.         [ Links ]

34 W. Ott, M.A. Rivas and J. West, Observing Lyapunov exponents of infinite-dimensional dynamical systems, J. Stat. Phys., 2015, 161, 1098-1111.         [ Links ]

35 Z.R. Novakovic, Solving systems of nonlinear equations using the Lyapunov direct method, Comput. Math. Appl., 1990, 20, 19-23.         [ Links ]

 

 

Received 8 February 2016
Revised 1 April 2017
Accepted 2 April 2017

 

 

* To whom correspondence should be addressed. E-mail: rsimoyi@pdx.edu