Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Chemistry
versión On-line ISSN 1996-840X
versión impresa ISSN 0379-4350
S.Afr.j.chem. (Online) vol.66 Durban ago. 2013
RESEARCH ARTICLE
Thermal behaviour and detonation characterization of N-benzoyl-3, 3-dinitroazetidine
Biao YanI, II; Ning Ning ZhaoI; Hai Xia MaI, *; Ji Rong SongI, III; Feng Qi ZhaoIV ; Rong Zhu HuIV
ISckool of Chemical Engineering/Shaanxi Key Laboratory of Physico-Inorganic Chemistry,Northwest University, Xi'an, 710069, China
IISchool of Chemistry and Chemical Engineering, Shaanxi Key Laboratory of Low Metamorphic Coal Clean Utilization, Yulin University, Yulin, 719000, China
IIIDepartment of Conservation Technology, The Palace Museum, Beijing, 100009, China
IVScience and Technology on Combustion and Explosion Laboratory, Xi'an Modern Chemistry Research Institute, Xi'an, 710065, China
ABSTRACT
N-benzoyl-3,3-dinitroazetidine(BDNAZ) is a derivative of 3,3-dinitroazetidine (DNAZ). Its thermal behaviour was studied by DSC methods. The results show that there are one melting process and two exothermic decomposition processes. The kinetic parameters of the intense exothermic decomposition process were obtained from the analysis of the DSC curves. The apparent activation energy, pre-exponential factor and the mechanism function are 170.77 kJ mol-1,1014.12 s-1 and f(α) = (1-a)-1/2, respectively. The specific heat capacity of BDNAZ was determined with a continuous Cp mode of a micro-calorimeter. The standard mole specific heat capacity of BDNAZ was 286.31 J mol1 K-1 at 298.15 K. Using the relationship between Cp and T with the thermal decomposition parameters, the time of the thermal decomposition from initialization to thermal explosion (adiabatic time-to-explosion, tTIAD), the self-accelerating decomposition temperature (TSADT), thermal ignition temperature (TTIT), critical temperatures of thermal explosion (Tb) and period of validity (t0.9) were obtained to evaluate its thermal safety. The detonation velocity (D) and pressure (P) of BDNAZ were estimated by using the nitrogen equivalent equation according to the experimental density.
Keywords: N-benzoyl-3,3-dinitroazetidine(BDNAZ), thermal behaviour, non-isothermal kinetics, thermal safety, detonation characterization.
1. Introduction
Dinitro- and trinitro-derivatives of azetidine are of interest because they contain strained ring systems during decomposition. This makes them good candidates for energetic materials (propellants or explosives). Initial reports concentrate on the synthesis of 1,3,3-trinitroazetidine (TNAZ) and 3,3-dinitro-azetidine (DNAZ).1,2 As one of the important derivatives of TNAZ, DNAZ2,3 can be used to prepare a variety of solid energetic materials with a high oxygen-balance.3-12 N-benzoyl-3,3-dinitroazetidine (BDNAZ, Fig. 1) is a novel insensitive high energy explosive. Presently, there are no reports about the thermal behaviour and detonation characterization of BDNAZ. In this paper, the thermal behaviour, non-isothermal decomposition reaction kinetics and thermal safety of BDNAZ were studied by DSC and TG/DTG methods. The detonation velocity and pressure were also calculated to estimate its detonationproperties.
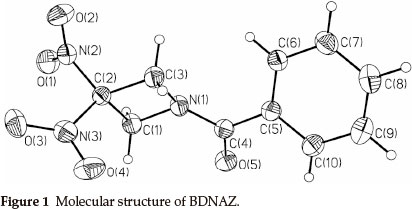
2. Experimental
A single crystal of BDNAZ was prepared by a reported method.12 The thermal behaviour of BDNAZ was studied by using a Q2000 DSC (TA, USA) by the DSC method under atmospheric pressure. The sample mass was about 2.742 mg at the heating rates of 3.0, 5.0,10.0 and 15.0 K min-1 with nitrogen as the purge gas and a flow rate of 50 mL min-1. The temperature and heat were calibrated by using pure indium and tin particles.
The specific heat capacity of BDNAZ was determined by a continuous Cp mode within 283-353 K at a heating rate of 0.15 K min-1 on a Micro-DSCIII (Seteram, France) instrument with a sample mass of 330.60 mg under atmospheric pressure.
3. Results and Discussion
3.1. Thermal Behaviour
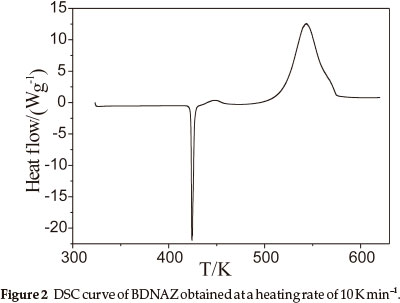
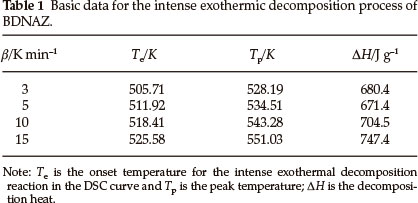
The DSC heat flow curve for BDNAZ at the heating rate of 10 K min-1 by DSC is shown in Fig. 2. It indicates that the thermal decomposition of BDNAZ can be divided into three stages. The first stage is a melting process, the extrapolated onset temperature (Te) and peak temperature (Tp) at a heating rate of 10 K min-1 are 423.27 K and 424.31 K, respectively. The second stage is a feeble exothermic decomposition process where Te and Tp are 432.28 K and 446.23 K, respectively. The third stage is an intense exothermic decomposition process, where Te and Tp are 518.41 K and 543.28 K, respectively. The basic data for the intense exothermic decomposition process are listed in Table 1.
3.2. Non-isothermal Reaction Kinetics
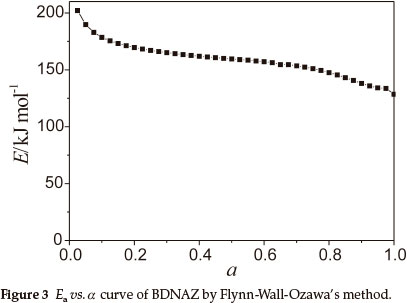
To explore the reaction mechanism of the intense exothermic decomposition process of BDNAZ and obtain the corresponding kinetic parameters [apparent activation energy (Ea/kJ mol-1), pre-exponential constant (A/s-1)] and the most probable kinetic model functions, the DSC curves at the heating rates of 3.0, 5.0, 10.0 and 15.0 K min-1 were dealt with by mathematic means, and the temperature data corresponding to the conversion degrees (α) were found. Six integral methods (MacCallum-Tanner, Satava-Šesták, Agrawal, General integral, Universal integral, Flynn-Wall-Ozawa) and one differential method (Kissinger) were employed.4-7,13 The values of Ea were obtained by Ozawa's method from the iso-conversional DSC curves at the heating rates of 3.0, 5.0, 10.0 and 15.0 K min-1, and the Ea-α relation is shown in Fig. 3. From Fig. 3, one can see that the activation energy slightly changes in the section of 0.10-0.60 (α), and the ranges were selected to calculate the non-isothermal reaction kinetics.
Forty-one types of kinetic model functions and the basic data were put into the integral and differential equations for calculation. The kinetic parameters and the probable kinetic model function were selected by the logical choice method and satisfying the ordinary range of the thermal decomposition kinetic parameters for energetic materials (Ea = 80-250 kJ mol-1, log A = 7-30 s-1). These data together with their appropriate values of linear correlation coefficient (r), standard mean square deviation (Q) and believable factor (d, where d = (1-r)Q), are presented in Table 2. The values of Ea and log A obtained from a single non-isothermal DSC curve is in good agreement with the calculated values obtained by Kissinger's method and Ozawa's method. Therefore, we conclude that the reaction mechanism of the intense exothermic decomposition process of BDNAZ is classified as Reaction order G(α) = 1-(1-α)2,f(α) = (1-a)-1/2. Substituting f(α) with (1-a)-1/2, E with 170.77 kJ mol-1 and A with 1014.12 s-1 in Eq. (1), the kinetic equation of the intense exothermic decomposition reaction may be described as dα/dT= 101382(1-a)-1exp(-2.05 x 104/T)/β.

3.3. Specific Heat Capacity
Figure 4 shows the results obtained for the specific heat capacity of BDNAZ by using the continuous specific heat capacity mode of a Micro-DSCIII apparatus. The specific heat capacity of BDNAZ presents a good cubic equation relationship with temperature in the temperature range studied. The specific heat capacity equation is shown as:
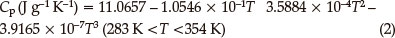
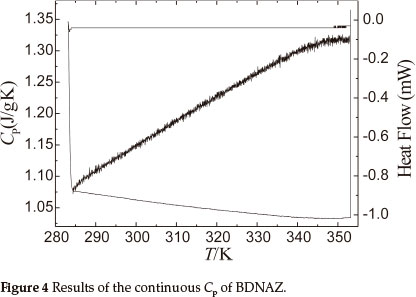
The standard molar specific heat capacity of BDNAZ is 286.31 J mol-1 K-1 at 298.15 K.
3.4. Thermal Safety Studies
The values (Te0 and Tp0) of the onset temperature (Te) and peak temperature (Tp) corresponding to β → 0 were obtained by Eq. (3), and the self-accelerating decomposition temperature (TSADT) was obtained by Eq. (4).4-7,13 The values (TSADT and Tp0) are 489.13 K and 513.44 K. respectively.
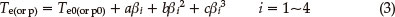
where a, b and c are coefficients.

The thermal ignition temperature (Tbe0 or TTIT) was obtained by substituting Eeo and Te0 into the equation of Zhang et al. [Eq. (5)],14 and the critical temperatures of thermal explosion (Tbp0 or Tb) were obtained by substituting Epo and Tp0 into equation (5). The values (TTIT and Tb) are 501.04 K and 527.52 K, respectively.
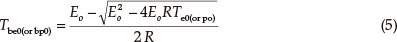
The entropy of activation (ΔS≠), enthalpy of activation (ΔΗ≠) and Gibbs energy of activation (ΔG≠) of the main exothermic decomposition reaction of BDNAZ corresponding to T = Tpo, Ea = Ek and A = Ak were obtained from Eqs (6) - (8),4-7 and are 13.99 J mol-1 K-1,163.80 kJ mol-1 and 156.62 kJ mol-1, respectively. The positive value of (ΔG≠), indicates that the exothermic decomposition reaction of BDNAZ must proceed under the heating condition.
where kB is the Boltzman constant and h is the Plank constant.
After the kinetic parameters (Ea and A) were obtained, the rate constant (k) for the decomposition reaction could be calculated by the following equation:

The period of validity of the BDNAZ could be determined by the equation:

where k was the rate constant and could be obtained by Eq. (9), where α is 0.1 and G(α) is the decomposition reaction mechanism function. For the temperature of 298.15 K and using the values of the activation energies (Ea) and frequency factors (A) obtained in the above, Eq. (10) could be solved. The period of validity for BDNAZ is 38.04 million years, which indicates that BDNAZ is very stable at 298.15 K.
The adiabatic time-to-explosion (tTIAD) of energetic materials is the time of decomposition transiting to explosion under the adiabatic conditions and is an important parameter for assessing the thermal stability and the safety of energetic materials.
where Qd decomposition heat, 700.9 J g-1. A, pre-exponential constant, A = 1014.12 s-1; Cp as Eq. (2) expressed, J g-1 K-1, E, activation energy, 170.77 kJ mol-1; R, the gas constant, 8.314 J mol-1 K-1; ƒ (α), differential mechanism function ƒ (α) = (1-a)-1/2.
Substituting the corresponding data into the Smith equation [Eqs (11) and (12)],15-16 the value of tTIAD is 550.97 s, which is longer than that of DNAZ-HClO4 (3,3-dinitroazetidinium perchloric acid),4 DNAZ-PA (3,3-dinitroazetidinium picrate),5 DNAZ DNS (3,3-dinitroazetidinium 3,5-dinitrosalicylate),6 NTO DNAZ (3-nitro-1,2,4-triazol-5-one 3,3-dinitroazetidinium)7 and TNAZ17. In the calculation process of adiabatic time-to-explosion, a little change in the activation energy located in the integral equation with exponential form can make a great difference in the result, and a small increase of the activation energy can induce tTIAD to rise greatly.
3.5. Characterization of Detonation Velocity and Pressure
Detonation velocity (D) and detonation pressure (P) are the most important targets of scaling the detonation characteristics of energetic materials. The detonation velocity and pressure of an explosive can be predicted with the nitroge n equivalent equation (NE equation) shown as formulas (13)-(15).18

in which VD represents detonation velocity of an explosive, p0 represents density of an explosive, ΣN represents nitrogen equivalent of the detonation products, Ni is the nitrogen equivalent index of certain detonation products, xi is the mole number of certain detonation products produced by a mole of explosive.
The detonation products produced by general explosives together with their nitrogen equivalent indices are listed in Table 3. According to the order of H2O-CO-CO2 in forming detonation products, the detonation products of BDNAZ are calculated as follows:
C10H9N3O5 = (4.5)H2O + (0.5)CO + (9.5)C +(1.5)N2.

According to Eq. (15), in which M = 251.20 g mol-1,ρ = 1.504 g cm-3,12 total nitrogen equivalents of BDNAZ are obtained through the nitrogen equivalent indices of the detonation products in Table 3:
ΣN =100 x (4.5 x 0.54 + 0.5 x 0.78 + 9.5 x 0.15 + 1.5 x 1)/251.2 = 2.287
According to Eqs (13) and (14), the calculated detonation velocity and pressure of BDNAZ are 5568.08 m s-1 and 12.34 GPa, respectively.
4. Conclusions
The thermal behaviour of BDNAZ under non-isothermal conditions by DSC methods was studied. The apparent activation energy and pre-exponential factor of the intense exothermic decomposition reaction are 170.77 kJ mol-1 and 1014.12 s-1, respectively. The reaction mechanism of the intense exothermic decomposition process of BDNAZ is classified as Reaction order G(α) = 1-(1-a)2, f(α) = (1-a)-1/2. The specific heat capacity was determined with a Micro-DSC method. The specific heat capacity equation is Cp(J g-1 K-) = 11.0657 - 1.0546 x 10-1T + 3.5884 x 10-4T2 - 3.9165 x 10-7T3 (283 K < T < 353 K) and the standard molar specific heat capacity is 286.31 J mol-1K-1 at 298.15 K. The self-accelerating decomposition temperature, the thermal ignition temperature and the critical temperatures of thermal explosion are 489.13 K, 501.04 K and 527.52 K, respectively. The values of (ΔS≠), (ΔΗ≠) and (ΔG≠) of this reaction are 13.99 J mol-1 K-1,163.80 kJ mol-1 and 156.62 kJ mol-1, respectively. The period of validity is 38.04 million years. The adiabatic time-to-explosion was calculated to be 550.97 s. The detonation velocity and pressure are 5568.08 m s-1 and 12.34 GPa, respectively.
Acknowledgements
This work was supported by the Program for New Century Excellent Talents in University, the National Natural Science Foundation of China (No. 21073141), the Education Committee Foundation of Shaanxi Province (Nos. 11JK0564 and 11JK0582) and the Project-sponsored by SRF for AT, YLU (Grant No. 09GK019).
References
1 T.G. Archibald, R. Gilardi, K. Baum and C. George, J. Org. Chem, 1990, 55, 2920-2924. [ Links ]
2 M.A. Hiskey, M.D. Coburn, M.A. Mitchell and B.C. Benicewicz, J. Heterocyclic. Chem., 1992, 29, 1855-1856. [ Links ]
3 M.A. Hiskey, M.M. Stincipher and J.E. Brown, J. Energ. Mater., 1993, 11, 157-165. [ Links ]
4 H.X. Ma, B. Yan, Y.H. Ren, Y.L. Guan, F.Q. Zhao, J.R. Song and R.Z. Hu, J. Therm. Anal. Calorim., 2011, 103, 569-575. [ Links ]
5 H.X. Ma, B. Yan, J.F. Li, Y.H. Ren, Y.S. Chen, F.Q. Zhao, J.R. Song and R.Z. Hu, J. Mol. Struc., 2010, 981, 103-110. [ Links ]
6 H.X. Ma, B. Yan, Z.N. Li, J.R. Song and R.Z. Hu, J. Therm. Anal. Calorim., 2009, 95, 437-444. [ Links ]
7 H.X. Ma, B. Yan, Z.N. Li, Y.L. Guan, J.R. Song, K.Z. Xu and R.Z. Hu, J. Hazard. Mater., 2009, 169, 1068-1073. [ Links ]
8 Z.N. Li, H.X. Ma, B. Yan, Y.L. Guan and J.R. Song, Chinese. J. Chem., 2009, 27, 2284-2290. [ Links ]
9 H.X. Ma, B. Yan, J.R. Song, X.Q. L and L.J. Wang, Chem. J. Chinese. U, 2009, 30, 377-381. [ Links ]
10 R. Gao, H.X. Ma, B. Yan, J.R. Song and Y.H. Wang, Chem. J. Chinese. U, 2009, 30, 577-582. [ Links ]
11 B. Yan, H.X. Ma, Y. Hu, Y.L. Guan and J.R. Song, Acta Crystallogr. E, 2009, 65, o3215. [ Links ]
12 B. Yan, H.X. Ma, J.F. Li, Y.L. Guan and J.R. Song, Acta Crystallogr. E. 2010, 66, o57. [ Links ]
13 H.X. Ma, J.R. Song, F.Q. Zhao, R.Z. Hu and H.M. Xiao, J. Phys. Chem. A., 2007, 111, 8642-8649. [ Links ]
14 T.L. Zhang, R.Z. Hu, Y. Xie and F.P. Li, Thermochim. Acta, 1994, 244, 171-176. [ Links ]
15 L.C. Smith, Thermochim. Acta, 1975, 13, 1-6. [ Links ]
16 R.Z. Hu, H. Zhang, Z.M. Xia, P.J. Guo, S.L. Gao, Q.Z. Shi, G.E. Lu and J.Y. Jiang, Chin. J. Energ. Mater., 2003, 11, 130-133. [ Links ]
17 H.A. Zhao, R.Z. Hu, X.J. Wang, F.Q. Zhao, H.X. Gao, H. Zhang, X.L. Zhang, Y. Feng, and H.X. Ma, Acta. Chim. Sinica, 2009, 67, 2536-2540. [ Links ]
18 H.X. Chen, S.S. Chen, L.J. Li, Q.Z. Jiao, T.Y. Wei, and S.H. Jin, J. Hazard. Mater., 2010, 175, 569-574. [ Links ]
Received 21 June 2012
Revised 14 November 2012
Accepted 13 December 2012
* To whom correspondence should be addressed. E-mail: donghuhai@qq.com














