Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Chemistry
On-line version ISSN 1996-840X
Print version ISSN 0379-4350
S.Afr.j.chem. (Online) vol.66 Durban Aug. 2013
RESEARCH ARTICLE
Carbonyl substitution in β-diketonatodicarbonyl-rhodium(I) by cyclo-octadiene: Relationships with experimental, electronic and calculated parameters
Jeanet ConradieI, II, *
IDepartment of Chemistry, University of the Free State, Bloemfontein, P.O. Box 339, 9300, South Africa
IIDepartment of Chemistry and Centre for Theoretical and Computational Chemistry, University of Tromsø, N-9037 Tromsø, Norway
ABSTRACT
The substitution rate constant of the reaction between [Rh(β-diketonato)(CO)2] and cyclo-octadiene is related to various empirical parameters and density functional theory calculated energies and charges, β-diketonato = R'COCHCOR. Results indicate that especially the Hammett meta substituent constants (σ), the Lever electronic parameters (EL) and the density functional theory calculated energies and charges predict the substitution rate constant to a high degree of accuracy, for example: ln k2 = 8.48 (σr + σr,) - 2.24 (R2 = 0.99) = 31.8 ΣEl - 63.0 (R2 = 0.99) = - 9.16 EHOMO - 52.1 (R2 = 0.97) = 101 ΣQMulliken(Rh(CO)2) - 49.9 (R2 = 0.99).
Keywords: BETA-diketone, rhodium, substitution; dicarbonyl, cyclo-octadiene, DFT.
1. Introduction
The first [Rh(β-diketonato)(CO)2] complexes were reported by Bonati and Wilkinson in 1964.1 They showed that the carbon monoxide groups in [Rh(p-diketonato)(CO)2] can be completely substituted by olefins such as cyclo-octa-1,5-diene (cod) (Scheme 1). The reverse reaction, i.e. treatment of [Rh(β-diketonato)(cod)] with CO resulted in better yields of [Rh(β-diketonato)(CO)2] than the conventional synthetic pathway by treating [Rh(Cl)(CO)2]2 with the β-diketone in certain cases.2 Reactions of [Rh(β-diketonato)(CO)2] involving triphenylphosphine (PPh3) or triphenylarsine (AsPh3) lead to substitution of only one of the carbonyl ligands.1,3-6 Rhodium(I) complexes with bi-dentate β-diketonato ligands are well-known catalysts for hydroformylation of olefins.7-9 We have recently shown that experimental second-order substitution rate constants of the [Rh(R'COCHCOR)(cod)] + phen → [Rh(phen)(cod)]+ + (R'COCHCOR)- reaction relate to the density functional theory calculated energies of the highest occupied molecular orbital of thermodynamically stable reactant [Rh(R'COCHCOR)(cod)] (phen = 1,10-phenanthroline).10 We were interested to see if a similar relationship exists if [Rh(R'COCHCOR)(cod)] is the product of a substitution reaction. An experimental study of the kinetics of the substitution reaction [Rh(R'COCHCOR)(CO)2] + cod → [Rh(R'COCHCOR)(cod)] + 2(CO) (Scheme 1) showed that the order of the effect of the β-diketonato ligands (R'COCHCOR)- on the reactivity of the [Rh(β-diketonato)(CO)2] complexes was (CH3COCHCOPh)- < (PhCOCHCOPh)- < (CF3COCHCOCH3)- < (CF3COCHCOPh)- < (CF3COCHCOCF3)-, i.e. more electronegative substituents R or R' of the β-diketone led to a faster substitution rate.11
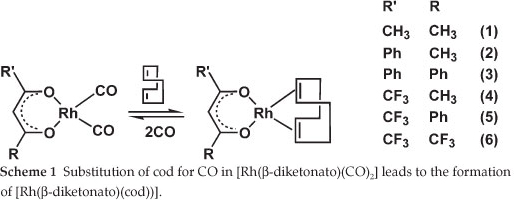
The aim of this study is to establish relationships and trends between density functional theory (DFT) calculated, empirical and experimental data in order to be able to predict the reactivity of β-diketonatodicarbonyl-rhodium(I)- systems from calculated descriptors.
2. Methods
Density functional theory (DFT) calculations were carried out using the ADF (Amsterdam Density Functional) 2012 programme12-14 with the GGA (Generalized Gradient Approximation) functional PW91 (Perdew-Wang 1991).15 The TZ2P (Triple ζ polarized) basis set, with a fine mesh for numerical integration and tight convergence criteria, was used for minimum energy searches. Throughout, all calculations have been performed with no symmetry constraints (C1) and all structures have been calculated as spin-restricted singlet states. All calculations have been done in the gas phase. Optimized geometries obtained were used to perform an NBO analysis by the NBO 3.1 module.16
3. Results and Discussion
3.1. Kinetic Rate Constant and Electronic Parameters
The experimentally measured second-order rate constant k2for the substitution of cod for CO in [Rh(R'COCHCOR)(CO)2]is tabulated in Table 1 (cod = 1,5-cyclooctadiene).11 Empirical parameters that are related to the electron donating property of the R and R' groups on the β-diketonato ligand (R'COCHCOR)-, the sum of the Gordy scale group electronegativities (χR + χR'),17,18 the sum of the Hammett meta substituent constants, (σR + σR),19,20 and the sum of the Lever electronic parameter ΣEL21-24 for the [Rh(R'COCHCOR)(CO)2] complexes are also given in Table 1. Figure 1 visualizes the linear relationships between ln k2and the electronic parameters.
In k2 = 4.25 (χR + χR') - 20.9 (R2 = 0.91)
In k2 = 8.48 (σR + σR') - 2.24 (R2 = 0.99)
In k2 = 31.8 ΣΕL - 63.0 (R2 = 0.99)
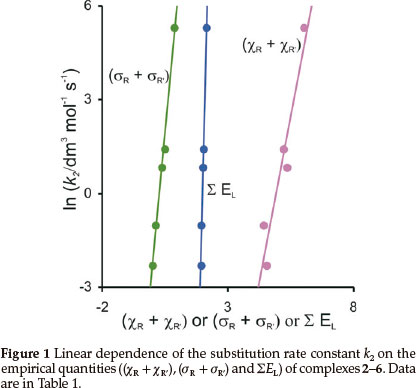
A lower (more acidic) pKa value of the free β-diketone generally resulted in a faster substitution rate (see data in Table 1), but did not give a good linear fit. The Hammett constants and Lever parameters originate from substitution rate constants and electrochemical potentials respectively. The Hammett constants σR are empirical constants that relate the logs of rate or equilibrium constants for reactions of the substituted (kR, R = substituent) and the unsubstituted (kH, no substituent) benzoic acid derivatives to the reaction rate ρ: log (kR/kH) = (σR)ρ. σR depends solely on the nature and position of the substituent R.25 In as much as the substituents on the β-diketonato chelate ring are meta with respect to rhodium, the σ values used are those for meta position substitution.26 Since the β-diketonato ligand in [Rh(R'COCHCOR)(cod)] has two meta substituents relative to rhodium, the σ value is taken as the sum of the values for the two groups present. The Lever parameter is a redox potential parameterization approach,21 involving an empirical relationship between the oxidation potential (in volts vs. SHE) of the redox couple M(q)/M(q+1) of a complex and the Lever electrochemical parameters determined by the ligands and the metal centre, Εredox (vs.SHE) =SM ΣΕL + IM. ΣΕL is the sum of the values of the Lever ligand ΕL parameters for all the ligands (additive effects) in the complex and SM and IM represent the slope and intercept (dependent on the metal, redox couple, spin state and stereochemistry). We observe that both the Hammett constants and the Lever parameters give excellent descriptions of reactivity patterns of the [Rh(R'COCHCOR)(CO)2] complexes containing different R and R' substituents as experimentally measured by the substitution rate constant k2.
3.2. Kinetic Rate Constant, Electronic Parameters and DFT Calculated Energies
The reactivity of the rhodium complexes is in many respects due to the nature of ligand surroundings27 and determined largely by the relative frontier orbital energies.28-30 The Frontier Molecular Orbital Theory (FMO Theory) simplifies reactivity to interactions between the HOMO of one species and the LUMO of the other31 The reactivity of the [Rh(R'COCHCOR)(CO)2] complex is therefore related to the energy of its HOMO. The high correlation found between the DFT calculated energy of the HOMO (highest occupied molecular orbital) of the [Rh(R'COCHCOR)(CO)2] complexes 2-6, Εhomo and the substitution rate constant (Figure 2 (a)) shows that the substitution reaction is frontier controlled:
ln k2= -9.16 Εhomo- 52.1 (R2 = 0.97)
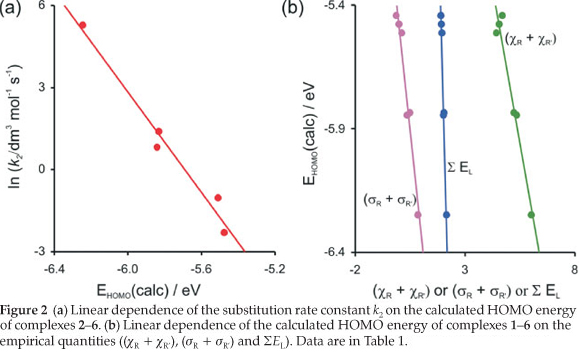
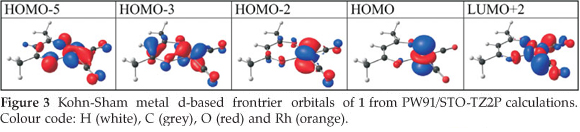
The d-occupation of the [Rh(R'COCHCOR)(CO)2] complexes 1-6 is dxz2 dyz2 dxy2 dz22 dx2-y20 with the HOMO mainly dz2 on rhodium, see Fig. 3. The calculated HOMO energy is largely influenced by the electronic effect of the substituent groups R and R' on rhodium. Figure 2 (b) displays the relationships between the various empirical parameters describing the electron-donating/withdrawing power of the R and R' groups and the energy of the HOMO of complexes 1-6:
Εhomo = -0.502 (χR + χR') - 3.20 (R2 = 0.95)
Εhomo = -0.835 (σr + σR') - 5.49 (R2 = 0.96)
Εhomo = -3.34 ΣΕl + 0.928 (R2 = 0.99)
The above relationships all show that more electron withdrawing R and R' substituent groups lead to a more negative ΕHOMO, i.e. a more stable HOMO.
Experimental rate constants k2 relate to the activation energy Εa by the Arrhenius equation:
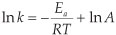
where, R = gas constant, T = temperature and A = pre-expo-nential factor. We have previously shown that the relationship between the DFT calculated activation energy and the experimentally measured kinetic parameter ln k2 of the oxidative addition reaction [Rh(β-diketonato)(P(OPh)3)2] + CH3l is less accurate than the relationship between EHOMO and ln k2.32Therefore we do not consider relationships involving transition states in this study.
3.3. Kinetic Rate Constant, Electronic Parameters and DFT Calculated Charges
A detailed quantum chemical examination of electron state variations of an active metal-containing centre versus different ligand characteristics may lead to a better understanding of the relationship between the activity and catalyst structure, as well as to ways of predicting catalytic activity. The wavefunction population analysis methods assign a partial charge to each atom. Although the absolute magnitudes of the atomic charges yielded by population analysis have little physical meaning,33 the relative magnitude of the numbers can be interpreted and can yield useful information.34,35 The Mulliken population analy-sis36 is one of the oldest, simplest and most common population analysis methods. The calculated Mulliken charge on the Rh(CO)2 fragment in the reactant [Rh(R'COCHCOR)(CO)2] complexes 1-6 relates to the experimental and empirical parameters tabulated in Table 1 (average R2 = 0.95, see Figs 4 and 5):
ln k2 = 101 ΣQMulliken(Rh(CO)2) - 49.9 (R2 = 0.99)
ΣQMulliken(Rh(CO)2) = 0.0470 (χr +χr') + 0.257 (R2 = 0.84)
ΣQMulliken(Rh(CO)2) = 0.0851 (σr + σr') + 0.470 (R2 = 1.00)
ΣQMulliken(Rh(CO)2) = 0.333 ΣEL - 0.170 (R2 = 0.98)
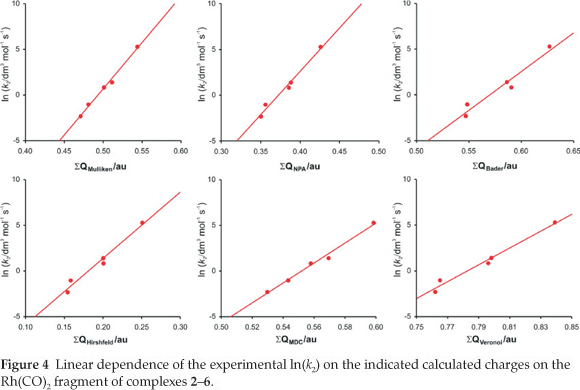
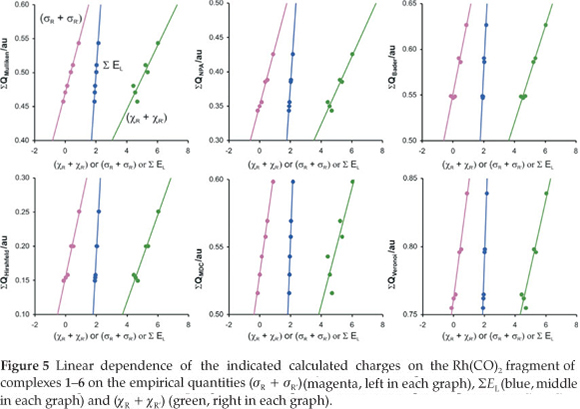
The natural population analysis (NPA), another wavefunction population analysis method, yields natural charges. The natural charge on rhodium generally increased (became less negative) in going from complex 1 to 6 (fastest substitution rate, most reactive). The charge alteration of the rhodium-dicarbonyl fragment correlates with the different experimental and empirical parameters (see Figs 4 and 5, data are in Table 1):
ln k2 = 94.7 ΣQNPA(Rh(CO)2) - 35.2 (R2 = 0.98)
ΣQnpa(Rh(CO)2) = 0.0493 (Xr +Xr')+ 0.127 (R2 = 0.93)
ΣQnpa(Rh(CO)2) = 0.0841 (σr + σr') + 0.351 (R2 = 0.98)
ΣQNPA(Rh(CO)2) = 0.334 ΣEL + 0.290 (R2 = 0.99)
From the relationships obtained above, we note that the calculated charges are valuable indicators of chemical behaviour. Other computational methods37 of atomic charge determination include the partitioning of electron density distributions (e.g. Bader charges obtained from an atoms in molecules analysis38 and Hirshfeld39 charges) and charges derived from density-dependent properties (e.g. MDC, Multipole derived atomic charges40). See Figs 4 and 5 for a visualization of the good relationships obtained between the calculated charges and experimental and empirical parameters (data are in Table 1):
ln k2 = 84.7 ΣQBader(Rh(CO)2) - 48.3 (R2 = 0.95)
ΣQBader(Rh(CO)2) = 0.0527 (Xr +Xr') + 0.309 (R2 = 0.98)
ΣQBader(Rh(CO)2) = 0.0848 (σr + σr') + 0.551 (R2 = 0.93)
ΣQBader(Rh(CO)2) = 0.341 ΣEL + 0.104 (R2 = 0.96)
ln k2= 72.6 ΣQHirshfeld(Rh(CO)2) - 13.1 (R2 = 0.97)
ΣQHirshfeld(Rh(CO)2) = 0.0633 (χR + χR') + 0.134 (R2 = 0.95)
ΣQHirshfeld(Rh(CO)2) = 0.105 (σR + σR') + 0.156 (R2 = 0.96)
ΣQHirshfeld(Rh(CO)2) = 0.421 ΣEL + 0.653 (R2 = 0.99)
ln k2 = 109 ΣQMDC(Rh(CO)2) - 60.3 (R2 = 0.99)
ΣQMDC(Rh(CO)2) = 0.0434 (χR +χR') + 0.334 (R2 = 0.79)
ΣQMDC(Rh(CO)2) = 0.0805 (σR + σR') + 0.530 (R2 = 1.00)
ΣQMDC(Rh(CO)2) = 0.313 ΣEL + 0.0714 (R2 = 0.97)
Voronoi deformation density (VDD) is a method based on the partitioning of space into non-overlapping atomic areas modelled as Voronoi cells and then computing the deformation density within those cells.41 The relationship between the calcu-lated Voronoi charges and the experimental substitution rate and empirical electronic parameters is illustrated in Figs 4 and 5 (data are in Table 1):
ln k2 = 91.9 ΣQVoronoi(Rh(CO)2) - 72.0 (R2 = 0.98)
ΣQVoronoi(Rh(CO)2) = 0.0505 (χR + χR') + 0.531 (R2 = 0.94)
ΣQVoronoi(Rh(CO)2) = 0.08545 (σR + σR') + 0.762 (R2 = 0.97)
ΣQVoronoi(Rh(CO)2) = 0.341 ΣEL + 0.107 (R2 = 0.99)
In all the above relationships that involved calculated partial charges, the sum of the charges on the Rh(CO)2 fragment gave relationships with a better fit than the charge on Rh alone. The thermodynamic trans infiuence of the two Oβ-diketonato atoms of the chelate ring trans to the carbonyl groups of [Rh(R'COCHCOR) (CO)2] may contribute to this phenomenon. The trans influence of the Oβ-diketonatoo is due to the electron withdrawing power of the R group nearest to it. The Rh-CO bonding (CO-to-M σ bond) and back-bonding (M-to-CO π bond) may also contribute to this phenomenon. Shor similarly found that for [Rh(R'COCHCOR) (CO)2] complexes the NPA charge alteration of the metal-di-carbonyl fragment (and not on Rh alone) in [Rh(R'COCHCOR) (CO)2] correlated with CO bond lengths and vibration frequencies of carbonyl group.
The above relationships show the same trend; stronger electron attracting R and R' substituent groups decrease the electron density on Rh(CO)2 in going from complex 1 to 6, making the complex a stronger Lewis acid. The five-coordinate transition state42 of the substitution reaction [Rh(R'COCHCOR)(CO)2]+ cod is therefore more stabilized as R and R' become more elec-tron attracting. This leads to an increase of the reactivity of the complex towards substitution reactions.
The relationships obtained from DFT charges make the estimate of k2 for any [Rh(R'COCHCOR)(CO)2] complex possible with an accuracy of >97 %.
4. Conclusions
The aim of this study was to establish relationships and trends between caicuiated, empiricai and experimentai data in order to predict the reactivity as experimentally measured by the chemical substitution rate (k2) of cod for CO in [Rh(R'COCHCOR)(CO)2]. From the DFT optimized structures of [Rh(R'COCHCOR)(CO)2] complexes 1-6 we found that both the HOMO energy and the charges on Rh(CO)2 are valuable indicators of chemical behaviour. Results show that k2 can be predicted with a high degree of accuracy by the following equations:
ln k2 = 4.25 (χR+ χR') - 20.9 (R2 = 0.91)
= 8.48 (σR + σR') - 2.24 (R2 = 0.99)
= 31.8 ΣEL- 63.0 (R2 = 0.99)
= - 9.16 ΕHOMO- 52.1 (R2 = 0.97)
= 101 ΣQMulliken(Rh(CO)2) - 49.9 (R2 = 0.99)
= 94.7 ΣQNPA(Rh(CO)2) - 35.2 (R2 = 0.98)
= 84.7 ΣQBader(Rh(CO)2) - 48.3 (R2 = 0.95)
= 72.6 ΣQHirshfeld(Rh(CO)2) - 13.1 (R2 = 0.97)
= 109 ΣQMDC(Rh(CO)2) - 60.3 (R2 = 0.99)
= 91.9 ΣQVoroni(Rh(CO)2) - 72.0 (R2 = 0.98)
A lower (more negative) ΕHOMO, i.e. a more stable HOMO, therefore systematically resulted in a faster substitution rate. The complex is therefore more reactive, due to the stabilization of the five-coordinate transition state of the substitution reaction. The electronic influence of R and R' groups in [Rh(R'COCHCOR) (CO)2] complexes is reflected in the stability of the HOMO of the complex. Higher group electronegativities (χR + χR'), higher Hammett meta substituent constants (σR + σR'), higher Lever electronic parameters ΣΕL and lower pΚa values of the free β-diketone result in a more stable HOMO with a lower (more negative) energy. Relationships between calculated and experimental parameters allow for the design of ligands that can enhance the substitution rate.
Acknowledgements
The South African National Research Foundation and the Central Research Fund of the University of the Free State, Bloemfontein for funding.
References and Notes
1 F. Bonati and G. Wilkinson, J. Chem. Soc. 1964, 3156-3160. [ Links ]
2 J. Conradie, T.S. Cameron, M.A.S. Aquino, G.J. Lamprecht and J.C. Swarts, Inorg Chim Acta, 2005, 358, 2530-2542. [ Links ]
3 A.M. Trzeciak and J. J Ziólkowski, Inorg. Chim. Acta, 1985, 96, 15-20. [ Links ]
4 S. Serron, J. Huangand S.P. Nolan, Organometallics, 1998, 17, 534-539. [ Links ]
5 N.F. Stuurman and J. Conradie J. Organomet Chem, 2009, 694, 259-268. [ Links ]
6 M.M. Conradie and J. Conradie 2008, Inorg. Chim. Acta, 2008, 361, 208-218. [ Links ]
7 E. Mieczynska, A.M Trzeciak and J.J. Ziólkowski, J. Mol. Catal, 1993, 80, 189-200. [ Links ]
8 A.M. Trzeciak, M. Mieczynska and J.J. Ziólkowski, Topics in Catalysis, 2000, 11/12, 461-468. [ Links ]
9 H. Jin, B. Subramaniam, A. Ghosh and J. Tunge, AIChE Journal, 2006, 52, 2575-2581. [ Links ]
10 J. Conradie, J. Organomet. Chem., 2012, 719, 8-13. [ Links ]
11 J.G. Leipoldt, S.S. Basson, J.J.J. Schlebush and E.C. Grobler Inorg. Chim. Acta, 1982, 62, 113-115. [ Links ]
12 G. te Velde, F.M Bickelhaupt, E.J. Baerends, C. Fonseca Guerra, S.J.A. van Gisbergen, J.G. Snijders and T. Ziegler, J. Comput. Chem. 2001, 22, 931-967. [ Links ]
13 C. Fonseca Guerra, J.G. Snijders, G. te Velde and E.J. Baerends, Theor. Chem. Acc., 1998, 99, 391-403. [ Links ]
14 ADF2012.01 SCM Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands [ Links ]
15 J.P. Perdew, J.A. Chevary, S.H. Vosko, K.A. Jackson, M.R. Pederson, D.J. Singh and C. Fiolhais, Phys. Rev. 1992, B 46, 6671-6687. [ Links ] Erratum: J.P. Perdew, J.A. Chevary, S.H. vosko, K.A. Jackson, M.R. Perderson, D.J. Singh and C. Fiolhais, Phys. Rev. 1993, B 48, 4978-4978. [ Links ]
16 E.D. Glendening, J.K. Badenhoop, A.E. Reed, J.E. Carpenter, J.A. Bohmann, C.M. Morales and F. Weinhold, NBO 31, Theoretical Chemistry Institute University of Wisconsin, Madison, WI, 2001, [ Links ]
17 Gordy scale group electronegativities χR are empirical numbers that express the combined tendency of not only one atom but a group of atoms like R = CF3 or CH3 to attract electrons including those in a covalent bond, as a function of the number of valence electrons n and the covalent radius r in Ǻ, of groups as discussed in (a) P.R. Wells in Progress in Physical Organic Chemistry, vol. 6, John Wiley & Sons, New York, 1968, pp. 111-145, and (b), R.E. Kagarise, J. Am. Chem. Soc., 1955, 77, 1377-1379. [ Links ]
18 A. Kuhn, K.G. von Eschwege and J. Conradie, Electrochim. Acta, 2011, 56, 6211-6218. [ Links ]
19 L.P. Hammett, Chem. Rev., 1935, 17, 125-136. [ Links ]
20 C. Hansch, A. Leo and R.W. Taft, Chem. Rev., 1991, 91, 165-195. [ Links ]
21 A.B.P. Lever, Inorg. Chem., 1990, 29, 1271-1285. [ Links ]
22 M.F.C. Guedes da Silva, A.M. Trzeciak, J.J. Ziólkowski and A.J.L. Pombeiro, J. Organomet. Chem, 2001, 620, 174-181. [ Links ]
23 A.M. Trzeciak, B. Borak, Z. Ciunik, J.J. Ziólkowski, M.F.C. Guedes da Silva and A.J.L. Pombeiro, Eur. J. Inorg. Chem, 2004, 1411-1419. [ Links ]
24 I. Kovacik, O. Gevert, H. Werner, M. Schmittel and R. Söllner, Inorg. Chim. Acta, 1998, 435, 275-276. [ Links ]
25 D.H. McDaniel and H.C. Brown, J. Org. Chem., 1958, 420, 420-427. [ Links ]
26 R.L. Lintvedt, H.D. Russell and H.F. Holtzclaw, Inorg. Chem, 1966, 5, 1603-1607. [ Links ]
27 E.A. Shor, A.M. Shor, V.A. Nasluzov and A.I. Rubaylo, J. Struct. Chem, 2005, 46, 220-229. [ Links ]
28 I. Fleming, Frontier Orbitals and Organic Chemical Reactions, Wiley, New York, 1976. [ Links ]
29 K. Fukui, Top. Curr. Chem., 1970, 15, 1-85. [ Links ]
30 G. Klopman, J. Am. Chem. Soc., 1968, 90, 223-234. [ Links ]
31 K. Fukui, T. Yonezawa and H. Shingu, J. Chem. Phys. 1952, 20, 722-725. [ Links ]
32 J. Conradie, Inorg. Chim. Acta, 2012, 392, 30-37. [ Links ]
33 E.R. Davidson and S. Chakravorty, Theor. Chim. Acta, 1992, 83, 319-330. [ Links ]
34 M.D. Segall, C.J. Pickard, R. Shah and M.C. Payne, Mol. Phys., 1996, 89, 571-577. [ Links ]
35 M.D. Segall, R. Shah, C.J. Pickard and M.C. Payne, Phys. Rev. B, 1996, 54, 16317-16320. [ Links ]
36 R.S. Mulliken, J. Chem. Phys., 1955, 23, 1833-1840. [ Links ]
37 J. Meister and W.H.E. Schwarz, J. Chem. Phys., 1994, 98, 8245-8252. [ Links ]
38 R. Bader, Chem. Rev., 1991, 91, 893-928. [ Links ]
39 F.L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129-138. [ Links ]
40 M. Swart, P.Th. van Duijnen and J.G. Snijders, J. Compt. Chem., 2001, 22, 79-88. [ Links ]
41 C.F. Guerra, J.W. Handgraaf, E.J. Baerends and F.M Bickelhaupt J. Comp. Chem., 2004, 25, 189-210. [ Links ]
42 J.K. Burdett, Inorg. Chem., 1977, 16, 3013-3025. [ Links ]
43 J. Starý, The Solvent Extraction of Metal Chelates, MacMillan Company, New York, 1964, Appendix. [ Links ]
44 M. Ellinger, H. Duschner and K. Starke, J. Inorg. Nucl. Chem, 1978, 40, 1063-1067. [ Links ]
45 W.C. du Plessis, T.G. vosloo and J.C. Swarts, J. Chem. Soc. Dalton Trans, 1998, 2507-2514. [ Links ]
46 R.E. Kagarise, J. Am. Chem. Soc., 1995, 77, 1377-1379. [ Links ]
Received 14 December 2012
Accepted 5 February 2013
* E-mail: conradj@ufs.ac.za
Submitted by invitation in support of the 2012 celebrations "100 years of SACI: The Past, The Present, The Future".














