Metabolizable energy requirements, dry matter intake and feed selection of sable antelope (Hippotragus niger)

 

 

C.A. Shepstone^{I, #}; H.H. Meissner^II; J.H.C. Van Zyl^I; P. Lubout^III; L.C. Hoffman^{I, IV}

^IDepartment of Animal Sciences, Stellenbosch University, Private Bag X1, Matieland, Stellenbosch, 7602, South Africa
^IINo 3 Die Hoewes, 276 von Willich Street, Centurion 0157, South Africa
^IIIDepartment of Animal Science, Faculty of Natural and Agricultural Science Mahikeng Campus, North-West University, Mafikeng 2735, South Africa
^IVCentre for Nutrition and Food Sciences, Queensland Alliance for Agriculture and Food Innovation (QAAFI), The University of Queensland, Australia

 

 

---

ABSTRACT

The large animal unit, grazing unit, and browsing unit methods for determining carrying capacity of wildlife use only metabolic weight as a factor to determine the energy requirements of game, whereas the large stock unit method uses metabolic weight and energy requirements of the animal at a specific well-defined physiological production stages. The metabolizable energy requirement in megajoules per day (MJ ME/day) was regressed on weight in kg using a log-log transformation to ascertain whether the large animal unit method was suitable for defining and determining the ME requirements of game. The resulting equations were used to compare the calculated ME and large stock unit values with the published values. Six of the seven categories had values higher than 0.75 with R² values of >0.99, the exception being calf/lamb data with a value of 0.742 with an R² = 0.97. The physiological production stages that were analysed were calf/lamb, young dry cow/ewe, mature dry cow/ewe, young cow/ewe with calf/lamb, mature cow/ewe with calf/lamb, young bull/ram, and mature bull/ram. These results indicated that metabolic weight was neither conceptually correct nor sufficiently accurate to calculate ME requirements for game, confirming the acceptance of the alternative hypothesis. Therefore, the large animal unit (metabolic weight method) cannot replace the large stock unit (metabolizable energy method). The derived log-log transformation equation provided a more accurate method for determining the metabolizable energy requirements and dry matter intake values for sable antelope (Hippotragus niger) and other game species.

Keywords: browsing unit, carrying capacity, grazing unit, large animal unit, large stock unit, stocking rate, wildlife ranching

---

 

 

Introduction

Ecologists, rangeland and animal scientists have different approaches to determining the carrying capacity of a game ranch or reserve. This is particularly true of the animal unit (AU) component when calculating the short- and long-term carrying capacity for certain vegetation types. The approaches that have been used to estimate carrying capacity have led to ambiguities when interpreting the results. The methods include the large stock unit (LSU) (Meissner, 1982), AU (animal unit) (Scarnecchia, 1985), the large animal unit (LAU), browsing unit (BU) and grazing unit (GU) (Peel et al., 1994; Van Rooyen & Bothma, 2016).

The Amendment to the South African Animal Improvement Act, no 62 of 1998 (Government Gazette, 2019), and the classification of certain game animals on privately owned land as livestock, enabled ranchers to manage game animals similarly to domestic livestock. This amendment highlighted the importance of understanding carrying capacity and its use as a management tool in animal and veld management, ensuring sustainable use of the natural resources.

In terms of nutritional wellbeing of game and livestock species, it is important to have guidelines to determining their energy and other nutrient requirements. From the comparative nutrition perspective, research on cattle and other domestic livestock has shown that if the weight of the animal, dry matter intake (DMI) and digestibility of the feed are known, it is possible to assess whether the available feed will supply sufficient nutrients for the animal's physiological production stage. For example, to keep a 550 kg domestic beef cow in her first month of lactation in positive energy balance, she would need to consume 12.1 kg feed with a total digestible nutrient content of 60%. This feed would supply approximately 112.28 MJ ME per day. A 550 kg dry cow eating 11.1 kg of the same diet would consume 103.00 MJ ME. Thus, the cow in the first month of lactation would require 9.28 MJ more metabolizable energy per day (NRC, 2016). This highlights that game ranchers could use similar information to improve animal production and veld management if the energy requirements for various physiological stages can be estimated for game.

To simplify the prediction of energy requirements of grazing and browsing game species, the authors scrutinized the work of Meissner (1982) for common denominators that could be used to develop a mathematical model to calculate the energy requirements for ungulate species not included in the article. Thus, the aim of this article was to ascertain whether metabolic weight could be incorporated in a mathematical model to determine the energy requirements and DMI of the sable antelope (Hippotragus niger) and other ungulate species at their own physiological production stages and in terms of their feeding habits. These calculations could be used to re-evaluate the GU and BU methods (Van Rooyen & Bothma, 2016), resulting in improved carrying capacity and better stocking rate estimates on game reserves and ranches.

 

Material and Methods

This study involved only mathematical modelling, and approval from an institutional animal care and use committee was not necessary. Its main objective was to ascertain whether metabolic weight could be used to determine the ME requirements of game. Metabolizable energy in megajoules per day (MJ ME/day) was regressed on weight in kilograms with a log-log transformation for herbivores in the first three columns of Table 5 of the appendix (Meissner, 1982). These regressions were used to ascertain the efficacy of the LAU method (Van Rooyen & Bothma, 2016) for determining the ME requirements of game. The physiological production stages incorporated in the analyses included calf/lamb, young dry cow/ewe, mature dry cow/ewe, young cow/ewe with calf/lamb, mature cow/ewe with calf/lamb, young bull/ram, and mature bull/ram. The log-transformed data are shown in Table 1. The predicted values for ME intake and LSU from the regression equations were compared with published values from Meissner (1982). Sable antelope (Hippotragus niger) weights for the various categories were entered into the model to obtain predictions of ME consumed per day, making it possible to calculate DMI. Finally, the results were compared with those of the grazing and browsing unit method of Van Rooyen & Bothma (2016).

 

Results and Discussion

Could metabolic weight alone be used to determine the ME requirements for game? The results in Table 2 represent the inter-species equations for wildlife species from the springbok (Antidorcas marsupialis) to the elephant (Loxodonta africana). This diverse group of herbivores was used to determine whether the b-value of the allometric equation (ME = aW^b) would differ significantly from 0.75. To explain the rationale, ME requirements and weight (W) are believed to be allometrically (ME = aW^b ) related (Brody, 1945; Kleiber, 1961). The assumption is that if the value of 'b' is approximately equal to 0.75, then the LAU method is correct and equivalent to the LSU value presented in Meissner (2020). Alternatively, if the null hypothesis (b =0.75) is rejected, then the LAU values based on metabolic weight do not correspond to the LSU values and should not be used in their stead. The results (Table 2) indicated that b-values for the calf/lamb, mature dry female, mature female with offspring, and mature male did not differ significantly from the expected value of 0.75. However, the b-values for the young non-lactating (dry) female, young female with offspring, and young male were all significantly greater than the hypothesized value. In the NRC (2007, 2016) the equation ME = aW^0.75 is used to calculate the ME that is required for maintenance. Each of the physiological stages for which the b-value exceeded 0.75 have recognized energetic requirements for production beyond maintenance. These results indicated that metabolic weight might not provide sufficient information to calculate the energy requirements for game species that are growing or lactating.

The predicted ME (MJ/day) values were compared with the published data (Meissner, 1982) and the results for the largest and smallest species are shown in Table 3. Results for the remaining 11 species are shown in Supplementary Tables S1-S11. The present results for energy requirements and large stock units differ from those of Meissner (1982) as a result of a scaling effect, being consistently greater across all of the species and physiological states. Could the newly developed equations be used to estimate the ME requirements for sable antelope (Hippotragus niger) as an example of animals not found in Meissner (1982)? Table 3 and Supplementary Tables 1 -11 illustrate applicability of the allometric equation across a diverse collection of species indicating its generality.

Table 4 shows the general equations that are proposed for these physiological states, regardless of species, and an example of their application for the sable antelope (Hippotragus niger). For example, in terms of the mature lactating female and using the bodyweights for sable antelope from Bothma et al. (2016) the ME required could be estimated:

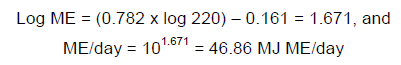
Finally if an LSU is equivalent to 75 MJ ME, then the value for this animal is 0.63.

Could DMI be calculated using selected forage? As Meissner (1982) stated, it is possible to estimate DMI from ME in MJ/day if the weight of the animal, forage digestibility, DE content of the forage and calculated ME value in MJ/day are known. Sable antelope graze and browse in various proportions, usually 85% graze and 15% browse (Van Rooyen & Bothma, 2016). Assuming the grass has an energy digestibility of 50% and the browse an energy digestibility of 55%, the weighted average digestibility is 0.51 (0.85*0.50 + 0.15*0.55 = 0.51). By using digestibility values in this calculation that reflect average to poor quality veld, the possibility of overestimating intake can be avoided. An example of the calculations that are necessary to calculate DMI as a percentage of bodyweight is shown here.

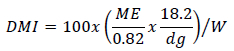
where: the constants 0.82 and 18.2 represent the fraction of digestible energy that can be metabolized (ARC, 1965) and the average gross energy value of roughage, respectively, and = metabolizable energy intake per day, dg = digestibility of the diet consumed, and W = bodyweight of the animal. Predictions of DMI as a percentage of bodyweight for sable antelope are shown in Table 5.

How do these predictions compare with those derived from the GU and BU concepts, which consider what animals select naturally, and derive values relative to their metabolic weight. Metabolizable energy is the base line for these calculations. However, these methods reflect an animal only at or near maintenance and do not consider the physiological stage of production. The predicted intake of 220 kg for a mature sable antelope cow raising offspring was 46.86 MJ ME per day, whereas a mature non-lactating cow of the same bodyweight required 36.21 MJ ME per day. The latter value reflected the prediction of her ME intake under the GU and Bu concepts, which underestimate the intake of the mature lactating female by about 29% (46.86/36.21 *1.29). Taking a 180 kg animal at maintenance as representing one grazing unit, the calculated grazing units for sable antelope in various physiological stages are shown in Table 6. The mature non-lactating cow and the mature bull represent animals at approximately maintenance. The mature cow with calf compared with the mature cow that was not lactating represented he increment in energy required for lactation. Finally, comparing young animals with their mature counterparts at the same bodyweights reflected the increment in energy that was required for growth.

Carrying capacity represents the number of animals of a particular species for which a given area of veld can provide feed (Grossman et al.., 1999) and may be described broadly as a function of veld or pasture management, which includes the effects of trampling, water point distribution, amount and availability of palatable and nutritious plant species, inter-species competition, animal behaviour, rainfall, and fire regime (Meissner, 1982; Grossman et al.., 1999). Rangeland scientists calculate carrying capacity by focusing on livestock, where the physiological production stages are considered, whereas ecologists evaluate the carrying capacity of a game reserve in terms of an average game animal at maintenance. Managers of game and livestock use estimates of carrying capacity to determine when supplementary feedstuffs need to be provided.

The forage intake by an herbivore is related to its energy needs and the ability to fulfil its nutrient requirements from the available forage (Meissner, 1982). In practice, there seems to be movement away from keeping animals on large fenced tracts of land such as game reserves towards raising game species in ways that are more similar to ranching livestock (Oberem & Oberem, 2016). This more intensive management of game species necessitates additional managerial interventions such as strategic feeding of balanced rations. The present study documented the need to consider the physiological stage of an animal when formulating these interventions to avoid underestimation of its energy requirements. The use of a single allometric equation to predict energy required by a population of herbivores would undoubtedly be inadequate for this reason, yet the LAU, AU, GU and BU approaches rely on this assumption. Yet these methods have been used widely on ranches that breed game intensively (Van Rooyen & Bothma, 2016).

Energy consumption or requirement is a function of metabolic weight, expressed as kg⁰⁷⁵ rather than as linear function of bodyweight (Mentis, 1977). These relationships were investigated in detail (e.g., Brody, 1945; Kleiber, 1961; Schmidt-Nielsen, 1972; Heusner, 1982; Hayssen & Lacy, 1985) by researchers who provided evidence that bodyweight was not an accurate basis for comparison. A better method would be to express animal size in terms of energy requirements, in which a less commonly studied animal (wild ungulate) is compared with a well-studied one (domestic livestock), using the common denominator of metabolic weight to calculate energy requirements (Mentis & Duke, 1976; Mentis, 1977). When this approach is used, it is assumed that differences are proportional only to a particular exponent, that is, the animal's bodyweight to the power of 0.75. This inferred that feed consumption per unit of metabolic weight would be the same for all animals at the same physiological production stage.

When the allometric relationships of ME required were estimated for lactating and growing animals, the b-values (exponents) applied to bodyweight were greater than 0.75 (Bothma & Du Toit, 2014) in the formulation of LAU. Thus, the LAU and LSU concepts were not equivalent. Other comparable published research used 'field metabolic rate', which measures the total energy expenditure of the animal when all basic energy costs are accounted for (Costa & Maresh, 2018). Field metabolic rate is calculated as the basal metabolic rate (Heusner, 1982; Hayssen & Lacy, 1985) multiplied by 1.35 for low activity animals and by 1.85 for medium activity animals (Karasov, 1992). The average of the low and medium activity values compares well with maintenance energy requirements for animals of similar weight in Meissner (1982) and NRC (2007). Similar procedures were used to estimate energy requirements for a wide group of species in feed formulation software (Zootrition© 2.7 Software, St. Louis, USA) (Dierenfeld, 2021; personal communication).

Complications in the application of these predictions could be expected for several reasons, namely i) animals are gregarious, but are not at a uniform physiological stage at any point, ii) for predictions that rely on bodyweight, random variation in the recorded weight values and measurement errors must be acknowledged, and iii) because required ME is not a linear function of bodyweight, the use of average bodyweight for a group of animals that vary in weight might be misleading.

In practice the DMI of game species is almost always unknown. Feed intake is usually expressed on a dry matter basis as a percentage of bodyweight. If the ME required for a particular animal at a specific weight is known, it is possible to calculate the DMI as a percentage of bodyweight t. However, direct measurement of DMI and the proximate analysis of the diet being consumed would obviously be preferred. Also it would be desirable to measure directly the requirements for pregnancy and lactation of game species.

 

Conclusions

Methodologies that are currently used to determine the carrying capacity of various wildlife species appear inadequate. Approaches that include the particular physiological stage appear more desirable. The calculated values for required ME and LSU in this study would enable game reserves and ranches to estimate carrying capacity more accurately. This methodology could contribute to more nearly sustainable animal production systems and veld management through improved carrying-capacity estimates.

 

Acknowledgements

The authors would like to thank G. Jordaan for helping with the statistical analysis in this article. Second, the authors thank L.D. van Esson for his ecological contributions.

Authors' contributions

CAS drafted and wrote the manuscript and asked how the animal component could be simplified in determining carrying capacity. HHM guided the statistical analysis, and suggested the methods. BVZ, PCL and LCH assisted in supervising and editing the manuscript.

Conflict of interest declaration

The authors declare there is no conflict of interests regarding the publication of the manuscript.

 

References

ARC, 1965. The nutrient requirements of farm livestock. 2nd ed. Agricultural Research Council, London        [ Links ]

Bothma, Du P.J. (editor), 2002. Game Ranch Management (4th edition). Van Schaik, Pretoria, South Africa.         [ Links ]

Bothma, Du P.J., Van Rooyen, N. & Du Toit, J.G., 2016. Antelope and other smaller herbivores. In J. du P Bothma & J.G. du Toit (editors). Game ranch management. 6th edition. Pp. 194-231. Van Schaik, Pretoria, South Africa        [ Links ]

Brody, S., 1945. Bioenergetics and growth. Reinhold, New York, USA.         [ Links ]

Costa, D.P. & Maresh, J.L., 2018. Energetics. In: B. Wursig, J.G.M. Thewissen, & K.M. Kovacs (eds). Encyclopedia of marine mammals. 3rd edition. Pp. 329-335. Academic Press, Washington DC. https://www.elsevier.com/books/encyclopedia-of-marine-mammals/wursig/978-0-12-804327-1        [ Links ]

Grossman, D., Holden, P.L. & Collinson, R.F.H., 1999. Veld management on a game ranch. In: N.M. Tainton (ed). Veld management in South Africa. Pp. 261-279). University of Natal Press, Pietermaritzburg, South Africa.         [ Links ]

Hayssen, V., & Lacy, R.C., 1985. Basal metabolic rates in mammals: Taxonomic differences in the allometry of BMR and body mass. Comparative Biochemistry and Physiology Part A: Physiology 81(4), 741-754.         [ Links ]

Heusner, A.A., 1982. Energy metabolism and body size I. Is the 0.75 mass exponent of Kleiber's equation a statistical artifact? Respiration Physiology 48(1), 1-12. https://doi.org/10.1016/0034-5687(82)90046-9        [ Links ]

Karasov, W.H., 1992. Daily energy expenditure and the cost of activity in mammals. Integrative and Comparative Biology 32(2), 238-248. https://doi.org/10.1093/icb/32.2.238        [ Links ]

Kleiber, M., 1961. The fire of life: An introduction to animal energetics. John Wiley, New York, USA.         [ Links ]

Meissner, H.H., 1982. Theory and application of a method to calculate forage intake of wild southern African ungulates for purposes of estimating carrying capacity. South African Journal of Wildlife Research 12(2), 41 -47. http://www.csa.com/partners/viewrecord.php?requester=gs&collection=ENV&recid=263358

Mentis, M.T., 1977. Stocking rates and carrying capacities for ungulates on African rangelands. South African Journal of Wildlife Research 7(2), 89-98.         [ Links ]

Mentis, M.T. & Duke, R.R., 1976. Carrying capacities of natural veld in Natal for large herbivores. South African Journal of Wildlife Research 6(2), 65-74.         [ Links ]

NRC, 2007. Nutrient requirements of small ruminants. 8th edition. National Academies Press. Washington DC, USA. https://doi.org/10.17226/11654        [ Links ]

NRC, 2016. Nutrient requirements of beef cattle. 8th edition. National Academies Press. Washington DC, USA. https://doi.org/10.17226/19014        [ Links ]

Oberem, P. & Oberem, P.T., 2016. The new game rancher. 1st edition. Briza, Pretoria, South Africa        [ Links ]

Peel, M., Pauw, J.C. & Snyman, D.D., 1994. The concept of grazer and browser animal units for African savanna areas. Bulletin of the Grassland Society of Southern Africa 5, 61        [ Links ]

Scarnecchia, D.L., 1985. The animal-unit and animal-unit-equivalent concepts in range science. Journal of Range Management 38(4), 346-349.         [ Links ]

Schmidt-Nielsen, K., 1972. How animals work. Cambridge University Press, Cambridge, United Kingdom        [ Links ]

Van Rooyen, N. & Bothma, Du P.J., 2016. Veld management. In: J. du P Bothma & J. G. du Toit (eds). Game ranch management. 6th edition. Pp. 808-872. Van Schaik, Pretoria, South Africa.         [ Links ]

 

 

Submitted 31 May 2021
Accepted 5 March 2022
Published 12 June 2022

 

 

# Corresponding author: craig.shepstone@gmail.com

 

 

Supplementary Data

The supplementary data is available in pdf: [Supplementary data]