Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Animal Science
versão On-line ISSN 2221-4062
versão impressa ISSN 0375-1589
S. Afr. j. anim. sci. vol.52 no.3 Pretoria 2022
http://dx.doi.org/10.4314/sajas.v52i3.5
Predicting feed intake from weaning to maturity in South African sheep reared on high-energy grain-based diets
D.A. van der MerweI; T.S. BrandI, II, #; P.G. TheronI; L.C. HoffmanI, III
IDepartment of Animal Sciences, Stellenbosch University, Private Bag X1, Matieland, 7602, South Africa
IIDirectorate: Animal Sciences, Department of Agriculture, Western Cape Government, Private Bag X1, Elsenburg, 7607, South Africa
IIIThe University of Queensland, Health and Food Sciences, Precinct, Level 0, Block 10, 39 Kessels Rd, Coopers Plains, 4108, Australia
ABSTRACT
Feed intake models seldom take breed differences into account. This study investigated various approaches to describing and predicting the feed intake of certain breeds (Dohne Merino, Dormer, Dorper, Meatmaster, Merino, South African Mutton Merino (SAMM) and White Dorper). On weaning at 90 days old, four ram and four ewe lambs from each breed were housed under feedlot conditions and reared on a high-energy concentrate-based diet until they reached maturity at about 12 months. Bodyweight and feed intake were recorded weekly. Daily dry matter intake was modelled with bodyweight for each breed using a quadratic function. Feed intake increased to a peak and then tended to decrease as lambs neared maturity. Dormer lambs had the highest peak intake (2202.02 g/day) and Merinos the lowest (1558.8 g/day). However, this model accounted for less than 50% of the variation in the groups. Linear regressions of percentage intake of bodyweight (R2 = 0.732) and cumulative feed intake with bodyweight (R = 0.941) were deemed more reliable in predicting voluntary feed intake. The change in feed conversion ratio was modelled with an exponential relationship. At 75 kg live weight, Dormer rams had the highest feed conversion ratio (20.44) and SAMM rams the lowest (6.48). Generally, lambs with larger frame sizes (Dormer, Dorper and SAMM) presented higher feed intakes at a given bodyweight than smaller-framed breeds. Dorper rams and SAMM lambs proved to have better lifetime feed efficiency than the earlier maturing breeds.
Keywords: breeds, dry matter intake, feed efficiency, percentage intake
Introduction
In livestock production, the level of feed intake and the utilization of feed influence the productive performance of an animal. Voluntary feed intake (VFI) in growing animals provides the organism with the nutrients for tissue growth and development according to its genetic potential if nutrient requirements are met. In a sheep feedlot operation, the goal is to add value to the conformation and size of the lamb by subjecting the animal to an intensive feeding regime that would accelerate growth to obtain a more desirable carcass. Although growth is dependent on the amount of feed that the lamb consumes, intake varies with the physical size of the animal, along with changes in maintenance requirements (Finlayson et al., 1995). In a precision sheep feedlot or finishing system it is important to be able to predict the change in VFI with the change in bodyweight of the growing lamb to determine the amount of feed required to rear the lamb to a desired slaughter weight. It is also necessary to adjust the nutrient composition in relation to the level of VFI to meet the requirements of growing lambs. Aside from the cost of purchasing weaner lambs, the nutritional outlay to rear lambs is a major operational expenditure, which influences the profitability of the system directly. It is therefore important to be able to predict VFI to ensure sustainable management for profitable production.
Multiple models have been formulated to predict intake (Thompson & Parks, 1983; Cannas et al., 2004; Vieira et al., 2013). The inputs of these models varied depending on the situation or production system for which the model was specified. The prediction and regulation of feed intake is complex, because it is influenced by animal factors, feed composition, bulkiness, passage rate and environmental elements such as photoperiod and ambient temperature (Ingvartsen, 1994; Allen, 1996; Pulina et al., 2013). Many of these factors were incorporated in these models, depending on the design and purpose. One of the main drivers included under the animal factors of an intake model was the influence of live weight on VFI. Emmans (1997) stated that the first step in modelling intake in growing animals was to predict intake as a function of live weight. From there, additional factors could be included in the model to improve its fit and application (Vieira et al., 2013). Although the National Research Council (NRC, 2007) provided models to predict VFI for growing sheep, they were based on an approach in which a standard reference size weight was used to account for maturity, and thus similar predictions were provided for breeds of different maturity types. The breed was seldom accounted for (Ingvartsen, 1994) and therefore the use of bodyweight as a predictor of VFI was confounded by the degree of maturity of the animal. Earlier models to predict intake did not include South African sheep breeds. It was thus postulated that because breeds varied in mature bodyweight and maturation rate, the parameters to predict the intake characteristics of the breeds would also vary.
The aim of this study was to develop and fit models that could be used to predict feed intake characteristics from weaning up to mature bodyweight of feedlot-reared ram and ewe lambs of various sheep breeds that differed in terms of growth and maturity.
Materials and Methods
The protocol for this study was approved by the Departmental Ethical Committee for Research on Animals (DECRA R14/110), Western Cape Department of Agriculture. Lambs (four rams and four ewes) from seven breeds were weaned at about 90 days old (average weight of 30.4 kg ± 4.03) and housed under feedlot conditions on Elsenburg Research Farm. These seven breeds were selected as the most popular in South African commercial lamb production systems and consisted of Dohne Merino, Dormer, Dorper, Meatmaster, Merino, South African Mutton Merino (SAMM) and White Dorper. The lambs were obtained from stud flocks to be representative of the breeds in terms of good growth performance. Owing to spatial restrictions in the housing facility, four ram lambs and four ewe lambs per breed were used to investigate intake trends in growing lambs from weaning to one year old, when the lambs were assumed to have attained their mature bodyweight and the growth curve had reached the plateau phase. Live weights of the animals at this time are given in Table 1.
On weaning, the lambs were drenched and vaccinated with a broad-spectrum vaccine against Clostridia and Pasteurella bacterial infections and assigned to individual pens (1 m x 2 m) in the housing facility. The lambs were gradually adapted to the concentrate feedlot diet from an oat hay-based roughage ration using a step-up programme over a seven-day period. After adaptation, lambs were supplied the feedlot diet (Table 2) ad libitum, and the troughs was replenished twice a day. For each lamb, 7 kg of feed was weighed into a bag at the start of the week and used to replenish the feed troughs. As the bags were emptied, they were refilled with 7 kg of feed. Troughs were managed to ensure that at least 100 g of feed was available before replenishing. At the end of the week, the orts in the troughs and the feed remaining in the bags were weighed to determine intake. The feedlot diet in this study resembled a high-energy commercial lamb finisher concentrate, formulated according to specifications for optimal growth rates (300400 g/day) (National Research Council, 2007). The feed was pelleted through an 8.8 mm diameter sieve, and the length of the pellets supplied was about 25 mm. Water was freely available.
The lambs were weighed at the same time each week in the morning before feeding. Weekly feed refusals were also weighed then to determine feed intake. The refusals were subtracted from the amount of feed supplied and divided by the number of days to give daily feed intake on a dry matter basis (DMI). Feed samples and refusal samples were oven dried at 100 °C for 24 hours to determine dry matter content. The DMI was also expressed as a percentage of the bodyweight of the lambs of the previous week to give the percentage intake (PI). The cumulative feed intake (CFI) was also calculated over the study period. The relative feed conversion ratio (FCR) was also calculated by dividing the DMI by the average daily gain (ADG) at that bodyweight. The ADG was determined by differentiating the Gompertz growth curve: fitted to the cumulative bodyweights of the individual lambs to determine the growth rate:
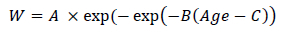
fitted to the cumulative bodyweights of the individual lambs to determine the growth rate. In this growth curve W refers to weight, A represents the asymptotic mature weight, B is the proportion of mature weight to be gained after birth, and C is the age at the inflection point.
Growth and feed intake data were analysed statistically with SAS Enterprise Guide (SAS, 2006). Data points deviating more than three standard deviations from the mean trends of the dataset were considered outliers and removed from the dataset. Polynomial or linear trends in the data were subsequently identified from the adjusted dataset. A quadratic polynomial function was fitted to describe the relationship between DMI and bodyweight of the individual lambs using the PROC NLIN function of SAS. Iteration of the parameter estimates was performed using the Gauss-Newton method. Similarly, the exponential function was fitted to describe the relationship between FCR and bodyweight using the same procedure. To obtain the ADG to calculate FCR, the Gompertz function was fitted to the growth curves of each individual by the PROC NLIN function. The parameter estimates were then obtained for each individual and the function differentiated to obtain the growth rate at weight W. Linear regressions were performed to describe the relationships of cumulative feed intake and PI with bodyweight using PROC REG of SAS. The parameter values of these regression models were compared between the main effects of breed and sex and the interaction between these effects, using the general linear model procedure (PROC GLM) of SAS. The parameter values were then expressed as least square means with accompanying standard errors. Means were compared using the Bonferroni test, identifying statistical differences at the 5% (P <0.05) and tendencies at the 10% (P <0.10) levels.
Results and Discussion
In this study, the DMI of each of the groups increased with bodyweight of the lambs in a curvilinear fashion. Therefore, a quadratic polynomial function was deemed most appropriate in describing this bell-shaped trend, and was fitted to the individual curves presented by the animals. The model parameters or coefficients were compared to demonstrate differences between breed and sex (Table 3). No differences were observed between ewes and rams for any of the model parameters (P >0.05), although there was a tendency for ewes to have lower A parameter estimates than rams (-0.696 and -0.531) (P <0.10). Dohne Merino and Meatmaster lambs displayed the highest estimates for the A (-0.371 and -0.409, ) and C (546.11 and 316.23, ) parameters, whereas the lowest estimates were obtained by the White Dorper lambs (-0.964 and -1374.66 for the A and C parameters ). Conversely, the opposite trend was observed with the B parameter. The lowest B parameter estimates were obtained by the Dohne Merino (42.163) and Meatmaster (48.938) breeds, whereas the White Dorper group obtained the highest estimate of 112.012 (P <0.05). The parameter values of the Dormer, Dorper, Merino and SAMM breeds did not differ from those of any of the other breeds for A, B or C parameter estimates of the quadratic function describing the change in DMI with bodyweight. The estimated quadratic curves for the various breeds were also plotted (Figure 1).
Separate regression equations are presented for the groups (Table 4), although significant interactions were not observed between breed and sex for the quadratic relationship of DMI and bodyweight, Although these models described the general pattern that DMI follows with an increase in bodyweight, the quadratic effects accounted for only a small portion of the variation in the traits. The highest R2 value was observed for the model describing DMI of Dormer ewes, whereas the lowest values were found for Merino ewes and rams, and White Dorper rams. With less than 50% of the variation between actual and predicted values being described by these models, it could be concluded that DMI cannot be predicted reliably from bodyweight of growing lambs using the quadratic function.
The regressions of daily VFI, expressed as a percentage of bodyweight, on bodyweight of the growing lambs are summarized in Tables 5 and 6. Percentage intake decreased linearly with bodyweight. The parameter estimates of the linear equations were compared to evaluate the main effects of sex and breed (Table 5). Interactions were not observed between the main effects and either the slope or intercept of the linear regression of PI on bodyweight. Neither sex nor breed influenced the A parameter (P >0.05), giving an average value of 6.082 for the intercept of the regression equation, although a tendency was observed for the intercept of Dormer lambs to be higher than that of Merino lambs (6.835 vs. 5.434) (P <0.10). The slope was negative for all production groups and was 19% lower for rams than for ewes (P <0.05). The slope for the change of PI with bodyweight did not vary between breeds (P >0.05) with an average value of -0.0499.
Separate equations are presented for the various production groups to predict PI for the specific group (Table 6), although interactions were not observed for the parameter estimates of the linear regression of PI with bodyweight. The R2 values showed that more than 50% of the variation of the data in the production groups was accounted for by the linear models. The R2 values were generally high, with the exception of the Dorper and Merino rams (R2 <0.600), whereas the highest value was realised by the model describing PI in Dohne Merino rams (R2 =0.878).
Cumulative feed intake increased linearly with the rise in bodyweight (Table 7). Significant interactions were not observed between breed or sex and the intercept of the curve A (P >0.05), although , the effect of breed influenced the magnitude of the A parameter (P =0.03), with the Dormer and Merino breeds presenting higher values than the Dohne Merino and Dorper. The intercept for the SAMM and Meatmaster breeds did not differ from the other breeds (P >0.05), whereas it was lower for Dormer lambs than for White Dorper lambs (P <0.05), and did not differ from Dohne Merino and Dorper (P >0.05). The slope of the regression (B parameter) was lower for SAMM rams compared with Dohne Merino, Meatmaster and White Dorper ewes and rams and for Dormer, Dorper, Merino and SAMM ewes. On the other hand, the slope of the equations for Dormer, Dorper and Merino rams did not differ from the other groups (P >0.05) with an average value of 6.8. The coefficients of determination for the models of these groups were quite high, indicating that bodyweight explained more than 87% of the variation CFI.
An exponential function was used to model the change in FCR with bodyweight of the lambs, with varying levels of accuracy (Table 8). The curves for the increase in FCR are depicted in Figure 2 for ram and ewe lambs. The highest R2 value was obtained by the model to predict FCR of Merino ram lambs. However, the Dormer groups, Dorper ewes and Merino ewes presented R-squares with less than 50% of the variation being accounted for by these models. An interaction (P <0.05) was observed between breed and sex for the A parameter of the model, with the parameter estimate of Dohne rams (2.883) being significantly greater than that of SAMM ewes (0.892) (P <0.05), whereas the other groups did not differ (P >0.05). Although no significant interactions were observed between breed and sex for the B parameter, ewes had higher B values than their male counterparts (P =0.045). The effect of breed did not significantly influence the magnitude of the B parameter estimates of the exponential models to predict FCR from bodyweight of the lambs.
Sheep and goats consume feed to satisfy their nutritional requirements for maintenance as a first priority (Faverdin, 1999; Illius et al., 2000; Brand et al., 2017). The main factors influencing the potential level of feed intake are related to body size of the animal, and its physiological status, which determine its maintenance requirements (Tolkamp et al., 2006; Zereu, 2016). Cannas et al., (2004) took bodyweight and production level of sheep into account in models to predict the level of intake. On low-energy high roughage-based diets the physical form and bulk density of the feed becomes a strong limiting factor, which influences the passage rate and the amount of feed consumed (Allen, 1996).
The size of the animal determines the capacity for feed consumption and the maintenance requirements for body tissues. As lambs grow, increasing amounts of energy are required for protein and fat tissue growth until a point is reached at which the maintenance requirements exceed the growth requirements (Johnson et al., 2012). Daily feed intake of the lambs in this study increased before peaking in a curvilinear fashion relative to bodyweight for all breed groups during the study (Tables 2 and 3). A quadratic function was found to represent this relationship between DMI and bodyweight accurately. This function was characterised by an initial increase in DMI until a maximum was reached, after which there was an apparent decrease in DMI with further increase in bodyweight. The intake of Suffolk sheep was modelled with the same function (Lewis & Emmans 2010). In addition, Ministry of Agriculture, Fisheries and Food (1975) proposed a simple quadratic function to predict DMI from bodyweight for growing cattle. Cannas et al. (2004), however, used a linear representation incorporating metabolic bodyweight and growth rate to predict the intake of growing lambs. Using factor analysis, the inclusion of growth rate in addition to bodyweight did not provide any significant improvement to DMI prediction models. Thus growth rate was thus not incorporated in the models to predict DMI. This approach may be bordering on a mechanistic model describing the growth of tissues, whereas the aim of this study was to present a simple empirical model to predict feed intake from bodyweight.
With the quadratic relationship between DMI and bodyweight, the initial increase in feed intake can be ascribed to the lambs increasing their level of feed intake to meet their metabolic requirements for growth, as their bodies grow in size and mass. It would be expected that a maximum DMI would be reached as the lambs neared maturity, which would then plateau. However, in this study DMI decreased after attaining a maximum, which may be the result of increased fat deposition in the growing lambs. Johnson et al. (2012) stated that there was a high variation in intake as a ruminant neared maturity, which might be accompanied by fat loss. It is hypothesised that increased fat deposition in the abdominal cavity of lambs caused physical restrictions, displacing rumen contents and slowing down passage rate and intake (Forbes, 2007). Another possible effect of increased fat deposition is that it is expected to amplify plasma leptin levels from adipose tissue suppressing hunger feedback systems. An increase in plasma leptin concentrations was associated with a suppression of appetite and reduced feed intake (Marie et al., 2001). The provision of a high energy diet in the feedlot along with reduced movement might lead to high levels of fat deposition in lambs as they became heavier, which could result in higher levels of leptin being released from adipose tissue.
The quadratic model for predicting the absolute DMI from bodyweight of lambs accounted for only a small portion of the variation of the trait in the groups (<46%). More factors should be incorporated in the model to improve its accuracy of fit. Tolkamp et al., (2006) also described the curvilinear relationship between intake and bodyweight, and stated that bodyweight alone was insufficient to account for the variation in feed intake. Feed factors that are easy to quantify and detect could be incorporated into the model as variables along with environmental factors to improve the accuracy of prediction (Blaxter et al., 1966; Pulina et al., 2013). The number of animals included in the study should be increased to give a better representation of within breed variation. Although the addition of these mechanisms improved the accuracy of prediction and understanding of the results, the models will still be heavily dependent on the empirical relationship of the change in intake with bodyweight (Illius et al., 2000).
Expressing intake as a percentage of bodyweight and regressing against bodyweights of the lambs improved the accuracy of prediction, with 53-87% of the variation being accounted for (Table 6). Percentage intake decreases in relation to bodyweight and is accepted to decrease from 4% to 3% as lambs grow from 30 kg to 80 kg bodyweight, provided that the growth rate remained constant (nrc, 2007). The linear decline in PI occurred at a similar rate for all of the breeds in this study with intakes predicted to range from 4% to 5% in lambs weighing 30 kg and dropping to 2-3% in lambs weighing about 70 kg. Cumulative feed intake was also expressed linearly in relation to the increase in bodyweights of the lambs over the study period with high accuracies (R2 >0.87). The slope of the regression also represented the average FCR of the lambs over the rearing period. Because lambs are often introduced to the rearing conditions at various ages and bodyweights and reared for different periods, the points at which the curve intercept the axes should vary between production systems. The factors by which the cumulative feed intake increases with bodyweights were then expected to remain constant for the production groups. Thus, the model for cumulative feed intake must be adjusted for the starting weight of the production system, though the relative proportion by which it increased with bodyweight would remain constant. This can be achieved easily without correction between breeds, because of the lack of differences between the intercepts of the groups. Although these models to predict PI from bodyweight and cumulative intake give a better prediction of feed intake than the proposed quadratic model, the prediction results still have to be converted back to DMI. This may be complicated when using cumulative feed intake, as growth rate needs to be taken into account. In addition there may be other factors affecting intake and feed digestibility that should be taken into account when applying these models when feeding different levels of grain.
The absolute amount of feed required to gain a unit of bodyweight at regular intervals presents a large amount of variation within an individual animal with no clear pattern. Therefore, FCR must be considered over specific rearing periods (weight intervals) or determined in relation to the sigmoidal growth curve rather than the absolute growth rate. In this study, the growth rates were determined as the slopes of the Gompertz growth curves of the individual lambs (Emmans, 1989) and FCR was expressed as feed intake as a proportion of this growth rate at that bodyweight. An exponential relationship could then be observed between FCR and bodyweight (Table 8). These models depicted an increase in FCR, indicating bodyweights at which it became unfeasible to rear lambs in a finishing system. These points of inflection were often expected to relate to the level of fat deposition in lambs, as fat tissue growth increased as the lamb grew, increasing the amount of energy per unit bodyweight gain (Johnson et al., 2012).
Differentiating the quadratic functions of the seven breeds revealed the peak feed intakes predicted by the curves. Dormers had the highest estimated peak intakes of 2203 g/day at a weight of 61.3 kg, followed by Dorper (2007 g/day, 63.8 kg), SAMM (1958 g/day, 72.0 kg), White Dorper (1879 g/day, 58.1 kg), Meatmaster (1780 g/day, 59.8 kg), Dohne Merino (1744 g/day, 56.8 kg) and Merino (1560 g/day, 58.6 kg) (Figure 1). On average, the peak intakes of ewes was 13.4% lower than that of rams, which were attained at 16.2% lower bodyweights. These trends in DMI resemble the intake trends calculated by Meissner et al. (1983) for South African wool, dual-purpose and Dorper lambs, although the peak intakes of rams in the current study were estimated to be 4.5% higher for wool sheep (Merino), 28.1% higher for dual-purpose sheep (SAMM) and 10.6% higher for the Dorpers. It is expected that breeds with larger body conformations such as the Dormer, SAMM and Dorper would consume larger quantities of feed because of their greater metabolic demand than the smaller framed and wool breeds. Trends in the current study mimicked those of Meissner et al. (1983), in which intakes were calculated using the energy requirements of the various breeds, although these values were lower than those demonstrated in the present study. [?]
More of the variation in the data can be explained by describing VFI in terms of PI than by using the quadratic polynomial function for DMI, meaning more accurate predictions of VFI can be made. Lewis & Emmans (2010) described the use of a standardised intake to express intake as a proportion of bodyweight relative to the degree of maturity. When VFI was presented as a percentage of bodyweight, the linear decline in percentage intake with an increase in bodyweight occurred at a similar rate for all breeds (0.05% per kg bodyweight). The intercept values of the regressions approached significance, indicating that Dormer lambs had the highest PI, whereas Merino lambs tended to have the lowest PI. This can again be ascribed to the larger body size and greater proportion of metabolic tissue of Dormer sheep, which have been bred for enhanced meat production traits compared with the smaller frame size of the wool producing Merino sheep (Cloete et al., 2003).
The slopes of the cumulative intake curves indicate that SAMM rams were more efficient in converting feed into body growth over the study period by obtaining the lowest regression slope. Figure 2 illustrates that at a given bodyweight SAMM lambs generally presented the lowest FCR values. The FCR curves of ewe lambs (Figure 2) generally increased at a greater rate than that of ram lambs, because ewes start to deposit fat at lower live weights than rams, thus increasing their metabolic requirements and reducing the efficiency of feed utilization for growth (Owens et al., 1993). The Dormer showed higher rates of FCR increase with bodyweight, again owing to higher levels of fat deposition. Alternatively, the SAMM is later maturing and therefore had lower levels of fat deposition and exhibited better feed efficiency (Cloete et al., 2004). The Dorper, an early maturing breed, was expected to show a relatively sharp increase in FCR with bodyweight. However, the curve for Dorper rams followed a similar trend to SAMM rams, indicating high feed efficiency. Figure shows that the trends of the DMI curves for Dorper and SAMM resemble each other closely. Because Dorper rams maintained high growth rates and similar intakes to SAMM during this study, they showed similar trends in feed efficiency, although the Dorper is known to deposit fat at an earlier age. The FCR of Merino ewes mimicked the trend of Dormer ewes (Figure 2), which was possibly because of the lower growth rates exhibited by Merino ewes relative to other breeds (Van der Merwe et al., 2019).
Because of the variation in the level of feed intake, and feeding efficiency, of the seven breeds and sexes at the same bodyweights, separate models are required to predict feed intake trends of the groups (Tables 3, 5, 6 and 7). The necessity for these models can be attributed mainly to the diversity in frame size, maturity type, growth rate and production potential for meat or wool of the breeds. The same model can only be used for breeds with different mature weights if DMI is similar at the same bodyweight (Lewis & Emmans, 2010). Figure 1 shows that the trends up to 55 kg bodyweight of Dorper, SAMM and White Dorper were similar, whereas the intakes of Meatmaster and Dohne lambs were similar to each other, but distinct from the former groups. This study defined the changes in feed intake characteristics observed in lambs reared on a pelleted concentrate diet as they increased in bodyweight from weaning to maturity. The models in this study were empirical in nature and the inclusion of feed and environmental factors might be necessary to improve the accuracy of prediction. These models were aligned with trends in the literature and predicted levels that could be expected for the various breeds, reared under optimal sheep feedlotting conditions, as in this study.
Conclusion
Modelling DMI with the quadratic function in this study gave an indication of the dynamics of VFI and the changes in trends that occurred with the growth of lambs of various breeds. However, this model was not deemed accurate in predicting the actual level of DMI. By modelling feed intake as a percentage of bodyweight, more reliable models were obtained to predict DMI values. The use of cumulative feed intake accounted for the greatest proportion of variation in the data, although it was more indicative of the feed efficiency over the rearing period and might change depending on the rearing conditions. The models of FCR showed that feed efficiency was subject to change with the weight of the lambs, which must be considered when adopting cumulative feed intake for a specific rearing period. Although it is relatively simple to determine DMI from PI at a given bodyweight, to determine DMI from CFI, knowledge of the growth rates of lambs at a given bodyweight is required. Generally higher levels of VFI were observed in larger framed sheep breeds to supply sufficient nutrients for tissue growth than for smaller framed animals with slower growth rates. Overall, SAMM lambs and Dorper rams presented the most desirable feeding efficiencies at a given bodyweight, whereas early maturing breeds with higher degrees of fatness presented the highest FCRs at heavier bodyweights.
Acknowledgements
The authors would like to thank the Western Cape Department of Agriculture for the use of their facilities, and the Western Cape Agricultural Research Trust (0300-001), Cape Wools SA, and National Research Foundation of South Africa (RTF150512117948) for their financial support in making this study possible. This work is also based on the research supported by the South African Research Chairs Initiative of the Department of Science and Technology and National Research Foundation of South Africa (Grant No. UID 84633). Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s), and the National Research Foundation does not accept any liability in this regard.
Authors' contributions
DAVDM was responsible for data collection, statistical analysis, interpretation of the results and writing manuscript. TSB and LCH collaborated in conceptualizing the hypothesis, designing the experiment, interpreting the results and reviewing the final manuscript critically. PGT assisted with revising and editing the manuscript. All authors read and approved the manuscript.
Conflicts of interest statement
The authors declare that they have no affiliations or involvement with any organisation or entity with financial or non-financial interest in the matter described in this manuscript.
References
Allen, M.S., 1996. Physical constraints on voluntary intake of forages by ruminants. J. Anim. Sci. 74, 3063-3075. https://doi.org/10.2527/1996.74123063x [ Links ]
Blaxter, K.L., Clapperton, J.L. & Wainman, F.W., 1966. The extent of differences between six British breeds of sheep in their metabolism, feed intake and utilization, and resistance to climatic stress. Br. J. Nutr. 20, 283-294. https://doi.org/10.1079/BJN19660029 [ Links ]
Brand, T.S., Van der Merwe, D.A., Swart, E. & Hoffman, L.C., 2017. Comparing the effect of age and dietary energy content on feedlot performance of Boer goats. Small Rumin. Res. 157, 40-46. https://doi.org/10.1016/j.smallrumres.2017.10.009 [ Links ]
Cannas, A., Tedeschi, L.O., Fox, D.G., Pell, A.N. & Van Soest, P.J., 2004. A mechanistic model for predicting the nutrient requirements and feed biological values for sheep. J. Anim. Sci. 82, 149-169. https://doi.org/10.2527/2004.821149x [ Links ]
Cloete, J.J.E., Hoffman, L.C., Cloete, S.W.P. & Fourie, J.E., 2004. A comparison between the body composition, carcass characteristics and retail cuts of South African Mutton Merino and Dormer sheep. S. Afr. J. Anim. Sci. 34, 44-51. DOI: 10.4314/sajas.v34i1.4040 [ Links ]
Cloete, S.W.P., Cloete, J.J.E., Durand, A. & Hoffman, L.C., 2003. Production of five Merino type lines in a terminal crossbreeding system with Dormer or Suffolk sires. S. Afr. J. Anim. Sci. 33, 223-232. DOI: 10.4314/sajas.v33i4.3778 [ Links ]
Emmans, G.C., 1989. The growth of turkeys. In: C. Nixen & T.C. Grey (eds.) Recent advances in turkey science. Butterworths, London, UK. Pp. 135-165. [ Links ]
Emmans, G.C., 1997. A method to predict the food intake of domestic animals from birth to maturity as a function of time. J. Theor. Biol., 186,189-199. https://doi.org/10.1006/jtbi.1996.0357 [ Links ]
Erasmus, L.J., Prinsloo, J. & Meissner, H.H., 1988. The establishment of a protein degradability data base for dairy cattle using the nylon bag technique. 1. Protein sources. S. Afr. J. Anim. Sci. 18, 23-29. [ Links ]
Erasmus, L.J., Prinsloo, J., Botha, P.M. & Meissner, H.H., 1990a. The establishment of a ruminal protein degradation data base for dairy cattle using the in situ polyester bag technique. 2. Energy sources. S. Afr. J. Anim. Sci. 20, 124-129. [ Links ]
Erasmus, L.J., Prinsloo, J., Botha, P.M. & Meissner, H.H., 1990b. The establishment of a ruminal protein degradation data base for dairy cattle using the in situ polyester bag technique. 3. Roughages. S. Afr. J. Anim. Sci. 20, 130-135. [ Links ]
Faverdin, P., 1999. The effect of nutrients on feed intake in ruminants. Proc. Nutr. Soc. 58, 523-531. https://doi.org/10.1017/S0029665199000695 [ Links ]
Finlayson, J.D., Cacho, O.J. & Bywater, A.C., 1995. A simulation model of grazing sheep: I. Animal growth and intake. Agric. Syst. 48, 1-25. https://doi.org/10.1016/0308-521X(95)93643-R [ Links ]
Forbes, J.M., 2007. A personal view of how ruminant animals control their intake and choice of food: minimal total discomfort. Nutr. Res. Rev. 20, 132-146. https://doi.org/10.1017/S0954422407797834 [ Links ]
Illius, A.W., Jessop, N.S. & Gill, M., 2000. Mathematical models of food intake and metabolism in ruminants, in: P.B. Cronjé (ed). Ruminant physiology, digestion, metabolism growth and reproduction. CABI, Wallingford, UK. Pp.21-40. [ Links ]
Ingvartsen, K.L., 1994. Models of voluntary food intake in cattle. Livest. Prod. Sci. 39, 19-38. https://doi.org/10.1016/0301-6226(94)90149-X [ Links ]
Johnson, I.R., France, J., Thornley, J.H.M., Bell, M.J. & Eckard, R.J., 2012. A generic model of growth, energy metabolism, and body composition for cattle and sheep. J. Anim. Sci. 90, 4741 -4751. https://doi.org/10.2527/jas.2011-5053 [ Links ]
Lewis, R.M. & Emmans, G.C., 2010. Feed intake of sheep as affected by body weight, breed, sex, and feed composition. J. Anim. Sci., 88, 467-480. https://doi.org/10.2527/jas.2008-1735 [ Links ]
Marie, M., Findlay, P.A., Thomas, L. & Adam, C.L., 2001. Daily patterns of plasma leptin in sheep: effects of photoperiod and food intake. J. Endocrinol. 170, 277-286. https://doi.org/10.1677/joe.0.1700277 [ Links ]
Meissner, H.H., Hofmeyr, H.S., Van Rensburg, W.J.J. & Pienaar, J.P., 1983. Classification of livestock for realistic prediction of substitution values in terms of a biologically defined Large Stock Unit. Technical Communication 175. Department of Agriculture, Republic of South Africa. [ Links ]
Ministry of Agriculture, Fisheries and Food, 1975. Energy allowances and feeding systems for ruminants. Tech Bull. 33, Ministry of Agriculture and Fisheries. HMSO, London. Pp. 79. [ Links ]
NRC (National Research Council), 2007. Nutrient requirements of small ruminants: Sheep, goats, cervids and New World camelids. National Academic Press, Washington D.C., U.S.A. Pp. 256-261. [ Links ]
Owens, F.N., Dubeski, P. & Hanson, C.F., 1993. Factors that alter the growth and development of ruminants. J. Anim. Sci. 71, 3138-3150. https://doi.org/10.2527/1993.71113138x [ Links ]
Pulina, G., Avondo, M., Molle, G., Francesconi, A.H.D., Atzori, A.S. & Cannas, A., 2013. Models for estimating feed intake in small ruminants. R. Bras. Zootec. 42, 675-690. https://doi.org/10.1590/S1516-35982013000900010 [ Links ]
Thompson, J.M. & Parks, J.R., 1983. Food intake, growth and mature size in Australian Merino and Dorset horn sheep. Anim. Sci. 36, 471-479. https://doi.org/10.1017/S0003356100010527 [ Links ]
SAS Institute, 2006. SAS/Stat user's guide version 9, 1st printing, Volume 3, SAS Institute Inc, Cary, North Carolina 27513. [ Links ]
Tolkamp, B.J., Emmans, G.C. & Kyriazakis, I., 2006. Body fatness affects feed intake of sheep at a given body weight. J. Anim. Sci. 84, 1778-1789. https://doi.org/10.2527/jas.2005-514 [ Links ]
Van der Merwe, D.A., Brand, T.S. & Hoffman, L.C., 2019. Application of growth models to different sheep breed types in South Africa. Small Rumin. Res. 178, 70-78. https://doi.org/10.1016/j.smallrumres.2019.08.002 [ Links ]
Vieira, P.A.S., Pereira, L.G.R., Azevêdo, J.A.G., Neves, A.L.A., Chizzotti, M.L., dos Santos, R.D., de Araújo, G.G.L., Mistura, C. & Chaves, A.V., 2013. Development of mathematical models to predict dry matter intake in feedlot Santa Ines rams. Small Rumin. Res. 112, 78-84. https://doi.org/10.1016/j.smallrumres.2012.10.007 [ Links ]
Zereu, G., 2016. Factors affecting feed intake and its regulation mechanisms in ruminants - A Review. Int. J. Livest. Res. 6, 19-40. https://www.bibliomed.org/?mno=220064 [ Links ]
Submitted 24 April 2020
Accepted 24 December 2021
Published 27 May 2022
# Corresponding author: tersb@elsenburg.com














