Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Animal Science
On-line version ISSN 2221-4062
Print version ISSN 0375-1589
S. Afr. j. anim. sci. vol.51 n.6 Pretoria 2021
http://dx.doi.org/10.4314/sajas.v51i6.5
ARTICLES
Optimization of response to selection using genomic selection in indigenous chicken breeding programmes
C.W. Ndung'u#; T.K. Muasya; T.O. Okeno
Animal Breeding and Genomics Group, Department of Animal Sciences, Egerton University, P.O. Box 536-20115, Egerton, Kenya
ABSTRACT
This study tested the hypothesis that the use of pooled genetic and phenotypic parameters and genomic selection would optimize selection response in indigenous chicken breeding programmes. This premise was tested with deterministic simulation in three breeding schemes based on the sources of information used to estimate breeding values. These schemes used a conventional breeding scheme with non-pooled parameters (CSN), pooled parameters (CSP), and genomic information in a genomic selection scheme (GSS). A one-tier closed nucleus breeding programme was considered with a mating ratio of 1 to 5 for males to females, Four traits were used in the breeding goal, namely live weight at twelve weeks (LW), egg number for twelve weeks (EN), age at first egg (AFE), and antibody response (Ab). The genetic gain for CSN was 1.5 times higher than that of CSP. The rate of inbreeding for CSN was 19% lower than in CSP. The accuracy of selection followed the same trend with CSN producing 9% higher accuracy of selection than CSP. The GSS scheme resulted in an additional 59.3% genetic gain and 30% accuracy compared with CSP. The GSS scheme also had a reduced rate of inbreeding by 46% compared with CSP. When compared with CSN, GSS produced 38.7% greater genetic gain, a 27% lower rate of inbreeding and 21.0% higher accuracy of selection. Use of pooled parameter estimates and genomic information optimized response to selection, whereas non-pooled inputs overestimated and underestimated rates of genetic gain and inbreeding.
Keywords: deterministic simulation, economic gain, genetic gain, inbreeding
Introduction
Most developing countries recognized the social, economic and nutritional roles of indigenous chickens (IC) in improving the livelihoods of resource-poor rural households (Kattel, 2016; Moussa et al., 2019). This was confirmed by their attempts to improve productivity of IC in growth and egg production. These attempts focused on genetics, nutrition, health, housing and capacity building of farmers and on general management and marketing (Wondmeneh et al., 2014; Ayieko et al., 2015; Mpenda et al., 2018). Genetic improvements were initiated through experiments modelled to provide information for informed decision making before investing in breeding programmes. Modelling of breeding programmes, however, requires population-specific input parameter estimates and constant monitoring of loss in genetic variance owing to intense selection and adoption of new technologies such as genomic selection for sustainable long-term genetic gains (Rutten et al., 2002; Lillehammer et al., 2016; Miyumo et al., 2018).
Population-specific parameter estimates require pedigree and performance recording, which is the biggest challenge in developing countries owing to small flock sizes and lack of commitment by smallholder farmers (Wasike et al., 2011; Mrode et al., 2020). The IC breeding programmes therefore were modelled with input parameters sourced from single studies, as recommended by Koots and Gibson (1996). However, bias can arise in predicting response to selection because certain parameters were picked, whereas others were omitted. First, parameters were generated from studies carried out in different geographical zones with various data sizes. Second, data analysis used different methods (Haunshi & Shanmugam, 2012; Niknafs et al., 2013). To overcome these challenges, the use of pooled parameters from a number of studies was proposed as they accounted for variability in geographical conditions, data source, size and analytical procedure (Akanno et al., 2013).
Genetic variance was demonstrated to decrease over time owing to selection (Willoughby et al., 2015; Seyedsharifi et al., 2018). Selection can also lead to increased rates of inbreeding, because the chances of two related animals being selected together are higher, especially in small populations (Mwangi et al., 2016). Inbreeding may eventually lead to reduction in additive genetic variance owing to fixation of alleles (Esfandyari et al., 2017). A high rate of inbreeding affects response to selection for individual traits negatively, and levels beyond 0.1% would not be optimal for evolution (Franklin & Frankham 1998; Tongsiri et al., 2019). Ignoring loss in genetic variance and inbreeding and not accounting for mitigation strategies such as genomic selection against these factors could be detrimental to long-term genetic gain in a breeding programme.
Genomic selection was demonstrated to be more efficient in making selection decisions that simultaneous manage inbreeding in animal populations (Liu et al., 2017; Thomasen et al., 2020). it generates information on Mendelian sampling terms more accurately, leading to less co-selection of sibs, because estimated breeding values between individuals within families can be differentiated better, hence reduced rates of inbreeding (Daetwyler et al., 2007; Júnior et al., 2016). It also accelerates the rate of genetic gain, as it increases the accuracy of selection and reduces the generation interval (Miller, 2010). But its adoption in developing countries, especially in IC breeding programmes has been limited owing to high genotyping costs being assumed without the returns being considered. This study therefore investigated the premise that using pooled input parameter estimates, accounting for loss in genetic variance, and adopting genomic selection in IC breeding programmes in developing countries would accelerate genetic gains. This hypothesis was tested with deterministic simulation of breeding schemes (Lwelamira et al., 2008; Ebrahimpourtaher et al., 2018) that resembled those used in IC breeding programmes in developing countries.
Materials and Methods
Deterministic simulation was used to model various breeding schemes in a closed single-tier nucleus breeding system in SelAction software (Rutten et al., 2002). The breeding schemes were conventional and genomic. The conventional schemes mimicked the current chicken breeding programmes in developing countries, whereas the genomic schemes represented alternative breeding systems. A single tier was considered, since the chickens produced from the breeding stations were regarded as being sold to farmers for production. This implied that the breeding goals in the breeding stations and those of the farmers were in tandem.
A breeding goal was adopted in the current study that targeted the improvement of IC as dual purpose. Most farmers raise IC for multiple roles, which include provision of meat and eggs (Okeno et al., 2013). Three breeding goals for IC in Kenya were developed in consultation with farmers, traders and consumers (Okeno et al., 2013). These included IC-broiler, IC-layer and IC-dual purpose, which targeted improvement of IC for meat, eggs and both. The traits in the breeding goal in the current study were live weight at twelve weeks (LW), egg number for twelve weeks (EN), age at first egg (AFE), and antibody response (Ab) ( Bett et al., 2011; Okeno et al., 2013). Antibody response (Ab) was used as an indicator trait for disease tolerance. Inclusion of traits of economic importance in the breeding goal required estimation of their economic values (Amer et al., 2001; Bytyqi et al., 2015). The values for traits of economic importance for IC in Kenya had been estimated (Okeno et al., 2012) and the traits in the breeding goal were weighted with these values (Table 1).
The genetic and phenotypic parameters were sourced from studies in the tropics. Non-pooled parameters were obtained from single studies, whereas pooled parameters were obtained from a number studies for each trait and subjected to meta-analysis (Ndung'u et al., 2020). The aim was to account for variances in data size, geographical conditions, and the statistical evaluation model (Jembere et al., 2017). Parameters estimated in a certain location could be used in other populations owing to minimal or no differences between parameters obtained from different populations (Koots & Gibson, 1996). The pooled and non-pooled parameters that were used in this research were drawn from the studies of Okeno et al. (2013) and Ndung'u et al. (2020) (Table 1).
A single-tier closed nucleus breeding structure was considered that resembled those in developing countries. The activities within the nucleus included chicken identification with wing tags, phenotyping, genotyping, predicting breeding values, selecting, and mating. The best candidates were selected by truncation of estimated breeding values (EBV) calculated by best linear unbiased prediction (BLUP) and used as replacement stock, whereas the rest of the flock was culled. Three breeding schemes were considered.
The CSN used non-pooled estimates of the input parameters and assumed that the parents were selected based on pedigree and phenotypic information only. This represented the current breeding programme in most developing countries, where selection is based on performance records. The input parameter estimates were sourced from various studies in the tropics. This mimicked most breeding models that were used to develop livestock breeding programmes in developing countries such as Kenya (Okeno et al., 2013).
The CSP used pooled estimates of the input parameters. This scheme was similar to CSN, but the input parameter estimates resulted from meta-analysis. The aim was to obtain pooled parameter estimates that accounted for variances in data size, geographical condition and statistical evaluation model. The scheme aims at reducing the biasness that could be attributed to use of non-pooled parameter estimates (Safari et al., 2005; Akanno et al., 2013).
The GSS was similar to CSP, but selection of candidates was based on genetic markers as an additional source of information to phenotypes. It represented the selection technologies used in developed countries to optimize response to selection, but its adoption in developing countries has been slow (Ebrahimpourtaher et al., 2018).
A base population of 4800 chickens with a sex ratio of 0.5 was assumed. Ninety-six (96) males were selected from a population of 2400 males, whereas 480 hens were selected as parents of the base generation from a population of 2400 females for one round of selection. This proportion was chosen because few males are required for breeding compared with females. The mating ratio was assumed to be one cock to five hens. Each hen was assumed to lay 15 eggs per clutch with a hatchability of 95% and survival rate to sexual maturity of 70% (Yitbarek & Atalel, 2013). Selection was by truncation using EBV. For the sex-limited traits and those phenotyped later in life such as EN, AFE, and Ab, the candidates were selected based on phenotypic data from their female ancestors and sib performances. On the other hand, selection for LW was based on own performance before maturity, phenotypic data from male and female ancestors, and sib performances. Since all the birds were raised in the same environment, the common environmental effect was assumed constant. The effect of the nucleus size and mating ratios on response to selection was considered by increasing the number of breeding females in the population from 480, 960, 1440, 1920, 2400, and 2880. The mating ratio of males to females ranged from 1 to 5 with 96 males and 480 females to 1 to 30 with 2880 females and 576 males. Starting from a population of 1440, artificial insemination (AI) was considered to be in use since the semen from one cock could be used to inseminate 100 hens with extenders (Mohan et al., 2018).
The rates of genetic gain and inbreeding per generation were computed and compared under conventional and genomic breeding schemes. In CSP, the response to selection was computed for all the traits in the breeding goal (H) which was the sum of the true breeding values (TBV) of traits, weighted by their economic weights. A selection index, which was the sum of the TBVs for the traits in the breeding goal and their economic weights, was computed as (Rutten et al., 2002):
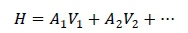
where: A are true breeding values, and
V are weighting factors for each trait.
In the GSS, genomic traits were included in the selection index as extra correlated traits with heritability equal to one (Dekkers, 2007). Estimates of the genetic and phenotypic correlations between the true breeding value and the extra trait (hrggand rgg) where h equals the square root of the heritability of the trait and is the accuracy of the genomic estimated breeding values. The was determined by the size of the reference population (np), the effective number of loci in the base population (nG), and the correlation of the true breeding values of the genotyped individuals and their phenotypes (r), and were based on the model below (Van Grevenhof et al., 2012):
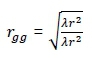
where: λ = 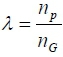 and r is the heritability,
and r is the heritability,
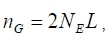
where: NEis the historic effective size of the base population and
L is the size of the genome in Morgan.
The IC genome was assumed to be 32 in Morgan units (Groenen et al., 2009), and the effective population size was 16.02 (Okeno et al., 2012). The genetic and phenotypic correlations between the genomic traits were calculated according to the procedure of Dekkers (2007). The response to selection for each trait was calculated as:
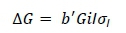
where: 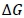 is a vector containing selection response for each trait,
is a vector containing selection response for each trait,
b is a vector of index weights,
G is a matrix of co-variances between information sources and true breeding values of selection candidates,
I is the selection intensity, and
σ, is the standard deviation of the index.
The total gain in the breeding goal in economic units was calculated as:
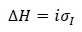
where: ΔH, is the breeding goal.
The rate of inbreeding was calculated in three steps. In the first step, a regression model was used to predict the long term contributions:
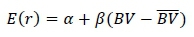
where: E(r) is the expected contribution,
α, the contribution of an individual with an average breeding value, AND
βaccounts for the increase of the contribution of parents with higher breeding value implying that the parents with high breeding values will have more selected offsprings (Rutten et al., 2002).
Second, the square of the expected contributions was calculated. And finally, inbreeding was calculate as:

where: N is the number of parents, and
E(r)2, is the square of the expected contributions.
Results and Discussion
The findings of the current study confirmed the authors' premise that using pooled input parameter estimates, accounting for loss in genetic variance, and adopting genomic selection would optimize response to selection. The rate of genetic gain was lower and the accumulation of inbreeding was higher in CSP compared with CSN. The genomic scheme (GSS) on the other hand outperformed the conventional scheme in response to selection. The genetic gain, loss of genetic variance, and accuracy of selection per generation in the three breeding schemes are presented in Table 2.
The genetic gain for CSN was 1.5 times higher than that of CSP (Table 2). The rate of inbreeding for CSN was 19% lower than for CSP. The accuracy of selection followed the same trend with CSN resulting in 9% higher accuracy of selection than CSP. The GSS scheme produced an additional 59.3% genetic gain and 30% accuracy compared with CSP. The GSS scheme also had a reduced rate of inbreeding by 46% compared with CSP. When compared with CSN, GSS had 38.7% greater genetic gain, 27% lower rate of inbreeding and 21.0% higher accuracy of selection. The GSS scheme had the lowest rate of inbreeding at 0.22% compared with 0.49% and 0.68% for CSN and CSP.
The genetic gains for individual traits in the breeding goal in the three breeding schemes are presented in Table 3. The genetic gain for individual traits followed the same trend as observed in the overall genetic gains for each scheme in Table 2. For instance, the genetic gain for EN was -0.39 in CSN as compared with -0.49 in CSP. The live weight in CSN was 27.64 g higher than that of CSP. Age at first egg was reduced by 1.40 days in CSN, but increased by 0.34 days in CSP. Immune antibody system changed by -0.24 in CSN and -0.27 in CSP. In all the traits except for EN and Ab, GSS realized higher genetic gain compared with CSP. The genetic gain for LW was at least doubled in GSS compared with CSP. The highest genetic gain was obtained from the live weight trait in all the schemes.
The effect of nucleus size and mating ratio of males to females on rates of genetic gain and inbreeding were investigated by changing nucleus size and mating ratios. Since the trends for CSN and CSP were identical, only CSP and GSS are presented. The rate of change in genetic gain and inbreeding when the nucleus size was increased is presented in Figure 1. Although genetic gain realized in GSS ranked above CSP, the rate of gain in the two schemes increased at diminishing rate with increase in nucleus size. A similar trend was observed in the rate of inbreeding, but with GSS ranking below CSP.
The change in rates of genetic gain and inbreeding with increased mating ratio is presented in Figure 2. The genetic gain increased with increase in the mating ratio for both CSP and GSS. It increased with increase in the number of hens per cock from 5 to 30, although at a diminishing rate in both schemes. The rate of increase, however, was higher for GSS than for CSP. The rate of inbreeding increased with increase in the mating ratio for the CSP, whereas it decreased with the increase in the mating ratio for GSS.
These findings supported the hypothesis that not accounting for variation in sources of input parameter estimates and ignoring loss in genetic variance over time overestimated response to selection. It also confirmed that adoption of genomic selection in an IC breeding programme would optimize response to selection. These findings were supported by Akanno et al. (2013), who demonstrated that utilization of input parameters from a single study could lead to bias. This implies that in the event that primary data is not available to estimate the genetic parameters, there is need to subject parameters sourced from different studies to meta-analysis to obtain pooled parameters (Jembere et al., 2017; Gathura et al., 2020). As demonstrated in the findings (Table 2), the genetic gain realised in CSN was higher than that obtained in CSP. This could be attributed to differences in input parameters used in the two breeding schemes.
The input parameters for CSN were obtained from various literature sources, which had higher heritability values, compared with those adopted in CSP, where pooled parameters were used after meta-analysis (Table 1). The difference in heritability values obtained in CSN could be because of data size, evaluation model, and the year in which the data were collected (Giannotti et al., 2005; Akanno et al., 2013). These values have direct impact on accuracy of selection and therefore true breeding values (Toghiani, 2012; Zhang et al., 2019). When comparing the impact of different levels of heritability on accuracy of selection, Toghiani (2012) and Zhang et al. (2019) found that heritability had a significant effect on both conventional and genomic breeding programmes. These studies found that higher heritability values resulted in higher accuracies. This could explain the higher accuracy of selection realized in CSN compared with CSP (Table 2) in the current study. Similarly, in Ellen et al. (2007), high accuracy of individual selection was found when heritability was higher compared with selection based on the performance of full sibs. Since all other input parameters were constant in these two schemes, the economic and individual trait responses presented in Tables 2 and 3 could be attributed to differences in selection accuracies. This implies that it would be highly recommendable for each breeding programme to be evaluated based on primary data generated from the breeding programme to obtain a more precise estimation of response to selection. Where that is not feasible, meta-analysis of sampled input parameters should be carried out. Meta-analysis was conducted to obtain the input parameters in this study in which lower heritability estimates were obtained for CSP as compared with CSN. The parameters in CSN had been obtained directly from the literature as found in Okeno et al. (2013).
The lower heritability values could be the reason for the higher rate of inbreeding in CSP compared with CSN (Table 2). According to Woolliams and Bijma. (2000) when heritability estimates are low and BLUP is used, the information from relatives is given more weight, which increases the possibility of relatedness and therefore high rates of inbreeding. This is consistent with the findings of the current study in which low heritabilities in CSP resulted in higher rates of inbreeding (Table 2). The high rate of inbreeding was demonstrated to affect response negatively to selection for individual traits in the breeding goal in poultry (König et al., 1999; Tongsiri et al., 2019). Inbreeding has also been shown to affect negatively traits such as milk production, growth and health in cattle (Mészáros et al., 2014).This could explain the low genetic gain for individual traits and subsequent economic response realized under CSP in the current study. Generally, all three breeding schemes had higher rates of inbreeding than the recommended levels of 0.1% for evolutionary potential (Franklin & Frankham, 1998). This could be explained by the low effective population size of 320, since rate of inbreeding is determined by population size (Wang et al., 2016). This size was lower than the recommended 500 to 1000 for conservation in animal populations (Frankham & Franklin, 1998; Krupa et al., 2015; Lopes et al., 2019).The highest genetic gains and lowest rates of inbreeding for GSS compared with CSN and CSP implied that this scheme could yield more response to selection in IC breeding.
Genomic selection was superior to conventional breeding programmes in response to selection and reduction in rates of inbreeding in various species (Thomasen et al., 2020). The high response to selection in GSS compared with CSP (Table 2) was attributed to high accuracy of selection and lower rates of inbreeding in GSS. This accuracy could be attributed to the power of GSS to trace the inheritance of chromosomal segments and estimate relationships between selection candidates (Stock & Reents, 2013). A genomic information-based relationship matrix has been demonstrated to provide accurate relationship coefficients among individuals (VanRaden et al., 2009; Zhang et al., 2020). Establishment of close relationships optimizes utilization of information from different related candidates and therefore increases accuracy of selection, which has a direct impact on EBV and genetic gain (Dekkers, 2007; Meuwissen et al., 2013). The impact of increased accuracy on individual traits was evident in Table 3 in this study where all the traits in the breeding goal had higher responses in GSS than CSP. On the other hand, the independent management of ancestral contributions owing to the use of genomic selection unlocked the association between the genetic gain and relationships (Henryon et al., 2014). This was owing to the establishment of more accurate relationships, which increased the accuracy of Mendelian sampling terms (Avendano et al., 2005; Henryon et al., 2014; Liu et al., 2017). This constrained identity-by-descent among the parents, leading to a low rate of inbreeding. This could explain the lower rates of inbreeding in GSS compared with CSP in the current study. This study therefore shows that adoption of GSS in IC breeding programmes would optimize response to selection, even with small nucleus sizes.
The effect of increasing the nucleus size was also investigated under the current CSP and alternative GSS breeding programme. In the two schemes, response to selection increased with population size, but with diminishing returns (Figure 1). These findings were supported by Lillehammer et al. (2011) and Henryon et al. (2012), who demonstrated marginal diminishing returns in a pig genomic selection strategy. In these two studies, there were diminishing returns as more candidates were genotyped based on truncation selection. The diminishing returns in the current study could be attributed to the truncation selection method, in which animals that were ranked at the top were selected based on their estimated breeding values (Caballero et al., 1996). This implied the best ranking animals would have higher breeding values than low-ranking selection candidates. Therefore, as more candidates were added to the nucleus population after truncation selection, the low ranking candidates could not outperform the high-ranking candidates. This meant that the benefits from the genetic gains derived from the low ranking candidates were not as great as those obtained from the high-ranking candidates. This led to diminishing returns to selection as more candidates were being recruited into the nucleus. Although the genetic gain increased with nucleus size for both CSP and GSS strategies, only the population size of 2880 attained a rate of inbreeding of around 0.1% for CSP, which is required to maintain genetic diversity and long-term viability for animal populations (Franklin & Frankham 1998; FAO, 2000). A larger nucleus size would lead to a higher costs in inputs and resources such as feeding, genotyping and recording (Kahi & Nitter, 2004; Janssen et al., 2018). There was also an increase in genetic gain with rise in mating ratio (Figure 2), although at diminishing return. This could be attributed to the increase in the selection intensity of the males as it is one of the factors that affect genetic gain (Lopes et al., 2019). Previous studies demonstrated that increasing selection intensity, especially that of males, had a huge positive impact on genetic gain (Abdel-Salam et al., 2010; Battagin et al., 2016; Granleese et al., 2017). The diminishing return in response to selection could be attributed to the increase in relatedness and reduction of genetic variability owing to selection of more related animals for breeding (Doublet et al., 2019).
The decreasing rate of inbreeding with increased number of candidates in the nucleus population in the GSS scheme could be explained by capability of this scheme to rank full sibs. The GSS scheme uses genomic rather than numerator relationship matrix leading to generation of different breeding values for the full sibs (Su et al., 2018; Chu et al., 2019). Such breeding values can be used to rank full sibs, hence minimise chances of mating related individuals (Dekkers et al., 2007) leading to a low rate of inbreeding, as observed in the current study. On the other hand, the decreasing rate of inbreeding in CSP could be attributed to the increase in the breeding population for both males and females because the increase in the mating population increases the effective population size, which is indirectly proportional to the rates of inbreeding (Ghafouri-Kesbi, 2010; Biscarini et al., 2015). This could explain the increasing trend of rate of inbreeding realized in Figure 2 as the number of males was kept, whereas the female population increased. This implied each male was mated to more females and hence would result in close relationships in future generations. Although this study demonstrated that adoption of GSS would optimize response to selection, conventional breeding schemes would still play a significant role in establishing breeding programmes for IC in developing countries, because the GSS scheme would require reference population with phenotyped and genotyped candidates (Lee et al., 2017; Eynard et al., 2018). However, the level of recording for traits of economic importance for IC, in particular in developing countries, is rudimentary because resource-poor rural households do not see the value of recording or have no capacity.
Conclusion
The use of non-pooled estimates of input parameters rather than pooled estimates results in over-and underestimation of the rates of genetic gain and inbreeding. The use of pooled parameter estimates minimizes overestimation because the parameters are subject to meta-analysis, which puts into account the accuracy with which they have been estimated. In the absence of population-specific input parameters, the information sampled from various studies should be subject to meta-analysis to obtain pooled estimates as it would avoid overestimation of the genetic response. Genomic selection could be used to optimize response to selection in IC breeding programmes. This is achieved from attainment of improved genetic gain and reduction of rates of inbreeding. To realize potential benefits from genomic selection, establishment of necessary infrastructure is recommended in some research institutions, especially in developing countries. This would include setting up sequencing and genomic data analysis tools, which would help in obtaining data to conduct genomic evaluations before selection and mating of indigenous chickens in the breeding plans.
Acknowledgment
The authors acknowledge Transforming African Agricultural Universities to contribute meaningfully to Africa's Growth and Development (TAGDev) and Centre of Excellence in Sustainable Agriculture and Agribusiness Management (CESAAM) of Egerton University for their support.
Authors' Contributions
CWN was involved in data analysis, interpretation of the results and writing of the original draft. TKM was involved in the design of the study, interpretation of the results and revision of the manuscript. TOO was involved in the design of the study, data analysis, interpretation of the results and revision of the manuscript.
Conflict of Interest Declaration
The authors declare that they have no conflicts of interest.
References
Abdel-Salam, S.A., Sayed, A.I., Elsayed, M. & Abou-Bakr, S., 2010. Genetic gain in open nucleus breeding scheme to improve milk production in Egyptian buffalo. Livest. Sci. 131, 162-167. https://doi.org/10.1016/jlivsci.2010.03.013 [ Links ]
Akanno, E.C., Schenkel, F.S., Quinton, V.M., Friendship, R.M. & Robinson, J.A.B., 2013. Meta-analysis of genetic parameter estimates for reproduction , growth and carcass traits of pigs in the tropics. Livest. Sci. 152, 101-113. https://doi.org/10.1016/j.livsci.2012.07.021 [ Links ]
Amer, P.R., Simm, G., Keane, M.G., Diskin, M.G. & Wickham, B.W., 2001. Breeding objectives for beef cattle in Ireland. Livest. Prod. Sci. 67, 223-239. https://doi.org/10.1016/S0301-6226(00)00201-3 [ Links ]
Avendano, S., Woolliams, J.A. & Villanueva, B., 2005. Prediction of accuracy of estimated Mendelian sampling terms. J. Anim. Breed. Genet. 122, 302-308. DOI: 10.1111/j.1439-0388.2005.00532.x [ Links ]
Ayieko, M.O.D., Bett, E.K. & Kabuage, L.W., 2015. Analysis of indigenous chicken marketing participation decisions: The case of producers from Makueni county, Kenya. East African Agric. For. J. 81, 12-17. https://doi.org/10.1080/00128325.2015.1040643 [ Links ]
Battagin, M., Gorjanc, G., Faux, A.M., Johnston, S.E. & Hickey, J.M., 2016. Effect of manipulating recombination rates on response to selection in livestock breeding programs. Genet. Sel. Evol. 48, 1-12. DOI: 10.1186/s12711-016-0221-1 [ Links ]
Bett, H.K., Bett, R.C., Peters, K.J., Kahi, A.K. & Bokelmann, W., 2011. Estimating farmers' preferences in selection of indigenous chicken genetic resources using non-market attributes. Anim. Genet. Resour. 49, 51-63. DOI: 10.1017/S2078633611000348 [ Links ]
Bytyqi, H., Fuerst-Waltl, B., Mehmeti, H. & Baumung, R., 2015. Economic values for production traits for different sheep breeds in Kosovo. Ital. J. Anim. Sci. 14, 603-609. https://doi.org/10.4081/ijas.2015.3808 [ Links ]
Caballero, A., Santiago, E. & Toro, M.A., 1996. Systems of mating to reduce inbreeding in selected populations. Anim. Sci. 62, 431-442. DOI: 10.1017/S1357729800014971 [ Links ]
Daetwyler, H.D., Villanueva, B., Bijma, P. & Woolliams, J.A., 2007. Inbreeding in genome-wide selection. J. Anim. Breed. Genet. 124, 369-376. DOI: 10.1111/j.1439-0388.2007.00693.x [ Links ]
Dekkers, J.C.M., 2007. Prediction of response to marker-assisted and genomic selection using selection index theory. J. Anim. Breed. Genet. 124, 331-341. DOI: 10.1111/j.1439-0388.2007.00701.x [ Links ]
Doublet, A.C., Croiseau, P., Fritz, S., Michenet, A., Hozé, C., Burge, C.D., Laloë, D. & Restoux, G., 2019. The impact of genomic selection on genetic diversity and genetic gain in three French dairy cattle breeds. Genet. Sel. Evol. 51, 1-13. https://doi.org/10.1186/s12711-019-0495-1 [ Links ]
Ebrahimpourtaher, S., Alijani, S., Rafat, S.A. & Sharifi, A.R., 2018. Potential of genomic breeding program in Iranian native chickens. Iran. J. Appl. Anim. Sci. 8, 519-525. [ Links ]
Ellen, E.D., Muir, W.M., Teuscher, F. & Bijma, P., 2007. Genetic improvement of traits affected by interactions among individuals: sib selection schemes. Genetics 176, 489-499. https://doi.org/10.1534/genetics.106.069542 [ Links ]
Esfandyari, H., Henryon, M., Berg, P., Thomasen, J.R., Bijma, P. & S0rensen, A.C., 2017. Response to selection in finite locus models with nonadditive effects. J. Hered. 108, 318-327. https://doi.org/10.1093/jhered/esw123 [ Links ]
Eynard, S.E., Croiseau, P., Laloë, D., Fritz, S., Calus, M.P. & Restoux, G., 2018. Which individuals to choose to update the reference population ? Minimizing the loss of genetic diversity in animal genomic selection programs. Genes, Genomes, Genet. 8, 113-121. DOI: 10.1534/g3.117.1117 https://pubmed.ncbi.nlm.nih.gov/29133511/ [ Links ]
FAO, 2000. Secondary guidelines for development of farm animal genetic resources management plans. Management of small populations at risk. FAO, Rome, Italy. [ Links ]
Franklin, I.R. & Frankham, R., 1998. How large must populations be to retain evolutionary potential? Anim. Conserv. 1, 69-70. DOI: 10.1111/j.1469-1795.1998.tb00228.x [ Links ]
Gathura, D.M., Muasya, T.K. & Kahi, A.K., 2020. Meta-analysis of genetic parameters for traits of economic importance for beef cattle in the tropics. Livest. Sci. 242, 104306. https://doi.org/10.1016/j.livsci.2020.104306 [ Links ]
Ghafouri-Kesbi, F., 2010. Change in genetic size of small-closed populations: Lessons from a domestic mammal population. Genet. Mol. Biol. 33, 657-662. https://pubmed.ncbi.nlm.nih.gov/21637574/ [ Links ]
Giannotti, J.D.G., Packer, I.U. & Mercadante, M.E.Z., 2005. Meta-analysis for heritability of estimates growth traits in beef cattle. Rev. Bras. Zootec. 34, 1173-1180. https://doi.org/10.1590/S1516-35982005000400011 [ Links ]
Granleese, T., Clark, S.A., Swan, A.A. & Van der Werf, J.H.J., 2017. Increased genetic gains in multi-trait sheep indices using female reproductive technologies combined with optimal contribution selection and genomic breeding values. Anim. Prod. Sci. 57, 1984-1992. https://doi.org/10.1186/s12711-015-0151-3 [ Links ]
Groenen, M.A.M., Wahlberg, P., Foglio, M., Cheng, H.H., Megens, H.J., Crooijmans, R.P.M.A., Besnier, F., Lathrop, M., Muir, W.M., Wong, G.K.S., Gut, I. & Andersson, L., 2009. A high-density SNP-based linkage map of the chicken genome reveals sequence features correlated with recombination rate. Genome Res. 19, 510-519. https://genome.cshlp.org/content/19/3/510 [ Links ]
Haunshi, S. & Shanmugam, M., 2012. Evaluation of two Indian native chicken breeds for reproduction traits and heritability of juvenile growth traits. Trop. Anim. Health Prod. 44, 969-973. https://link.springer.com/article/10.1007/s11250-011-9994-y [ Links ]
Henryon, M., Berg, P. & S0rensen, A.C., 2014. Animal-breeding schemes using genomic information need breeding plans designed to maximise long-term genetic gains. Livest. Sci. 166, 38-47. https://doi.org/10.1016/j.livsci.2014.06.016 [ Links ]
Janssen, K., Saatkamp, H. & Komen, H., 2018. Cost-benefit analysis of aquaculture breeding programs. Genet. Sel. Evol. 50, 1-16. [ Links ]
Jembere, T., Dessie, T., Rischkowsky, B., Kebede, K., Okeyo, A.M. & Haile, A., 2017. Meta-analysis of average estimates of genetic parameters for growth, reproduction and milk production traits in goats. Small Rumin. Res. 153, 71-80. [ Links ]
Júnior, G.A.F., Rosa, G.J., Valente, B.D., Carvalheiro, R., Baldi, F., Garcia, D. A., Gordo, D.G.M., Espigolan, R., Takada, L., Tonussi, R.L., De Andrade, W.B.F., Magalhães, A.F.B., Chardulo, L.A.L., Tonhati, H. & De Albuquerque, L.G., 2016. Genomic prediction of breeding values for carcass traits in Nellore cattle. Genet. Sel. Evol. 48, 1-8. DOI: 10.1186/s12711-016-0188-y [ Links ]
Kahi, A.K. & Nitter, G., 2004. Developing breeding schemes for pasture based dairy production systems in Kenya: I. Derivation of economic values using profit functions. Livest. Prod. Sci. 88, 161-177. https://doi.org/10.1016/j.livprodsci.2003.10.008 [ Links ]
Kattel, P., 2016. Socio-economic importance of indigenous poultry in Nepal. Poultry, Fish. Wildl. Sci. 4, 9-11. DOI: 10.4172/2375-446X.1000153 [ Links ]
König, S., Tsehay, F., Sitzenstock, F., Von Borstel, U.U., Schmutz, M., Preisinger, R. & Simianer, H., 1999. Evaluation of inbreeding in laying hens by applying optimum genetic contribution and gene flow theory. Poult. Sci. 89, 658-667. DOI: 10.3382/ps.2009-00543 [ Links ]
Koots, K.R. & Gibson, J.P., 1996. Realized sampling variances of estimates of genetic parameters and the difference between genetic and phenotypic correlations. Genetics 143, 1409-1416. DOI: 10.1093/genetics/143.3.1409 [ Links ]
Krupa, E., Žáková, E., & Krupová, Z.,, 2015. Evaluation of inbreeding and genetic variability of five pig breeds in Czech Republic. Asian-Australasian J. Anim. Sci. 28, 25-36. DOI: 10.5713/ajas.14.0251 [ Links ]
Lee, S.H., Clark, S., & Van der Werf, J.H.J., 2017. Estimation of genomic prediction accuracy from reference populations with varying degrees of relationship. PLoS One 12, 1-22. DOI: 10.1371/journal.pone.0189775 [ Links ]
Lillehammer, M., Sonesson, A.K. & Meuwissen, T.H.E., 2016. Use of field data in pig genomic selection schemes: A simulation study. Animal 10, 1025-1032. DOI: 10.1017/S1751731115002669 [ Links ]
Lillehammer, M., Meuwissen, T.H.E. & Sonesson, A.K., 2011. Genomic selection for maternal traits in pigs. J. Anim. Sci. 89, 3908-3916. DOI: 10.2527/jas.2011-4044 [ Links ]
Liu, H., Henryon, M. & Sorensen, A.C., 2017. Mating strategies with genomic information reduce rates of inbreeding in animal breeding schemes without compromising genetic gain. Animal 11, 547-555. DOI: 10.1017/S1751731116001786 [ Links ]
Lopes, J.S., Rorato, P.R.N., Mello, F.C.B., Freitas, M.S.D., Prestes, A.M., Garcia, D.A. & Oliveira, M.M.D., 2019. Strategies to control inbreeding in a pig breeding program: A simulation study. Ciência Rural 49, 1-9. https://doi.org/10.1590/0103-8478cr20180994 [ Links ]
Lwelamira, J., Kifaro, G.C. & Gwakisa, P., 2008. Breeding strategies for improving performance of Kuchi chicken ecotype of Tanzania for production under village conditions. Livest. Res. Rural Dev. 20. [ Links ]
Mészáros, R.K.G., Kadlečík, O., Hazuchová, E., Šidlová, V. & Pavlík, I.,, 2014. Influence of mating systems and selection intensity on the extent of inbreeding and genetic gain in the Slovak Pinzgau cattle. Czech J. Anim. Sci., 219-226. DOI: 10.17221/7402-CJAS [ Links ]
Meuwissen, T., Hayes, B. & Goddard, M., 2013. Accelerating improvement of livestock with genomic selection. Annu. Rev. Anim. Biosci. 1, 221-239. DOI: 10.1146/annurev-animal-031412-103705 [ Links ]
Miller, S., 2010. Genetic improvement of beef cattle through opportunities in genomics. Rev. Bras. Zootec. 39, 247-255. https://doi.org/10.1590/S1516-35982010001300027 [ Links ]
Miyumo, S., Wasike, C.B. & Kahi, A.K., 2018. Genetic and phenotypic parameters for feed efficiency in indigenous chicken in Kenya. Livest. Sci. 207, 91-97. https://doi.org/10.1016/j.livsci.2017.11.011 https://www.cabdirect.org/cabdirect/abstract/20183055427 [ Links ]
Mohan, J., Sharma, S.K., Kolluri, G. & Dhama, K., 2018. History of artificial insemination in poultry, its components and significance. World's Poult. Sci. J. 74, 475-488. DOI: https://doi.org/10.1017/S0043933918000430 [ Links ]
Moussa, H.O., Keambou, T.C., Hima, K., Issa, S., Motsa'a, S.J. & Bakasso, Y., 2019. Indigenous chicken production in Niger. Vet. Anim. Sci. 7, 1-19. https://doi.org/10.1016/j.vas.2018.11.001 [ Links ]
Mpenda, F.N., Schilling, M.A., Campbell, Z., Mngumi, E.B. & Buza, J., 2018. The genetic diversity of local african chickens: A potential for selection of chickens resistant to viral infections. J. Appl. Poult. Res. 28, 1-12. DOI: 10.3382/japr/pfy063 [ Links ]
Mrode, R., Dzivenu, C.E., Marshall, K., Gift, M., Chagunda, G., Muasa, B.S., Ojango, J.O. & Okeyo, A.M., 2020. 2020. Phenomics and its potential impact on livestock development in low-income countries: Innovative applications of emerging related digital technology. Anim. Front. 10, 6-11. DOI: 10.1093/af/vfaa002 [ Links ]
Mwangi, S., Muasya, T.K., Ilatsia, E.D., Kahi. & A.K., 2016. Assessment of the genetic variability using pedigree analysis of the Sahiwal breed in Kenya. Anim. Genet. Resour. 59, 7-14.https://www.researchgate.net/publication/312049672_Assessment_of_the_genetic_ variability_using_pedigree_analysis_of_th e_Sa hiwal_breed_i n_Kenya [ Links ]
Ndung'u, C.W., Okeno, T.O. & Muasya, T.K., 2020. Pooled parameter estimates for traits of economic importance in indigenous chicken in the tropics. Livest. Sci. 239, 1-34. https://doi.org/10.1016/j.livsci.2020.104102 [ Links ]
Niknafs, S., Abdi, H., Fatemi, S.A., Zandi, M.B. & Baneh, H., 2013. Genetic trend and inbreeding coefficients effects for growth and reproductive traits in Mazandaran indigenous chicken. J. Biol. 3, 25-31. [ Links ]
Okeno, T.O., Kahi, A.K. & Peters, K.J., 2013. Evaluation of breeding objectives for purebred and crossbred selection schemes for adoption in indigenous chicken breeding programmes. Br. Poult. Sci. 54, 62-75. DOI:10.1080/00071668.2013.764492 [ Links ]
Okeno, T.O., Magothe, T.M., Kahi, A.K. & Peters, K.J., 2012. Application of risk-rated profit model functions in estimation of economic values for indigenous chicken breeding. Trop. Anim. Health Prod. 44, 1279-1287. DOI: 10.1007/s11250-011-0069-x [ Links ]
Rutten, M.J.M., Bijma, P., Woolliams, J.A., & Van Arendonk, J.A.M., 2002. SelAction: Software to predict selection response and rate of inbreeding in livestock breeding programs. J. Hered. 93, 456-458. https://doi.org/10.1093/jhered/93.6.456 [ Links ]
Safari, E., Fogarty, N.M. & Gilmour, A.R., 2005. A review of genetic parameter estimates for wool, growth, meat and reproduction traits in sheep. Livest. Sci. 92, 271-289. https://doi.org/10.1016/j.livprodsci.2004.09.003 [ Links ]
Seyedsharifi, R., Azizyan, S., Boustan, A., Seifdavati, J. & Mojtahedin, A., 2018. Investigating the bias resulted from ignoring Bulmer effect on the genetic and economic output in progeny test and genomic selection program. Kafkas Üniversitesi Vet. Farkultesi Derg. 24, 137-144. [ Links ]
Stock, K. & Reents, R., 2013. Genomic selection: Status in different species and challenges for breeding. Reprod. Domest. Anim. 48, 2-10. DOI: 10.1111/rda.12201 [ Links ]
Thomasen, J.R., Liu, H. & S0rensen, A.C., 2020. Genotyping more cows increases genetic gain and reduces rate of true inbreeding in a dairy cattle breeding scheme using female reproductive technologies. J. Dairy Sci. 103, 597-606. DOI: 10.3168/jds.2019-16974 [ Links ]
Toghiani, S., 2012. Quantitative genetic application in the selection process for livestock production. Livest. Prod. InTech., 3-32. DOI: 10.5772/51027 [ Links ]
Tongsiri, S., Jeyaruban, G.M., Hermesch, S., van der Werf, J.H., Li, L. & Chormai, T., 2019. Genetic parameters and inbreeding effects for production traits of Thai native chickens. Asian-Australasian J. Anim. Sci. 32, 930-938. DOI: 10.5713/ajas.18.0690 [ Links ]
Van Grevenhof, E.M., Van Arendonk, J.A. & Bijma, P., 2012. Response to genomic selection: The Bulmer effect and the potential of genomic selection when the number of phenotypic records is limiting. Genet. Sel. Evol. 44, 272-298. https://doi.org/10.1186/1297-9686-44-26 [ Links ]
VanRaden, P.M., Van Tassell, C.P., Wiggans, G.R., Sonstegard, T.S., Schnabel, R.D., Taylor, J.F. & Schenkel, F.S., 2009. Invited review: Reliability of genomic predictions for North American Holstein bulls. J. Dairy Sci. 92, 1624. https://doi.org/10.3168/jds.2008-1514 [ Links ]
Wang, J., Santiago, E. & Caballero, A., 2016. Prediction and estimation of effective population size. Heredity 117, 193-206. https://doi.org/10.1038/hdy.2016.43 [ Links ]
Wasike, C.B., Magothe, T.M., Kahi, A.K. & Peters, K.J., 2011. Factors that influence the efficiency of beef and dairy cattle recording system in Kenya: A SWOT-AHP analysis. Trop. Anim. Health Prod. 43, 141-152. DOI: 10.1007/s11250-010-9666-3 [ Links ]
Willoughby, J.R., Fernandez, N.B., Lamb, M.C., Ivy, J.A., Lacy, R.C. & Dewoody, J.A., 2015. The impacts of inbreeding, drift and selection on genetic diversity in captive breeding populations. Mol. Ecol. 24, 98-110. DOI: 10.1111/mec.13020 [ Links ]
Wolc, A., Zhao, H.H., Arango, J., Settar, P., Fulton, J.E., O'Sullivan, N.P., Preisinger, R., Stricker, C., Habier, D., Fernando, R.L., Garrick, D.J., Lamont, S.J. & Dekkers, J.C.M., 2015. Response and inbreeding from a genomic selection experiment in layer chickens. Genet. Sel. Evol. 47, 1-12. https://doi.org/10.1186/s12711-015-0133-5 [ Links ]
Wondmeneh, E., Van der Waaij, E.H., Dessie, T., Okeyo Mwai, A. & Van Arendonk, J.A., 2014. A running breeding program for indigenous chickens in Ethiopia: evaluation of success. In: Proc.10th World Cong. Genetics Appl. Lvstck. Prod., 17-22 August 2014, Vancouver, British Columbia, Canada. [ Links ]
Woolliams, J. A. & Bijma, P., 2000. Predicting rates of inbreeding in populations undergoing selection. Genetics 154, 1851-1864. DOI:10.1093/genetics/154.4.1851 [ Links ]
Yitbarek, M.B. & Atalel, W., 2013. Constraints and opportunities of village chicken production in Debsan Tikara Keble at Gonder Zuria Woreda, North Gonder, Ethiopia. Sci. J. Vet. Adv. 2, 118-124. [ Links ]
Zhang, H., Yin, L., Wang, M., Yuan, X. & Liu, X., 2019. Factors affecting the accuracy of genomic selection for agricultural economic traits in maize, cattle and pig populations. Front. Genet. 10, 1-10. DOI: 10.3389/fgene.2019.00189 [ Links ]
Zhang, J., Song, H., Zhang, Q. & Ding, X., 2020. Assessment of relationships between pigs based on pedigree and genomic information. Animal 14, 697-705. https://doi.org/10.1017/S1751731119002404 [ Links ]
Zhang, Z., Zhang, Q. & Ding X.D., 2011. Advances in genomic selection in domestic animals. Anim. Genet. 56, 2655-2663. DOI: 10.1007/s11434-011-4632-7 [ Links ]
Submitted 10 September 2020
Accepted 24 July 2021
Published 5 December 2021
# Corresponding author: catendungu11@yahoo.com














