Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Animal Science
versão On-line ISSN 2221-4062
versão impressa ISSN 0375-1589
S. Afr. j. anim. sci. vol.47 no.6 Pretoria 2017
http://dx.doi.org/10.4314/sajas.v47i6.13
Using path analysis to predict bodyweight from body measurements of goats and sheep of communal rangelands in Botswana
O. TemosoI, #; M. ColemanII; D. BakerI; P. MorleyIII; L. BalesengIV; A. MakgekgeneneIV; S. BahtaV
IUNE Business School, University of New England, Armidale, NSW, 2351, Australia
IISchool of Environmental and Rural Science, University of New England, Armidale, NSW, 2351, Australia
IIIInstitute for Rural Futures, School of Behavioural, Cognitive and Social Sciences, University of New England, Armidale, NSW, 2351, Australia
IVDepartment of Agricultural Research, Private Bag 0033, Gaborone, Botswana
VInternational Livestock Research Institute, PO Box 30709, Nairobi, 00100, Kenya
ABSTRACT
The objective of this study was to determine the practicality of using linear body measurement traits to predict live weight of goats and sheep under communal grazing in three districts of Botswana, namely Central, Kweneng, and Kgalagadi. Pairwise (Pearson) correlations were estimated using bodyweight (BW) and morphological trait measurements, namely heart girth (HG), shoulder height (SH), and body condition score (BCS) for a sample of 1447 goats and 588 sheep. These ranged from 0.19 to 0.94 for goats and 0.44 to 0.94 for sheep, and were statistically significant. In both animals, regardless of sex, the highest positive correlations were found between BW and HG, followed by BW and SH, then BW and BCS. The direct and indirect relationship between BW and morphological traits using a path analysis approach were also estimated. This analysis suggested that the direct effect of HG on BW was higher at 0.761 for male and 0.662 for female goats, respectively. Similarly, the direct effect of HG on BW was higher among sheep at 0.764 for males and 0.882 for females. The direct effects of SH in all the animals were also positively influenced by BW. It was concluded that among these three morphological traits, the most valuable for estimating the BW for goats and sheep in Botswana is HG, followed by SH. BCS was found non-significant. Path analysis therefore has an advantage over previous empirical studies by providing more detailed information on the relationships (direct and indirect) between these variables. A further implication of this study is that a conversion table could be constructed to help smallholder farmers to estimate the live weight of their sheep and goats from linear measurements. This would aid in the management and marketing of their livestock.
Keywords: Body condition score, heart girth measurement, live weight, shoulder height measurement, small ruminants
Introduction
The importance of small ruminant livestock to the socio-economic welfare of people in developing countries cannot be overemphasised, in terms of nutrition, income, insurance against emergencies, and for cultural and ceremonies purposes (Kosgey et al., 2008; Gwaze et al., 2009). Goats and sheep play a particularly important role in the socio-economic status of smallholder farmers in rural Botswana, with the majority of households (85 per cent) owning goats and/or sheep, while only 40 per cent are estimated to keep cattle (Statistics Botswana, 2015). The popularity of goats and sheep among rural households has been associated with their cheaper maintenance and upkeep costs, their tendency to require less land, and their greater tolerance of harsh environments in comparison with cattle (Nsoso et al., 2003; Alexandre & Mandonnet, 2005; Gwaze et al., 2009). The small body size of goats and sheep, their high digestive efficiency, low metabolism and efficient nitrogen economy, and efficient use of water all contribute to their capacity to cope with drought (Alexandre & Mandonnet, 2005). Alexandre & Mandonnet (2005) predicted that indigenous Tswana goats could survive up to 72 hours without water. These characteristics help to explain why governments and international development organizations recognise that goats and sheep provide an ideal vehicle to generate income, help to address food security, and improve the socio-economic welfare of many households in developing countries (Gwaze et al., 2009).
Livestock weighing machines are not usually available to small-scale farmers in Botswana, because of their high cost and users' lack of technical skills in operating and maintaining them. This suggests that small-scale farmers rely instead on visual estimation of the animal's BW (Yakubu, 2009). In Botswana, goats and sheep are usually slaughtered for social events, such as weddings, funerals, and traditional ceremonies, or sold to local butcheries and abattoirs. Marketing and sale prices of livestock in rural areas for these activities are primarily dependent on the live weight of the animal (Sebolai et al., 2012; Norris et al., 2015). When smallholder farmers have little experience with weight scales, their ability to estimate animal weight 'by eye' is likely to be relatively limited, and may result in incorrect weight being utilized to determine sale price (Sebolai et al., 2012). Having some knowledge of the weight and growth rates of goats and sheep is therefore vital information for smallholder farmers in making livestock management decisions and evaluating alternative strategies (ESGPIP, 2009).
In addition to their relevance to livestock transactions, estimated BWs are an informative measure of animal performance, and could be used to examine growth rates, responses of animals to different environmental conditions, nutritional requirements and strategies (Kunene et al., 2009; Moela, 2014). In arid grazing systems, BW measurements could provide a monitoring tool for assessing animal performance when pasture cover is monitored on grazing land, especially in communal systems. There is potential to address these issues by developing simple and reasonably accurate methods for estimating the BW of goats and sheep, using prediction equations based on linear body measurements that have been obtained with a metric tape rule (Worman et al., 1980; Sebolai et al., 2012).
The interrelationships between linear body dimensions and BW of goats and sheep in Botswana have been investigated (Owen et al., 1977; Worman et al., 1990; Nsoso et al., 2003; Sebolai et al., 2012). Owen et al. (1977) used linear regression models to estimate the relationship between live weight and HG for castrated indigenous goats and sheep in southern Botswana. They found a higher degree of correlation between the two variables in goats than in sheep. Nsoso et al. (2003) sought to explore the relationship between BW, BCS and HG in indigenous Tswana goats during dry and wet seasons in south-east Botswana. They concluded that BCS was the most useful of these indicators in identifying seasonal nutritional defects in goats. In a more recent study, Sebolai et al. (2012) applied a multiple regression model to estimate the relationship between live weight and linear traits in indigenous goats at various ages, identifying a significant increase in BW and linear associations relating to older animals.
However, the common methods of estimating the associations of BW and body measurements in Botswana do not adequately explain all the aspects of the relationship between variables, and may be inadequate in investigating the causal effects among biologically related variables. The main objective of this study was therefore to estimate the phenotypic relationships among BW and linear body measurements - HG, SH, and BCS - of indigenous goats and sheep. The authors used a path analysis approach to explore these relationships, which permits the determination of explanatory variables that largely affect the response variable, and have the potential to produce forecast indices at a higher degree of accuracy (Alwin & Hauser, 1975; Norris et al., 2015). Optimum regression equations were also estimated, and these could serve as useful practical tools for weight estimation in the field and for selection.
Materials and Methods
The purpose of this analysis was to present practical issues of measurement, and to identify path dependency among the variables being examined. The authors used primary data collected on BW, HG, SH, and BCS of goats and sheep aged one year or less. The age of 'less than one year' was chosen because it provided a well understood and easily identifiable class of animal on the farm that could always be checked by farm staff and enumerators by examining animals' teeth. The sample size of 1447 goats (749 males and 698 females) and 588 sheep (264 males and 324 females) was used to estimate the models. These data were collected from three agricultural districts in Botswana, namely Kweneng in the south, Central in the east and Kgalagadi in the south west, from September to November 2015 (Figure 1). Central and Kweneng districts can generally be classified as having a semi-arid climate, with an average annual rainfall of 400 mm to 460 mm (Burgess, 2006). On the other hand, Kgalagadi district can be classified as a desert climate with considerably lower average annual rainfall of 310 mm (Burgess, 2006).
The majority of farmers in the three districts were found to keep goats and sheep of the indigenous Tswana breed. Some farmers kept Dorper and Karakul sheep, while others kept Boer, Savannah and Kalahari goat breeds. Furthermore, some farmers kept cross-bred goats (Tswana/Boer). However, in this study only indigenous goats and sheep data were used in the analysis. This was because of difficulties in obtaining positive identification of breed for all non-indigenous animals owing to variations in local language and expressions, and also unfamiliarity with the breeding history of animals by on-farm staff at the time that the animals were weighed and measured. The livestock were maintained under a semi-intensive management system, whereby animals were released during the day, usually between 10:00 and 11:00, to forage in communal grazing areas, and housed overnight in kraals (fenced enclosures). Communal grazing areas were the main supply of feed for the majority of participating farmers, with only a small proportion undertaking supplementary feeding. Supplementary feed was usually used during the dry season, or given only to breeding animals (pregnant and nursing animals). Breeding was carried out throughout the year.
During data collection, animals measured across all farms and in all three districts were ear-tagged as a form of identification for repetitive collection of data. Initial measurements (BW, HG, and SH) were taken before the goats or sheep were released for grazing, while BCS was also measured. A second series of measurements was taken approximately four weeks after the initial measurement, to allow determination of growth rate.
The biological relationship between BW and morphological traits is complex (Norris et al., 2015). There are several analytical methods for estimating the relationship between BW and linear body measurements. Most are related to common statistical procedures such as analysis of covariance (ANCOVA), multiple regression, and residual analysis (Nespolo et al., 2003). The most commonly used approach to determine the degree and direction of the relationship between BW and other body measurements is a simple correlation analysis. However, one of its limitations is that it fails to explain all aspects of the relationships between variables, and therefore may be inadequate in investigating causal effects among biologically related variables (Yakubu, 2009; Yakubu & Mohammed, 2012; Norris et al., 2015). According to Nespolo et al. (2003), most statistical methods are good for treating physiological variables separately, but may be less effective in handling multiple variable analyses, especially when physiological variables differ in their dependence variable. In such cases, alternative models may be required to predict the BW of animals in various environmental conditions, management scenarios, and for different breeds.
One of the approaches that can be used to address some of these limitations is a path analysis model, involving structural equation modelling (SEM) (Nespolo et al., 2003). Path analysis measures the direct and indirect effects of one variable on another, and separates the correlation coefficients of variables into components of direct effect, indirect effect and compound path (Cankaya & Abaci, 2012; Norris et al., 2015). Path analysis uses only observed variables, and each variable has only one indicator (Alwin & Hauser, 1975). A path analysis model does not replace regression analysis. It is a complementary methodology that provides flexibility in determining the relationships between variables. Path analysis extends a multiple regression model by permitting the determination of explanatory variables that largely affect the response variable, and thus offers an opportunity to estimate BW with a higher degree of accuracy using linear body measurements (Norris et al., 2015). The concept of path analysis can be represented graphically using a path diagram to explain the relationship between the response variable and explanatory variables (Figure 2).
In Figure 2, straight arrows represent the direct effect of a body measurement trait on BW, while a curved double-headed arrow shows the covariance or correlation among variables. e1 is the residual effect. Mathematically, the path coefficient from an explanatory variable (X) to a response variable (Y) can be represented as follows (Cankaya & Abaci, 2012; Norris et al., 2015):

Where: PYXi represents a path coefficient (direct effect) from Xi to Y (i = HG, SH, and BCS)
bi represents the partial regression coefficient
Sxi is the standard deviation of Xi
Sy is the standard deviation of Y
It is assumed that the residuals (error terms) in path analysis are uncorrelated with variables in the model or with each other (Yakubu, 2010). Equation (1) produces direct effects, which is a part of its total effect that is not transmitted through intervening variables and has been held constant (Alwin and Hauser, 1975).
The indirect effects tell us how much of a given effect occurs due to manipulation of the predecessor variable of integrates, leading to changes in other variables, which in turn change the consequent variable (Alwin & Hauser, 1975).
The indirect effect of Xi on Y through Xj can be calculated as follows (Norris et al., 2015):

Where: IEYXi = the direct effect of Xi via Xj on Y
rXiXj = correlation coefficient between ith and jth independent variables
PY.Xj = path coefficient indicating the direct effect of jth independent variable on the dependent variable
rij is the correlation coefficient
The following regression model was used to estimate the relationship between BW and other body measurements traits:

Where: Y= the predicted response variable (BW)
b0 = intercept; b's= regression coefficients
x's= explanatory variables (HG, SH and BCS)
e = error term
The authors estimated the correlation coefficients of body measurements and BW for both sexes in all the animals using a Pearson correlation in STATA Statistical Software version 14 (StataCorp, 2015). These estimated correlation coefficients are presented in Table 2. This was followed by path analysis estimation, which produced the direct effect (beta coefficient) of each body measurement on BW (Tables 3 and 4). Based on the estimated direct effects, the authors used Equation 2 to calculate the indirect effect of each body measurement for each sex and animal combination. Path analysis procedures in the STATA software package were used to assess relationships between variables and the way in which these influenced BW. Pairwise correlations and regression models among BW and morphometric traits were determined separately for each sex of goats and sheep, respectively. The authors used R-squared as a statistical measure of how closely the data fitted the regression line. After estimating a regression model, they used a variance inflation factor (VIF) to detect multicollinearity, that is, to quantify how much the variance was overestimated. This produces a tolerance, which is defined as 1/VIF and was used to check the degree of collinearity.
Results and Discussion
Descriptive statistics, namely means, standard deviations and coefficient variation of BW and body measurements, are shown in Table 1. Male goats had higher average BW, HG, SH and BCS than their female counterparts. Male sheep also had higher average BW, HG and SH, though the female sheep recorded a slightly higher average BCS. Table 1 shows the differences between males and females in goats and sheep in all body measurements. Sebolai et al. (2012) similarly found significant differences in live weight between male and female indigenous goats, and among age groups. Given the differences between sex groups, illustrated in Table 1, the implication for the current analysis was that models may be more usefully developed within sex groups.
Pairwise correlations between BW and other body measurements were also estimated, and are presented in Table 2. All correlations between BW and the other body measurements were found to be positive, and statistically significant at 95 per cent (P <0.05). In both sheep and goats, regardless of sex, the highest correlations were found between BW and HG, followed by BW and SH, and then BW and BCS. The correlation between HG and BCS was lowest for female goats and male sheep. These results are consistent with those elsewhere for indigenous goats (Norris et al., 2015) and sheep (Kunene et al., 2009) in South Africa.
The calculations of path coefficients are presented in Tables 3 and 4. These allow direct comparison of values that reflect the relative importance of independent variables in explaining variation in the dependent variable. The correlation coefficient between HG and BW was positive and higher than other measurements. Also, its direct effect on BW was higher, at 0.761 for male and 0.662 for female goats. Similar results were observed by Sebolai et al. (2012) for Tswana goats, and Norris et al. (2015) for indigenous goats in South Africa. For both male and female goats, the authors found the direct effect on BW was lower than its total indirect effect (0.874 and 0.702, realized mostly through SH). The correlation coefficient between BCS and BW in goats was lower than other measurements, but still significant. Its direct effect on BW was low in both male and female goats, but not significant for male goats (P >0.05). Also, its direct effect (0.0222 for male goats and 0.021 for female goats) was higher than its indirect effect (0.014 for male goats and 0.007 for female goats).
The correlation coefficient between HG and BW was positive and higher (0.933 for male and 0.938 for female) than other traits (Table 4). Its direct effect on BW was also higher, at 0.764 for male and 0.882 for female sheep. The direct effect of BCS on BW was low, but significant (at P <0.05) in both male and female sheep. Although the correlation coefficient between SH and BW was high and significant for male sheep (0.809 at P <0.05) and for female sheep (0.769 at P <0.05), its direct effect was low, but significant for male sheep (0.17 at P <0.05), and low and insignificant for female (0.339 at P >.05). For both male and female sheep, the direct effect of other body measurements on BW was lower than its total indirect effect (0.874 and 0.702, realized mostly through SH). The correlation between BCS and BW in goats was lower than other measurements, but still significant. Its direct effect on BW was low in both male and female goats, but not significant for male goats (P >0.05). Its direct effect (0.0737 for male sheep and 0.0571 for female sheep) was also higher than its indirect effect (0.049 for male sheep and 0.048 for female sheep).
Tables 5 and 6 present the results of the regression analysis, in which standardised regression coefficients, standard error, t-statistical significance levels and VIF values are given to explain the relationship between the other body measurements and BW of goats and sheep. For male goats and female goats, HG and SH had positive and significant effect on BW (P <0.05), while BCS was not significant (Table 5). The other measurements explained 83.5 per cent of variance in the bodyweight of male goats and 91 per cent for female goats. Moreover, the VIF values for the explanatory variables were less than 10 in both cases, meaning that the problem of multicollinearity was not detected. For sheep, all other body measurements had a positive and significant effect on BW (P <0.05) in male sheep, while in female sheep the effect of SH was insignificant on BW. The other measurements explained 88.3 per cent and 88.2 per cent of variance for male and female sheep, respectively. Nor did the authors find any problem of multicollinearity in sheep, since the VIF of explanatory variables was less than 10.
From Table 5 the results of the regression analysis for male and female goats can be derived:

After deleting insignificant predictor variables, the optimum regression model was found to be:

Similarly, from Table 6, the results of regression analysis for sheep may be derived:

After deleting insignificant predictor variables, the optimum regression model was
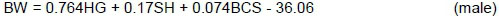

Generally, in both goats and sheep, the authors found HG was most important in the prediction of BW from the other body measurements. A number of previous studies had also found HG was the most important predictor for BW in goats (Yakubu, 2009; Sebolai et al., 2012; Norris et al., 2015) and in sheep (Kunene et al., 2009; Yakubu, 2010). Therefore, based on the current findings, it could be concluded that among the three physical traits measured for this study, the most valuable in the estimation of BW for both goats and sheep is HG. It has been argued that a high correlation between HG and BW could be because of muscle and less fat, together with bone structure, contribute to the formation of HG (Yakubu, 2010). On the other hand, correlation coefficients between BW and BCS were shown to be low compared with other measurements. This implies that attempts to predict BW based only on BCS would be of little value. Nsoso et al. (2003) also found that changes in the BW of Tswana goats did not always parallel BCS. They attributed this to the concept that BCS reflects body fat, as it appeared to be a more useful trait than BW for assessing nutritional consequences of the dry versus the wet season under conditions of extensive management (Nsoso et al., 2003).
Conclusion
The implications of this study are that the BW of goats and sheep may be predicted using body measurements, and that this is particularly relevant to poor smallholder farmers, for whom scales are not readily available. The predicted equations could also serve as useful practical tools for livestock farmers, researchers and rural development workers for breeding selection. From these equations, conversion tables could be constructed and provided to smallholder farmers to use to estimate the live weight of their animals via simple linear measurement. Further, the conversion table should be simplified to encourage efficient utilization by uneducated rural poor smallholder farmers.
Acknowledgements
This work was supported by the Food and Agriculture Organization of the United Nations project titled Improving Methods for Estimating Livestock Production and Productivity, which was implemented as part of the Global Strategy for Improving Agricultural Statistics. The authors gratefully acknowledge the support of Botswana Department of Agricultural Research (DAR), including provision of transport and technical and logistical support from DAR researchers, technical officers and extension officers during fieldwork activities. They are grateful to all farmers who gave their time to participate in this research.
Authors' Contributions
All authors of this research paper participated directly in the planning, implementation and analysis of this study. All the authors read and approved this final version. The manuscript has not been published or accepted for publication or under editorial review for publication anywhere. The contents of this manuscript will not be copyrighted, submitted, or published elsewhere, while evaluation by this journal is under consideration.
Conflict of Interest Declaration
There are no conflicts of interest.
References
Alexandre, G. & Mandonnet, N., 2005. Goat meat production in harsh environments. Small Rumin. Res. 60(1), 53-66. [ Links ]
Alwin, D. F. & Hauser, R. M., 1975. The decomposition of effects in path analysis. Am. Sociol. Review, 40(1), 37-47. [ Links ]
Burgess, J., 2006. Country pasture/forage resource profiles. Food and Agriculture Organization of the United Nations (FAO), Rome, Italy. [ Links ]
Cankaya, S. & Abaci, H. S., 2012. Path analysis for determination of relationships between some body measurements and live weight of German Fawn x Hair crossbred kids. Kafkas Üniversitesi Veteriner Fakültesi Dergisi, 18(5), 769-773. [ Links ]
ESGPIP (Ethiopia Sheep and Goat Productivity Improvement Program). 2009. Estimation of weight and age of sheep and goats. ESGPIP Technical Bulletin No. 23. [ Links ]
Gwaze, F. R., Chimonyo, M. & Dzama, K., 2009. Communal goat production in Southern Africa: A review. Trop. Anim. Health and Prod. 41(7), 1157-1168. [ Links ]
Kosgey, I. S., Rowlands, G. J., Van Arendonk, J. A. M. & Baker, R. L., 2008. Small ruminant production in smallholder and pastoral/extensive farming systems in Kenya. Small Rumin. Res. 77(1), 11-24. [ Links ]
Kunene, N. W., Nesamvuni, A. E. & Nsahlai, I. V., 2009. Determination of prediction equations for estimating bodyweight of Zulu (Nguni) sheep. Small Rumin. Res. 84(1), 41-46. [ Links ]
Moela, A. K., 2014. Assessment of the relationship between bodyweight and body measurement in indigenous goats using path analysis. MSc Agric. dissertation, University of Limpopo, Turfloop Campus. [ Links ]
Nespolo, R. F., Arim, M. & Bozinovic, F., 2003. Body size as a latent variable in a structural equation model: thermal acclimation and energetics of the leaf-eared mouse. J. Exp. Biology. 206(13), 2145-2157. [ Links ]
Norris, D., Brown, D., Moela, A. K., Selolo, T. C., Mabelebele, M., Ngambi, J. W. & Tyasi, T. L., 2015. Path coefficient and path analysis of body weight and biometric traits in indigenous goats. Indian J. Anim. Res. 49(5), 573-578. [ Links ]
Nsoso, S. J., Aganga, A. A., Moganetsi, B. P. & Tshwenyane S. O., 2003. Body weight, body condition score and heart girth in indigenous Tswana goats during the dry and wet seasons in southeast Botswana. Liv. Res. Rural. Dev. 15 (32). [ Links ]
Owen, J. E., Norman, G. A., Fisher, I. L. & Frost, R. A., 1977. Studies on the meat production characteristics of Botswana goats and sheep. Part I: Sampling, methods and materials, and measurements on the live animals. Meat. Sci. 1(1), 63-85. [ Links ]
Sebolai, B., Nsoso, S. J., Podisi, B. & Mokhutshwane, B. S., 2012. The estimation of live weight based on linear traits in indigenous Tswana goats at various ages in Botswana. Trop. Anim. Health Prod. 44(4), 899-904. [ Links ]
StataCorp. 2015. Stata Statistical Software: Release 14. College Station, TX: StataCorp LP. [ Links ]
Statistics Botswana. 2015. 2013 Annual Agricultural Survey Report. Statistics Botswana, Gaborone. [ Links ]
Worman, F. D., Thedford, T. R., Kelemogile, K. M. & Baathodi, J. A., 1990. Heart girth measurement as an estimate of weight for Tswana goats. ATIP Working paper no. WP-30, Botswana. [ Links ]
Yakubu, A., 2009. Fixing collinearity instability in the estimation of body weight from morpho-biometrical traits of West African Dwarf goats. Trakia J. Sci. 7(2), 61-66. [ Links ]
Yakubu, A., 2010. Path coefficient and path analysis of body weight and biometric traits in Yankasa lambs. Slovak J. Anim. Sci. 43(1), 17-25. [ Links ]
Yakubu, A. & Mohammed, G. L., 2012. Application of path analysis methodology in assessing the relationship between body weight and biometric traits of red Sokoto goats in northern Nigeria. Bio. Anim. Hus. 28(1), 107-117. [ Links ]
Received 19 June 2017
Accepted 30 August 2017
First published online 5 October 2017
# Corresponding author: otemoso2@une.edu.au














