Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Animal Science
versão On-line ISSN 2221-4062
versão impressa ISSN 0375-1589
S. Afr. j. anim. sci. vol.45 no.2 Pretoria 2015
http://dx.doi.org/10.4314/sajas.v45i2.1
REVIEW
Genetic prediction models and heritability estimates for functional longevity in dairy cattle
V.E. Imbayarwo-ChikosiI, #; K. DzamaI; T.E. HalimaniIII; J.B. van WykIV; A. MaiwasheII; C.B. BangaII
IDepartment of Animal Sciences, University of Stellenbosch, Private Bag X1, Matieland 7602, South Africa
IIAgricultural Research Council, Animal Breeding and Genetics Institute, Private Bag X2, Irene 0062, South Africa
IIIDepartment of Animal Science, University of Zimbabwe, P.O. Box MP167, Mt. Pleasant, Harare, Zimbabwe
IVDepartment of Animal, Wildlife & Grassland Sciences, University of the Free State, P.O. Box 339, Bloemfontein 9300, South Africa
ABSTRACT
Longevity is a major component of the breeding objective for dairy cattle in many countries because of its high economic value. The trait has been recommended for inclusion in the breeding objective for dairy cattle in South Africa. Linear models, random regression (RR) models, threshold models (TMs) and proportional hazard models (PH) have been used to evaluate longevity. This paper discusses these methodologies and their advantages and disadvantages. Heritability estimates obtained from these models are also reviewed. Linear methodologies can model binary and actual longevity, while RR and TM methodologies model binary survival. PH procedures model the hazard function of a cow at time t derived from survival from first calving to culling, death or censoring. It is difficult to compare methodologies for sire evaluation and ranking across countries because of the variation in the definition of longevity and the choice of model. Sire estimated breeding values (EBVs) are derived differently for the models. Sire EBVs from PH models are expressed as deviations of the culling risk from the mean of the base sires, expected percentage of daughters still alive after a given number of lactations, expected length of productive life in absolute terms or as standard deviation units. In linear, TM and RR modelling, sire EBVs for longevity have been expressed as deviations of survival from the mean estimated with Best Linear Unbiased Prediction (BLUP). Appropriate models should thus be developed to evaluate functional longevity for possible inclusion in the overall breeding objective for South African dairy cattle.
Keywords: Dairy cattle, proportional hazards, random regression, survival analysis
Introduction
In line with global trends in dairy cattle breeding, the South African dairy industry has adopted the balanced breeding concept (Banga et al., 2014). This entails the inclusion of all economically relevant traits in the breeding objective. Traits such as longevity, cow fertility, udder health and functional efficiency have increasingly become important in national selection objectives, which were previously based on milk and component production traits alone (Carlén et al., 2005; Miglior et al., 2005; Sewalem et al., 2005a). The breeding objective for South African Holstein cattle has already incorporated calving interval and somatic cell count (Banga, 2009). Recent studies (Banga et al., 2013; 2014) recommend the inclusion of other traits such as live weight and longevity.
The economic value of longevity cannot be overemphasized, as it is directly related to total herd profit and profit per day (Gill & Allaire, 1976). The trait has been reported to be important in South African dairy cattle, more so for the Holstein than the Jersey breed (Banga et al., 2013). Length of productive life is reported to account for as much as 50% of the economic value of production traits (Jairath & Dekkers, 1994). The high economic value of longevity has been attributed to the dynamics of the trait in herds that depend on the extent of voluntary and involuntary culling. A decrease in involuntary culling increases opportunities for voluntary culling and retention of high-yielding cows for longer periods. The corresponding increases in the proportion of higher-yielding mature cows and subsequent decline in the proportion of young cows allows older cows to reach their age-dependent maximum milk yield (Vukasinovic et al., 2001; Strapák et al., 2005). This lowers costs associated with the supply of energy and protein to young cows, which require the nutrients to attain physiological maturity, pregnancy and lactation. Subsequently, farmers will have better control of production costs associated with rearing and purchasing replacement of heifers as there will be more heifers to sell (Van Arendonk, 1986; Forabosco et al., 2004; Banga et al., 2013). Despite these obvious economic advantages, studies in South African dairy cattle have observed a decline in longevity and other fitness traits (Banga et al., 2002; Dube et al., 2008; Makgahlela et al., 2008), probably because these traits were not included in the dairy cattle breeding objective in the past. To be included, this objective, longevity has to be evaluated. Accurate estimation of breeding values is thus a prerequisite to including the trait in the breeding objective.
Various approaches have been used to estimate breeding values for longevity, namely linear (e.g. Du Toit, 2011; Kern et al., 2014), random regression (RR) (e.g. Van Pelt & Veerkamp, 2014), threshold (TM) (e.g. Kern et al., 2014) and PH models (e.g. Sasaki et al., 2012). Linear, TM and RR models generally produce lower estimates of heritability (0.01 - 0.10) for longevity than PH models on original scale (0.15 -0.22). Linear, TM and RR methodologies can handle multiple trait models, thereby giving direct estimates of genetic correlations between longevity and other traits. However, PH models cannot handle multiple-trait models and can only perform univariate analysis. They are therefore unable to give direct correlations between longevity and type traits. Instead, through stepwise inclusion of type traits in the PH model, the contribution of each type trait to the relative risk of culling can be determined by estimating relative risk ratios. If all the other covariates in the model are kept constant, the contribution of the various type traits to the risk of culling can be determined.
Survival analysis was first proposed for use in animal breeding by Smith & Quaas (1984) for studying longevity in dairy cattle. Since then, the availability of appropriate tools and software to analyse longevity has seen many countries rapidly including the trait in the composite selection strategy for increased production and ultimately herd profitability (Sewalem et al., 2005b; M'hamdi et al., 2010). This has not been the case with South African dairy cattle, although there has been some research on longevity (e.g. Setati et al., 2004; Du Toit, 2011). In his study, Du Toit (2011) highlighted the shortcomings of the linear model approach authors were using to evaluate longevity in South African Jersey cattle and recommended the application of survival analysis through PH models. This paper reviews the various ways in which longevity has been defined in several studies, its economic importance in different populations and the models that have been applied for its genetic prediction. The estimates of heritability obtained from various models are summarised.
Trait definition
Longevity or survival measures follow-up time from a defined starting point to the occurrence of a given event (Beswick et al., 2004; Flynn, 2012). It can be true or functional longevity. In true longevity, the reasons that animals leave the herd are not considered (Ducrocq et al., 1988). When true longevity is adjusted for production, it gives an approximation of functional longevity (Ducrocq & Solkner, 1998). Functional longevity therefore refers to the ability of an animal to delay involuntary culling, that is, the ability of the cow to avoid culling for reasons other than its milk production. This indicates the health, fertility and overall fitness of an animal (Bunger & Swalve, 1999; Zavadilová & Stípková, 2012) and is therefore of particular interest to the breeder (Vukasinovic, 1999). Many measures of functional longevity have been proposed, namely age, number of lactations, length of productive life and lifetime production at time of disposal (Ducrocq et al., 1988).
Longevity has assumed various trait definitions (Vollema & Groen, 1997; Brotherstone et al., 1998), all of which are based on age at culling or death (uncensored) or censoring and survival to a given age or predetermined period within or across lactations (Jamrozik et al., 2008; Forabosco et al. 2009). It has been scored as a binary trait (e.g. Ajili et al., 2007; Holtsmark et al., 2009; Du Toit, 2011), in which animals are scored based on whether they have survived up to a specific time, age or event, and analysed with linear regression (e.g. Du Toit et al., 2009) RR (e.g. Veerkamp et al., 2001; Van Pelt & Veerkamp, 2014) or TM models (e.g. Boettcher et al., 1999; Van der Westhuizen et al., 2001; Holtsmark et al., 2009). The survival period could be limited to within lactation (e.g. Holtsmark et al., 2009) or could be across all lactations (e.g. Caraviello et al., 2004a; b; M'hamdi et al., 2010). This definition is constrained because only animals with an opportunity to survive the entire specified period can be used in genetic analysis while records from the most recent animals are excluded. Besides, cows that are culled or where recording ended before the specified time are usually considered missing and excluded from analysis (Veerkamp et al., 2001). In South Africa, longevity in Holstein cattle has been expressed as the number of lactations initiated among dairy cattle (Setati et al., 2004). Maiwashe et al. (2009) and Van der Westhuizen et al. (2001) regarded longevity in South African beef cattle as stayability, defined as the probability that a cow would reach a certain age, given the opportunity to reach that age. However, Du Toit (2011) expressed survival in South African Jersey cattle as a binary trait, in which survival to the next lactation was determined based on the presence or absence of a subsequent lactation. Survival in a given lactation was coded 1 if the cow survived during that lactation; and 0 if the cow was culled during that lactation or if the number of days between the current calving and extraction date exceeded 581.
Sewalem et al. (2005a; b) defined the length of productive life as time in days from one calving to the next calving, death or culling. Holtsmark et al. (2009) expressed longevity variously as herd life in the first lactation, calculated as number of days from calving to culling, censoring or second calving; and as herd life in the first five lactations, calculated as number of days from first calving to culling, death, censoring or sixth calving. Longevity was also expressed as survival scores for lactations 1 to 5, as well as survival to 365 days after first calving, after which an animal was scored 0 if it was culled before the 365 days, otherwise it was scored 1. Tsurunta et al. (2005) defined longevity as the total number of lactation days up to 84 months of age with restrictions of fewer than or equal to 305, 500 or 999 days per lactation, as well as number of days from first calving date to the culling date, including dry periods. Elsewhere, longevity was expressed as functional herd life (e.g. Chirinos et al., 2007), which is the herd life of a cow adjusted for individual milk yield relative to milk production of the entire herd. Table 1 shows the longevity trait definitions that have been adopted for national genetic evaluation of dairy cattle for countries that participate in Interbull multiple-trait across-country evaluations (MACE) programme (Interbull, 2014).
Economic value of longevity
The economic value of a trait is defined as the amount by which profit is expected to increase for each unit improvement in the genetic merit of that trait while all other traits in the breeding objective are held constant (Hazel, 1943). Vargas et al. (2002) defined the economic value of a trait in dairy cattle as change in farm profit per average lactating cow per year because of one unit change in genetic merit of the trait of interest. Profit can be expressed as profit per day of herd life, profit per herd year and lifetime profit. In South Africa, Banga et al. (2013) reported increases in profit of between ZAR 3.59 and ZAR 3.68 for both pasture-raised and concentrate-fed Holstein cattle and between ZAR 1.09 and ZAR 2.29 for pasture-raised Jersey cattle per day increase in longevity. Corresponding values for concentrate-based Jersey cattle systems ranged from ZAR 1.54 to ZAR 2.29. Elsewhere, Vargas et al. (2002) noted an increase of US$ 2.42 per cow per year per 1% increase in survival rate in Costa Rican Holsteins, which was within the range of US$ 1.35 to US$ 4.90 reported by Visscher et al. (1994) for Australian Holsteins. Rogers et al. (1988) observed an increase in net revenue per cow per year of US$ 22.00 following a reduction of 2.9% in involuntary culling rates and the subsequent associated increase in longevity.
In Iranian Holsteins, economic values for longevity were estimated under three schemes: profit maximization, maximum economic benefit, and economic minimization. Absolute profit increased with longevity by $ 6.20 and $ 36.33 per month under profit maximisation and maximum economic benefit schemes, respectively. However, profits declined by $ 20.40 per month for increasing in longevity with the economic minimization scheme (Sadeghi-Sefidmazgi et al., 2009). Positive economic values support the incorporation of longevity in the selection objective for dairy cattle as a strategy for improving selection for net economic merit. These values have been reported to be sensitive to a reduction in the price of milk solids and population mean (Vargas et al., 2002; Banga et al., 2014).
Modelling survival data
Nature of survival data
Longevity manifests itself as a threshold trait. Threshold traits are not continuous in their expression and exhibit distinct categorical phenotypes. The inheritance of such traits lies in the understanding that the trait has an underlying continuity with a threshold manifestation that imposes a discontinuity on its expression (Falconer & Mackay, 1996). When plotted, longevity data are characteristically skewed to the left because a larger proportion of cows are usually in early lactation (Caraviello et al., 2004b). Environmental factors that influence an animal's risk of culling at any given time may differ dramatically, based on prevailing conditions, and will probably change throughout its lifetime, rendering the factors time dependent (Caraviello et al., 2004a; Zavadilová et al., 2011; Flynn, 2012). In any instance, survival data will have complete and incomplete records. Events such as culling and death may be known to have occurred and will therefore be uncensored. At the same time, animals may have been lost to follow-up and events such as culling and death may not be known to have occurred. Animals may also still be alive at time of analysis, so that only the lower bounds of their productive life will be known. Such records cannot be excluded from evaluation of survival, as this might lead to bias, and are therefore censored (Beswick et al., 2004). Appropriate modelling strategies for such data should accommodate these unique characteristics without losing important phenotypic, additive and environmental variance information necessary for genetic evaluation (Weigel et al., 2003).
Models for analysis
Linear, TM, RR and PH models have all been used in the genetic evaluation of animals for longevity. Table 1 shows the models used for national genetic evaluations of survival, depending on the definition of the survival trait by country. As of 2014, of the 20 countries on Interbull that were evaluating longevity at national level, more than 50% were using sire-maternal grandsire (S-MGS) of sire Weibull models to evaluate longevity. These included France, Netherlands, Spain, Germany, Czech Republic, Hungary, Poland and Italy (Interbull, 2014). A sizeable number of countries were using the linear models in which survival is usually evaluated in single- or multi-trait analysis with animal, sire, maternal grandsire or sire-maternal grandsire survival models (Holtsmark et al., 2009). In South African cattle, survival has been evaluated using a multiple-trait BLUP animal model (e.g. Setati et al., 2004; Du Toit, 2011) and TM models (e.g. Maiwashe et al., 2009). Until 2006, genetic parameters for functional longevity in Japanese dairy cattle were estimated using a linear multi-trait animal model with direct effects of milk yield and seven conformation traits (Sasaki et al., 2012). Countries such as Australia, Canada, Ireland and New Zealand use a multi-trait linear animal model to evaluate longevity in all dairy breeds. Great Britain uses a bivariate animal model for all breeds, while the USA and Israel evaluated longevity with a single-trait BLUP animal model for all breeds. Belgium is the only country that uses RR lactation survival animal models to evaluate longevity (Interbull, 2014). Modelling survival for genetic evaluation of functional longevity has therefore not been standard across countries. These variations in modelling methods imply that sires cannot be compared and ranked across countries, although this depends largely on the correlation between these differently defined traits. Therefore, there is no universal system for sire evaluation and comparison as with production traits (Sewalem et al., 2005b).
1. Linear models
Linear animal and sire models have been used by a number of researchers to evaluate survival (e.g. Caraviello et al., 2004a; Holtsmark et al., 2009; Du Toit, 2011; Zavadilová & Stípková, 2012). In these analyses, indicators of longevity such as whether the animal was still alive at a particular time or at the beginning of a given lactation period were discussed and used (Vukasinovic, 1999; Holtsmark et al., 2009). A value of time (t) on a time scale is decided upon and the record of each animal is converted into a 0 or 1 trait, depending on whether the animal is alive at time t or not. Longevity in this case is considered a binary trait, the analysis of which, excluding fixed effects, is based on the model:
yij(t) = μ + si + eij (i)
where yij(t) is 0 if the jth progeny of sire i is not alive at time t, and 1 otherwise; μ is the population mean; si is breeding value of sire i on the binary scale and eij are random residuals. Linear modelling of binary survival has been carried out in Canadian Holsteins (Boettcher et al., 1999), Czech Fleckvieh (Zavadilová et al., 2009), Norwegian Red (Holtsmark et al., 2009), South African Jersey cattle (Du Toit, 2011), Italian Brown Swiss (Samoré et al., 2010) and others (e.g. Jamrozik et al., 2008; Zavadilová & Stípková, 2012). Linear models have also been used to analyse survival based on actual and projected records, using currently available information (VanRaden & Klaaskate, 1993). Models have been developed for projecting the herd life of cows still alive at time of analysis (e.g. Brotherstone et al. 1998; Caraviello et al., 2004a; Zavadilová & Stípková, 2012) and then applying linear models to the combined datasets with the actual and the projected herd life.
The major advantage of linear modelling is its relative simplicity (Boettcher et al., 1999) and, as demonstrated by a number of researchers (e.g. Du Toit, 2011), its ability to run a univariate or multi-trait analysis with an animal, sire, maternal or maternal grandsire model, which is not possible with PH modelling. The major criticisms of linear models are that they make many incorrect assumptions, that the true survival times are continuous, and that they are not necessarily normally distributed (Yazdi et al., 2002). Many reference times can be chosen, leading to loss of substantial information. Besides, animals that are culled or die one day or one year before the reference time are all treated in the same way, leading to incorrect evaluation of individual animals (Ducrocq et al., 1988). In addition, survival times are derived from a product, rather than a sum of time-dependent and independent factors that influence longevity (Beilharz et al., 1993; Vukasinovic, 1999) so that if at least one of these factors is defective, the longevity of an individual animal is impaired (Ducrocq & Skolner, 1998). This reduces the applicability and value of linear models in estimating genetic parameters for survival. Linear models are less appropriate for analysis of binary traits than for continuous variables such as milk yield (Boettcher et al., 1999) since the distribution of binary traits is discontinuous and therefore categorical. Analysing such data with linear procedures on the assumption of continuous phenotypic distributions ignores the discontinuity of such threshold traits. According to Gianola (1982), the main theoretical objection to using BLUP with categorical data is that breeding values and residuals are not independent of each other.
Although the variable of interest is time to death, culling or censoring, when data are analysed, culling or death may not have occurred for some animals. Where these events have occurred, the effect of independent variables on the variable of interest should be assessed, which, again is not easily accomplished through linear models. Furthermore, linear models assume that non-genetic factors that influence the time to culling or death have a constant effect throughout the life of the animal. The conditions to which animals are exposed are time dependent. Nor can linear models account optimally for time dependency of variables or non-linearity in data (Vukasinovic, 1999; Caraviello et al., 2004a; Zavadilová et al., 2011). Nevertheless, linear models have been used to evaluate binary survival and absolute longevity in a number of studies (e.g. Tsurunta et al., 2005; Zavadilova et al., 2009; Du Toit, 2011).
2. Random regression survival animal models
The RR models were first proposed by Henderson (1982) and Laid & Ware (1982) for use in cattle evaluation. However, it was not until 1994 that Schaeffer & Dekkers (1994) proposed their use for analysis of test-day production records in dairy cattle breeding. In 1999 Veerkamp et al. (1999) proposed their use for evaluation of survival through longitudinal generalization of the multiple-trait models. In RR modelling, binary observations (0 = culled, 1 = survived) are assigned to each discrete unit in the cow's lifetime, such as per lactation or per month after first calving, after which a linear model with RRs for an animal genetic effect can be fitted to this data for genetic evaluation. Breeding values for survival can then be generated for both cows and sires and for each point on the trajectory (Jamrozik et al., 2008). Linear regression of observations of the trait under consideration on indicator variables is performed with the animals' additive genetic effects fitted as random effects. Since functions of time such as days in milk can easily be modelled within the mixed-model framework (Henderson, 1982), trajectories can be described. The covariables are usually non-linear functions such as polynomials or splines relating time to the traits. Fitting sets of RR coefficients for each individual random factor (e.g. additive genetic and permanent environmental effects) produces estimates of the corresponding trajectories (Dzomba et al., 2010). The univariate RR model can be extended to survival analysis and presented as follows (Schaeffer, 2004):
Yijkimnoit = (YS : Ht)ij + (YSAP:t)ik| + r(a,x,m1)n + r(pe,x,m2)k + eukimno:t (ii)
where yijklmno:tis the nth observation on the kth animal at time t belonging to the ith fixed factor and jth group; YS is the ith year-season of first calving, H is the jth herd, A is the kth age at first calving group, P is the lth production level as a deviation from herd average in first lactation, r(a, x, m1)k = 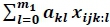 is the notation adopted for RR function where a denotes the additive genetic effects of the kth animal, x are appropriate orthogonal polynomials of time, t, after first calving, a are the RR coefficients for additive genetic value of animal n, pe are the RR coefficients for permanent environmental effects of animal n and eijklmn:o is the residual effect.
is the notation adopted for RR function where a denotes the additive genetic effects of the kth animal, x are appropriate orthogonal polynomials of time, t, after first calving, a are the RR coefficients for additive genetic value of animal n, pe are the RR coefficients for permanent environmental effects of animal n and eijklmn:o is the residual effect.
The basic idea underlying RR models consists of modelling the additive genetic values as a function of an observed dependent variable through a set of random coefficients. Models used in genetic evaluation of animals through RR involve continuous functions to describe fixed and random effects. The EBVs are then predicted by continuous functions of deviations from each animal, considered random, in relation to average curve, considered fixed (Mota et al., 2013). RR models have been used in dairy cattle breeding to evaluate production traits (e.g. Jamrozik & Schaeffer, 1997; Mrode & Swanson, 2004) and other traits such as susceptibility to mastitis and fertility (e.g. Carlen et al., 2005; Tsurunta et al., 2009), conformation, body condition scores, feed intake, heart girth measures (Schaeffer, 2004) and survival (Jamrozik et al., 2008).
The RR models can generate sire and dam proofs for survival for each point on the trajectory. They are relatively more robust to censoring data (Veerkamp et al., 1999) and have direct links with PH and generalized linear models. RR models can handle time-dependent fixed effects and offer scope for using multiple-trait analysis of yield, functional traits and survival (Veerkamp et al., 2001). In addition, they can handle random animal effects, unlike PH models. The number of distinct genetic effects per animal can be optimized and it should be straightforward to estimate genetic and environmental correlations with other predictors of longevity, for example linear-type traits (Brotherstone et al., 1998; Jairath et al., 1998). When compared with the multi-trait linear model approach to analysis of survival data, RR models have the advantage that fewer parameters are required to explain the genetic variation in lifespan (Veerkamp et al., 2001).
Practical applications of RR models in animal breeding have been limited, however, owing to problems associated with the large number of parameters to be estimated, poor polynomial approximation and the need to analyse much larger sets of data, implausible estimates at the extremes of trajectories, and associated high computational requirements (Dzomba et al., 2010). Besides, in extremes of the age range or when data are insufficient, the estimated parameters may not be accurate (Meyer, 1999). By treating binary data as if they were continuous, and assuming uncorrelated normally distributed residuals in each lactation, the procedure ignores the effect of repeated records. More appropriate error structures would therefore be required (Veerkamp et al., 2001).
3. Threshold models
The TMs include sequential threshold models (STMs), threshold repeatability models (TRMs) and threshold cross-sectional models (TCMs). In threshold modelling, survival is considered a binary trait, as in some linear modelling (e.g. 0 = alive at time t and 1 = dead at time t). The probit model postulates that a linear model with a non-linear relationship between the observed and underlying scale describes the underlying variable called liability (Gianola & Foulley, 1983). A generalized linear model is therefore linked to the binomial trait with a probit link function. TMs have been used to evaluate survival to weaning in pigs (Cecchinato et al., 2010), reproductive traits in South African beef cattle (Van der Westhuizen et al., 2001) and survival in dairy cattle (Holtsmark et al., 2008; 2009). Holtsmark et al. (2009) evaluated survival within the first five lactations of Norwegian Red dairy cattle using a TRM, assuming a probit link function, and the threshold cross-sectional probit link model (TCM). Survival in this study was scored 1 if the cow had a calving k + 1; 0 if the cow was culled in lactation k; and missing if the cow was culled before the lactation or if recording period ended during lactation k. Animals that were culled on the same day they calved were given a herd life of 1.
The STMs (described by Albert & Chib, 2001) have been used to analyse the number of lactations per cow (functional discrete time survival) that occur in a sequential order (Gonzalez-Recio & Alenda, 2007; Holtsmark et al., 2009). The basic principle of STM is that for an observation to be present in a given lactation, it must have survived through all previous lactations. This means that for any observation at a given stage, the animal must have passed through all previous stages (Gonzalez-Recio & Alenda, 2007) and, by implication, the method accounts for what occurred in the previous stages, thereby increasing reliability of the estimates obtained from it. This approach can describe the physiological or decision processes that occur in sequential order, and the model can handle large datasets. Sequential modelling, unlike PH modelling, is capable of using an animal model, but this increases computation time. Furthermore, STMs can accommodate time-dependent covariates and censoring (Gonzalez-Recio & Alenda, 2007; Cecchinato et al., 2010).
The major drawback of TMs is that the heritability estimates obtained from them are from an underlying scale, yet the observed phenotypes are on the same scale as those for linear models. Selection on the EBVs from TMs would not yield greater genetic progress on the observed scale than selection on EBVs from linear model (Boettcher et al., 1999). Further studies are needed to improve knowledge of the behaviour of STMs.
4. Proportional hazard models
The use of PH models in dairy cattle breeding was initially suggested by Smith & Quaas (1984) and is now widely accepted for analysis of functional longevity (e.g. Durr et al., 1999; Caraviello et al., 2004a; b; Mészáros et al., 2008; M'hamdi et al., 2010; Jovanovic & Raguz, 2011). More than 50% of all member countries of Interbull that evaluate longevity use PH models with sire or sire-maternal grandsire models, although countries such as New Zealand, Ireland, Australia, Great Britain and USA still use the multi-trait animal or sire models (Potocnik et al., 2009; Interbull, 2014). PH models are based on modelling the survival function, that is, the probability that an animal will survive past a specified time t; and the hazard function, that is, the instantaneous rate of failure (Ducrocq, 2005). These two functions can differentiate between a cow that died at exactly time t and a cow that was last seen alive at time t, but may have survived several additional months or years. The model is based on the assumption that the hazard rate or risk is a product of a time-dependent baseline hazard and an exponential function of a series of explanatory variables, covariates (Ducrocq, 1997). PH models assume that the covariates have a multiplicative effect on the baseline hazard rate. This implies that the ratio of the hazard rates of any two animals observed at any time t associated with any set of two covariates will be a constant with respect to time and proportional to each other.
These models do not always give the highest fit with current data, yet they are expected to estimate accurately the performance of future offspring of a sire (Holtsmark et al., 2009). Furthermore, they assume that survival is the same trait throughout life, yet correlation between longevity in lactations 1 to 3 has been shown to be less than 1, implying that it is not one trait throughout life. Unlike linear models, PH models cannot account for non-random mating among animals (Jairath & Dekkers, 1994; Boettcher et al., 1999). Besides, the software that is commonly used for survival analysis with PH models currently uses only univariate analyses (Veerkamp et al., 2001; Holtsmark et al., 2009) and therefore is unable to adjust for correlations between traits, a requisite for increased accuracy of evaluation of animals. Since there are no multivariate analyses, it is difficult to use indicator traits to estimate longevity early in life as most important information at that stage comes from predictor traits (Brotherstone et al., 1998). Another limitation is that the software is not able to process the full animal model, restricting analysis to sire and sire-maternal grandsire models (Holtsmark et al., 2009). This ignores the contribution of the cows mated to these sires to production performance of the daughters, especially when there is assortative or disassortative mating. Although PH models are considered optimal in a statistical sense, they may not be economically optimal (VanRaden et al., 2006).
Despite the limitations associated with this approach, PH models have become the method of choice for analysing survival data because of their ability to handle censored data, to accommodate the non-normal distribution of survival data appropriately, and to incorporate time-dependent environmental effects (Ducrocq et al., 1988; Ducrocq & Casella, 1996). Moreover, like mixed linear models, PH models can be extended to include random genetic effects (Ducrocq, 1997), in which case these mixed survival models are referred to as frailty models. The PH models that are normally used in cattle evaluations are parametric Weibull models. Semi-parametric models, including Cox models, are not usually used. Weibull models have several advantages over Cox models. They allow stronger inferences to be made about survival times than Cox models. The output from the Weibull model relates directly to duration of survival, thereby allowing inferences to be made about the true event. Moreover, Weibull models incorporate non-constant hazard functions, unlike Cox models, which assume that the risk of an event remains constant throughout time (Flynn, 2012). However, the Cox model is more flexible, since the hazard function is not restricted to any specific form. Although Cox models simultaneously explore the effects of several covariates on longevity, and allow the isolation of the effects of these covariates, the Weibull model assumes that the baseline hazard function, λ0(t) can be parameterized according to a specific model for the distribution of the survival times (Walters, 2009).
5. Model comparison
Statistically, it is difficult to compare results from models for binary data such as TM and RR with those for models for continuous data, for example linear models, because the models are on different numeric scales (Littell et al., 1996; Matos, 1997). Different mathematical models have different link functions and different distribution functions are assumed for the response trait. Different link functions contribute to the problem of comparing mathematical models on different numeric scales. However, some comparisons have been carried out. The criteria used for such model comparisons include predictive abilities, estimated variance components, heritability estimates (e.g. Holtsmark et al., 2009), correlations of estimated and true breeding values, proportion of sires' daughters that survived to specified end points, and ranking of sires between models (Jamrozik et al., 2008).
Holtsmark et al. (2009) compared TRMs, TCMs, linear multi-trait, linear repeatability, linear cross-sectional and Weibull frailty models in terms of estimated variance components, heritability estimates, sire EBVs and predictive abilities. Sire variances for the first five lactations obtained with TRMs and TCMs were higher, at 0.09, than those obtained from the Weibull frailty model (0.0107) and linear models (0.01). Heritability estimates for survival for the first five lactations obtained from linear repeatability and cross-sectional models, at 0.02, were lower than those obtained from TM and Weibull frailty models, both of which were 0.04. Predictive abilities for survival 365 days after first calving were highest for linear multi-trait models, followed by cross-sectional models (linear and threshold), repeatability models (linear and threshold) and Weibull frailty models. In the same study, the performance of sire EBVs from linear cross-sectional models and TCMs was similar to those obtained by linear and TRMs. This probably explains why in an earlier study, Meijering & Gianola (1985) found no practical differences in rankings of individual animals from linear models or TMs when traits were binary. However, sire EBVs from Weibull frailty models with data from first lactation only performed better than those from linear repeatability models, TRMs and Weibull frailty models with data from lactations 1 to 5 (Holtsmark et al., 2009). This was probably because linear repeatability, TRM and Weibull frailty models for lactations 1 to 5 assumed genetic correlation of unity between survival in different lactations, although previous studies (e.g. Boettcher et al., 1999; Sewalem et al., 2007) indicated that survival in first lactation was distinct from survival in later lactations because the genetic correlation between survival in first and in later lactations was below unity.
In a simulation study, Jamrozik et al. (2008) compared Weibull, multi-trait linear and linear RR models based on the correlation between true and estimated breeding values (the accuracy of evaluation), proportion of sires' daughters that survived to specified end-points and sire ranking. With Weibull models, this correlation remained constant through time, while in evaluations with random regressions and multi-trait models, the accuracy of evaluation, measured by the correlation between true and estimated breeding values, increased with time, but remained lower than that obtained from Weibull models. Estimated breeding values obtained from multi-trait and Weibull models gave more similar sire rankings than those from PH models. Jamrozik et al. (2008) also reported better prediction of survived daughters from evaluations with multi-trait models than Weibull models. In fact, Weibull models showed poor performance in predicting the percentage of sires' daughters than MT models in early of a cow's lifetime.
Overall, sire EBVs from linear and TMs were found to perform equally well and better than those from Weibull models when predicting survival 365 days after first calving in second-crop daughters (Holtsmark et al., 2009). Comparison of the models also showed that Weibull models were better at predicting functional longevity, while linear random models and linear multi-trait models were better at predicting overall survival (Jamrozik et al., 2008). However, when examining the abilities of sire EBVs to predict survival to a given point, average general survival is measured rather than functional survival. This favours linear models (Jamrozik et al., 2008). Earlier studies by Caraviello et al. (2004a) reported no significant differences in the predictive abilities of the Weibull frailty linear animal models for survival to second, third, fourth and fifth lactations. It would therefore be difficult to identify which of the models that are currently available is better for evaluating longevity in dairy cattle. Although operationally, linear models are simple to implement and require the least computing resources, they have been reported to be the least statistically appropriate for categorical and censored data. Neither linear multi-trait nor RR models were optimal in terms of statistical correctness (Jamrozik et al., 2008), while TMs were found to be more appropriate for binary survival than linear models (Boettcher et al., 1999).
Heritability estimates
Heritability estimates for survival traits differ among models. Unlike estimates obtained with linear, TM and RR sire models, those from PH models are expressed on a log linear scale, on an original scale or as effective heritability (Yazdi et al., 2002). Heritability estimates from linear sire models have been found to be generally lower than those from threshold sire models. Table 2 shows heritability estimates for longevity estimated with PH sire, RR, threshold and linear animal and sire models.
1. Linear models
Linear models have generally been reported to produce lower estimates of heritability for longevity than PH models, suggesting increased accuracy of selection from the PH models (Boettcher et al., 1999; Ducrocq, 2002; Roxstrom et al., 2003; Sewalem et al., 2005b). In his study, Du Toit (2011) reported heritability estimates in a range of 0.01 to 0.03 in South African Jersey cattle with both sire and animal models, in a multivariate linear model analysis of length of productive life as binary trait. Setati et al. (2004) published slightly higher estimates of 0.06 for South African Holsteins, using a linear animal model. Elsewhere, Zavadilová et al. (2009) reported estimates of 0.05 with a linear animal model in Czech Fleckvieh, while Tsurunta et al. (2005) published estimates of 0.08 to 0.10 in American Holsteins with a linear animal model and Gibbs sampling, respectively. Generally, these heritability estimates ranged from as low as 0.01 to as high as 0.20, depending on the type of linear model. Despite this wide variation, Holtsmark et al. (2009) pointed out that heritability estimates for survival as a binary trait, obtained with linear models, were frequency dependent, and heritability values from different studies could therefore not be compared directly.
2. Random regression models
In their study, Van Pelt & Veerkamp (2014) estimated genetic parameters for longevity in Dutch dairy cattle using RR models. Models used records of monthly survival up to 72 months from first calving and heritability estimated for monthly survival. If an animal survived to month i + 1, it was considered alive and scored 100. Those culled in month were considered dead and scored 0. Using a sire-maternal grandsire (S-MG) model, heritability estimates for monthly survival ranged between 0.002 and 0.011 with higher estimates of heritability for the later periods. The cumulative heritability for the entire 72-month period was 0.15. These estimates for monthly survival were lower than those of 0.02 to 0.181 reported for national evaluations (Forabosco et al., 2009) and estimates of 0.01 to 0.07 from an earlier study by Veerkamp et al. (2001) with RR models in British dairy cattle. Estimates from Van Pelt & Veerkamp (2014) were also significantly lower than estimates of 0.12 - 0.36 obtained from Canadian Jersey cattle using RR models (Jamrozik et al., 2008). Generally, however, RR models produce lower heritability estimates than PH models.
3. Threshold models
Heritability for longevity has been estimated with TMs in Canadian Holsteins (Boettcher et al., 1999), Spanish Holsteins (Gonzalez-Recio & Alenda, 2007), South African beef cattle (Van Westhuizen et al., 2001), South African Angus (Maiwashe et al., 2009), Norwegian Red (Holtsmark et al., 2009) and Brazilian Holsteins (Kern et al., 2014). Heritability estimates in dairy cattle breeds were generally low, ranging from 0.04 (Holtsmark et al., 2009) to 0.15 (Kern et al., 2014). Estimates in beef cattle breeds, however, were higher, ranging from 0.08 (Van Westhuizen et al., 2001) to 0.30 (Maiwashe et al., 2009) probably owing to differences in trait definition between dairy and beef cattle. Heritability estimates obtained with a sequential threshold model were slightly higher at 0.11 (Gonzalez-Recio & Alenda, 2007) than those obtained for dairy cattle with threshold models, as expected, since STMs are known to increase reliability by accounting for what may have occurred in the previous stages. Estimated heritability estimates obtained with records from within lactation 1 and those from across all lactations up to lactation 5 were also reported to be low, but significantly higher than estimates obtained with linear models (Holtsmark et al., 2008; Holtsmark et al., 2009), despite the different definitions of longevity. Earlier studies observed that if longevity was expressed as a binary trait, the difference in heritability estimates expressed on the underlying scale was negligible when linear and non-linear models were used. Theoretical and empirical results indicate higher estimates of heritability from TMs than from linear models (Boettcher et al., 1999).
4. Proportional hazards models
Heritability estimates for functional longevity have been expressed on an original or a logarithmic scale with PH models. Ducrocq & Casella (1996) defined heritability on a logarithmic scale and modified under simulation to incorporate the tri-gamma function (γ) as used by Sasaki et al. (2012) and Terawaki & Ducrocq (2009). Estimates of heritability on a logarithmic scale were deficient in terms of biological interpretation and were reported to have a weak relationship with reliabilities for genetic evaluations (Ducrocq, 1999). Ducrocq (1999) transformed heritability on a log scale to the original scale (ho), using Taylor series expansion, and found this provided good results for reliability of genetic evaluations when the Weibull parameter relating to the shape of the distribution (ρ) was close to 2. Large biases, however, were obtained if ρ was less than or close to 1 (Chirinos et al., 2007). The heritability estimate on the original scale has a major advantage over the logarithmic scale. It gives good approximations of the true prediction error variance of the bulls, based on survival of their offspring. However, as a limitation, it estimates heritability using one of the two Weibull parameters, namely shape (ρ) and scale. These parameters have a relatively strong negative correlation, implying that different combinations can lead to similar fit of the data, but produce different heritability estimates (Yazdi et al., 2002). Moreover, in some research the derivation and interpretation of heritability on the original scale have been considered dubious. Because of these limitations, Yazdi et al. (2002) developed an alternative formula to compute heritability under a normal Weibull PH model, expressed as effective heritability. This has been modified and extended for use in various situations (e.g. Roxstrom et al., 2003) because it accounts for censoring, unlike original and logarithmic heritability. Effective heritability calculates expected reliabilities of estimated breeding values as a function of the expected number of animals still alive at any given time (Mészáros et al., 2010).
Generally, heritability for survival estimated on the original scale has been reported to be higher than estimates obtained on a log linear scale, which are consistent with estimates from linear models (Ducrocq & Skolner, 1998). Heritability estimates on a log linear scale range from 0.05 to 0.10 (Caraviello et al., 2004b), while on average they range from 0.15 to as high as 0.20 when determined on the original scale (Caraviello et al., 2004a). Using the Weibull PH models, Mészáros et al. (2008) reported heritability estimates of 0.05 on a logarithmic scale in Croatian Pinzgau cattle. This concurred with the logarithmic estimates of 0.04 reported earlier by Van der Linde et al. (2006) and Chirinos et al. (2007). However, these were much lower than earlier estimates of 0.16 to 0.22 (Ducroq, 1997), 0.12 (Egger-Danner et al., 2005) as well as 0.21 and 0.22 for true productive life and functional productive life, respectively, on an original scale (Bunger & Swalve, 1999).
The wide variation in heritability estimates for animals in different regions and countries, as in linear modelling, can be attributed to differences in the magnitude of the genetic variation in cow longevity among regions, although this could be because of differences in the accuracy of sire identification, record keeping (Caraviello et al., 2004b) and precision of data analyses. Table 2 shows heritability estimates for survival obtained with various models.
Predictors of functional longevity
A number of traits are used to predict longevity in dairy animals. These include conformation traits, production traits, somatic cell score, calving traits, cow fertility traits and likeability. Predictor traits may be included in net merit indices on their own or in combination with direct longevity, as in the USA, France and Belgium (Forabosco et al., 2009). Recent studies have evaluated dairy form, body capacity, conformation score, rear leg set, hock quality, rump angle and udder traits as early predictors of functional longevity (Zavadilová et al., 2011; Zavadilová & Stípková, 2012). The positive correlations between some of these traits and longevity imply the possibility of predicting longevity from other structural traits. Although the relationships between functional longevity and some type and conformation traits appear linear, other traits may have an intermediate optimum, beyond which culling risk increases when type scores deviate from this optimum (Caraviello et al., 2003).
Type and udder traits
Using linear models, genetic correlation between conformation/type traits and longevity were reported to range between -0.26 and 0.27 in Czech Holsteins (Zavadilová & Stípková, 2012). Slightly higher estimates ranging between 0.36 and 0.50 were reported by Rodgers et al. (1999) and Tsurunta et al. (2005). Earlier studies in Dutch Friesian cattle found higher correlations between subjective score for udder traits and longevity of between 0.77 and 0.93, which were attributed to probable upgrading of the Friesian breed by the Holstein (Vollema & Groen, 1997). In South African Holstein cattle, Setati et al. (2004) reported correlations values of between -0.15 and 0.48 between conformation/type traits and longevity. Such correlations are relatively high and could probably be due to low emphasis on selection against poor type traits or durability at the time of study. Although linear models have been used widely to estimate correlation between type traits and longevity, they have their limitations, since the joint distributions are difficult to describe with common methods, if not impossible (Gonzalez-Recio & Alenda, 2007). Damgaard & Korsgaard (2006) presented a Gibbs sampler for joint Bayesian analysis as an appropriate method for estimating correlation between a threshold character and a survival trait. This procedure, however, was reported to be computationally demanding. Gonzalez-Recio & Alenda (2007) proposed a bivariate sequential linear censored TM model for joint analysis of survival to next lactation and either 305-day standardised milk production, days open or number of inseminations to conception.
Type traits with the greatest influence on the risk of culling in dairy cattle have been reported to be those linked to udder traits (Larroque & Ducrocq, 2001; Schneider et al., 2003; Setati et al., 2004; Bouska et al., 2006; Zavadilová et al., 2009). Udder-type traits contribute to culling, and hence affect longevity, probably through their influence on mastitis and other disease incidence. Cows with good udders are more likely to avoid voluntary culling than those with poor udders. The relative contribution of udder-type traits to risk of culling and hence likelihood of survival has been well documented (e.g. Bunger et al., 2001; Dadpasand et al., 2008; Zavadilová et al., 2011). Some researchers have listed udder traits as having a significant impact on longevity. These udder traits, according to order of importance, are udder depth, fore udder attachment, front teat placement, udder support, udder cleft and teat length (Boettcher et al., 1999; Bunger & Swalve, 1999; Caraviello et al., 2003). Dadpasand et al. (2008) observed a slightly different order for the risk of culling, which ranged between 0.78 and 1.73 for fore udder attachment, 0.89 and 1.64 for udder depth, 0.98 and 1.26 for fore teat placement and 0.75 and 1.07 for suspensory ligament, against a reference score class of 5 within the score range of 1 to 9. Udder depth has been reported to have the highest relative contribution to survival likelihood, and therefore had the highest effect on cow survival after correction for milk production (Bunger & Swalve, 1999; Caraviello et al., 2003; Zavadilová et al., 2011). Dadpasand et al. (2008), Sewalem et al. (2005a) and Caraviello et al. (2003; 2004b) reported an intermediate optimum for udder depth, implying that cows with very deep or very shallow udders were at high risk of being culled from the herds. Among US Jersey cows, udder depth scores of between 6 and 10 on a scale of 1 to 100 had 1.60 times more relative risk of involuntary culling than cows with scores between 21 and 25, while cows with udder depth scores of 41 to 45 had a relative risk of 0.70 times that of cows with scores of 21 to 25 (Caraviello et al., 2003). In the same study, cows with udder support scores of 6 to 10 on a scale of 1 to 100 were found to have a relative risk of culling of nearly 1.80 times that of cows with intermediate scores, especially at the lower end of the scale.
In Croatian Simmental cattle, cows that scored lower for suspensory ligament attachment, rear udder length and teat thickness had approximately 1.50 to 2.00 times higher risk of being culled than those with scores of at least 4 (Jovanovac & Raguz, 2011). This concurred with results from Zavadilová et al. (2011). Teat placement has also been reported to influence culling and therefore longevity in dairy cattle, probably because cows with extremely closely placed rear teats are more likely candidates for culling than those with extremely wide rear teats (Ducrocq, 2002; Schneider et al., 2003; Sewalem et al., 2005a) as they present problems of teat-cup placement, resulting in delays in the milking process, especially in large herds. In contrast, Zavadilová et al. (2011) reported a small contribution of teat placement to survival likelihood and hence functional longevity. Other studies, however, reported similar importance of fore-udder attachment, but observed the central ligament to contribute more to the relative risk of culling than rear-udder height and rear-udder attachment (Sewalem et al., 2004; Schneider et al., 2005). Regardless of the order of importance, Larroque & Ducrocq (2001) pointed out that traits related to udder support, particularly udder depth and central ligament attachment, explained culling differences better than teat length and placement.
Conclusion
The relatively high economic importance of functional longevity justifies the decision to evaluate the trait genetically for inclusion in the overall breeding objective for dairy cattle. Multi-trait linear, TM, random and Weibull PH models can all be used to evaluate longevity in dairy cattle. The performance of these models depends on the definition of survival trait. No practical differences were observed in the ranking of animals when linear and TM models were used with longevity as a binary trait. In terms of statistical correctness, TM models are more appropriate for binary survival than linear and RR models. The high correlations between sire EBV from linear, TM and Weibull PH models observed in some studies imply that the survival trait in the linear sire model and TM models can be considered the same trait in PH modelling. Estimates of heritability for longevity obtained with Weibull PH models are generally higher than estimates obtained with TM, linear and RR models. Although RR models showed greater predictive abilities for overall survival than the Weibull and multi-trait linear models, the Weibull PH model is relatively better than linear and RR models for genetic evaluation of dairy cattle for functional survival, because it can handle time dependency and censoring in a relatively more robust way than the RR and TM models. Linear modelling cannot even handle these two phenomena, leading to possible loss of information from the analyses. Models that should be developed that use all the information optimally to accurately derive and apply genetic parameters estimated in genetic evaluation of animals for accurate sire ranking. Meanwhile countries can use any of the four models, namely linear, TM, RR and PH, depending on the nature and quality of the data.
References
Ajili, N., Rekik, B., Ben Gara, A. & Bouraoui, R., 2007. Relationships among milk production, reproductive traits and herd life for Tunisian Holstein-Friesian cows. AJAR 2 (2), 47-51. [ Links ]
Albert, J.H. & Chib, S., 2001. Sequential ordinal modelling with applications to survival data, Biometrics 57, 829-836. [ Links ]
Banga, C.B., 2009. The development of breeding objectives for Holstein and Jersey cattle in South Africa. PhD thesis, University of Free State, RSA. [ Links ]
Banga, C.B., Theron, H.E., Mostert, B.E. & Jordaan, F., 2002. Analysis of longevity in South African Holstein cattle. Proc. South African Society of Animal Science Congress, Christiana, 11-15 May 2002. [ Links ]
Banga, C.B., Neser, F.W.C. & Garrick, D.J., 2013. Derivation of economic values of longevity for inclusion in the breeding objectives for South African dairy cattle. International Proceedings of Chemical Biological and Environmental Engineering. 60 (14), 69-73. [ Links ]
Banga, C.B., Neser, F.W.C. & Garrick, D.J., 2014. Breeding objectives for Holstein cattle in South Africa. S. Afr. J. Anim. Sci. 44, 199-214. [ Links ]
Beilharz, R.G., Luxford, B.G. & Wilkinson, J.I., 1993. Quantitative genetics and evolution: Is our understanding of genetics sufficient to explain evolution? J. Anim. Breed. Genet. 10, 161-170. [ Links ]
Beswick, V., Cheek, L. & Ball, J., 2004. Review: Statistics review. 12: Survival analysis. Critical Care 2004 8, 389-394. [ Links ]
Boettcher, P.J., Jairath, L.K. & Dekkers, J.C.M., 1999. Genetic evaluation of herd life in Canada: Current status and future outlook. GIFT workshop; Longevity Jouy-En-Josas, France May, 1999. Bulletin 21, 23-30. [ Links ]
Bouška, J., Vacek, M., Štipkova, M. & Nemec, A., 2006 The relationship between linear type traits and styability of Czech Fleckvieh cows. Czech J. Anim. Sci. 51 (7), 299-304. [ Links ]
Brotherstone, S.R., Veerkamp, R.F. & Hill, W.G., 1998. Predicting breeding values for herd life of Holstein-Friesian dairy cattle from lifespan and type. J. Anim. Sci. 67, 405-411. [ Links ]
Bünger, A. & Swalve, H.H., 1999. Analysis of survival in dairy cows using supplementary data on type scores and housing systems. Interbull Bulletin No. 21, Uppsala, Sweden. pp. 128-135. [ Links ]
Bünger, A., Ducrocq, V. & Swalve, H.H., 2001. Analysis of survival in dairy cows with supplementary data on type scores and housing systems from a region of Northwest Germany. J. Dairy Sci. 84, 1531-1541. [ Links ]
Caraviello, D.Z., Weigel, K.A. & Gianola, D., 2003. Analysis of the relationship between type traits, inbreeding and functional survival in Jersey cattle using a Weibull proportional hazards model. J. Dairy Sci. 86, 2984-2989. [ Links ]
Caraviello, D.Z., Weigel, K.A. & Gianola, D., 2004a. Comparison between a Weibull Proportional Hazards Model and a Linear Model for predicting the genetic merit of US Jersey sires for daughter longevity. J. Dairy Sci. 87, 1469-1476. [ Links ]
Caraviello, D.Z., Weigel, K.A. & Gianola, D., 2004b. Analysis of the relationship between type traits and functional survival in US Holstein cattle using a Weibull proportional hazards model. J. Dairy Sci. 87, 2677-2686. [ Links ]
Carlén, E, Schneider, M.delP. & Strandberg, E., 2005. Comparison between linear models and survival analysis for genetic evaluation of clinical mastitis in dairy cattle. J. Dairy Sci. 88, 797-803. [ Links ]
Cecchinato, A., Gonzalo-Recio, O, Lopez de Maturana, E., Gallo, L. & Carnier, P., 2010. A comparison between different survival and threshold models with an application to piglet preweaning survival in a dry-cured ham-producing crossbred line. J. Anim. Sci. 88, 1990-1998. [ Links ]
Chirinos, Z., Carabaňo, M.J. & Hernández, D., 2007. Genetic evaluation of length of productive life in the Spanish Holstein-Friesian population. Model validation and genetic parameters estimation. Livest. Sci. 106, 120-131. [ Links ]
Damgaard, L.H. & Korsgaad, I.R., 2006. A bivariate quantitative genetic model for a threshold trait and a survival trait. Genet. Sel. Evol. 38, 565-581 [ Links ]
. Dadpasand, M., Mirael-Ashtiani, S.R., Moradi Shahrebabak, M. & Vaez Torshizi, R., 2008. Impact of conformation traits on functional longevity of Holstein cattle of Iran assessed by a Weibull proportional hazards model. Livest. Sci. 118, 204-211. [ Links ]
Dube, B., Banga, C.B., Dzama, K. & Norris, D., 2008. Genetic analysis of somatic cell score and linear type traits in South African Holstein cattle. S. Afr. J. Anim. Sci. 8, 229-232. [ Links ]
Ducrocq, V., 1997. Survival analysis, a statistical tool for longevity data. Proc: 48th Annual Meeting of the EAAP: 25-28 August 1997, Vienna, Austria. [ Links ]
Ducrocq, V., 1999. Two years of experience with the French genetic evaluation of dairy bulls on production adjusted longevity of their daughters. Proceedings of the International Workshop on EU Concerted Action Genetic Improvement of Functional Traits (GIFT); Longevity. Jouy-en-Josas, France, May, 1999, Interbull Bulletin 21, 60-68. [ Links ]
Ducrocq, V., 2002. A piecewise Weibull mixed model for the analysis of length of productive life of dairy cows. Proc. 7th WCGALP 32, 505-508. [ Links ]
Ducrocq, V., 2005. An improved model for the French genetic evaluation of dairy bulls on length of productive life of their daughters. Anim. Sci. 80, 249-256. [ Links ]
Ducrocq, V & Casella, G., 1996. A Bayesian analysis of mixed survival models. Genet. Sel. Evol. 28, 205-529. [ Links ]
Ducrocq, V. & Sölkner, J., 1998. "The Survival Kit'- V3.0, a package for large analyses of survival data. In: 6th World Cong. Genet. Appl. Livest. Prod. 27, 447-448. Anim. Genetics and Breeding Unit, Univ. of New England, Armidale, Australia. [ Links ]
Ducrocq, V., Quaas, R.L., Pollak, E.J. & Casella, G., 1988. Length of productive life of dairy cows. 1. Justification for a Weibull model. J. Dairy Sci. 71, 3061-3070. [ Links ]
Durr, J.W., Monardes, H.G. & Cue, R.I., 1999. Genetic analysis of herd life in Quebec Holsteins using Weibull models. J. Dairy Sci. 82, 2503-2513. [ Links ]
Du Toit, J., 2011. A genetic evaluation of productive herd life in dairy cattle. PhD dissertation. University of the Free State, Bloemfontein, South Africa. [ Links ]
Dzomba, E.F., Nephawe, K.A., Maiwashe, A.N., Cloete, S.W.P., Chimonyo, M., Banga, C.B., Muller, C.J.C. & Dzama, K., 2010. Random regression test-day model for the analysis of dairy cattle production data in South Africa: Creating the framework. S. Afr. J. Anim. Sci. 40, 273-284. [ Links ]
Egger-Danner, C., Kadlečík, O., Fuerst, C. & Kasarda, R., 2005. Joint genetic evaluation for functional longevity for Pinzgau cattle. 56th Annual Meeting of the European Association for Animal Production, Uppsala, Sweden, June 5-8. [ Links ]
Falconer, D.S. & Mackay, T.F.C., 1996. Introduction to Quantitative Genetics. Longman, New York. [ Links ]
Flynn, R., 2012. Approaches for data analysis: Survival analysis. J. Clinical Nursing 21, 2789-2797. [ Links ]
Forabosco, F., Bozzi, R., Boettcher, P., Filipine, F., Bijma, P. & Van Arendonk, J.A.M., 2004. Relationship between profitability, type traits and deviation of economic values in Chianina beef cows. J. Anim. Sci. 83, 2043-5738. [ Links ]
Forabosco, F., Jakobsen, J.H. & Fikse, W.F., 2009. International genetic evaluation for direct longevity in dairy bulls. J. Dairy Sci. 92, 2338-2347. [ Links ]
Gill, G.W. & Allaire, F.R., 1976. Relationship of age at first calving, days open, days dry and herd life to a profit function of dairy cattle. J. Dairy Sci. 59, 1131-1139 [ Links ]
Gianola, D., 1982. Theory and analyses of threshold characters. J. Anim. Sci. 54, 1078-1096. [ Links ]
Gianola, D. & Foulley, J.L., 1983. Sire evaluation for ordered categorical data with a threshold model. Genet. Sel. Evol. 15, 201-224 [ Links ]
González-Recio, O. & Alenda, R., 2005. Genetic parameters for female fertility traits and a fertility index in Spanish dairy cattle, J. Dairy Sci. 88, 3282-3289. [ Links ]
Gonzalez-Recio, O. & Alenda, R., 2007. Genetic relationship of discrete-time survival with fertility and production in dairy cattle using bivariate models. Genet. Sel. Evol. 39, 391-404. [ Links ]
Hazel, L.N., 1943. The genetic basis for constructing selection indexes. Genetics 28, 476-490. [ Links ]
Henderson Jr., C.R., 1982. Analysis of covariance in the mixed model: higher-level, nonhomogeneous, and random regressions. Biometrics 38, 623-640. [ Links ]
Holtsmark, M., Heringstad, B., Madsen, P. & Ødegård, J., 2008. Genetic relationship between culling, milk production, fertility, and health traits in Norwegian Red cows. J. Dairy Sci. 91, 4006-4012. [ Links ]
Holtsmark, M., Heringstad, B. & Ødegárd, J., 2009. Predictive abilities of different statistical models for analysis of survival in dairy cattle. J. Dairy Sci. 92, 5730-5738. [ Links ]
Interbull, 2014. Description of national genetic evaluation systems for dairy cattle traits as applied in different Interbull member countries. http://www-interbull.org/ib/geforms Accessed September 19, 2014. [ Links ]
Jairath, L. & Dekkers, J.C.M., 1994. Genetic parameters of functional and true lactational survival, and relationships with milk production and conformation traits in registered Canadian Holsteins. J. Dairy Sci. 77 (Supplement 1), 146. [ Links ]
Jairath, L., Dekkers, J.C.M., Schaeffer, L.R., Liu, Z., Burnside, E.B. & Kolstad, B., 1998. Genetic evaluation for herd life in Canada. J. Dairy Sci. 81, 550-562. [ Links ]
Jamrozik, J. & Schaeffer, L.R., 1997. Estimates of genetic parameters for a test day model with random regressions for yield traits of first lactation Holsteins. J. Dairy Sci. 80, 762-770. [ Links ]
Jamrozik, J., Fatehi, J. & Schaffer, L.R., 2008. Comparison of models for genetic evaluation of survival traits in dairy cattle: a simulation study. J. Anim. Breed. Genet. 125, 75-83. [ Links ]
Jovanovac, S. & Raguz, N., 2011. Analysis of the relationships between type traits and longevity in Croatian Simmental cattle using survival analysis. Agric. Conspec. Sci. 76, 249-253. [ Links ]
Kern, E.L., Cobuci, J.A., Costa, C.N., McManus, C.M., Campos, G.S., Almeida, T.P. & Campos, R.V., 2014. Genetic association between herd survival and linear type traits in Holstein cows under tropical conditions. Ital J. Anim. Sci. 13, 665-672. [ Links ]
Kumar, D. & Klefsö, B., 1994. Proportional hazards model: A review. Reliab. Eng. & System Safety 44, 177-188. [ Links ]
Laird, N.M. & Ware, J.H., 1982. Random-effects models for longitudinal data. Biometrics 38, 963-974. [ Links ]
Larroque, H. & Ducrocq, V., 2001. Relationships between type and longevity in the Holstein breed. Genet. Sel. Evol. 33, 39-59. [ Links ]
Littell, R.C., Milliken, G.A., Shroup, W.W. & Wolfinger, R.D., 1996. SAS Systems for Mixed Models. SAS Inst. Inc. Cary, N.C., USA. [ Links ]
Maiwashe, A., Nephawe, K.A. & Theron, H.E., 2009. Analysis of stayability in South African Angus using a threshold model. S. Afr. J. Anim. Sci. 39, 55-60. [ Links ]
Makgahlela, M.L., Banga, C.B., Norris, D., Dzama, K. & Ngambi, J.W., 2008. Genetic analysis of age at first calving and calving interval in South African Holstein cattle. Asian J. Anim. Vet. Adv. 3, 197-205. [ Links ]
Matos, C.A., Ritter, P., Gianola, C.D. & Thomas, D.L., 1993. Bayesian analysis of lamb survival using Monte Carlo numerical integration with importance sampling. J. Anim. Sci. 71, 2047-2051. [ Links ]
M'hamdi, N., Aloulou, R., Bouallegue, M., Brar, S.K. & Hamouda, M.B., 2010. Study on functional longevity of Tunisian Holstein dairy cattle using a Weibull proportional hazard model. Livest. Sci. 132, 173-176. [ Links ]
Meijering, A. & Gianola, D., 1985. Linear versus nonlinear methods of sire evaluation for categorical traits: a simulation study. Genet. Sel. Evol. 17, 115-132. [ Links ]
Mészáros, G., Fuerst, C., Fuerst-Waltl, B., Kadlečík, O., Kasarda, R. & Solkner, J., 2008. Genetic evaluation for length of productive life in Slovak Pinzgau cattle. Arch. Tierz., Dummerstorf 51, 438-448. [ Links ]
Mészáros, G., Pálos, J., Ducrocq, V. & Sölkner, J., 2010. Heritability of longevity in Large White and Landrace sows using continuous time and grouped data models. Genet. Sel. Evol., 42, 1-13. [ Links ]
Meyer, K., 1999. Estimates of genetic and phenotypic covariance functions for postweaning growth and mature weight of beef cows. J. Anim. Breed. Genet. 116, 181-205. [ Links ]
Miglior, F., Muir, B.L. & Van Doormaal, B.J., 2005. Selection indices in Holstein cattle of various countries. J. Dairy Sci. 88. 1255-1263. [ Links ]
Mota, R.R., Marques, L.F.A., Lopes, P.S., da Silva, L.P., Neto, F.R.A., de Resende, M.D.V. & Torres, R.A., 2013. Genetic evaluation using multi-trait and random regression models in Simmental beef cattle. Gen. Mol. Res. 12 (3), 2465-2480. [ Links ]
Mrode, R.A. & Swanson, G.J.T., 2004. Calculating cow and daughter yield deviations and partitioning of genetic evaluations under a random regression model. Livest. Prod. Sci. 86, 253-260. [ Links ]
Potocnik, K., Jovanovac, S., Krsnik, J., Gantner, V., Stepec, M., Raguz, N., Gorjanc, G. & Logar, B., 2009. Estimation of genetic parameters for longevity in Slovenian dairy cattle populations. Proc: 44th Croatian & 4th International Symposium on Agriculture. pp. 757-761. [ Links ]
Rogers, G.W., McDaniel, B.T., Dentine, M.R. & Johnson, L.P., 1988. Relationships among survival rates, predicted differences for yield and linear type traits. J. Dairy Sci. 71, 214-222. [ Links ]
Roxström, A., Ducrocq, V. & Strandberg, E., 2003. Survival analysis of longevity in dairy cattle on a lactation basis. Genet. Sel. Evol. 35, 305-318. [ Links ]
Sadeghi-Sefdmazgi, A., Moradi-Shahrbabak, M., Nejati-Javaremi, A. & Shadpavar, A., 2009. Estimation of economic values in three breeding perspectives for longevity and milk production traits in Holstein dairy cattle in Iran. Ital J. Anim. Sci. 8, 359-375. [ Links ]
Samoré, A.B., Rizzi, R., Rossoni, A. & Bagnato, A., 2010. Genetic parameters for functional longevity, type traits, SCS, milk flow and production in the Italian Brown Swiss. Ital J. Anim. Sci. 9, 145-152. [ Links ]
Sasaki, O., Aihara, M., Nishiura, A., Ishii, K. & Satoh, M., 2012. Genetic evaluation of the longevity of the Holsteins population in Japan using a Weibull proportional hazards model. Anim. Sci. J. 83, 95-102. [ Links ]
Schaeffer, L.R., 2004. Application of random regression models in animal breeding. Livest. Prod. Sci. 86, 35-45. [ Links ]
Schaeffer, L.R. & Dekkers, J.C.M., 1994. Random regressions in animal models for test-day production in dairy cattle. Proceedings of Fifth World Congress of Genetics Applied to Livestock Production, vol. XVIII. Guelph, Ont., Canada. pp. 443-446. [ Links ]
Schneider, M.del P., Durr, J.W., Cue, R.I. & Monardes, H.G., 2003. Impact of type traits on functional herd life of Quebec Holsteins assessed by survival analysis. J. Dairy Sci. 86, 4083-4089. [ Links ]
Setati, M.M., Norris, D., Banga, C.B. & Benyi, K., 2004. Relationships between longevity and linear type in Holstein cattle population of southern Africa. Trop. Anim. Hlth Prod. 36, 807-814. [ Links ]
Sewalem, A., Kistemaker, G.J., Miglior, F. & Van Doormaal, B.J., 2004. Analysis of the relationship between type traits and functional survival in Canadian Holsteins using a Weibull proportional hazards model. J. Dairy Sci. 87, 3938-3946. [ Links ]
Sewalem, A., Kistemaker, G.J. & Van Doormaal, B.J., 2005a. Relationship between type traits and longevity in Canadian Jerseys and Ayrshires using a Weibull Proportional Hazards Model. J. Dairy Sci. 88, 1552-1560. [ Links ]
Sewalem, A., Kistemaker, G.J., Ducrocq, V. & Van Doormaal, B.J., 2005b. Genetic analysis of herd life in Canadian dairy cattle on a lactation basis using a Weibull proportional hazards model. J. Dairy Sci. 88, 368-375. [ Links ]
Sewalem, A., Miglior, F., Kistemaker, G.J., Sullivan, P., Huapaya, G. & Van Doormaal, B.J., 2007. Modification of genetic evaluation of herd life from a three-trait to a five-trait model in Canadian dairy cattle. J. Dairy Sci. 90, 2025-2028. [ Links ]
Smith, S.P. & Quaas, R.L., 1984. Productive lifespan of bull progeny groups: Failure time analysis. J. Dairy Sci. 67, 2999-3007. [ Links ]
Strapák, P., Candrák, J. & Aumann, J., 2005. Relationship between longevity and selected production, reproduction and type traits. Czech J. Anim. Sci. 50 (1), 1-6. [ Links ]
Terawaki, Y. & Ducrocq, V., 2009. Non-genetic effects and genetic parameters for length of productive life of Holstein cows in Hokkaido, Japan. J. Dairy Sci. 92, 2144-2150. [ Links ]
Tsuruta, S., Misztal, I. & Lawlor, T.J., 2005. Changing definition of productive life in US Holstein: Effect on genetic correlations. J. Dairy Sci. 88, 1156-1165. [ Links ]
Tsuruta, S., Misztal, I., Huang, C. & Lawlor, T.J., 2009. Bivariate analysis of conception rates and test-day milk yields in Holsteins using a threshold-linear model with random regressions. J. Dairy Sci. 92, 2922-2930. [ Links ]
Van Arendonk, J.A.M., 1986. Economic importance and possibilities for improvement of dairy cow herd life. Third World Congt. Genet. Appl. Livest. Prod., Lincoln, NE: 95. [ Links ]
Van der Linde, C., de Jong, G., Simai, S.Z., Gombacsi, P. & Wellisch, P., 2006. Genetic evaluation for longevity in Hungary. Interbull Bull. 35, 3-8. [ Links ]
Van der Westhuizen, R.R., Schoeman, S.J., Jordaan, G.F. & Van Wyk, J.B., 2001. Heritability estimates derived from threshold analyses for reproduction and stayability traits in a beef cattle herd. S. Afr. J. Anim. Sci. 31, 25-32. [ Links ]
Van Pelt, M.L. & Veerkamp, R.F., 2014. Genetic analysis of longevity in Dutch Dairy Cattle using Random Regression. Proceeding of the 10th World Congress of Genetics Applied to Livestock Production. Canada, 2014. [ Links ]
Van Raden, P.M. & Klaaskate, E.J.H., 1993. Genetic evaluation of length of productive life including predicted longevity of live cows. J. Dairy Sci. 76, 2758-2764. [ Links ]
VanRaden, P.M., Dematawewa, C.M., Pearson, R.E. & Tooker, M.E., 2006. Productive life including all lactations and longer lactations with diminishing credits. J. Dairy Sci. 89, 3213-3220. [ Links ]
Vargas, B., Groen, A.F., Herrero, M. & Van Arendonk, J.A.M., 2002. Economic values for production and functional traits in Holstein cattle of Costa Rica. Livest. Prod. Sci. 75, 101-116. [ Links ]
Veerkamp, R.F., Brotherstone, S. & Meuwissen, T.H.E., 1999. Survival analysis using random regression models. Proc. International Workshop on EU Concerted Action Genetic Improvement of Functional Traits in Cattle; Longevity. Interbull Bull. 21, 36-40. [ Links ]
Veerkamp, R.F., Brotherstone, S., Engel, B. & Meuwiwissen, T.H.E., 2001. Analysis of censored survival data using random regression models. Anim. Sci. 72, 1-10. [ Links ]
Visscher, P.M., Bowman, P.J. & Goddard, M.E., 1994. Breeding objectives for pasture based dairy production systems. Livest. Prod. Sci. 40, 123-137. [ Links ]
Vollema, A.R. & Groen, A.F., 1997. Genetic correlations between longevity and conformation traits in an upgrading dairy cattle population. J. Dairy Sci. 80, 3006-3014. [ Links ]
Vukasinovic, N., 1999. Application of survival analysis in breeding for longevity. Proceedings of the 4th International Workshop on Genetic Improvement on functional traits in cattle. Jouy-en-Josas. Interbull Bulletin No. 21, Uppsala: 3-10. [ Links ]
Vukasinovic, N., Moll, J. & Casanova, L., 2001. Implementation of a routine genetic evaluation for longevity based on survival analysis techniques in dairy cattle populations in Switzerland. J. Dairy Sci. 84, 2073-2080. [ Links ]
Walters, S.J., 2009. What is a Cox model. What is? Series. 1st Edition. Hayward Group. Accessed on 12 February 2013 from www.whatisseries.co.uk. [ Links ]
Weigel, K.A., Palmer, R.W. & Caraviello, D.Z., 2003. Investigation of factors affecting voluntary and involuntary culling in expanding dairy herds in Wisconsin using survival analysis. J. Dairy Sci. 86, 1482-1486. [ Links ]
Weller, J.I. & Ron, M., 1992. Genetic analysis of fertility traits in Israeli Holsteins by linear and threshold models. J. Dairy Sci. 75, 2541-2548. [ Links ]
Wiebelitz, J., Reinhardt, F., Liu, Z., Erbe, M. & Simianer, H., 2014. Genetic evaluation of survival traits in Germany Holstein dairy cattle using a six trait linear model. In: Proceeding of the 10th World Congress of Genetics Applied to Livestock Production. Canada, 2014. [ Links ]
Yazdi, M.H., Visscher, P.M., Ducrocq, V. & Thompson, R., 2002. Heritability, reliability of genetic evaluations and response to selection in proportional hazards models. J. Dairy Sci. 85, 1563-1577. [ Links ]
Zavadilová, L. & Štípková, M., 2012. Genetic correlations between longevity and conformation traits in the Czech Holstein population. Czech J. Anim. Sci. 57, 2012 (3), 125-136. [ Links ]
Zavadilová, L. & Štípková, M., 2013. Effect of age at first calving on longevity and fertility traits for Holstein cattle. Czech J. Anim. Sci. 58, 47-57. [ Links ]
Zavadilová, L., Štípková, M., Němcova, E., Bouška, J. & Matějičkova, J., 2009. Analysis of the phenotypic relationships between type traits and functional survival in Czech Fleckvieh cows. Czech J. Anim. Sci. 54, 521-531. [ Links ]
Zavadilová, L., Němcova, E. & Stípková, M., 2011. Effect of type traits on functional longevity of Czech Holstein cows estimated from a Cox proportional Hazards model. J. Dairy Sci. 94, 4090-4099. [ Links ]
Received 11 December 2013
Accepted 10 February 2015
First published online 9 May 2015
# Corresponding author: vichikosi@gmail.com














