Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Animal Science
On-line version ISSN 2221-4062
Print version ISSN 0375-1589
S. Afr. j. anim. sci. vol.43 n.1 Pretoria Jan. 2013
Estimates of variance components for postweaning feed intake and growth in Bonsmara bulls and evaluation of alternative measures of feed efficiency
M.D. MacNeilI, II, III, #; M.M. ScholtzI, III; A. MaiwasheI
IARC-Animal Production Institute, Private Bag X2 Irene 0062, South Africa
IIDelta G, 145 Ice Cave Road Miles City, MT 59301, USA
IIIUniversity of the Free State, P.O. Box 339, Bloemfontein 9301, South Africa
ABSTRACT
Feed efficiency is of major economic importance in beef production. The objective of this work was to evaluate alternative measures of feed efficiency for use in genetic evaluation. To meet this objective, genetic parameters were estimated for the components of efficiency. These parameters were then used in multiple-trait animal model genetic evaluations and alternative genetic predictors of feed efficiency were derived from the results. Corresponding single-trait evaluations for residual feed intake (RFI), residual daily gain (RDG), and residual intake and gain (RIG) were also conducted. The data contained 3 331 animals with records and an additional 6 322 animals in their pedigree. The alternative measures of feed efficiency were compared using Spearman rank correlations. Heritability estimates for metabolic body weight (MBW), average daily gain (ADG) and average daily feed intake (DFI) were 0.38 ± 0.05, 0.25 ± 0.05 and 0.37 ± 0.05, respectively. Estimates of the genetic correlations among these traits were 0.79 ± 0.07, 0.54 ± 0.08 and 0.66 ± 0.08 for MBW with ADG, MBW with DFI, and ADG with DFI, respectively. The various measures of feed efficiency were highly correlated. However, RFI and RDG did provide different rankings of candidates for selection. The combination of RFI and RDG to form RIG appears to provide an effective harmonization of the former two biological measures of efficiency. It is recommended that genetic evaluation systems include analyses of ADG and DFI, and breeders are advised to base selection decisions on the basis of multiple-trait selection indexes that incorporate feed intake and performance.
Keywords: Genetic evaluation, residual feed intake, residual gain
Introduction
Conversion of feedstuffs into food through animal tissues is the essence of livestock production. The more efficiently this process occurs, the more sustainable livestock production becomes. An additional benefit of increased efficiency is increased production of highly nutritious food for people, from a finite resource.
Ratio measures of efficiency have seen long-standing use in the animal sciences. For example, feed conversion ratio (FCR) has been and continues to be used widely to select for efficiency. However, these ratio measures suffer theoretical defects that make them less than desirable as a basis for genetic improvement (Gunsett, 1986; Iwaisaki, 1989). Following Koch et al. (1963), measures of residual feed intake (Arthur et al., 1996) and residual gain (MacNeil et al., 2011) have been suggested as alternatives. Furthermore, Berry & Crowley (2012) suggested the combination of these measures expressed on a standardized scale as a further refinement. Yet combining feed intake and growth to calculate a single measure of feed efficiency does not add additional information to that which can be obtained directly from the component traits (Kennedy et al., 1993).
In the current study, data emanating from performance recording of Bonsmara bulls in South Africa, originally presented by Van der Westhuizen et al. (2005), were re-examined. Van der Westhuizen et al. (2005) accepted phenotypic residual feed intake as being the appropriate residual-based measure of feed efficiency and estimated genetic parameters for it and other routinely recorded traits. Here, alternative expressions for feed efficiency are considered with a goal of putting forth recommendations for a system of genetic evaluation to facilitate improvement of feed efficiency. Specific objectives are to estimate genetic parameters for components of efficiency: namely metabolic body weight, average daily gain and feed intake; and to compare various measures of efficiency derived from them.
Materials & Methods
The data used in this research were originally described by Van der Westhuizen et al. (2005). Briefly, data were collected from the centralised bull testing stations under the supervision of South Africa's Agricultural Research Council. Records from Bonsmara bulls that were tested between 1989 and 2001 were used. The data set consists of the individual feed intake and weights of 3 331 bulls. This data set differs from that of Van der Westhuizen et al. (2005) in that observations of magnitude greater than 3.5 standard deviations removed from the mean of each trait were removed from the data set and that only animals with measured feed intake were included. Individual feed intake and body measurements were taken on a weekly basis. Following a 4-week adaptation period, data were collected during a test period of at least 12 weeks.
In this study, concern was with three primary traits: average daily feed intake (DFI), average daily gain (ADG), and mid-test metabolic body weight (MBW). As stated by Koch et al. (1963), efficiency of feed use is not a directly measurable trait and it must be calculated from component traits. Thus, from these primary traits several measures of efficiency were derived. Phenotypic values for residual feed intake (RFIp) and residual gain (RDGp) were calculated from the linear regressions of DFI on ADG and MBW, and ADG on DFI, respectively. Phenotypic residual intake and gain (RIGp, Berry & Crowley, 2012) was calculated by transformation of RFIp and RDGp to z-scores (mean = 0.0, variance = 1.0) and then subtracting the z-score for RFIp from the z-score for RDGp.
A 3-trait animal model analysis was conducted to estimate genetic variances and covariances for the primary traits using MTDFREML (Boldman et al., 1993). The model can be described as:

where, Yi is the vector of data for the ith trait; i = 1 to 3 for MBW, ADG, and DFI, respectively. The Xi, are design matrices relating the data to their respective fixed herd of origin and contemporary group classification effects (a concatenation of test year and number), and linear age of calf effects (βi). The Zi, are design matrices relating the data to their respective random additive genetic effects (ui, i = 1 to 3). The ei denotes the unexplained residual effects for each trait. The random genetic effects were assumed to have null means and variances (VAR):
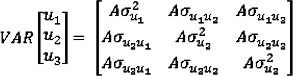
where, A represents the numerator relationship matrix with rank equal to the number of animals in the three generation pedigree (n = 9 653) used for this analysis. The random residual effects were assumed to have null means and

where, I represents an identity matrix with rank equal to number of animals with records (n = 3 331).
After solving the 3-trait mixed model equations, functions of the ü indicative of genetic measures of efficiency were calculated as follows:
Genetic residual gain (RDGg):
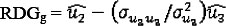
Genetic residual feed intake (RFIg):

Finally,

Genetic residual intake and gain (RIGg):

where, σRDG and σrfig were computed from variances of the linear functions used to predict RDGg and RFIg, respectively. The search for parameter estimates was assumed to have converged when the variance of the simplex was less 10-10 and the solution vector was confirmed in two independent restarts from different starting values.
In addition to the multi-trait analyses described above, single trait animal model analyses were conducted to estimate genetic parameters and predict breeding values for RFIp, RDGp and RIGp. As above, the model of the data included fixed effects for the classification variables herd and contemporary group, and a linear covariate for age of calf, and a random genetic effect for each animal in the pedigree. Spearman rank correlations were calculated to quantify the relationships among RDGp, RFIp and RIGp, their predicted breeding values from single trait mixed model analyses, and RDGg, RFIg, and RIGg calculated following the multi-trait mixed model analysis of MBW, ADG and DFI.
As a final step in interpreting these data, the concept of equivalent indexes (Kennedy et al., 1993) was used to derive economic weights for alternative selection indexes. The alternative indexes that were examined, contained either EBV for: 1) ADG and DFI assuming relative economic values of 7 and 1, respectively; 2) MBW, ADG, and RFI; or 3) RDG and DFI.
Results & Discussion
Means and phenotypic standard deviations (in parentheses) of MBW, ADG, and DFI were 79.7 (4.19) kg0.75, 1.74 (0.22) kg/d, and 10.4 (0.95) kg, respectively. Phenotypic correlations among these traits were 0.50, 0.50, and 0.58 for MBW and ADG, MBW and DFI, and ADG and DFI, respectively. Thus, these data exhibit the well-recognized antagonism between desired feed intake and desired growth. Shown in Table 1 are results from partitioning phenotypic (co)variances into their genetic and environmental components, and parameter estimates derived from them. Estimates of heritability, previously reported in the literature, for feed intake include 0.54 for mixed breeds of cattle in Canada (Nkrumah et al., 2007), 0.48 for Charolais cattle in France (Arthur et al., 2001a), 0.48 for Brangus heifers in Texas (Lancaster et al., 2009), 0.45 for Hereford and Angus cattle in the Northern Plains of North America (MacNeil et al., 1991), 0.39 for Angus cattle in Australia (Arthur et al, 2001b), 0.36 for Angus cattle in the USA (MacNeil et al, 2011), 0.34 for Japanese Black cattle (Hoque et al., 2006), and 0.27 for tropically adapted breeds in Australia (Robinson & Oddy, 2004). Estimates of heritability for ADG ranged from 0.20 to 0.59 in these studies. Likewise, recent prior estimates of the genetic correlation between DFI and ADG were 0.55 in both MacNeil et al. (2011) and Berry & Crowley (2012). Thus, the bivariate genetic distribution of DFI and ADG presented here seems consistent with prior literature. Both the genetic and environmental correlations of ADG with DFI indicate the antagonism between these traits arises from both genetic and non-genetic causes. This positive relationship between ADG and DFI makes improvement of efficiency challenging. However, the estimated correlations were not so large as to make this challenge infeasible.
Equations, with parameters estimated from the data, for calculating phenotypic RFI and RDG were:
RFIp = DFI - 0.7833 - 0.0718*MBW - 2.1861*ADG, and
RDGP = ADG - 0.5037 - 0.1198*DFI
All regression coefficients in these equations were highly significant (P <0.001). The genetic regression of ADG on DFI used to calculate RDGg was 0.1293. The genetic regressions of DFI on MBW and ADG used to calculate RFIg were 0.1153 and 0.1305, respectively.
For the 3 331 animals with recorded phenotypic data, Spearman rank correlations among the different measures of efficiency are shown in Table 2. Previously, Crowley et al. (2010) estimated the genetic correlation of RDG with RFI as -0.46 and MacNeil et al. (2011) found the rank correlation of animals evaluated with multiple-trait genetic predictors of RDG and RFI was -0.78. Based on the present data and the previous studies, it is clear that RFI and RDG may provide for quite different rankings of candidates for selection. To arrive at a weight constant endpoint, selection for RDG would reduce feed used by reducing the number of days for which maintenance requirements are met, and RFI would reduce feed used by directly reducing daily consumption. If either is to be used as a selection criterion, a decision must be made whether candidates that have superior performance when provided an average amount of feed or candidates that eat less to achieve average performance are preferred. In the former case RDG would be the criterion of choice and in the latter case RFI would be the criterion of choice. If Robertson's (1959) suggestion that correlations of magnitude greater than 0.8 reflect alternative measures of the same trait were adopted, then combining RFI and RDG to form RIG appears to provide an effective harmonization of both efficiency measures. As expected, the single-trait EBVs were highly correlated with the respective phenotypes and the multiple-trait EBV were slightly less so due to the incorporation of information from the correlated traits. The preceding discussion is not intended to imply advocacy for selection based on any single biological trait, or in this case efficiency measure.
Use of EBV for evaluation of candidates for selection is preferable to use of phenotypes due to the greater accuracy of EBV for predicting genetic merit. Relative to the residual phenotypes, single-trait EBV are more accurate as a result of their including and properly weighting information from related animals (Belonsky & Kennedy, 1988). In addition, animals without an own phenotype for efficiency may thus be evaluated. Here, this results in an additional 6 322 animals being evaluated. Some of the related animals lacking observed phenotypes may have evaluations equivalent in accuracy to those of animals with records (MacNeil et al., 2011). Further gains in accuracy can result from multiple-trait evaluation (Henderson & Quaas, 1976) of the primary traits with subsequent prediction of efficiency EBV. These gains result from the value of MBW and ADG as indicator traits useful for predicting DFI. With prior calculation of phenotypic residual measures of efficiency, this opportunity may be substantially negated. However, reliance on indicator traits alone will not facilitate breaking the genetic antagonism between intake and performance (MacNeil et al, 1991). It is important to recognize that the most desirable animals, with respect to efficiency, will be outliers to the general bivariate relationship of intake and performance and thus measurement of both traits will be essential to their identification.
Breeders have often been advised to make selection decisions based on carefully constructed breeding objectives and selection indexes (e.g. Harris & Newman, 1992; MacNeil et al, 1997). Here, discussion is limited to aspects arising from consideration of feed intake and growth in this process. Given the economic values for the EBV of ADG and DFI to be used in a selection index (I), an equivalent index incorporating the EBV for RFI or the EBV for RDG could be derived, following Kennedy et al. (1993). If the hypothetical magnitude of the economic value for ADG (kg/d) is 7 times the economic value for feed intake (kg/d); then:
I1 = 7*EBVADG - EBVDFI, and since
EBVdfi = 0.1153*EBVmbw + 0.1305*EBVadg + EBVrfi
I2 = 6.8695*EBVadg - 0.1153*EBVmbw - EBVrfi
Thus, while the economic value for RFI remains the same as it was for DFI, the economic value for ADG must be adjusted to account for the expected amount of feed consumed to produce it and MBW must also be included in the index. Following similar logic:
EBVadg = 0.1293*EBVdfi + EBVrdg
I3 = 7*EBVrdg - 0.0949*EBVdfi
While these three indexes are equivalent (I1 = I2 = I3, given the estimated genetic parameters), the first of them seems straightforward, potentially necessitates genetic evaluation for fewer traits, and has economic values that are more transparent to farmers.
Selection based on the EBVrfi or EBVrdg has also been advocated to improve feed efficiency (e.g. Eisen, 1977; Herd et al., 2003; Crews 2005). However, it should be noted that single trait selection on EBVRFI or EBVRDG is equivalent to selection on a restricted selection index (Kennedy et al, 1993). Further, it has been shown that restricted indexes are always suboptimal economically and can cause severe losses in potential economic gain (Gibson & Kennedy, 1990). Thus, if it can be assumed that the farmers' interests are best served by selection for economic merit, then selection index based on the primary traits can be recommended for improving feed efficiency.
Conclusions
There exists a significant genetic antagonism between ADG and DFI that potentially compromises selection programmes. Evaluation of candidates for selection based on RFI and RDG provide quite different ranking of their merit. Selection index is an efficient approach for breaking this antagonism. Applying economic weights to the EBV for ADG and DFI directly is straightforward and likely to be most transparent to farmers when compared to selection indexes using residual measures of efficiency. An obvious consequence of this work is the recommendation that genetic evaluation systems include analyses of the primary traits ADG and DFI.
References
Arthur, P.F., Herd, R.M., Wright, J., Xu, G., Dibley, K. & Richardson, E.C., 1996. Net feed conversion efficiency and its relationship with other traits in beef cattle. Proc. Aust. Soc. Anim. Prod. 21, 107-110. [ Links ]
Arthur, P.F., Renand, G. & Krauss, D., 2001a. Genetic and phenotypic relationships among different measures of growth and feed efficiency in young Charolais bulls. Livest. Prod. Sci. 68, 131-139. [ Links ]
Arthur, P.F., Archer, J.A., Johnston, D.J., Herd, R.M., Richardson, E.C. & Parnell, P.F., 2001b. Genetic and phenotypic variance and covariance components for feed intake, feed efficiency, and other postweaning traits in Angus cattle. J. Anim. Sci. 79, 2805-2811. [ Links ]
Belonsky, G.M. & Kennedy, B.W., 1988. Selection on individual phenotype and best linear unbiased predictor of breeding value in a closed swine herd. J. Anim. Sci. 66, 1124-1131. [ Links ]
Berry, D.P. & Crowley, J.J., 2012. Residual intake and body weight gain: a new measure of efficiency in growing cattle. J. Anim. Sci. 90, 109-115. [ Links ]
Boldman, K.G., Kriese, L.A, Van Vleck, L.D. & Kachman, S.D., 1993. A manual for use of MTDFREML. USDA-ARS, Clay Center, Nebraska. [ Links ]
Crews Jr., D.H., 2005. Genetics of efficient feed utilization and national cattle evaluation: a review. Genet. Mol. Res. 4, 152-165. [ Links ]
Crowley, J.J., McGee, M., Kenny, D.A., Crews Jr., D.H., Evans, R.D. & Berry, D.P., 2010. Phenotypic and genetic parameters for different measures of feed efficiency in different breeds of Irish performance tested beef bulls. J. Anim. Sci. 88, 885-894. [ Links ]
Eisen, E.J., 1977. Restricted selection index: an approach to selecting for feed efficiency. J. Anim. Sci. 44, 958-972. [ Links ]
Gibson, J.P. & Kennedy, B.W., 1990. The use of constrained selection indexes in breeding for economic merit. Theor. Appl. Genet. 80, 801-805. [ Links ]
Gunsett, F.C., 1986. Problems associated with selection for traits defined as a ratio of two component traits. Proc. 3rd World Congr. Genet. Appl. Livest. Prod. XI, 437-440. [ Links ]
Harris, D.L. & Newman, S., 1992. How does genetic evaluation become economic improvement? Proc. Symp. Appl. of Expected Progeny Differences (EPDs) to Livest. Improve. Am. Soc. Anim. Sci. 84th Ann. Mtg. 10 August 1992. Pittsburgh, PA. pp. 3-1 to 3-30. [ Links ]
Henderson, C.R. & Quaas, R.L., 1976. Multiple trait evaluation using relatives' records. J. Anim. Sci. 43, 1188-1197. [ Links ]
Herd, R.M., Archer, J.A. & Arthur, P.F., 2003. Reducing the cost of beef production through genetic improvement in residual feed intake: Opportunity and challenges to application. J. Anim. Sci. 81 (E. Suppl. 1), E9-E17. [ Links ]
Hoque, M.A., Arthur, P.F., Hiramoto, K. & Oikawa, T., 2006. Genetic relationship between different measures of feed efficiency and its component traits in Japanese Black (Wagyu) bulls. Livest. Sci. 99, 111-118. [ Links ]
Iwaisaki, I., 1989. Distributional and genetic properties of and selection for ratio indexes. Ph.D. thesis. Univ. of Guelph. Guelph, Ontario, Canada. [ Links ]
Kennedy, B.W., Van der Werf, J.H.J. & Meuwissen, T.H.E., 1993. Genetic and statistical properties of residual feed intake. J. Anim. Sci. 71, 3239-3250. [ Links ]
Koch, R.M., Swiger, L.A., Chambers, D. & Gregory, K.E., 1963. Efficiency of feed use in beef cattle. J. Anim. Sci. 22, 486-494. [ Links ]
Lancaster, P.A., Carstens, G.E., Crews Jr., D.H., Welsh Jr., T.H., Forbes, T.D.A., Forrest, D.W., Tedeschi, L.O., Randel, R.D. & Rouquette, F.M., 2009. Phenotypic and genetic relationships of residual feed intake with performance and ultrasound carcass traits in Brangus heifers. J. Anim. Sci. 87, 3887-3896. [ Links ]
MacNeil, M.D., Bailey, D.R., Urick, J.J., Gilbert, R.P. & Reynolds, W.L., 1991. Heritabilities and genetic correlations for postweaning growth and feed intake of beef bulls and steers. J. Anim. Sci. 69, 3183-3189. [ Links ]
MacNeil, M.D., Nugent, R.A. & Snelling, W.M., 1997. Breeding for profit: An introduction to selection index concepts. Proc. Range Beef Cow Symp. 9-11 Dec. 1997. Rapid City, SD. Paper 142. http://digitalcommons.unl.edu/rangebeefcowsymp/142 [ Links ]
MacNeil, M.D., Lopez-Villalobos, N. & Northcutt, S.L., 2011. A prototype national cattle evaluation for feed intake and efficiency of Angus cattle. J. Anim. Sci. 89, 3917-3923. [ Links ]
Nkrumah, J.D., Basarab, J.A., Wang, Z., Li, C., Price, M.A., Okine, E.K., Crews Jr., D.H. & Moore, S.S., 2007. Genetic and phenotypic relationships of feed intake and measures of efficiency with growth and carcass merit of beef cattle. J. Anim. Sci. 85, 2711-2720. [ Links ]
Robertson, A., 1959. The sampling variance of the genetic correlation coefficient. Biometrics 15, 469-485. [ Links ]
Robinson, D.L., & Oddy, V.H., 2004. Genetic parameters for feed efficiency, fatness, muscle area and feeding behavior of feedlot finished beef cattle. Livest. Prod. Sci. 90, 255-270. [ Links ]
Van der Westhuizen, R.R., Van der Westhuizen, J. & Schoeman, S.J., 2004. Genetic variance components for residual feed intake and feed conversion ratio and their correlations with other production traits in beef bulls. S. Afr. J. Anim. Sci. 34, 257-264. [ Links ]
Received 2 August 2012
Accepted 14 January 2013
First published online 9 March 2013
# Corresponding author: macneil.deltag@gmail.com














