Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Animal Science
On-line version ISSN 2221-4062
Print version ISSN 0375-1589
S. Afr. j. anim. sci. vol.40 n.4 Pretoria Jan. 2010
REVIEW
Random regression test-day model for the analysis of dairy cattle production data in South Africa: creating the framework
E.F. DzombaI,1; K.A. NephaweII; A.N. MaiwasheIII; S.W.P. CloeteI,IV; M. ChimonyoV; C.B. BangaIII; C.J.C. MullerIV; K. DzamaI,#
IDepartment of Animal Science, University of Stellenbosch, Private Bag X1, Matieland 7602, South Africa
IILimpopo Department of Agriculture, 69 Biccard Street, Private Bag X9487, Polokwane 0700, South Africa
IIIAgricultural Research Council, Animal Breeding and Genetics, Private Bag X2, Irene 0062, South Africa
IVInstitute for Animal Production, Private Bag X1, Elsenburg 7607, South Africa
VDiscipline of Animal & Poultry Science, University of KwaZulu Natal, Private Bag X01, Scottsville, Pietermaritzburg 3209, South Africa
ABSTRACT
Genetic evaluation of dairy cattle using test-day models is now common internationally. In South Africa a fixed regression test-day model is used to generate breeding values for dairy animals on a routine basis. The model is, however, often criticized for erroneously assuming a standard lactation curve for cows in similar contemporary groups and homogeneity of additive genetic variances across lactation and for its inability to account for persistency of lactation. The random regression test-day model has been suggested as a more appropriate method and is currently implemented by several Interbull member-countries. This review traces the development of random regression methods and their adoption in test-day models. Comparisons are drawn with the fixed regression test-day model. The paper discusses reasons for suggesting the adoption of the random regression approach for dairy cattle evaluation in South Africa and identifies the key areas where research efforts should focus.
Keywords: Genetic evaluation methods, lactation yield traits
Introduction
Genetic evaluation of dairy sires and cows has evolved immensely over the years. From the initial stages when simple dam-daughter comparisons were made, rapid advances in computer hardware and improvements in computing algorithms have made it possible to implement modern methods for analysis. Several countries are now using best linear unbiased prediction (BLUP) under animal models for national genetic evaluations based either on lactation yields or test-day yields.
In South Africa, estimates of breeding values (BV) for production traits and somatic cell scores of dairy cattle are based on test-day (TD) yields of milk, protein, fat, as well as somatic cell count. Within the National Dairy Animal Improvement Scheme of South Africa, daily yields of milk, protein and fat percentages are recorded every five weeks. These recordings are subsequently used directly in genetic evaluations using a fixed regression test-day model (Mostert et al., 2006b) instead of yields aggregated over 305-days of lactation. A test-day model (TDM) is a statistical procedure which considers all genetic and environmental effects directly on a test-day basis (Swalve, 1995). Data for test-day production of dairy cows provide an example of repeated measures or longitudinal data, the essential feature of which is the presence of correlations between tests on the same animal. It is important to explore the potential of any statistical and computing technique which allows a direct and more efficient utilization of all available test-day records for genetic evaluation of dairy cattle.
Use of the TDM approach allows a more detailed statistical model to be developed, which accounts for environmental variation specific to individual TD yields and genetic effects associated with individual animals. It offers the opportunity to directly account for short-term environmental factors specific to individual yields such as gestation period. The TDM also overcomes the need to predict 305-day yields or for projection of incomplete lactations. Furthermore, the TDM allows for precise definition of the contemporary group (CG). With the TD approach, definition of CG including test-month improves the properties of the statistical model. Solutions emanating from such CG effects can be utilized to improve herd management.
Within the TDM approach, the genetic component of the lactation curve can be modelled by fitting regression coefficients for each animal, commonly referred to as random regression (RR) coefficients (Schaeffer & Dekkers, 1994). The additive genetic solutions can be extracted from the BV estimates for the RR coefficients (Jamrozik et al., 1997). It becomes possible to genetically rank animals for each TD yield by estimating a BV of each animal for each TD yield. The estimated BV is given as a product of the RR coefficients and the days in milk (DIM) dependent covariates. Monitoring of management of individual herds and of individual cows within a herd is also an added advantage through the simple comparison between actual and expected production.
For the South African Holstein and Jersey cow populations, Mostert et al. (2004; 2006a) reported genetic correlations between TD milk yields of different lactations to differ from one. This study led to the implementation of a fixed regression TD model, but recommended the use of RR functions in the genetic evaluation of South African dairy cattle. A random regression TDM approach was first implemented in Canada (Schaeffer et al., 2000) in 1999 and several countries that are members of Interbull have since adopted various forms of the methodology, including Belgium, Germany, the Netherlands, Italy, Finland, Denmark and Sweden (Interbull, 2009). Interbull is an international non-profit making organization responsible for promotion, development and standardization of genetic evaluation of dairy cattle. There are currently 27 countries, including South Africa, participating in Interbull evaluations. South Africa participates in international genetic evaluations of dairy cattle conducted by Interbull for which it has been a member since 1999.
The purpose of this review is to describe the random regression methodology in dairy cattle genetic evaluation and explore how a framework of their adoption for TD data analysis in South Africa can be built.
Methods for genetic evaluation of TD records
Interest has grown in changing the data used in genetic evaluation of dairy cattle from combined 305-day mature equivalent lactation yields to individual TD yields. The 305-day mature equivalent adjusts the current production record for a cow to what she would be producing after three years in lactation or greater as a mature cow. The current method for genetic evaluation uses several daily measurements usually taken once a month (test-day) on an individual cow over the course of the lactation. The idea of using TD measurements in genetic evaluation has been a subject for research for a long time (Searle, 1961; Meyer et al., 1989; Stanton et al., 1992; Ptak & Schaeffer, 1993; Meyer & Hill, 1997; Wiggans & Goddard, 1997).
Data from the milk recording scheme are often analyzed by regarding TD records from a cow in single or multiple trait analyses or as repeated measurements of the same trait along a lactation curve, potentially applying some correction for DIM or age at recording. Various methods have been used to analyze TD records which represent longitudinal data (Swalve, 1995; 2000; Misztal et al., 2000; Schaeffer et al., 2000; Jensen, 2001). Most of these methods can be regarded as being derived from a model in which the traits have a patterned covariance matrix, but these methods vary in assumptions about the structure of the covariance matrix (White et al., 1999).
Firstly, in single trait analysis with a repeatability model, constant genetic variance over DIM and a genetic correlation of one between TD records taken at different DIM, is assumed (Ptak & Schaeffer, 1993).
Secondly, multivariate analysis treats each TD record at different DIM as a different trait (Meyer et al., 1989; Pander et al., 1992). Swalve (1995) observed that some authors arbitrarily divided the DIM range into intervals (early, mid and late lactation) that represent individual, but correlated traits and treated the measurements of these different intervals as different traits. The approach has major drawbacks that include inadequate use of information provided at test-days, hence fails to account for constraints imposed on the covariance structure.
Thirdly, lactation curves have been fitted at a phenotypic level and the parameters of the curve have subsequently been analyzed as new traits (Stanton et al., 1992). However, this approach results in failure to fully account for the systematic environmental effects (VanRaden, 1997).
Fourth, as a way of improving the current model for dairy cattle data analysis, the random regression approach has been proposed for South Africa (Mostert, 2007) and is already being applied in some countries' dairy cattle genetic evaluations (Hammami et al., 2008).
The random regression approach
The additive genetic values (estimated breeding values, EBV) of animals are usually obtained from mixed model analyses. For the trait under consideration, a linear regression of observations on indicator variables is performed. Animals' additive genetic effects are fitted as random effects. Because functions of time, such as DIM, can be readily modelled in the mixed model framework (Henderson, 1982), trajectories (e.g. lactation curve) can be described. The covariables are usually nonlinear functions such as polynomials or splines relating time to the traits e.g. milk, fat or protein yield. Fitting sets of RR coefficients for each individual random factor (e.g. additive genetic and permanent environmental effects) produces the estimates of the corresponding trajectories. This in short, describes the RR model.
For the evaluation of TD records, the RR test-day animal model is considered the most appealing statistically. It is often used to fit the RR coefficients in a linear model to obtain genetic parameters and breeding values. There are two approaches to the RR model (RRM): RR on lactation curve functions (e.g. the Wilmink's function) or RR on polynomials or splines. The number of parameters that can be fitted to describe a lactation curve is flexible with the RR where a lactation curve function is used. Jamrozik & Schaeffer (2002) found that the TDM with Legendre polynomials outperformed the TDM with a lactation curve function, considering the same number of parameters in terms of statistics on the goodness of fit.
History of random regression models in dairy cattle genetic evaluation
The general concept of using RR for analysis of covariance in an animal breeding context was suggested by Henderson (1982). Kirkpatrick & Heckman (1989) and Kirkpatrick et al. (1990; 1994) introduced the infinite-dimensional model for traits measured repeatedly per individual, and suggested to model genetic covariances of trajectories through covariance functions. However, initial applications of the RRM were in genetic evaluation of dairy cows, using records from individual test-days to model the lactation curve (Schaeffer & Dekkers, 1994; Jamrozik et al., 1997). Since then, the RRM has become a standard for analyses of repeated measured records from animal breeding schemes. Other areas of animal breeding that have already utilized RRM include conformation traits (Uribe et al., 2000), body condition scores (Berry et al., 2003a), feed intake (Veerkamp & Thompson, 1999); growth in pigs (Lorenzo Bermejo, 2003), sheep (Lewis & Brotherstone, 2002) and beef cattle (Nephawe, 2004; Meyer, 2005a); and litter size in pigs (Lukovic et al., 2004). The RRM has also been used for analysis of survival data (Veerkamp et al., 2001) and for assessing genotype by environment interactions using a continuum of an environmental parameter as covariance functions in reaction norms (Strandberg et al., 2000; Calus & Veerkamp, 2003; Berry et al., 2003b; Shariati et al., 2007).
Differences between random regression and fixed regression test -day models
The fixed regression TDM in current use for dairy cattle genetic evaluation in South Africa uses an animal model with test-day records that includes Wilmink's (1987) covariables to describe the general shape of the lactation curve within fixed subclasses for age and season of calving (Mostert et al., 2006b). Contemporary groups include cows tested on the same day within a herd (herd-test date, HTD) which reduces residual variation substantially more than would herd-year-season of calving groups (Ptak & Schaeffer, 1993). Further, the model assumes a standard fixed lactation curve for all cows in the same age-season subclass, and the estimated additive genetic effects of animals reflect differences in the height of these curves. Thus, differences in lactation persistency are ignored. Correlations between yields at different days in milk are assumed to be the same regardless of time elapsing between test-day measures. The assumption that the variances are homogenous throughout the lactation is difficult to justify. Studies on heterogeneity of variance have been conducted in South Africa. Specifically, it had been discovered that older sire proofs were much higher than for younger bulls with progeny still active in the herds (Mostert et al., 2006a). As a result, the SA fixed regression test-day model incorporates a fixed calving year effect to account for this. However, failure to pre-adjust for heterogeneous variance in test-day models often inflates genetic variances resulting in biased estimated breeding values and lowers their accuracy (Strabel et al., 2006) This is likely due to a set of nonspecified factors in the model equation (e.g. days open, pregnancy status, characteristics of the dry period, body condition at calving, etc.) that make the temporary measurement errors larger and highly variable at the beginning and at the end of the lactation (Lopez-Romero et al., 2003). The reasons for pre-adjustment for heterogeneous variance due to DIM and parity in the South African fixed regression model are twofold; firstly, it is meant to correct the bias due to residual variances being higher in the beginning and end of lactation than in mid-lactation and secondly, it corrects for first lactations having higher residual variances compared to second and third lactations (Mostert et al., 2006a).
A simplified scalar version of the fixed regression model would be:
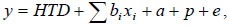
where HTD is the fixed herd TD effect, a is the random additive genetic effect of the cow, p is the random permanent environmental effect associated with each cow and e is the random residual (Swalve, 2000; Jensen, 2001). The lactation curve is modelled using the regression parameters bi and xi are the corresponding time (days in milk) covariates.
An extension of the fixed regression TDM to a RRM would be desirable in several ways. It will allow for the inclusion of random regression coefficients for the lactation curve for each cow (Henderson, 1982). The lactation curve for an individual cow could be viewed as two sets of regressions on DIM. Fixed regressions for all cows belonging to the same subclass of age-season of calving describe the general shape for that cow, and the random regressions for a cow describe the deviations from the fixed regressions, which allow cows to have differently shaped lactation curves.
A random regressions test-day model (RR-TDM) is an extension of the TDM with fixed regressions. The basic structure of RRM is similar in most applications. The shape of the lactation curve is assumed to be influenced by random genetic and permanent environmental effects. As such, genetic and permanent environmental correlations between yields at different DIM can take values less than one. An added advantage is that the model can accommodate heterogeneous additive genetic and permanent environmental variances during lactation, the degree of which varies according to the regression functions chosen to model the trajectory of lactation. The covariates used in the regression part of TDM are usually functions of the day in lactation when the measurements were made.
In simplified scalar form, the model is:

where y is an observation on an animal belonging to a certain fixed factor grouping at a certain time, HTD the herd-test date effect is independent of the time scale for the observations, 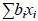 is a linear or nonlinear function or functions that account for the phenotypic trajectory of the average observations across all animals (it accounts for different lactation curve shapes for groups of animals defined by years of birth, parity number, and age and season of calving within parities, for example), aj is the additive genetic effect corresponding to regression coefficient j, xj are the corresponding time covariates, and similarly for the permanent environmental effect subscripted by k, m1 and m2 denote the order of the regression function, e is a random residual effect with mean zero and with possibly different variances for each time or functions of time (Swalve, 2000; Jensen, 2001). The different subscripts indicate that the covariates in different parts of the model are not necessarily the same. When compared with the fixed regression TDM, this corresponds to using regressions to model the additive genetic and the permanent environmental effects. In principle, the covariates xi can be any covariate but are usually relatively simple functions fitted on DIM such as polynomials, orthogonal polynomials (e.g. Legendre polynomials), splines or the parameters of lactation functions proposed by Wood (1967), Ali & Schaeffer (1987) and Wilmink (1987).
is a linear or nonlinear function or functions that account for the phenotypic trajectory of the average observations across all animals (it accounts for different lactation curve shapes for groups of animals defined by years of birth, parity number, and age and season of calving within parities, for example), aj is the additive genetic effect corresponding to regression coefficient j, xj are the corresponding time covariates, and similarly for the permanent environmental effect subscripted by k, m1 and m2 denote the order of the regression function, e is a random residual effect with mean zero and with possibly different variances for each time or functions of time (Swalve, 2000; Jensen, 2001). The different subscripts indicate that the covariates in different parts of the model are not necessarily the same. When compared with the fixed regression TDM, this corresponds to using regressions to model the additive genetic and the permanent environmental effects. In principle, the covariates xi can be any covariate but are usually relatively simple functions fitted on DIM such as polynomials, orthogonal polynomials (e.g. Legendre polynomials), splines or the parameters of lactation functions proposed by Wood (1967), Ali & Schaeffer (1987) and Wilmink (1987).
The results of the genetic evaluations for the South African dairy herd have had a fixed regression model defined by the following parameter sizes shown in Table 1 (Personal communication: B. Mostert, 2010, ARC, Private Bag X02, Irene 0062, South Africa). Using a random regression model would probably increase the number of dairy cattle evaluated thereby improving the accuracy of estimating their proofs.
Choice of basis functions
Theoretically, any function can be used in RRM as a basis function (Swalve, 2000; Meyer, 2005b). Legendre polynomials are the most common, because the correlations between parameters are lower than with other functions (Kirkpatrick et al., 1990; 1994; Van der Werf, 1997). Orthogonal polynomials are able to model lactation curves for a range of covariance structures, but they also have undesirable properties (Misztal, 2006). Fit at the extremes of the trajectories may be poor especially for high orders of fit (Meyer, 2005b) and there may be problems of convergence for large data sets. Several alternatives have been proposed and these include fractional polynomials and linear and B-splines. Fractional polynomials use roots and logs and were advocated for by Robert-Granie´ et al. (2002). Splines are curves constructed from piece-wise lower degree polynomials which are joined smoothly at selected points (knots). Splines are readily fitted within the mixed model analyses (Verbyla et al., 1999; Ruppert et al., 2003). White et al. (1999) used cubic splines, while Torres & Quaas (2001) used B-splines with 10 knots in separate RR analyses of test-day records of dairy cows. Too many knots would increase model complexity, while too few knots would reduce accuracy in estimates (Meyer, 2005b). It is important to compare RR models with South African data using lactation curve functions, orthogonal polynomials and splines.
Advantages of random regression models
Advantages of RR test-day models over other approaches of evaluating test-day records are now widely acknowledged (Bohmanova et al., 2008; Hammami et al., 2008):
1. This type of model provides a continuous treatment of observation over time and is able to incorporate heterogeneous variances and covariances among measures along time (including days that were not sampled) with a potentially reduced number of parameters compared with the multiple trait approach (Schaeffer & Dekkers, 1994; Lidaeur et al., 2003).
2. Every record contributes information at the value of the control variable at which it is measured. Arbitrary or inappropriate corrections for the differences in the control variable are therefore rendered useless (Van der Werf, 1997).
3. With regards to estimation of variance components, random regression models facilitate parsimonious description of changing and potentially complex covariance structures, thereby utilizing the data more efficiently and generating breeding values of higher accuracies (Jamrozik & Schaeffer, 1997; Meyer, 1998).
4. Because the lactation curve is allowed to differ for each cow, this facilitates accounting for the variability in persistency and makes possible the prediction of evaluations for persistency, thereby providing additional information for selection (Jamrozik et al., 1998; Swalve & Gengler, 1999; Lin & Togashi, 2005).
5. The RRM also allows a cow to be evaluated on the basis of any number of TD records during lactation. Related to this, as only eight to 10 TD yields per cow per lactation may be collected, this could result in lower costs of recording (Schaeffer et al., 2000). However, there are issues of accuracy associated with this. EBVs based on one test tend to be of low accuracy. A number of countries require a minimum of three test-day records per lactation for inclusion in genetic evaluation.
6. The RRM for TD yields can account more precisely for environmental factors that could affect cows differently during lactation (Schaeffer & Dekkers, 1994).
7. Due to emphasis on more yield information, a RRM results in top animals which are less related and hence results in reduced rates of inbreeding compared to lactation models (Mrode & Coffey, 2008).
While being conceptually appealing, practical applications of random regression models in animal breeding have been plagued by problems associated with large numbers of parameters to be estimated, poor polynomial approximation and therefore the necessity of analysing much larger sets of data, implausible estimates at the extremes of trajectories, and associated high computational requirements (Swalve, 2000; Jensen, 2001; Schaeffer, 2004; Meyer, 2005b; Misztal, 2006).
Partitioning variance with random regression model
The first estimates of variance components for test-day milk yields obtained by RRM were published by Jamrozik & Schaeffer (1997). The RRM were used for modelling genetic effects only. Meyer & Hill (1997) and Meyer (1998) demonstrated the use of covariance functions to model additive genetic and permanent environmental effects in random regression TDMs. The covariance function describes the covariance structure of an infinite-dimension character, such as test-day milk yields, as a function of time. The covariance function is equivalent to a RRM if the same functions are used (Meyer & Hill, 1997; Van der Werf et al., 1998). The equivalence of the RRM with the covariance function is useful when analyzing data observed at many time periods, because the number of regression coefficients determines the number of covariances to be estimated for each source of variation in a RRM. In a univariate RRM, k regression coefficients result in k(k+1)/2 covariance estimates. The covariance function is used to reduce the rank of the covariance matrix from n, the number of traits, to k, the number of functions, when starting from a multiple trait approach (Meyer & Fitzpatrick, 2005).
The further development of the variance component estimation by RRM included modelling of permanent environmental effects by random regressions (Van der Werf et al., 1998; Olori et al., 1999; Rekaya et al., 1999; Strabel & Misztal, 1999). In addition, other authors modelled the heterogeneity of residual variance across the lactations (Jamrozik & Schaeffer, 1997; Jamrozik et al., 1998; Brotherstone et al., 2000; Jaffrezic et al., 2000).
Parameters obtained in various models and with various data sets showed great variability in both average values and shapes of trajectories (Misztal et al., 2000). The heritability estimates of the first lactation milk yield for particular DIM resulting from RR models ranged between 0.14 (Strabel & Misztal, 1999) and 0.51 (Olori et al., 1999). Some authors reported high heritabilities at the beginning and at the end of lactation (Jamrozik & Schaeffer, 1997; Olori et al., 1999; Kettunen et al., 2000). Other authors found the highest heritabilities in the middle of lactation (e.g. Swalve, 1995; Rekaya et al., 1999; Liu et al., 2000; Pool et al., 2000; Jakobsen et al., 2002; Druet et al., 2003).
Standard mixed-model-based variance component procedures (i.e. Restricted maximum Likelihood: REML or Bayesian methods based on Markov chain Monte Carlo methodology: MCMC) can be used to estimate covariance functions directly from the data (Jensen, 2001). High computational demands limit the size of the datasets and the nature of the models that can be analyzed using REML, but algorithms for multivariate analyses via AIREML are readily adapted to the estimation of covariances among random regression coefficients (Meyer & Kirkpatrick, 2005).
Sorensen & Gianola (2002) noted that Bayesian estimation is now standard for quantitative genetic analyses. Particularly popular are schemes that sample from fully conditional posterior distributions of the parameters of interest. These are computationally easy to implement. Jamrozik (2004) discussed implementation issues of Markov chain Monte Carlo methods for random regression analyses.
Modelling environmental effects in the random regression model
Milk production is influenced by exactly the same environmental factors whether a TDM or lactation model is used in genetic evaluation. However, for a TDM, the stage of lactation is an important consideration, because of the curvilinear relationship that exists between the stage of lactation and milk production (Swalve, 1995; 2000). The TDMs often use types of covariates or mathematical functions, in a regression, to account for stage of lactation. Meyer (2005a) and Meyer & Kirkpatrick (2005) noted that the resultant lactation curve parameters can be considered as examples of 'function-valued traits' implying that mathematical functions are in use.
The adoption of TDM over the lactation model replaced the use of herd-year-season (HYS) with herd-test-date (HTD). The HTD accounts for the effects of herd and the year and the season of production whereas HYS effect is commonly used to account for the effects of the individual herd, the year, and the season of calving and the interactions among them. With a TDM, further effects that can be fitted in the analysis include age at calving, parity and pregnancy (Swalve, 1995).
The random regression TDM can account for many environmental factors that could affect cows differently during the lactation (Schaeffer & Deckers, 1994). The lactation curve is split into two parts: a fixed part (average lactation curve) and a random animal specific part (deviation from the average curve). To account for the variability within lactation stage, an appropriate sub-model is fitted on stage of lactation, nested within parts of the model that account for environmental effects. There are profound differences in the manner in which environmental variation is accounted for with RRM in respect to definition of subgroups for fixed regression on the stage of lactation (Zavadilova et al., 2005). Frequently used factors are season of calving and/or classes of age at calving (Reents et al., 1998; Strabel & Misztal, 1999; Lidauer et al., 2000; Schaeffer et al., 2000). Other models used include the effects of days carried calf (Lidauer et al., 2000). For South Africa, it is important to investigate how best the information collected when testing herds can be used in genetic analysis to account for the environmental variation. Mostert et al. (2006b) defined a fixed regression TD-model which passed the necessary trend validation tests required by Interbull to ensure that the model sufficiently accounts for all environmental effects. Such studies can also attempt to recommend inclusion of valuable variables that the current milk recording system ignores or encourage inclusion of some traits such as fertility measures in the routine genetic evaluations. The SA Dairy Animal Improvement Scheme records artificial insemination information. Unfortunately, the participants of the Scheme are still reluctant to participate.
Persistency of lactation
Dairy breeders focus on modelling the individual genetic curves of the cows and estimating genetic parameters of the lactation curves to select for lactation yields or persistency (Shanks et al., 1981; Danell, 1982; Ferris et al., 1985; Gengler, 1996; Jamrozik & Schaeffer, 1997). Although the definition of persistency varies, generally it refers to the rate of decline in production after peak milk yield production has been reached (Swalve & Gengler, 1999). High persistency is associated with a slow rate of decline in production whereas low persistency is associated with a rapid rate of decline. Persistent cows are more desirable because they are more efficient in roughage usage, suffer less metabolic stress due to high peak yield and are thus more disease-resistant (Solkner & Fuchs, 1987). Genetic modification of the lactation curves are concerned with the artificial redistribution of total lactation responses among different stages of the lactation (Lin & Togashi, 2005). In a recent study, Mostert et al. (2008) laid out the framework for inclusion of persistency of lactation in genetic evaluation of South African dairy cattle based on the Canadian Persistency Index. As a result, persistency of production has been implemented in routine genetic evaluations thereby highlighting the economic importance of persistency.
In describing the persistency of milk production during lactation, the choice of a parameter that gives a correct description of the shape of a lactation curve is important. It is therefore important to develop an evaluation method in which genetic differences in persistency can be evaluated on a routine basis.
A key issue in genetic evaluation of persistency is trait definition. Gengler (1995; 1996) identified three types of measures of persistency which are: measures based on ratios of yields, measures based on variation of yields and measures developed out of functions that describe lactation yields. There is, however, no clear consensus on how best to mathematically model persistency. The procedure most widely used to measure lactation persistency nowadays is based on the by-product of the random regression test day model. Druet et al. (2005) showed that the first and second eigenvectors of the estimated genetic covariance matrix in a random regression model may serve as proxies for yield and persistency. Use of these eigenvectors in random regression test-day models is computationally advantageous but there is still no clear biological interpretation of the eigenvectors.
Conclusion
Attempts to improve the accuracy of estimated breeding values, reduce the generation interval and boost response to selection for dairy cattle and the quest to provide more comprehensive management information to dairy farmers are stimulating interest in advancing the conceptual framework of the TDM. The RRM approach probably wields the potential to realize these benefits from the South African dairy cattle genetic evaluation programme. Replacing the current TDM with a RRM requires research to demonstrate the benefits. Currently research should be focused on defining the RRM to be implemented, investigating the environmental effects to be included in the model and estimating the covariance structure among observations and genetic parameters for traits to be included in the breeding programme for dairy cattle in South Africa. These are the requisite steps towards adoption of a RRM framework for analysis of dairy TD records.
Acknowledgements
This paper is made possible due to financial support from the Harry Crossley Foundation, Western Cape Animal Production Research Trust and the National Research Foundation (NRF). Thanks to Raphael Mrode for his useful comments on the manuscript.
References
Ali, T.E. & Schaeffer, L.R., 1987. Accounting for covariances among test day milk yields in dairy cows. Can. J. Anim. Sci. 67, 637-644. [ Links ]
Berry, D.P., Buckley, F., Dillon, P., Evans, R.D., Rath, M. & Veerkamp, R.F., 2003a. Genetic parameters for body condition score, body weight, milk yield and fertility estimated using random regression models. J. Dairy Sci. 86, 3704-3717. [ Links ]
Berry, D.P., Buckley F., Dillon, P., Evans, R.D., Rath, M. & Veerkamp, R.F., 2003b. Estimation of genotype X environment interaction, in a grass-based system, for milk yield, body condition score, and body weight using random regression models. Livest. Prod. Sci. 83, 191-203. [ Links ]
Bohmanova, J., Miglior, F., Jamorozik, J., Misztal, I. & Sullivan, P.G., 2008. Comparison of random regression models with legendre polynomials and linear splines for production traits and somatic cell score of Canadian Holstein cows. J. Dairy Sci. 91, 3627-3638. [ Links ]
Brotherstone, S., White, I.M.S. & Meyer, K., 2000. Genetic modeling of daily milk yield using orthogonal polynomials and parametric curves. Anim. Sci. 70, 407-415. [ Links ]
Calus, M.P.L. & Veerkamp, R.F., 2003. Estimation of environmental sensitivity of genetic merit for milk production traits using a random regression model. J. Dairy Sci. 86, 3756-3774. [ Links ]
Danell, B., 1982. Studies on lactation yield and individual test-day yield of Swedish dairy cows. III. Persistency of milk yield and its correlation with lactation yield. Acta Agric. Scand. 32, 93-101. [ Links ]
Druet, T., Jaffrezic, F., Boichard, D. & Ducrocq, V., 2003. Modelling lactation curves and estimation of genetic parameters for first lactation test-day records of French Holstein cows. J. Dairy Sci. 86, 2480-2490. [ Links ]
Druet, T., Jaffrezic, F. & Ducrocq, V., 2005. Estimation of genetic parameters for test day records of dairy traits for the first three lactations. Genet. Sel. Evol. 37, 257-271. [ Links ]
Ferris, T.A., Mao, I.L. & Anderson, C.R., 1985. Selecting for lactation curve and milk yield in dairy cattle. J. Dairy Sci. 68, 1438-1448. [ Links ]
Gengler, N., 1995. Use of mixed models to appreciate the persistency of yields during the lactation of milk cows. PhD thesis, Faculte Universitaire des Science Agronomiques de Gembloux, Gembloux, Belgium. [ Links ]
Gengler, N., 1996. Persistency of lactation yields: A review. INTERBULL Bulletin No. 12, 87-96. [ Links ]
Hammami, H., Rekik, B., Soyeurt, H., Ben Gara, A. & Gengler, N., 2008. Genetic parameters for Tunisian Holsteins using a test-day random regression model. J. Dairy Sci. 91, 2118-2126. [ Links ]
Henderson Jr., C.R., 1982. Analysis of covariance in the mixed model: higher level, nonhomogeneous, and random regressions. Biometrics 38, 623-640. [ Links ]
Interbull, 2009. Interbull routine genetic evaluation for dairy production traits, August 2009. http://www-interbull.slu.se/eval/framesida-prod.htm Accessed December 4, 2009. [ Links ]
Jaffrezic, F., White, I.M.S., Thompson, R. & Hill, W.G., 2000. A link function approach to model heterogeneity of residual variances over time in lactation curve analysis. J. Dairy Sci. 83, 1089-1093. [ Links ]
Jakobsen, J.H., Madsen, P., Jensen, J., Pedersen, J., Christensen, L.G. & Sorensen, D.A., 2002. Genetic parameters for milk production and persistency for Danish Holsteins estimated in random regression models using REML. J. Dairy Sci. 85, 1607-1616. [ Links ]
Jamrozik, J., 2004. Implementation issues for Markov Chain Monte Carlo methods in random regression test-day models. J. Anim. Breed. Genet. 121, 1-13. [ Links ]
Jamrozik, J. & Schaeffer, L.R., 1997. Estimates of genetic parameters for a test day model with random regressions for yield traits of first lactation Holsteins. J. Dairy Sci. 80, 762-770. [ Links ]
Jamrozik, J. & Schaeffer, L.R., 2002. Bayesian comparison of random regression models for test-day yields in dairy cattle. Proceedings of the 7th World Congress on Genetics Applied to Livestock Production. CD-ROM Commun., no 01-03, INRA and CIRAD, Montpellier. [ Links ]
Jamrozik, J., Kistemaker, G. J., Dekkers, J.C.M. & Schaeffer, L.R., 1997. Comparison of possible covariates for use in random regression model for analyses of test day yields. J. Dairy Sci. 80, 2550-2556. [ Links ]
Jamrozik, J., Jansen, G., Schaeffer, L.R. & Liu, Z., 1998. Analysis of persistency of lactation calculated from a random regression test day model. INTERBULL Bulletin No. 17, 64-69. [ Links ]
Jensen, J., 2001. Genetic evaluation of dairy cattle using test-day models. J. Dairy Sci. 84, 2803-2812. [ Links ]
Kettunen, A., Mantysaari, E.A. & Poso, J. 2000. Estimation of genetic parameters for daily milk yield of primiparous Ayrshire cows by random regression test-day models. Livest. Prod. Sci. 66, 251-261. [ Links ]
Kirkpatrick, M. & Heckman, N., 1989. A quantitative genetic model for growth, shape, reaction norms, and other infinite-dimensional characters. J. Math. Biol. 27, 429-450. [ Links ]
Kirkpatrick, M., Lofsvold, D. & Bulmer, M., 1990. Analysis of the inheritance, selection, and evolution of growth trajectories. Genetics 124, 979-993. [ Links ]
Kirkpatrick, M., Hill, W.G. & Thompson, R., 1994. Estimating the covariance structure of traits during growth and ageing illustrated with lactations in dairy cattle. Genet. Res. 64, 57-67. [ Links ]
Lewis, R.M. & Brotherstone, S., 2002. A genetic evaluation of growth in sheep using random regression techniques. Anim. Sci. 74, 63-70. [ Links ]
Lidauer, M., Mäntisaari, E.A., Strandèn, I. & Pösö, J., 2000. Multiple-trait random regression test-day model for all lactations. INTERBULL Bulletin No. 25, 81-86. [ Links ]
Lidauer, M., Mäntisaari, E.A. & Strandèn, I., 2003. Comparison of test-day models for genetic evaluation of production traits in dairy cattle. Livest. Prod. Sci. 79, 73-86. [ Links ]
Lin, C.Y. & Togashi, K., 2005. Maximization of lactation milk production without decreasing persistency. J. Dairy Sci. 88, 2975-2980. [ Links ]
Liu, Z., Reinhardt, F. & Reents, R., 2000. Estimating parameters of a random regression test day model for first three lactation milk production traits using the covariance function approach. INERBULL Bulletin No. 25, 74-80. [ Links ]
Lopez-Romero, P., Rekaya, R. & Carabano, M.J., 2003. Assessment of homogeneity vs. heterogeneity of residual variance in random regression test-day models in a Bayesian analysis. J. Dairy Sci. 86, 3374-3385. [ Links ]
Lorenzo Bermejo, J., 2003. Random regression to model genetically the longitudinal data of daily feed intake in growing pigs. Livest. Prod. Sci. 82, 189-200. [ Links ]
Lukovic, Z., Malovrh, S., Gorjanc, G. & Kovac, M., 2004. A random regression model in analysis of litter size in pigs. S. Afr. J. Anim. Sci. 34, 241-248. [ Links ]
Meyer, K., 1998. Estimating covariance functions for longitudinal data using a random regression model. Genet. Sel. Evol. 30, 221-240. [ Links ]
Meyer, K., 2005a. Random regression analyses using B-splines to model growth of Australian Angus cattle. Genet. Sel. Evol. 37, 473-500. [ Links ]
Meyer, K., 2005b. Advances in methodology for random regression analyses. Aust. J. Exp. Agric. 45, 847-858. [ Links ]
Meyer, K. & Hill, W.G., 1997. Estimates of genetic and phenotypic covariance functions for longitudinal or 'repeated' records by restricted maximum likelihood. Livest. Prod. Sci. 47, 185-200. [ Links ]
Meyer, K. & Kirkpatrick, M., 2005. Up hill, down dale: quantitative genetics of curvaceous traits. Phil. Trans. R. Soc. B. 360, 1443-1455. [ Links ]
Meyer, K., Graser, H.U. & Hammond, K., 1989. Estimates of genetic parameters for first lactation test-day production of Australian Black and White cows. Livest. Prod. Sci. 21, 177-199. [ Links ]
Misztal, I., 2006. Properties of random regression models using linear splines. J. Anim. Breed. Genet. 123, 74-80. [ Links ]
Misztal, I., Strabel, T., Jamrozik, J., Mantysaari, E.A. & Meuwissen, T.H.E., 2000. Strategies for estimating the parameters needed for different test-day models. J. Dairy Sci. 83, 1125-1134. [ Links ]
Mostert, B.E., 2007. The suitability of test-day models for genetic evaluation of dairy cattle in South Africa. PhD thesis, University of Pretoria, South Africa. [ Links ]
Mostert, B.E., Groeneveld, E. & Kanfer, F.H.J., 2004. Testday models for production traits in dairy cattle. S. Afr. J. Anim. Sci. 34, 35-37. [ Links ]
Mostert, B.E., Theron, H.E., Kanfer, F.H.J. & Van Marle-Köster, E., 2006a. Adjustment for heterogeneous variances and a calving year effect in test-day models for national genetic evaluation of dairy cattle in South Africa. S. Afr. J. Anim. Sci. 36, 165-174. [ Links ]
Mostert, B.E., Theron, H.E., Kanfer, F.H.J. & Van Marle-Köster, E., 2006b. Fixed regression test-day models for South African dairy cattle for participation in international evaluations. S. Afr. J. Anim. Sci. 36, 58-70. [ Links ]
Mostert, B.E., Van der Westhuizen, R.R. & Theron, H.E., 2008. Procedures for estimation of genetic persistency indices for milk production for the South African dairy industry. S. Afr. J. Anim. Sci. 38, 224-230. [ Links ]
Mrode, R. & Coffey, M., 2008. Understanding cow evaluations in univariate and multivariate animal and random regression models. J. Dairy Sci. 91, 794-801. [ Links ]
Nephawe, K., 2004. Application of random regression models to the genetic evaluation of cow weight in Bonsmara cattle in South Africa. S. Afr. J. Anim. Sci. 34, 166-173. [ Links ]
Olori, V.E., Hill, W.G., McGuirk, B.J. & Brotherstone, S., 1999. Estimating variance components for test day milk records by restricted maximum likelihood with a random regression animal model. Livest. Prod. Sci. 61, 53-63. [ Links ]
Pander, B.L., Hill, W.G. & Thompson, R., 1992. Genetic parameters of test day records of British Holstein-Friesian heifers. Anim. Prod. 55, 11-21. [ Links ]
Pool, M.H., Jans, L.L.G. & Meuwissen, T.H.E., 2000. Genetic parameters of Legendre polynomials for first parity lactation curves. J. Dairy Sci. 83, 2640-2649. [ Links ]
Ptak, E. & Schaeffer, L.R., 1993. Use of test day yields for genetic evaluation of dairy sires and cows. Livest. Prod. Sci. 34, 23-34. [ Links ]
Reents, R., Dopp, L., Schmutz, M. & Reinhardt, F., 1998. Impact on application of a test day model to dairy production traits on genetic evaluations of cows. INTERBULL Bulletin No. 17, 49-54. [ Links ]
Rekaya, R., Carabano, J. & Toro, M.A., 1999. Use of test day yields for the genetic evaluation of production traits in Holstein-Friesian cattle. Livest. Prod. Sci. 57, 203-217. [ Links ]
Robert-Granie', C., Maza, E., Rupp, R. & Foulley, J.L., 2002. Use of fractional polynomial for modelling somatic cell scores in dairy cattle. In: Proceedings of the 7th World Congress of Genetics Applied to Livestock Production, Montpellier (France), 19-23 August 2002, CD-ROM, comm. no 16-05, Montpellier, France. [ Links ]
Ruppert, D., Wand, M.P. & Carroll, R.J., 2003. Semiparametric Regression. Cambridge University Press, New York, USA. [ Links ]
Schaeffer, L.R., 2004. Application of random regression models in animal breeding. Livest. Prod. Sci. 86, 35-45. [ Links ]
Schaeffer, L.R. & Dekkers, J.C.M., 1994. Random regressions in animal models for test-day production in dairy cattle. 5th World Congr. Genet. Appl. Livest. Prod. 18, 443-446. [ Links ]
Schaeffer, L.R., Jamrozik, J., Kistemaker, G.J. & Van Doormaal, B.J., 2000. Experience with a test-day model. J. Dairy Sci. 83, 1135-1144. [ Links ]
Searle, S.R., 1961. Part lactations. II. Genetic and phenotypic studies of monthly fat yield. J. Dairy Sci. 44, 282-295. [ Links ]
Shanks, R.D., Berger, P.J., Freeman, A.E. & Dickinson, F.N., 1981. Genetic aspects of lactation curves. J. Dairy Sci. 64, 1852-1860. [ Links ]
Shariati, M.M., Su, G., Madsen, P. & Sorensen, D., 2007. Analysis of milk production traits in early lactation using a reaction norm model with unknown covariates. J. Dairy Sci. 90, 5759-5766. [ Links ]
Solkner, J. & Fuchs, W., 1987. A comparison of different measures of persistency with special respect to variation of test-day milk yields. Livest. Prod. Sci. 16, 305-319. [ Links ]
Sorensen, D. & Gianola, D., 2002. Likelihood, Bayesian, and MCMC Methods in Quantitative Genetics. Springer-Verlag, New York. [ Links ]
Stanton, T.L., Jones, L.R., Everett, R.W. & Kachman, S.D., 1992. Estimating milk, fat, and protein lactation curves with a test-day model. J. Dairy Sci. 75, 1691-1700. [ Links ]
Strabel, T. & Misztal, I., 1999. Genetic parameters for first and second lactation milk yield of Polish Black and White cattle with random regression test-day models. J. Dairy Sci. 82, 2805-2810. [ Links ]
Strabel, T., Jankowiski, T. & Jamrozik, J., 2006. Adjustments for heterogeneous herd-year variances in a random regression model for genetic evaluations of Polish Black and White cattle. J. Appl. Genet. 47 (2), 125-130. [ Links ]
Strandberg, E., Kolmodin, R., Madsen, P., Jensen, J. & Jorjani, H., 2000. Genotype by environment interaction in Nordic Dairy Cattle studied by use of reaction norms. INTERBULL Bulletin No. 25, 41-45. [ Links ]
Swalve, H.H., 1995. Test day models in the analysis of dairy production data- a review. Arch. Tierzucht. 38, 591-612. [ Links ]
Swalve, H.H., 2000. Theoretical basis and computational methods for different test-day genetic evaluation methods. J. Dairy Sci. 83, 1115-1124. [ Links ]
Swalve, H.H. & Gengler, N., 1999. Genetics of lactation persistency. Occ. Publ. Br. Soc. Anim. Sci. 24, 75-82. [ Links ]
Torres, R.A. & Quaas, R.L., 2001. Determination of covariance functions for lactation traits on dairy cattle using random-coefficient regressions on B-splines. J. Anim. Sci. 79 (Suppl. 1), 112 (abstract). [ Links ]
Uribe, H., Schaeffer, L.R., Jamrozik, J. & Lawlor, T.J., 2000. Genetic evaluation of dairy cattle for conformation traits using random regression models. J. Anim. Breed. Genet. 117, 247-259. [ Links ]
Van der Werf, M., 1997. Random Regressions in Animal Breeding. Course notes available at: http://www-personal.une.edu.au/~jvanderw/CFcoursenotes.pdf Accessed 4 December, 2009. [ Links ]
Van der Werf, J.H.J., Goddard, M.E. & Meyer, K., 1998. The use of covariance functions and random regressions for genetic evaluation of milk production based on test day records. J. Dairy Sci. 81, 3300-3308. [ Links ]
VanRaden, P.M., 1997. Lactation yields and accuracies computed from test-day yields and (co)variances for best prediction. J. Dairy Sci. 80, 3015-3022. [ Links ]
Veerkamp, R.F. & Thompson, R., 1999. A covariance function for feed intake, liveweight and milk yield estimated using a random regression model. J. Dairy Sci. 82, 1565-1573. [ Links ]
Veerkamp, R.F., Brotherstone, S., Engel, B. & Meuwissen, T.H.E., 2001. Analysis of censored survival data using random regression models. Anim. Sci. 72, 1-10. [ Links ]
Verbyla, A.P., Cullis, B.R., Kenward, M.G. & Welham, S.J., 1999. Smoothing splines in the analysis of designed experiments and longitudinal data. Appl. Stat. 48, 269-311. [ Links ]
White, I.M.S., Thompson, R. & Brotherstone, S., 1999. Genetic and environmental smoothing of lactation curves with cubic splines. J. Dairy Sci. 82, 632-638. [ Links ]
Wiggans, G.R. & Goddard, M.E., 1997. A computationally feasible test day model for genetic evaluation of yield traits in the United States. J. Dairy Sci. 80, 1795-1800. [ Links ]
Wilmink, J.B.M., 1987. Adjustment of test day milk, fat and protein yield for age, season and stage of lactation. Livest. Prod. Sci. 16, 335-348. [ Links ]
Wood, P.D.P., 1967. Algebraic model of the lactation curve in cattle. Nature 216, 164-165. [ Links ]
Zavadilova, L., Nemcova, E., Pribyl, J. & Wolf, J., 2005. Definition of sub-groups for fixed regression in test-day animal model for milk production of Holstein cattle in the Czech Republic. Czech J. Anim. Sci. 50 (1), 7-13. [ Links ]
# Corresponding author. E-mail: kdzama@sun.ac.za
1 Current address: Discipline of Genetics, University of KwaZulu Natal, Private Bag X01, Scottsville, Pietermaritzburg 3209, South Africa














