Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Animal Science
On-line version ISSN 2221-4062
Print version ISSN 0375-1589
S. Afr. j. anim. sci. vol.39 n.4 Pretoria Jan. 2009
Non-linear model analysis of categorical traits related to female reproduction efficiency in beef cattle
T. RustI,II,III,#; S.J. SchoemanII; J. van der WesthuizenIII; J.B. van WykIV
IDohne ADI, Private Bag X15, Stutterheim 4930, South Africa
IIUniversity of Stellenbosch, Private Bag X1, Matieland 7602, South Africa
IIIARC-Animal Production Institute, Private Bag X2, Irene 0062, South Africa
IVUniversity of the Free State, P.O. Box 339, Bloemfontein, South Africa
ABSTRACT
The utilization of non-linear threshold models and linear animal models to estimate variance components for categorical reproductive traits in beef cattle was investigated. Three traits, retention (RET), stayability (STAY) and calf tempo (CT) were defined. The data set consisted of 36 880 Afrikaner beef cattle measurements recorded over a period of 10 years. After editing, the records of 7 746 females from 473 sires were available for the genetic parameter estimation for RET. The corresponding number of records for STAY and CT were 3 018 (243 sires) and 7 653 (465 sires), respectively. Using GFCAT, sire variances for RET, STAY and CT were estimated as 0.202, 0.072 and 0.114, respectively. With error variances pre-set to one, the heritability estimates on the underlying scale were calculated as 0.67, 0.27 and 0.41 for RET, STAY and CT, respectively. From the three traits analyzed in this study CT probably reflects the true fertility of the bull's female progeny best.
Keywords: Calf tempo, fertility, GFCAT, retention, stayability, sire variance
Introduction
Threshold traits are governed by polygenic inheritance, expressing themselves in two or more phenotypic categories. The genotype of the additive genetic effect is a component of the liability that varies according to the closeness to the threshold. The first category individuals may differ widely in whether they are near the threshold or far below it. Likewise, some will almost reach the threshold and are genetically close to those just above it (Lush, 1994). Even a large change in an individual's genotype will have no observable phenotypic effect unless the change moves the specific individual across the threshold. If it does, even a small change in the genotype will have a large phenotypic effect. Threshold models assume the existence of an underlying, unobservable normal distribution that is categorized through fixed thresholds. The phenotypes that are observed depend on the underlying tendency to develop in one form rather than the other, depending on where it is situated relative to the threshold (Wright, 1920; 1926; Bliss, 1935; Dempster & Lerner, 1950).
Female reproductive potential is often defined in the literature as a threshold trait because of the categorical nature of the observation, i.e. the cow either calved or she did not. Exposure to harsh environmental conditions such as drought, extreme heat or cold, and low levels of nutrition, will show the breeder which individuals and families are the most tolerant to the adverse conditions. Falconer (1989) referred to this as "genetic assimilation" and referred to earlier work described by Waddington (1953). Year-to-year fluctuations in the threshold, because of changes in the general environment, will inevitably cause year-to-year fluctuations in the expression of fertility.
Spangler et al. (2006) investigated two approaches of analyzing the data. Firstly, a threshold model ignoring uncertainty, and secondly, a threshold model accounting for uncertainty via fuzzy logic classification. They concluded that a threshold model has advantages over alternative methods when the data is of binary nature in order to avoid bias when estimating genetic parameters.
Given the restrictions of the South African recording system in the past as described by Rust & Groeneveld (2001; 2002) and Rust (2007), an attempt was made to define new additional traits in order to utilize the historically available data to its full potential. The aim of this study was to define some additional categorical traits related to female reproduction efficiency and to estimate the variance components for these traits using non-linear threshold (GFCAT) models.
Materials and Methods
Data from the National Beef Cattle Improvement Scheme (NBCIS) of the Afrikaner beef breed in South Africa were used. The data spanned 10 years and the original selected data set consisted of 36 880 animals. Three traits, considered to describe aspects of female fertility potential and efficiency, were defined as follows:
1. Retention (RET): Heifers were considered that were present in the herd at the age of 18 months. If she proceeded to record the birth of a calf at any stage later in her lifetime, she was placed in category 1. If she failed, and the birth of a calf was never recorded for her, she was placed in category 0.
2. Stayability (STAY): If a cow calved at any stage for any number of times before she reached the age of six years, she was placed in category 0. If she calved again at any stage for any number of times after the age of six years, she was placed in category 1.
3. Calf Tempo (CT): Heifers were considered that were present in the herd at the age of 18 months and evaluated up to the age of five years. Thus, only females that were weighed at 18 months and then stayed in the herd to the age of at least five years or older, qualified for inclusion in the analysis. If she recorded the birth of a calf once before reaching the age of five years, she was placed in category 1, and if she recorded two or more calves before the age of five years, she was placed in category 2. If the heifer failed to record the birth of a calf before she reached the age of five years, she was placed in category 0. Since the definition of the rate of calving in this study differs from that of Meyer et al. (1990) and Rust & Groeneveld (2002), it was decided to refer to this trait as CT rather than calving rate to avoid confusion.
The first trait, RET, identifies heifers that are retained in the herd as breeding cows. In beef cattle breeding, it is preferable that female animals stay in the herd as breeding cows for longer periods. Animals that rebreed after the first and second calving are often the animals that stay in the herd for longer, displaying good genetic merit as breeding animals. Breeders tend to cull animals that fail to rebreed after the first or second calving opportunity.
The second trait, STAY, is defined as an indicator of the staying ability of a cow in the herd once she is selected as a breeding heifer. The STAY of cows in a herd can vary from breed to breed and will determine the manner and intensity of selection for other fertility traits since it influences the age structure of the breed. Therefore, STAY is an important trait to include in a study regarding female fertility of a breed. Animals that tend to stay in herds for many years display good adaptation with the consequence of breeding good adapted offspring.
The third trait, CT, describes the rate at which a cow calved up to a specific age after being chosen as a breeding heifer in the herd. In beef cattle herds it is not economically viable to keep cows that do not breed every year. Therefore, if breeders can select cows that tend to breed regularly, such an animal will have a better economic value than an animal that skips a calving opportunity. Thus, being adapted to the environment and staying in the herd for many years alone will only be economically beneficial if that cow gives birth to a calf every year she is given the opportunity to do so.
For the Afrikaner breed, heifers are rarely bred to calve before the age of three years. Rebreeding after first calving is often a challenge, and once a cow can overcome this hurdle, she will usually be retained as a breeding cow in the herd. CT will allow the breeder to make a distinction between cows that rebreed after the first calving and those that tend to delay before rebreeding. The cut-off ages of 18 months, five years and six years were chosen arbitrarily. It is assumed that heifers still present in the herd at the age of 18 months are kept as replacement heifers and will usually be mated at some future time, depending on the management system employed by the farmer. Heifers not suitable as replacement heifers are usually culled before 18 months of age. For CT it was reasoned that a breeding heifer should show her reproductive potential by the time she is five years old, overlapping the critical second calving period when many heifers often falter. For STAY, the aim is to determine the retention of cows in the herd. Since the Afrikaner cow is known to often breed up to an age of 16 - 20 years it was decided to extend the defining cut-off age for STAY in the Afrikaner breed to six years. Similarly, Silva et al. (2003) defined STAY as whether a cow had calved in a herd at a specific age given that she had calved at an earlier age. The cut-off ages Silva et al. (2003) studied were five, six and seven years.
The general statistics of the data for the three traits, RET, STAY and CT, are presented in Table 1. Initially 7 746 Afrikaner female records from 473 sires calving in 78 herds were used for the genetic parameter estimation using threshold models for RET. The corresponding numbers were 3 018 Afrikaner females from 243 sires calving in 51 herds for STAY and 7 653 Afrikaner females from 465 sires calving in 82 herds for CT. All sires and herds were represented in both categories for RET and STAY and in at least two categories for CT. Since the definition of the three traits depend on whether a cow calved given the chance to do so, only data of cows giving birth from natural mating were considered and data of animals subjected to embryo transfers were omitted from the data.
The basic theory of threshold models has been given by Gianola & Foulley (1983), Harville & Mee (1984), Gilmour et al. (1985) and Misztal et al. (1989). By adding an additional subroutine in the existing programmes for linear models Misztal et al. (1989) were able to accommodate threshold models. The modified model used in this study was as follows:
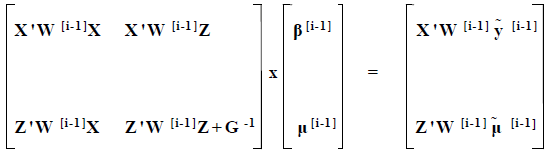
where:
| X, Z | = | design matrices | |
| W | = | diagonal matrix | |
| β | = | vector associated with fixed effects (herd, year and season of birth of animal) | |
| µ | = | vector of sires | |
| G | = | variance-covariance matrix of sire effects | |
| G-1 | = | A-1/σ2s | |
| where: | A-1 = inverse of the relationship matrix | ||
| σ2s = sire variance | |||
The software used in these threshold analyses, GFCAT, was adapted by the University of the Free State, South Africa (Konstantinov, 1992). It is a set of Fortran programmes calculating variance components and breeding values using threshold mixed models. A relationship matrix due to sire relationships was used to support the model. For the GFCAT procedure the fixed effect herd*birth year*season concatenation was included in the model. Season was defined as follows: January to February as Summer, March to May as Autumn, June to August as Winter and September to November as Spring.
Since sire models were fitted, heritability on the underlying scale was estimated for all three traits as:
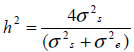
where:
h2 = design matrices
σ2s = sire variance
σ2e = residual variance
Results
The sire variances and derived heritability estimates on the underlying scale for RET, STAY and CT are presented in Table 2. A large sire variance of 0.202 with a resulting heritability of 0.67 on the underlying scale was estimated for RET.
As for the STAY of a bull's female progeny, a sire variance of 0.072 with a heritability estimate on the underlying scale of 0.27, which was considerably lower, was obtained. For the rate at which a bull's female progeny calved before they reached the age of five years, a moderate to high sire variance of 0.114 (with heritability on the underlying scale of 0.41) was estimated. Unfortunately, the adapted GFCAT software used for this study did not produce standard errors for the sire variances.
Discussion
Failure to reproduce is the most common cause for culling beef cows reared under extensive farming conditions. Thus, by assuming that other culling reasons are unimportant, the ability of a cow to be retained in the breeding herd may be considered as an indicator trait for female fertility.
The large sire variance estimated for RET enables the beef breeder to effectively select progeny as sires for the next generation from those bulls of which the female progeny was more likely to be retained in the national herd as breeding heifers. Eler et al. (2002) recommended that estimated progeny differences for the binary trait heifer pregnancy should only be used for the selection of bulls when selecting for improved heifer precocity because the accuracy of prediction is higher for bulls (depending on their number of daughters). The heritability estimate for RET of 0.67 on the underlying scale is much higher than expected. RET does, however, not only reflect the fertility of the female progeny of a bull, but may also reflect a preference of breeders for a specific bull and its female progeny. The fertility reflected by this trait is an indication of the fertility displayed by a bull's heifers, as it is often the practice in beef breeding to mate more heifers than needed in a time limited breeding season and then to select only those that fall pregnant. The subjective preferences of the breeder for specific animals will also be reflected by RET. So, using RET as a primary predictor of the fertility of a bull can be misleading in some instances, since some breeders give preferential treatment to those heifers from, for example, an expensive bull or females that display specific breed characteristics very well.
STAY reflects the ability of a bull's female progeny to remain in the national herd as breeding cows for a few years after initially being selected as breeding heifers and thus also reflects the retention of bull's female progeny. A lower sire variance of 0.072 for STAY was estimated with the heritability estimated on the underlying scale as 0.27. This estimate is higher than the heritablities estimated for STAY by Snelling et al. (1995) 0.09 and 0.20; Doyle et al. (2000) of 0.15; Van der Westhuizen et al. (2001) which ranged between 0.03 and 0.08 and Silva et al. (2003) with heritabilities ranging 0.11 to 0.17 for Nelore cattle. However, it corresponds to heritability estimates using threshold models by Martinez et al. (2002) on Hereford cattle ranging from 0.13 to 0.49. As is the case with RET, STAY will reflect a component of fertility differences among the female offspring of bulls, since breeders tend to cull cows that do not calve every year. The way STAY was defined, however, gave no indication of the number of calves she produced but merely an indication whether she was still present after a given time. The stayability of cows in a herd can vary from breed to breed and herd to herd depending on what criteria the breeder uses to decide whether he should keep or cull a heifer. This will determine the manner and intensity of selection for STAY. This will allow for a bull with female progeny to which the breeder is favourably disposed, to have good breeding values even if his female progeny did not calve regularly, but were kept in the herd for other reasons than good fertility. However, as the production of beef becomes more economically and efficiency orientated, few breeders still employ this practice. Brumatti et al. (2002) estimated the economical value of STAY as corresponding to 44% of the total economic value when obtaining economical values of the traits used in beef cattle production.
Calf tempo is a binary trait for cows with a single parity, but becomes more continuous as the number of parities increase. It has similarities to calving rate as defined by Meyer et al. (1990), Rust & Groeneveld (2002) and Rust (2007). Calving rate is a lifetime measure of the reproductive performance of a cow. Meyer et al. (1990) defined calving rate as the number of calves born divided by the number of opportunities a cow has had to calve. They estimated the heritability for calving rate at 0.07 for Hereford, 0.11 for Angus and 0.17 for tropical cross breeds. Rust & Groeneveld (2002) and Rust (2007) defined calving rate as the number of calves born divided by the age of the cow and estimated a heritability of 0.04 using linear mixed model methodology. In this study a relatively large sire variance of 0.114 and resulting heritability of 0.41 were estimated for CT.
Taking into account that heritability estimates for female fertility traits are often low (Rust et al., 2001), the sire variances and heritabilities estimated for RET and CT were high. This may be as a result of the breed and breeding practices in the breed. Bos indicus breeds have on average later ages at puberty than Bos taurus breeds. Eler et al. (2004) argues that because puberty is later, genetic variability for fertility traits like heifer pregnancy rate seems to be much higher than that in Bos taurus breeds These findings correspond with the results of this study. The Afrikaner is an indigenous breed to South Africa and classified as Bos taurus africanus (Frisch et al., 1997; Hanotte et al., 2002); animals that have similar characteristics to both Bos indicus and Bos taurus breeds.
For this study the assumption was made that any heifer still present in the herd at an age of 18 months was selected as a breeding heifer and mated. However, the information as to whether she was in the herd at the age of 18 months relied on a weight measurement taken at this age. For most cases the fact that she was weighed at 18 months will also mean that she was part of the heifer group initially selected for breeding purposes. Unfortunately many heifers may have been bred without being weighed. Therefore no records of such animals would be available, resulting in a loss of information.
It is possible that due to the restrictions of GFCAT (each sire and herd had to be represented in all or at least two categories per trait), data editing was too severe, leaving only offspring from sires that have produced many offspring that performed well. Also, the contemporary groups were small due to the exclusion of homogenous groups. When Eler et al. (2004) used the weaning management of heifers as contemporary groups, they found that it led to the exclusion of 23% of the data (due to homogenous groups) but concluded that heifer pregnancy is highly heritable, regardless of the contemporary group definition. Using Method R to analyse fertility traits in Bos indicus beef cattle, Evans et al. (1999), Doyle et al. (2000) and Eler et al. (2004) estimated heritabilities of similar magnitude to those estimated in this study.
A multivariate analysis was not considered due to the fact that the traits defined in this study were not component traits but aggregates of the components. The three traits, RET, STAY and CT were all defined using the same dataset combining some of the same components of reproduction. Analyzing RET, STAY and CT in a multivariate was thus not a viable option since the three aggregate traits explained, to a degree, the same variance. This fact rendered the correlations estimated between RET, STAY and CT as meaningless. If all components of reproduction could be defined clearly and measured accurately, multivariate analysis will be an option. However, most components of reproduction are ill defined and rarely measured.
Conclusions
From the three traits analyzed in this study, CT is the trait that probably best reflects the true fertility of the bull's female progeny, since it takes the rate at which female progeny calved between two given ages into account. It is therefore a measure of the reproductive performance of the female offspring of a bull.
From this study it seems that utilizing GFCAT threshold models is not always the best option. The first limitation is that only sire models can be fitted; therefore only breeding values for sires can be derived and only when such a sire has reached an advanced age. Secondly, restrictions when using GFCAT threshold models resulted in severe editing of the data. Using GFCAT results in heavy restrictions on the structure of the data and rigorous editing must be performed on the data, losing potentially valuable information. To overcome this limitation, it can be considered to change the definition of the contemporary groups so that there are fewer groups where zero variation is observed. Another consideration can be to adjust each herd for herd-specific fixed effects.
References
Bliss, C.I., 1935. The calculation of the dosage mortality curve. Ann. Appl. Biol. 22, 134-167. [ Links ]
Brumatti, R.C., Ferraz, J.B.S., Formigoni, I.B. & Eler, J.P., 2002. Application of a bio-economical model to estimate economical weights for traits used in selection index in beef cattle. Proc. 7th World Congr. Gen. Appl. Livest. Prod., (Montpellier, France), August 2002, CD-ROM communication No 23, 1-4. [ Links ]
Dempster, E.R. & Lerner, I.M., 1950. Heritability of threshold characters. Genetics 35, 212-236. [ Links ]
Doyle, S.P., Golden, B.L., Green, R.D. & Brinks, J.S., 2000. Additive genetic parameter estimates for heifer pregnancy and subsequent reproduction in Angus females. J. Anim. Sci. 78, 2091-2098. [ Links ]
Eler, J.P., Silva IIV, J.A., Ferraz J.B.S., Dias, F., Oliveira, H.N., Evans, J.L. & Golden B.L., 2002. Genetic evaluation of the probability of pregnancy at 14 months for Nelore heifers. J. Anim. Sci. 80, 951-954. [ Links ]
Eler, J.P., Silva IIV, J.A., Evans, J.L., Ferraz J.B.S., Dias, F. & Golden B.L., 2004. Additive genetic relationships between heifer pregnancy and scrotal circumference in Nelore cattle. J. Anim. Sci. 82, 2519-2527. [ Links ]
Evans, J.L., Golden, B.L., Bourdon, R.M. & Long, K.L., 1999. Additive genetic relationships between heifer pregnancy and scrotal circumference in Hereford cattle. J. Anim. Sci. 77, 2621-2628. [ Links ]
Falconer, D.S., 1989. Introduction to Quantitative Genetics. (3rd ed.). Longman Group Ltd, Bath, UK. [ Links ]
Frisch, J.E., Drinkwater, R., Harrison, B. & Johnson, S., 1997. Classification of the Southern African sanga and East African shorthorned zebu. Anim. Genet. 28, 77-83. [ Links ]
Gianola, D & Foulley, J.L., 1983. Sire evaluation for ordered categorical data with threshold model. Genet. Sel. Evol. 15, 201. [ Links ]
Gilmour, A.R., Anderson, R.D. & Rae, A.L., 1985. The analysis of binomial data by a generalized linear mixed model. Biometrica 72, 593-599. [ Links ]
Hanotte, O., Bradley, D.G., Ochieng, J.W., Verjee, Y., Hill, E.W. & Rege, J.E.O., 2002. African Pastoralism: Genetic imprints of origins and migrations. Science 296, 336-339. [ Links ]
Harville, D.A. & Mee, R.W., 1984. A mixed model procedure for analyzing ordered categorical data. Biometrics 40, 393-408. [ Links ]
Konstantinov, K.V., 1992. GFCAT is a set of programs for analysis of mixed threshold models with support from REML-TYPE variance components estimation. University of the Orange Free State, P.O. Box 339, Bloemfontein, 9300, RSA. [ Links ]
Lush, J.L., 1994. The Genetics of Populations. College of Agriculture, Iowa State University, Ames, Iowa. Eds Chapman, A.B. & Shrode, R.R., Special Report 94. [ Links ]
Martinez, G.E., Koch, R.M., Cundiff, L.V., Gregory, K.E., Kachman, S.D. & Van Vleck, L.D., 2002. Genetic parameters and genetic trends for stayability in Hereford cows. Proc. 7th World Congr. Gen. App. Livest. Prod. (Montpellier, France), August 2002, CD-ROM communication No 2, 0-4. [ Links ]
Meyer, K., Hammond, K., Parnell, P.F., Mackinnon, M.J. & Sivarajasingam, S., 1990. Estimates of heritability and repeatability for reproductive traits in Australian beef cattle. Livest. Prod. Sci. 25, 15-30. [ Links ]
Misztal, I.D., Gianola, D. & Foulley, J.L., 1989. Computing aspects of a nonlinear method of sire evaluation for categorical data. J. Dairy Sci. 72, 1557. [ Links ]
Rust, T., 2007. An evaluation of genetic improvement in reproductive efficiency in beef cattle through the unraveling of composite reproductive traits. PhD Agric. thesis, University of Stellenbosch, Stellenbosch, South Africa. [ Links ]
Rust, T. & Groeneveld, E., 2001. Variance component on female fertility traits in beef cattle. S. Afr. J. Anim. Sci. 31, 131-141. [ Links ]
Rust, T. & Groeneveld, E., 2002. Variance component estimation of female fertility traits in two indigenous and two European beef cattle breeds of South Africa. S. Afr. J. Anim. Sci. 32, 23-29. [ Links ]
Silva II, J.A.V., Eler, J.P., Ferraz, J.B.S., Golden, B.L. & Oliveira, H.N., 2003. Heritability estimate for stayability in Nelore cows. Livest. Prod. Sci. 79, 97-101. [ Links ]
Snelling, W.M., Golden, B.L. & Bourdon R.M., 1995. Within-herd genetic analyses of stayability of beef females. J. Anim. Sci. 73, 993-1001. [ Links ]
Spangler, M.L., Sapp, R.L., Rekaya, R. & Bertrand, J.K., 2006. Success at first insemination in Australian Angus cattle: Analysis of uncertain binary responses. J. Anim. Sci. 84, 20-24. [ Links ]
Van der Westhuizen, R.R., Schoeman, S.J., Jordaan, G.F. & Van Wyk, J.B., 2001. Heritability estimates derived from threshold analyses for reproduction and stayability traits in a beef cattle herd. S. Afr. J. Anim. Sci. 31, 25-32. [ Links ]
Waddington, C.H., 1953. Genetic assimilation of an acquired character. Evolution 7, 118-126. [ Links ]
Wright, S., 1920. The relative importance of heredity and environment in determining the piebald pattern of guinea pigs. Proc. Nat. Acad. Sci. 6, 320-332. [ Links ]
Wright, S., 1926. A frequency curve adapted to variability in percentage occurrence. J. Am. Stat. Ass. 21, 162-178. [ Links ]
# Corresponding author. E-mail: tinarust@mweb.co.za














