Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Animal Science
On-line version ISSN 2221-4062
Print version ISSN 0375-1589
S. Afr. j. anim. sci. vol.39 n.1 Pretoria Jan. 2009
Analysis of stayability in South African Angus cattle using a threshold model
A. MaiwasheI; K.A. NephaweII; H.E. TheronI
IAgricultural Research Council, Animal Production Institute, Private Bag X2, Irene 0062, South Africa
IILimpopo Department of Agriculture, Private Bag X9487, Polokwane 0700, South Africa
ABSTRACT
The objectives of the study were to estimate genetic parameters for stayability in the South African Angus cattle and to compare the sire and animal threshold models. Data and pedigree information were obtained from the Integrated Registration and Genetic Information System of South Africa. Stayability was defined as a probability that a cow remained in the herd until four (STAY4), five (STAY5), six (STAY6), seven (STAY7) and eight years of age (STAY8), given that she was a dam. Cows that were in the herd by a specific age were assigned a "1" or a "0", otherwise. The proportions of successful stayability were 0.63, 0.57, 0.49, 0.42, and 0.37 for STAY4, STAY5, STAY6, STAY7 and STAY8, respectively. Estimates of genetic parameters were obtained from sire and animal threshold models using AIREML algorithm. The model included the fixed effect of contemporary group and random effects of sire or animal genetic effect and the residual. Heritability estimates from the sire model were 0.26 ± 0.08, 0.26 ± 0.09, 0.30 ± 0.09, 0.24 ± 0.10 and 0.27 ± 0.11 for STAY4, STAY5, STAY6, STAY7 and STAY8, respectively. Corresponding estimates from the animal model were 0.20 ± 0.11, 0.20 ± 0.11, 0.20 ± 0.12, 0.18 ± 0.13 and 0.20 ± 0.14. Estimates from the sire and animal models were consistent. Results from the current study indicate that direct selection for stayability could be effective. However, the long generation interval required to obtain accurate estimates of genetic merit may slow genetic progress for stayability at older ages.
Keywords: Genetic parameters, longevity, beef cattle
Introduction
Female fertility is a trait of economic importance in beef cattle production. Despite its importance, fertility receives little attention in most beef genetic evaluation programmes. For example, calf tempo and scrotal circumference are the only fertility traits in a list of 17 traits that forms part of the national beef cattle evaluation programme in South Africa. Historically, the lack of genetic prediction on fertility was motivated by the perception that heritability for this type of trait is low. Recent application of more appropriate analytical techniques indicates that heritability for fertility traits range from low to high (e.g. Evans et al., 1999; Doyle et al., 2000; Eler et al., 2004; Martinez et al., 2005; Van Melis et al., 2007). The complex nature of fertility is another reason for its neglect in breeding programmes.
Recently, cow stayability or productivity to a predetermined point in life has received attention in most beef and dairy cattle genetic evaluation programmes. Stayability is an economically relevant trait due to its direct relationship with profitability of the production system. Increased stayability is associated with a decrease in annual cost of the replacement of cows, increased herd production and increase in voluntary culling. There are several definitions of stayability in the literature (e.g. Hudson & Van Vleck, 1981; Snelling et al., 1995; Martinez et al., 2004). All these definitions attempt to reflect the potential of a cow to pay for her development and maintenance costs through the number of calves that she produces and possibly weans throughout her productive life. The most common definition of stayability is the probability that a cow reaches a specific age given the opportunity to reach that age (Hudson & Van Vleck, 1981).
Several studies have reported heritability estimates for stayability in beef cattle (Snelling et al., 1995; Doyle et al., 2000; Van der Westhuizen et al., 2001; Silva et al., 2003; Martinez et al., 2005). In general, estimates of heritability for stayability range from low to high. Snelling et al. (1995) conducted within-herd analyses of different measures of stayability using an animal model and reported heritability estimates ranging from 0.019 to 0.195, and 0.025 to 0.227 from a marginal maximum likelihood and Method R, respectively. Martinez et al. (2005) reported heritability estimates ranging from 0.09 to 0.30 from a threshold model. Heritability estimates from the linear model in the same study were lower (0.05 to 0.19) than those from the threshold model. However, transformation of results from the linear model led to similar estimates (0.09 to 0.35).
The first step in the implementation of genetic evaluation for a specific trait is a knowledge of the genetic parameters. Genetic parameters could be obtained from literature estimates from populations similar to the population under consideration or estimated if sufficient data for variance component estimation are available. The primary objective of this study was to estimate genetic parameters for stayability to different ages using data on South African Angus cattle. The secondary objective was to compare the sire and animal threshold models in the analysis of stayability traits.
Materials and Methods
Data considered in the current study were obtained from the Integrated Registration and Genetic Information System of South Africa and included calving records on 28 671 cows born between 1931 and 2006. Pedigree information was also available on these cows. The trait of interest was stayability and defined as a probability that a cow remains in the herd until a specific age, given that she was a dam and had an opportunity to reach that age. This definition is similar to that of Martinez et al. (2005). Five stayability traits were defined: (1) a cow survived to four years given that she was a dam (or had at least one calf) and was 4 yr or older (STAY4), 5 yr or older (STAY5), 6 yr or older (STAY6), 7 yr or older (STAY7) and 8 yr or older (STAY8). Thus, cows that have not reached a specific age (e.g. 4 yr) will not receive stayability observation for that trait. In other words, stayability for that cow is undefined. These traits were considered genetically distinct traits. The management practice for Angus in South Africa is such that about one third of the heifers are bred to calf at two years and the remainder at three years of age. Thus, the cows considered in the current study would have a minimum of one calf and a maximum of six calves for different stayability measures. Stayability at a specific age was a binary trait and an observation for stayability was assigned as follows: cows that remained in the herd until a specific age were assigned a "1" or a "0", otherwise.
Contemporary group was a concatenation of the breeder of the cow and year of birth, and subsequent breeder and year of birth of each calf until a specific age. For cows that left the herd before a specific age or skipped calving, breeder and year of birth of the last or previous calf were used for subsequent years until specific age. This definition of a contemporary group takes into account the fact that a cow may have calves in more than one herd. Data were edited to exclude records from single sire contemporary groups and contemporary groups without variation. Cows with unknown sires were also excluded from the analysis. Summary statistics of the edited data are presented in Table 1. The numbers of contemporary groups were 684, 678, 616, 542 and 451 for STAY4, STAY5, STAY6, STAY7 and STAY8, respectively. The corresponding average contemporary group sizes were 9.25, 8.71, 8.34, 8.06 and 7.86.
Statistical analyses for different stayability traits were conducted using a single trait generalized linear mixed model for threshold traits. The threshold model postulates a conceptual underlying continuous variable (liability) that relates to the observed scale through the thresholds (Wright, 1934). The probability that an observation falls in a given category is a function of the linear predictor (η) and the threshold (τ).
For a binary case such as in the current study, a single threshold divides the observations into the two categories. The linear predictor is a function of the fixed and random effects and was modelled as follows:
η = Xb + Zs [1]
where η is a vector of linear predictors; b is a vector of fixed effects; s is a vector of random sire transmitting abilities and X, Z are known incidence matrices relating conditional expectation, E[yi | ηi] = h(ηi) = pi, to fixed and random effects, respectively; yi is the stayability observations (i.e. yi = 1 or 0). The residual variance on the underlying scale is constrained to 1 because the residual variance and the threshold are not identifiable for binary data (Gianola & Foulley, 1983; Harville & Mee, 1984). The link function was the probit function η= Φ-1(pi) with inverse link function:
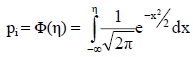
where Φ is the cumulative normal density function and pi denotes the probability of survival (success) for the ith cow. The above model was used to obtain estimates of genetic parameters using the MATVEC software package of Wang et al. (2002). This package implements the Average Information Residual Maximum Likelihood (AIREML) algorithm which estimates variance components using the penalized quasi-likelihood function. Several restarts were conducted using current estimates to ensure convergence of the estimates of the variance components. Estimates of heritability were calculated as follows:
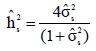
where 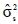 is the estimate of the sire genetic variance. Equation [1] was also used to estimate genetic parameters using an animal model and heritability was calculated as:
is the estimate of the sire genetic variance. Equation [1] was also used to estimate genetic parameters using an animal model and heritability was calculated as:
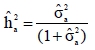
where 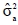 is the estimate of the animal genetic variance. Standard errors for estimates of heritability were computed using the delta method of Searle et al. (1992).
is the estimate of the animal genetic variance. Standard errors for estimates of heritability were computed using the delta method of Searle et al. (1992).
Three generation pedigrees for the sire and animal models were constructed to allow for the inclusion of the relationship among sires (animals) in the estimation of genetic parameters. The pedigree was built considering only cows with stayability observations and their ancestors.
Results and Discussion
The summary statistics for stayability to different ages are provided in Table 1. The rates of success for stayability to different ages in the current study were within the range of estimates from other studies. Martinez et al. (2005), using a similar definition of stayability as in the current study, reported higher stayability values in Hereford cattle for all the traits but STAY8. In a study by Van der Westhuizen et al. (2001), estimates were 0.56, 0.38, and 0.27 for the stayability to four, five and six years of age, respectively. The proportion of cows that had successful observation for stayability to six years was 0.38 in a study by Doyle et al. (2000). It should, however, be noted that stayability depends on the management system (e.g. culling of non-pregnant cows) in a particular herd and therefore direct comparison of the rate of success for stayability in different herds is often not possible.
Estimates of components of variance, heritability and their standard errors for stayability from the sire and animal models are presented in Tables 2 and 3, respectively. Estimates of heritability from the sire model were similar but somewhat higher than those from the animal model. The difference between estimates from the sire and animal model was more pronounced for STAY6. Both models indicate that stayability traits are moderately heritable. Estimates of heritability for stayability traits were similar
(h2 = 0.20) for the animal model except for STAY7 (h2 = 0.18). Estimates of heritability for STAY4 and STAY5 were similar (h2 = 0.26) for the sire model and different (h2 = 0.30) from that for STAY6. Similar estimates of heritability for STAY5 and STAY6 have been reported by Van Melis et al. (2007) in Nellore cattle. Martinez et al. (2005) found different heritability estimates for stayability to different ages. However, their estimates were not significantly different from each other. A similar pattern was observed by Snelling et al. (1995) using animal model Method R. Contrary to the agreement in the estimates of heritability from the sire and animal model observed in the current study, Snelling et al. (1995) studied heritability estimates from the animal and sire model marginal maximum likelihood and found estimates from the sire model that were 4 to 10 times greater than that of the animal model. They attributed these results to lack of sire information since 60% of the sires of the dam were unknown in one of the herds.
Estimates of heritability for the five stayability traits from both the sire and animal model obtained in the current study were within the range of literature estimates. Rasali et al. (2005) analysed stayability to three years of age in Canadian Angus cattle and obtained estimates of heritability (h2 = 0.23 to 0.24) that were consistent with those found in the current study. Van Melis et al. (2007) reported heritability estimates of 0.25 and 0.22 for STAY5 and STAY6 from a threshold model analysis of stayability in Nellore cattle. Likewise, Snelling et al. (1995) reported heritability estimates ranging from 0.16 to 0.21 from an animal model Method R . Martinez et al. (2005) found an estimate of heritability (0.25) for STAY6 that is consistent with that obtained in the current study but lower estimates for STAY4 and STAY5. Recently, Beckman et al. (2006) reported estimates of heritability for stayability to six years of age between 0.08 and 0.19. Doyle et al. (2000) using a similar data set to that of Snelling et al. (1995) reported average and median heritability estimates of 0.15 and 0.14. These estimates were not significantly different from those obtained in the current study.
Contrary to results found in the current study, Van der Westhuizen et al. (2001) obtained estimates of heritability for different stayability traits (i.e. 36 to 86 months) that were considerably lower than that found in the current study. It should, however, be noted that Van der Westhuizen et al. (2001) considered data from a single herd.
Estimates of heritability from the sire and animal model in Tables 1 and 2 were transformed to the observed scale to facilitate comparison with estimates from analyses conducted on the observed scale using linear models. Heritability estimates on the observed scale from the sire and animal models ranged from 0.12 to 0.19. These estimates were higher than most of the estimates from studies on dairy cattle where analyses were conducted on the observed scale (e.g. Hudson & Van Vleck, 1981; Van Doormaal et al., 1985). Hudson & Van Vleck (1981) reported low estimates of heritability for stayability for different opportunity groups (i.e. from 36 to 84 months of age) in U.S. Holstein cattle in the order of 0.02 to 0.05. It was interesting to note that heritabilities increased with age until 72-months of age and then declined at 84-months in the Hudson & Van Vleck (1981) study. This pattern was similar to that obtained in the current study where heritability peaked at six years of age. Vollema & Groen (1996) also reported an increasing trend in estimates of heritability in an upgrading population of dairy cattle. According to Hudson & Van Vleck (1981) the increase in heritability as age at which stayability is measured increases may be due to the reduction in proportion of cows surviving to successive ages, because variance of a binomial trait increases with more equal proportions in each category.
Results from the current study indicate that estimates of heritability for stayability at younger ages are similar to that of stayability at older ages. This implies that selection for stayability at younger ages should be as effective as that for older ages. The use of stayability at younger ages has an added advantage that higher accuracy could be achieved earlier thereby reducing the generation interval. Stayability to six years is used in most national cattle evaluations. Given the prolonged generation interval associated with stayability at six years of age an economic analysis is required to examine the appropriate break-even point for South African Angus cattle.
Conclusions
Estimates of heritability for stayability to different ages were obtained in the current study. Results indicate that measures of stayability between four and eight years are similarly and moderately heritable. All the stayability traits were equally heritable based on the animal model but somewhat different for the sire model with STAY6 tending to be more heritable compared to the other stayability traits. The sire model yielded higher estimates of heritability compared to the animal model despite the fact that the sire model does not account for all the known relationships among the animals. The heritability estimates obtained in the current study indicate that direct selection for stayability should be effective. However, selection for stayability to older ages may be less effective compared to that for earlier stayability traits due to prolonged generation interval associated with later stayability traits. Further research should focus an economic analysis of stayability to determine the appropriate break-even point specific to South African Angus beef cattle production system.
Acknowledgement
This research was jointly funded by the National Research Foundation Technology and Human Resources for Industry Programme (THRIP) and the Red Meat Research and Development Trust of South Africa.
References
Beckman, D.W., Speidel, S.E., Brigham, B.W., Garrick, D.J. & Enns, R.M., 2006. Genetic parameters for stayability and body condition score in beef females. Proceedings, Western Section, American Society of Animal Science. 57, 93-95. [ Links ]
Doyle, S.P., Golden, B.L., Green, R.D. & Brinks, J.S., 2000. Additive genetic parameter estimates for heifer pregnancy and subsequent reproduction in Angus females. J. Anim. Sci. 78, 2091-2098. [ Links ]
Eler, J.P., Silva, J.A.IIV., Evans, J.L., Ferraz, J.B.S., Dias, F. & Golden, B.L., 2004. Additive genetic relationships between heifer pregnancy and scrotal circumference in Nellore cattle. J. Anim. Sci. 82, 2519-2527. [ Links ]
Evans, J.L., Golden, B.L., Bourdon, R.M. & Long, K.L., 1999. Additive genetic relationships between heifer pregnancy and scrotal circumference in Hereford cattle. J. Anim. Sci. 77, 2621-2628. [ Links ]
Gianola, D. & Foulley, J.L., 1983. Sire evaluation for ordered categorical data with a threshold model. Genet. Sel. Evol. 15, 201-224. [ Links ]
Harville, D.A. & Mee, R.W., 1984. A mixed-model procedure for analyzing ordered categorical data. Biometrics 40, 393-408. [ Links ]
Hudson, G.F.S. & Van Vleck, L.D., 1981. Relationship between production and stayability in Holstein Cattle. J. Dairy Sci. 64, 2246-2250. [ Links ]
Martinez, G.E., Koch, R.M., Cundiff, L.V., Gregory, K.E. & Van Vleck, L.D., 2004. Genetic parameters for six measures of length of productive life and three measures of lifetime production by 6 yr after first calving of Hereford cows. J. Anim. Sci. 82, 1912-1918. [ Links ]
Martinez, G.E., Koch, R.M., Cundiff, L.V., Gregory, K.E., Kachman, S.D. & Van Vleck, L.D., 2005. Genetic parameters for stayability, stayability at calving, and stayability at weaning to specified ages for Hereford cows. J. Anim. Sci. 83, 2033-2042. [ Links ]
Rasali, D.P., Crow, G.H., Shrestha, J.N.B., Kennedy, A.D. & Brûlé-Babel, A., 2005. Genetic association between cows' stayability to three years of age and juvenile growth traits in Canadian Angus herds. Can. J. Anim. Sci. 85, 139-143. [ Links ]
Searle, S.R., Casella, G. & McCulloch, C.E., 1992. Variance Components. John Wiley & Sons, Inc., New York, N.Y., USA. [ Links ]
Silva, J.A.IIV., Eler, J.P. & Ferraz, J.B.S., 2003. Heritability estimate for stayability in Nellore cows. Livest. Prod. Sci. 79, 97-101. [ Links ]
Snelling, W.M., Golden, B.L. & Bourdon, R.M., 1995. Within-herd analyses of stayability of beef females. J. Anim. Sci. 73, 993-1001. [ Links ]
Tanida, H., Hohenboken, W.D. & DeNise, S.K., 1988. Genetic aspects of longevity in Angus and Hereford cows. J. Anim. Sci. 66, 640-647. [ Links ]
Van der Westhuizen, R.R., Schoeman, S.J., Jordaan, G.F. & Van Wyk, J.B., 2001. Heritability estimates derived from threshold analyses for reproduction and stayability traits in beef cattle herd. S. Afr. J. Anim. Sci. 31, 25-32. [ Links ]
Van Doormaal, B.J., Shaeffer, L.R. & Kennedy, B.W., 1985. Estimation of genetic parameters for stayability in Canadian Holsteins. J. Dairy Sci. 68, 1763-1769. [ Links ]
Van Melis, M.H., Eler, J.P., Oliveira, H.N., Rosa, G.J.M., Silva, J.A.IIV., Ferraz, J.B.S. & Pereira, E., 2007. Study of stayability in Nellore cows using a threshold model. J. Anim. Sci. 85, 1780-1786. [ Links ]
Vollema, A.R. & Groene, A.B., 1996. Genetic parameters of longevity traits of an upgrading population of dairy cattle. J. Dairy Sci. 79, 2261-2267. [ Links ]
Wang, T., Fernando, R.L. & Kachman, S.D., 2002. Matvec User's Guide. Version 1.03. Available: http://statistics.unl.edu/faculty/steve/software/matvec/ (Accessed July 1, 2008). [ Links ]
Wright, S., 1934. An analysis of variability in number of digits in an inbred strain of guinea pigs. Genetics 19, 506-536. [ Links ]
 Correspondence:
Correspondence:
E-mail: norman@arc.agric.za














