Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Animal Science
On-line version ISSN 2221-4062
Print version ISSN 0375-1589
S. Afr. j. anim. sci. vol.38 n.2 Pretoria Feb. 2008
Estimates of genetic parameters and effect of inbreeding on milk yield and composition in South African Jersey cows
A. MaiwasheI; K.A. NephaweII; H.E. TheronI
IARC-Livestock Business Division, Private Bag X2, Irene 0062, South Africa
IILimpopo Department of Agriculture, Private Bag X9487, Polokwane 0700, South Africa
ABSTRACT
The effect of inbreeding on the 305-d yields of milk, fat and protein, and the percentages of fat and protein in the first three lactations was estimated using records on the South African Jersey cows that participated in the National Dairy Animal Improvement Scheme. Inbreeding coefficients were estimated using the entire pedigree records of the Jersey breed and ranged from 0 to 42%. Data were analyzed using a repeatability animal model. The statistical model included the fixed effects of herd-year-season, age of the cow at calving, calving interval, inbreeding as a discrete or continuous variable and random effects of direct additive genetic, permanent environment of the cow and the residual effects. The multitrait derivative-free REML algorithm was used to obtain estimates of the variance components, ratios and empirical best linear unbiased estimates of the effects of inbreeding. Estimates of heritability were 0.26 (±0.009), 0.19 (±0.008), 0.23 (±0.008), 0.39 (±0.009), and 0.53 (±0.009) for milk, fat and protein yields and fat and protein percent, respectively. Corresponding estimates of the ratio of permanent environmental effect of the cow to total phenotypic variance were 0.20 (±0.008), 0.18 (±0.007), 0.21 (±0.007), 0.14 (±0.008) and 0.13 (±0.008). The regression coefficients for yields (kg) of milk, fat and protein were -15.42 (±1.13), -0.64 (±0.05), and -0.59 (±0.04), and 0.0011 (±0.0005) and 0.0003 (±0.0003) for percent (%) of fat and protein for each 1% increase in inbreeding, respectively. These results provide evidence of inbreeding depression for milk yield and composition traits in the South African Jersey population.
Keywords: Dairy cattle, inbreeding depression, 305-d yield
Introduction
The practical importance of inbreeding in livestock improvement programs is two-fold. Firstly, inbreeding reduces the additive genetic variation in the population, which negatively impacts on the prospects for long-term genetic response to selection. Secondly, inbreeding decreases mean phenotypic performance particularly for those traits that are related to fitness (Thompson et al., 2000a; b; Caraviello et al, 2003; Adamec et al, 2006; VanRaden & Miller, 2006; González-Recio et al, 2007). This phenomenon is called inbreeding depression (Falconer & Mackay, 1996). The effect of inbreeding on performance is of particular interest in the dairy cattle industry where the typical production animal is a purebred. An increase in inbreeding in dairy cattle has been shown to be associated with major economic losses in the form of reduced lifetime performance (Smith et al., 1998). In the U.S. marketplace, relative net income adjusted for opportunity cost was reduced by $14.79 for a fluid market and $12.40 for manufacturing pricing system per 1% increase in inbreeding (Smith et al., 1998). Croquet et al. (2006) have also reported a reduction in lifetime economic profitability associated with an increase in inbreeding in the Holstein breed in the Walloon region of Belgium.
Maiwashe et al. (2006) reported recent increases in the mean level of inbreeding in the South African (RSA) Jersey cattle breed. The increase in inbreeding in dairy cattle was mainly due to widespread use of certain sires through reproductive technologies such as artificial insemination. The rate of inbreeding was estimated at 0.07% per year in this study; which was the highest rate of inbreeding among the four South African dairy cattle breeds studied (Maiwashe et al., 2006). Weller & Ezra (2005) reported a similar rate of inbreeding of 0.08% per year for Israeli Holstein cows. The rate of inbreeding for the South African Jersey population is considerably lower than the rate of 0.20% per year reported for the U.S. Jersey population (Wiggans et al, 1995).
In a population undergoing selection, effects of inbreeding on performance depend on the rate of inbreeding, selection pressure, and mean production levels for traits under consideration. In the United States, Hudson & Van Vleck (1984a) reported estimates of -27.1, -39.5, -19.3, -21.2, and -14.8 kg per 1% increase in inbreeding for 305-d milk yield in the Ayrshire, Brown Swiss, Guernsey, Holstein and Jersey breeds, respectively. A subsequent study on major dairy cattle breeds in the U.S. by Wiggans et al. (1995) found the following estimates of inbreeding depression for milk yield: -30.2, -24.6, -19.6, -29.6, and -21.3 kg per 1% increase in inbreeding for Ayrshire, Brown Swiss, Guernsey, Holstein and Jersey, respectively. Casanova et al. (1992) reported an estimate of -26.0 kg per 1% increase in inbreeding of Swiss Braunvieh for 305-d milk yield. In Canada, Miglior et al. (1992) found a decrease of -9.84 kg per 1% increase in inbreeding for 305-d milk yield in a Jersey population. Furthermore, significant decline in fat and protein yields associated with increasing levels of inbreeding have been reported (Hermas et al., 1987; Wiggans et al., 1995). These reports show that the effect of inbreeding on production in dairy cattle is variable across production environments. It is therefore important that the effect of inbreeding be evaluated in each production environment.
To date no research has been conducted to evaluate the effect of inbreeding on performance in South African dairy cattle despite the fact that recent increases in mean inbreeding levels have been reported in South African dairy cattle breeds (Maiwashe et al., 2006). The objective of the current study was to estimate the effect of inbreeding on 305-d yield of milk, fat and protein, and percentages of fat and protein using the first three lactation records of South African Jersey cows that participated in the National Dairy Animal Improvement Scheme.
Materials and Methods
A pedigree file of the South African Jersey breed (n = 724 229) was obtained from the Integrated Registration and Genetic Information System (INTERGIS). These data were checked for integrity (e.g. animals were ordered chronologically and no animals appeared as both a sire and dam) using the stack_ped tool of the Animal Breeder's Tool Kit (ABTK: Golden et al., 1995). The percentages of animals in the pedigree file with at least one unknown parent and both parents known were 41% and 59%, respectively. The inbreeding coefficient for each animal in the pedigree was calculated using the ainv tool of the ABTK. The ainv tool implements the algorithm of Meuwissen & Luo (1992) to compute the inbreeding coefficients.
Phenotypic data considered in the current study comprised records on first three lactations for 305-d milk, fat and protein yields for the South African purebred Jersey cows that participated in the National Dairy Cattle Improvement Scheme between 1961 and 2006. To obtain a sample of data of manageable size only phenotypic data from 1990 to 2006 were considered. The implementation of this criteria resulted in the exclusion of about 34% of the data. Furthermore, cows that had a missing observation for the first lactation were also excluded. Observations were restricted within three standard deviations from their respective overall phenotypic mean. Only records from cows that calved within a specified age range in different lactations were considered: 17 to 40, 29 to 53 and 41 to 67 months at the first, second and third lactation, respectively. Following Mostert (2006), cows were assigned into one of the following age at calving classes on a lactation basis: 17 - 23, 24 - 26, 27 - 29, 30 - 32 and 33 - 40 months for the first lactation; 29 - 35, 36 - 38, 39 - 41, 42 - 46 and 47 - 53 months for the second lactation; and 41 - 47, 48 - 56, 57 - 60 and 61 - 67 months for the third lactation.
Contemporary groups were defined as a concatenation of the herd, year and season of calving. Two seasons of calving were defined: Season 1 - cows that calved between April and September and Season 2 -cows that calved between October and March. Records from contemporary groups with a single sire, or less than 10 cows or no genetic ties were excluded from the analysis. Contemporary groups with genetic ties were those that had at least one sire with daughters in another contemporary group.
To account for the effect of calving interval (CI) on the second and third lactation 305-d yields, cows were assigned into calving interval classes following the criteria employed by Mostert (2006) in the analysis of test day records. Calving interval classes were created using standardized calving interval (CI ) as follows: unknown CI, CI* < -1, -1 < CI* < +1, CI* > +1.
After editing, the individual inbreeding coefficients were merged with the phenotypic data for all the cows with performance records. A pedigree file was created for these cows by tracing each cow's ancestry as far back as possible. The pedigree file is required in the construction of the inverse of the numerator relationship matrix useful in setting up the mixed model equations. The summary statistics for traits analysed are presented in Table 1. The cows in the data were daughters of 2 748 sires and 48 633 dams, respectively.
A repeatability animal model was used to analyse 305-d milk, fat and protein yields and their percentages. The matrix representation of the model is as follows:
y = Xβ + Zu + Wc + e
where y is a vector of observations for 305-d milk, fat or protein yields and their percentages in the first, second and third lactations; X, W and Z are the incidence matrices relating the fixed and random effects to the observations in y ; β is a vector of fixed effects of herd-year-season of calving, age at calving, calving interval and inbreeding coefficient (fitted as a discrete and continuous independent variable) - for the discrete case, inbreeding coefficients were assigned into the following classes: F = 0, 0 < F < 6.25, 6.25 < F < 12.5, 12.5 < F < 18.5 and F > 18.5%. A similar classification strategy was used by Miglior et al. (1992) and Mc Parland et al. (2007); u is a vector of unobservable random direct additive genetic effects for all the animals in pedigree; c is a vector of permanent environmental effect of the cow; e is a vector of random residual effects unique to each observation. The random effects were assumed to be normally distributed with the expectation equal to zero and the following covariance structure:
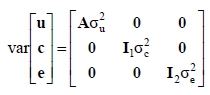
where 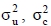 and
and 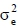 e are the additive genetic, permanent environment and residual variances, respectively. The I1 and 1e are the identity matrices of the order equal to number of records and cows respectively and A is Wright's numerator relationship matrix of the order equal to number of animals in the pedigree. The pedigree for each cow was traced as far back as possible. The number of records in the pedigree file were similar for all traits, e.g. there were 121 813 animals in the pedigree for milk yield.
e are the additive genetic, permanent environment and residual variances, respectively. The I1 and 1e are the identity matrices of the order equal to number of records and cows respectively and A is Wright's numerator relationship matrix of the order equal to number of animals in the pedigree. The pedigree for each cow was traced as far back as possible. The number of records in the pedigree file were similar for all traits, e.g. there were 121 813 animals in the pedigree for milk yield.
Estimates of variance components and the effect of inbreeding (empirical best linear unbiased estimates - eBLUES) for all the traits were obtained using the MTDFREML programs (Boldman et al., 1995). Convergence was assumed when the variance of the simplex was less than 10-9. To ensure convergence to a global maximum, several restarts were run with the estimates at apparent convergence as initial values. In addition, the MTDFREML was used to conduct statistical test of significance for the effect of inbreeding using the t-test. The t-statistic (tobs) is given by (Croquet et al., 2006):
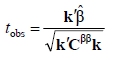
where 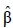 is the solution vector for fixed effects, k is a vector of contrasts, Cββ is the block of the inverse of the coefficient matrix of the mixed model (C-1) corresponding to the fixed effects.
is the solution vector for fixed effects, k is a vector of contrasts, Cββ is the block of the inverse of the coefficient matrix of the mixed model (C-1) corresponding to the fixed effects.
Results and Discussion
Descriptive statistics of the data are presented in Table 1. The number of records suitable for analysis was similar across traits. However, the distribution of records per lactation was highly skewed and typical of livestock production populations where the numbers decline with time. For milk yield, the proportion of records was 60%, 28%, and 12% for the first, second and third lactations, respectively. The same pattern was observed for other traits. The distribution of records by inbreeding class was 45.23%, 50.49%, 3.03%, 0.95%, and 0.31% for F = 0, 0 < F < 6.25, 6.25 < F < 12.5, 12.5 < F < 18.5 and F > 18.5%, respectively. That is, majority of the cows (95.72%) fell into the first two classes of inbreeding while a small proportion of cows (4.29%) were in the next three classes. Mc Parland et al. (2007) found a similar distribution of inbreeding coefficients in Irish Holstein-Friesians. The distribution of inbreeding coefficients observed in the current study is typical in livestock populations where mating of close relatives is often avoided. Low frequency of highly inbred animals might also be due to difficulties in detecting inbreeding as a result of incomplete pedigree information (Smith et al., 1998; Lutaaya et al., 1999; Cassell et al., 2003). Inbreeding coefficients ranged from 0 to 42% with an average of 1.61% in the current study. The mean level of inbreeding was 2.43% for the Irish Holstein-Friesian used in the study of inbreeding by Mc Parland et al. (2007). It should be noted that Mc Parland et al. (2007) only considered cows with a minimum of three complete generations of pedigree information.
Estimates of variance components and their ratios for all the traits are presented in Table 2. The ratios for the additive genetic and permanent environmental effects indicate that the two components were almost equally important for yield traits but the additive genetic effect was somewhat higher. Weller & Ezra (2004) used a repeatability animal model and reported a similar but slightly higher heritability of 0.29 for milk yield using data on first five lactations in Israeli Holstein cows. Their estimate for the permanent environmental ratio (0.22) for milk yield was similar to that obtained in the current study. Gulisija et al. (2007) reported a heritability estimate of 0.34 for first lactation 305-d mature equivalent milk yield for the U.S. Jersey population. Smith et al. (1998) also found a higher heritability estimate for first lactation mature equivalent fat yield of 0.34. In a comprehensive study including data from 13 countries Weigel & Rekaya (2000) obtained heritability estimates ranging from 0.28 to 0.39 for first lactation milk yield. Miglior et al. (2007) used a test-day random regression model and reported average heritabilities for milk yield of 0.52, 0.43 and 0.47 for first, second and third lactation, respectively.
Heritability estimates for fat and protein yield obtained in the current study were lower than those reported by Weller & Ezra (2004). Estimates of heritability for fat and protein yield obtained by Miglior et al. (2007) were almost double those found in the current study. In general, estimates of heritability found in other studies were similar or higher than those found in the current study (de Jager & Kennedy, 1987; Meinert et al., 1989; Welper & Freeman, 1992; Du Toit et al., 1998). Estimates of the ratios for the permanent environmental effect for fat and protein yield found in the current study were similar to those reported by Weller & Ezra (2004).
Estimates of heritability for fat and protein percent are presented in Table 2. Contrary to the results for yield traits, the additive genetic effect was about three times more important than the permanent environmental effect for percentage fat and protein. Heritability estimate for fat yield is lower than estimates from the literature (Meinert et al., 1989; Welper & Freeman, 1992; Miglior et al., 2007).
Estimates of the effect of inbreeding and their standard errors for all the traits are presented in Table 3. These results show a strong negative unfavourable linear relationship (P <0.05) between inbreeding and production traits (i.e. 305-d yields of milk, fat and protein). For example, an 1% increase in inbreeding is associated with 15.42, 0.64 and 0.59 kg reduction in 305-d milk, fat and protein yield, respectively. These magnitudes of inbreeding depression are within the range of estimates reported in the literature (Hodges et al, 1979; Hudson & Van Vleck, 1984a; b; Casanova et al, 1992; Miglior et al, 1992; Smith et al, 1998; Croquet et al., 2006; Croquet et al., 2007). While results from this study confirm the linear relationship between inbreeding and production, the existence of non-linear relationship was not explicitly investigated using higher-order polynomials in the current study. Curvilinear relationship between inbreeding and production has been reported in other studies (Thompson et al., 2000b; Croquet et al., 2007; Gulisija et al., 2007; Mc Parland et al., 2007).
The results obtained from the analysis where inbreeding was fitted as a class variable were in agreement with those from the regression analysis in terms of the negative unfavourable relationship between inbreeding and production. The solutions for the effect of inbreeding on production traits were expressed as deviation from non-inbred cows (F = 0). For example, cows with inbreeding coefficients ranging from 1% to 6.25% produced 58.02 kg, 2.65 kg and 2.00 kg less milk, fat and protein, respectively, compared to the non-inbred cows. Among the three production traits the reduction for fat yield was somewhat lower for the F > 18.5 class than that of the 12.5 < F < 18.5. However, there was no difference (P >0.05) in the reduction in fat yield for the two classes. Similar results where the effect of inbreeding for high inbreeding classes (levels) were lower than that of the preceding lower inbreeding classes have been reported in other studies (Hudson & Van Vleck, 1984a; b). For example, in a study of the effect of inbreeding on first lactation milk yield in U.S. Guernsey cattle Hudson & Van Vleck (1984b) found an estimate of -346.2 kg for inbreeding class 10 < F < 15% and 87.5 kg for inbreeding class 15 < F < 25%.
However, it should be noted that the distribution of records per inbreeding class was highly unbalanced and solutions from higher inbreeding classes should be interpreted with caution. For example, the number of records within the F > 18.5 class was about 0.31% of the entire data.
Table 3 presents estimates of the effect of inbreeding on fat and protein percent. In general, increases in inbreeding were associated with an increase in the percentage of fat and protein. An increase in percent fat for each 1% increase in inbreeding (0.0011%) was somewhat higher than that for percent protein (0.0003%). The linear relationship between inbreeding and fat percent was different from zero (P <0.05) while that for protein percent was not (P >0.05). A positive but non-significant estimate for fat percent (0.002%) has been reported elsewhere (Hermas et al., 1987). Casanova et al. (1992) found a positive but slightly higher estimate of 0.0010% for percent protein in Swiss Braunvieh. Contrary to the results in the current study, they reported a small negative estimate of -0.0005% for percent fat. Miglior et al. (1992) also observed a negative linear relationship (-0.0011%) between inbreeding and percentage fat in Canadian Jersey population.
Conclusions
This study examined the effect of inbreeding on 305-d yield of milk, fat and protein, and percentage of fat and protein in the South African Jersey breed. There was strong evidence of inbreeding depression affecting all yield traits and fat percent. Estimates of inbreeding depression obtained in the current study were comparable to those in the literature. Given that the inbreeding coefficient of majority of the cows is below 6.25% in the current study, it can be concluded that the effect of inbreeding on 305-d production and composition traits is currently minimal in the South African Jersey population. However, results from the current study indicate that levels of inbreeding greater than 6.25% may lead to significant reduction in production and composition traits.
Acknowledgements
The authors wish to acknowledge contributions by M. MacNeil from the ARS-USDA and B.E. Mostert of the ARC-LBD. Financial support from the Technology and Human Resources for Industry Programme (THRIP) and the Professional Research Development Programme of the Department of Science and Technology is greatly appreciated.
References
Adamec, V., Cassell, B.G., Smith, E.P. & Pearson, R.E., 2006. Effects of inbreeding in the dam on dystocia and stillbirths in US Holsteins. J. Dairy Sci. 89, 307-314. [ Links ]
Boldman, K.G., Kriese, L.A., Van Vleck, L.D., Van Tassell C.P. & Kachman, S.D., 1995. A manual for use of MTDFREML. A set of programs to obtain estimates of variances and covariances. [ Links ] [Draft], USDA-ARS, Lincoln, N.E., USA.
Caraviello, D.Z., Weigel, K.A. & Gianola, D., 2003. Analysis of the relationship between type traits, inbreeding and functional survival in Jersey cattle using Weibull proportional hazards model. J. Dairy Sci. 86, 2984-2989. [ Links ]
Casanova, C., Hagger, C. & Kuenzi, N., 1992. Inbreeding in Swiss Braunvieh and its influence on breeding values predicted from a repeatability animal model. J. Dairy Sci. 75, 1119-1126. [ Links ]
Cassell, B.G., Adamec, V. & Pearson, R.E., 2003. Effect of incomplete pedigrees on estimates of inbreeding and inbreeding depression for days to first service and summit yield in Holsteins and Jerseys. J. Dairy Sci. 86, 2967-2976. [ Links ]
Croquet, C., Mayeres, P., Gillon, A., Hammami, H., Soyeurt, H., Vanderick, S. & Gengler, N., 2007. Linear and curvilinear effects of inbreeding on production traits for Walloon Holstein cows. J. Dairy Sci. 90, 465-471. [ Links ]
Croquet, C., Mayeres, P., Gillon, A., Vanderick, S. & Gengler, N., 2006. Inbreeding depression for global and partial economic indexes, production, type, and functional traits. J. Dairy Sci. 89, 2257-2267. [ Links ]
de Jager, D. & Kennedy, B.W., 1987. Genetic parameters of milk yield and composition and their relationships with alternative breeding goals. J. Dairy Sci. 70, 1258-1266. [ Links ]
Du Toit, J., Van Wyk, J.B. & Van der Westhuizen, J., 1998. Genetic parameter estimates in the South African Jersey breed. S. Afr. J. Anim. Sci. 28, 146-152. [ Links ]
Falconer, D.S. & Mackay, T.F.C., 1996. Introduction to Quantitative Genetics. Longman Group, Essex, UK. [ Links ]
Golden, B.L., Snelling, W.M. & Mallinckrodt, C.H., 1995. Animal Breeder's Tool Kit 2.0. User's Guide and Reference Manual. Department of Animal Sciences, Colorado State University, Ft Collins, USA. [ Links ]
González-Recio, O., Lopez de Maturana, E. & Gutierrez, J.P., 2007. Inbreeding depression of female fertility and calving ease in Spanish dairy cattle. J. Dairy Sci. 90, 5744-5752. [ Links ]
Gulisija, D., Gianola, D. & Weigel, K.A., 2007. Nonparametric analysis of the impact of inbreeding on production in Jersey cows. J. Dairy Sci. 90, 493-500. [ Links ]
Hermas, S.A., Young, C.W. & Rust, J.W., 1987. Effects of mild inbreeding on productive and reproductive performance of Guernsey cattle. J. Dairy Sci. 70, 712-715. [ Links ]
Hodges, J., Tannen, L., McGillivray, B.J., Hiley, P.G. & Ellis, S., 1979. Inbreeding levels and their effect on milk, fat and calving interval in Holstein-Friesian cows. Can. J. Anim. Sci. 59, 153-158. [ Links ]
Hudson, G.F.S. & Van Vleck, L.D., 1984a. Inbreeding of artificially bred dairy cattle in the Northeastern United States. J. Dairy Sci. 67, 161-170. [ Links ]
Hudson, G.F.S. & Van Vleck, L.D., 1984b. Effects of inbreeding on milk and fat production, stayability, and calving interval of registered Ayrshire cattle in the Northeastern United States. J. Dairy Sci. 67, 171-179. [ Links ]
Lutaaya, E., Misztal, I., Bertrand, J.K. & Marry, J.W., 1999. Inbreeding in populations with incomplete pedigrees. J. Anim. Breed. Genet. 166, 475-480. [ Links ]
Maiwashe, A., Nephawe, K.A., Van der Westhuizen, R.R., Mostert, B.E. & Theron, H.E., 2006. Rate of inbreeding and effective population size in four major South African dairy cattle breeds. S. Afr. J. Anim. Sci. 36, 50-57. [ Links ]
Mc Parland, S., Kearney, J.F., Rath, M. & Berry, D.P., 2007. Inbreeding effects on milk production, calving performance, fertility, and conformation in Irish Holstein-Friesians. J. Dairy Sci. 90, 4411-4419. [ Links ]
Meinert, T.R., Korver, S. & Van Arendonk, J.A.M., 1989. Parameter estimation of milk yield and composition for 305 days and peak production. J. Dairy Sci. 72, 1534-1539. [ Links ]
Meuwissen, T.H.E. & Luo, Z., 1992. Computing inbreeding coefficients in large populations. Genet. Sel. Evol. 24, 305-313. [ Links ]
Miglior, F. & Burnside, E.B., 1995. Inbreeding of Canadian Holstein cattle. J. Dairy Sci. 78, 1163-1167. [ Links ]
Miglior, F., Burnside, E.B. & Dekkers, J.C.M., 1995. Nonadditive genetic effects and inbreeding depression for somatic cell counts of Holstein cattle. J. Dairy Sci. 78, 1168-1173. [ Links ]
Miglior, F., Sewalem, A., Jamrozik, J., Bohmanova, J., Lefebvre, D.M. & Moore, R.K., 2007. Genetic analysis of milk urea nitrogen and lactose and their relationships with other production traits in Canadian Holstein cattle. J. Dairy Sci. 90, 2468-2479. [ Links ]
Miglior, F., Szkotnicki, B. & Burnside, E.B., 1992. Analysis of levels of inbreeding and inbreeding depression in Jersey cattle. J. Dairy Sci. 75, 1112-1118. [ Links ]
Mostert, B.E., 2006. An investigation into the suitability of test-day models for genetic evaluation of dairy cattle in South Africa. PhD dissertation, University of Pretoria, South Africa. [ Links ]
Smith, L.A, Cassell, B.G. & Pearson, R.E., 1998. The effects of inbreeding on the lifetime performance of dairy cattle. J. Dairy Sci. 81, 2729-2737. [ Links ]
Thompson, J.R., Everett, R.W. & Hammerschmidt, N.L., 2000a. Effects of inbreeding on production and survival in Holsteins. J. Dairy Sci. 83, 1856-1864. [ Links ]
Thompson, J.R., Everett, R.W. & Wolfe, C.W., 2000b. Effects of inbreeding on production and survival in Jerseys. J. Dairy Sci. 83, 2131-2138. [ Links ]
VanRaden, P.M. & Miller, R.H., 2006. Effects of nonadditive genetic interactions, inbreeding, and recessive defects on embryo and fetal loss by seventy days. J. Dairy Sci. 89, 2716-2721. [ Links ]
Weigel, K.A & Rekaya R., 2000. A multiple-trait herd cluster model for international dairy sire evaluation. J. Dairy Sci. 83, 815-821. [ Links ]
Weller, J.I. & Ezra, E., 2004. Genetic analysis of the Israeli Holstein dairy cattle population for production and nonproduction traits with a multitrait animal model. J. Dairy Sci. 87, 1519-1527. [ Links ]
Weller, J.I. & Ezra, E., 2005. Analysis of inbreeding in the Israeli Holstein dairy cattle population. Proc. 2005 Interbull meeting, Uppsala, Sweden, June 2-4, pp. 85-87. [ Links ]
Welper, R.D. & Freeman, A.E., 1992. Genetic parameters for yield traits of Holsteins, including lactose and somatic cell score. J. Dairy Sci. 75, 1342-1348. [ Links ]
Wiggans, G.R., VanRaden, P.M. & Zuurbier, J., 1995. Calculation and use of inbreeding coefficients for genetic evaluation of United States dairy cattle. J. Dairy Sci. 78, 1584-1590. [ Links ]
 Correspondence:
Correspondence:
E-mail: norman@arc.agric.za














