Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
HTS Theological Studies
versión On-line ISSN 2072-8050
versión impresa ISSN 0259-9422
Herv. teol. stud. vol.78 no.4 Pretoria 2022
http://dx.doi.org/10.4102/hts.v78i4.7144
ORIGINAL RESEARCH
Inaccurate volume values in the discussion of Solomon's sea in Yerushalmi Eruvin 1:5
Uri ZurI; David GarberII
IDepartment of Moreshet Israel, Faculty of Social and Humanities, Ariel University, Ariel, Israel
IIDepartment of Applied Mathematics, Faculty of Science, Holon Institute of Technology, Holon, Israel
ABSTRACT
Solomon's sea (a brass basin used in the First Temple) was discussed in the Yerushalmi Talmud Eruvin 1:5 (as well as in BT Eruvin 14a-b), and it revolved around the shape of Solomon's sea. However, inaccurate volume values of the basin were cited in the Yerushalmi. The aim of this article was to offer a new explanation for one problem arising in connection with these values. The setting of this study was the inaccurate volume values of the basin appearing in the Yerushalmi. The background of the issue at stake is the fact that Jewish scholars cannot accept that Scripture contains discrepancies (cf. BerR. 4:6). Our methods were to review the different explanations given by different commentators and to introduce a discussion by R. Avraham Ben Hiyya ha-Nassi and the Book of Tashbetz dealing with an explanation of verses related to the basin's shape. We suggested a new idea based on the above-mentioned discussion: by reducing the basin's width by one handbreadth as the verse states, one could reach exactly the values appearing in the Yerushalmi for the volumes of a squared basin and a circular basin. Based on our suggestion, one could settle the volume values appearing in the Yerushalmi without correcting them.
CONTRIBUTION: The key insight was that one could settle the volume values appearing in the Yerushalmi without correcting them. This insight was connected with the textual history of the Rabbinic literature, which exactly fit HTS's scope
Keywords: Solomon's sea; volume values; incorrect values; Yerushalmi; Eruvin.
Introduction
Solomon's sea, referred to in the Bible as the 'molten sea' or 'brazen sea' (henceforth, the basin), was a large brass (II R. 25:13, Jer. 52:17, I Ch. 18:8) basin built by King Solomon for accumulating water ('This crafted brass object was called a sea because of its size' [Flavius 1985; Wright 1941]) in the First Temple and was used for the priests' ritual bathing (II Ch. 4:6; yYoma 3:8). Additional uses of Solomon's sea were for immersion of the showbread table (bPesachim 109b) or filling the laver from within the basin (Ben Maimon 1959b; Jechielis 1955; Zevin 1999).
The verses in I R. 7:23-26 describe the basin as follows:
[23] And he made a molten sea, ten cubits from the one brim to the other: it was round all about, and its height was five cubits: and a line of thirty cubits did circle it round about.
[24] And under the brim of it round about there were colocynths compassing it, ten cubits, compassing the sea round about: the colocynths were in two rows, cast with it in the same casting.
[25] It stood upon twelve oxen, three looking towards the north, and three looking towards the west, and three looking towards the south, and three looking towards the east: and the sea was set above upon them, and all their hinder parts were inward.
[26] And it was a hand breadth thick, and its brim was wrought like the brim of a cup, like the petals of a lily: it contained two thousand bat. (Koren edition)
In the Yerushalmi Tractate Eruvin 1:5, the structure of the basin is discussed in an attempt to reconcile its shape as described in verse 23 (10 cubits wide and 5 cubits high) with its volume in verse 26 (2000 bat). In the context of this discussion, the volume values appear to be incorrect, as we show below in section 'Difficulties in the Words of the Yerushalmi'.
In this article, we present the inaccurate volume values from the Yerushalmi, review the various suggestions for explaining the inaccurate volumes (section 'Explanations given for the difficulties in the Yerushalmi') and offer a new explanation for these values (section 'Our proposal for explaining the volumes in the Yerushalmi's discussion of Solomon's sea').
Discussion
The discussion regarding Solomon's sea in the Yerushalmi
The Yerushalmi in Eruvin discusses Solomon's sea as follows:
'Then he made the molten sea; it was round, ten cubits'… It is not possible to say that it is round, for it already has been indicated … that it is square. It furthermore is not possible to say that it is square, for it already has been indicated that it was round [in the cited verse].
If you say it was square [Venice edition: round (UZ, DG)], you turn out to say that one hundred sixty-[six] [Venice edition: sixty (UZ, DG)] parts of [water for the purpose of] purification did the sea contain, and if you say it was round [Venice edition: square (UZ, DG)], you turn out to say that one hundred twenty-[five] [Venice edition: twenty-two (UZ, DG)] parts of [water for the purpose of] purification did the sea contain. Accordingly, you must conclude that the two upper cubits [of the sea] were round, and the three lower cubits [of the full height of five cubits] were square. You turn out to rule that the sea held one hundred fifty parts of [water for the purpose of] purification. (Neusner 1991)
Short explanation
The discussion in the Yerushalmi is based on the verse in I R. 7:23 that describes the basin Solomon made in the Temple, and says that it (lit., can, read:) cannot (Assis 2010) be said to be round because it was already said to be square (the source for the square shape of the basin is the verse in I R. 7:24 (Frankel 2012). Another commentator maintains that there is no source for the fact that the basin was square in the verses describing the basin (I R. 7:23-26), rather he proves this from the fact that if the basin were entirely circular - its volume would not match the volume mentioned in the verse I R. 7:26 (Margalit 2012) (see the calculation for this at the end of section 'Difficulties in the words of the Yerushalmi'), and it (lit., can, read:) cannot (Assis 2010) be said to be square because it was already said to be round (agol saviv = 'it was round all about', in the verse).
If the basin had been entirely circular, it should have been able to hold the equivalent of 160 ritual baths (yadot taharah = water for the purpose of purification; the expression yadot taharah is unique to the Bavli and Yerushalmi Talmud [Amrami 1949]). If the basin had been completely square, it should have been able to hold the equivalent of 122 ritual baths.
In view of I R. 7:26, whereby the basin contained 2000 bat, which is the equivalent of 150 ritual baths, as follows: according to Menachot 77a, the volume measure 'bat' is equal in volume to 3 seah. Therefore, the volume of the basin is 2000*3 = 6000 seah. A ritual bath contains 40 seah, which are 3 cubic cubits according to Eruvin 14a-b: 'cubit by cubit with a height of 3 cubits', and therefore, the volume of the basin is the volume of 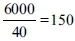 ritual baths, whose total volume is 3*150=450 cubic cubits. Therefore, it should be said that the two upper cubits of the basin were circular and the three lower cubits were square.
ritual baths, whose total volume is 3*150=450 cubic cubits. Therefore, it should be said that the two upper cubits of the basin were circular and the three lower cubits were square.
Methods
Difficulties in the words of the Yerushalmi
In the Yerushalmi's version, two difficulties arise:
1. It would appear that if the basin were square, its volume should be larger than if the basin were circular (because it is a circle inscribed in a square); while according to the volume values that appear in the Yerushalmi, the ratio is the reverse: the volume suggested for a circular basin is greater than the volume suggested for a square basin (in Ms. Or. 4720 Scal.3, p. 456, the words 'square' and 'circular' are marked as puzzling version).
2. Moreover, even if the words 'circular' and 'square' were switched, such that the volume suggested for a square vessel was greater than the volume suggested for a circular vessel - the problem of the incorrect volume values in the Yerushalmi would remain:
a. A vessel that is entirely square - The volume should be the equivalent of 166.66 ritual baths (as opposed to the Yerushalmi, which states 160 ritual baths): a square vessel 10 cubits long and wide and 5 cubits high contains 10*10*5= 500 cubic cubits. As the volume of a ritual bath is 3 cubic cubits, then this vessel contains the equivalent of
ritual baths.
b. A vessel that is entirely circular - The volume should be the equivalent of 125 ritual baths (as opposed to the Yerushalmi, which states 122 ritual baths): a round vessel with 10 cubits in diameter and 5 cubits high contains (3*5*5)*5 = 375 cubic cubits (using the approximation π = 3. For the history of number π, (see, for example, Berggren, Borwein & Borwein 2004). The Rhind Mathematical Papyrus, which dates to 2000-1500 B.C.E., which preceded King Solomon's time by at least several centuries, already discusses how to determine the volume of a cylindrical granary if one knows its diameter, and the formula given in that text indicates that the ancient Egyptians used 256:81 = 3.1604… as an approximation for π). As the volume of a ritual bath is 3 cubic cubits, this vessel contains the equivalent of
ritual baths.
Explanations given for the difficulties in the Yerushalmi
Korban ha-Edah and Pnei Moshe
Korban ha-Edah and Pnei Moshe corrected the Yerushalmi's version and switched the words 'circular' and 'square' (Frankel 2012; Margalit 2012; Liebermann 1995). In this way, they solved the first difficulty as stated above. According to their explanation, the large measure refers to the volume of the basin if it is a box, and the small measure if the shape of the basin is a cylinder.
With respect to the difficulty of erroneous volumes with regard to the volume of the basin, if it is circular or square, addressed in the second difficulty as listed above, Korban ha-Edah corrected both volume values to the mathematically correct values: that is, according to this correction, a circular vessel should contain the equivalent of 125 ritual baths, instead of 122 as stated in the Yerushalmi, and a square vessel should contain 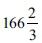 ritual baths, instead of 160 as in the Yerushalmi (Liebermann 1995). On the other hand, Pnei Moshe corrected only the volume of a round basin to 125 instead of 122 as in the Yerushalmi, and did not change the volume of a square vessel, leaving it at 160 as in the Yerushalmi. In his opinion, the correct value for the volume of the square basin is greater than 160, but only 150 are needed according to the verse: 'contains 2000 bat'.
ritual baths, instead of 160 as in the Yerushalmi (Liebermann 1995). On the other hand, Pnei Moshe corrected only the volume of a round basin to 125 instead of 122 as in the Yerushalmi, and did not change the volume of a square vessel, leaving it at 160 as in the Yerushalmi. In his opinion, the correct value for the volume of the square basin is greater than 160, but only 150 are needed according to the verse: 'contains 2000 bat'.
Explanation by a contemporary commentator
D. Makover proposed two assumptions to resolve most of the problems regarding the erroneous volume values in the Yerushalmi (Makover 2012): His suggestion is based on the rationale that the Yerushalmi assumes that a volume of 40 seah is equal to two cubic cubits. This is in contrast to that assumed above, that a volume of 40 seah is equal to 3 cubic cubits.
According to Makover, it may be said that the square part is actually a square inscribed in a circle, 10 cubits in diameter, and therefore, the side of the square is about 7 cubits  . This is in contrast to the assumption in the difficulty stated in the earlier section ('Difficulties in the words of the Yerushalmi', 2.a) that the size of the square part of the basin is 10 cubits × 10 cubits, and it inscribes a circle of 10 cubits in diameter. According to this possibility, the volume of the basin if square is indeed smaller than the volume of the sea in its circular form, as appears in the Yerushalmi's version.
. This is in contrast to the assumption in the difficulty stated in the earlier section ('Difficulties in the words of the Yerushalmi', 2.a) that the size of the square part of the basin is 10 cubits × 10 cubits, and it inscribes a circle of 10 cubits in diameter. According to this possibility, the volume of the basin if square is indeed smaller than the volume of the sea in its circular form, as appears in the Yerushalmi's version.
In view of these two assumptions, Makover explains the incorrect volume values in the Yerushalmi as follows:
1. If the basin is entirely circular: A circular vessel with a 10 cubit diameter and 5 cubits high contains (3*5*5)*5=375 cubic cubits (using the approximation π = 3). As according to Makover's assumption - the volume of a ritual bath is 2 cubic cubits - the basin holds the equivalent of
ritual baths, in contrast to the Yerhushalmi's version that has 160 ritual baths.
2. If the basin is entirely square: A square vessel 7 cubits long and wide (because it is a square inscribed in a circle as assumed above) and 5 cubits high contains 7*7*5 = 245 cubic cubits. As according to his assumption, the volume of a ritual bath is 2 cubic cubits, this basin holds the equivalent of
ritual baths, consistent with the Yerushalmi's version (122 ritual baths).
3. If the basin is a vessel whose lower part is square and 3 cubits high, and its upper part is circular and 2 cubits high - It contains in its square part 7*7*3 = 147 cubic cubits, and in its circular part (3*5*5)*2 = 150 cubic cubits (using the approximation π = 3). Thus, the volume of the entire vessel is 147 + 150 = 297 cubic cubits. As the volume of a ritual bath is 2 cubic cubits, the basin holds a volume equivalent to
ritual baths, which is a good approximation of the volume obtained from the verse which states that the basin contains 2000 bat, which is the equivalent of 150 ritual baths.
Results
Our proposal for resolving the inaccurate volume values mentioned in the Yerushalmi's version
At this stage, we are unable to explain the first difficulty because the volume of a square vessel should be greater than the volume of a circular vessel with the same width. Therefore, it is necessary to switch the words 'circular' and 'square' in the Yerushalmi, as done by Korban ha-Edah and Pnei Moshe.
It could be suggested that the words from the Yerushalmi 'ein teimar' do not mean 'if you say', but rather 'you should not say', and in this way, we would change the meaning of the words, and there would be no need to make a correction and switch the words 'circular' and 'square'. However, we found no support for this, neither linguistically nor exegetically.
However, we would like to propose a new explanation to explain the volumes of 160 and 122 ritual baths - for the square and circular shapes, respectively - in the Yerushalmi's version, which appear to be incorrect, such that there will be no need to correct these volumes as done by the Korban ha-Edah and Pnei Moshe.
The rationale of our proposed explanation is based on the words of R. Avraham Bar Hiyya ha-Nassi (henceforth RABH) (Bar Hiyya 1913), and the words of Enballshum in the Book of Tashbetz (Duran 1998) regarding the discussion of the basin that Solomon made in Bavli Eruvin 14a-b. In the next two sections, we briefly present the RABH's explanation and explain, in light of their remarks, the erroneous volume values in the Yerushalmi.
The suggestion of R. Avraham Bar Hiyya ha-Nassi and the Book of Tashbetz regarding the structure of the basin in Bavli Eruvin 14a-b
The suggestion made by RABH was in view of the difficulty that arose in Bavli Eruvin 14a-b, namely the lack of reference by the Bavli (and also by the Yerushalmi) to the words in verse 26: 'and its thickness is a handbreadth', relating to the structure of the basin (I R. 7:26). That is, if the thickness of the basin wall is a handbreadth, why is this not reflected in the calculation of the basin's volume? (Ben Gershom 2001; Levi 2011).
Thus, in view of the words of the verse 'and its thickness is a handbreadth', they assumed that there was a difference of a handbreadth between the round part and the square part (see Figure 1).
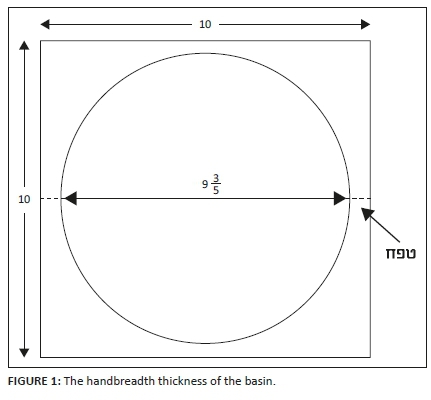
In view of this assumption, RABH and Enballshum calculated the size of the circular part of the basin, and calculated its area accordingly. The width of the square part is 10 cubits, and according to their assumption, removing a handbreadth (which is a fifth of a cubit according to R. Yehudah ha-Nassi in Kelim 17:10 [Duran 1998]) from each side would bring the diameter of the round part to 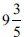 cubits. Hence, they calculated the circumference of a circle with a diameter of
cubits. Hence, they calculated the circumference of a circle with a diameter of 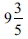 cubits, and the circumference obtained is approximately
cubits, and the circumference obtained is approximately 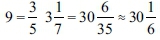 cubits, where the value
cubits, where the value 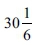 was stated by RABH, and the value
was stated by RABH, and the value 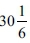 by Enballshum in the Book of Tashbetz.
by Enballshum in the Book of Tashbetz.
Verse 23 says that the circumference of the basin was exactly 30 cubits, and therefore, the difference of 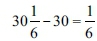 cubits reflects the circumference, because of the thickness of the basin's rim that was 'like the brim of a cup, like the petals of a lily' (verse 26). Accordingly, the thickness of the rim is
cubits reflects the circumference, because of the thickness of the basin's rim that was 'like the brim of a cup, like the petals of a lily' (verse 26). Accordingly, the thickness of the rim is 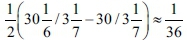 cubits, which is equal to
cubits, which is equal to  fingers (as one cubit equals 24 fingers, usually according to the thumb [Ben Maimon 2011] and Maimonides maintains that a large cubit is 24 fingers [Ben Maimon 1959a]).
fingers (as one cubit equals 24 fingers, usually according to the thumb [Ben Maimon 2011] and Maimonides maintains that a large cubit is 24 fingers [Ben Maimon 1959a]).
Using the diameter and circumference data, they calculated the area of the round part according to the mathematical rule, stating that the area of a circle equals the product of half the diameter by half the circumference, and the result they obtained is that the area of the round part is 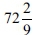 square cubits (notably, they made a mistake in the mathematical calculation. The area of the internal circle, without the rim, is
square cubits (notably, they made a mistake in the mathematical calculation. The area of the internal circle, without the rim, is 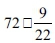 square cubits, and the area of the internal circle with the addition of the rim is
square cubits, and the area of the internal circle with the addition of the rim is 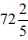 square cubits. Thus, there is no case where the result obtained is
square cubits. Thus, there is no case where the result obtained is  , as they obtained).
, as they obtained).
However, it remains for them to explain how Bavli Eruvin (14a-b) reached the conclusion that the area of the round part of the basin is 75 square cubits, because their calculation of the area of the round part is  square cubits, as shown above.
square cubits, as shown above.
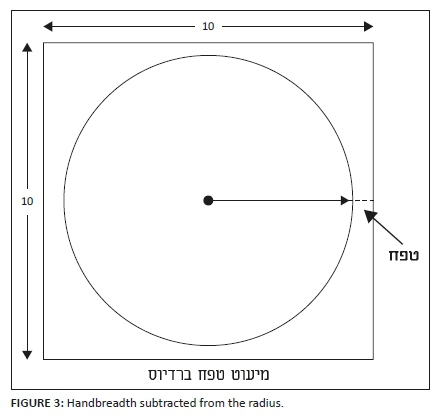
Their cause for uncertainty was the meaning of the words 'and its thickness is a handbreadth' in verse 26. Is the circular part narrower than the square part by a total of one handbreadth (see Figure 2), or is the round part narrower than the square part by a handbreadth on each side, and therefore, the width of the round part is narrower than the square part by two handbreadths (see Figure 3)?
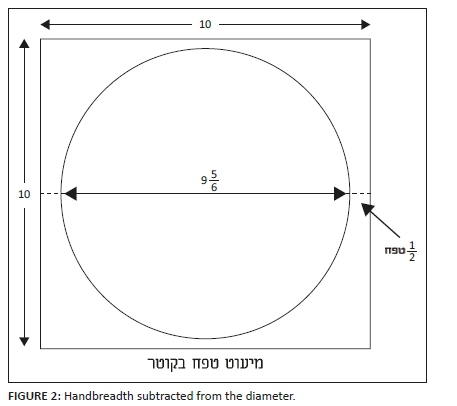
They calculated the difference in the area of the circular part in the two options, according to the assumption that a cubit contains six handbreadths (they explained this with the fact that the rabbis had taken a stringency, that according to a six handbreadth cubit, they obtained a large volume in relation to the basin). According to the first option, the diameter of the round part is:  cubits, and thus, the area of the circular part is
cubits, and thus, the area of the circular part is 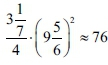 square cubits (according to the approximation
square cubits (according to the approximation 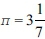 ). According to the other option, the diameter of the round part is:
). According to the other option, the diameter of the round part is:  cubits, and therefore, the area of the round part is
cubits, and therefore, the area of the round part is  square cubits (R. Duran took an approximation that was somewhat less close: 73 square cubits [Duran 1998]). As they were in doubt, they settled for an intermediate value for the area of the round part: 75 square cubits (Duran 1998).
square cubits (R. Duran took an approximation that was somewhat less close: 73 square cubits [Duran 1998]). As they were in doubt, they settled for an intermediate value for the area of the round part: 75 square cubits (Duran 1998).
Our proposal for explaining the volumes in the Yerushalmi's discussion of Solomon's sea
Our proposal is based on the RABH and the Book of Tashbetz, and in their interpretation of the words 'and its thickness is a handbreadth' as referring to the thickness of the basin wall. Accordingly, the thickness of the wall should be subtracted from the width of the basin when calculating its volume. We explain the volume values that appear in the Yerushalmi's version:
1. If the basin is completely square, then it holds the equivalent of 160 ritual baths: According to the assumption made above, a cubit of vessels contains five handbreadths and in conjunction with the assumption mentioned above regarding one option, that the thickness of the wall is half a handbreadth on each side (and therefore the total effect of the thickness of the wall on the internal space is one handbreadth), then the width of the space inside the basin is
cubits. According to these two assumptions, and in view of the fact that the height of the basin was five cubits, the volume of the basin obtained is 9.8*9.8*5 = 480.2 cubic cubits, almost exactly equal to the volume of 160 ritual baths:
, as in the Yerushalmi's version.
2. If the basin is completely circular, then it can hold the equivalent of 122 ritual baths: If we use the known approximation: π = 3, then the ratio between the volume of the basin if it were round and the volume of the basin if it were square is 3:4. Accordingly, if the volume of the basin if it were square is the equivalent of 160 ritual baths according to the Yerushalmi (and our calculation above), then the volume of the basin if it were circular is the equivalent of
ritual baths, which is a small deviation from the Yerushalmi's version - 122 ritual baths.
Perhaps, it may be suggested that in the Yerushalmi, they used a slightly larger approximation for π = 3.1415… : If we select, for example, the approximation π = 3.05, then the ratio between the volume of the basin if it were round and the volume of the basin if it were square is 3.05:4. Accordingly, the volume of the basin if it were round is the equivalent of 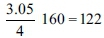 ritual baths, exactly as in the Yerushalmi's version. The difficulty with this suggestion for the approximation of π is that we did not find whether any of the commentators used the π = 3.05 approximation as a (known) approximation of π.
ritual baths, exactly as in the Yerushalmi's version. The difficulty with this suggestion for the approximation of π is that we did not find whether any of the commentators used the π = 3.05 approximation as a (known) approximation of π.
Conclusion
In this article, we reviewed the various possibilities for explaining the inaccurate volume values that appear in the Yerushalmi's discussion regarding the basin that Solomon made. We offered a new suggestion based on the idea that originated with R. Avraham Ben Hiyya ha-Nassi and the Book of Tashbetz: reducing the width of the basin by one handbreadth as the verse states, one can reach exactly the value that appears in the Yerushalmi for the volume of a squared basin, and accordingly, one can almost reach the value that appears in the Yerushalmi for the volume of a circular basin.
Our suggestion can explain the volume values that appear in the Yerushalmi, because the only correction required is switching the words 'square' and 'circular', which is a logical correction based on the consensus amongst most of the commentators mentioned in this article.
Acknowledgements
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors' contributions
U.Z. and D.G. contributed to the design and implementation of the research, to the analysis of the results and to the writing of the manuscript.
Ethical considerations
This article followed all ethical standards for research without direct contact with human or animal subjects.
Funding information
This research received no specific grant from any funding agency in the public, commercial or not-for-profit sectors.
Data availability
Data sharing is not applicable to this article as no new data were created or analysed in this study.
Disclaimer
The views and opinions expressed in this article are those of the authors and do not necessarily reflect the official policy or position of any affiliated agency of the authors.
References
Amrami, M., 1949, Paths in the Sea, vol. 3, Amrami, Jerusalem, p. 41. [ Links ]
Assis, M., 2010, A concordance of Amoraic terms expressions and phrases in the Yerushalmi, vol. 1, The Jewish Theological Seminary of America, Jerusalem, p. 71. [ Links ]
Bar Hiyya, A., 1913, Chibbur ha-Meschicha weha-Tischboreth, vol. 2, Mekize Nirdamim, Berlin, pp. 112-114 (para. 193-194). [ Links ]
Ben Gershom, L., 2001, Ralbag commentary to Melakhim Alef, vol. 4, Jerusalem, Ha-Ma'or. [ Links ]
Ben Maimon, M., 1959a, Mishne Torah, Hilkhot Meʻilah (8:5), vol. 4, Pardes, Jerusalem, p. 155. [ Links ]
Ben Maimon, M., 1959b, Mishne Torah, Hilkhot Biʿat ha-Mikdash (5:15), vol. 4, Pardes, Jerusalem, p. 60. [ Links ]
Ben Maimon, M., 2011, Mishne Torah, Hilkhot Eruvin (1:12), Kapach ed. vol. 3, Moshe Institute, Kiryat Ono, p. 651. [ Links ]
Berggren, L., Borwein, J.M. & Borwein, P., 2004, Pi: A source book, 3rd edn., Springer, Berlin. [ Links ]
Duran, S., 1998, The book of Tashbetz, vol. 1, Jerusalem Institute, Jerusalem, pp. 369-371. [ Links ]
Flavius, J., 1985, Jewish antiquities, Book VIII, vol. 1, transl. A. Schalit, Bialik Institute, Jerusalem, p. 275. [ Links ]
Frankel, D., 2012, Korban ha-Edah, Yerushalmi Eruvin (1:5), ha-Maʿor, Jerusalem, p. 8a. [ Links ]
Jechielis, N., 1955, Aruch ha-Shalem, vol. 5, Kohut edn., Pardes, New York, NY, pp. 136-137. [ Links ]
Levi, D.M., 2011, 'How does the Holy Scripture regarding "Solomon Sea" coincide with mathematical knowledge?', BDD 25, 51-54. [ Links ]
Liebermann, S., 1995, HaYerushalmi Kiphshuto, vol. 1, The Jewish Theological Seminary of America, Jerusalem, p. 234. [ Links ]
Makover, D., 2012, 'Shiʻur Reviʻit', Sinai 145, 99-100. https://doi.org/10.1111/j.1467-9736.2012.00796.x [ Links ]
Margalit, M., 2012, Pnei Moshe, Yerushalmi Eruvin (1:5), ha-Maʿor, Jerusalem, p. 8a. [ Links ]
Neusner, J., 1991, The Talmud of the Land of Israel, Erubin, vol. 12, The University of Chicago Press, Chicago, IL, p. 44. [ Links ]
Wright, G.E., 1941, 'Solomon's temple resurrected', The Biblical Archaeologist 4(2), 18-31. https://doi.org/10.2307/3209118 [ Links ]
Zevin, S.J., 1999, Talmudic encyclopedia, vol. 24e, eds. S.J. Zevin et al., Talmudic Encyclopedia Institute, Jerusalem, p. 576. [ Links ]
 Correspondence:
Correspondence:
Uri Zur
uriz@ariel.ac.il
Received: 15 Sept. 2021
Accepted: 05 Nov. 2021
Published: 25 Jan. 2022














