Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
SAMJ: South African Medical Journal
versión On-line ISSN 2078-5135
versión impresa ISSN 0256-9574
SAMJ, S. Afr. med. j. vol.99 no.6 Pretoria jun. 2009
ORIGINAL ARTICLES
A simple clinical formula for predicting fetal weight in labour at term – derivation and validation
Eckhart BuchmannI, *; Karabo TlaleII
IFCOG (SA), MSc (Med), PhD, Department of Obstetrics and Gynaecology, University of the Witwatersrand, Johannesburg
IIFCOG (SA), Department of Obstetrics and Gynaecology, University of the Witwatersrand, Johannesburg
ABSTRACT
OBJECTIVES: To derive and validate a simple formula for birth weight based on symphysis-fundal height (SFH) measurement during labour, and to determine a useful SFH cut-off value for prediction of birth weight >4 000 g.
METHODS: In a derivation study, SFH was measured in women at term in the active phase of labour. A simplified formula for birth weight was derived from a regression equation. The best cut-off SFH measurement was obtained for prediction of birth weight >4 000 g. After this, a similar study was done to validate these findings.
RESULTS: In the derivation study (N=504), birth weight was predicted by the equation: birth weight in g=301+78 (SFH in cm). This was transformed to the simplified formula: birth weight in g=100 ([SFH in cm]–5). Using this formula for the data set, 68.1% of birth weight estimates were correct to within 10% of the birth weight. For prediction of birth weight >4 000 g, an SFH measurement of 40 cm had a sensitivity of 82% and a specificity of 80%. In the validation study (N=294), the derived simplified formula gave 65.0% of estimates correct to within 10% of the birth weight. The predictive values of the 40 cm SFH cut-off were similar to those in the derivation study.
CONCLUSION: The derived simplified formula was validated in the second study. The formula may be useful for intrapartum use in term pregnancies. A cut-off SFH measurement of 40 cm may identify labours at risk for cephalopelvic disproportion or shoulder dystocia.
Clinicians frequently estimate fetal weight when examining women in labour at term. This may help in predicting cephalopelvic disproportion when labour progress is poor,1 or give early warning of possible shoulder dystocia.2 In experienced hands, intrapartum clinical estimates of birth weight for term infants are at least as good as ultrasound-based predictions, being correct to within 10% of the birth weight in 55 - 72% of estimations.3-10 A more objective estimate of fetal weight may be offered by measurement of symphysis-fundal height (SFH) using a tape measure.11-13 This requires minimal experience, relying only on identifying the upper edge of the pubic symphysis and the highest point on the uterus. However, there is no simple formula that converts SFH measurement into fetal weight. The Johnson formula is frequently quoted, where birth weight in g=(SFH in cm–13)×155, with further adjustments based on maternal obesity and engagement of the fetal head.12 A South African study found good correlation of intrapartum SFH measurement with birth weight (r=0.56), and derived a regression equation, but the authors stated that the derived formula was 'not sufficiently accurate to be clinically useful'.14 A problem with fetal weight estimation is that all methods are least accurate at extremes of birth weight.15-17 Macrosomia (birth weight of 4 000 g and above) is notoriously difficult to predict.2,18,19 Where a formula is inaccurate at the upper extreme of birth weight, the most useful tool may be a cut-off measure of SFH to assist prediction of macrosomia. This study was done to derive and validate a simple formula for birth weight based on SFH, and to determine a useful SFH cut-off value for prediction of fetal macrosomia (birth weight >4 000 g).
Methods
Derivation study
The derivation study was a prospective cross-sectional study undertaken from 2003 to 2005 at Chris Hani Baragwanath Maternity Hospital. The study was approved by the Human Research and Ethics Committee of the University of the Witwatersrand. This investigation of SFH measurement was part of a larger study, which was to evaluate clinical assessment in prediction of cephalopelvic disproportion. The methods have been described previously.20,21 The study population was women at 37 or more completed weeks of gestation in the active phase of labour (cervix fully effaced and at least 3 cm dilated) with singleton live fetuses and vertex presentations. Women with pre-existing or gestational diabetes mellitus were excluded. A consecutive sampling method was used on days that the researcher (EB) was available to collect data in the labour ward. All the researcher's measurements were done at the time of the routine labour ward rounds of the attending clinicians. Written informed consent was obtained from all participants.
The researcher palpated the woman's abdomen and estimated the level of head above the pelvic brim in fifths.22 The head was considered engaged if two-fifths or less was palpable above the brim. This was followed by marking the highest point on the uterine fundus, not necessarily in the midline, with a pen using a horizontal line.23 Between uterine contractions, he identified the highest point on the fundus by gentle downward vertical pressure with the left index finger. The SFH was measured with a soft tape-measure from the superior edge of the symphysis pubis in the midline to the line identifying the highest point on the fundus, and recorded to the nearest 1 cm. Women with palpably full bladders were asked to void or were catheterised before proceeding with measurement. The state of the membranes was recorded as intact or ruptured, and cervical dilatation (in cm) was noted. After completing these observations, the researcher recorded race, age, parity, maternal height, maternal weight and gestation in weeks. Maternal weights were recorded from the first antenatal visit. Birth weights were measured on scales frequently calibrated by the researcher, and provided readings to the nearest 10 g.
Statistical analysis was performed using Microsoft Excel and Epi-Info 6 statistical software. Categorical data were presented as frequencies and percentages, and continuous data as means ± standard deviations (SD). Univariate linear regression analysis was done to study the relationship between SFH and birth weight. A scatter plot with regression line and equation was derived, with SFH as the independent variable and birth weight as the dependent variable. This was modified into a simplified formula for easy recall by clinicians, to offer estimations correct to within 10% of the birth weight in at least 60% of estimations, if possible. The influence of body mass index (BMI), membrane rupture and engagement of the fetal head was studied by comparing mean SFH measurements and birth weight, using Student's t-test with statistical significance defined as p<0.05. To determine the most predictive cut-off measurement for macrosomia, a receiver-operating characteristic plot was made. A two-by-two contingency table was used to determine sensitivity, specificity, positive predictive value and negative predictive value of the SFH cut-off for macrosomia.
Validation study
The validation study was done using similar methods. Sample size calculation suggested that 340 participants would be needed to give a precision of 5% around an observed percentage of estimated fetal weights correct to within 10% of the birth weight. For example, such a sample size would give a 95% confidence interval (CI) of 55 - 65% if the observed percentage was 60%. The researcher who made measurements in the derivation study (EB) instructed a second researcher (KT) in recording SFH and collection of other data, as described above. Measurement was refined by measuring the SFH twice, 5 - 20 minutes apart, and recording the mean of the two measurements. This part of the study was done from July to September 2007 in the labour wards of Johannesburg Hospital and Chris Hani Baragwanath Maternity Hospital. Approval for the validation study was given by the Human Research and Ethics Committee of the University of the Witwatersrand. If it were found that the simple formula could provide fetal weight estimates with 10% of the birth weight in over 60% of estimations in this validation, the formula would be acceptable for use in clinical practice.
Results
Derivation study
The researcher examined 504 women, 489 (97.0%) of black African ethnic origin. The mean age was 25.0±5.8 years, and the mean gestation was 39.3±1.6 weeks. Three hundred and twenty women (63.5%) were nulliparous. The mean maternal height was 157.4±6.4 cm and the mean weight 69.2±13.9 kg. The fetal head was engaged in 128 cases (25.4%), and the membranes were found to be ruptured in 263 (52.2%). The mean cervical dilatation at the time of examination was 5.9±1.9 cm. The mean SFH was 37.0±3.6 cm, with a range of 27 - 53 cm. The mean birth weight was 3 190±436 g, with a range of 1 880 - 4 890 g.
Univariate linear regression of SFH with birth weight gave a correlation coefficient of 0.64. The regression equation (y=301+78.0x) suggests that for each cm increase in SFH, birth weight increased by 78 g (solid line in Fig. 1). Since a 78 g/cm increase could be rounded up to 100 g, this was adjusted, with minimal change to the regression line, to the simplified formula: birth weight in g=100 ([SFH in cm]–5), giving an increase of 100 g in fetal weight for each cm SFH (dotted line in Fig. 1). It is evident from the regression line in the figure that the simplified formula prediction follows the statistical regression line most closely in the SFH range of 32 - 40 cm, equivalent to birth weights of 2 700 - 3 500 g. Using this formula to translate SFH measurements to birth weights, 343 (68.1%; 95% CI 63.8 - 72.1%) of estimates were accurate to within 10% of the birth weight. Accuracy within 20% of the birth weight was achieved in 470 estimations (93.3%; 95% CI 90.6 - 95.2%).

A BMI of 30 kg/m2 or more was associated with higher mean SFH (38.9 cm v. 36.4 cm; p<0.0001) and greater mean birth weight (3 298 g v. 3 155 g; p=0.0009) than a BMI less than 30 kg/m2. The mean SFH was lower (36.5 cm v. 37.2 cm; p=0.03) with an engaged fetal head than with an unengaged fetal head, with no difference in birth weight. Status of the membranes (ruptured or intact) was not associated with any difference in SFH or birth weight (Table I).
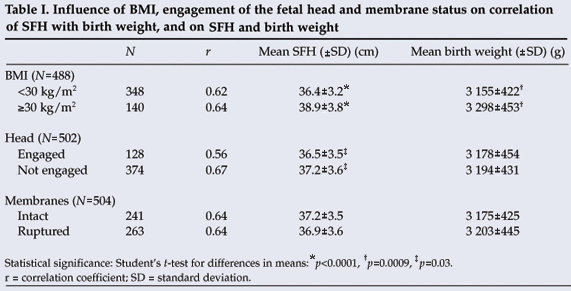
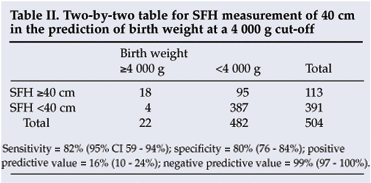
A receiver-operating characteristic plot (not shown) indicated that the 40 cm SFH cut-off provided the best predictive value for macrosomia. A cut-off of 41 cm was less sensitive (59%) but more specific (87%) and a cut-off of 39 cm less specific (70%) but more sensitive (91%). A 40 cm cut-off gave a sensitivity of 82% and a specificity of 80% for predicting a birth weight of 4 000 g or more. The positive and negative predictive values for 40 cm were 16% and 99% respectively (Table II).
Validation study
There were 294 participants, of whom 289 (98.3%) were of black African ethnic origin. One hundred and ninety-five were investigated at Johannesburg Hospital and 99 at Chris Hani Baragwanath Maternity Hospital. Their mean age was 26.6±5.8 years, 111 (37.8%) were primiparous, the mean gestational age at delivery was 39.2±1.4 weeks, and the mean weight was 73.9±15.8 kg. Membranes were ruptured at the time of measurement in 152 cases (51.7%) and the mean cervical dilatation was 5.5±1.4 cm. The fetal head was engaged in 60 cases (20.4%) at the time of examination. The mean SFH, in each case using the average of two measurements, was 37.0±3.3 cm. The mean birth weight was 3 221±417 g.
Univariate linear regression of SFH and birth weight revealed a correlation coefficient (r) of 0.56. The regression equation (y=585+71.3x) suggested an increase in birth weight of 71.3 g for each cm SFH. Using the derived simplified formula: birth weight in g=100 ([SFH in cm]–5), 191 estimations (65.0%; 95% CI 59.2 - 70.4%) were accurate within 10% of the birth weight. Accuracy within 20% of the birth weight was achieved in 275 estimations (93.5%; 95% CI 89.9 - 96.0%). A BMI of 30 kg/m2 or above (N=100) was associated with greater mean SFH (38.4 cm v. 36.3 cm; p<0.0001) and greater mean birth weight (3 363 g v. 3 148 g; p=0.0009) than a BMI less than 30 kg/m2 (N=178). The mean SFH was lower (35.8 cm v. 37.3 cm; p=0.001) with an engaged fetal head than with an unengaged fetal head. Rupture of membranes appeared to have no significant effect on SFH or birth weight (ruptured v. unruptured: 36.8 cm v. 37.1 cm respectively). The 40 cm SFH cut-off for macrosomia yielded a sensitivity of 83% (10/12), a specificity of 82% (232/282), a positive predictive value of 17% (10/60) and a negative predictive value of 99% (232/234).
Discussion
The simplified formula derived in the first study was successfully validated in the second. The formula offers an easy conversion of SFH to birth weight for midwives or obstetricians looking after women in the active phase of labour at term. The formula is best memorised as a subtraction of 5. Examples are an SFH measurement of 33 cm giving an estimated fetal weight of 2.8 kg or one of 41 cm predicting a fetal weight of 3.6 kg. The method provided estimates (68% of estimations in the first study and 65% of estimations in the second study within 10% of the birth weight) that fell in the upper range of accuracies of clinical estimates reported in the literature.3-10 Membrane rupture had no influence on estimations, while an engaged head was associated with an under-estimation of birth weight by about 100 g. Users of the formula could add 100 g to the estimated fetal weight if the head is engaged. The data also suggested that a high BMI could lead to overestimation of fetal weight, possibly because of increased abdominal subcutaneous fat content. However, women with a high BMI tended to give birth to larger infants, thus compensating for such over-estimation.
An SFH cut-off value of 40 cm had good sensitivity and specificity for predicting a birth weight of 4 000 g or more. The greatest strength of this cut-off was its negative predictive value (99%). This means that an SFH of less than 40 cm in a woman in the active phase of labour at term gives a 99% likelihood that the newborn will weigh less than 4 000 g. However, this applies only in populations where macrosomia at birth (birth weight of 4 000 g or more) is relatively rare. Studies of women of black African ethnic origin in southern Africa suggest that the rate of macrosomia at birth is 2.3 - 3.4%,24,25 much less than in Europe or North America.26,27 Therefore, the predictive findings here related to an SFH of 40 cm should not be applied in communities or environments different from the one studied. The 40 cm cut-off can be recommended for general use in southern Africa for term parturients of black African ethnic origin, to identify women at high and low risk of complications such as shoulder dystocia and cephalopelvic disproportion. This adds to findings from a previous study from Pretoria,13 where a 30 cm cut-off was found useful in predicting birth weights of less than 2 000 g in women in preterm labour.
Interpretation of these results must take into account some limitations. While the validation study found the results of the derivation study to be repeatable and therefore probably reliable, it is important that the method of SFH measurement be followed exactly as recommended23 for the results to be reproduced elsewhere. The derived formula should only be used at term in women in the active phase of labour. Simple inspection of the derived regression line (dotted line in Fig. 1) shows that the formula becomes unreliable at the extremes of birth weights at term. Therefore, with SFH measurements of greater than 40 cm it is enough to consider that the infant will have a birth weight above the average, without aiming to predict the birth weight with any precision. For SFH measurements less than 33 cm there is similar inaccuracy, and a guess that the infant will be of below-average weight is sufficient. The results of this study are not able to give information about SFH in small babies, because the study specifically excluded all gestations of less than 37 weeks. Also, SFH measurement as described here may not be meaningful if the gestation is unknown. Careful clinical palpation or ultrasound scanning would need to be done first to determine whether the pregnancy is likely to be at term or not.
SFH measurement in labour, with or without the use of formulas or cut-offs, can assist in the prediction of birth weight. However, only randomised controlled trials will be able to demonstrate whether SFH measurements during labour will make a difference in terms of intrapartum interventions such as referral, oxytocin use and caesarean section, or fetal outcomes such as asphyxia, birth trauma and perinatal death.
This study was supported by a research grant from the South African Society of Obstetricians and Gynaecologists.
References
1. Handa VL, Laros RK. Active-phase arrest in labor: predictors of cesarean delivery in a nulliparous population. Obstet Gynecol 1993; 81: 758-763. [ Links ]
2. O'Reilly-Green C, Divon M. Sonographic and clinical methods in the diagnosis of macrosomia. Clin Obstet Gynecol 2000; 43: 309-320. [ Links ]
3. Chauhan SP, Lutton TC, Bailey KJ, Morrison JC. Intrapartum prediction of birth weight: clinical versus sonographic estimation based on femur length alone. Obstet Gynecol 1993; 81: 695-697. [ Links ]
4. Barnhard Y, Bar-Hava I, Divon MY. Accuracy of intrapartum estimates of fetal weight. Effect of oligohydramnios. J Reprod Med 1996; 41: 907-910. [ Links ]
5. Sherman DJ, Arieli S, Tovbin J, Siegel G, Caspi E, Bukovsky I. A comparison of clinical and ultrasonic estimation of fetal weight. Obstet Gynecol 1998; 91: 212-217. [ Links ]
6. Shamley KT, Landon MB. Accuracy and modifying factors for ultrasonographic determination of fetal weight at term. Obstet Gynecol 1994; 84: 926-930. [ Links ]
7. Baum JD, Gussman D, Wirth III JC. Clinical and patient estimation of fetal weight vs. ultrasound examination. J Reprod Med 2002; 47: 194-198. [ Links ]
8. Chauhan SP, Hendrix NW, Magann EF, Morrison JC, Kenney SP, Devoe LD. Limitations of clinical and sonographic estimates of birth weight: experience with 1034 parturients. Obstet Gynecol 1998; 91: 72-77. [ Links ]
9. Noumi G, Collado-Khoury F, Bombard A, Julliard K, Weiner Z. Clinical and sonographic estimation of fetal weight performed during labor by residents. Am J Obstet Gynecol 2005; 192: 1407-1409. [ Links ]
10. Hall MH. Guessing the weight of the baby. Br J Obstet Gynaecol 1996; 103: 734-736. [ Links ]
11. Johnson RW, Toshach CE. Estimation of fetal weight using longitudinal mensuration. Am J Obstet Gynecol 1954; 68: 891-896. [ Links ]
12. Johnson RW. Calculations in estimating fetal weight. Am J Obstet Gynecol 1957; 74: 929. [ Links ]
13. Jeffery BS, Pattinson RC, Makin J. Symphysis-fundal measurement as a predictor of low birthweight. Early Hum Dev 2001; 63: 97-102. [ Links ]
14. Bothner BK, Gulmezoglu AM, Hofmeyr GJ. Symphysis fundus height measurements during labour: a prospective, descriptive study. Afr J Reprod Health 2000; 4: 48-55. [ Links ]
15. Loeffler FE. Clinical fetal weight prediction. J Obstet Gynaecol Br Cwlth 1967; 74: 675-677. [ Links ]
16. Niswander KR, Capraro VJ, Van Coevering RJ. Estimation of birth weight by quantified external uterine measurements. Obstet Gynecol 1970; 36: 294-298. [ Links ]
17. Woo JS, Ngan HY, Au KK, Fung KP, Wong VC. Estimation of fetal weight in utero from symphysis-fundal height and abdominal girth measurements. Aust N Z J Obstet Gynaecol 1985; 25: 268-271. [ Links ]
18. Chauhan SP, Cowan BD, Magann EF, Bradford TH, Roberts WE, Morrison JC. Intrapartum detection of a macrosomic fetus: clinical versus 8 sonographic models. Aust N Z J Obstet Gynaecol 1995; 35: 266-270. [ Links ]
19. Sadah-Mestechkin D, Walfisch A, Shachar R, Shaham-Vardi I, Vardi H, Hallak M. Suspected macrosomia? Better not tell. Arch Gynecol Obstet 2008; 278: 225-230. [ Links ]
20. Buchmann EJ, Libhaber E. Accuracy of cervical assessment in the active phase of labour. BJOG 2007; 144: 833-837. [ Links ]
21. Buchmann EJ, Libhaber E. Sagittal suture overlap in cephalopelvic disproportion: blinded and non-participant assessment. Acta Obstet Gynecol Scand 2008; 87: 731-737. [ Links ]
22. Notelowitz M. The graphic monitoring of labour. S Afr J Obstet Gynaecol 1973; 11: 3-10. [ Links ]
23. Theron GB. Perinatal Education Programme. Manual I. Maternal Care. Cape Town: Perinatal Education Trust, 1993. [ Links ]
24. Essel JK, Opai-Tetteh ET. Macrosomia – maternal and fetal risk factors. S Afr Med J 1995; 85: 43-46. [ Links ]
25. Buchmann EJ. Perinatal health in the Chiawelo district of Soweto. Maternal characteristics and clinical outcomes. CHASA J Compr Health 1996; 7: 118-123. [ Links ]
26. Boulet SL, Alexander GR, Salihu HM, Pass M. Macrosomic births in the United States, outcomes and proposed grades of risk. Am J Obstet Gynecol 2003; 188: 1372-1378. [ Links ]
27. Chauhan SP, Grobman WA, Gherman RA, et al. Suspicion and treatment of the macrosomic fetus: a review. Am J Obstet Gynecol 2005; 193: 332-346. [ Links ]
Accepted 24 February 2009.
* Corresponding author: E Buchmann (eckhart.buchmann@wits.ac.za)














