Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Education
On-line version ISSN 2076-3433
Print version ISSN 0256-0100
S. Afr. j. educ. vol.41 n.3 Pretoria Aug. 2021
http://dx.doi.org/10.15700/saje.v41n3a1909
ARTICLES
The influence of project-based learning on student achievement in elementary mathematics education
Bojan D. LazicI; Jelena B. KnezevicII; Sanja M. MaricicIII
IFaculty of Education in Sombor, University of Novi Sad, Serbia. lazicbsaa@yahoo.com
IIPrimary school Miroslav Antic in Futog, Novi Sad, Serbia
IIIFaculty of Education in Uzice, University of Kragujevac, Serbia
ABSTRACT
An effective instructional approach in elementary mathematics education has a significant role in the understanding of mathematical concepts and overall student achievement. We point out the characteristics, significance and effects that may be achieved in mathematics education through the application of project-based learning. The aim of the study was to examine the effects of project-based learning on student achievement in lower elementary mathematics education and examine whether the project-based model was equally acceptable to students with different marks. We arranged quasi-experimental research instruction (experiment with parallel groups), on a sample (N = 147) in order to examine whether an instructional approach based on the principles of project-based work would achieve better effects of learning and student achievement compared to the usual way of learning implemented in mathematics education. Results of the final measurements show that students in the experimental group, who worked according to the model of project-based work, achieved better compared to students who worked in the usual way. With this study we have shown that project-based instruction has significant effects on student achievement in lower elementary mathematics education, and that it can undoubtedly contribute to the methodological empowerment of teachers in their teaching practice.
Keywords: content integration; elementary mathematics education; instruction; mathematics; project-based learning; student achievement; teacher
Introduction
The exceptional importance of elementary education, especially mathematics education, demands constant innovations of the teaching practice which would bring about improved rationalisation and efficiency of the teaching process, as well as positively influence the quality and duration of student knowledge (Reigeluth, Beatty & Myers, 2017; Umugiraneza, Bansilal & North, 2017). General intentions are nowadays focused on education and learning which emphasises the acquisition of functional knowledge that students may apply to solve specific real-life problems, on cooperative work, collaboration with others, and teamwork. One's success in mathematics largely depends on how the knowledge is acquired (Arends, Winnaar & Mosimege, 2017; Umugiraneza et al., 2017). Instruction based on active student participation in the learning process, activities that encourage students to explore, work in groups, solve real-life problems and integrate mathematics with other content areas achieves better results (Lazic, Maricic & Milinkovic, 2015). Modern mathematics should be a means of communication and a "tool" used in everyday life, it should create a link between the children's perception of the world and mathematical structures, and mathematics education should be viewed as a creative activity in which students participate with determination and enthusiasm. One of the ways to achieve this is through project-based learning.
Literature Review
Initial ideas about project-based instruction can be found in the works of W. Kilpatrick, who believed that the traditional teaching strategy of lecturing, together with its inactivity and rigidity, should be replaced with student participation and activity in a social environment. The basic idea is to have students participate in the learning process, to allow them to think, ask questions and explore. The aim of this approach is to get students to take part willingly/consciously in all aspects of their learning process and to allow them to ask questions, make decisions and think about their own learning. Learning should be inquiry-based, where students are able to step in and discuss the topics they find interesting (Bell, 2010).
The beginnings of project-based instruction can be found in the philosophy of pragmatism according to which knowledge that people acquire has genuine value only if it may be used as a means for solving practical, real-life situations (Sutinen, 2013). Best education is that which allows students to learn through work and which prepares them for a successful encounter with reality (Vilotijevic & Vilotijevic, 2016). The foundations of project-based instruction rely on the principles of constructivist and sociocultural theories, the basic postulates of which read that students acquire knowledge through active construction and construction of knowledge in a social context.
Research shows that students who have learned within a project-based model show greater intrinsic motivation for learning, express greater autonomy in learning, are more self-sufficient and possess better
developed metacognitive skills, as well as greater autonomy compared with students who worked within a traditional model of instruction (Ali, Akhter, Shahzad, Sultana & Ramzan, 2011; Gerhana, Mardiyana & Pramudya, 2017; Loyens, Magda & Rikers, 2008; Roh, 2003; Schmidt, Rotgans & Yew, 2011). Studies show that a project-based model in instruction helps improve academic performance in mathematics (Ali, Hukamdad, Akhter & Khan, 2010).
Research-based learning has many advantages in the development of conceptual understanding and skills related to problem-solving (Dordevic, 2007; Kirschner, Sweller & Clark, 2006; Wilhelm, Sherrod & Walters, 2008). To enable learning means to fully involve students in the process, to hand over the control of what they learn to them, and to confront them with personal, social and practical problems. It is vitally important to allow students to assess their progress and achievement by themselves (Vizek Vidovic, Vlahovic-Stetic, Rijavec & Miljkovic, 2003). In project-based work, the student becomes more actively involved in the process of learning, whereas the teacher is there to organise, channel, encourage and assess student work (Hrvatic & Pirsl, 2007; Vilotijevic & Vilotijevic, 2016).
Theoretical Framework
A project-based strategy of learning mathematics is an open, inquisitive learning process which is primarily student-centred (Bell, 2010), and focused on engaging students to take active part in the research through instruction which integrates acquired theoretical knowledge with practical skills, including real-world projects within mathematical concepts (Bender, 2012; Savery, 2006). Learning content comprises real-world projects which include interwoven problems or tasks, integrated into several disciplines, and associated with the mathematical content (Barell, 2007, 2010; Grant, 2002). In the project-based model of instruction, students work in groups on an open problem, set up research tasks and hypotheses that are to be tested by themselves, using the knowledge they possess. Through real-life situations, mathematics may become more relatable to the student. For this purpose, we may use simple problems which can be explored during one school period, or more complex problems of which the resolution requires the collaboration of several students, longer time for organisation and project preparation, and often integration and multidisciplinarity as well.
The main goal of project-based learning is to simplify the acquisition of the skills which include critical thinking competencies and deep content knowledge typical for the 21st century (Darling-Hammond, Barron, Pearson, Schoenfeld, Stage, Zimmerman, Cervetti & Tilson, 2008) as well as "skills such as creativity and innovation, problem solving, and communication and collaboration" (Kim & Choi, 2016:136). Students of the same age with their teacher become a tool which will make it easier for students to activate previous knowledge and higher-order thinking (Gavin, Casa, Adelson, Carroll & Sheffield, 2009).
As stated in Muschla and Muschla (2006), when students work on authentic problems in project-based instruction, they begin to realise how the mathematical skills that they are learning can be implemented in the real world. Mathematical projects open doors for the incorporation of other subjects and disciplines in mathematics classes, and students will soon realise that mathematics is present in many aspects of their lives. Mathematical projects also give students the opportunity to collaborate, where one person is in charge. In project-based learning activities, students with different abilities have a chance to contribute to the solution. Everyone has a role to play and everyone can contribute to the success of the team.
Project-based learning gives students the opportunity to learn content within a context, to use previous knowledge and to collaborate with other students. There is also an opportunity of integration of different disciplines through one project (Capraro & Slough, 2013). This innovative model of schooling (Doppelt, 2009) encourages students' independence of choice, their thinking, and intrinsic motivation. Positives of this programme have been noticed at students' engagement in the learning process (Lam, Cheng & Ma, 2009; Quek, Wong, Divaharan, Liu, Peer & Williams, 2007). Project-based learning shows students to think creatively and innovatively (Lee & Breitenberg, 2010), and includes the possibility to work independently (Doppelt, 2009). "It allows students to learn content within a context, apply prior knowledge, and gain skills not found in traditional education, such as how to collaborate" (Jacques, 2017:428).
Project-based learning implies that the knowledge specified in the curriculum is acquired through a project. The main question is what the essence is of what we want students to acquire, which should be challenging, original and meaningful. In project-based instruction, students explore, they work independently, develop social skills, and solve real-life problems (Janes, 2007). Implementation of this type of instruction requires interdisciplinary content integration, as well as implementation of acquired knowledge, skills and techniques. Through the integration of individual disciplines, which provide depth and focus, we get a wider context, change of perspective, but also knowledge transfer, i.e. functional knowledge.
Fabijanic (2014) states that the main aim of project-based instruction is focus on reality where one creates a product through one's own work and awareness. Through work on project tasks, students acquire new knowledge, skills, abilities and habits that are applicable in real life. They develop an interest in research and exploration, planning skills and cooperative relationships with others. Through their work, they use different means and evaluate resources at their disposal. Group work develops their communication skills, tolerance, as well as a critical attitude toward their own work, and the work of others. Teachers who apply project-based learning contexts must be able to find mathematic in those projects, to present that mathematic to the students and to be able to involve students in an authentic way (Lee & Breitenberg, 2010).
Although there is a large number of empirical studies on the implementation of a project-based model in instruction, when it comes to the implementation of project-based instruction in lower elementary mathematics education in Serbia, there is a dearth of studies. For this reason, we focus on the empirical examination of the effects of the project-based model of instruction in lower elementary mathematics education. Given that project-based mathematics education has a number of effects, monitoring all these effects exceeds the scope of this article. Therefore, we wanted to examine the extent to which a project-based model of work in lower elementary school improves learning efficiency in the realisation of mathematical content. The aim of the study was to examine the effects of project-based learning on student achievement in lower elementary mathematics education and examine whether the project-based model was equally acceptable to students with different marks. Performance indicators for this type of instruction have been assessed based on the level of students' academic performance. The results of this research should help in the popularisation of the project-based model of instruction in lower elementary mathematics education.
Methodology
Research Sample
Our study was conducted on a sample (N = 147) selected from the population of third grade elementary students in Serbia. Given that our study was based on an experiment with parallel groups, we formed two uniform student groups - an experimental (E) and a control (C) group. The experimental group comprised third grade students from three classes of one elementary school (N = 77), whereas the control group comprised third grade students from three classes of another elementary school (N = 70). To equate our research groups, we used overall student achievement, and student achievement in mathematics at the end of the second grade, as well as the results of the pretest knowledge.
Research Course Description
The study was conducted during 3 months of the academic year 2017/2018 (from March to Jun). The teaching content was according to the current mathematics curriculum for the third grade of elementary schools in Serbia. The experimental programme was implemented during the second semester over 11 classes on Measuring and Measurements on the following topics: measuring mass, measuring length, measuring time, measuring liquid volume, money, and through six projects: Funfair, Hurdles track, We are baking cookies, Doll clothing, Mathematical fairy tale, History on tape (Knezevic, Lazic, Maricic & Petojevic, 2019). Measuring is directly related to objective knowledge and is present in everyday life, which perfectly fits into the didactic and instructional approach of the project-based model in mathematics education.
All exercises within the experimental programme have been designed in the form of projects closely related to students' daily lives and real problems regarding measuring (they measured the volume and mass while baking cookies, they measured time required to complete some competitive activities, and used money to buy and sell cookies and toys).
The History on tape project was realised over two school classes by connecting and integrating the content of multiple objects while the stages preceding the realisation had been organised within other school subjects. The learning content was primarily related to the school subject, nature and society, within the teaching topic: The past of my place. The students discovered the most significant events from the historic Serbian people and the individuals that assigned them. Content from literature was also integrated through the introduction of elements from culture and folk tradition. Content from the musical culture through the introduction of elements of the musical folk tradition was also integrated. The content was then incorporated into mathematics through content aimed at introducing units for measuring time (year, decade, century, millennium), by connecting to a number law, a place number in a number series, representing time units on the timeline (through a series of events in time series), comparisons of multi-digit numbers (through comparisons of years of significant events and years of births and deaths of significant individuals), that is, determining the decade and century of events.
Project elaboration followed after identifying the connection between the number line and the timeline studied through the history of one' s people. The aim of the project was to have students design a timeline on a number line where they would mark time periods (units of time) and connect these using major historic events and distinguished individuals. Students were divided in two groups. Each group was given a time period to study. Members of each group distributed tasks among themselves, so each student could actively share in project realisation. Information was found in their textbooks, magazines, and online. They researched when a significant historical event took place, when it ended, how long it lasted and what exactly happened. After collection, data were analysed and evaluated, after which members of both groups were given new tasks: to draw a number line, add time markers, write text, add pictures in appropriate places, and to draw on the timeline. While drawing the number line, they used the same unit length in all groups because they eventually merged all the works into one, class timeline. They marked time determinants, counted their mutual distances on a number line, and expressed it to different units of measure for length. Besides that, they calculated the time difference between historical events and expressed them in different time units (month, year, century). Members of the same group together analysed the results and designed a presentation. Presentation of the results and observations of each group were realised according to the chronology of the periods they had studied. Before the presentation, each group added their own timeline, extending it on the previous timeline to complete a time period. At the end of the History on tape project, all students analysed and evaluated the project using different criteria: acquisition and implementation of the knowledge about units of time and the past, converting larger into smaller units of time and vice versa, comparing time intervals, student independence and commitment to the project, etc. Students also analysed what was good about the project and what could have been better, as well as which elements could be applied in real life and subsequent projects.
The Funfair project included content from the following lessons: Money and Addition and Subtraction, and its aim was to train students to trade, use money and solve mathematical problems over the course of two school periods. During the Hurdles track project, students used a tape measure to measure the length of the track, constructed and positioned hurdles, whereas the aim of the Doll clothing project was to have them revise the content of the lesson Units of length: metre, decimetre, centimetre, millimetre over two school periods through different activities related to measurements, tailoring and sewing clothes for dolls. The We are baking cookies project required students to measure the mass of selected ingredients in gram and kilogram, mix them together and bake cookies.
In the Mathematical fairy tale project students were required to present mathematical problems through a story, and these problems included equations with a missing addend, subtrahend and minuend, inequalities, units of measurement, and fractions.
Lessons taught within the afore-mentioned projects were thematically related to the idea of project-based instruction, and their content matched the activities of project-based work. At the same time, the projects were inter-related because they all dealt with mathematical measurements and could form part of an integrative week. Students' activities were engaging and interesting and activated different students' potential in different ways. By working on the projects, students had an opportunity to solve real-life problems and knowledge acquired in this manner would be more permanent and more applicable in situations outside the school context.
Exercises within the experimental programme were conducted and supervised by teachers who had been previously provided with the necessary explanations, instructions, preparation for classes, material, as well as their duties and responsibilities for each of 11 school periods which had been designated for programme realisation through the implementation of a project-based model. Within the control group, the same teaching units were implemented at the same time as in the experimental group. The only difference was the approach to learning, which meant that the students in the control group did not learn content through inter-subject connecting, through projects and broader topics, but in the usual lecturing way, that is the isolated processing of mathematical program content without integration with other subjects or an interdisciplinary approach. Teachers who participated in the control classes were not given any instructions, nor were they aware of the content and the way in which it was taught in the experimental group.
Our study implemented the quasi-experimental method and the parallel study mode. Effects of the experimental programme have been determined through testing. We performed two tests: pre-testing before the introduction of the experimental programme, and post-testing, after the implementation of the experimental programme.
We performed a pilot test on a sample of 43 students, after which instrument adjustments were performed and the final test form was constructed. Students who participated in the pilot test did not participate in the study.
We created test tasks modelled on standardised mathematics tasks classified by achievement level (Markovic, Kirovski, Mrkalj, Rikalo, Vukovic, Madaras, Prodanovic & Perovanovic, 2006), and on the prescribed education standards related to student achievement (Opsti standardi postignuca - obrazovni standardi za kraj prvog ciklusa obaveznog obrazovanja, 2011) with descriptors at three levels: basic, intermediate and advanced level of expected knowledge for that age, designed by expert teams of the Republic of Serbia's Ministry of Education. Tests comprised 10 tasks each. The tasks were not identical in these two forms.
Ten tasks from the pre-test included content from Measuring and Measurements. They were designed to include all achievement levels: basic, intermediate and advanced. The first four tasks were intended for the basic achievement level (simpler examples with maximum two operations per task, equations involving addition and subtraction), the fifth, sixth and seventh tasks were on the intermediate level (converting from larger to smaller units, determining which operation takes precedence, tasks with three operations), whereas the eighth, ninth and tenth tasks were on the advanced level of achievement (textual tasks, conversion between units of measurement, implementation of the acquired knowledge). The test was carried out before the introduction of the project-based experimental programme model. The tasks were assessed against the identification key and the maximum score was 100.
The post-test was introduced after implementing the project-based model to measure the effects of the content covered through the 10 tasks on Measuring and measurements and it was an equivalent of the pre-test, both in form and elements.
All students were placed in approximately identical examination conditions during the tests, and tests were reviewed uniformly, using the instructions from the identification key to ensure test objectivity. In analysing achievement on the tests for each student, the total achievement was observed. We confirmed the logical and content validity of the tests by establishing that they met the requirements of the curriculum, and the content they referred to. Instrument reliability was established by calculating Cronbach' s alpha coefficient (a = .88), which indicates high instrument reliability (Pallant, 2011). The discriminant coefficient (corrected point-biserial correlation) for each task ranged between .389 and .651, which is very good.
Data obtained in the tests were processed using the IBM Statistics SPSS23 software package for system analysis. One-way analysis of variance (ANOVA) was used to monitor the effects of the experimental programme in the experimental group, whereas analysis of covariance (ANCOVA) was used for statistical control of uniformity between the groups in the tests.
Results and Discussion
The aim of this study was to determine the effectiveness of implementing a project-based model of instruction on student achievement in lower elementary mathematics education. Results of the pre-test showed more or less uniform results of the tests in both student groups: experimental group (M = 63.01, SD = 19.626), and control group (M = 62.84, SD = 21.489) (Table 1).
Variance analysis of differences obtained between the experimental and the control group during the initial measurement ((Fx(1,145) = .003, p = .960) shows that there was no statistically significant difference in student performance on the pre-testing, whereas Levene' s test (p = .389) shows that the assumption of homogeneity of variance has not been violated (Pallant, 2011:253) (Table 2).
After the pre-testing, the experimental group was introduced to the experimental programme, i.e. project-based model of work, whereas the control group continued to work in the usual way. After carrying out the experimental programme, we conducted the post-testing. Comparing the results (Table 1), we can see that the project-based model of instruction helped students from the experimental group to score highers on the post-test (M = 69.34, SD = 17.893) compared to students from the control group (M = 63.14, SD = 19.744). Variance on the post-test (Fy(1, 145) = 3.982, p = .048) indicates the existence of a statistically significant difference in the performance of students on the test in favour of the experimental group. Levene' s test shows that the assumption of equality of variances has not been violated (p = 1.119, p = .275) and that the result is reliable.
To remove all doubt that the difference was as a result of a lack of uniformity between the experimental and the control group, we calculated the ANCOVA. The result on the initial measurement was taken as the covariate. The result (F = 39.686, p < .001) proves beyond doubt that the differences were not as a result of the lack of uniformity between the experimental and the control group, but rather a result of the experimental programme (Table 3).
The strength of the effects of the experimental programme, i.e. project-based model, can be best seen on the resulting partial Eta squared (.216) which indicates strong effects (Cohen, 1988). This means that the variance of 21.6% on the post-test measurement can be explained by the effects of the experimental programme. The effects of the covariate (initial measurement) on the results of the post-test are also significant (F = 1372.64, p = .000), provided we eliminate the effects of the independent variable (group). Moreover, there was a strong correlation between the results of examination of the project-based model's effects on student performance in mathematics before and after the experimental programme had been introduced (partial Eta squared equals .905), and it may explain the 90.5% variance in the post-test results.
Based on the results obtained, we can conclude that the project-based model of work in mathematics education has caused a significant improvement of student performance in mathematics. These results have been confirmed by other authors (Ayan, 2012; Cengizhan, 2007; Chang & Tseng, 2011; Kanter & Konstantopoulos, 2010; Korkmaz & Kaptan, 2002).
The second aim of this study was to determine whether observed differences between groups depended on students' marks in mathematics in addition to instructional approach, in other words, whether the project-based model of instruction improved the performance of students with different marks in mathematics. We wanted to specifically examine whether the project-based model was equally acceptable to students with different marks and whether it improved their performance. If we compare the results from the pre-testing, we can see that students from the experimental group and students from the control group achieved approximately the same scores, the most successful students in both groups being those with excellent scores (5) (Table 4). However, all students from the experimental group achieved a significant improvement of performance on the post-test. What' s especially encouraging is the fact that even students with the lowest marks achieved a significant improvement of performance after implementation of the project-based model.
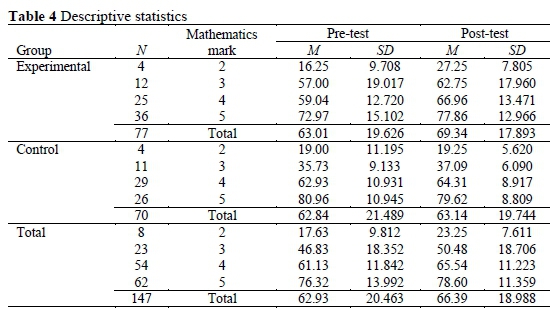
Levene' s test for equality of variances shows that the assumption of equality of variances has been verified (F = 1.694, p = .115) (Table 5).
We saw that students with better marks also achieved improved scores on the test. When we remove the covariate (initial measurement), we see that those differences are statistically significant (F = 75.597, p = .000), whereas the partial Eta squared (.620) indicates that 62% variance can be explained by the marks, which is a very strong effect (Cohen, 1988).
After removing the covariate (results of the initial measurement), we determined that there was a statistically significant effect of the interaction between teaching methodology in mathematics education (project-based model) and the mark in mathematics on student performance (F = 8.040, p = .000). Partial Eta squared is .148, which is a strong effect (Cohen, 1988).
Results of the tests mentioned above have shown that students from the experimental group (project-based model of instruction) have achieved better scores on the test compared to students from the control group (usual method of instruction), which means that the project-based model of learning contributes to improved performance in mathematics. These results confirm the value of project-based instruction and further emphasise its possible role in lower elementary mathematics education. Results from other studies also confirm the advantages of the project-based model of instruction and its positive impact on student achievement. One such study (Özdemir, 2006) underlines that there are several reasons for obtaining such results. Özdemir (2006) believes that the project-based model of instruction is pleasant for students. Gültekin (2005) points out that students look happy during project-based instruction, learning the material at the same time. To conclude, actively engaging students increases their desire to work and improves attention, which in turn positively influences their achievement (Özdemir, 2006).
Conclusion
The results of this research show that the project-based teaching method contributes to the better educational achievement of students in mathematics teaching, in the younger grades of primary school. Progress in student achievement is achieved by all students, regardless of the success they have achieved in mathematics teaching. This is especially important from the point of view of students who have poor achievement in mathematics, who have achieved better results in learning arranged according to the principles of project work.
The results are particularly significant if they are observed in the light of the importance of project teaching, and above all since such teaching contributes to inter-subject connecting, learning that is based on the student's activity in the learning process, learning that is embedded in the student' s real life and connecting learning to the student' s personal experience. The knowledge gained in such a process is of greater value to the student, not isolated, but linked to their experiences and the student sees the meaning of learning. In this way, the abstract world of mathematics is understood by students as a science that benefits them in life.
It should be emphasised that the introduction of project teaching should start from the beginning of schooling. If such a model of teaching mathematics and other fields is embedded from the beginning of students' education, then students will begin to view mathematics and its importance in life differently, and they will see its applicability and connection with other fields.
However, it should be kept in mind that the project teaching of mathematics is very complex and requires significant teacher and student skills. Preparing this type of learning requires much more time, engagement and a more inclusive approach. First of all, it is necessary to find links to the content of other subjects and the students' experience.
Stronger commitment and increased effort of a creative and innovative teacher who studiously plans and systematically adapts project-based activities to the preferences, interests and abilities of students will result in a high-quality knowledge applicable in everyday life. Project-based learning is not just a way of learning, it is a way of working with others. This approach to learning demands a competent, highly motivated and creative teacher who is able to find the best way to plan, organise and implement it in his or her teaching practice, but it also demands adaptations of the curriculum and the textbook to match the principles of project-based instruction (Lazic et al., 2015). The results of this study may be useful for mathematics teachers in lower elementary schools towards empowering them in applying this effective instructional approach when creating mathematics classes.
Authors' Contribution
All authors, BL, JK and SM, equally contributed to the data collection, data analysis and writing of the manuscript. All authors reviewed the final manuscript.
Notes
i. Published under a Creative Commons Attribution Licence.
ii. DATES: Received: 23 August 2019; Revised: 19 March 2020; Accepted: 6 July 2020; Published: 31 August 2021.
References
Ali R, Akhter A, Shahzad S, Sultana N & Ramzan M 2011. The impact of motivation on students' academic achievement in problem based learning environment. International Journal of Academic Research, 3(1):306-309. [ Links ]
Ali R, Hukamdad, Akhter A & Khan A 2010. Effect of using problem solving method in teaching mathematics on the achievement of mathematics students. Asian Social Science, 6(2):67-72. Available at https://citeseerx.ist.psu.edu/viewdoc/download7doi=10.1.1.889.2447&rep=rep1&type=pdf. Accessed 31 August 2021. [ Links ]
Arends F, Winnaar L & Mosimege M 2017. Teacher classroom practices and Mathematics performance in South African schools: A reflection on TIMSS 2011. South African Journal of Education, 37(3):Art. #1362, 11 pages. https://doi.org/10.15700/saje.v37n3a1362 [ Links ]
Ayan M 2012. The influence of project based learning on elementary school students' academic achievement in science education. Journal of Turkish Educational Sciences, 10(1):167-183. [ Links ]
Barell J 2007. Problem-based learning: An inquiry approach (2nd ed). Thousand Oaks, CA: Corwin Press. [ Links ]
Barell J 2010. Problem-based learning: The foundation for 21st century skills. In J Bellanca & R Brandt (eds). Twenty-first century skills: Rethinking how students learn. Bloomington, IN: Solution Tree Press. [ Links ]
Bell S 2010. Project-Based Learning for the 21st century: Skills for the future. The Clearning House: A Journal of Educational Strategies, Issues and Ideas, 83(2):39-43. https://doi.org/10.1080/00098650903505415 [ Links ]
Bender W 2012. Project-based learning: Differentiating instruction for the 21st century. Thousand Oaks, CA: Crown. [ Links ]
Capraro RM & Slough SW 2013. Why PBL7 Why STEM? Why now? An introduction to STEM project-based learning: An integrated science, technology, engineering, and mathematics (STEM) approach. In RM Capraro, MM Capraro & JR Morgan (eds). STEM project-based learning: An integrated science, technology, engineering, and mathematics (STEM) approach (2nd ed). Rotterdam, The Netherlands: Sense. [ Links ]
Cengizhan S 2007. The effects of project based and computer assisted instructional designs on those students' who have depended, independed and cooperative learning styles, academic achievement and learning retention. Journal of Turkish Educational Sciences, 5(3):377-101. [ Links ]
Chang CC & Tseng KH 2011. Using a Web-based portfolio assessment system to elevate project-based learning performances. Interactive Learning Environments, 19(3):211-230. https://doi.org/10.1080/10494820902809063 [ Links ]
Cohen J 1988. Statistical power analysis for the behavioral sciences (2nd ed). Hillsdale, NJ: Lawrence Erlbaum Associates. [ Links ]
Darling-Hammond L, Barron B, Pearson PD, Schoenfeld AH, Stage EK, Zimmerman TD, Cervetti GN & Tilson JL 2008. Powerful learning: What we know about teaching for understanding. San Francisco, CA: Jossey Bass. [ Links ]
Doppelt Y 2009. Assessing creative thinking in design-based learning. International Journal of Technology and Design Education, 19(1):55-65. https://doi.org/10.1007/s10798-006-9008-y [ Links ]
Dordevic V 2007. Inovativni modeli nastave (integrativna nastava, projektna nastava i interaktivna nastava) [Innovative teaching models (integrative teaching, project teaching, and interactive teaching)]. Obrazovna Tehnologija, 4:76-97. Available at http://www.edu-soft.rs/cms/mestoZaUploadFajlove/7_OT_4_2007_VESNA_DJORDJEVIC_.pdf. Accessed 31 August 2021. [ Links ]
Fabijanic V 2014. Projektna nastava: Primena u izradi istrazivackih radova ucenika [Project education: Application in the design of student research]. Educatio Biologiae, 1:89-96. Available at https://hrcak.srce.hr/index.php?show=clanak&id_clanak_jezik=219231. Accessed 31 August 2021. [ Links ]
Gavin MK, Casa TM, Adelson JL, Carroll SR & Sheffield LJ 2009. The impact of advanced curriculum on the achievement of mathematically promising elementary students. Gifted Child Quarterly, 53(3):188-202. https://doi.org/10.1177/0016986209334964 [ Links ]
Gerhana MTC, Mardiyana M & Pramudya I 2017. The effectiveness of Project Based Learning in trigonometry. Journal of Physics: Conference Series, 895:012027. https://doi.org/10.1088/1742-6596/895/1/012027 [ Links ]
Grant MM 2002. Getting a grip on project-based learning: Theory, cases and recommendations. Meridian: A Middle School Computer Technologies Journal, 5(1):83. [ Links ]
Gültekin M 2005. The effects of project-based learning on learning outcomes in the 5th grade social studies course in primary education. Educational Sciences: Theory & Practice, 5(2):548-556. [ Links ]
Hrvatic N & Pirsl E 2007. Kurikulum pedagoske izobrazbe ucitelja [Curriculum of pedagogical training of teachers]. In V Previsic (ed). Kurikulum [Curriculum]. Zagreb, Croatia: Skolska Knjiga. [ Links ]
Jacques LA 2017. What does project-based learning (PBL) look like in the mathematics classroom. American Journal of Educational Research, 5(4):428-433. https://doi.org/10.12691/education-5-4-11 [ Links ]
Janes S 2007. Borba za ucenika i njegovo znanje [The struggle for the student and his knowledge]. Metodicki Obzori, 2:155-163. [ Links ]
Kanter DE & Konstantopoulos S 2010. The impact of a project-based science curriculum on minority student achievement, attitudes, and careers: The effects of teacher content and pedagogical content knowledge and inquiry-based practices. Science Education, 94(5):855-887. https://doi.org/10.1002/sce.20391 [ Links ]
Kim SH & Choi SY 2016. Exploring the influences of global learning using web technologies on 21st century skills and global learning attitudes. Advanced Science and Technology Letters, 127:135-139. https://doi.org/10.14257/astl.2016.127.27 [ Links ]
Kirschner PA, Sweller J & Clark RE 2006. Why minimal guidance during instruction does not work: An analysis of the failure of constructivist, discovery, problem-based, experiential, and inquiry-based teaching. Educational Psychologist, 41(2):75-86. https://doi.org/10.1207/s15326985ep4102_1 [ Links ]
Knezevic J, Lazic B, Maricic S & Petojevic A 2019. Uvodenje projektnog rada u razrednu nastavu matematike [Introduction of project work in upper elementary teaching of mathematics]. Létünk, 2019(1):59-73. Available at http://www.letunk.rs/documents/archivum/Letunk_2019_1.pdf. Accessed 30 August 2021. [ Links ]
Korkmaz H & Kaptan F 2002. The effects of project-based learning on elementary school students' academic achievement, academic self concepts and study time in science education. Hacettepe Üniversitesi Egitim Fakültesi Dergisi, 22:91-97. [ Links ]
Lam SF, Cheng RWY & Ma WYK 2009. Teacher and student intrinsic motivation in project-based learning. Instructional Science, 37(6):565-578. https://doi.org/10.1007/s11251-008-9070-9 [ Links ]
Lazic B, Maricic S & Milinkovic J 2015. ПРОПЕДЕВТИЧКО УЧЕЊЕ РАЗЛОМАКА ЗАСНОВАНО НА ИНТЕГРАЦИЈИ САДРЖАЈА У ПОЧЕТНОЈ НАСТАВИ МАТЕМАТИКЕ [Propedeutic fraction learning based on content integration in the initial teaching of mathematics]. Nastava i Vaspitanje, 65(4):679-697. https://doi.org/10.5937/nasvas1504679L [ Links ]
Lee HK & Breitenberg M 2010. Education in the new millennium: The case for design-based learning. The International Journal of Art & Design Education, 29(1):54-60. https://doi.org/10.1111/j.1476-8070.2010.01631.x [ Links ]
Loyens SMM, Magda J & Rikers RMJP 2008. Self-directed learning in problem-based learning and its relationships with self-regulated learning. Educational Psychology Review, 20:411-427. https://doi.org/10.1007/s10648-008-9082-7 [ Links ]
Markovic S, Kirovski N, Mrkalj Z, Rikalo M, Vukovic L, Madaras M, Prodanovic R & Perovanovic M 2006. Zbirka modela zadataka po nivoima postignuca: Srpski jezik i matematika za treci razred osnovne skole [Collection of model Serbian language and math tasks for the third grade of elementary school]. Beograd, Serbia: Zavod za Vrednovanje Kvaliteta Obrazovanja i Vaspitanja. [ Links ]
Muschla JA & Muschla GR 2006. Hands-on math projects with real-life applications (2nd ed). San Francisco, CA: Jossey-Bass. [ Links ]
Opsti standardi postignuca - obrazovni standardi za kraj prvog ciklusa obaveznog obrazovanja [General achievement standards - Education standards at the end of the first cycle of compulsory education, mathematics] 2011. Beograd, Serbia: Zavod za Vrednovanje Kvaliteta Obrazovanja i Vaspitanja. [ Links ]
Özdemir E 2006. An investigation on the effects of project-based learning on students' achievement in and attitude towards geometry. Master's thesis. Ankara, Turkey: Middle East Technical University. Available at https://open.metu.edu.tr/bitstream/handle/11511/15935/index.pdf. Accessed 26 August 2021. [ Links ]
Pallant J 2011. SPSS: Prirucnik za prezivljavanje: Postupni vodic kroz analizu podataka pomocu SPSS-a [SPSS: Survival guide: A step-by-step guide to analyzing data using SPSS]. Beograd, Serbia: Mikro Knjiga. [ Links ]
Quek CL, Wong AFL, Divaharan S, Liu WC, Peer J & Williams MD 2007. Secondary school students' perceptions of teacher-student interaction and students' attitudes towards project work. Learning Environments Research, 10(3):177-187. https://doi.org/10.1007/s10984-007-9030-3 [ Links ]
Reigeluth CM, Beatty BJ & Myers RD (eds.) 2017. Instructional-design theories and models (Vol. IV). New York, NY: Routledge. [ Links ]
Roh KH 2003. Problem-based learning in Mathematics (EDO-SE-03-07). Educational Resources Information Center. Available at https://files.eric.ed.gov/fulltext/ED482725.pdf. Accessed 24 May 2019. [ Links ]
Savery JR 2006. Overview of problem-based learning: Definitions and distinctions. The Interdisciplinary Journal of Problem-Based Learning, 1(1):9-20. https://doi.org/10.7771/1541-5015.1002 [ Links ]
Schmidt HG, Rotgans JI & Yew EHJ 2011. The process of problem-based learning: What works and why. Medical Education, 45(8):792-806. https://doi.org/10.1111/j.1365-2923.2011.04035.x [ Links ]
Sutinen A 2013. Two project methods: Preliminary observations on the similarities and differences between William Heard Kilpatrick's project method and John Dewey's problem-solving method. Educational Philosophy and Theory, 45(10):1040-1053. https://doi.org/10.1111/j.1469-5812.2011.00772.x [ Links ]
Umugiraneza O, Bansilal S & North D 2017. Exploring teachers' practices in teaching Mathematics and Statistics in KwaZulu-Natal schools. South African Journal of Education, 37(2):Art. # 1306, 13 pages. https://doi.org/10.15700/saje.v37n2a1306 [ Links ]
Vilotijevic M & Vilotijevic N 2016. Modeli razvijajuce nastave II [Models of evolving teaching II]. Belgrade, Serbia: Uciteljski Fakultet. [ Links ]
Vizek Vidovic V, Vlahovic-Stetic V, Rijavec M & Miljkovic D 2003. Psihologija obrazovanja [Psychology of education]. Zagreb, Croatia: IEP-VERN. [ Links ]
Wilhelm J, Sherrod S & Walters K 2008. Project-based learning enviroments: Challenging perservice to act in the moment. The Journal of Educational Research, 101(4):220-233. https://doi.org/10.3200/JOER.101.4.220-233 [ Links ]














