ARTICLES

 

Pre-service teachers' mathematical engagement in learning about the total surface areas of geometrical solids

 

 

Sibawu Witness Siyepu^I; Siphokazi Winniefred Vimbelo^II

^IDepartment of Mathematics, Faculty of Education, Cape Peninsula University of Technology, Cape Town, South Africa
^IITeacher Professional Development, Faculty of Education, Cape Peninsula University of Technology, Cape Town, South Africa svimbelo@gmail.com, vimbelos@cput.ac.za

 

 

---

ABSTRACT

In this article we report on pre-service teachers' mathematical engagement regarding the total surface areas of geometric solids. Despite several attempts at improvement, the poor performance of South African learners in mathematics persists. This is attributed to instructional approaches. In the study reported on here we explored how pre-service teachers communicate conjectures, justifications, and generalisations to develop formulae for geometric solids. We employed a qualitative descriptive case study within the interpretive paradigm. Data were collected through document analysis and students' written tasks. Four tasks were administered to 30 pre-service teachers to enable the researchers to reflect on their performance. Students' written tasks were analysed with the aid of the model of mathematical knowledge for teaching, which served as the theoretical underpinning of the study. The findings of the study reveal that students can develop mathematical engagement and reasoning when appropriate tasks are designed to facilitate understanding of key concepts that are the cornerstone of learning about geometric solids. Certain concepts, notably, circles, radii, pi, rectangles, cones, Pythagoras' theorem, slanting height, congruence, and prism, were crucial elements that should be explored prior to the introduction of the topic of the total surface areas of geometric solids. The study was an eye-opener to South African policy makers, mathematics teachers and lecturers in terms of identifying students' weaknesses at pre-service level on how to develop logical methods to make sense in the learning of geometrical solids.

Keywords: areas of three-dimensional shapes; areas of two- dimensional shapes; conjectures; deductions; formulae; generalisations; justifications; mathematical concepts; pre-service teachers; understanding

---

 

 

Introduction and Background

In the South African context, the poor performance of learners in mathematics gives stakeholders cause for concern. In this context, the term "stakeholders" refers to people who are interested in education systems worldwide.

In this study we focused on the development of mathematical engagement among first-year pre-service teachers to enable them to make sense of learning about geometrical solids, which includes cylinders, cuboids, triangular prisms, and cones.

The Department of Basic Education, Republic of South Africa (2011:12) recommends that "teachers should facilitate conjecture about the properties of special triangles, quadrilaterals, and other polygons, and test conjectures using any logical method." In this context "logical method" refers to students' ability to identify relationships among shapes and use appropriate reasoning to justify their solutions. Siyepu (2018) suggests that teachers should facilitate the processes of deriving formulae of finding total surface areas of complex solid shapes.

The poor performance of learners in mathematics has been attributed to poor instructional approaches that do not make sense (Feza & Webb, 2005; Siyepu, 2013; Skemp, 1976). This problem does not only apply in South Africa; it is a global issue. Mathematics researchers in Colombia such as Pino-Fan, Assis and Castro (2015:1429) refer to "the importance of teachers knowing school mathematics in depth and breadth, with the general consensus being that this knowledge in turn impacts upon pedagogical content knowledge and therefore the effectiveness of instruction." They further claim that many elementary teachers lack conceptual understanding of mathematics and that pre-service and in-service teachers' limited knowledge of mathematical content and their confidence in doing mathematics, are of particular concern.

European countries distinguish successful students in mathematics based on factors such as anxiety, self-efficacy, self-belief, self-concept and motivational interest (RadisiC, Videnovic & Baucal, 2018). This reveals that there are problems in the learning of mathematics that should be addressed in European countries. Countries such as Hungary, The Slovak Republic and Sweden achieve below the average in a comparison across European countries (Radisic et al., 2018). Radisic et al. (2018) further explain that students with high anxiety, low self-efficacy, low self-belief, and low interest in the learning of mathematics tend to perform poor in classroom activities. These factors assumingly apply in South Africa as well.

Asian countries claim that their high performance in mathematics is attributed to the culture of learning mathematics and language competence (Leung, 2017). All countries with high levels of understanding mathematics have a good culture of learning mathematics and a content balance with the years of schooling (Leung, 2017). In the South African situation, there is a low culture of learning mathematics and there is no content balance with the years of schooling.

Mathematical Thinking and Reasoning

Mathematical thinking is a highly complex activity (Stacey, 2006). In order for students to enjoy mathematics, they have to develop mathematical thinking in the learning process. This suggests that learning should be facilitated in such a way that students conduct mathematical investigations by themselves (Stacey, 2006). Students should be able to trace how rules, procedures and formulae applied in mathematics were developed (Siyepu, 2013). In order for students to develop mathematical thinking and reasoning, teachers should be familiar with the concepts informing the following questions:

• What is mathematical thinking and reasoning?

• What are the core concepts to be studied by students in order to develop mathematical thinking and mathematical reasoning?

Mathematical thinking and reasoning are considered to be processes of making justified inferences using deductive, inductive and adductive processes (Mata-Pereira & Da Ponte, 2017). Mata-Pereira and Da Ponte (2017) elaborate that "mathematical thinking and reasoning processes include formulating questions and solving strategies, formulating and testing generalisations and other conjectures and justifying them" (p. 170). Our study focused on the teaching for understanding as key mathematical thinking and reasoning processes necessary to learn about areas of geometric solids.

Lannin, Ellis, Elliott and Zbiek (2011:13) argue that "conjecturing involves reasoning about mathematical relationships to develop statements that are tentatively thought to be true but are not known to be true." Lesseig (2016:3) emphasises that "this element of doubt distinguishes conjectures from proofs and provides an access point for further mathematical reasoning." Generalising involves identifying commonalities in cases or extending mathematical reasoning to consider a wider range of objects (Ellis, 2011). Staples, Bartlo and Thanheiser (2012:448) argue that "justifying is the act of developing arguments to demonstrate the truth (or falsehood) of a conjecture, using mathematical forms of reasoning."

The purpose of our study was to explore conjecturing, generalising and justifying patterns to develop mathematical thinking and reasoning among first-year Bachelor of Education students (pre-service teachers) specialising in mathematics for the Senior Phase and the Further Education And Training Phase at a University in South Africa.

We sought to answer the following main research question:

1) What is the nature of the activities performed by lecturers to facilitate mathematical engagement, so as to make sense of learning about the areas of geometric solids.

This research question was divided into the following sub-questions:

a) How do mathematics lecturers facilitate pre-service teachers' mathematical engagement to enable them to understand the development of formulae for finding the total surface areas of geometric solids?

b) What kind of knowledge should lecturers possess to build proficiency among pre-service teachers in conjecturing, generalising and justifying the development of formulae for the total surface areas of geometric solids?

Literature Review

In this research we explored ways of facilitating mathematical reasoning and engagement among pre-service teachers when learning about the total surface areas of geometric solids. Several researchers argue that mathematical reasoning can be defined as comprising five interrelated processes of mathematical engagement: sense-making, conjecturing, convincing, reflecting, and generalising (Bjuland, 2002, 2007; Borgersen, 1994). This suggests that in order for students to develop mathematical engagement and reasoning, teachers should develop activities that promote all five interrelated processes.

Sense-making in learning about the areas of geometric solids

Rehmeyer (2014:4) highlights that "the Greek root of the word 'mathematics' means 'the learnable thing.'" However, many students perceive mathematics as a difficult subject that does not make sense (Rehmeyer, 2014). Sukirwan, Darhim and Herman (2018) define sense-making as the ability to build a schema of problems and represent knowledge. They add that sense-making is a process of the adaptation and association of new information acquired with prior knowledge (Sukirwan et al., 2018). This process occurs when the mathematical situation is understood and communicated in mathematical language (Sukirwan et al., 2018). This forcibly reminds us that in order for students to enjoy the learning of mathematics it must make sense to them. Mathematics is entirely about making sense and reasoning; reasoning being the very foundation of mathematics (Rehmeyer, 2014). Lithner (2008) explains four characteristics of reasoning as follows:

• Novelty, which refers to the new fact requiring reasoning to be created or recreated.

• Flexibility, which means the ability to use different approaches and adaptations for specific problems.

• Plausibility, which means that there are arguments in favour of the chosen strategy explaining why the conclusion is true or plausible.

• A sound mathematical foundation, meaning that the argument is based on solid mathematical conceptual characteristics.

Conjecturing in learning about the areas of geometric solids

Conjecturing involves predicting theoretical activities and conclusions based on incomplete facts (Sukirwan et al., 2018). As mentioned above, conjecturing is a first attempt to develop a theory or a proof without adequate valid reasons. In learning about the areas of geometric solids, mathematicians use conjecturing to make sense of developing formulae.

Convincing in learning about the areas of geometric solids

Convincing is the ability to cause someone to believe that a given statement is true. Conjectures developed through the completion strategies of arguing and communicating mathematical activity are convincing. The process of convincing entails cognitive development that makes students assemble elements of basic knowledge to develop new knowledge such as postulates, theorems and formulae.

Reflecting in learning about the areas of geometric solids

Reflecting refers to the interpretation of what is happening in the students' minds when they are learning about the total surface areas of solids. In the context of mathematics, reflecting leads to the development of a theory. The development of theories, postulates, rules and formulae is called generalising.

Pre-service teachers' understanding of mathematics depends to a large extent on the knowledge of lecturers. As they are preparing to start a teaching career, they need proper guidance on how to develop mathematical reasoning and engagement among learners in the schooling system. Mata-Pereira and Da Ponte (2017:171) claim that "mathematical reasoning requires that students get involved in a variety of engagement and sense-making processes." In our study we engaged pre-service teachers in a variety of activities, focusing on the development of formulae for the total surface areas of geometric solids.

Students' mathematical reasoning can be traced through their interaction in the classroom (Brodie, 2010). Researchers such as Brodie (2010) and Christiansen and Walther (1986) assert that appropriate tasks are essential to support students' mathematics learning and tasks that aim at developing mathematical reasoning. Teachers should know which tasks guide learners to engage in mathematical reasoning, and in what ways these tasks can be used in class (Brodie, 2010; Mata-Pereira & Da Ponte, 2017).

Theoretical Framework

The Model of Mathematical Knowledge for Teaching underpins this study. With this study we focus teachers' attention on what Shulman (1987:4) claims to be "qualities, skills, abilities and understandings" to be developed by pre-service teachers to be known as competent teachers. She further elaborates that "teachers should learn how particular kinds of content knowledge and pedagogical strategies necessarily interacted in the minds of teachers" (Shulman, 1987:5). In order for students to gain understanding in the learning of mathematics, teachers should be experts in two domains: (a) knowledge of content and (b) pedagogical knowledge (Chua, 2018; Shulman, 1986). Knowledge of content is a measure of teachers' level of proficiency in the subject matter they are expected to teach, while pedagogical knowledge is a measure of how they are able to manage classrooms, design activities, frame assignments, develop and implement lessons, and assess learners' understanding (Chua, 2018). Chua (2018) supports researchers such as Depaepe, Verschaffel and Kelchtermans (2013:13-14) who claim that teachers should have an understanding of knowledge of content and curriculum, specialised content knowledge, knowledge of instructional design, knowledge of students' misconceptions and difficulties, and knowledge of instructional strategies. Hill, Rowan and Ball (2005) provide valid evidence for the purported link between teacher knowledge and student achievement in mathematics. In our study we pursued the processes of designing activities and developing assessment strategies that lead to improvement in the quality of students' understanding.

Siyepu (2018) asserts that it is of the utmost importance for pre-service teachers to be experts in facilitating the development of mathematical reasoning in learners by exposing them to conjecturing, generalisation, deduction and justification in the learning of mathematics. He emphasises that students should be familiar with activities that can serve to enhance mathematical reasoning (Siyepu, 2018).

Pre-service teachers should have expert knowledge of the mathematics for the phases in which they are trained to be specialists. This suggests that pre-service teachers should be able to interpret the curriculum recommended for the grades of their specialisation. We investigated the kind of mathematical content knowledge that pre-service teachers possessed regarding the areas of geometric solids, and assessed their level of mathematical knowledge for teaching in this regard. The focus of the study was on what pre-service teacher knew about the mensuration of the areas of geometric solids. Mathematical knowledge for teaching entails the kind of knowledge that teachers need to perform the recurring tasks of teaching mathematics in their specific phases of specialisation.

We investigated pre-service teachers' knowledge, focusing on six domains. Ball, Thames and Phelps (2008) briefly outline these domains as follows:

• Common content knowledge (CCK) as subject-specific knowledge required to solve mathematics problems. The reason why it is called "common" is because this knowledge is not specific to teaching -non-teachers are likely to have it and use it.

• Ball et al. (2008:400) describe subject content knowledge (SCK) as "mathematical knowledge and skills unique to teaching." Although teachers need this knowledge for effective teaching, it is probably not needed for any other purpose.

• Horizon content knowledge is an awareness of how mathematical topics are related.

• Knowledge of content and students (KCS) is knowledge that combines knowing about students and knowing about mathematics; it helps teachers predict students' thinking.

• Ball et al. (2008) describe knowledge of content and teaching (KCT) as knowledge that combines knowing about teaching and knowing about mathematics.

• Knowledge of content and curriculum implies that teachers need knowledge of the available materials that they can use to support student learning.

The main aim of our study was to demonstrate how lecturers facilitate pre-service teachers' mathematical engagement in learning about the total surface areas of geometrical solids.

 

Research Design and Methods

This study comprised a single qualitative descriptive case study. Labaree (2016:1) asserts that a "case study is an in-depth study of a particular research problem rather than a sweeping statistical survey or comprehensive comparative inquiry." We investigated mathematical knowledge for teaching areas of geometric solids among pre-service teachers at a South African university. Labaree (2016:1) further elaborates that a "case study research design is also useful for testing whether a specific theory and model actually applies to phenomena in the real world."

Research Participants

The research participants were 30 first-year students registered for mathematics in Bachelor of Education, Further Education and Training, in the 2018 academic year. All participants (18 females and 12 males) were full-time students studying in English, although English was only one student's first language. Participants, whose ages ranged from 19 to 25, were purposefully chosen to investigate their levels of knowledge and understanding with regard to geometric solids at university entry level. Baseline assessment tasks were administered to the participants in order to assist lecturers to gain background of what the participants knew about geometric solids.

Data Collection

We collected data through different tasks that were developed to explore how students understood the inter-connectedness of various shapes in a geometric solid. The tasks were developed according to what the Curriculum and Assessment Policy Statement documents recommend to be taught at secondary school level in South Africa. The South African curriculum requires teachers to investigate and form conjectures about the properties of special triangles, quadrilaterals and other polygons, and then go on to validate or prove these conjectures.

Our study focused on cylinders, cuboids, triangular prisms, triangular pyramids and cones. A cylinder comprises two circles and a curved rectangle. Thus, in order for students to be able to see or identify relationships among these shapes, they need an adequate understanding of the areas of circles, triangles, rectangles, cones, and prisms.

Task 1

Task 1.1 was to assess students' understanding in developing conjectures for the total surface area of a cylinder. The instruction was as follows: Use the net of a cylinder in Figure 1 below to demonstrate how the formula for the total surface area of a cylinder can be derived.

 

 

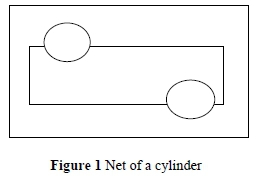
In order for students to be able to develop a conjecture, they need to understand what a conjecture is and how it is formed. Students should be able to make deductions linking the areas of circles and a curved rectangle to develop a calculation for the total surface area of a cylinder. This task assists pre-service teachers to demonstrate to their learners how the formula of a cylinder was developed by mathematicians.

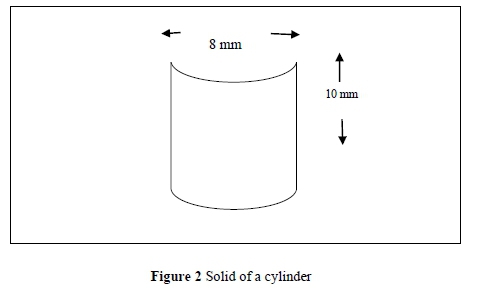
Task 1.2 was to assess pre-service teachers' understanding of the application of the formula for the total surface area of a cylinder.

The instruction was as follows: Given that the diameter of the base of a cylinder is 8 mm and the height is 10 mm, find the total surface area of a cylinder as shown in Figure 2. Students were expected to know that the radius of a circle is always half the diameter.

 

 

Task 2

Task 2 was to assess pre-service teachers' understanding of basic concepts in solids, notably, faces, edges and vertices. Task 2 also assessed whether pre-service students were able to deduce the interconnections between shapes used to build a rectangular prism. Alternatively, this task was to determine whether pre-service students were able to make conjectures to develop the formula for finding the total surface area of a rectangular prism.

Participants were supplied with match a box as in Figure 3, below, to perform the following three tasks:

 

 

Task 2.1: Count the number of faces, edges and vertices in a rectangular prism.

Task 2.2: Draw a net of a rectangular prism.

Task 2.3: Derive the formula for the total surface area of a rectangular prism.

Task 3

Task 3 was to assess pre-service student teachers' understanding of the formulae for calculating the areas of triangles and rectangles. Task 3 also assessed whether students were able to deduce and make interconnections between the triangles and rectangles used to build a triangular prism. Alternatively, this task was to determine whether pre-service student teachers were able to calculate the areas of triangles and rectangles when certain units were given, and were able to identify and use congruent triangles and rectangles to reach a solution to a given problem.

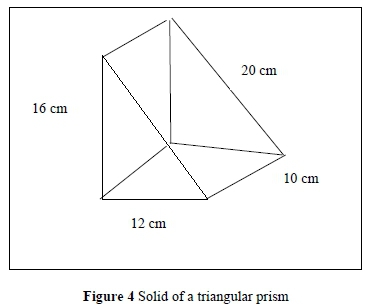
Task 3.1

Task 3.1 was as follows: Use Figure 4 to calculate the total surface area of the triangular prism. Consider the fact that only one pair of opposite faces are congruent.

 

 

Task 4

Task 4 was to assess pre-service student teachers' understanding of key concepts that determine the formulae for the area of a cone and assess whether they were able to deduce and trace the interconnections between concepts such as circle, circumference, diameter, radius, slant height, triangles and Pythagoras's theorem used to calculate the area of a cone. The question was: Given that the radius of a closed cone is 5 cm and its total surface area is 100∏ cm² , what is the slant height of the cone?

Data Analysis

In this study we employed a qualitative content analysis approach. Hsieh and Shannon (2005:1278) claim that "qualitative content analysis is a research method for the subjective interpretation of the content of text data through the systematic classification process of coding and identifying themes or patterns."

Analysis was done through examining students' responses to the questions administered in the form of tasks. Students' written tasks were marked and grouped together according to common themes. The data analysis process involved reading and re-reading students' written work to interpret it to make sense on how to answer research questions of the study. This included identification of the errors made in pursuit of a solution. The identification of errors assisted us to trace root causes of errors, to obtain students' shortcomings (see Table 1). We grouped students' written tasks according to themes that emerged during the process of data analysis.

 

Results of the Study and Discussion

In this study we report on pre-service student teachers' understanding of areas of geometric solids, based on exercises involving the development of formulae for the areas of a cylinder and rectangular prism. The application of formulae for the areas of a triangular prism and cone were explored to ascertain the students' understanding of key concepts such as circle, radius, circumference, apothem, altitude, Pythagoras' theorem, slant height and trigonometric ratios, notably tangent.

Pre-Service Student Teachers' Understanding with regard to Task 1

Twelve of 30 students (40%) demonstrated an understanding of how the formula for the total surface area of a cylinder was derived. These 12 students showed an understanding that the area of a circle is A ∏r . This suggests that these students knew that ∏ is the relationship between the circumference and the diameter of a circle. They also knew that the radius is always half the diameter of a circle.

Twelve of 30 students' (40%) interpretations showed that they knew that congruent circles shared the same area. As a result they were able to deduce that the areas of the two congruent circles add up to 2∏r² . They were also able to deduce from the understanding of a rectangle that the area of the curved surface of a cylinder is 2∏r². Figure 5 shows an example of how a student demonstrated understanding of how the formula of a cylinder is derived.

Twelve of 30 students (40%) demonstrated horizon content knowledge through their awareness of how mathematical topics are related. They identified the relationship between two congruent circles and a curved rectangular shape that combines with the two circles to build a cylinder. Indeed, these students formed conjectures that led to generalisation that the formula of the area of a cylinder is A = 2∏r² + 2∏rh. Their developing of conjectures regarding the total surface area of a cylinder thus shows that they have adequate content knowledge of the relationship between shapes that are used to build a cylinder. To be precise, the students who participated in the study showed an understanding of certain key concepts, notably, circle, circumference, radius, diameter, and the formula for the area of a circle which is ∏r².Five of 30 students (17%) showed poor understanding of how to derive a formula for the total surface of a cylinder. These students understood that the area of a circle is ∏r² and succeeded in adding ∏r² +∏r² =2∏r² as the sum of two congruent circles in a cylinder. Yet they failed to deduce that the area of a curved surface is 2∏r, assuming this rather to be and ending up with the mistaken formula A = 2∏r² + ∏rh . Figure 6 shows an example of how a student incorrectly derived the formula for the area of a cylinder.

These students' errors suggest that while they knew how to build up the composite area of a geometric solid, they did not know the formula for all the parts (viz. the formula for the circumference of a circle). Lecturers should lay a foundation for students to form conjectures using the given geometric solids. Students should know the formulae specific to each shape used to build a special kind of a geometric solid. These findings support Brodie's (2010) claim that students' mathematical reasoning can be traced through their interaction in the classroom.

Pre-Service Students' Understanding with regard to Task 1.2

Students who could not correctly conjecture regarding the surface area of a cylinder failed to complete Task 1.2 as they resorted to an incorrect formula, TSA = 2∏r2 +∏rh, instead of TSA = 2∏r² + 2∏r². students who came up with the correct formula for the surface area of a cylinder substituted correctly, using the formula.

TSA = 2∏r² + 2∏rh. This suggests that teachers and lecturers should emphasise that the application of a formula is only possible when students have some insight into the formula. Students should be given plenty of time to explore the derivation of the formula and how it can be applied to solve problems involving solid geometry.

Pre-Service Students' Understanding with regard to Task 2

Twenty-seven of 30 students demonstrated an understanding of all the concepts in Task 2, notably, faces, edges and vertices, and also correctly derived a formula for the total surface area of a rectangular prism. This indicates that these 27 students entered university with sufficient knowledge to be able to conjecture, justify and generalise to create formulae for total surface areas in solid geometry, in this instance, a cuboid. One student even demonstrated the ability to draw a model of a cuboid together with its net. The student also demonstrated how to derive the formula for the total surface area of a cuboid. Figure 7 shows the work of the student who demonstrated insight in deriving the formula for the area of a cuboid.

Six of 30 students (20%) could not draw a net for a rectangular prism despite the fact that a matchbox was supplied. This suggests that these six students should be familiarised with the use of the net of an object to develop a formula for the total surface area of any object. Alternatively, these students could have been shown the use of a net, but failed to understand it. In either event, the students who could not draw a net of a rectangular prism were not able to deduce the formula for the total surface area of the prism as TSA = 2lb+ 2bh+ 2lh. The total surface area of a rectangular prism resembled by a matchbox in the study as in Figure 3 can be written as TSA = 2lb+ 2bh+ 2lh (TSAstands for total surface area, 2lbstands for two times length times breadth, 2bh stands for two times breadth times height and 2lhstands for two times length times height).

The findings of the study indicated that some pre-service student teachers could not make conjectures, justify and generalise in their attempts to solve problems involving the total surface areas of geometric solids, in this case, a cuboid. This suggests that pre-service student teachers should be taught how to make conjectures, justify and generalise to develop mathematical engagement and reasoning in their learning of solid geometry. These tasks and their results point to the kind of mathematical knowledge that should be emphasised in the classroom - not only in South Africa but worldwide - to develop competent mathematics teachers. For the community as a whole, raising achievement for the lowest achievers brings many benefits, including higher levels of Gross Domestic Product (GDP) (Thompson, 2016). A number of countries - Brazil, Germany, Italy, Mexico, Poland, Portugal, The Russian Federation, Tunisia and Turkey - all decreased their proportion of low achievers in mathematics, showing that it is possible, with the will and the right policies, to change things (Thompson, 2016).

Pre-Service Students' Understanding with regard to Task 3

Twenty-three of 30 students (77%) identified that a triangular prism, as shown in Figure 3, can be separated into different shapes. They then calculated the area of each shape and added them together to obtain the total surface area of the given solid. They used various correct approaches. Four of 30 students (13%) changed the model given to a net and then used the net they drew to calculate the area of each shape before adding them to get the total surface area of a triangular prism. This indicates that these students could deduce and discern relationships between shapes used to build a model of a triangular prism. They could make conjectures, justifications and generalisations in their learning how to calculate the total surface area of a triangular prism.

The study shows that mathematical engagement and reasoning could be developed in pre-service student teachers through facilitating the process of making conjectures, justifications and generalisations to link different types of shapes used to build a solid. Task 3 guided students in the KCT. The fact that pre-service students knew that, in order to calculate the total surface area of a triangular prism, one should combine knowing about teaching and knowing about mathematics, indicates that they were able to explain the strategies followed to reach a solution. Figure 8 portrays an example of how a student demonstrated insight into applying the various formulae for areas of different shapes to calculate the total surface area of a triangular prism.

However, seven of 30 students (23%) could not understand that in order to find the total surface area of a triangular prism they had to calculate the area of each shape and add them together. This suggests that these students should be guided on how to make conjectures, justify and generalise. This can surely be rectified by giving them several tasks that reinforce the process of understanding through conjecturing, deduction, justifying and generalising. The findings of our study confirm what researchers such as Brodie (2010) and Christiansen and Walther (1986) state, that appropriate tasks are essential to support students' mathematics learning, in particular, tasks that aim at developing mathematical reasoning.

Pre-Service Students' Understanding with regard to Task 4

Thirteen of 30 students (43%) recognised that a cone consists of a circle and a sector of a circle. They understood that the area of a cone can be represented by A ∏r² ∏r² + ∏rl. They understood that in order to calculate the total surface area of a cone they required an understanding of the Theorem of Pythagoras, the area of a circle, its radius and circumference, the area of triangle, perpendicular height and slanting height. They applied all the concepts appropriately to reach a solution to the problem posed to them in Task 4. This indicates that these students were familiar with the calculation of the total surface area of a cone, or could deduce it by conjecture from the key concepts involved.

Seventeen of 30 students (57%) could not calculate the total surface area of a cone correctly. These seventeen students seemingly did not know that the correct formula for the area of a cone is A = ∏r² + ∏rl, and were not familiar with this calculation. Alternatively, they had been taught the formula but did not understand it. The instruction was: Given that the radius of a closed cone is 5 cm and its total surface area is 100∏ cm² , what is the slant height of the cone? Five of 30 students (17%) knew the correct formula for the total surface area of a cone but could not make the height the subject of the formula; in other words, they had not grasped the practice of making one variable in an algebraic equation the subject of the formula. These findings confirm Siyepu's (2018) emphasis that students should be familiar with activities that can serve to enhance mathematical reasoning.

This indicates that lecturers should reinforce students' understanding of the formula for the area of a cone, with an emphasis on making different variables the subject of the formula.

 

Conclusion

The result from our study shows that student teachers have some insight into the process of conjecturing, justifying, convincing and generalising to develop formulae for the total surface areas of geometric solids such as cylinders, rectangular prisms, triangular prisms and cones. Although a few students could not develop appropriate formulae for finding the total surface area of various solids, they were outnumbered by students who did demonstrate such understanding, as evidenced by the examples given above. Students were able to see the relationship between shapes used in the activities to build a certain kind of solid. For instance, several students recognised that circles and a curved rectangle were used to build a cylinder. They were also able to deduce the formula for finding the total surface area of a cylinder as TSA 2∏r² + 2∏rh . The students demonstrated insight regarding the key concepts to be used in deriving formulae. The fact that they were able to identify interconnectedness among the different shapes used to build solids is evidence that they had developed mathematical engagement and mathematical reasoning in the learning of geometric solids.

The nature of the activities used in the study confirmed that it is required to know which tasks lead students to engage in mathematical reasoning, and in what ways these tasks may be used in the classroom (Brodie, 2010; Mata-Pereira & Da Ponte, 2017). The activities and students' understanding demonstrated that pre-service student teachers should be guided towards thorough knowledge of the mathematical content they are expected to teach. The students' performance also demonstrated that teachers should be aware of what kinds of mathematical concepts should be emphasised in the classroom to develop proficiency among students.

The results of the study indicate that students should be taught the formulae for areas of two-dimensional shapes as a prerequisite for their learning about the total surface areas of three-dimensional shapes. Once students know formulae of areas of two-dimensional shapes, it becomes simple for them to calculate the area of each shape in a solid and add them together to obtain the total surface area.

The results show that pre-service student teachers require an understanding of key concepts that serve as cornerstones for the development of mathematical engagement and reasoning in the learning of solid geometry, such as conjecturing, generalising, and justifying. Once students become proficient in the deployment of these key concepts, they can be guided with ease to develop formulae for the total surface areas of geometric solids. Based on the results of the study, it is recommended that teachers be exposed to in-service training that will guide them in the development of mathematical engagement and reasoning in learning about the surface areas of geometric solids. It is also recommended that these kinds of activities should be duplicated to reduce low achievement of learners in mathematics worldwide. Learners' achievement in mathematics will boost the economy of the world as there will be an increased number of students who have access to prestigious careers.

The limitation of the study is that this research focused only on pre-service teachers' mathematical engagement about the total surface areas of geometrical solids. There should be further research to explore learners' mathematical engagement and reasoning in various sections of mathematics that are recommended to be taught in South African high schools. The study is an eye-opener to South Africa policy makers, mathematics teachers and lecturers in terms of identifying students' weaknesses at pre-service level on how to develop logical methods to make sense in the learning of geometrical solids.

 

Authors' Contributions

S.W. Siyepu collected the data as we used his group of students, and wrote the theoretical framework. S.W. Vimbelo wrote the manuscript, drew figures 2, 3 and 5. Both authors contributed to the data analysis, literature review, and reviewed the final version before submitting.

 

Notes

i. Passed away in 2020.

ii. Published under a Creative Commons Attribution Licence.

iii. DATES: Received: 3 March 2019; Revised: 1 February 2020; Accepted: 11 March 2020; Published: 31 May 2021.

 

References

Ball DL, Thames MH & Phelps G 2008. Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5):389-107. https://doi.org/10.1177/0022487108324554        [ Links ]

Bjuland R 2002. Problem solving in geometry. Reasoning processes of student teachers working in small groups: A dialogical approach. PhD dissertation. Bergen, Norway: University of Bergen.         [ Links ]

Bjuland R 2007. Adult students' reasoning in geometry: Teaching mathematics through collaborative problem solving in teacher education. The Montana Mathematics Enthusiast, 4(1):1-30. Available at https://scholarworks.umt.edu/cgi/viewcontent.cgi?article=1056&context=tme. Accessed 18 March 2021.         [ Links ]

Borgersen HE 1994. Open ended problem solving in geometry. NordiskMatematikk-Didaktikk, 2(2):6-35.         [ Links ]

Brodie K 2010. Teaching mathematical reasoning in secondary school classrooms. New York, NY: Springer. https://doi.org/10.1007/978-0-387-097428        [ Links ]

Christiansen B & Walther G 1986. Task and activity. In B Christiansen, AG Howson, & M Otte (eds). Perspectives on mathematics education (Vol. 2). Dordrecht, The Netherlands: Springer. https://doi.org/10.1007/978-94-009-4504-3_7        [ Links ]

Chua VCG 2018. Mathematical knowledge for teaching: A literature review on ideology, instrumentation, and investigations. Available at https://www.researchgate.net/publication/327043331. Accessed 3 February 2019.         [ Links ]

Depaepe F, Verschaffel L & Kelchtermans G 2013. Pedagogical content knowledge: A systematic review of the way in which the concept has pervaded mathematics educational research. Teaching and Teacher Education, 34:12-25. https://doi.org/10.1016/j.tate.2013.03.001        [ Links ]

Department of Basic Education, Republic of South Africa 2011. Curriculum and Assessment Policy Statement Mathematics FET Phase. Pretoria: Author. Available at https://www.clarkebury.co.za/wp-content/uploads/2018/04/mathematicss-caps-fet-jan-2011.pdf. Accessed 25 March 2021.         [ Links ]

Ellis AB 2011. Generalizing-promoting actions: How classroom collaborations can support students' mathematical generalizations. Journal for Research in Mathematics Education, 42(4):308-345. https://doi.org/10.5951/jresematheduc.42A0308        [ Links ]

Feza N & Webb P 2005. Assessment standards, Van Hiele levels, and grade seven learners' understandings of geometry. Pythagoras, 62:3647.         [ Links ]

Hill HC, Rowan B & Ball DL 2005. Effects of teachers' mathematical knowledge for teaching on student achievement. American Educational Research Journal, 42(2):371-406. https://doi.org/10.3102/00028312042002371        [ Links ]

Hsieh HF & Shannon SE 2005. Three approaches to qualitative content analysis. Qualitative Health Research, 15(9):1277-1288. https://doi.org/10.1177/1049732305276687        [ Links ]

Labaree RV 2016. Organizing your social sciences research paper. Available at http://libguides.usc.edu/content.php?pid=83009&sid=8180722. Accessed 18 March 2021.         [ Links ]

Lannin JK, Ellis AB, Elliott R & Zbiek RM 2011. Developing essential understanding of mathematical reasoning for teaching mathematics in pre-kindergarten-Grade 8. Reston, VA: National Council of Teachers of Mathematics.         [ Links ]

Lesseig K 2016. Conjecturing, generalizing and justifying: Building theory around teacher knowledge of proving. International Journal for Mathematics Teaching and Learning, 17(3):1-31. Available at http://www.cimt.org.uk/ijmtl/index.php/IJMTL/article/view/27. Accessed 9 March 2021.         [ Links ]

Leung FKS 2017. Making sense of mathematics achievement in East Asia: Does culture really matter? In Kaiser G (ed). Proceedings of the 13th International congress on mathematics education. ICME-13 Monographs. Cham, Switzerland: Springer. https://doi.org/10.1007/978-3-319-62597-3_13        [ Links ]

Lithner J 2008. A research framework for creative and imitative reasoning. Educational Studies in Mathematics, 67(3):255-276. https://doi.org/10.1007/s10649-007-9104-2        [ Links ]

Mata-Pereira J & Da Ponte JP 2017. Enhancing students' mathematical reasoning in the classroom: Teachers' actions facilitating generalization and justification. Educational Studies in Mathematics, 96(2):169-186. https://doi.org/10.1007/s10649-017-9773-4        [ Links ]

Pino-Fan LR, Assis A & Castro WF 2015. Towards a methodology for the characterization of teachers' Didactic-Mathematical Knowledge. Eurasia Journal of Mathematics, Science & Technology Education, 11(6):1429-1456. https://doi.org/10.12973/eurasia.2015.1403a        [ Links ]

Radisic J, Videnovic M & Baucal A 2018. Distinguishing successful students in mathematics - A comparison across European countries. Psihologija, 51(1):69-89. https://doi.org/10.2298/PSI170522019R        [ Links ]

Rehmeyer J 2014. Reasoning and sense-making in the math curriculum. Berkeley, CA: Mathematical Sciences Research Institute.         [ Links ]

Shulman L 1987. Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57(1):1-23. https://doi.org/10.17763/haer.57.Lj463w79r56455411        [ Links ]

Shulman LS 1986. Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2):4-14. https://doi.org/10.3102/0013189X015002004        [ Links ]

Siyepu S 2013. The zone of proximal development in the learning of mathematics. South African Journal of Education, 33(2):Art. 714, 13 pages. https://doi.org/10.15700/saje.v33n2a714        [ Links ]

Siyepu SW 2018. Learners' understanding of the total surface area of a cylinder. In R Govender & K Junqueira (eds). Proceedings of the 24th Annual National Congress of the Association for Mathematics Education of South Africa (Vol. 1). Johannesburg, South Africa: Association for Mathematics Education of South Africa (AMESA). Available at http://www.amesa.org.za/AMESA2018/VolumeLpdf. Accessed 24 March 2021.         [ Links ]

Skemp RR 1976. Relational understanding and instrumental understanding. Mathematics Teaching, 77:20-26.         [ Links ]

Stacey K 2006. What is mathematical thinking and why is it important? Melbourne, Australia: University of Melbourne. Available at https://www.researchgate.net/publication/254408829. Accessed 10 February 2019.         [ Links ]

Staples ME, Bartlo J & Thanheiser E 2012. Justification as a teaching and learning practice: Its (potential) multifaceted role in middle grades mathematics classrooms. The Journal of Mathematical Behavior, 31(4):447-462. https://doi.org/10.1016/j.jmathb.2012.07.001        [ Links ]

Sukirwan, Darhim & Herman T 2018. Analysis of students' mathematical reasoning. Journal of Physics: Conference Series, 948:012036. https://doi.org/10.1088/1742-6596/948/1Z012036        [ Links ]

Thompson S 2016. Lifting Australian performance in mathematics. In The Australian Council for Educational Research Conference 2016: Improving STEM learning: What will it take? Melbourne, Australia: Australian Council for Educational Research. Available at https://www.acer.org/files/2016_Research_Conference_Proceedings_150.pdf. Accessed 10 February 2019.         [ Links ]