ARTICLES

 

The concept of prime number and the strategies used in explaining prime numbers

 

 

Nejla Gürefe^I; Gülfem Sarpkaya Aktas^II

^IDepartment of Mathematics Education, Faculty of Education, Usak University, Usak, Turkey, nejlacalik@gmail.com
^IIDepartment of Mathematics Education, Faculty of Education, Cukurova University, Adana, Turkey

 

 

---

ABSTRACT

The teaching of mathematics does not only require the teacher to have knowledge about the subject, but the teacher also needs mathematical knowledge that is useful for the teaching and explaining thereof, as the teacher's knowledge effects the students' knowledge. A teacher should use appropriate mathematical explanation to be understood well by her/his students. In the study reported on here we investigated how prospective mathematics teachers defined the concept of prime number and which strategies they employed to explain the concept. The study was a descriptive survey within qualitative research. Forty-eight participants took part in the study and all completed the abstract algebra courses where they learned about the concept in question. The data collection tool was a form comprising 3 open-ended questions challenging what the concept of prime number was and how this concept could be explained to secondary/high school students. The data were analysed and the results show that the preservice teachers experienced great difficulty in defining the concept of prime number and that they used rules to explain prime numbers.

Keywords: explanatory strategies; prime number; prospective mathematics teachers

---

 

 

Introduction

The National Council of Teachers of Mathematics (NCTM, 2000) states that, for all class levels, it is important to understand numbers, the ways of in which they are represented and the relations between them. Understanding numbers and the multiplicative relation between them requires the comprehension of prime numbers (PNs) (Zazkis & Liljedahl, 2004). PNs is a very important concept encountered by students in all class levels from 6th grade and in numerous learning domains. NCTM (2000:214) asserts that students use PNs to find denominators, factors, prime factors and to solve problems. Even at the university level PNs are related to various domains of mathematics such as the principal theorem of arithmetic, modular arithmetic, group theory, Galois Theory and the theory of numbers, and has particular importance for prospective mathematics teachers (PMTs). However, studies indicate that prospective teachers (PTs) find the use of PNs and prime factorisation in operations difficult (Lenstra, 2000; Zazkis, 1999) and even more PTs struggle with multifarious conceptual mistakes (Özdeş, 2013; Zazkis & Campbell, 1996a). Zazkis and Liljedahl (2004) show that prospective teachers could define what a PN was, however, they struggled to put this knowledge into practice. We also assert that PMTs find this topic difficult since it lacks a clear representation, i.e. PNs could not be represented as a product. The incomplete comprehension of this topic by PMTs, who would explain it to their students in the future, will hinder the correct conveyance of the topic to the students. The teachers' knowledge and the manner in which they explain the topic to their students are significant. Literature reveals that PMTs make conceptual mistakes such as accepting 0 and 1, the multiples of the factors in prime factoring, the negatives of the PNs as PNs, and thinking that 2 and odd numbers are not PNs (Özdeş, 2013); thinking that greater numbers have greater factors and that PNs are small (Zazkis & Campbell, 1996b; Zazkis & Gadowsky, 2001). In this study we aimed to reveal how PMTs defined PNs and how they explained the concept.

Although certain studies focus on PNs (Zazkis, 2005; Zazkis & Campbell, 2006), others address PMTs' understanding of prime factoring (Zazkis & Campbell, 1996a, 1996b) and PNs (Zazkis & Liljedahl, 2004); designate PMTs' conceptual mistakes about PNs and factors (Zazkis & Campbell, 1996b; Zazkis & Gadowsky, 2001); reveal PMTs' understandings about 20 concepts, such as PNs, factors, denominators, etc. via conceptual maps (Bolte, 1999); and investigating the potential definitions of PNs by the students (Cavey, Kinzel, Walen & Rohrig, 2015). In addition, some studies propose various methods on how PNs should be taught. Burkhart (2009) used real building blocks to form visual representations of prime factorisations, and enabled the students to explore the concept of prime factors physically. Kurz, Garcia, Breyfogle and Wallace (2010) exploited tiles to prime factorisation and Griffiths (2010) used prime factor trees to teach prime factorisation, while Baştürk Şahin, Şahin and Tapan Broutin (2017) used didactic theories. We could not find any studies on what PMTs know about PNs and how they would explain this topic to the students. We thus sought to fill this gap by studying PMTs' knowledge of the concept of PNs, and how they would teach this to students (explanatory strategies). The teaching of mathematics does not only require of the teacher to have knowledge about the subject, but also to have useful mathematical knowledge for teaching and explaining the subject. A teacher should be able to select and clarify appropriate mathematical explanations for the teaching of any concept and link these with the approach used to teach the concept (Kazima, Pillay & Adler, 2008).

Theoretical Framework

Explanatory strategies

Mathematical explanations do not always consist of formal proofs in school mathematics. Individuals sometimes use abstract mathematical argument (AMA), analogy, and rules strategies to explain mathematical concepts (Cofer, 2015). AMA is the use of abstract mathematical thought and formal reasoning techniques to explain a definition (Cofer, 2015). In this strategy, the use of mathematical definitions, theorems, axioms and formulas is relevant. In the undergraduate mathematics courses such as abstract algebra, PMTs are taught formal justification and explanatory techniques, which apply to mathematical formulas and definitions. For example, any conceptual and abstract explanation that might be given by a lecturer or a teacher at university or school is AMA (Cofer, 2015). Analogy is a strategy in which concrete contexts or concrete materials are used to explain mathematical concepts, and it is expressed as concrete mathematical representation to build reasoning (Cofer, 2015). The context can be a palpable representation. That is, using concrete materials such as apples, pencils, etc. in explaining a mathematical concept. For example, PMTs in this study used flowers and their petals to express PN. The concept may also be an explanation that depends entirely and fundamentally on a specific mathematical context or representation such as the use of a number table. Rules are strategies that individuals use to form alternative rules and explanations of the correct statements using expressions such as "they are already defined in the book like this." However, these rules refer to what the individual believes, i.e. they are mathematical definitions remembered and acknowledged by the individual (Cofer, 2015). For example, PMTs used especially false explanations or expressions such as "I remembered …" when they were asked how they would explain the concept of PN to secondary school or high school students.

 

Method

Research Model

This study was a qualitative research study, and a descriptive survey model was adopted as the design since we aimed at determining the concept explanations of PMTs about PNs and their explanatory strategies.

Participants

The participants were selected PMTs who had completed the abstract algebra courses and had learned the concepts in question in these courses. The participants comprised of 48 fourth-year PMTs (the PMTs were educated in the same class) in the Department of Mathematics Teaching and graduates of the Department of Mathematics (the PMTs were educated in the same class of the pedagogical formation training) receiving teacher's training. The students in the Department of Mathematics Teaching will become secondary school mathematics teachers and the students in the Department of Mathematics will become high school mathematics teachers.

Data Collection

A survey comprising of three open-ended questions was used. The questions were: 1) "What is a PN?," 2) "Are there any other alternative definitions for PNs? If so, please explain these definitions" and 3) "How would you explain the concept of PN to secondary school or high school students?" The opinions from two faculty members, one of which taught the abstract algebra course, were taken into consideration in creating the survey form. The open-ended questions were printed out and distributed to the participants, and the prospective mathematics teachers were given 50 minutes in which to answer the questions.

Data Analysis

Content analysis was used in the analysis of the data. The degree of correctness of the PMTs' definitions of PNs were categorized into two categories, namely appropriate (essential and adequate) and inappropriate (essential and inadequate, partly essential and inadequate, neither essential nor adequate). The explanatory strategies introduced to the literature by Cofer (2015) were used as a basis on how they would explain PNs.

In order to determine the correct definition, training books, course books and mathematics dictionaries were scanned and the Wolfram MathWorld Dictionary (Weisstein, 2017) and the study by Arıkan and Halıcıoğlu, which were thought to have had the most appropriate definitions, were used as reference. Arıkan and Halıcıoğlu (2012) define PN such as let p ≥ 2 an integer. If the denominators are only ±1 and ±p, then p is a PN. Weisstein (2005) defines PN as a positive number, which does not have positive denominators other than 1 and itself, and is greater than 1. According to these definitions, the key features that provide the definition of PN are determined as not having a positive denominator other than 1 and itself, 2 and the positive integer of a natural number greater than 2, not having any denominator other than ±1 and ±1 itself. The explanations that provided all these features were evaluated in the essential and adequate category; those that provided two of the features in the essential and inadequate category; those that provided only one feature in the partly essential and inadequate category, and those that provided none of the features in the neither essential nor adequate category.

In the data analysis, one of the researchers conducted the analysis after which another researcher re-analysed the data at a different time to ensure the reliability of the encoding. The encoding consistency was found to be 90%. The controversial codes were discussed in detail and consensus was achieved between the researchers.

 

Findings

In this section, the definition and the alternative definition of PNs and the strategies used to explain this concept to the students are addressed.

Findings Concerning the First and the Second Questions

The PMTs were asked 1) "What is a PN?" and 2) "Are there any other alternative definitions for PNs? If so, please explain these definitions." The accuracy of the PMTs' answers to the second question were analysed (Table 1). The total frequencies in Table 1 are greater than the number of the participants. The reason for this is that some participants provided answers that could be placed in more than one category.

 

 

The findings presented in Table 1 show that the accuracy conditions of the PN definitions supplied by the PMTs comprised of appropriate and inappropriate definitions; while appropriate definitions have the essential and adequate criteria, inappropriate definitions were categorised as essential but inadequate, partly essential but inadequate and neither essential nor adequate. However, it was seen that the definitions for PN fall into the categories essential and adequate and essential but inadequate. A great majority of PMTs gave definitions of PN, which were essential but inadequate (45 responses placed the definition within to this category). The definitions presented by the PMTs are presented in Table 2. The alphabet letters (a), (b), etc. used in the following discussion refer to the corresponding entries in Table 2.

In none of the explanations by PMTs, -1 and the negative counterpart of the numbers were taken as the denominators of the number; all explanations focused on positive integers as denominators. In the definition provided in the Wolfram MathWorld dictionary, the positive denominators were taken into consideration. From this definition, it is understood that a PN has only 1 and itself as the positive denominators, but that it may have negative denominators, and the definition directs us to the statement that a PN is a positive integer greater than 2 with ±1 and ±p as the only denominators (Arıkan & Halıcıoğlu, 2012). When the PMTs used these definitions as reference in the assessment of the explanations, the explanation in (a) by the PMTs were a valid one, and this definition was assessed as essential and adequate. It was found that the explanations other than (a) used the division definition for PNs, and they were assessed in the essential but inadequate category. In (b), all numbers that do not have any denominators other than 1 and itself were acknowledged as PNs. This definition allows negative numbers, zero and even all rational and irrational numbers to be PNs. The majority of the students (n = 33) defined PNs as such. In (d) and (e) the set of natural numbers, with only 1 and themselves as the denominators, was defined as the PNs. While 1 was left out of the set of numbers in (e), it was included in (d). These definitions even allow zero to be a PN. The PNs, which were only positive integers, were expanded to the set of all integers (with 1 and themselves as denominators) in (j). According to this definition, negative numbers with 1 and themselves as the only denominators were acknowledged as PNs. The statement "positive integers, which do not have any denominators other than 1 and themselves" was expressed verbally in (i) and with the 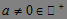condition in (c), and it was stated that positive integers were greater than 1. In (f) it was stated that "natural numbers, which only have two positive integers as denominators" were PNs. It was stated that the denominator set of PNs was a two-element set, but it was not stated what these elements were, and the set of natural numbers was greater than 1. If the negative counterparts of the denominators had been stated in definitions (h) and (g), the definitions would have been complete. It would have been sufficient if it were stated that the denominators were only positive denominators.

In response to the second question, the PMTs should have provided an alternative definition for PNs. The responses were examined and in the answers to this second question, the explanations other than the ones in the first question were included (Table 3). Once again, the alphabet letters (a), (b), etc. used in the following discussion refer to the corresponding entries in Table 3.

When the alternative definitions for the PNs were examined (Table 3), definitions did not resort in the essential and adequate category, 14 in the essential but inadequate category, seven in the partly essential but inadequate category and 12 in neither the essential nor the adequate category. Eleven participants left this question unanswered. The findings indicate that the PMTs were unsuccessful in inadequately defining PN. It was also clear that participants who defined PNs generally with negative expressions such as "… which cannot be divided …" in the first question, made their own definitions with positive expressions such as "… which has denominators …" or "… which has factors … ." It was also interesting to note that the PMTs' first statements referred to the negative, while the alternative statements referred to the positive. While the majority of the participants mentioned 1 and the number itself as the denominators, one participant (in category j) mentioned -1 and the negative counterpart of the number itself as the denominators. In fact, this definition would have been in the essential and adequate category, but the definition of PNs was explained as negative integers and the fact that a PN is a positive integer was overlooked. Thus, this definition was included in the essential but inadequate category. In Table 3, the explanations in (b) and (c) appear to be closed statements. It is stated that the number is the prime number if the sum of the divisors, divisors in (b) are positive and divisors in (c) are positive and negative, is equal to 1 surplus. The statement in (b) leads us to the definition that a PN is a number, which has only 1 and itself as the denominators. In statement (c) the negative numbers were also included in the denominators. Let us accept -1 and -5 as denominators of 5. The sum of these denominators is -6 and one more of this number is -5. However, the number in question was 5. Since -5 is not equal to 5, the definition in (c) is categorised as essential but inadequate. The definition in (h) is the same as the (b) definition in Table 2. While definition (b) in Table 2 is a verbal statement, definition (h) in Table 3 uses more complex notation. In (g) it is stated that a PN is a number, which has only two positive integer denominators, but it was not stated what these numbers were, and whether these were different from each other. In (d), (e), (f) and (i), the factors of the PN were mentioned, and in (e), different from others, more complex symbols were used. The definition set or the number of the denominators were not defined correctly in the explanations provided. The statements in the partly essential but inadequate category were rather inadequate and they were in fact not essential either. For instance, in (l) it is stated that 2n-1 is prime while n is prime. In (l), which tries to determine which numbers were prime in the condition of a given PN, inadequate definitions were seen. The participants' answers in the neither essential nor adequate category were not even remotely close to the definition and were completely inaccurate. For instance, responses (v) and (q) mentioned being relatively prime, instead of defining PNs.

Findings Concerning the Third Questions

Responses to the third question, "How would you explain the concept of PN to secondary school or high school students?," were categorised according to the explanatory strategies proposed by Cofer (2015), the AMA, and Analogy and Rules (Table 4). In this question, one of the participants used AMA, two used analogy and 25 used rules. The answers of the other 14 participants were included in the other category.

The use of rules was the strategy most frequently used by PMTs to explain PNs (Table 4). The answers of the majority of the participants (n = 16) indicated that they would explain PN to the students using a definition, "Numbers, which are divisible by 1 and itself only, are PNs." This definition is a rule. Because, the definition taught in abstract mathematics courses is that PNs were positive integers and greater than 1, and their positive denominators were 1 and themselves and the negative denominators were -1 and the negative counterparts of themselves; and this definition is an AMA. However, most of the participants remembered and acknowledged that the denominators were 1 and the numbers themselves. Therefore, the definition adopted by the participants was considered as a rule. Student's use of rules reflects the incomplete comprehension of the PMTs with regard to the concept in question. In addition, rules contain expressions such as "it was like this in the course books," "the teacher said so," "since it is the definition." One of the participant's explanations revealed this feature of the rule. The participant commented: "I remember that there is a sieve of Eratosthenes. If this method is to be explained, we write the positive integers until the number we wish (except for 1) ... ." From the explanation it was clear that a previously learned method was active in the participant's memory, but the explanation was rather inadequate, as the explanation provided more questions than answers.

Only two participants used analogy. One of the participants indicated that they would use handmade cardboard daises to explain PN (Table 4). This definition limited the set of PNs to ±1 and ± themselves as denominators to a set of numbers, which have only positive denominators, because it is not possible to explain negative denominators with the petals of the flower. In fact, use of analogy occurs independently from common mathematical thought.

Only one of the participants used AMA. The participant stated that he/she would explain PN to the student by giving the definition, "With the definition a positive integer, which does not have a positive denominator other than 1 and itself (except for 1)." This definition corresponds to the definition in the Wolfram MathWorld dictionary, and it is based on abstract and theoretical mathematical techniques. The participant determined the definition domain of PNs as positive integers greater than 1 (with 1 and the number itself as the only denominators), and this definition corresponds to the common and appropriate mathematical definition.

 

Conclusion and Implications

We found that PMTs provided accurate and inaccurate explanations in defining the concept of PN. The majority of definitions were found to be inaccurate. Only three of the PMTs emphasised that the positive denominators of PNs were 1 and the number itself, and used the definition in the Wolfram MathWorld dictionary, and thus gave an accurate explanation. However, apart from these explanations, all other included inadequate or unrelated explanations and were thus categorised as inaccurate explanation, which revealed that the PMTs were rather uncertain about this topic. The following errors occurred in their reasoning: the definition of PNs in wider definition sets such as "number," "integer" or "natural number," without thinking that they were positive integers; acknowledging zero, 1 and negative integers as PNs; failing to acknowledge the existence of negative denominators among the denominators of the number; trying to explain relative PNs or which numbers would be PNs under the condition of one PN. Cavey et al. (2015) indicate that students displayed similar errors in their study in which they investigated the usability and openness preferences in explaining PNs. In addition, they found that most of the definitions by PMTs included negative expressions such as "… which does not have denominators … ." When the PN definition in Wolfram MathWorld dictionary is considered, it is seen that "a positive number, which is greater than 1 and does not have positive denominators other than 1 and itself" is defined as PN and thus the definition includes a negative expression. Zazkis (2005), too, indicates that PMTs use negative expressions in defining the PN. However, Zazkis and Campbell (1996a, 1996b) acknowledge the use of negative expression in the definition as an obstacle before the comprehension of the concept of PN. In addition, Zandieh and Rasmussen (2010) mention the significance of handling familiar concepts in an unfamiliar context. As many individuals were familiar with the concept of PN, they were not familiar with alternative definitions (Cavey et al., 2015). When asked for alternative definitions, the PMTs answered the question with positive expressions such as "… which has denominators …" or "… which has factors …" concordantly. It was also interesting that the PMTs' first statements referred to the negative, while the alternative statements referred to the positive. However, except for one PT, in none of the explanations by PMTs, -1 and the negative counterpart of the numbers were taken as the denominators of the number, and all explanations focused on positive integers as denominators.

The use of rules was the explanatory strategy used most frequently by PMTs (25 individuals) to explain PNs. Some of the answers in this category contained inappropriate or inadequate explanations, which had been formed based on the experiences or emotions of the individuals. For instance, answers such as "I remember that there is a sieve of Eratosthenes. If this method is to be explained, we write the positive integers until the number we wish (except for 1). Then we circle two and cross out the multiples of 3. If we continue like this, the circled numbers (2, 3, 5) give us the PNs" were in the form of PMTs remembering some previous topics. However, PMTs remembered their previous knowledge incompletely; they expressed themselves in an incomplete manner and thus they made incorrect explanations. They said that they would circle 2 but they forget to express that they should cross out multiples of 2 and that they should also cross out the multiples of the numbers greater than 5; they reached an early generalisation and thus their explanations were incomplete. In addition, the majority of the participants who used the rules to explain (n = 16) expressed that they would explain PNs to the students with a definition such as "numbers that can only be divided by 1 and itself were PNs." In fact, PMTs learn the correct definition in the abstract algebra courses. However, the latter learning, much as they were correct, might not have positively affected the previous learning since PMTs began these courses with concept images they had obtained during their previous experiences (Tall & Vinner, 1981). In fact, courses like abstract mathematics should reduce the gap between the algebra concept images of individuals and the real concept images (Cofer, 2015). Thus, the instructor should be so careful in forming definitions of concepts and their real images in the courses at the university so that the PMTs are able to transfer the concept to the students accurately in the future. Among the explanatory strategies, analogy was used by only two participants. The participants wanted to convey the PNs via a concrete representation; however, the explanation of one participant (the daisy example) was not appropriate due the physical properties of the example given. The explanation was inadequate to explain the concept; because the PT, who thought of the daisy as the PN and its petals as the denominators, resorted to memorisation by saying that the petals of the daisy were represented by 1 and the number itself. Here, the representation of the PN denominators by the petals was an inappropriate example. Another PT stated that he or she would show the PN via a 100s of blocks and provided an explanation. Only one PT used the AMA and provided an accurate explanation. Cofer (2015) found that PMTs gave inappropriate examples while explaining what 0/0 was. Explanatory strategies provide information about the inadequate and inappropriate concept images of the PMTs (Cofer, 2015). When considered holistically, the explanatory strategies used by the PMTs provided us with information about their incorrect concept images. In addition, the results obtained reveal that the assessment in the mathematics courses was not done appropriately and that the PMTs fell short of developing effective strategies to teach. Under these circumstances it can be suggested that the syllabi of the courses at university should be planned and conducted to ensure that the PMTs make the connection between the concepts in the abstract mathematics courses and the concepts in school mathematics. In addition, the PMTs need to develop their skills with regard to pedagogy to reflect their conceptual comprehension.

The university curriculum contains courses such as abstract mathematics, which includes prime numbers that enables us to cope with structurally presented concepts (Dubinsky, Schwingendorf & Mathews, 1995). As we know, the concepts in abstract mathematics are associated with the concepts in the secondary school mathematics curriculum (Conference Board of the Mathematical Sciences, 2001).

In this study we focused on how PMTs formed the relationship between the two curricula and the results revealed that PMTs were found to have difficulty in establishing this relationship, as the PMTs were more rule-oriented in explaining the concept. AMA strategy show theoretical mathematics experience. This experience occurs from the explanation of mathematical fundamental concepts. The analogy strategy shows use of concrete materials.

The results of this study reveal that a few PMTs applied these two strategies. This situation proved that PMTs couldn't explain PNs using mathematical definitions and concrete materials. However, it is expected that teachers who will teach in secondary schools will have an in-depth understanding of the concept rather than memorisation. It will also be in the students' best interests to explain the concepts by going the concrete way. Therefore, teaching at university should result in meaningful learning rather than memorisation in courses such as abstract mathematics.

 

Authors' Contributions

Both authors contributed to the completion of the article. N.G. completed the literature review, did the data analysis and wrote the original draft. G.S.A. contributed to the data collection, checked the reliability of coding, completed the final reading and edited the document by shaping the results section.

 

Notes

i. A part of this study was presented as an oral presentation at the International Congress on Science and Education (ICSE), Afyonkarahisar, Turkey, 23-25 March 2018.

ii. Published under a Creative Commons Attribution Licence.

iii. DATES: Received: 11 July 2018; Revised: 26 July 2019; Accepted: 29 September 2019; Published: 31 August 2020.

 

References

Arıkan A & Halıcıoğlu S 2012. Soyut matematik [Abstract mathematics]. Ankara, Turkey: Palme Yayıncılık.         [ Links ]

Baştürk Şahin BN, Şahin G & Tapan Broutin MS 2017. Didaktik durumlar teorisi ışığında asal sayılar kavramının öğretimi: Bir eylem araştırması [Teaching the concept of prime numbers regarding to the theory of didactical situations: An action research]. Necatibey Eğitim Fakültesi Elektronik Fen ve Matematik Eğitimi Dergisi [Necatibey Faculty of Education Electronic Journal of Science and Mathematics Education], 11(2):156-171. https://doi.org/10.17522/balikesirnef.373146        [ Links ]

Bolte L 1999. Enhancing and assessing preservice teachers' integration and expression of mathematical knowledge. Journal of Mathematics Teacher Education, 2:167-186. https://doi.org/10.1023/A:1009900320337        [ Links ]

Burkhart J 2009. Building numbers from primes. Mathematics Teaching in the Middle School, 15(3):156-167.         [ Links ]

Cavey L, Kinzel M, Walen S & Rohrig K 2015. Students talk about prime: What we heard about definitions. School Science and Mathematics, 115(4):168-178. https://doi.org/10.1111/ssm.12117        [ Links ]

Cofer T 2015. Mathematical explanatory strategies employed by prospective secondary teachers. International Journal of Research in Undergraduate Mathematics Education, 1:63-90. https://doi.org/10.1007/s40753-015-0007-9        [ Links ]

Conference Board of the Mathematical Sciences 2001. Issues in mathematics education (Vol. 11). Providence, RI: American Mathematical Society.         [ Links ]

Dubinsky E, Schwingendorf K & Mathews DM 1995. Calculus, concepts and computers (2nd ed). New York, NY: McGraw-Hill.         [ Links ]

Griffiths M 2010. Thematic mathematics: The combinatorics of prime factorization. Teaching Mathematics and its Applications: An International Journal of the IMA, 29(1):25-40. https://doi.org/10.1093/teamat/hrp019        [ Links ]

Kazima M, Pillay V & Adler J 2008. Mathematics for teaching: Observations from two case studies. South African Journal of Education, 28(2):283-299. Available at http://www.sajournalofeducation.co.za/index.php/saje/article/view/168/110. Accessed 25 May 2020.         [ Links ]

Kurz TL, Garcia J, Breyfogle ML & Wallace AH 2010. Prime decomposition using tools. Teaching Children Mathematics, 17(4):256-259.         [ Links ]

Lenstra AK 2000. Integer factoring. Designs, Codes and Cryptography, 19:101-128.         [ Links ]

National Council of Teachers of Mathematics 2000. Principles and standards for school mathematics. Reston, VA: Author. Available at https://epdf.pub/queue/principles-and-standards-for-school-mathematics.html. Accessed 1 June 2020.         [ Links ]

Özdeş H 2013. 9. sınıf öğrencilerinin doğal sayilar konusundaki kavram yanilgilari [Ninth grade students' misconceptions about natural numbers]. Master's thesis. Aydın, Turkey: Adnan Menderes University. Available at http://adudspace.adu.edu.tr:8080/xmlui/bitstream/handle/11607/1380/459478.pdf?sequence=1&isAllowed=y. Accessed 19 May 2020.         [ Links ]

Tall D & Vinner S 1981. Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, 12:151-169. https://doi.org/10.1007/BF00305619        [ Links ]

Weisstein EW 2005. Prime numbers. Available at http://www.ericweisstein.com/encyclopedias/books/PrimeNumbers.html. Accessed 12 May 2020.         [ Links ]

Weisstein EW 2017. Prime number. Avaible at http://mathworld.wolfram.com/PrimeNumber.html. Accessed 14 January 2017.         [ Links ]

Zandieh M & Rasmussen C 2010. Defining as a mathematical activity: A framework for characterizing progress from informal to more formal ways of reasoning. The Journal of Mathematical Behavior, 29(2):57-75. https://doi.org/10.1016/j.jmathb.2010.01.001        [ Links ]

Zazkis R 1999. Intuitive rules in number theory: Example of 'The more of A, the more of B' rule implementation. Educational Studies in Mathematics, 40:197-209. https://doi.org/10.1023/A:1003711828805        [ Links ]

Zazkis R 2005. Representing numbers: Prime and irrational. International Journal of Mathematical Education in Science and Technology, 36(2-3):207-217. https://doi.org/10.1080/00207390412331316951        [ Links ]

Zazkis R & Campbell S 1996a. Divisibility and multiplicative structure of natural numbers: Preservice teachers' understanding. Journal for Research in Mathematics Education, 27(5):540-563. https://doi.org/10.2307/749847        [ Links ]

Zazkis R & Campbell SR 1996b. Prime decomposition: Understanding uniqueness. Journal for Mathematical Behavior, 15:207-218. Available at http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.588.2379&rep=rep1&type=pdf. Accessed 12 May 2020.         [ Links ]

Zazkis R & Campbell SR (eds.) 2006. Number theory in mathematics education: Perspectives and prospects. Mahwah, NJ: Lawrence Erlbaum Associates.         [ Links ]

Zazkis R & Gadowsky K 2001. Attending to transparent features of opaque representations of natural numbers. In AA Cuoco & FR Curcio (eds). The roles of representation in school mathematics: 2001 yearbook. Reston, VA: National Council of Teachers of Mathematics.         [ Links ]

Zazkis R & Liljedahl P 2004. Understanding primes: The role of representation. Journal for Research in Mathematics Education, 35(3):164-186. https://doi.org/10.2307/30034911        [ Links ]