Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Education
On-line version ISSN 2076-3433
Print version ISSN 0256-0100
S. Afr. j. educ. vol.40 n.1 Pretoria Feb. 2020
http://dx.doi.org/10.15700/saje.v40n1a1727
ARTICLES
Exploring female learners' perceptions of learning geometry in mathematics
Jayaluxmi NaidooI; Winfilda KapofuII
IMathematics and Computer Science Education, School of Education, University of KwaZulu-Natal, Pinetown, South Africa. naidooj2@ukzn.ac.za
IIDurban Girls Secondary School, Durban, South Africa
ABSTRACT
In this article we explore female learners' perceptions of learning Grade 11 geometry. Many learners have difficulty in learning geometry in mathematics, thus, teachers and researchers are constantly searching for reasons why learners have challenges with learning geometry with the aim of developing suitable pedagogic strategies to alleviate these challenges. An improvement in female learner performance advances learners' pass rates in mathematics, which has the potential to improve the economic status of South Africa. Data was generated from 1 secondary school for girls in the KwaZulu-Natal province, South Africa. Qualitative data was generated through the use of learner journal entries and focus group interviews. All generated data was coded and analysed using the NVivo software program. Employing Piaget's constructivist theory as a lens to analyse the data generated, the article highlights that the participants (N = 30) held both positive and negative perceptions of learning Grade 11 geometry. Findings from this study suggest that if teachers wanted to improve female learners' performance in mathematics, then important steps needed to be taken to alleviate learners' negative perceptions of learning Grade 11 geometry. Some suggestions are provided.
Keywords: analytical geometry; Euclidean geometry; female learners; learning; mathematics; perceptions
Introduction
Globally, the lack of female learner participation in mathematics has been of concern to researchers (Mandina, Mashingaidze & Mafuta, 2013; Yazilitas, Saharso, De Vries & Svensson, 2017), since mathematics is an essential requirement to pursue careers that are important for a country's economic growth and development. These career fields include among others, medicine, mathematics, physical sciences, chemical sciences, agricultural sciences, engineering, computer and information sciences. Currently in South Africa there is a shortage of qualified individuals in these fields, and this shortage is as a result of fewer tertiary students graduating within these fields (Alexander, Lotriet & Pieterse, 2014). This dwindling interest in mathematics-related subjects is a concerning matter in developing countries such as South Africa. This declining interest could be due to gender differences, ability levels of learners, curriculum transformations, or the increased intricacy of mathematics content (Frenzel, Goetz, Pekrun & Watt, 2010). Moreover, geometry in mathematics has also been considered challenging for many learners (Hanna & De Villiers, 2012).
Hence, in the study reported on in this article, we aimed at exploring the following research questions:
1) What are female learners' perceptions of learning geometry in Grade 11?
2) How can teachers accommodate these perceptions when designing appropriate learning tasks?
Literature Review
Exploring the teaching of mathematics in South Africa
Secondary school learners in South Africa write an exit examination called the National Senior Certificate (NSC) examination at the end of their Grade 12 year. The NSC exit examination is considered significant since learners who are successful in the examination are allowed admittance to higher education to study for a higher certificate, diploma or bachelor's degree (Grussendorff, Booyse & Burroughs, 2010). The mathematics examination comprises of two papers. Paper 1 focusses on algebra and equations; patterns and sequences; finance, growth and decay; functions and graphs; differential calculus and probability. Paper 2 focusses on statistics; analytical geometry; trigonometry and Euclidean geometry and measurement. Geometry is considered a challenging subject at secondary school level (Luneta, 2014), and in recent years learners have found Euclidean geometry problematic (Siyepu & Mtonjeni, 2014). Similarly, research (Van Putten, Howie & Stols, 2010) maintains that learners in South Africa who want to become mathematics teachers do not have a comprehensive understanding of geometric concepts.
It must be noted that only a small percentage of the learners who choose to study mathematics in the FETi phase achieve university entrance requirements in mathematics at the end of their Grade 12 year (Alexander et al, 2014). Furthermore, Barry (2000) maintains that learners are intimidated by mathematics due to the statistics published regarding the poor performance of learners in the national examinations. Considering the current economic realities of South Africa, it is crucial for mathematics teachers and researchers to take steps to ensure that more students choose to study mathematics and pass mathematics in the FET phase.
The importance of learning geometry in mathematics
Geometry involves learning about the geometric properties of a figure that do not change when the figure is revolved or transformed (Tabak, 2004). These properties include points, lines, planes, angles, different shapes, and dimensions. Geometry is an important discipline of mathematics and has been acknowledged as a domain of mathematics which has the capacity to enliven mathematics (Chambers, 2008). Geometry appeals to our different (visual, instinctive, and aesthetic) senses and captures the attention of learners when we use shapes and constructions that learners may relate to within their real-world contexts (Siyepu & Mtonjeni, 2014).
Learner's thinking abilities are enhanced when working with geometric constructions (Hanna, 1998) and this notion is supported within the current South African mathematics curriculum. The South African Curriculum Assessment and Policy Statements (CAPS) captures the notion that it is imperative for learners of mathematics to be able to question, examine, conjecture, and experiment (Department of Basic Education, 2014). The skills necessary to examine, question, conjecture, and experiment may be acquired through learning geometry. These attributes promote logical thinking in learners and engage them in analytical and rigorous thinking.
The importance of learner perceptions of learning geometry in Grade 11
Perceptions may be defined as the comprehension of our environment created from information acquired by way of our senses (Johnson, 1994). This comprehension provides individuals with the opportunity to create meaning of their environment (Cunningham, 1989). Perceptions in this article refers to a learner's opinion of learning Grade 11 geometry within their classroom contexts. The influence of aspects such as challenges in completing activities in geometry, teaching and learning resources, interest in geometry, and views about learning geometry were acknowledged as notions of perceptions that influenced learners' performance in geometry in mathematics.
The understanding of perceptions in this article revolves around the views of Sharma (2015). Sharma (2015) proposes the opinion that perceptions are founded by the manner in which individuals shape and understand the stimuli they acquire to assign significance to their milieu. Learners are unique, thus they hold different insights of the same object and what they observe may not be an exact replica of reality. Perceptions are important because they shape an individual's behaviour and every individual is distinctive because of their perceptions (Abou Elnaga, 2012). Moreover, if a learner has not grasped the fundamental ideas in mathematics, the learner may find it difficult to interact within a lesson (Department of Basic Education, 2014).
Perceptions also have an effect on one's accomplishments in mathematics (Pehkonen & Torner, 1998). Hence, if minimal connections are developed within a learner's understanding of mathematical concepts, this may have an undesirable influence on the learner's achievement in mathematics. It is therefore essential that learners' perceptions of mathematics, more specifically perceptions of Euclidean and analytical geometry, be explored in order for teachers to consider these perceptions to enrich their teaching of Euclidean and analytical geometry.
Theoretical Framework
In this study we sought to explore female learners' perceptions of learning Grade 11 geometry. This exploration was premised on constructivist ideas. According to Von Glasersfeld (1990), constructivism encompasses psychological theories that emphasise how knowledge is constructed rather than how knowledge is transmitted. Using this perspective, all learning is viewed as involving mental constructions as learners create and adjust their internal mental schema to accommodate their growing and evolving knowledge. Thus, within a constructivist educational milieu teaching is learner-centred, whereby teachers differentiate activities based on learners' thinking (Bosman & Schulze, 2018). Learning is motivated by experiences and incited by an external environment or a teacher (Piaget, 1964).
Moreover, Piaget, in his theory of constructivism, argues that learners create knowledge and shape meaning based on their experiences (Bada, 2015). Thus, within the ambits of Piaget's theory of constructivism, knowledge is viewed as distinctive to the learner regardless of the process through which it is learnt (Muthivhi, 2009). This implies that although learners are taught within the same classroom milieu, all learners do not develop the same understanding of the concepts being taught. These notions assisted in developing the research instruments which were essential in generating data for this study.
Individual learner perceptions, through the use of personal journals, were solicited from all participants. Additionally, focus group interviews were used to provide the opportunity for each participant to share their perceptions and experiences. The participants interacted freely, as peers, in a group, rather than in individual one-on-one interviews. Such engagement provided a form of legitimisation and validation of the views expressed. This is in line with Piaget's constructivist frame of thought since every learner's input is valued. Learning is regarded as a shared practice, hence learners learn collaboratively through debates and the discussion of concepts - as was evident during the focus group interviews. Thus, through the use of a constructivist lens, focus group interviews were used in an attempt to explore learners' experiences and perceptions of learning geometry in Grade 11 within their educational milieu.
Methodology
We sought to explore female learners' perceptions of learning geometry in Grade 11. Although the focus of the study was on female learners' perceptions of learning geometry in Grade 11, the learners were also asked questions regarding learning mathematics in general. The idea was to obtain an overall impression of learners' perceptions of mathematics as a subject. Data was generated through the use of focus group interviews (FGIs) and personal journal entries (JEs), which were completed by each participant for the duration of the study.
Participants
One Grade 11 mathematics class at Ulwazi Secondary School (USS)ii was selected for this study. This is a school for girls, which is situated in KwaZulu-Natal, South Africa. In this school there were two Grade 11 mathematics classes; learners from one class participated in the pilot study, and learners from the second class participated in the main study. Two focus groups with eight participants each were used to generate data through focus group interviews (FGI 1 and FGI 2) (see Table 1). The learners who participated in the focus group interviews in the main study were selected by their peers to represent the class. Our aim was to investigate the learners' perceptions and perspectives on learning mathematics in general and geometry in particular.
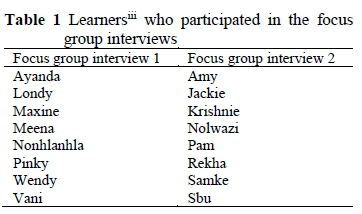
The participants indicated that the 16 participants (Table 1), would best represent the Grade 11 mathematics class with respect to providing a greater insight into why learners have specific perceptions of learning mathematics in general and geometry in particular. In addition, all participants completed personal journals during the course of the study.
Instruments and Methods
Participants' views and perceptions of learning geometry were solicited through learner journals and focus group interviews. Before commencing with the pilot study, the focus group interview schedule was peer reviewed by colleagues within similar research fields. The questions in the focus group interview schedule were formulated to explore participants' views and perceptions of learning mathematics in general and learning Grade 11 geometry.
The focus group interview schedule comprised of both open and closed-ended questions. The main questions in the focus group interviews included:
-
What are your perceptions of learning mathematics in Grade 11?
-
What are some of your experiences of learning mathematics in Grade 11?
-
What are your perceptions of learning geometry in Grade 11?
-
What are some of your experiences of learning geometry in Grade 11?
Prompts were used to ensure that the conversation flowed freely. All data generated during the focus group interviews was video or audio recorded and transcribed.
Working within the ambits of constructivism, personal journal entries were useful in capturing individual learner's experiences and perceptions of learning Grade 11 geometry. Since the study spanned two school terms, learners were asked to write their experiences and perceptions of learning mathematics in general and Grade 11 geometry in particular in their personal journals. Learner journals were collected, and entries were transcribed and analysed. Data analysis began during the focus group interview stage and was completed when all personal journal entries were collected.
Transcriptions of all focus group interviews and learner journal entries were typed. These transcriptions were useful since they could be examined throughout the data analysis stage. The NVivo software programiv was used to analyse the transcribed video and audio recordings of the focus group sessions.
Ethical Considerations
Permission to conduct this study was granted by the university, the Department of Education, the school governing body, the parents/guardians of the participants as well as the participating learners. Letters of informed consent were issued to and signed by all participants. Once transcriptions were completed the learners were asked to read each transcript to ensure that their views were correctly captured and represented.
Findings and Discussion
Within the ambits of constructivism, an important part of the learning process involves learners reflecting on, and discussing, their perceptions and experiences. One needs to acknowledge that learners arrive in the classroom with prior perceptions and knowledge. This prior knowledge is the foundation for new knowledge that learners will construct. Thus, using the principles of constructivism as a ba-
sis, during the focus group interviews, learners were prompted and encouraged by the researcher to reflect on their perceptions and experiences of learning mathematics in general and geometry in particular.
In exploring learners' perceptions of learning geometry in mathematics, consideration had to be given to learners' perceptions of mathematics in general before moving specifically to learners' perceptions of learning geometry. While an attempt was made to include data collected from all data sources, selected extracts from learner JEs and FGI transcripts that best highlight the emerging themes are included in this article. Content analysis was used to manually code, classify, and organise focus group interview data. Coding was an important method used to shape data so that the underlying significance depicted by the data may become clearer (Theron, 2015).
Thus, through the use of coding, the following themes emerged: mathematics is difficult, confusing and stressful; mathematics is time-consuming; Euclidean geometry is difficult and confusing; and geometry is all about proofs. These themes are discussed in more detail in the section that follows.
Mathematics is Difficult, Confusing and Stressful
This notion was a result of learner perception that mathematics is confusing and stressful. When the participants were asked about their perceptions of learning mathematics in Grade 11, they responded by claiming that mathematics was:
… very hard and confusing … (Amy, FGI 2).
… very difficult, especially geometry … (Maxine, FGI 1).
... demanding … a lot of effort is needed … (Krishnie, FGI 2).
… a little bit confusing and stressful because one minute you are in class and you understand everything … the next minute you go home and you attempt the homework and, eish, you can't remember anything. You don't know whether to start from A or whether to start from Z … . (Nolwazi, FGI 2)
The participants believed that they were able to work independently on the mathematics problems during lesson time, however when they went home and were required to complete mathematics problems on their own, they could not "remember anything." They found the mathematics "hard and confusing" and as a result, could not solve the mathematics problems independently. Curtis (2016) supports the participants' opinions and concedes the view that mathematics is a confusing subject. Similar views permeated throughout the learners' JEs where some learners acknowledged the necessity to learn mathematics although it was difficult and stressful for them to grasp certain concepts. Selected learners' perceptions of their experiences of learning mathematics are depicted in Figure 1.
The perceptions exhibited in the preceding journal entries resonate with those found in a study by Nardi and Steward (2003) in that mathematics was perceived as being a difficult subject at school level. This perception was ascribed to the difficulty of the subject and stress felt by some learners when confronted with difficult concepts in mathematics (Curtis, 2016). Some of these difficult concepts include constructing mathematical meanings of symbols or proving theorems involving circle geometry (Euclidean geometry) (Charles-Ogan & George, 2015). Additionally, Curtis (2016) highlights learners' thoughts of feeling inferior to their peers as a reason why they stressed when confronted with difficult concepts in mathematics. Beilock and Willingham (2014) maintain that mathematical stress is another reason for learners' feelings of confusion when working with mathematical problems.
Moreover, based on anecdotal evidence, learners are generally not provided with an overall view of the different mathematics sections and how they are related to each other, but rather their interaction with mathematics is syllabus driven and limited to what is of importance for the final examinations. Through this examination-driven teaching of mathematics, learners are subjected to what is tested in the examination, which fragments learners' knowledge and results in a loss of content consistency (Julie, 2013). It is in this way that the teaching and learning of background information and key preliminary notions revolving around specific mathematical concepts are incomplete or marginalised.
Furthermore, Ireland (2016) proposes that learner difficulties in mathematics could be related to prior negative encounters when learning mathematics and the lack of confidence when working with problems in mathematics. The lack of confidence in executing mathematical procedures was also prevalent in the current study as can be seen from the following journal entries (JE).
As is evident from Figure 2 above, as was the case in the focus group interviews, participants indicated that mathematics was a difficult, stressful and confusing subject. Learners did not "understand what the maths symbols are" and "using the formulae to calculate and remember … was … tricky."
Mathematics is Time-Consuming
Participants expressed the belief that mathematics was demanding and time-consuming. This view seemed to have emerged from the fact that learners spent a copious amount of time over the same mathematics question, sometimes without success. When learners were asked about their experiences when learning mathematics, learners indicated that:
… it takes too long to arrive at a solution … many steps and processes … (Londy, FGI 1).
… yes … it does take time … I am always running out of time in the exam too …(Wendy, FGI 1).
… I find mathematics demanding, maths needs your time, like your 99.9% time … you have to think about it, in your mind you have to think only about maths. You cannot think about two things at the same time. It needs your full time … . (Jackie, FGI 2)
… you are trying to do it … it doesn't work out … it takes hours … (Rekha, FGI 2).
… because I can't solve the problem … it takes longer … just too many steps … (Pam, FGI 2).
… to be successful … try and practice as much as possible … one problem … too long to solve … (Samke, FGI 2).
Gafoor and Kurukkan (2015) suggest that the difficulty in comprehending concepts in mathematics is related to the need for more time to grasp concepts. The journal entries that follow in Figure 3 posit that the participants tended to easily forget what they had learnt.
Generally, the participants indicated that mathematics was not only time-consuming, but required one's total dedication and focus although they did "try and practice as much as possible … one problem … too long to solve." This proposition is in line with the comments made by Ashbacher (2015). Additionally, we maintain that to do mathematics a learner ought to consider the problem from different points of view. Ireland (2016) compares mathematics to playing a sport, where constant and consistent practice is required to achieve success. This implies that a learner is required to invest time and effort when engaging with mathematics to be able to master mathematical concepts. This may be problematic since at Grade 11 level in South Africa learners are also expected to study at least six other subjects besides mathematics. To realise academic success, learners ought to have adequate time to focus on their other six subjects apart from focussing on mathematics.
Another perception of the participants was that mathematics revolved around numbers. Learners indicated that "when the word mathematics is mentioned numbers comes to mind." They did not acknowledge that shape and space were also contained in the mathematics curriculum. The participants were of the view that anything that was presented to them as mathematics had to be represented in an algebraic arrangement. Such a view is substantiated by the following excerpts:
… when the word mathematics is mentioned numbers comes to mind … (Pinky, FGI 1).
… it is all about working with numbers … (Vani, FGI 1).
… you cannot do maths if you don't know how to work with numbers … the most important aspect … (Pam, FGI 2).
... if we were good at working with numbers we will do well in maths … I don't know about that anymore … (Amy, FGI 2).
… I have no interest in anything with numbers … (Maxine, FGI 1).
It is evident from the preceding excerpts that the participants could not link anything to mathematics that was not algebraic in nature. This is supported by research findings (Özerem, 2012), which indicate that learners have problems learning mathematical concepts and how they are related. This could be as a result of a teacher-centred, examination-driven or textbook-oriented approach to teaching mathematics, whereby learners are not provided with the opportunity to experiment and discover relationships between mathematical concepts independently. Mathematics is taught in a traditional manner in which learners' imagination and background knowledge are ignored (Moloi, 2013).
Another notable finding was that the participants in general viewed mathematics negatively, however they did favour certain sections in mathematics. When asked about their experiences of learning mathematics, the participants spoke about mathematics topics they enjoyed learning. This is evident in the excerpts that follow:
… when working with the Theorem of Pythagoras we had to learn using the discovery learning method … I learnt new work and also had fun …(Vani, FGI 1).
… this section was interesting, as I usually learn to use the theorems not actually proving or looking at how they were invented … (Nonhlanhla, FGI 1).
I really learnt something very good because I didn't know how the Pythagoras' Theorem came about … (Pam, FGI 2).
As is evident, participants did not dislike all sections of mathematics; participants enjoyed mathematics lessons that were interesting and fun, which was as a result of an innovative method of teaching called discovery learning. Discovery learning is a constructivist-based pedagogic strategy that enhances inquiry-based learning (Baker, 2016). Learners are engaged in interesting lessons that are designed for learners to discover the concepts and principles through their own constructions (Herdiana, Wahyudin & Sispiyati, 2017). This notion is corroborated by the excerpts that follow:
… the lesson was mind awakening …(Samke, FGI 2).
… the lesson was very interesting …(Londy, FGI 1).
… being able to do it by ourselves, on our own, it was like a victory, like you have won a battle … you could do it yourself, you could prove it right without actually getting frustrated, being stressed trying to figure out a way forward … . (Ayanda, FGI 1)
… the lesson was fun and realistic because we were using objects we can see and we were doing our work all by ourselves, interesting because we were proving what we did, on our own … (Rekha, FGI 2).
Based on the interviews it was evident that participants felt that when creative learning was encouraged in the mathematics classroom, the lessons became more interesting. Learners were of the view that "the lesson was fun and realistic" and that the "lesson was very interesting" since they were using objects that they could "see" as well as "we were doing our work all by ourselves." Participants also felt that through the use of concrete manipulatives (objects), and group work, mathematics became more stimulating. Effectively, Yadav (2016) maintains that children learn better when they interact with each other and manipulate concrete objects as a group within their educational milieu.
Euclidean Geometry is Difficult and Confusing
When learners were asked about their perceptions of learning geometry in Grade 11, their responses were generally discouraging. Learners perceived Euclidean geometry to be difficult and confusing. When probed further during the interviews, the following reasons were provided by the participants:
… mathematics is very difficult, especially geometry … (Maxine, FGI 1).
… geometry is very confusing and it is difficult to make sense of … theorems … (Rekha, FGI 2).
… Euclidean geometry is so difficult … (Wendy, FGI 1).
… with the circles, the lines and angles, it has theorems so it's like all varied … that it is why it is so hard … we can't understand … (Ayanda, FGI 1).
… if we are asked to provide reasons then this becomes … a nightmare to us … (Sbu, FGI 2).
In the learners' minds, their understanding of geometry was limited to Euclidean geometry only. When working within Euclidean geometry learners seek to understand the geometry of flat, two-dimensional planes. Learners work with axioms and theorems to solve problems involving plane and solid geometry and they use knowledge from previous grades as a foundation to work from. Ayanda's perception that Euclidean geometry was difficult was due to the assortment of theorems. This appeared to be a sign that the learners had problems with calculating given angles while justifying their answers using appropriate theorems. Work by other researchers such as Hanna and De Villiers (2012) suggest that learners do have difficulties with Euclidean geometry. These sentiments were also evident from the learners' personal journal entries depicted in Figure 4.
Based on Ayanda and Londy's perceptions, it appeared as though learners perceived geometry as the mathematics that dealt with "circles, lines and angles." It was their view that geometry dealt with finding the length of sides and missing angles, which they did not perceive as problematic as long as the question was (i) numeric in nature and (ii) did not require of them to give reasons to justify how they arrived at their solutions. It was only when the activity required of them to provide reasons and justifications for their solutions that geometry became "a nightmare" as suggested by Sbu. Nightmares are considered to be exceedingly terrifying dreams and extremely emotional encounters (Thünker, Norpoth, Von Aspern, Özcan & Pietrowsky, 2014). Sbu's response suggests that geometry created an emotional experience of fear for him. Fear may further obstruct the achievement of knowledge as learners may reject the notion of understanding as a result of this fear (Van Putten et al., 2010).
This defeats the purpose of learning proofs, since proofs assist in understanding the Euclidean geometry being taught as it explains why a statement is true (Magajna, 2013). Moreover, proof is believed to be one of the foundations of mathematics, which assist in solving real-world problems and requires logical and critical thinking skills (Bayuningsih, Usodo & Subanti, 2018). In this regard, it may be deduced from Sbu's experience that the objectives that participants set for themselves during the proving process may have been contradictory to what the teacher expected of them (Zazkis, Weber & Mejía-Ramos, 2015).
Comprehending learners' thoughts during the problem-solving process improves a teacher's perception of their learners (Canturk Gunhan, 2014). Not being aware of what your learners understand and what your learners do not understand creates a challenge for the teacher with respect to which concepts ought to be emphasised when teaching a lesson. Thus, through improved perception, teachers become aware of how their learners think and also gain insight into whether or not learners have grasped the different mathematical concepts crucial for problem-solving activities. This awareness may also equip teachers with ideas on how to develop future lessons to assist with remediating challenges learners may experience.
Geometry is All about Proofs
When participants were asked about their experiences of learning geometry, the view that geometry became difficult when proofs were required to solve problems was maintained by all learners in both focus group interviews. This is captured in the excerpts that follow:
… the moment I have to prove to find the solution it becomes difficult … (Meena, FGI 1).
… solving using the proof or making links to the proof is always a challenge … (Pinky, FGI 1).
… all about proving … and locating angles and linking one angle to the next … we then need to remember the theorem and what it says to try and solve the problem … sometimes we have to try and link more than one theorem … . (Sbu, FGI 2)
… proving this is this and this is equal to this and this is what this is … it is so hard and confusing … I can't keep up and I can't make the link … I can't see the link … . (Samke, FGI 2)
… yes, just solve for x, proving with reasons, no it's difficult … I can't see what is happening in the diagram … (Krishnie, FGI 2).
Based on comments made during the interviews, Euclidean geometry became challenging in instances where learners had to remember, link different proofs, and think about the problem as well as carry out proofs involving different statements and theorems. Proof in geometry involves critical thinking and integrating this type of thinking within the problem-solving process. Similarly, Jones (2002) attributes difficulties learners experience in geometry to the complexity of learning to prove the given concepts, theorems, and axioms. These challenges may lead learners to make false interpretations or limit the learners' ability to make acute inferences that are needed to write a proof (Zazkis et al., 2015).
Since proving involves representing interpretations, the results from this study show that the absence of an algebraic solution, and providing reasons to justify the steps taken to arrive at some conclusion, became challenging for the learners. These perceptions were also apparent from the personal journal entries as depicted in Figure 5.
The perception that geometry was difficult as maintained by the participants in both focus group interviews and journal entries is supported by research (Makgato & Mji's, 2006).
What emerged from our study was that participants' perceptions of Euclidean geometry were in many ways similar to their perceptions of mathematics, that is, they all had both positive and negative perceptions of mathematics. This position was further exemplified when indicated that they enjoyed the section on analytical geometry, which they did not consider to be geometry.
The main reason for the perception that analytical geometry was not part of geometry was that no reasoning or proofs were required of learners in that section. During the interviews learners maintained that analytical geometry required a simple application of the formulae learnt. Within analytical geometry learners worked with space and shape using algebraic formulas and a coordinate system within a Cartesian plane. It was of interest to note the learners' use of vocabulary when referring to analytical geometry. They used words like "simple and easy" compared to words such as "challenging, stressful, difficult," which were used to refer to Euclidean geometry and mathematics in general.
Moreover, during the interviews learners alluded that analytical geometry was an easy section due to the use of pre-determined formulae. This statement is corroborated by excerpts from the interview transcripts that follow:
… in analytical geometry the formulae do not change ... this makes working on these questions easy … (Wendy, FGI 1).
… its formulae are so easy to remember such that you cannot forget them … so it's simple to solve … (Ayanda, FGI 1).
… it is easy to remember as opposed to other sections of mathematics like Euclidean geometry ... (Sbu, FGI 2).
… I know what's happening in analytical geometry … it is easy to follow and it is easy to solve the questions … (Rekha, FGI 2).
In general, the participants agreed and seemed to appreciate some sections of mathematics, for example analytical geometry, provided that it did not involve critical thinking. Analytical geometry involves the study of geometry using a coordinate system and encompasses algebraic notions and notations (Pierce, 2014). For the learners it was important that they continued using the same formulae which they would have mastered either by rote learning or repeated use. The participants were reluctant to venture into new situations that involved applying acquired knowledge within a critical and novel context.
Conclusion
In this study we sought to explore female learners' perceptions of mathematics at Grade 11 level. After an analysis and interpretation of the results, it would appear that the participants had both negative and positive perceptions of learning mathematics in general and Euclidean geometry in particular. The findings reveal that the participants experienced mathematics as difficult, confusing and stressful, that mathematics was time-consuming, that Euclidean geometry was difficult and confusing, and that geometry was all about proofs. Learners, however, did perceive the learning of the Theorem of Pythagoras and analytical geometry positively and found mathematics interesting and fun when innovative teaching strategies and concrete manipulatives were used during the teaching process.
Teaching strategies, which prioritise teaching to accommodate national norms have become recognised as suitable, however this may not always be the most appropriate or relevant teaching strategy for a specific group of learners or may not work within a particular educational milieu. Therefore, an exploration of learners' perceptions prior to the teaching of concepts or topics may assist teachers in identifying the tacit perceptions that may exist among learners concerning that specific topic in mathematics or any other subject.
The teaching of geometry enhances learners' thinking skills using visual images (Tieng & Kwan Eu, 2014) and promotes critical, logical, analytical, and rigorous thinking (Canturk Gunhan, 2014). These enhanced thinking skills assist learners in improving their performance in mathematics (Chukwuyenum, 2013). With an improvement in performance, learners would then have positive perceptions of learning geometry in mathematics. Thus, once the teaching of a section in mathematics is complete, it may be useful for the teacher to interrogate learners' perceptions of learning the section to develop the necessary tasks to support learners with challenges experienced during learning. Learning tasks may support learning and transform learners' existing perceptions of specific topics or sections in mathematics. This may be done over and above the traditional assessment of learners' understanding and content knowledge development of each mathematics concept or section that needs to be taught.
Acknowledgements
This study was partially funded by the National Research Foundation: NRF Grant Number: TTK170408226284.
Authors' Contributions
Both authors conceptualised the article. Jayaluxmi Naidoo restructured a draft version of the article to improve the focus, added literature, analysed the data and wrote the final version of the article. Winfilda Kapofu conducted the original theoretical and empirical research.
Notes
i . Learners in secondary schools in South Africa are in the Further Education and Training (FET) phase (Grades 10-12).
ii . Pseudonyms were used to protect the identity of the research site.
iii . Pseudonyms were used to protect the identity of the participants.
iv . The NVivo software program supports qualitative research and is designed to assist researchers to organise, analyse, and find interpretations in unstructured or qualitative data.
v . Published under a Creative Commons Attribution Licence.
References
Abou Elnaga A 2012. The impact of perception on work behavior. Kuwait Chapter of Arabian Journal of Business and Management Review, 2(2):56-71. Available at http://www.arabianjbmr.com/pdfs/KD_VOL_2_2/6.pdf. Accessed 30 January 2020. [ Links ]
Alexander PM, Lotriet HH & Pieterse V 2014. Self-perceived intrinsic and extrinsic differences between Information Systems and Computer Science university students. South African Computer Journal, 52:13-28. https://doi.org/10.18489/sacj.v52i0.225 [ Links ]
Ashbacher M 2015. Mathematicians and mathematics. In P Casazza, SG Krantz & RD Ruden (eds). I, Mathematician. Washington, DC: Mathematical Association of America. Available at https://en.b-ok2.org/book/3274699/4a9307. Accessed 30 January 2020. [ Links ]
Bada SO 2015. Constructivism learning theory: A paradigm for teaching and learning. IOSR Journal of Research & Method in Education, 5(6):66-70. https://doi.org/10.9790/7388-05616670 [ Links ]
Baker W 2016. Discovery method and teaching research. In B Czarnocha, W Baker, O Dias & V Prabhu (eds). The creative enterprise of mathematics teaching research: Elements of methodology and practice - from teachers to teachers. Rotterdam, The Netherlands: Sense. [ Links ]
Barry DT 2000. Mathematics in search of history. Mathematics Teacher, 93(8):647-650. Available at http://calcnet.cst.cmich.edu/faculty/stjohn/mth553/history_papers/math_in_search_of_history.pdf. Accessed 15 March 2018. [ Links ]
Bayuningsih AS, Usodo B & Subanti S 2018. Critical thinking level in geometry based on self-regulated learning. Journal of Physics: Conference Series, 983:1-6. https://doi.org/10.1088/1742-6596/983/1/012143 [ Links ]
Beilock SL & Willingham DT 2014. Math anxiety: Can teachers help students reduce it? American Educator, 38(2):28-32, 43. Available at https://files.eric.ed.gov/fulltext/EJ1043398.pdf. Accessed 12 March 2018. [ Links ]
Bosman A & Schulze S 2018. Learning style preferences and Mathematics achievement of secondary school learners. South African Journal of Education, 38(1):Art. # 1440, 8 pages. https://doi.org/10.15700/saje.v38n1a1440 [ Links ]
Canturk Gunhan B 2014. A case study on the investigation of reasoning skills in geometry. South African Journal of Education, 34(2):Art. # 910, 19 pages. https://doi.org/10.15700/201412071156 [ Links ]
Chambers P 2008. Teaching mathematics: Developing as a reflective secondary teacher. London, England: Sage. [ Links ]
Charles-Ogan G & George NR 2015. Investigating difficult concepts in senior secondary school mathematics curriculum as perceived by students. International Journal of Academic Research and Reflection, 3(6):67-74. Available at https://www.idpublications.org/wp-content/uploads/2015/07/Paper-INVESTIGATING-DIFFICULT -CONCEPTS-IN-SENIOR-SECONDARY-SCHOOL-MATHEMATICS-CURRICULUM.pdf. Accessed 25 January 2020. [ Links ]
Chukwuyenum AN 2013. Impact of critical thinking on performance in Mathematics among senior secondary school students in Lagos State. IOSR Journal of Research & Method in Education, 3(5):18-25. Available at https://s3.amazonaws.com/academia.edu.documents/34729010/berpikir_kritis.pdf?response-content-disposition=inline%3B%20filename%3DImpact_of_Critical_thinking_on_Performan.pdf&X-Amz-Algorithm=AWS4-HMAC-SHA256&X-Amz-Credential=AKIAIWOWYYGZ2Y53UL3A%2F20200124%2Fus-east-1%2Fs3%2Faws4_request&X-Amz-Date=20200124T211519Z&X-Amz-Expires=3600&X-Amz-SignedHeaders=host&X-Amz-Signature=6cc06512f0d5bca0b75a732822186cab72bbb3a8403d12bfa3d5b28e7f16f06e. Accessed 24 January 2020. [ Links ]
Cunningham S 1989. Perception, meaning, and mind. Synthese, 80(2):223-241. Available at https://www.jstor.org/stable/pdf/20116678.pdf?casa_token=6NROYTm_wagAAAAA:KeG3abolPQlmzWiqe5JamuPXpZ HPaiiL4epIIRitmKMq6D53CeS7nxjtc5FXS7APAXazj_AoiSQo4y_d6bpYqepjGXNxDJpuMh2MIzAqFZX6vNBkuDu_0Q. Accessed 24 January 2020. [ Links ]
Curtis W 2016. How to improve your mathematics grades: Why is mathematics difficult? [ Links ]
Department of Basic Education 2014. Matric results analysis report (Grade 12). Pretoria, South Africa: Author. [ Links ]
Frenzel AC, Goetz T, Pekrun R & Watt HMG 2010. Development of mathematics interest in adolescence: Influences of gender, family, and school context. Journal of Research on Adolescence, 20(2):507-537. https://doi.org/10.1111/j.1532-7795.2010.00645.x [ Links ]
Gafoor KA & Kurukkan A 2015. Why high school students feel mathematics difficult? An exploration of affective beliefs. Paper presented at the national seminar on Pedagogy of Teacher Education- Trends and Challenges, Kerala, India, 18-19 August. Available at https://files.eric.ed.gov/fulltext/ED560266.pdf. Accessed 1 February 2020. [ Links ]
Grussendorff S, Booyse C & Burroughs E 2010. Evaluating the South African National Senior Certificate in relation to selected international qualifications: A self-referencing exercise to determine the standing of the NSC (Overview Report). Pretoria, South Africa: UMALUSI. Available at https://www.umalusi.org.za/docs/research/2010/iq_overview_report.pdf. Accessed 1 February 2020. [ Links ]
Hanna G 1998. Proof as explanation in geometry. Focus on Learning Problems in Mathematics, 20(2/3):4-13. Available at https://www.researchgate.net/profile/Gila_Hanna/publication/234693181_Proof_as_Explanation _in_Geometry/links/581a225208aeffb294131379/Proof-as-Explanation-in-Geometry.pdf. Accessed 19 January 2020. [ Links ]
Hanna G & De Villiers M (eds.) 2012. Proof and proving in mathematics education: The 19th ICMI study. Dordrecht, The Netherlands: Springer. https://doi.org/10.1007/978-94-007-2129-6 [ Links ]
Herdiana Y, Wahyudin & Sispiyati R 2017. Effectiveness of discovery learning model on mathematical problem solving. In C Kusumawardani, AM Abadi, S Suyanto & I Wilujeng (eds). AIP Conference Proceedings (Vol. 1868). Melville, NY: AIP Publishing. https://doi.org/10.1063/1.4995155 [ Links ]
Ireland L 2016. Maths phobia and how to beat it. Available at https://www.academia.edu/32499486/Maths_phobia_and_how_to_beat_it. Accessed 22 October 2016. [ Links ]
Johnson NA 1994. The pervasive, persuasive power of perceptions. Alberta Journal of Educational Research, 40(4):475-497. [ Links ]
Jones K 2002. Issues in the teaching and learning of geometry. In L Haggarty (ed). Aspects of teaching secondary school mathematics: Perspectives on practice. London, England: Routledge. [ Links ]
Julie C 2013. Can examination-driven teaching contribute towards meaningful teaching? Paper presented ISTE International Conference on Mathematics, Science and Technology Education, Limpopo, South Africa. Available at http://uir.unisa.ac.za/bitstream/handle/10500/22503/Cyril%20Julie.pdf?sequence=1&isAllowed=y. Accessed 4 February 2020. [ Links ]
Luneta K 2014. Foundation phase teachers' (limited) knowledge of geometry. South African Journal of Childhood Education, 4(3):71-86. Available at http://www.scielo.org.za/pdf/sajce/v4n3/06.pdf. Accessed 18 January 2020. [ Links ]
Magajna Z 2013. Overcoming the obstacle of poor knowledge in proving geometry tasks. CEPS Journal, 3(4):99-116. Available at https://www.pedocs.de/volltexte/2014/8503/pdf/cepsj_2013_4_Magajna_Overcoming_the_obstacle.pdf. Accessed 18 January 2020. [ Links ]
Makgato M & Mji A 2006. Factors associated with high school learners' poor performance: A spotlight on mathematics and physical science. South African Journal of Education, 26(2):253-266. Available at http://www.sajournalofeducation.co.za/index.php/saje/article/view/80/55. Accessed 17 January 2020. [ Links ]
Mandina S, Mashingaidze SS & Mafuta J 2013. Increasing female participation in advanced level mathematics: A perspective from students and teachers in Zimbabwe. African Educational Research Journal, 1(3):183-190. Available at https://files.eric.ed.gov/fulltext/EJ1216892.pdf. Accessed 30 December 2017. [ Links ]
Moloi TJ 2013. An analysis of challenges in the teaching of problem solving in Grade 10 mathematics [Special edition]. TD The Journal for Transdisciplinary Research in Southern Africa, 9(3):480-492. https://doi.org/10.4102/td.v9i3.192 [ Links ]
Muthivhi A 2009. A dialogue between Piaget and Vygotsky on the developmental acquisition of the notions of necessity and possibility: A South African case study. Journal of Educational Studies, 8(1):68-90. Available at http://www.iapo.uct.ac.za/sites/default/files/image_tool/images/104/jes09.pdf. Accessed 17 January 2020. [ Links ]
Nardi E & Steward S 2003. Is mathematics T.I.R.E.D? A profile of quite disaffection in secondary mathematics classroom. British Educational Research Journal, 29(3):345-367. https://doi.org/10.1080/0141192031000155999 [ Links ]
Özerem A 2012. Misconceptions in geometry and suggested solutions for seventh grade students. Procedia - Social and Behavioral Sciences, 55:720-729. https://doi.org/10.1016/j.sbspro.2012.09.557 [ Links ]
Pehkonen E & Torner G (eds.) 1998. The state-of-art in mathematics-related belief research: Results of the MAVI activities. Helsinki, Finland: University of Helsinki, Department of Teacher Education. [ Links ]
Piaget J 1964. Part 1. Cognitive development in children: Piaget. Development and learning. Journal of Research in Science Teaching, 2(1):176-186. [ Links ]
Pierce D 2014. Analytic geometry. Istanbul, Turkey: Mathematics Department, Mimar Sinan Fine Arts University. [ Links ]
Sharma A n.d. Perception: Meaning, definition, principles and factors affecting in perception. Available at http://www.psychologydiscussion.net/perception/perception-meaning-definition-principles-and-factors-affecting-in-perception/634. Accessed 15 January 2018. [ Links ]
Siyepu SW & Mtonjeni T 2014. Geometrical concepts in real-life context: A case of South African traffic road signs. In M Lebitso & A Maclean (eds). Proceedings of the 20th Annual National Congress of the Association for Mathematics Education of South Africa (Vol. 1). Johannesburg: Association for Mathematics Education of South Africa (AMESA). Available at http://www.amesa.org.za/AMESA2014/Proceedings/papers/Long%20Papers/18.%20SW%20SIYEPU%20-%20Geometrical%20concepts%20in%20real%20life.pdf. Accessed 4 February 2020. [ Links ]
Tabak J 2004. Geometry: The language of space and form. New York, NY: Facts on File. [ Links ]
Theron PM 2015. Coding and data analysis during qualitative empirical research in Practical Theology. In die Skriflig, 49(3):Art. #1880, 9 pages. https://doi.org/10.4102/ids.v49i3.1880 [ Links ]
Thünker J, Norpoth M, Von Aspern M, Özcan T & Pietrowsky R 2014. Nightmares: Knowledge and attitudes in health care providers and nightmare sufferers. Journal of Public Health and Epidemiology, 6(7):223-228. https://doi.org/10.5897/JPHE2013.0565 [ Links ]
Tieng PG & Kwan Eu L 2014. Improving students' van Hiele level of geometric thinking using Geometer's Sketchpad. The Malaysian Online Journal of Educational Technology, 2(3):20-31. Available at https://files.eric.ed.gov/fulltext/EJ1086363.pdf. Accessed 9 January 2020. [ Links ]
Van Putten S, Howie S & Stols G 2010. Making Euclidean geometry compulsory: Are we prepared? Perspectives in Education, 28(4):22-31. [ Links ]
Von Glasersfeld E 1990. An exposition of constructivism: Why some like it radical. In RB Davis, CA Maher & N Noddings (eds). Monographs of the Journal for Research in Mathematics Education, #4. Reston, VA: National Council of Teachers of Mathematics. Available at http://www.vonglasersfeld.com/127. Accessed 4 February 2020. [ Links ]
Yadav AK 2016. Teach elementary mathematics using manipulative. International Journal of Current Research, 8(5):30299-30301. Available at http://www.journalcra.com/sites/default/files/issue-pdf/14637.pdf. Accessed 28 March 2017. [ Links ]
Yazilitas D, Saharso S, De Vries GC & Svensson JS 2017. The postmodern perfectionist, the pragmatic hedonist and the materialist maximalist: Understanding high school students' profile choices towards or away from mathematics, science and technology (MST) fields in the Netherlands. Gender and Education, 29(7):831-849. https://doi.org/10.1080/09540253.2016.1166185 [ Links ]
Zazkis D, Weber K & Mejía-Ramos JP 2015. Two proving strategies of highly successful mathematics majors. The Journal of Mathematical Behavior, 39:11-27. https://doi.org/10.1016/j.jmathb.2015.04.003 [ Links ]
Received: 30 July 2018
Revised: 10 April 2019
Accepted: 16 July 2019
Published: 29 February 2020















