Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Education
On-line version ISSN 2076-3433
Print version ISSN 0256-0100
S. Afr. j. educ. vol.40 n.1 Pretoria Feb. 2020
http://dx.doi.org/10.15700/saje.v40n1a1792
ARTICLES
Implications of the quantitative literacies test results of the National Benchmark Test Project (NBTP) for teachers
Benita P Nel
Centre for Educational Testing for Access and Placement (CETAP), Centre of Higher Education and Development (CHED), University of Cape Town, Cape Town, South Africa bnel@uwc.ac.za
ABSTRACT
Learners intending to enter some higher education (HE) institutions in South Africa write the National Benchmark Tests (NBTs) that are expected to provide a measure of their readiness for HE. A large gap exists between the quantitative literacy competencies of many of these learners and expectations at HE level. In this article I explore the following research question: Which quantitative literacy competencies required in HE, as identified through the National Benchmark Test Project (NBTP), are not well developed in the test takers, and what does this imply for teachers? Twelve test-item results in which candidates performed the poorest were analysed (N = 2348). The focus areas identified for teachers included quantity, number and operations, data representation, and change. The research indicates that, to enhance learners' competence in these areas, teachers should provide them with more challenging tasks than, for example, reading a single value from a graph, chart or table. Instead, learners should be required to integrate information from more than one graph/chart.
Keywords: errors; mathematics teachers; NBT; quantitative literacy; test takers
Introduction
Learners seeking to enter some of the HE institutions in South Africa are required to write the NBTs, of which the test results are incorporated into the application, selection, or placement process. The NBT results provide a measure of candidates' readiness for HE. These tests have three components: academic literacy (AL), quantitative literacy (QL), and mathematics (MAT); each of which has its own set of specific sub-domains. In this paper I focus on the Quantitative Literacies test. Indeed, many prospective HE candidates' results reveal the existence of a large gap between their quantitative literacy competencies and expectations at HE level (Prince & Frith, 2017). Candidates' test-based competencies can enable HE to establish what it needs to focus on in interventions aimed at supporting students to enable them to cope with the curriculum. Moreover, these test results can also be of significance to schoolteachers. The results can guide teachers in preparing learners for HE and critical citizenship. In this article I investigate the main gaps in tested candidates' competencies, as identified through analysing a sample of the QL test results, and I discuss some of the implications for teachers.
The identification of specific conceptual gaps - through the analysis of the QL NBT - might result in teachers focussing more on the identified areas. In turn, this can increase HE candidates' chances of successfully coping with the QL demands of the different courses (and those of adult life situations).
The research question guiding this article is: Which quantitative literacy competencies required in HE, as identified through the NBTP, are not well developed in the test takers, and what does this imply for teachers?
Quantitative Literacy as NBTP entity and Mathematical Literacy as School Subject
The NBTP defines QL as "the ability to manage situations or solve problems in practice, and involves responding to quantitative (mathematical and statistical) information that may be presented verbally, graphically, in tabular or symbolic form; it requires the activation of a range of enabling knowledge, behaviours and processes and it can be observed when it is expressed in the form of a communication, in written, oral or visual mode" (Frith & Prince, 2006:30). In South African schools learners who opt not to take pure Mathematics, may take Mathematical Literacy (ML) as subject. ML intends to enhance learners' ability to flourish in a "world characterised by numbers, numerically based arguments and data represented and misrepresented in a number of different ways" (Department of Basic Education, Republic of South Africa, 2011:8). The five key elements of this subject include the use of elementary mathematical content, authentic real-life contexts, familiar and unfamiliar problems, decision-making and communication, as well as the use of integrated content and/or skills in solving problems. Quantitative literacy is also needed and developed by other subject fields such as Biology and Geography, where quantitative information is used in context.
The NBTP test items assess quantitative literacy competencies where the mathematical content is embedded in authentic contexts and graphs, charts, diagrams, and tables in which data is displayed. The test under investigation was in English, and calculators were not allowed during the test. The academic and quantitative literacy test components were combined in one test where the QL part comprised two fifths of the combined 3-hour test. However, the candidates received separate results for AL and QL. All 50 QL test items were multiple-choice questions with four options from which learners were required to choose one; distractors as possible options to answers were carefully selected to reveal possible misconceptions. The identification of misconceptions through the selections made by candidates as possible answers, is an important aspect that teachers can incorporate in their teaching.
The NBTP QL items were classified in the following mathematical and statistical ideas: 1) relationships, pattern and permutation, 2) quantity, numbers and operations, 3) data handling, 4) change, 5) shape, dimension and space, and 6) chance and uncertainty. The mathematical and statistical ideas with which test candidates experienced the greatest difficulty were 1) quantity, numbers and operations, 2) data representation and analysis, and 3) change. The classification of items in "change" in the NBTP might however differ from how they are classified in other tests.
"Quantity, numbers and operations" items assess candidates' ability to order quantities, as well as to calculate and estimate the answers to computations using numbers and simple operations. This includes expressing the same decimal number in other ways, interpreting the words and phrases used to describe ratios, converting phrases to numerical representations, and doing calculations and interpretations of tables and charts. "Data representation and analysis" items evaluate candidates' capacity to derive and use information from representations of data contextualised in tables, charts, graphs and diagrams, as well as to interpret the meaning of this information. "Change" items gauge candidates' ability to distinguish between changes expressed in absolute and relative terms, quantify and reason about changes or differences, and calculate the average rates of change.
Literature Review
Many reasons account for the gaps between learners' knowledge and skills and the QL required of them at HE level. These include changed content, shifted emphasis, and different forms of assessment due to changing school curricula in South Africa (Bohlmann, Prince & Deacon, 2017). I also trace learners' mathematical errors to a poor understanding of the basics and foundational concepts taught even before the Further Education and Training (FET) phase. Consequently, I recommend that the understanding of mathematical terminology should be emphasised. In addition, because the NBT items are embedded in a context involving language use, second-language speakers of English may be disadvantaged regarding contextualised tasks where the interpretation of information might be linguistically complex (Helme, 1995).
Assessments can be used as a tool that informs teaching and learning. Through the analysis of tested candidates' alternative (incorrect) NBT answers, common misconceptions and fallacious thinking are revealed (Prince & Frith, 2017) and can thus direct teachers to areas that need more focus in schools. It is useful for all teachers to become aware of the specific conceptual gaps that learners still have after completing their school careers. When this happens, teachers are in a better position to reflect and adjust their lesson plans, their teaching, and the design of assessment tasks.
Quantity, numbers and operations (QNO)
A study by Parker and Leinhardt (1995) revealed that most of the learners struggled with percentage problems. This was especially valid where conversion was required between fractions, percentages, and decimals of common numerical value, as well as problems with percentages greater than 100%. As I will show later, this situation prevails among the candidates constituting the sample for the study reported on here.
Proportional reasoning is fundamental to understanding many everyday-life situations. However, ratios and proportions are topics poorly understood by learners, resulting in many of them not being able to distinguish between quantities expressed in absolute and relative terms, leading to difficulties in reasoning with numbers such as percentages or rates. Learners have become calculator-dependent to the extent that they have a limited understanding of the number system, a prerequisite for many algebraic operations (Bohlmann et al., 2017).
Data representation (DR)
As indicated in the Curriculum and Assessment Policy Statement (CAPS) (Department of Basic Education, Republic of South Africa, 2011:8), data representation is a crucial skill that learners need to develop in a world "characterised by numbers, numerically based arguments and data represented and misrepresented in a number of different ways." Learners need to acquire the ability to read and understand data representation to be competent citizens in today's world. Data is represented in different forms such as line graphs, tables, pie charts, bar graphs (single, stacked, vertical or horizontal), or histograms. The use of graphical representations in newspapers and reports has increased. As such, learners need to not only be able to read graphs, but also to integrate information from different data sources.
Change (C)
One of the areas under the sub-domain, change, is percentage increase/decrease. An understanding of percentage change is a pre-requisite for understanding and interpreting mark-up/down prices, salary changes, or the cost of an item that includes value-added tax (VAT) (Ngu, 2019). Bansilal (2017) refers to the complexities pertaining to applying the percentage change procedure within a particular context. She also alludes to the challenges that learners experience when two consecutive percentage changes come into play. It suffices to note that percentage is linked to many misconceptions and basic incorrectness in the application thereof (Bansilal, 2017). Similarly, Chen and Rao (2007) observe that calculations involving percentages are not second nature to the average person and that students mistakenly do mathematical operations on percentages as if they are whole numbers. For example, if an item is marked down by 30% and again discounted by 30%, it does not lead to a 60% (30 + 30) markdown. Furthermore, Ngu (2019) highlights students' lack of awareness of the multiplicative relationship when determining percentage change.
The afore-mentioned problem is compounded by the fact that learners are mainly exposed to a procedural approach to percentage calculations, instead of a conceptual understanding (Parker & Leinhardt, 1995), which reduces their meaning‑making capacity. Consequently, learners struggle with data interpretation in percentage form.
Problem-solving related to mark-up consists of many steps and requires the understanding of concepts such as 100% of a cost and 115% of a value. General misconceptions exist among learners regarding the meaning of a percentage that exceeds 100. For instance, when a question requires learners to determine the initial value, given that a 15% mark-up results in a value of 60, they tend to determine it by applying the following operation:  . It seems that learners do not always realise that mark-up implies an increase in an unknown original amount that leads to the value of 60 (Ngu, Yeung, Phan, Hong & Usop, 2018).
. It seems that learners do not always realise that mark-up implies an increase in an unknown original amount that leads to the value of 60 (Ngu, Yeung, Phan, Hong & Usop, 2018).
Methodology
In the study in which the results of an NBTP QL test written in 2017 were analysed, a mixed-methods approach was followed. The scores obtained by a large, representative sample (N = 2348) of school-leavers from across South Africa were used. The fact that the test was written in 2017 implies that some of the test takers entered HE in 2018.
For each item, a facility value was calculated. This value is the proportion of candidates who attempted the item and gave the correct answer. Of the 50 items in the test, only those from the bottom 30% in terms of the facility value were selected for analysis. This generated a cut-off facility value (p-value) of 0.37. For an item with a facility value of 0.37, at least 63% of the test candidates did not provide the correct answer. The performance data for the selected items was analysed with reference to the different mathematical and statistical ideas described in the test construct.
Ethical Considerations
Ethical clearance was granted by the Research Ethics Committee of the University of Cape Town's Centre for Higher Education Development. The candidates who sat for NBTs signed consent forms allowing the use of their scores for research purposes. In turn, they were assured of anonymity. In this regard, the results were presented and discussed in terms of the sample, not with reference to individual candidates. In other words, no names were divulged.
Data Analysis and Findings
Twelve of the 50 items in the test were identified as those where at least 63% of the candidates provided the incorrect answer. The most prominent mathematical and statistical difficulties identified in these 12 items were QNO, DR, and C. The number of items in each category, based on the dominant mathematical and statistical idea addressed, is shown in Table 1.
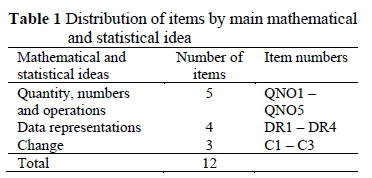
These ideas are used as themes that help to analyse the data and are further explored - per item - in the section below. The analysis bears in mind that almost all items usually draw on a combination of more than one mathematical and statistical idea.
Quantity, Numbers and Operations (QNO)
Item QNO1 focused on four different scenarios where the number of female rabbits and the number of births per 1,000 female rabbits - for four different rabbit colonies - were presented in a table. The colony with the highest number of births per female rabbit had to be identified. The correct answer was provided by 33% of the candidates, while 55% of the candidates selected an option with the same birth rate but a lower number of female rabbits - compared to the correct answer. This suggests that the candidates struggled to understand that, for the same birth rate, more females imply a higher number of births. The question then is what this test result implies for teachers? It might be that candidates did not grasp the context or that they were not clear about the meaning of births per 1,000 females. Nevertheless, assuming that they understood the context, it shows that they were unable to reason with proportions (fractions), i.e. to understand that to get a high number of births you need to find the colony with the highest birth rate and the largest female population. Therefore, teachers might want to emphasise the teaching of fractions and learners' ability to think about numbers in relative terms.
Item QNO2 was about assessing learners' ability to interpret the words used to describe the ratio between two quantities (expressed by the phrase "how many times as many") within a context. The answer had to be provided in fraction form. Only 33% of the candidates selected the correct
answer. A question similar to QNO2 was: "On a piece of land, there are 40 rose trees. Of these, 10 are white. The remainder are red. How many times as many red rose trees are there as white roses?" The mathematical terms used were "how many times as many" and "remainder." This item was badly answered. This may be because of candidates not knowing the meaning of these two mathematical terms within the context of the question. When this kind of mathematical language is used, teachers need to probe learners' understanding of its meaning, before allowing them to delve into the question. "How many times as many" signals a comparison that can be expressed as a fraction, and "remainder" indicates a subtraction: 40−10=30 red trees. red trees.

Thus, there are three times as many red rose trees as white rose trees. However, 19% of the candidates swopped this ratio around. This indicates that teachers should constantly revisit the importance of order when working with ratios.
The other most popular option chosen by 30% of the candidates reflected that candidates determined the fraction of the whole (not the ratio between two quantities) and disregarded the phrase "how many times as many." These candidates wrote the red rose trees in terms of the total number of rose trees, leaving 18% of the candidates writing the ratio as the total number of rose trees to the white rose trees. Clearly, misconceptions relating to ratios were at play here.
Item QNO3 assessed - in a particular context - the candidates' ability to identify the need for and perform more than one operation with fractions. In this item, the candidates had to perform two operations, namely, subtraction and division. An example of this type of question read as follows: "A coffee machine contained 2 litres when it was filled up. During the morning, five people had coffee using cups of the same size. During lunchtime, the assistant found that 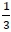 of a litre remained in the machine. How many litres of coffee did each cup contain?" Here some of the candidates only performed subtraction, ignoring the second part of the instruction. Another group took the initial amount and divided it by the five people
of a litre remained in the machine. How many litres of coffee did each cup contain?" Here some of the candidates only performed subtraction, ignoring the second part of the instruction. Another group took the initial amount and divided it by the five people 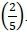 . This seemingly indicated that the candidates could not identify the operations that needed to be performed in this context.
. This seemingly indicated that the candidates could not identify the operations that needed to be performed in this context.
Only 30% of the candidates could answer item QNO3 correctly, while 24% and 21%, respectively, provided different answers that revealed that one of the two expected operations had been omitted. Experience and research (Coetzee & Mammen, 2017) have demonstrated that candidates struggle with problems involving fractions, of which the concept was included on the three items discussed thus far. The examination report on the 2012 exit examination flagged the lack of understanding of the basics of fractions as one of the factors contributing to low performance in Mathematics (Department of Basic Education, Republic of South Africa, 2012). Fractions - in more complex situations where more than one operation was involved - resulted in candidates' poor performance in the specific item. Coetzee and Mammen (2017) make several recommendations to teachers in seeking to address fractions-related conceptual difficulties. Due to accumulated gaps in learners' fractions-related knowledge - from their early development - teachers should offer learners remedial classes on fractions. This could enhance their conceptual knowledge, as their procedural knowledge might not have fostered conceptual knowledge development. Teachers should also ensure that learners understand that multiplication and division lead to different outcomes, depending on whether the involved numbers are bigger or smaller than one. Teachers should initiate a process enabling learners to understand why this is so. Challenges in the understanding of fractions can also be addressed by demonstrating the magnitude representation of fractions on a number line, jointly with the part-of-a-whole approach, to strengthen learners' conceptual understanding. Learners need to be exposed to questions where more than one operation needs to be identified and performed to sharpen their ability to identify all operations needed to solve a problem. This would combat their lack of conceptual understanding of fractions-related operations. Teachers might also consider prohibiting learners from using calculators to perform fractions-based operations to foster the development of conceptual understanding.
Item QNO4 dealt with understanding that ratios could be represented as decimals, fractions, percentages, and in the form a:b. Only 32% of the tested candidates selected the correct answer. The same percentage of candidates believed that a ratio could only be represented by a fraction, or in the form a:b, while 25% only chose the fraction representation. Teachers need to address these misconceptions by ensuring that learners can link percentages, ratios, proportions, and fractions. Teachers should also apply this understanding in various authentic contexts so that learners conceptualise real-situation representations.
Item QNO5 probed candidates' understanding of converting a given number to decimal form - in millions to scientific notation. Conversion to scientific notation is an area that learners are exposed to early in their high school career and are thus expected to be well versed in at the end of their school careers. However, most of the candidates (54%) chose the incorrect option where, for example, in 23,4 million the position of the comma was incorrectly interpreted. Only 35% converted it correctly. The candidates might have been used to this kind of question where the comma was already "in the correct place" (2,34 million). Therefore, teachers should expose their learners to questions requiring conversion to scientific notation where the position of the comma varies, to allow for further development of this concept.
Data Representation (DR)
It is important that learners are able to make sense of various data representations used to convey quantitative information in their disciplines and in everyday life. However, evidence demonstrates that this skill was not well developed in a significant number of tested candidates. To read the appropriate information from more than one given graph/table and then make decisions pertaining to the posed problem seems a daunting task. Item DR1, which tested this, combined data-handling with determining a percentage of a percentage. Only 19% of the candidates answered it correctly. A specific incorrect answer was chosen by 62% of the tested candidates who did not refer to a subset of the whole.
The CAPS document gives the following directive regarding data representation per grade (see Table 2).
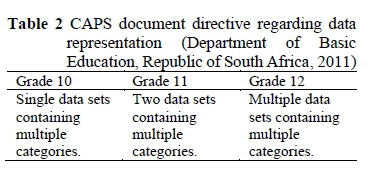
This indicates a progressive complexity of data sets, as learners advance through the different grades, and their increased capacity to use multiple data sets. This item required of candidates to combine data from a bar graph with those from a pie chart, thus only using two data sets, when three data sets were provided (bar graph, pie chart, and table). Most candidates (62%) chose the option where they only used the bar-graph data, meaning that they only used a subset of the whole that the question required them to consider. The survey revealed that only one in three adults could interpret and understand simple data and statistics in graphs and tables (Organisation for Economic Co-operation and Development [OECD], 2013). Hence, I argue that the candidates possibly chose this option because they did not understand the question or were unable to use more than one data set at a time. Helme (1995) stresses the existence of certain mathematical terms that learners should be familiar with and be able to apply in appropriate contexts. Examples include "at most" and "more than."
Item DR2 evaluated the meaning of these two terms in the context of reading data off a chart. Data points had to be read in terms of "more than" a value on the vertical axis and "at most," using a value on the horizontal axis. Thereafter, the number of points had to be converted into percentages. Only 28% of the candidates selected the correct answer. Most candidates interpreted "more than" as "that lower value and more" and "at most" as "less than (the upper limit)." Teachers should consider these errors as indicating that candidates either do not understand the meaning of these mathematical terms (whether they should include or exclude the upper/lower limit), or they cannot apply them to a chart with data points. These results may also indicate a combination of the previously mentioned misunderstandings. Another reason for candidates' inability to select the correct answer can be them experiencing challenges with converting values to percentages. Consequently, teachers need to be aware that the understanding of terminology is linked to mathematical language proficiency (Bohlmann et al., 2017). Thus, mathematical terminology needs to be carefully discussed in the classroom, so that learners first understand its meaning before being required to apply it. Teachers should not assume that learners understand terminology or concepts supposedly covered in earlier years.
In item DR3 the data of four different categories - subdivided into gender (number and percentage) - were presented in table form. The candidates were required to indicate the gender-related ratio of one category. Some of the numbers were in hundred thousands and millions. After deriving the ratio, the candidates had to simplify it to an approximate value, to suit the options. The correct answer was selected by only 34% of the candidates. Either the parts were in the incorrect order (21%) or the total was based on one part (44%). These results confirm the claim that candidates have difficulties interpreting table data, especially percentages (Prince & Frith, 2017:13). Teachers should support learners in reading and interpreting various information categories off tables, particularly when this information is in percentages. The meaning of percentages should be explained to learners - when the totals do/do not add up to 100%. Again, ratio is a concept that teachers need to thoroughly teach and allow learners to practise using different combinations of data categories.
The use of fractions was also challenging to a significant portion of the tested candidates. In item DR4 where data handling was combined with quantity, numbers, and operations, candidates had to read a given fraction off a combination of three different line graphs. Two of these represented different categories, while the third one reflected the two categories' totals. The correct answer was selected by only 32% of the candidates. The incorrect option closest to the correct answer was selected by 17% of the candidates, while the options further away from this option were selected by 27% and 22% of the candidates, respectively. Teachers need to be cognisant of the earlier recommendations pertaining to fractions. Exposure to the interpretation of more than one graph - on the same cartesian plane - and feedback after exercises need to be encouraged.
Change (C)
A question in which candidates were required to find a value after two successive annual percentage increases (C1) was answered poorly. Only 28% of the candidates selected the correct answer. The option most chosen (by 33% of the candidates) was using the same starting value for both years, not realising that the initial value for the next year would be different. The option where only the increase for the first year was calculated, despite the longer period indicated, was chosen by a quarter of the candidates. Another option chosen by 14% of the candidates involved incorrect percentage increase values and the incorrect percentage change period. The option chosen by most candidates revealed that learners ignored the cumulative effect of the percentage increase (Bansilal, 2017). The teaching of the concept of percentage is important for many subject fields, including Mathematics, and in everyday life - especially since learners and adults perceive this as a very difficult topic (Yapıcı & Kayhan Altay, 2017). It is recommended that teachers, when teaching percentage, support learners with concept formation that discourages dependency on operational rules and algorithms (Allinger & Payne, 1986). Teachers are also advised to encourage the development of estimation and mental computation skills when teaching percentage. A tip is to use reference points such as 10% and 50%, initially, to facilitate estimations. Teachers should also improve their learners' number sense, instead of focusing on operational skills, to enhance the development of the concept of percentage (Yapıcı & Kayhan Altay, 2017).
In item C2, the greatest percentage increase was assessed using a double bar chart. Only 13% of the candidates chose the correct answer. An evident misconception was candidates' challenge in distinguishing between reading the highest percentage increase and the highest measured value off a graph/chart. Almost half of the candidates chose the greatest absolute increase and not the percentage increase, while 32% of the candidates opted for the highest values on the chart. This indicates a lack of proportional comparison, an extremely challenging concept (Meyer & Land, 2003). Literature reveals that most adults (including a significant portion of teachers) experience difficulties in mastering of concepts related to fractions, ratio, and proportions (Lamon, 2007; Tourniaire & Pulos, 1985), which makes it understandable that it reflects in learners' performance. Therefore, it is recommended that "teacher content knowledge needs to be augmented by higher level training in pedagogical skills such that subject matter is not only taught by those who know more about it, but also know how to teach it" (Shepherd, 2013:21). Developing an understanding of the proportional comparison concept cannot happen over a short period of, for example, six months; learners should "have many opportunities in different authentic disciplinary contexts … to engage with troublesome quantitative concepts in situations where the need for critical thinking about quantitative information is inescapable" (Frith & Lloyd, 2014:959). This implies that teachers should teach and assess beyond mere calculations, they must include reasoning and appropriate language use to describe scenarios when developing these skills.
Item C3 required of the candidates to identify the correct verbal statements about information reflected in a stacked bar chart. The latter showed changes in the users' proportions of five different categories over five consecutive years. Most candidates (49%) chose the option that confused proportional/relative decrease with absolute decrease. Only 33% of the candidates could identify the correct verbal statement.
Here, the candidates confused proportion and absolute quantities. If a question refers to two values' proportional difference, then one needs to establish whether there is a percentage change in the one, compared to the other. However, if the question is about which of two values changed more (without referring to proportionality), then, absolute quantities are used. This concept also needs serious interventions by high school teachers to ensure that learners understand that proportions and absolute quantities are represented by different number types and operations, and to help learners distinguish between the different phrases used to express them.
Discussion and Conclusion
When gaps are identified in learners' performance, teachers need to address these and constantly ponder how best to support learners in closing these gaps. Teachers should adapt their teaching methods to optimally support learners' formation of the identified mathematical concepts. This can help learners to become self-managing individuals in a world where mathematical content is embedded in real life.
The NBT results clearly identify certain high school curriculum topics where learners demonstrate underdeveloped skills. The NBT questions were predominantly set within an authentic context. This is important in developing QL for citizenship and HE studies. Therefore, teachers should constantly work towards embedding their assessments and examples into authentic contexts.
Tested candidates' inability to reason using proportions (fractions) could be addressed through teachers emphasising fractions and learners' ability to think about numbers in relative terms. Teachers should build ways of addressing misconceptions about ratios and fractions into their lessons. Fractions-related remedial lessons should be offered to enhance candidates' conceptual knowledge. Teachers should also consider demonstrating fractions' magnitude representation on a number line, jointly with part-of-a whole, to ensure a better understanding of fractions. More exposure to fractions-related multi-operation questions is advised to strengthen fractions-based operations.
Candidates should also be cognisant of the links between percentages, ratios, proportions, and fractions, and their representations should happen in real-life situations. This study has shown that percentage change is a difficult concept for learners to understand. Thus, more effort and time should be invested to ensure learners' understanding and development. Concept development should include the use of graphs and data tables to ensure a deeper understanding of percentage change. Teachers might be underestimating the difficulty level of understanding percentage change. They should use examples of learners' errors to unpack the concept and enhance learners' understanding.
The understanding of the meaning of mathematical language and the terminology used must also be ensured before candidates attempt to solve presented problems. The conscious development of mathematical language understanding cannot be overemphasised. Thus, mathematical terminology should be carefully discussed in class.
The analysis of the NBT responses revealed that teachers should vary questions on similar topics regarding context and wording, and even include irrelevant information to be identified by learners. This might enhance conceptual development or even uncover misconceptions. Hence, I recommend that the position of the comma be changed, when assessing the conversion of numbers into decimal form.
The CAPS document specifies that learners should be widely exposed to analysing data related to their personal lives and broader social, national/global issues. Learners should be exposed to real, authentic contexts, not just those in textbooks. Developing learners' quantitative literacy skills enables their use in real life, stripped from a neatly packaged context.
Items where candidates needed to refer to more than one data source were particularly poorly answered. This skill should be practised from Grade 10 where only one data source is used. This should then be increased to two data sources in Grade 11 and to multiple data sets in Grade 12.
The ML curriculum states that, at the end of their school career, learners should be able to work with data comprising complex values in graphs and in tables, regardless of whether they can estimate or read these values accurately. Learners should also be exposed to large values like millions or complex values.
Therefore, teachers need to present learners with more challenging tasks than those simply requiring reading information from graphs/charts/tables. The reading of graphical information should include identifying the "whole sample" and its subsections. Learners need to be supported in analysing activities requiring critical thinking and exposing them to data and contextual real-life settings. One-step questions should lead to multi-step questions.
Thus, numerous ways exist for teachers to adapt their teaching to support learners in addressing the misconceptions identified in the NBT results analysis. Teachers should also use the analysis of learners' classroom assessment results to identify misconceptions/gaps in different curriculum topics. This could significantly improve learners' understanding of ML.
Suggestions for Future Research
More assessment research should be conducted to identify other gaps/misconceptions displayed by learners entering HE. Further research should also seek pedagogies that could successfully help alleviate mathematical misconception and conceptual gaps.
Acknowledgement
The author wishes to thank the University of Cape Town's National Benchmark Tests (NBT) project team and the Centre for Educational Testing for Access and Placement (CETAP) for providing her with the opportunity to conduct this research and thus contribute to the NBT project's four-fold purpose:
• To assess students' entry-level academic and quantitative literacy and mathematics proficiency;
• To assess the relationship between entry-level proficiencies and school-level exit outcomes;
• To provide a service to HE institutions requiring additional information on student admission and placement; and
• To inform the nature of foundation courses and curriculum responsiveness.
The author also wishes to thank M. Paxton, K. le Roux and V. Frith who acted as critical readers and gave valuable input regarding this article.
Notes
i. Published under a Creative Commons Attribution Licence.
References
Allinger GD & Payne JN 1986. Estimation and mental arithmetic with percent. In HL Schoen & MJ Zweng (eds). Estimation and mental computation. Reston, VA: National Council of Teachers of Mathematics. [ Links ]
Bansilal S 2017. The application of the percentage change calculation in the context of inflation in Mathematical Literacy. Pythagoras, 38(1):a314. https://doi.org/10.4102/pythagoras.v38i1.314 [ Links ]
Bohlmann CA, Prince RN & Deacon A 2017. Mathematical errors made by high performing candidates writing the National Benchmark Tests. Pythagoras, 38(1):a292. https://doi.org/10.4102/pythagoras.v38i1.292 [ Links ]
Chen H & Rao AR 2007. When two plus two is not equal to four: Errors in processing multiple percentage changes. Journal of Consumer Research, 34(3):327-340. https://doi.org/10.1086/518531 [ Links ]
Coetzee J & Mammen KJ 2017. Science and engineering students' difficulties with fractions at entry-level to university. International Electronic Journal of Mathematics Education, 12(3):281-310. Available at http://iejme.com/article/science-and-engineering-students-difficulties-with-fractions-at-entry-level-to-university. Accessed 16 August 2018. [ Links ]
Department of Basic Education, Republic of South Africa 2011. National Curriculum Statement (NCS). Curriculum and Assessment Policy Statement: Mathematical Literacy. Further Education and Training Phase Grades 10-12. Available at https://www.education.gov.za/Portals/0/CD/National%20Curriculum%20Statements%20and%20Vocational/ CAPS%20FET%20_%20MATHEMATICAL%20LITERACY%20_%20GR%2010-12%20_%20Web_DDA9.pdf?ver=2015-01-27-154330-293. Accessed 16 August 2018. [ Links ]
Department of Basic Education, Republic of South Africa 2012. National Senior Certificate examination: National diagnostic report on learner performance. Pretoria: Author. Available at https://www.gov.za/sites/default/files/gcis_document/201409/national-senior-certificate-examination-national-diagnostic-report-learner-performance-2012re.pdf. Accessed 15 October 2018. [ Links ]
Frith V & Lloyd P 2014. Students' difficulty with proportional reasoning in a university quantitative literacy course. South African Journal of Higher Education, 28(3):940-960. Available at https://journals.co.za/docserver/fulltext/high/28/3/high_v28_n3_a20.pdf?expires=1579698472&id=id&accname =guest&checksum=35117C8D93204C3581BB911C3AF8DB55. Accessed 2 September 2018. [ Links ]
Frith V & Prince R 2006. Quantitative literacy. In H Griesel (ed). Access and entry level benchmarks: The national benchmark tests project. Pretoria, South Africa: Higher Education South Africa. Available at http://www.cetap.uct.ac.za/sites/default/files/image_tool/images/216/2006_HESA_Access%20and%20 Entry%20Level%20Benchmarks.pdf. Accessed 28 January 2020. [ Links ]
Helme S 1995. 'Maths embedded in context; how do students respond?' Numeracy in Focus, 1(1):24- 32. [ Links ]
Lamon SJ 2007. Rational numbers and proportional reasoning: Towards a theoretical framework for research. In FK Lester Jr (ed). Second handbook of research on mathematics teaching and learning. Charlotte, NC: Information Age Publishing. [ Links ]
Meyer JHF & Land R 2003. Threshold concepts and troublesome knowledge: Linkages to ways of thinking and practising within the disciplines. In C Rust (ed). Improving student learning - ten years on. Oxford, England: OCSLD. Available at https://pdfs.semanticscholar.org/9fb9/db2c04b54574e70553d1a211a5020026e98a.pdf. Accessed 20 August 2018. [ Links ]
Ngu BH 2019. Solution representations of percentage change problems: The pre-service primary teachers' mathematical thinking and reasoning. International Journal of Mathematical Education in Science and Technology, 50(2):260-276. https://doi.org/10.1080/0020739X.2018.1494860 [ Links ]
Ngu BH, Yeung AS, Phan HP, Hong KS & Usop H 2018. Learning the solve challenging percentage-change problems: A cross-cultural study from a cognitive load perspective. The Journal of Experimental Education, 86(3):362-385. https://doi.org/10.1080/00220973.2017.1347774 [ Links ]
OECD 2013. OECD skills outlook 2013: First results from the survey of adult skills. Paris, France: OECD Publishing. https://doi.org/10.1787/9789264204256-en [ Links ]
Parker M & Leinhardt G 1995. Percent: A privileged proportion. Review of Educational Research, 65(4):421-481. https://doi.org/10.3102/00346543065004421 [ Links ]
Prince R & Frith V 2017. The quantitative literacy of South African school-leavers who qualify for higher education. Pythagoras, 38(1):a355. https://doi.org/10.4102/pythagoras.v38i1.355 [ Links ]
Shepherd DL 2013. The impact of teacher subject knowledge on learner performance in South Africa: A within-pupil across-subject approach. Paper presented at the fourth international workshop on Applied Economics of Education, Cantanzaro, Italy, 23-25 June. Available at http://www.iwaee.org/papers%20sito%202013/Shepherd.pdf. Accessed 31 January 2020. [ Links ]
Tourniaire F & Pulos S 1985. Proportional reasoning: A review of the literature. Educational Studies in Mathematics, 16:181-204. https://doi.org/10.1007/PL00020739 [ Links ]
Yapıcı A & Kayhan Altay M 2017. Ortaokul öğrencilerinin yüzdeler konusunda sayı duyularinin incelenmesi [An investigation of middle school students' number sense regarding the percent]. Abant İzzet Baysal Üniversitesi Eğitim Fakültesi Dergisi, 17(4):2221-2243. Available at https://dergipark.org.tr/en/download/article-file/340908. Accessed 14 August 2018. [ Links ]
Received: 19 November 2018
Revised: 30 May 2019
Accepted: 28 July 2019;
Published: 29 February 2020.














