Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Education
On-line version ISSN 2076-3433
Print version ISSN 0256-0100
S. Afr. j. educ. vol.37 n.3 Pretoria Aug. 2017
http://dx.doi.org/10.15700/saje.v37n3a1362
Teacher classroom practices and Mathematics performance in South African schools: A reflection on TIMSS 2011
Fabian Arends; Lolita Winnaar; Mogege Mosimege
Education and Skills Development, Human Sciences Research Council, Pretoria, South Africa. mmosimege@hsrc.ac.za
ABSTRACT
Teachers play an important role in the provision of quality education. The variety of classroom practices they use in interacting with learners play a critical role in the understanding of mathematical concepts and overall performance in Mathematics. Following the work done by Hattie (2009, 2012) in relation to classroom practices this study investigated the association between learner achievement and selected teacher classroom practices. The Mathematics teacher questionnaire, administered as part of the Trends in International Mathematics and Science Study (TIMSS) 2011, comprised questions pertaining to the classroom practices of Teacher Clarity, Classroom Discussion, Feedback, Formative Assessment, Problem Solving and Metacognitive Strategies, and Collaboration. The results showed a positive association between teachers' high endorsement of the selected classroom practices and learner performance. The study also investigated how collaboration between Mathematics teachers affected learner performance. The analysis shows that teachers observing each other's lessons affected the learners' performance positively, although most teachers were not keen on collaboration with their peers. This study showed that various teacher classroom practices affect learner performance in Mathematics significantly and that these practices should be identified and mechanisms put in place to support teachers in terms of these practices.
Keywords: hierarchical linear modeling; Mathematics performance; teacher classroom practice; TIMSS
Introduction
Access to quality education is recognised as a fundamental human right by the Constitution of the Republic of South Africa, and as a fundamental precondition for achieving national development goals. The 2015 Millennium Development Goal Report (Statistics South Africa, 2015) shows that South Africa has made progress with respect to the following: significant improvement towards achieving and securing universal enrolment of all children of primary school-going age; significant increase in the National Senior Certificate (NSC) pass rate to 76 percent in 2014.
Despite the progress made in securing access, the same is not true with regard to the quality of education received by learners. This is evident when looking at learner performance results in national and international studies such as the Annual National Assessments (ANA) and the Trends in International Mathematics and Science Study (TIMSS): South African learners perform far below the international mean. In identifying the determinants of education quality, various articles have focused on the issue of resources at schools as well as school management, both of which have been found to have an effect on learner performance. An area that has gained much attention internationally is the effect that teacher classroom practices have on learner performance - and hence on the quality of education.
Teacher classroom practices are clearly intended to improve learning, but may or may not do so, depending on the level of effectiveness (Leithwood & Jantzi, 2006). Coe, Aloisi, Higgins and Major (2014) define effective teaching as an activity which leads to improved student achievement using outcomes that matter to the future success of the students. They argue that, in order to judge whether or not teaching is effective, it must be evaluated against progress made by students.
Close monitoring, adequate pacing and classroom management, as well as clarity of presentation, well-structured lessons and informative and encouraging feedback - considered the key aspects of "direct instruction" - have generally been shown to have a positive impact on student achievement (OECD, 2009). The argument presented in the OECD report is that the learning opportunities provided by the teacher must be recognised and utilised by the student, if it is to be effective. It can also be deduced from the OECD report that teacher classroom practices are crucial to the performance of learners. This does not only apply to South Africa but to all the countries in an attempt to improve learner performance in Mathematics. Following the poor performance in most of the Trends in International Mathematics and Science Studies, the emerging economies need to look closely at teacher classroom practices and the impact thereof as one possible way of addressing this low performance.
Teacher Classroom Practices
The results of large-scale studies such as the Trends in International Mathematics and Science Study (TIMSS), the Programme for International Student Assessment (PISA) and the Progress in International Reading Literacy Study (PIRLS) indicate that student achievement is affected by multiple factors that originate from various social layers (Yetişir, 2014). A range of information about the context of gaining mathematical knowledge was collected for TIMSS 2011. The five contextual factor areas associated with students' Mathematics achievement are: students, teachers, classroom, school and curriculum.
A number of studies have investigated some variables in the TIMSS 2002 and 2011 datasets to understand which school and household factors have some impact on learner achievement. Some of the variables that have been explored in these studies are: English-language proficiency and science achievement (Dempster & Reddy, 2007); the relationship between attitude to science and science achievement (Juan, Reddy & Hannan, 2010); the relationship between Mathematics per-formance and reaching Grade 12 (Reddy, Van der Berg, Janse van Rensburg & Taylor, 2012); home and school resources as predictors of Mathematics performance (Visser, Juan & Feza, 2015); under-standing the factors within schools that explain the variation in student achievement levels (Winnaar, Frempong & Blignaut, 2015); and the relationship between language and achievement (Prinsloo & Rogers, 2013).
South African studies that focus on teacher knowledge and learner performance (Carnoy & Arends, 2012; Carnoy, Chisholm, Arends, Baloyi, Hoadley, Wa Kivilu, Winnaar, Addy, De Sorto, Marshall, Fleisch, Sapire, Cross, Muller, Johnson, Soudien, Moletsane, Wedekind, Mabogoane, Tay-lor, Christie & Reeves, 2008) have provided evidence of a positive relationship between teacher knowledge and learner performance, and that teachers with higher content knowledge - specific-ally pedagogical content knowledge (PCK) - are more likely to be teaching in wealthier schools that are independent or that fell under the former white and Indian school departments (Shepherd, 2013).
Although a sound knowledge of mathematics is generally regarded as a prerequisite for effective Mathematics teaching, there is scant evidence linking teacher preparation in mathematics directly to the achievement of students (Mullis, Martin, Foy & Arora, 2012). While teachers' educational ex-perience and credentials are often used by policy-makers and researchers as measures of teacher quality, these characteristics explain little of the variation in teacher performance in terms of improving student achievement (Filmer, Molina & Stacy, 2015).
We argue that, in addition to all the variables reported in the studies cited above, there are specific teacher classroom practices that contribute significantly to the achievement of learners. For this purpose, we have utilised the TIMSS 2011 dataset to investigate a number of teacher classroom practices that impact on learner per-formance in Mathematics. In order to improve mathematical performance of learners, it is im-portant to understand how teachers use classroom instruction to engage learners, how they adapt their teaching and interaction strategies, how confident they are in clarifying their expectations to learners, whether or not they apply classroom discussion as a learning tool, and how effective their formative assessment and feedback strategies are in benefitting the learning environment.
Hattie (2009, 2012) conducted over 800 meta-studies covering about 80 million students. His studies are regarded as among the largest collec-tions of evidence-based research about what works best in education. Hattie found that the ten most effective influences on student achievement are: student self-reporting grades; formative evalu-ation; teacher clarity; reciprocal teaching; feed-back; teacher-student relationships; metacognitive strategies; self-verbalisation/questioning; teacher professional development; and problem solving teaching.
Following the work of Hattie and the identification of the most effective influences, this study selected some of the influences and analysed the Mathematics teacher questionnaire as part of the TIMSS 2011 survey items to determine the effect of these influences on learner performance in Mathematics. The variables selected according to the TIMSS Survey are: 1) teacher clarity; 2) classroom discussion; 3) feedback; 4) formative assessment; 5) metacognitive, and problem solving strategies. For purposes of this study, we have combined metacognitive strategies and problem solving strategies into one variable, unlike in Hattie's work. The grouping was influenced by the grouping of items in the TIMSS 2011 Survey.
The variables mentioned above were chosen to provide in-depth understanding of what has been written and researched on the role of teacher classroom practices in improving student per-formance. Important to the concept of teaching clarity is the concept of clear teaching behaviour (Metcalf, 1992), which according to Hattie (2012) describes the skills, knowledge, attitudes and values that the student needs to learn. Classroom discussion can help students acquire better communication skills, as they learn to present ideas clearly and briefly; it also provides opportunities to practice listening to, and following what others are saying (Cashin, 2011; Kosko, 2012); and has been shown to have a positive impact on Mathematics achievement (Grouws, 2004; Koichu, Berman & Moore, 2007; Mercer & Sams, 2006).
Shute (2008) defines feedback as information communicated to the learner that is intended to modify the learner's thinking or behaviour for the purpose of improving learning. Hattie and Tem-perley (2007) consider feedback to be one of the most powerful influences on learning and achieve-ment, but cautions that this impact can either be positive or negative.
Efklides (2009) argues that students' problem-solving difficulties are not necessarily a con-sequence of a lack of mathematical knowledge, but also stem from ineffective activation of student knowledge, since students lack the metacognitive skill needed to control, monitor and reflect on the solution process. As a result, cognitive/meta-cognitive difficulties cause many students to develop negative feelings towards mathematics, thus hampering learning and achievement (Ef-klides, 2011; Efklides & Petkaki, 2005).
Formative assessment is defined as a process that involves teachers making adjustments to teaching and learning in response to assessment evidence; students receiving feedback about their learning and advice on what they can do to improve; and students participating in the process through self-assessment (Black & Wiliam, 2009).
In addition to the teacher classroom practices identified for this study, we also investigated the effect of teacher collaboration on Mathematics achievement by students. Collaboration between teachers seems to be uncommon, yet it promises major benefits for those who engage in it. As Mullis et al. (2012) argue, teacher collaboration with colleagues is important in building a pro-fessional community.
Methods
Sample
TIMSS uses a two-stage stratified systematic sampling methodology, with schools selected in terms of probability-proportional-to-size (PPS) at the first stage and with an intact Grade Nine class randomly selected at the second stage (Joncas & Foy, 2013; Wu, 2010). In South Africa, a total of 300 schools were sampled and provinces, language of learning and teaching and school type (public and independent) served as the strata.
Selection of Variables
TIMSS acknowledges that learning takes place in a context; hence, background questionnaires are administered to school leaders, teachers and learn-ers, in an effort to better understand the educational and social context, and so improve achievement. Data used for the current analysis was drawn from the teacher questionnaire, since the interest was teacher classroom practices.
Analysis of the TIMSS 2011 data in this study was done according to the fee-paying/no-fee cat-egorisation of South African schools. South African schools are delimited according to socio-economic quintiles, which are based on school resources and the socio-economic status of the area surrounding the school.
Poor schools that are ranked in quintiles 1, 2 and 3 are no-fee schools, and are allocated a higher state subsidy than the affluent schools in quintiles 4 and 5.
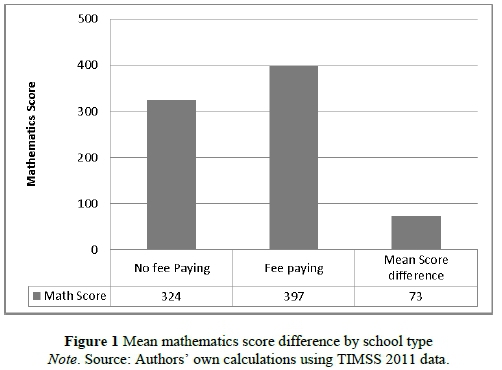
Figure 1 looks at the performance difference between fee-paying and no-fee-paying schools as well as the mean score difference between these groups. Univariate analysis performed showed that this difference is statistically significant (t = 10.57; p-value < 0.05).
Outcome variable
The TIMSS study consists of an extensive number of assessment items and new items are constantly added to the item bank from one assessment cycle to another. It is thus not possible for a particular learner to be tested in all the items. Using a matrix design, TIMSS items are spread over a set of 12 booklets, with overlapping blocks of items and a test booklet is assigned to a learner. Using Item Response Theory; learner responses to the TIMSS items together with background characteristics, five score estimates per learner are calculated and are referred to as plausible values. Details of the assessment framework and methodology used in the TIMSS study can be obtained from the International TIMSS user guide (Joncas & Foy, 2013).
Independent variables
Using the six broader classroom practice measures as outlined by Hattie and discussed in the literature, a number of variables were selected from the teacher questionnaire that met the definitions used for each of the six criteria.
Teacher Clarity included two concepts and eight variables within these concepts. Teachers were asked what limitation they faced with respect to teaching and included students' lack of prerequisite knowledge, disruptive students, and uninterested students. Teachers were also asked if they were confident to answer students' questions about mathematics; show students a variety of problem solving strategies; provide challenging tasks for capable students; adapt my teaching to engage students' interest; and help students appreciate the value of learning mathematics.
The set of variables included within the Classroom Discussions category asked teachers how often they summarised what students ought to have learnt from the lesson, as well as how they ensured the student related to the lesson, used questioning to elicit reasons and explanations, encouraged all students to improve their achieve-ment, praised students for good effort, and whether they brought interesting materials to class.
With respect to the Feedback section, teachers were asked whether they work on problems together in the whole class, apply facts and con-cepts and procedures to solve routine problems, explain their answer, and take a written test. In the Formative Assessment section, teachers were about the emphasis they placed on evaluation of students, classroom tests, national assessments, mathematics tests or examinations given to the class.
Problem Solving and Metacognitive Strat-egies included checking whether the learners listen to the teacher explain how to solve problems, memorise rules, procedures and facts, work on problems with teacher guidance, work on problems by themselves, relate what they are learning in mathematics, decide on their own procedure, work on problems for which there is no immediately obvious. With regard to Collaboration, teachers were asked if they discuss how to teach a particular topic, collaborate in planning, share what I have learnt about my teaching experiences, visit another classroom, and work together to try out new ideas with other teachers.
In recoding the original TIMSS variables, one of two things occurred: where needed, the variables were reverse coded, so that the most desirable (positive) responses had the highest value on the Likert scale type questions; secondly, variables were either dummy coded, or standardised using mean = 0 and standard deviation = 1 (see Appendix A).
Data Analysis
More complex analysis techniques are required to account for the nested nature of the education data. These techniques are typically referred to as multilevel modeling and, in this paper Hierarchical Linear Modeling (HLM) software has been used. HLM allows for effects to be estimated at both the learner level as well as the teacher level. It is then possible to determine the learners' home back-ground factors, which will serve as controls, as well as to isolate which of the six classroom practices influences are associated with learner achievement.
In South Africa, there are large variations in performance between schools (Van der Berg, 2008). An additional advantage of the multilevel approach is that, after identifying the extent of variance in performance between schools, factors at the learner and school level can be used to explain the variance in achievement.
The analysis used in this study employs a two-level HLM model, with learner achievement and background variables at level-1 and teacher background variables at level-2.
Three general steps were followed when running the HLM analysis. First, an unconditional model was run, which excluded all independent and teacher variables. This model provided in-formation pertaining to variations between schools. It was measured by calculating the intra-class correlation coefficient (ICC), which explains the distribution of inequality between schools. The second step was a level-1 model that included all the learner level variables; finally, the teacher variables were included at level-2. At the second level of analysis, a series of models were developed for each of the six teacher classroom practice measures.
Multilevel Analysis Results
The Unconditional Model
The learner background variables considered were: gender of learner (this was a dichotomy with Girl coded as 1 and Boy as 0); how often the learner spoke the language of the test at home; availability of home educational resources; learner engagement with mathematics in class; number of home study support; and time spent doing homework.
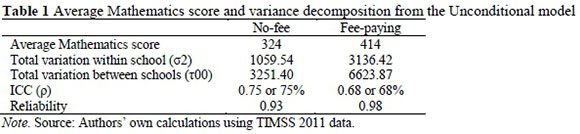
Table 1 provides the results of the uncon-ditional model and will be explained with reference to the ICC, which is defined as the between-group variance as a fraction of the total variance. The variance between schools for the two groups of schools is extremely large, with larger variation being observed in the no-fee paying schools (75%). This is indicative of large inequalities between schools, based on average Mathematics scores. Within the two groups, the situation within schools seems more homogenous, with less variation being observed.
Within School Model Results (Level-1 Model or Learner Background Variables)
Table 2 provides a summary of the within-school HLM model results. Learner engagement in Math-ematics lessons is positively associated with Mathematics performance, with learners who are engaged obtaining on average 19.5 points more than learners at non-fee public schools who are not engaged. In fee-paying schools, the average score difference is 15.6 points.
Another variable that is positively associated with performance is the language in which the test is written. The data shows that, in both school groups, when the language of the test is the same as the language spoken at home, improvement in average Mathematics performance is observed. In addition to these factors, two other factors are significantly associated with performance, but only in no-fee schools, i.e. a lack of educational re-sources in the home is negatively associated with performance, and time spent doing homework is positively related to Mathematics performance.
Between School Model Results (Level-2 or Teacher Level Model)
This section will provide the results of the multi-level models for the classroom practice measures by each of the two school types, viz. fee-paying and no-fee-paying schools.
Teacher Clarity
The results from the no-fee schools (Table 3) show a positive and significant association between Mathematics achievement, and teachers who are confident in showing learners the value of mathematics (β = 22.76, p-value < 0.01), and who are able to answer mathematical questions that learners have (β = 10.77, p-value < 0.05).
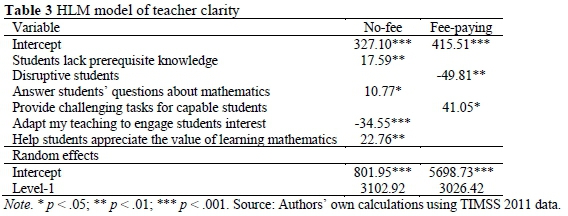
The results are slightly different at fee-paying schools (Table 3). Disruptive learners pose a huge problem at fee-paying schools, where a negative and significant association with learner per-formance (β = -49.81, p-value < 0.001) is observed. Learners who are taught by teachers who are able to provide capable learners with challenging problems score an average of 41 points more than learners who are taught by teachers who are not confident.
Classroom Discussion
With fee-paying schools, the results in Table 4 show that learners who are taught by teachers who spend more time summarising what was covered during a lesson perform better than learners who are taught by teachers who do not hold this as a priority (β = 16.52, p-value < 0.05). Interestingly, within this group, teachers who spent more time bringing interesting materials to class were associated with lower average mathematics scores (β = -16.3, p-value < 0.05).

A classroom discussion technique that is associated with lower scores at no-fee schools is the amount of time teachers spend eliciting reasons and explanations from learners.
Feedback
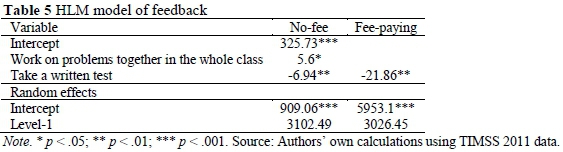
The results depicted in Table 5 show that in no-fee-paying schools, there was a positive significant association between Mathematics achievement and teachers who spent more time working on problems together with the entire class (β = 5.6, p-value < 0.05). A factor negatively associated with Mathe-matics achievement was teachers who administered tests and quizzes in almost all lessons. This was true at fee-paying schools, with the association being even more pronounced than at no-fee schools.
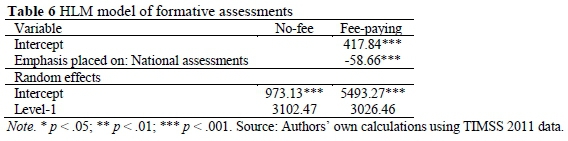
Formative Assessments
At no-fee-paying schools (Table 6), no significance was observed; however, at fee-paying schools, where major emphasis was placed on national or regional achievement tests, there appears to be a significant negative relationship with Mathematics achievement. Learners taught by teachers who place major emphasis on national assessments score an average of 59 points lower than learners who are taught by teachers who place little emphasis on national assessments.
Problem Solving and Metacognitive Strategies
Among the no-fee-paying schools (Table 7), a positive and significant association exists between mathematics performance and learners memorising rules, procedures and facts (β = 5.02, p-value < 0.05), as well as learners working on problems with the teachers' guidance (β = 7.93, p-value < 0.01).

In fee-paying schools, however, a statistically negative association is observed between two of the factors and Mathematics achievement.
Collaboration
Teachers observing one another's classes seem to have the largest association with Mathematics performance (β = 22.53, p-value < 0.05) as is seen in Table 8, with an average score difference of 23 points at fee-paying schools. Learners who attend schools where this method of collaboration is used show improved average Mathematics scores. Discussing how to teach a particular topic was associated with a decrease in average score (β = -9.56, p-value < 0.05). This seems to be the case in no-fee-paying schools.

Discussion
By applying work done by Hattie (2009, 2012) and identifying appropriate variables from the TIMSS 2011 teacher data, the analysis has provided some insights into the association between learner Mathematics performance and teacher classroom practices.
Important to the concept of teacher clarity is the identification of clear teaching behaviour, including variables such as communication skill, accommodating learner differences, clarity of ex-planations, and assessment procedures, all of which impact student achievement (Metcalf, 1992). This is in line with the results, which show that teachers who are able to provide the most clarity are those who are confident in what they know and are able to engage learners, adapt lesson to ensure that all students remain interested, and who are able to answer all content-related questions that learners may have.
Discussion in Mathematics classrooms involves students describing, explaining, defending and justifying their ideas about mathematics, which deepens students' understanding of mathematics (Lee, 2006). It has been shown to have a positive impact on mathematical achievement (Grouws, 2004; Koichu et al., 2007; Mercer & Sams, 2006).
The results of the study conducted by Kosko (2012) on student enrolment in classes with fre-quent mathematics discussions suggest that, even with a large amount of variability, student exposure to contexts with daily mathematics discussions has a significant and positive impact on Mathematics achievement. Described in another way, a student enrolled in a class with daily Mathematics dis-cussions will have larger gains in Mathematics achievement than a similar student enrolled in a class with little or no discussions about mathe-matics. Another study by Kosko and Miyazaki (2012) showed that there is no statistically significant mean difference in mathematical achievement between weekly and less-than-weekly discussion in fifth grade mathematics classrooms; but significant variability in the effect of discussion on achievement was found across classrooms and schools.
The results of the current study, however show a statistically significant association between achievement and classroom discussion but this association is negative, which could be indicative of a lack of content knowledge, and hence, learners are not able to become involved in discussions. This was also found in research done by Mercer and Sams (2006) and Sfard (2007), in which learners in Grade Five seemed not to have the necessary skills to engage in classroom discussions.
Hattie and Temperley (2007) argue feedback to be among the most critical influences on student learning, but this impact can be either positive or negative. Feedback is even more effective when it is combined with remediation, as shown by a study conducted by James and Folorunso (2012), in which they investigated the effect of feedback and remediation on student achievement in junior secondary school Mathematics. The results showed that students who were provided with feedback and remediation performed better that those who were provided with feedback without remediation. In this study, the analysis of the data shows positive significant association between Mathematics achievement and teachers who spent more time working on problems together with the entire class. This could be seen as feedback with remediation, which would then be in line with findings from James and Folorunso (2012). The data also shows a significant but negative association with taking tests, which could possibly be perceived as feedback without remediation.
Metacognition enables learners to plan and allocate learning resources, monitor their own knowledge and skills level, and evaluate their own learning levels at different points during the learning acquisition process (De Boer, Donker-Bergstra, Kostons, Korpershoek & Van der Werf, 2012). The data shows that it is important that learners are able to memorise mathematical facts and procedures, and that mathematical problems are solved with guidance from the teacher. Unfortunately, this contradicts the definition of metacognition stated by De Boer et al. (2012), since it refers to the learner being able to evaluate their own knowledge. In the case of the current study, the variables that relate to the definition is negatively associated with learner achievement. This could be indicative of the lack of content knowledge the learner has.
Teacher professional community refers to the extent to which teachers collaborate and work together to further their own learning as well as that of their students (Bryk, Camburn & Louis, 1999). With regard to the current analysis, a strong positive association exists between learner achieve-ment and teachers who visit one another's classrooms. Teachers, however, do not seem keen to share their knowledge and experiences with one another, and this negatively affects learner performance. There seems to be a degree of pride attached to these forms of collaboration.
Conclusion and Recommendations
The results of the analysis of the six measures of teacher classroom practices investigated in this study show that most of these indicate a positive and significant relationship with the Mathematics performance of learners. The results suggest that the manner in which teachers interact with learners has a significant bearing on their performance. The facilitation of learner interaction by the teacher is equally critical.
The differences between fee-paying schools and no-fee schools on some of the variables implies that this is an important consideration in the South African context. It is not sufficient to determine the impact of teacher classroom practices without considering how the dual system of education in South Africa affects such practices. This is an area that needs further research, in order to properly establish how the South African dual system affects performance in Mathematics classrooms. The results from the TIMSS studies (in this instance TIMSS 2011) suggest that further investigation is required in terms of the performance of learners in national and international assessments.
The impact of teacher collaboration and its effects on learner performance is instructive. Even though the results show that teachers do not fully embrace collaboration with fellow Mathematics teachers, as a form of support, it is not just a classroom practice that needs to be encouraged, but it can actually be regarded as a practice that goes beyond the confines of specific Mathematics classrooms. With the right support and imple-mentation, it could lead to higher learner per-formance in Mathematics.
Note
i. Published under a Creative Commons Attribution Licence.
Acknowledgement
This work is based on data contained in TIMSS 2011, conducted as part of the Education and Skills Development (ESD) Research Programme at the Human Sciences Research Council (HSRC).
References
Black P & Wiliam D 2009. Developing the theory of formative assessment. Educational Assessment, Evaluation and Accountability, 21(1):5-31. https://doi.org/10.1007/s11092-008-9068-5 [ Links ]
Bryk A., Camburn E & Louis KS 1999. Professional community in Chicago elementary schools: Facilitating factors and organizational consequences. Educational Administration Quarterly, 35(5):751-781. https://doi.org/10.1177/0013161X99355004 [ Links ]
Carnoy M & Arends F 2012. Explaining mathematics achievement gains in Botswana and South Africa. Prospects, 42(4):453-468. https://doi.org/10.1007/s11125-012-9246-6 [ Links ]
Carnoy M, Chisholm L, Arends F, Baloyi H, Hoadley U, Wa Kivilu M, Winnaar L, Addy N, De Sorto A, Marshall J, Fleisch B, Sapire I, Cross M, Muller J, Johnson Y, Soudien C, Moletsane R, Wedekind V, Mabogoane T, Taylor N, Christie P & Reeves C 2008. Towards understanding student academic performance in South Africa: A pilot study of grade 6 Mathematics lessons in South Africa. Pretoria, South Africa: Human Sciences Research Council (HSRC). [ Links ]
Cashin WE 2011. Effective classroom discussions. IDEA Paper #49. Manhattan, KS: The IDEA Center. Available at http://www.ideaedu.org/Portals/0/Uploads/Documents/IDEA%20Papers/IDEA%20Papers/IDEA_Paper_49.pdf. Accessed 24 July 2017. [ Links ]
Coe R, Aloisi C, Higgins S & Major LE 2014. What makes great teaching? Review of the underpinning research. London, UK: The Sutton Trust. Available at https://www.suttontrust.com/wp-content/uploads/2014/10/What-Makes-Great-Teaching-REPORT.pdf. Accessed 31 May 2016. [ Links ]
De Boer H, Donker-Bergstra AS, Kostons DDNM, Korpershoek H & Van der Werf MPC 2012. Effective strategies for self-regulated learning: A meta-analysis. Groningen, The Netherlands: Gion, Gronings Instituut voor Onderzoek van Onderwijs, Rijksuniversiteit Groningen. [ Links ]
Dempster ER & Reddy V 2007. Item readability and science achievement in TIMSS 2003 in South Africa. Science Education, 91(6):906-925. https://doi.org/10.1002/sce.20225 [ Links ]
Efklides A 2009. The role of metacognitive experiences in the learning process. Psicothema, 21(1):76-82. Available at http://www.redalyc.org/html/727/72711818013/. Accessed 15 July 2017. [ Links ]
Efklides A 2011. Interactions of metacognition with motivation and affect in self-regulated learning: The MASRL model. Educational Psychologist, 46(1):6-25. https://doi.org/10.1080/00461520.2011.538645 [ Links ]
Efklides A & Petkaki C 2005. Effects of mood on students' metacognitive experiences. Learning and Instruction, 15(5):415-431. https://doi.org/10.1016/j.learninstruc.2005.07.010 [ Links ]
Filmer D, Molina E & Stacy B 2015. What goes on inside the classroom in Africa? Assessing the relationship between what teachers know, what happened in the classroom, and student performance. Available at http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.690.7959&rep=rep1&type=pdf. Accessed 19 January 2016. [ Links ]
Grouws DA 2004. Mathematics. In G Cawelti (ed). Handbook of research on improving student achievement (3rd ed). Arlington, VA: Education Research Service. [ Links ]
Hattie J & Temperley H 2007. The power of feedback. Review of Educational Research, 77(1):81-112. https://doi.org/10.3102/003465430298487 [ Links ]
Hattie JA 2009. Visible learning: A synthesis of over 800 meta-analyses relating to achievement. New York, NY: Routledge. [ Links ]
Hattie JA 2012. Visible learning for teachers: Maximizing impact on learning. London, UK: Routledge. [ Links ]
James AO & Folorunso AM 2012. Effect of feedback and remediation on students' achievement in junior secondary school mathematics. International Education Studies, 5(5):153-162. [ Links ]
Joncas M & Foy P 2013. Sample design in TIMSS and PIRLS. In MO Martin & IVS Mullis (eds). Methods and procedures in TIMSS and PIRLS 2011. Chestnut Hill, MA: TIMSS & PIRLS International Study Center, Lynch School of Education, Boston College. [ Links ]
Juan AL, Reddy V & Hannan S 2010. Attitudes to science: part of the puzzle to improve educational achievement? Africa Growth Agenda, 7(1):13-16. [ Links ]
Koichu B, Berman A & Moore M 2007. The effect of promoting heuristic literacy on the mathematical aptitude of middle-school students. International Journal of Mathematical Education in Science and Technology, 38(1):1-17. https://doi.org/10.1080/00207390600861161 [ Links ]
Kosko KW 2012. Student enrollment in classes with frequent mathematical discussion and its longitudinal effect on mathematics achievement. The Mathematics Enthusiast, 9(1&2):111-148. [ Links ]
Kosko KW & Miyazaki Y 2012. The effect of student discussion frequency on fifth-grade students' mathematics achievement in U.S. schools. The Journal of Experimental Education, 80(2):173-195. https://doi.org/10.1080/00220973.2011.566588 [ Links ]
Lee C 2006. Language for learning mathematics: Assessment for learning in practice. Berkshire, UK: Open University Press. [ Links ]
Leithwood K & Jantzi D 2006. Transformational school leadership for large-scale reform: Effects on students, teachers, and their classroom practices. School Effectiveness and School Improvement, 17(2):201-227. https://doi.org/10.1080/09243450600565829 [ Links ]
Mercer N & Sams C 2006. Teaching children how to use language to solve maths problems. Language and Education, 20(6):507-528. https://doi.org/10.2167/le678.0 [ Links ]
Metcalf KK 1992. The effects of a guided training experience on the instructional clarity of pre-service teachers. Teaching and Teacher Education, 8(3):275-286. https://doi.org/10.1016/0742-051X(92)90026-Y [ Links ]
Mullis IVS, Martin MO, Foy P & Arora A 2012. TIMSS 2011 international results in Mathematics. Chestnut Hill, MA: TIMSS & PIRLS International Study Center, Lynch School of Education, Boston College. Available at https://timssandpirls.bc.edu/timss2011/downloads/T11_IR_Mathematics_FullBook.pdf. Accessed 31 July 2017. [ Links ]
OECD 2009. Creating effective teaching and learning environments: First results from TALIS. Paris, France: OECD Publications. Available at http://www.oecd.org/dataoecd/17/51/43023606.pdf. Accessed 31 May 2016. [ Links ]
Prinsloo C & Rogers S 2013. The missing link: language skills crucial to mathematics and science. HSRC Review, 11(2):26-27. Available at http://www.hsrc.ac.za/en/review/hsrc-review-may-2013/the-missing-link-language-skills-crucial-to-mathematics-and-science. Accessed 7 July 2017. [ Links ]
Reddy V, Van der Berg S, Janse van Rensburg D & Taylor S 2012. Educational outcomes: Pathways and performance in South African high schools. South African Journal of Science, 108(3/4): Art. #620, 8 pages. https://doi.org/10.4102/sajs.v108i3/4.620 [ Links ]
Sfard A 2007. When the rules of discourse change, but nobody tells you: Making sense of mathematics learning from a commognitive standpoint. Journal of the Learning Sciences, 16(4):565-613. https://doi.org/10.1080/10508400701525253 [ Links ]
Shepherd DL 2013. The impact of teacher subject knowledge on learner performance in South Africa: A within-pupil across-subject approach. Paper presented at the International Workshop on Applied Economics of Education, Italy, 23-25 June. Available at http://www.iwaee.org/papers%20sito%202013/Shepherd.pdf. Accessed 19 January 2016. [ Links ]
Shute VJ 2008. Focus on formative feedback. Review of Educational Research, 78(1):153-189. https://doi.org/10.3102/0034654307313795 [ Links ]
Statistics South Africa 2015. Millennium development goals: Country report 2015. Pretoria, South Africa: Statistics South Africa. Available at http://www.statssa.gov.za/MDG/MDG_Country%20Report_Final30Sep2015.pdf. Accessed 4 August 2017. [ Links ]
Van der Berg S 2008. How effective are poor schools? Poverty and educational outcomes in South Africa. Studies in Educational Evaluation, 34(3):145-154. https://doi.org/10.1016/j.stueduc.2008.07.005 [ Links ]
Visser M, Juan A & Feza N 2015. Home and school resources as predictors of mathematics performance in South Africa. South African Journal of Education, 35(1): Art. # 1010, 10 pages. https://doi.org/10.15700/201503062354 [ Links ]
Winnaar LD, Frempong G & Blignaut R 2015. Understanding school effects in South Africa using multilevel analysis: findings from TIMSS 2011. Electronic Journal of Research in Educational Psychology, 13(1):151-170. https://doi.org/10.14204/ejrep.35.13116 [ Links ]
Wu M 2010. Measurement, sampling, and equating errors in large‐scale assessments. Educational Measurement: Issues and Practice, 29(4):15-27. https://doi.org/10.1111/j.1745-3992.2010.00190.x [ Links ]
Yetişir MI 2014. Türkiye'de sekizinci sınıf öğrencilerinin fen başarısına öğrenci ve sınıf faktörlerinin çok düzeyli etkileri [The multilevel effects of student and classroom factors on the science achievement of eighth graders in Turkey]. Eğitim ve Bilim [Education and Science], 39(172):108-120. Available at http://eb.ted.org.tr/index.php/EB/article/view/2875/618. Accessed 8 August 2017.















