Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Education
On-line version ISSN 2076-3433
Print version ISSN 0256-0100
S. Afr. j. educ. vol.37 n.2 Pretoria May. 2017
http://dx.doi.org/10.15700/saje.v37n2a1306
Exploring teachers' practices in teaching Mathematics and Statistics in KwaZulu-Natal schools
Odette UmugiranezaI; Sarah BansilalI; Delia NorthII
ISchool of Education, University of KwaZulu-Natal, South Africa. odetteumugiraneza7@gmail.com
IISchool of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, South Africa
ABSTRACT
Teaching approaches and assessment practices are key factors that contribute to the improvement of learner outcomes. The study on which this article is based, explored the methods used by KwaZulu-Natal (KZN) teachers in teaching and assessing mathematics and statistics. An instrument containing closed and open-ended questions was distributed to seventy-five KZN mathematics teachers from Grade Four upwards. Teachers were encouraged to write freely about the different teaching methods and assessments that they used in the classroom. The findings revealed that teachers were more likely to report a single method in teaching statistics, but more than one method for teaching mathematics topics. In terms of assessments, the teachers generally reported the use of a single method. We also found that teachers mostly focus on teacher-led instructional methods and formal assessments. Furthermore, the findings revealed that teachers' demographic factors such as gender, age, teaching experience, participation in professional development course and further studies are associated with the choice of a variety of teaching and assessment methods. It is recommended that professional development courses ought to focus on helping teachers to increase their repertoire of teaching and assessment strategies.
Keywords: assessment methods; demographic factors; teaching mathematics and statistics; teaching methods
Introduction
In South Africa, the poor outcomes in mathematics has received much attention in recent times. For example, in the Grade 12 Mathematics examination in 2015, the percentage of learners who achieved 50% and above was only 20% (Department of Basic Education (DBE), Republic of South Africa, 2016:151). This means that 80% of the learners who wrote were only able to achieve a mark below 50 percent. Comments about poor results in mathematics naturally lead to questions about whether mathematics teaching is as effective as it could be. In looking at how mathematics teaching could be made more effective, a crucial issue is that of the actual methods of teaching employed by teachers to facilitate mathematics. To develop a sound understanding of mathematics and statistics with their learners, teachers need to continually update their existing teaching methods and assessments. Innovative teaching approaches can enable learners to link mathematics and statistics to real life and prepare learners to be investigators and problem solvers. Learners are expected to apply their knowledge to develop new perceptions and skills and to apply mathematical reasoning to problems in order to have the capacity to participate in today's and tomorrow's economy (Kilpatrick, Swafford & Findell, 2014:144).
Some novel teaching approaches, such as active learning methods based on investigation, discovery, cooperative learning, and simulation approaches, are more effective than concentrating on traditional approaches where teachers just apply "chalk and talk" (Serbessa, 2006:129-132). In South Africa, the Academy of Science of South Africa (Grayson, 2010:38) has emphasised an urgent need to increase the numbers of learners who are sufficiently proficient in mathematics and science. As an emerging resource economy, the limited numbers of mathematically proficient learners entering the workforce each year acts as a constraint to the growth of the country. Hence, the country ought to improve the learning outcomes in mathematics; to do that, mathematics teaching and assessment practices have to be improved. Barrows (1986:1) suggests that the integration of a variety of teaching methods and assessment strategies would be the most helpful factor to improve the effectiveness of teaching and learning practices. Furthermore, it may be the case that learners' preferred learning styles may not be their most effective learning styles. Therefore, the use of different teaching approaches has the advantage of challenging learners to think more laterally.
In this study, we adapt an instrument used by Beswick, Callingham and Watson (2012) to probe the use of teaching and assessment methods by a group of South African teachers. The instrument used by Beswick et al. (2012) aimed at measuring teachers' knowledge for middle school mathematics, by using Rasch analysis. These authors did not explore the various types of methods and assessments strategies that teachers were more likely to use, or the factors associated with the use of multiple teaching methods and assessments strategies, which are issues that we focus on in this study.
This research was underpinned by the following research questions:
• What are the different approaches used by teachers in their teaching and assessing of mathematics and statistics topics in KwaZulu-Natal schools?
• Is there any relationship between demographic factors of the teachers' profiles and the methods they use for teaching and assessment?
It is hoped that this study, which sheds light on the teaching practices of teachers, can help education authorities to find ways that support the use of innovative methods and assessments by teachers. Furthermore, the use of Beswick et al.'s (2012) instrument will provide greater insight into areas where teachers need more help, so that they can improve their teaching.
Literature Review
Teaching methods
According to Nyaumwe, Bappoo, Buzuzi and Kasiyandima (2004:33), traditional approaches, which involve "teacher-centred instructional me-thods that do not make learners develop conceptual understanding of mathematics", have been criti-cised because they do not encourage problem-solving skills in learners. Instructional methods based mainly on teacher talk, do not involve much questioning, discussion or individual development of understanding. In contrast, a learner-centred teaching approach is one that supports learners in developing mathematical reasoning, while en-couraging them to perceive the teacher as someone who is there to help them make sense of mathematics while creating contexts which help them develop meaning in mathematics (Brodie, 2006:543; Yashau, Mji & Wessels, 2005:20). However, learner-centred discourse is much harder to achieve in practice than it appears to be in policy. Chisholm and Leyendecker (2008:197) note that learner-centred education is one of the most pervasive ideas; yet it is very hard for them to take root in the classroom.
Such an approach requires teachers to have a variety of skills, as well as a sound knowledge of mathematics content. The use of a variety of teaching approaches and styles is recommended, because it can "encourage adapt-ability and lifelong learning in the teaching-learning process" (Vaughn & Baker, 2001:610). Shulman (1986:9), in his seminal definition of pedagogic content knowledge, articulates that "there are no single most powerful forms of representation, the teacher must have at hand a veritable armamentarium of alternative forms of representation." Shulman's definition focuses the need for teachers to have at their disposal a variety of ways to represent the subject matter, in order to make it meaningful to their learners.
Some common strategies in mathematics learning include direct instruction, cooperative learning and problem-based instruction. Other innovative teaching methods that can be added to teachers' repertoires, include manipulatives, real-life application, integration of technology devices, and games (Moore, 2012:4-18). Manipulatives can be effective in creating an external and more concrete representation of the mathematical con-cepts being taught (White, 2012:23). Another teaching approach that contributes to learners' achievement in mathematics is the integration of games in the teaching process (Moore, 2012:6). Using games to teach mathematics contributes to mathematical thinking and knowledge development (Nisbet & Williams, 2009:27). Ke and Grabowski (2007:256) add that "[p]laying games plays important roles in a child's psychological, social, and intellectual development." Boaler notes that there is a gap between what research has shown to work in teaching mathematics and what actually happens in schools. Boaler (2006, 2016:143-150) advises that teaching should draw upon rich mathematical activities, which have high intellec-tual demand, instead of resorting to rote learning, so that it can inculcate a positive mindset towards mathematics. Studies further argue that the connection of mathematics to real-world contexts gives teachers the opportunity of making mathe-matics seem more accessible and enjoyable to learners (Miller, 2009:4).
Researchers indicate that traditional methods, especially in teaching introductory statistics courses, are often viewed as unproductive, and result in students getting nervous about coursework because they consider statistics as a difficult field (Smith & Martinez-Moyano, 2012:107). Instead, researchers advocate that small-group or co-operative learning should replace traditional methods in order to encourage more critical engagement with statistics concepts (Garfield, 1993:30; Roseth, Garfield & Ben-Zvi, 2008:2-4). In recent years, there has been an increased emphasis on using real-life settings in the mathematics and statistics classroom so that learners can connect to the subject (Steen, 2001). In teaching statistics in particular, a data-driven approach can be very useful. Real data can be used to emphasise statistical principles and procedures, rather than using a traditional theoretical approach where the importance is on identifying the correct formula and performing a calculation (North, Gal & Zewotir, 2014:1). Experiential learning activities allow learners to see the ways in which statistics permeate current events. Such activities draw upon the use of newspaper articles or other news sources to teach statistics concepts thereby positively influencing learners' careers and lives.
Snee (1993:153) suggests incorporating a variety of learning methods so that the statistics curriculum accommodates a range of learning styles by mentioning that "using a variety of learning methods can also help some people discover new worlds that might be closed to them because the teaching methods used are not compatible with their preferred learning style." Mills (2015:63-66) adds that teachers of statistics need to search for new or alternative teaching methods to improve statistics instruction, in the hope of enhancing learning while also improving learner attitudes towards statistics.
Assessment strategies
Apart from using innovative teaching methods, the use of well-designed and creative assessments contributes to improvements in learning. Assess-ments are more than just tests and can be beneficial in mathematics; therefore, teachers are encouraged to design and use them in different ways (DBE, Republic of South Africa, 2011:293). The De-partment of Basic Education views assessments as the process of "generating and collecting evidence of achievement, evaluating this evidence, recording the findings and using this information to under-stand and thereby assist the learner's development in order to improve the process of learning and teaching" (DBE, Republic of South Africa, 2011:293).
Assessments go beyond merely evaluating what learners know and what they do not know. They generally include all activities that teachers and learners apply to acquire information that can be used diagnostically to adjust teaching and learning (Black & Wiliam, 1998:5). There are several types of assessments, namely diagnostic, formative, formal, informal and summative assessments (DBE, Republic of South Africa, 2011:292-294).
The Department of Basic Education, Republic of South Africa (2011:293) encourages teachers to use formal assessments such as tests, examinations, projects, assignments and investigations in teaching and learning mathematics. These tools are applied at the end of a mathematics topic or a group of related topics in relation to measuring the product of learning, or after a period of instruction in order to judge how learning has occurred (Boston, 2002:2).
Diagnostic assessments can provide infor-mation about learners' understanding of related prior knowledge and skills (Ketterlin-Geller & Yovanoff, 2009:1). Formative assessments contribute to sustaining the teaching and learning process (DBE, Republic of South Africa, 2011) by providing feedback of what learners can do and how the teaching needs to be adjusted to improve the learning. Formative work involves those activities undertaken by teachers, and/or by their students, which provide information to be used as feedback to adjust the teaching and learning activities undertaken (Black & Wiliam, 1998:1). Black and Wiliam add that in order for assessment to be formative, the feedback information has to be used. Wiggins (1998:60) says that "providing feedback in the middle of an assessment is sometimes the only way to find out how much a student knows" in terms of the final outcome. This information can be used by the teacher to support the development of the learners' understanding. Bansilal, James and Naidoo (2010:155) recommend that assessment should involve using feedback "to shape the construction of learners' understanding of mathematics." The authors also explain that scaffolding provided in the form of hints and prompts during assessment can support learners in attaining targets (Bansilal et al., 2010). Boaler (2006:41-44) provided a detailed description of an approach that led to high and equitable mathematics achievement. The mathematics classrooms across the school promoted a multi-dimensional perspective, where assessments valued many different abilities while the group work was structured so that all learners had specific roles and responsibilities.
Boaler (2016) asserts that Mathematics ass-essment practices should change so that they focus on improving understanding. Boaler (2016:149) reminds us that mistakes can present a powerful learning opportunity which teachers can take ad-vantage of by providing feedback on the actions and how this could be improved instead of focusing on the learner characteristics. Black, Harrison, Lee, Marshall and William (2004:14-15) further state that classroom dialogue, exercises and peer groups are forms of formative assessment, which are useful ways of helping students change from behaving as passive recipients of the knowledge offered, to becoming active learners who take responsibility for their own learning. Clark (2008:12-13) suggests that the use of a variety of teaching and assessment methods can stimulate learners' achievement, while pointing to the importance of specifying success criteria and learning intentions in any assessment settings. Foster (2003) articulates similarly that the integration of mixed teaching methods and assessments by involving both exercises and assignments, monitoring students' progress, advising on the progress, giving sufficient practices and giving feedback to practices in teaching mathematics and statistics, can contribute to effective learning. Based on this literature, we note that teaching and assessment methods play a primary role in fostering good learning and contributes to students' achievement. Therefore, when teaching, teachers have the responsibility to apply a variety of teaching and assessment methods to improve learning outcomes.
Methodology
The sample consisted of 75 mathematics teachers who attended a series of five professional develop-ment workshops at a university in KZN in early 2015 and who agreed to participate in the study. The Department of Education purposively selected these teachers, as coming from the worst performing schools in KZN, or schools in the province where help is urgently needed. Questionnaires requiring teachers to respond to open-ended questions (about the various methods and assessments used to develop their learners' understanding), as well as closed questions regarding demographic factors, were completed by the mathematics teachers, teaching at levels from Grade Four to Grade 12. Teachers were presented with a list of different mathematics and statistics topics and were asked to choose a single topic. Topics included: percentage, measurement, mental computation, ratio, fractions, algebra, relationships, simultaneous equations, exponents, data types, surveys, questionnaires, populations and samples, tally table, frequency, pictograms, bar graphs, pie graph, histogram, scatterplot, grouping data, mean, median, mode, range, stem and leaf plot, random experiment, events (certain, uncertain, impossible), frequency, probability, chance, etc.
They were then presented with the following instruction: 'Question 1: write down the teaching methods that you would use to teach the concept. Question 2: write down the assessment strategies that you would use to assess whether the concept was understood.' Similar types of items were previously used by Beswick et al. (2012) in their research on the nature and development of middle school mathematics teachers, which used a quan-titative approach only. In this study, we also used qualitative analysis to examine the type of teaching methods and assessments strategies. According to Creswell (2013:11-22), qualitative researchers tend to use open-ended questions so that participants can express their views. This process of qualitative research is largely inductive, with the inquirer generating meaning from the data collected in the field. The teachers' responses to the items regarding their methods of teaching and assessment were analysed for emerging themes using a general inductive analysis by two of the authors. The coding was then compared, and where there were differences, consensus was reached about the final coding into 11 categories of teaching methods (Table 3) and four main categories of assessment methods (Table 4). We then quantified the teachers' answers using quantitative coding to explore whether teachers focus on single or on more than one teaching and assessment method in teaching mathematics and statistics topics. Quantitative studies involve the process of identifying factors that influence an outcome, which in this case was the use of multiple teaching and assessment methods. The quantification of the qualitative data into quantitative data allowed us to run statistics tests (Driscoll, Appiah-Yeboah, Salib & Rupert, 2007; Sandelowski, Voils & Knafl, 2009) which enabled us to make inferences from the results. The summary of the teachers' responses appears in Table 1. The response variables are teaching methods and assessment strategies whereas the explanatory variables are age, domain of study, level of education, experience, using National Curriculum Statement (NCS) grades R-12 and attending mathematics workshops as professional learning.
Results and Discussion
The results of the study are presented in three sections, namely teaching methods, assessment methods and demographic factors. In this section, we report on the number of methods used for teaching mathematics and statistics in the class-room. Our interest is to know whether teachers apply a single method or a variety of teaching methods in the classroom, when teaching mathematics and statistics. To achieve this, we designed the codes for methods and assessments, with results as reported by teachers as presented in Table 2.

Table 2 and Figure 1 display the number of teaching and assessment methods reported by teachers in teaching mathematics and statistics. It can be noted that teachers were more likely to report a single method in teaching statistics topics (16 or 58%) than in mathematics topics (20 or 43%), whereas they are more likely to report more than one method in teaching mathematics (27 or 57%) than in teaching statistics topics (12 or 42%). Teachers are more likely to report a single type of assessment method in teaching statistics (19 or 65.5%) than is the case for teaching mathematics topics (25 or 53%). Furthermore, they are more likely to report more than one type of assessment in teaching mathematics (21 or 46%) than teaching statistics topics (34.5%).
This picture suggests that more than half of the teachers prefer to stick to one type of method in statistics topics, and should be encouraged to try multiple approaches. If teachers can take on a variety of methods and instruments, including systematic and creative aspects of mathematics, then their classrooms would become more interesting for their learners (Rico, 1993:9-20).
This picture suggests that many of the teachers find value in using multiple and multi-faceted assessment tools in developing mathematical understanding (Dandis, 2013:135). However, in this study some teachers have not reported the use of multiple strategies. It is a cause for concern that so many teachers seem to be limited to one or two types of assessments. Some reasons for this could be because they find it difficult to use the assessment tools or they may not have the resources to use the tool. Moreover, as teachers were given an opportunity to choose one topic from the list, it can be noted, in Table 2, that 46 teachers chose to teach mathematics topics while 29 selected statistics topics. The teachers' preference for mathematics concepts may be because statistics in school is a relatively new field compared to mathematics and only assumed prominence with the implementation of Curriculum 2005 (Wessels, 2008:1-2), indicating that teachers are clearly more comfortable with teaching mathematics topics.
Teaching Methods
Table 3 reports the different teaching methods reported by teachers in teaching mathematics and statistics. It was found that teachers mostly use teacher-led explanations (show and tell, ex-planations, illustrations, lecturing, etc.: 24 cases or 23.1%) followed by classroom discussion (dis-cussions, questions and answer, etc.: 17 cases or 16.4%), group work (cooperative learning, group activities, etc.: 17 cases or 16.4%) and practical instructional methods (using data from learners tests, examples they are familiar with, games, etc.). Figure 2 displays teaching methods by subject. The findings indicate that teacher-led instruction me-thod is applied more often in teaching mathematics (25%) than statistics topics (10%) while grouping methods is applied more often in teaching statistics (18%) than mathematics topics (15%). Moutal (1999:1) refers to teacher-led instruction as the method in which a teacher takes an active and central role in providing information and instructions to a class. Also described in Garrett (2008:35), "teacher-centred instruction" is not the most efficient way of facilitating content knowledge with learners, because it limits their active involvement in the learning process.
A learner-centred teaching approach, on the other hand, involves supporting learners to develop mathematical reasoning skills while making mean-ing in mathematics and it requires teachers to have variety of skills and sound knowledge of mathe-matics content (Brodie, 2006; Yashau et al., 2005:20). In this study, there were signs that some teachers were adopting progressive methods, albeit to a smaller extent than that of the traditional methods. It is encouraging to note reports on the use of co-operative learning strategies such as group work and classroom discussion. Brijlall (2008:60) noted that the learners in his study who worked in groups were able to share valuable information with one another, an approach that gave them an advantage over those learners who worked individually.
Snee (1993:151) finds that motivating stu-dents to collect their own data, and conduct experiments like testing paper helicopters, would be a way of creating fun, excitement, enthusiasm and joy in learning about data in the process.
Although 95% of teachers in the study (Ref. Table 3) reported using a well-defined teaching method to teach mathematics or statistics in the classroom, the remaining 5% showed a weakness in describing the methods they use in the classroom. One teacher described the procedure of converting fraction to percentage instead of giving the method to teach this concept, e.g. in cases where they convert fractions into percentages such as when the learners got 20 out of 30 marks, they convert to percentages.
Assessment Strategies
Table 4 represents the distribution of different forms of assessments implemented by teachers in assessing mathematics and statistics. In this study, we also found that most teachers use formal assessment methods (39 cases or 30.1%). More-over, Figure 3 displays the type of assessment strategy by subject. We note that teachers were more likely to apply formal and formative assessments methods in teaching mathematics (33%) than statistics (23%) topics while examples of skills appeared mostly in statistics topics (31%). Besides, informal assessments were also more apparent in teaching mathematics (18%) than statistics topics (11%).
These results can be seen in terms of the guideline given by the Department of Basic Edu-cation, namely that all formal assessment tasks are subject to self-control for the purpose of quality assurance (DBE, Republic of South Africa, 2011:294). The second-highest assessment method that was cited was Formative assessment (35 cases or 26.9%). Teachers mentioned that they also use informal, class and homework as assessments. Many teachers, instead of stating the strategies they used, provided examples of the skills or knowledge that they assessed. They cited reasoning, listening, and practical examples. The examples provided suggest that informal assessment methods play a role in these teachers' practices, but that they may need more help. Du Plessis, Conley and Du Plessis (2007) point out that the choice of assessment strategies is subject to and depends on the teacher's professional judgement, suggesting that teachers need advice and training in widening their repertoire of assessment strategies.
The DBE, Republic of South Africa (2014:23) has identified "the need to support teachers as well as subject advisors in the development of quality projects, assignments" as well as other assessment strategies. The findings indicate that around 93% of teachers (Ref. Table 4) cited a relevant type of assessment they use in the classroom. However, 7% did not report appropriate assessment methods, for instance one teacher, who chose fraction reported that "all learners in my class in order my lesson to be successful, I would give them more work" [all sic]. This finding indicates that this teacher is just reporting his/her belief about teaching and learning instead of reporting a type of assessment he/she uses in the classroom.
Other inappropriate examples that were given by the teachers included: the procedure for drawing a pie chart; drawing, measuring and naming angles, sorting and classifying angles, and constructing angles using protractors and compass.
Another irrelevant example given by a teacher was the rubric for drawing a bar graph was: "doing correct bars, labelling the x and y axis correct, writing heading, writing key is necessary." Knowledge of different assessment strategies is an essential component of teachers' pedagogic content knowledge which enables them to improve the effectiveness of their teaching. Formal testing techniques on their own cannot provide sufficient feedback to learners. Teachers may involve projects and investigations (Van den Bergh, Mortelmans, Spooren, Van Petegem, Gijbels & Vanthournout, 2006:347), as well as formative assessments as the way of improving teaching and learning about learners' update of work presented (Black & Wiliam, 1998).
Demographic Factors
In this section, we explore demographic factors which may influence teacher's decisions to use multiple teaching methods and assessments strat-egies. These factors were given in Table 1. We then grouped teachers' answers into two categories, those teachers who expressed a single method or single assessment and those who expressed at least two or more (multiple) methods or multiple assessments, as shown in Table 5. These two response variables were modelled using binary logistic regression (Harrell, 2015; Hellevik, 2009) at significant level alpha = .05. SAS 9.4 (SAS Institute, 2014). The description of the response variables is presented in Table 5.

Fit Statistics
In order to assure goodness of fit, we first checked with three chi-square tests such as likelihood ratio, score and Wald Test in order to guarantee that at least one of the predictors' regression coefficient is not equal to zero in the model. Table 6 indicates that all p-values from the all three tests are small (< .05); this leads us to conclude that at least one of the regression coefficients in the model is not equal to zero.
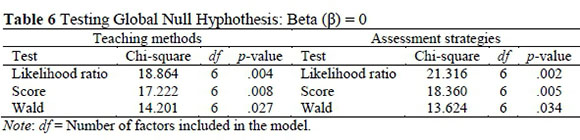
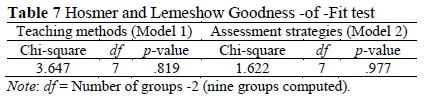
The Hosmer and Lemeshow (H-L) Test (Hosmer & Lemeshow, 2000) was also used. The finding from Table 7 indicates that the p-values of H-L test are large and non-significant (the values are greater than .05). This indicates that the model fits the data.
Parameters Estimates from Logistic Regression Model
We present the parameters estimates of each factor explored in Table 1 (methodology) in order to identify the effect of each factor in the model. These factors include gender, age, experience, level of education, using curriculum Grade R-12 and the attendance of professional courses. The parameters estimate of these factors, are presented in Table 8 and Table 9.
Gender
There is a statistically significant difference with respect to gender and the use of different types of teaching methods. It is observed from Table 8 that female teachers are more likely to use single method of teaching than males (OR = .158, p-value = .003) compared to male teachers, i.e. female teachers are more likely to use a single method of teaching than males are. This finding seems to be new, because gender differences in teaching practices do not appear to have been studied. This finding suggests that male teachers are more likely to be trying different methods; it could mean that male teachers may just be more confident about reporting their teaching and assessment practices.
Familiarity with the curriculum
Becoming more informed about the curriculum itself has positive effects on teachers' use of multiple teaching methods and assessments. We found a statistically significant difference between teachers working across the NCS Grades R-12 (2012) and the use of different types of teaching assessment. It is observed in Table 9 that the group of those who had not used NCS, is .272 (p-value = .023) times as likely to have used multiple assessment strategies than the group who has used NCS. This finding is unsurprising, because it confirms that teachers who are interested enough to consult the curriculum would be better placed to try different assessment strategies as endorsed in the curriculum documents (DBE, Republic of South Africa, 2011).
Age and teaching experience
The study found a significant difference between teachers' age and the use of different assessment strategies. It can be noted from Table 9 that teachers ≤ 40 years old are more likely to use more than one assessment strategies (OR = 5.309; p-value = .043) compared to teachers aged > 40 years old. Besides, the finding indicates a significant difference between teaching experience and the use of teaching methods and assessments strategies. Table 9 indicates that teachers whose teaching experience is ≤ 10 years are more likely to use more than one assessment strategies (OR = 5.543; p-value = .039) compared to teachers whose teaching experience is > 10 years respectively. It is surprising that less experienced teachers are more likely to use more than one assessment compared to more experienced teachers. We further noted that teachers aged ≤ 40 are also more likely than older teachers to cite the use of multiple assessment methods which provides further support to the finding that younger teachers seem to be more willing to discuss their use of multiple methods of assessments. Although teacher learning is dependent on the process of increasing participation in the practice of teaching (Adler, 2000), this does not necessarily mean that more experienced teachers are more inventive than their less experienced counterparts. Kini and Podolsky (2016:1) note that there is variation in teacher effectiveness at every stage of the teaching career, so not every inexperienced teacher is less effective, and not every experienced teacher is more effective. They emphasise that the benefits of teaching experience will be best realised when teachers are carefully selected and well-prepared at the point of entry into the teaching staff.
Level of education
With respect to teachers' level of education, the findings indicate that those who have bachelor's degree qualification are .277 (p-value = .032) times less likely to use multiple methods of teaching than the group with postgraduate qualifications. It is possible that the teachers who have studied further have been exposed to more diverse teaching me-thods during their postgraduate studies, making it easier for them to experiment with different me-thods.
Professional learning
Professional learning was also found to be a significant factor influencing teachers to report the use of multiple teaching methods. It can be noted from Table 9 that teachers who have attended mathematics or statistics workshops related to teaching and learning are more likely to report the use of multiple assessment strategies than those who did not attended these workshops (OR = .076, p-value = .021). This finding suggests that those who acquired some professional courses in teaching mathematics and statistics are more likely to apply multiple assessment strategies than those who did not do so. Kini and Podolsky (2016:1) emphasise that teachers who enter the professional tier of teaching have met a competency standard from which they can continue to expand their expertise throughout their careers.
Based on these findings, it is recommended that teachers be given support in developing more effective approaches that could stimulate their learners' creativity, and increase their interest. Such support could help teachers in teaching probability and statistics, improving the learners' graphical reasoning, and using concrete materials. Ulti-mately, the teachers would be increasingly able to apply a variety of approaches in order to help today's learners prepare for tomorrow's world, as reported in Steen (2001). Moreover, teachers are encouraged to develop projects which develop learners' abilities and skills to apply mathematics to real-life situations (DBE, Republic of South Africa, 2011:295). More specifically, as suggested by North et al. (2014:4), additional resources and additional programmes are required in order to build in more aspects of statistical literacy in teacher education programmes. A further need, identified by North et al. (2014:24), is to include teachers in small-group work or in extended open-ended discussions, so that they can practise the use of these types of teaching methods, while also developing a deeper understanding of the concepts of statistics. However, it remains a challenge to find such time in teacher development programmes that are offered by higher education institutions (North et al., 2014:18). The alternative is to offer in-depth teacher support programmes at the schools where teachers work, so that they can learn while they teach.
The findings show that most teachers are not applying multiple teaching methods and assess-ments approaches which are necessary to prepare learners to participate in a developing economy. Meeting the requirements of a global economy involves inculcating 21st century skills, and teaching as well as assessments must draw upon creative learning practices.
Conclusion
In this article, we used the teachers' responses to a questionnaire to analyse how likely they were to use more than a single method and assessment to teach mathematics and statistics. This study brings new insight into the extent to which progressive approaches are being implemented in relation to developing learners' understanding of mathematics. We found that the teachers seemed to be more comfortable in using a single approach in teaching statistics topics than in applying multiple methods. We also noted that teachers were more likely to apply more than one method in teaching mathe-matics than teaching statistics topics. This finding is surprising, given that statistics topics are generally more contextualised and it should therefore be easier to apply innovative pedagogies in the teaching of statistics. The teaching of statistics can be made more interesting by the use of real life examples such as media reports and newspapers articles in the classroom. These readily available resources can be used to develop learners' aptitude in terms of interpreting statistical ideas. Teachers could also build in opportunities of working with real data sets and simulated computer based activities, since statistics has so many real-life applications. Such activities could help learners explore statistical concepts while engaging in data collection and analysis. The use of these innovative pedagogies can promote statistical thinking, reasoning and construction of their knowledge.
In this study, it was found that teachers did try to engage in progressive methods such as classroom discussion, group work and practical examples in their classrooms; however, teacher-led instruction methods were still their first choice. The findings also showed that teachers need to build up their repertoire of formative assessment strategies, which would help them to provide regular feedback in order to enhance the learning experiences of their learners. For example, it would be useful to integrate projects, simulations, and investigations as they develop learners' reasoning in mathematics and statistics. The results of this study show that much work is needed before teachers can take on the variety of methods to the same extent that they use formal assessments. It is therefore incumbent upon the Department of Basic Education to explore possible classroom-based interventions that can encourage teachers to start increasing their reper-toire of assessment strategies. This suggests that teachers may need some support in trying to move to more innovative methods, which can enable learners to express themselves. The study has shown that teachers who attend workshops are more likely to cite several assessment methods than those who do not. This is an illustration of the value of attending professional development courses. To encourage teachers to attend more professional development programmes, these should ideally be carried out at the places where teachers work, so that they can learn while they practise and can be supported as they try to implement more progressive teaching methods. Through the professional development support programmes teachers can be given practical advice on how to design and assess projects using real data that they start using mathematics and statistics to solve problems in real life. The use of these methods can improve learners' critical thinking, reasoning, self-discovery and investigation skills. These different approaches will enable learners to look at different ways of finding solutions to mathematical and statistical tasks. This study furthermore brought a new understanding that teachers' tendencies to use different teaching app-roaches and assessments differs according to their gender, age and teaching experience. This means that all teachers of the same age, gender and teaching experience do not have the same pedagogical knowledge and confidence to integrate different methods into their teaching and learning. This underlines the importance of teachers taking on further studies in education so as to ensure that they become familiar with the curriculum. Teachers who used the national curriculum documents seem to have become aware of the need to improve their teaching by applying multiple methods in mathe-matics and statistics discourse. Generally, teachers should be encouraged to improve their way of teaching by moving beyond a reliance on teacher-led instruction. More particularly, training in statistics education is needed to help mathematics teachers manage the wider and more relevant statistics curriculum so that learners can be statistically literate when they leave school (Wessels, 2008:5).
As an emerging resource economy, South Africa is in urgent need of an increase in the number of mathematically proficient learners who enter the economy each year, which means that mathematics teachers' teaching and assessment practices need to be made more effective. This study has identified particular areas where teachers' teaching and assessment practices can be improved, as well as factors which are associated with progressive practices. The transformation of classrooms into sites where learners develop positive mindsets and become confident users of mathematics, is a difficult task (Boaler, 2016). Therefore, appropriate support from professional development initiatives can help the teachers move towards creating such classrooms.
Note
i. Published under a Creative Commons Attribution Licence.
References
Adler J 2000. Conceptualising resources as a theme for teacher education. Journal of Mathematics Teacher Education, 3(3):205-224. doi: 10.1023/A:1009903206236 [ Links ]
Bansilal S, James A & Naidoo M 2010. Whose voice matters? Learners. South African Journal of Education, 30(1):153-165. Available at http://www.sajournalofeducation.co.za/index.php/saje/article/view/236/177. Accessed 25 March 2016. [ Links ]
Barrows HS 1986. A taxonomy of problem‐based learning methods. Medical Education, 20(6):481-486. doi: 10.1111/j.1365-2923.1986.tb01386.x [ Links ]
Beswick K, Callingham R & Watson J 2012. The nature and development of middle school mathematics teachers' knowledge. Journal of Mathematics Teacher Education, 15(2):131-157. doi: 10.1007/s10857-011-9177-9 [ Links ]
Black P, Harrison C, Lee C, Marshall B & Wiliam D 2004. Working inside the black box: Assessment for learning in the classroom. Phi Delta Kappan, 86(1):8-21. doi: 10.1177/003172170408600105 [ Links ]
Black P & Wiliam D 1998. Inside the black box: Raising standards through classroom assessment. London, UK: School of Education, King's College. [ Links ]
Boaler J 2006. How a detracked Mathematics approach promoted respect, responsibility, and high achievement. Theory Into Practice, 45(1):40-46. doi: 10.1207/s15430421tip4501_6 [ Links ]
Boaler J 2016. Mathematical mindsets: Unleashing students' potential through creative Math, inspiring messages and innovative teaching. San Francisco, CA: Jossey-Bass. [ Links ]
Boston C 2002. The concept of formative assessment. Practical Assessment, Research & Evaluation, 8(9):1-4. Available at http://pareonline.net/getvn.asp?v=8&n=9. Accessed 23 March 2017. [ Links ]
Brijlall D 2008. Collaborative learning in a multilingual class. Pythagoras, 68:52-61. [ Links ]
Brodie K 2006. Teaching Mathematics for equity: learner contributions and lesson structure. African Journal of Research in Mathematics, Sciences and Technology Education, 10(1):13-24. [ Links ]
Chisholm L & Leyendecker R 2008. Curriculum reform in post-1990s sub-Saharan Africa. International Journal of Educational Development, 28(2):195-205. doi: 10.1016/j.ijedudev.2007.04.003 [ Links ]
Clark I 2008. Assessment is for learning: Formative assessment and positive learning interactions. Florida Journal of Educational Administration & Policy, 2(1):1-16. Available at http://files.eric.ed.gov/fulltext/EJ902994.pdf. Accessed 14 April 2017. [ Links ]
Creswell JW 2013. Research design: Qualitative, quantitative, and mixed methods approaches (4thed). Thousand Oaks, CA: Sage Publications, Inc. [ Links ]
Dandis MA 2013. The assessment methods that are used in a secondary mathematics class. Journal for Educators, Teachers and Trainers, 4(2):133-143. Available at http://digibug.ugr.es/bitstream/10481/39339/1/Vol4%282%29_010 _jett_dandis.pdf. Accessed 22 March 2017. [ Links ]
Department of Basic Education (DBE), Republic of South Africa 2011. Curriculum and Assessment Policy Statement Grades 4-6: Life Skills. Pretoria: DBE, Republic of South Africa. Available at http://www.education.gov.za/LinkClick.aspx?fileticket=OX12620gNnw %3D&tabid=572&mid=1568. Accessed 12 April 2017. [ Links ]
DBE, Republic of South Africa 2014. Report on the Annual National Assessment of 2014: Grades 1 to 6 & 9. Pretoria: DBE, Republic of South Africa. Available at http://www.education.gov.za/Portals/0/Documents/Reports/REPORT%20ON %20THE%20ANA%20OF%202014.pdf?ver=2014-12-04-104938-000. Accessed 31 March 2017. [ Links ]
DBE, Republic of South Africa 2016. National Senior Certificate examination 2015: Diagnostic report. Pretoria: DBE, Republic of South Africa. Available at http://www.education.gov.za/Portals/0/Documents/Reports /2015%20NSC%20Diagnostic %20Report.pdf?ver=2016-01-05-001418-000. Accessed 31 March 2017. [ Links ]
Driscoll DL, Appiah-Yeboah A, Salib P & Rupert DJ 2007. Merging qualitative and quantitative data in mixed methods research: How to and why not. Ecological and Environmental Anthropology, 3(1): Paper 18. Available at http://digitalcommons.unl.edu/cgi/viewcontent.cgi?article=1012&context=icwdmeea. Accessed 31 March 2017. [ Links ]
Du Plessis P, Conley L & Du Plessis E 2007. Teaching and learning in South African schools. Pretoria, South Africa: Van Schaik. [ Links ]
Foster B 2003. On‐line teaching of mathematics and statistics. Teaching Mathematics Applications, 22(3):145-153. doi: 10.1093/teamat/22.3.145 [ Links ]
Garfield J 1993. Teaching statistics using small-group cooperative learning. Journal of Statistics Education, 1(1):1-9. Available at https://ww2.amstat.org/publications/jse/v1n1/garfield.html. Accessed 21 March 2017. [ Links ]
Garrett T 2008. Student-centred and teacher-centred classroom management: A case study of three elementary teachers. The Journal of Classroom Interaction, 43(1):34-47. [ Links ]
Grayson DJ (ed.) 2010. Critical issues in school Mathematics and Science: Pathways to progress. Pretoria, South Africa: Academy of Science of South Africa (ASSAf). Available at https://www.assaf.org.za/files/2011/04/STEM-FINAL-WEB.pdf. Accessed 1 April 2016. [ Links ]
Harrell FE Jr. 2015. Regression modeling strategies: With applications to linear models, logistic and ordinal regression, and survival analysis (2nd ed). New York, NY: Springer-Verlag. [ Links ]
Hellevik O 2009. Linear versus logistic regression when the dependent variable is a dichotomy. Quality & Quantity, 43(1):59-74. doi: 10.1007/s11135-007-9077-3 [ Links ]
Hosmer DW & Lemeshow S 2000. Applied logistic regression (2nd ed). New York, NY: John Wiley & Sons, Inc. [ Links ]
Ke F & Grabowski B 2007. Game playing for maths learning: cooperative or not? British Journal of Educational Technology, 38(2):249-259. doi: 10.1111/j.1467-8535.2006.00593.x [ Links ]
Ketterlin-Geller LR & Yovanoff P 2009. Diagnostic assessments in Mathematics to support instructional decision making. Practical Assessment, Research & Evaluation, 14(16):1-11. Available at http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1. 459.7095&rep=rep1&type=pdf. Accessed 20 March 2017. [ Links ]
Kilpatrick J, Swafford J & Findell B (eds.) 2014. Adding it up: Helping children learn Mathematics. Washington, DC: National Academy Press. Available at https://www.ru.ac.za/media/rhodesuniversity/content/sanc/documents/Kilpatrick ,%20Swafford,%20Findell%20-%202001%20-%20Adding%20It%20Up%20Helping%20Children%20Learn%20Mathematics.pdf. Accessed 1 April 2017. [ Links ]
Kini T & Podolsky A 2016. Does teaching experience increase teacher effectiveness?: A review of the research. Palo Alto, CA: Learning Policy Institute. Available at https://learningpolicyinstitute.org/sites/default/files/product-files/Teaching_Experience_Report_June_2016.pdf. Accessed 1 April 2017. [ Links ]
Miller K 2009. Real world Math: Views from the researcher, teacher and student. Senior honors theses. Ypsilanti, MI: Eastern Michigan University. Available at http://commons.emich.edu/honors/172. Accessed 8 April 2016. [ Links ]
Mills J 2015. A conceptual framework for teaching statistics from a distance. The Journal of Effective Teaching, 15(1):59-68. Available at http://files.eric.ed.gov/fulltext/EJ1060441.pdf. Accessed 14 April 2017. [ Links ]
Moore ND 2012. Alternative strategies for teaching Mathematics. M.S.Ed. thesis. Brockport, NY: State University of New York. Available at http://digitalcommons.brockport.edu/cgi/viewcontent.cgi?article= 1132&context=ehd_theses. Accessed 1 April 2017. [ Links ]
Moutal V 1999. Teacher-led instructions. District Disc Discussion Paper. Available at http://www2.sd38.bc.ca/District%20Disc%20Papers/I0028BE0E. Accessed 10 January 2016. [ Links ]
Nisbet S & Williams A 2009. Improving students' attitudes to chance with games and activities. Australian Mathematics Teacher, 65(3):25-37. Available at http://files.eric.ed.gov/fulltext/EJ859754.pdf. Accessed 19 March 2017. [ Links ]
North D, Gal I & Zewotir T 2014. Building capacity for developing statistical literacy in a developing country: Lessons learned from an intervention. Statistics Education Research Journal, 13(2):15-27. Available at https://www.researchgate.net/profile/Temesgen_Zewotir/publication/269852720 _Building_capacity _for_developing_statistical_literac y_in_a_developing_country_Lessons _Learned_from_an_intervention/links/54be11830cf218da9391d5ff.pdf. Accessed 19 March 2017. [ Links ]
Nyaumwe L, Bappoo R, Buzuzi G & Kasiyandima O 2004. Students' perceptions of factors and gender differences that influence their achievement in 'O' level Mathematics in Mashonaland Central Region. The Zimbabwe Bulletin of Teacher Education, 13(1):21-39. Available at https://opendocs.ids.ac.uk/opendocs/bitstream/handle/123456789/4943/Nyaumwe %2c%20L%20%20%20ZBTE%20vo l.13%2c%20no.1.pdf?sequence=1&isAllowed=y. Accessed 19 March 2017. [ Links ]
Rico L 1993. Mathematics assessment in the Spanish educational system. In M Niss (ed). Cases of assessment in Mathematics Education: An ICMI study. Dordrecht, The Netherlands: Kluwer Academic Publishers. [ Links ]
Roseth CJ, Garfield JB & Ben-Zvi D 2008. Collaboration in learning and teaching statistics. Journal of Statistics Education, 16(1):1-15. Available at https://www.causeweb.org/cause/sites/default/files/workshops/aims/ Collaboration%20in%20 Learning%20and%20Teaching%20Statistics.pdf. Accessed 19 March 2017. [ Links ]
Sandelowski M, Voils CI & Knafl G 2009. On quantitizing. Journal of Mixed Methods Research, 3(3):208-222. doi: 10.1177/1558689809334210 [ Links ]
SAS Institute Inc. 2014. Base SAS® 9.4 procedures guide: Statistical procedures (3rd ed). Cary, NC: SAS Institute Inc. Available at https://support.sas.com/documentation/cdl/en/procstat/67528/PDF /default/procstat.pdf. Accessed 1 April 2017. [ Links ]
Serbessa DD 2006. Tension between traditional and modern teaching-learning approaches in Ethiopian primary schools. Journal of International Cooperation in Education, 9(1):123-140. Available at http://home.hiroshima-u.ac.jp/cice/wp-content/uploads/2014/03/9-1-10.pdf. Accessed 19 March 2017. [ Links ]
Shulman LS 1986. Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2):4-14. doi: 10.3102/0013189X015002004 [ Links ]
Smith AE & Martinez-Moyano IJ 2012. Techniques in teaching statistics: Linking research production and research use. Journal of Public Affairs Education, 18(1):107-136. [ Links ]
Snee RD 1993. What's missing in statistical education? The American Statistician, 47(2):149-154. [ Links ]
Steen LA (ed.) 2001. Mathematics and democracy: The case for quantitative literacy. Princeton, NJ: The Woodrow Wilson National Fellowship Foundation. Available at http://www.maa.org/sites/default/files/pdf/QL/MathAndDemocracy.pdf. Accessed 1 April 2017. [ Links ]
Van den Bergh V, Mortelmans D, Spooren P, Van Petegem P, Gijbels D & Vanthournout G 2006. New assessment modes within project-based education - the stakeholders. Studies in Educational Evaluation, 32(4):345-368. doi: 10.1016/j.stueduc.2006.10.005 [ Links ]
Vaughn L & Baker R 2001. Teaching in the medical setting: balancing teaching styles, learning styles and teaching methods. Medical Teacher, 23(6):610-612. doi: 10.1080/01421590120091000 [ Links ]
Yashau B, Mji A & Wessels DCJ 2005. The role of technology in fostering creativity in the teaching and learning of mathematics. Pythagoras, 62:12-22. [ Links ]
Wessels H 2008. Statistics in the South African school curriculum: Content, assessment and teacher training. In C Batanero, G Burril, C Reading & A Rossman (eds). Joint ICMI/IASE study: Teaching statistics in school Mathematics. Challenges for teaching and teacher education. Proceedings of the ICMI Study 18 and 2008 IASE Round Table Conference. Voorburg, The Netherlands: International Statistical Institute and International Commission on Mathematical Instruction. Available at http://iase-web.org/documents/papers/rt2008/T1P3_Wessels.pdf. Accessed 2 April 2017. [ Links ]
White KM 2012. The effect of an instructional model utilizing hands-on learning and manipulatives on Math achievement of middle school students in Georgia. Doctoral dissertation. Lynchburg, VA: Liberty University. Available at http://digitalcommons.liberty.edu/cgi/viewcontent.cgi?article= 1653&context=doctoral. Accessed 2 April 2017. [ Links ]
Wiggins G 1998. Educative assessment: Designing assessment to inform and improve student performance. San Francisco, CA: Jossey-Bass Inc., Publishers. [ Links ]














