Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Education
versão On-line ISSN 2076-3433
versão impressa ISSN 0256-0100
S. Afr. j. educ. vol.35 no.1 Pretoria Fev. 2015
Teacher training for mathematical literacy: A case study taking the past into the future
Sarah BansilalI; Lyn WebbII; Angela JamesIII
ISchool of Education, University of KwaZulu-Natal, Edgewood Campus, South Africa
IIFaculty of Education, Nelson Mandela Metropolitan University, South Africa lyn.webb@nmmu.ac.za
IIISchool of Education, University of KwaZulu-Natal, Edgewood Campus, South Africa
ABSTRACT
With the advent of the Minimum Requirements for Teacher Education Qualifications policy (MRTEQ), higher education institutions (HEIs) are rethinking curricula for teacher training in order to enable entree for in-service teachers to reskill, retrain and have access to higher qualifications. In the field of mathematical literacy (ML), most teacher training has been offered via government-funded Advanced Certificate in Education (ACE) qualifications, which have now largely been phased out. In this article we examine two ACE ML programmes offered in KwaZulu-Natal (KZN) in order to present some lessons that have been learnt. We put forward some elements that we consider to be essential for training ML teachers and also raise concerns about future training of ML teachers.
Keywords: contextual attributes; mathematical literacy; reflection; teacher training
Introduction
In 2003, the Department of Education (DoE, 2003) indicated that the introduction of a new curriculum was intended to be an international benchmark fostering the necessary knowledge and skills to participate in and contribute to a democratic society and economy. Globally, both developed and developing countries have engaged in curriculum revisions to take into account the knowledge and skills needed in a globalising 21st century (Gadebe, 2005). As a progressive economy in this century, South Africa was faced with large numbers of the population showing low levels of competence in mathematics. Since a lack of numerical competences has a negative effect on employment and economic development, it was incumbent on the government to take appropriate action to address this issue. In South Africa all pupils in Grades 10, 11 and 12 have to choose between either mathematics or ML as part of their National Senior Certificate curriculum.
According to the Department of Education (DoE, 2003) ML contributes to economic success. Learners will become citizens who can negotiate and function in the economic world with everyday mathematical calculations and problems. Learners are expected to use their skills "to enact their citizenry in a rapidly advancing scientific and technological world once they leave schooling" (Vithal & Bishop, 2006:3).
When the subject ML was introduced in 2006 there was an initial flurry of activity, with many universities offering formal programmes for retraining teachers, who wanted to take on the task of teaching ML in schools. In KZN, the DoE tasked two HEIs to develop programmes towards the ACE ML, in a bid to train sufficient teachers to teach the influx of pupils, who previously had not studied any form of mathematics in the Further Education and Training (FET) Phase. In-service teachers in KZN were identified by the DoE to attend the two-year part-time ML programmes. Subsequently, all DoE funding was phased out and the universities no longer offer part-time ACE ML qualifications. Presently there are no in-service programmes to reskill teachers in order to teach ML in KZN. There is also a silence regarding the continued professional development of those teachers who were retrained in the initial programmes. In this article, the two ACE qualifications will be examined in the light of recent literature, and suggestions will be made and concerns raised for the future training of teachers of ML. The research question that guides this study is: how can HEIs ensure quality teacher training for ML in order to serve the needs of South African pupils?
Background
Since the subject ML was introduced in 2006 as a compulsory subject for those pupils who do not enrol for mathematics in Grades 10-12, many well-known commentators such as Jansen (2011) and Ramphele (Child, 2012) have criticised the subject, because they perceive it to be a simpler form of mathematics. However, ML was intended for pupils who would otherwise not have engaged with any mathematics applications after Grade Nine level (Brombacher, 2010; North, 2013). As pointed out by North (2013), before the advent of ML, only 60% of pupils in the FET band chose to study Mathematics, made up of 10% who did Higher Grade Mathematics, and 50% who chose Standard Grade Mathematics (North, 2013:155). ML is described as follows in curriculum documents (DBE, 2011:8):
The competencies developed through Mathematical Literacy allow individuals to make sense of, participate in and contribute to the twenty-first century world - a world characterised by numbers, numerically based arguments and data represented and misrepresented in a number of different ways. Such competencies include the ability to reason, make decisions, solve problems, manage resources, interpret information, schedule events and use and apply technology.
These descriptions reveal that, "a life-preparation orientation, in which contextualisation in everyday-life situations is central, is a prevalent feature of the ML curriculum" (Venkat, 2010:55). A life-preparation perspective emphasises that ML seeks to produce pupils who will be participating citizens, contributing workers and self-managing people (DoE, 2003). Thus, a curriculum that attains these goals will develop pupils' skills at accessing, using, interpreting and critically assessing numerical information used in real-life contexts. There is an expectation that by engaging in life-related applications, pupils will not be intimidated when they encounter these contexts in their current or future lives, but will use it to make informed decisions.
The preceding discussion illustrates the need for teachers themselves to be clear about what they see the purpose of ML to be. In their study on teachers' views about the relationship between content and context in ML, Graven and Venkat (2007) identified a spectrum of four ML-teaching practices, which differ according to the nature of the link between content and context. These are: the context-driven agenda (to explore contexts that are relevant to pupils' current and future needs); and content and context driven agendas (to explore a context so as to deepen maths understanding and to learn maths (new or General Education and Training (GET) and to deepen understanding of that context); the mainly content-driven agenda (to learn mathematics and then to apply it to various contexts); and the content agenda (to give pupils a second chance to learn the basics of mathematics). Teachers' agendas are driven by their conceptions of the purpose of ML, and it is these conceptions that will ultimately affect the extent to which the curriculum will succeed. Teachers who believe ML to be 'mathematics for dummies' will clearly display the content agenda stream (Graven & Venkat, 2007). On the other hand, teachers who believe that ML can help pupils access and understand mathematically-based information, will draw upon activities involving numerical, graphical, statistical or spatial mathematical reasoning and arguments in their classrooms.
In order to understand how contexts are used in an ML classroom, we offer the framework discussed below (Bansilal, 2013; Bansilal & Debba, 2012).
A framework to describe the use of contexts in mathematical literacy
We draw on the work of Duranti and Goodwin (1992:3) in the field of linguistics, to discuss contexts. They use the term 'focal event' to identify the phenomenon being contextualised:
When the issue of context is raised it is typically argued that the focal event cannot be properly understood, interpreted appropriately, or described in a relevant fashion, unless one looks beyond the event itself to other phenomena.
The context is thus a frame for the event being examined and provides resources for its appropriate interpretation. It involves two entities: a focal event and a field of action within which the event is embedded. Duranti and Goodwin (1992:6-8) have identified attributes of contexts that need to be attained in order to participate in the contextual domain. Below we outline four attributes of contexts used in ML that need to be attained, using examples from previous ML contextualised tasks (see also Bansilal & Debba, 2012, for a more detailed account):
1. Contextual language. This refers to words or phrases, which hold a particular meaning within the context. Examples of the use of contextual language in ML tasks are provided below:
- 'Base occupancy' in accommodation bookings refers to the number of people that can stay in the room/chalet without incurring additional fees.
- '10 mg per kilogram of body weight, with up to four doses per day' is a phrase used in calculating the dosage of paracetamol that can be used (DBE, 2011:117).
2. Contextual signifiers refer to the signifiers used in the context to convey specific information, and which have a meaning that is bound by the parameters of the context. One example is given below:
The definition of the infant mortality rate appearing in the 2009 Grade 12 KZN ML trial examination paper (KZN DoE, 2009:9) was "the number of infant deaths during the first year of life per thousand live births". In the task, the statistics of infant mortality between 2004 and 2008 due to different illness was presented in a table form. In order to answer the questions, pupils needed to understand that, for example, the numeral 2 that was given for measles indicated that two children out of every 1,000 children that were born in 2004 (excluding still-born) died of measles within their first year. These numerals have a specific meaning that is bound to the context, and is different from the way it is used in a whole number discourse for mathematics.
3. Contextual rules are bound to the context and need to be interpreted within the context by the pupil, such as the description of the dosage of paracetamol and the definition of mortality rate appearing above. A further example of such a rule is given below.
The calculation of the body mass index of a person. In order to classify people as under- or overweight, we use the concept 'Body Mass Index (BMI)'. A person's BMI index is defined as a person's weight (in kilograms) divided by the square of the person's height (in metres).
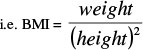
4. Contextual graphs are graphs used to present information about the context.
We consider these attributes as those tools that can be used with other contextual resources for understanding focal events located in contexts. Thus, in addition to engaging with the mathematics, ML pupils need to engage with these contextual resources. Hence, teachers of ML need more than just mathematical knowledge for teaching, and this argument is developed in the section that follows.
Mathematical literacy knowledge for teachers
Ball, Thames and Phelps (2008:395) use the term "mathematical knowledge for teaching" (MKT) to refer to "the mathematical knowledge needed to carry out the work of teaching mathematics". Their perspective is that MKT comprises two domains, namely subject matter for teaching and pedagogical content knowledge. Subject matter for teaching has been further divided into two subdomains of common content knowledge, which is "mathematical knowledge and skill used in settings other than teaching" and specialised content knowledge, which is "mathematics knowledge and skill unique to teaching" (Ball et al., 2008:399-400). They provide examples of common content knowledge: this kind of knowledge is apparent when teachers are themselves familiar with and understand the work that they assign to their pupils. Specialised content knowledge is beyond the knowledge taught to pupils and includes "understanding different interpretations of the operations in ways which students need not explicitly distinguish" (Ball et al., 2008:400). Depaepe, Verschaffel and Kelchtermans (2013) offer a comparison between the constructs described by Ball et al. (2008) and Shulman (1986).
According to Depaepe et al. (2013:13), MKT differs from Shulman's notion of pedagogical content knowledge (PCK). Shulman's concept of PCK was theoretical, whereas Ball et al. (2008) attempted to "refine and empirically validate PCK". Also, PCK and content knowledge are separated into two categories in Shulman's model whereas in the Ball et al. (2008) model, both PCK and content knowledge are integrated in the mathematics knowledge that teachers need to know for teaching. Intrinsic in the sense of MKT refers to the necessity of reflection.
Reviews of studies based on mathematics knowledge for teaching and our own conceptual analysis of ML topics, have convinced us of the role of three components: content knowledge, pedagogic content knowledge, and reflective practice), in ML teacher professional development programmes. These are elaborated below.
ML content knowledge
There are two aspects to ML content knowledge. Firstly, ML content knowledge involves knowledge of the "basic skills topics" mentioned in the curriculum documents (DBE, 2011:13) that is used to model relationships appearing in ML contexts.
Secondly, ML content knowledge also includes knowledge of the "application topics" provided in the curriculum document for ML (DBE, 2011:13). The application contexts are set within the topics of finance, measurement, maps and plans, data handling and probability.
Thus, ML teachers are required to teach the mathematics embedded in basic skills topics. The framework of Ball et al. (2008) provides a detailed description of the kinds of knowledge that mathematics teachers need. However, in addition, their knowledge of the contexts would include understanding of the contextual language, contextual signifiers, contextual graphs and contextual rules, in various settings. Furthermore, they need to be able to recognise arguments and reasoning used by people who are normally participants in the contextual domain. For example, discussions about tax tables would be set around the current regulations and rules pertaining to the law, or discussions about rules used to calculate scores in the case of rain during a cricket match, might also be informed by the ways in which the contextual attributes operate in reality.
ML pedagogic content knowledge
We describe this as the knowledge needed by the teacher to successfully mediate the teaching of the ML content. In discussing his seminal notion of PCK, Shulman (1986:9-10) explains as follows:
[...] for the most regularly taught topics in one's subject area, the most useful forms of representation of those ideas, the most powerful analogies, illustrations, examples, explanations, and demonstrations - in a word, the ways of representing and formulating the subject that make it comprehensible to others [...]. Pedagogical content knowledge also includes an understanding of what makes the learning of specific topics easy or difficult: the conceptions and preconceptions that students of different ages and backgrounds bring with them to the learning of those most frequently taught topics and lessons [...] teachers need knowledge of the strategies most likely to be fruitful in reorganizing [sic] the understanding of pupils [in order to deal with misconceptions].
The implication of Shulman's (1986) views on ML teaching is that the ML teacher also needs to know about the teaching of the mathematics entailed in the "basic skills topics" (DBE, 2011:13). Since the term 'basic skills topics' refers to mathematical skills that pupils have developed prior to their studies in ML, the implication is that ML teachers need to have a foundation of PCK for Senior Phase mathematics. Since many pupils who opt for ML have done poorly in mathematics at Grade Nine level, ML pupils are likely to have many misconceptions about the mathematics in the basic skills topics, which would hinder them from working with certain ML tasks. Hence an ML teacher ought to be able to teach mathematics at Senior Phase level as well, so that continuity can be established, and teachers will be able to guide pupils through the transition between phases.
The contextual attributes framework describeed earlier helps us understand some of the challenges of mediating the ML contextualised tasks with pupils. In view of Shulman's (1986) description, it is clearly incumbent on the teacher to be able to mediate the contextual signifiers, rules, language, and graphs with their pupils. Teachers need to be able to recognise similarities between certain contextual rules, and to be able to recognise which ones are more difficult than others, and why.
Contextual rules are often presented verbally, and these need to be translated into a numerical procedure, such as the rule to calculate the appropriate dosage of paracetamol, for example, is '10 mg per kg of body weight', given a weight of 39 kg, requires one to work out 10 x 39 = 390 mg. A further contextual rule appearing in the same task is that in syrup form paracetamol contains "120 mg per medicine measure (medicine spoon) (5 ml)", which has to then be translated into another procedure of dividing the total number of mg by 120 mg (390 ÷ 120) to give one the number of 5 ml doses that is needed (DBE, 2011:117). At this stage a pupil would need to make a decision about whether to round up or round down the quotient obtained.
In such tasks, teachers need to decide how they could help pupils decode the verbal contextual rules into mathematical operations. In the case of the contextual rules, which differ for each context, an ML teacher must decide whether pupils need further practice in carrying out a specific contextual rule using different numbers in order to understand which quantities are required for substitution into the procedure, or whether a pupil is able to cope with decoding the rule and carrying it out without any intervention by the teacher. Other decisions that a teacher could make could be about grouping tasks with similar rules together, so that similarities in the rules and language can be utilised to provide consolidation of these rules.
Another demand on ML teachers is that of designing appropriate and relevant tasks. Teachers know the context of the lives of their pupils and are best placed to design tasks that can help to fulfil the mandate of ML. In seeking to help pupils become "astute consumers of the mathematics reflected in the media" and other places (DBE, 2011:8), the teacher can decide on contexts that are relevant and appropriate to his/her pupils' situations. However designing tasks for ML requires much skill, ensuring that crucial information is presented clearly; in presenting necessary contextual rules in the simplest form; in providing meaning for the contextual language that is used; and in ensuring that any special meaning associated with contextual signifiers is clearly communicated.
Reflective practice of teachers
We also recommend that a crucial component of professional development programmes should be reflections in and on practice by the teachers. Thompson and Thompson (1994) point out that the relationship between a teacher's and a pupil's ways of knowing is a reflexive one. As pupils develop their understanding, their interactions with the teacher influence the way in which the teacher understands a concept. Steinbring (1998) provides insight into these mechanisms that facilitate learning of both pupils and teachers during a mathematics lesson. A modification of Zaslavsky's (2009) depiction of Steinbring's model is reproduced in Figure 1.
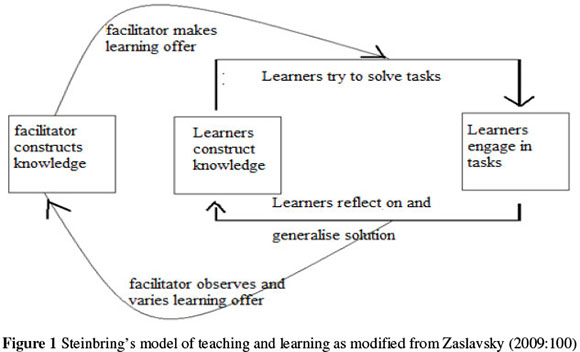
Figure 1 illustrates that the teacher's (facilitator's) learning is "an outcome of their observations of pupils' engagements in tasks" and their reflections on pupils' work (Zaslavsky, 2009:107). While pupils learn by engaging in a task, interpreting and making sense of their solutions, and reflecting on and generalising them, the teacher learns from observing the process pupils encounter, varying the learning offers, and reflecting upon the entire process. There are two loops of learning that are represented in this adapted model, one showing the learning by reflection of the pupils, and a second showing the learning of the teacher by reflection and observation of the process encountered by the pupils.
Hence, reflection can be seen as central to teachers' construction of knowledge. Thompson and Thompson (1996) suggest that teachers can come to understand a mathematical idea, in a way that enables them to teach it conceptually through sustained and reflective work with pupils and with the key ideas. As teachers reflect on the key ideas, their knowledge of the content is deepened. As they reflect on how the pupils interacted with the tasks, their PCK is strengthened over time.
As teachers develop habits of reflection, they learn to be critical of their own assumptions and knowledge. For Brookfield (1995), critical reflection involves 'hunting' the assumptions that underpin our teaching practices. This process involves questioning the assumptions and practices that seem to make our teaching lives easier, but actually work against our own best long-term interests. Paradigmatic assumptions are the hardest of all assumptions to uncover, because, as Brookfield (1995:2) explains,
[t]hey are the basic structuring axioms we use to order the world into fundamental categories and we seldom recognise them as assumptions, even after they have been pointed out to us. Instead, 'we insist that they're objectively valid renderings of reality, the facts as we know them to be true'.
Professional development programmes need to provide opportunities for teachers to engage in critical reflection about the ML they teach, about its purpose, how they teach it, and why they teach it in the way they do. We now briefly consider two ACE programmes that were offered in KZN Province, as an example of programmes run in the past. Data and findings from existing studies are highlighted to identify issues of future concern.
The past
This section reports on lessons learnt from two ML professional development programmes run by two universities in KZN Province, using data that emerged from related studies about these ACEs. We also refer to data from interviews that were analysed in two Master's dissertations by Brijlal (2014) and Thembela (2013). Interviews with Teachers 1 to 7 appear in Brijlal's study (2014), while interviews with ML teachers 8 to 10 appear in Thembela's study (2013). We use the shorthand T8, for example, to represent Teacher 8.
The two ACEs that were delivered in KZN were structured differently. Both qualifications consisted of 120 credits at NQF level 6. The cascade model was utilised in both universities, where university lecturers trained tutors who in turn went out into the field to train teachers either on Saturdays or in block sessions during holidays. As the teachers had been identified by the DoE, most of them were teachers of subjects that were in the process of being discontinued. The teachers' mathematics skills were, on the whole, not strong. Some teachers felt that a stronger background in mathematics content would have facilitated their understanding of ML. In Thembela's (2013) study, one teacher described her experience of realising the importance of a concept in Shape and Space:
I asked him 'what is a prism' and I don't know if he was shocked by me asking [...] I didn't understand it, I didn't do maths at school [...]. It made me study more of Shape and space [because] it was the one subject that was difficult for me. I didn't know these volumes - [in] what [way] and how am I going to explain to the kids what [...] those things [are] so concerning the tiling, which relates to the real life, [or] the volume of [...] for instance a can of coke, how much liquid must be in there [...] that was the new thing I learnt, it helped me a lot (T9: Thembela, 2013).
The teacher explained that the tutor was shocked that she did not know what a prism was, but this experience motivated her to work harder at the section so that she could handle the real life applications of the concept.
Another teacher from Brijlal's (2014) study found the opportunities for integration of mathematics across knowledge strands exciting.
In terms of content knowledge it added to my content in terms of the maths it self. With that content, I was able to use that to empower my learners in the classroom [...]. In terms of history, in terms of space and shape, where by I took the Taj Mahal [...] I was shocked to find the building inside is only 56 metre square, I was able to work out whether the length is short [and] using [what I learnt in] the programme, I was able to work out the formula (T2: Brijlal, 2014).
The first university offered three 30-credit content courses. The fourth module was designed as an ML pedagogical content module that enabled teachers to experience the curriculum imperative of combining content and context in order to develop mathematical competencies and to develop reflective skills. All teachers were required to have at least three years' prior teaching experience, where the emphasis was on reskilling teachers in a new subject area. The emphasis on content in the first ACE showed a leaning towards the imperative of skilling teachers in the content required for a particular curriculum, thus Ball et al.'s (2008) sections of specialised content knowledge and knowledge of content and curriculum were addressed; however, the section on knowledge of content and teaching was presumed to have been assimilated by the teachers during their prior teaching experiences. The teachers worked through many contextualised tasks, which they could later facilitate with their own pupils. This was done in order to help them become familiar with the contextual language, rules, signifiers and graphs pertinent to particular contexts. The participants welcomed the close alignment of the programme with the curriculum (Brijlal, 2014). Many of the teachers from the first ACE found it helpful that the textbook they used in the programme was one that they would later teach from. It provided a sense of direction for the teachers and gave them ideas about how they could approach the teaching of the same topics:
the lectures were very relevant to us as teachers, when we did the same thing in the class, it was not something out of context from the class, very practical and we were able to relate it to learners (T1: Brijlal, 2014).
The topics that were covered [reflected] what the learners were going to do in class [...] the teaching methods we learnt there like the methods you teach the learners [such as] to do the area or the perimeter (T4: Brijlal, 2014).
The comments by teachers 1 (T1) and 4 (T4) reported in Brijlal (2014) suggest that they appreciated the close alignment of the content and PCK to the school curriculum, because it helped them directly in their teaching. Another teacher, T2, found the project work that was part of the assessment in a module very practical and relevant to his ML lessons. The teacher (T2) continued to use the model that was built to scale for demonstrations in his ML classroom.
However, teachers were concerned about future support, and said that they would welcome more direct help in future, that was closely aligned to the curriculum delivery in teaching:
We should have an additional course to update our knowledge as the new work comes in [...] [We need] more training such that they don't teach [...] just the basic content but go into past year papers; because textbooks just give you a watered-down [sic] version, and the examiners will start chopping and changing question into different ways to challenge the children, so what they need to do is work with papers and show us exactly, the new students, how to handle it and how to give the learners the best knowledge (T5: Brijlal, 2014).
The second ACE consisted of eight 16-credit modules, four of which focused on content knowledge, one of which was devoted to PCK; two of which were on general pedagogy and one of which was a research model designed to improve the teachers' pedagogical practices. A section of the study revealed that there was a low correlation between the content and general pedagogy modules, and an even lower correlation between the content modules and the research module (Webb, Bansilal, James, Khuzwayo & Goba, 2012). This indicates that a teacher who understood the content was not necessarily capable in pedagogical skills. The reflective research module results also indicated that teachers were unused to descriptive and critical reflection (Webb et al., 2012). In fact, many teachers did not see the benefit of the modules based on reflective practice and learning theories in both ACEs. Some felt that these modules were not useful because they felt it involved "too much of reading" (T4), or "more theory and I didn't enjoy that" (T1).
One teacher recounted that a friend dropped out because he could not handle the amount of reading that was required:
my friend dropped [out] because he said "I cant read, I'm not a person who is good in reading. So I only need something to work on, like figures to solve problems [...] because I am a problem solver, not a researcher" (T8: Thembela, 2013).
This reluctance of teachers to read about theories of learning and to engage in reflections is supported by a study (Bansilal & Rosenberg, 2011), which found that many of the teachers' reflections were limited to descriptive writing and descriptive reflections (Hatton & Smith, 1995), where they simply stated the problem without giving much thought to its causes. However, all the teachers stated that their reflection skills improved and they saw new value in reflection, showing that they were starting the process of becoming reflective practitioners (Bansilal & Rosenberg, 2011).
Research emanating from the second ACE revealed that many teachers struggled with some of the real life concepts, as well as with some basic mathematics concepts. Bansilal (2011) investigated ML teachers' understandings of the inflation rate signifier. The findings revealed that most teachers were able to carry out a one-step calculation using the inflation rate concept, but struggled to use the inflation rate signifier in more complicated calculations. Bansilal (2011) also found that some teachers had weak conceptions of the basic mathematics concept of percentage and that this hindered them from attaining a robust understanding of the inflation rate signifier.
In terms of understanding contextual rules, a study by Bansilal and Debba (2012) identified three demands associated with contextual rules: the complexity of the rule, the degree of familiarity with the rule, and access to crucial information required in the rule. Furthermore, it was found that successful engagement with contextual rules was also influenced by the way in which the rule was used (Bansilal, Mkhwanazi & Mahlabela, 2012). In their study with 108 teachers, Bansilal et al., (2012) found that 82% of the teachers were able to use the contextual rule in an arithmetic manner by substituting the relevant inputs and calculating the outputs. However, only 55% of the group were able to use the rule in an algebraic manner, which required transformation of the contextual rule before the calculations could be carried out. Hence, these studies suggest that the in-service teachers need opportunities to work with these contextual signifiers and rules, which they are required to teach.
The studies by Brijlal (2014) and Thembela (2013) revealed that teachers found that their own personal understanding of ML was improved as an outcome of their participation in the ACE programmes. Three teachers from Thembela's (2013) study articulated their views about the differences between teaching mathematics and ML:
it made me realise the importance of learning ML by all people in society, as opposed to knowing your pure maths excellently [sic], because [...] the two subjects were not aimed to [address the pursuit of] the same purpose[s] in life [...] the educational courses of fered were also implicit in trying to help us use the correct classroom teaching strategies, [where] even a layman can easily see the connection of ML to everyday life situations (T8: Thembela, 2013).
It is the one subject that links with the real life situation that happen around us [...] there was this issue, which was recently discussed, about our increment, [which] it has been increased by 6.8%, so I asked them how much is 6.8% of your salary [...] but they didn't know that. So I said ML is [...] important, because it really links with what is happening around us (T9: Thembela, 2013).
[...] besides ML is a new subject for the learners, but for educators themselves [as well]. I am always complaining about teachers, where [...] teachers fail to calculate the increment of [their] salary, the salary increment when they are given percentages. [One can see] teachers going on strike and you find that the 3% they want is just a small amount [chuckles] (T10: Thembela, 2013).
These teachers' comments reveal that they saw ML as being relevant and of direct benefit to their own lives. Hence, it is expected that these teachers would convey a more informed view of ML than a teacher, who had not reflected in similar ways about the potential value of the subject.
Despite the benefits offered by these programmes, there have been no further plans by government agencies to continue with such programmes. In our study, it was identified that at the time of the delivery of the ACEs in KZN, there were 67,358 pupils in Grades 10, 11 and 12, who were studying ML in KZN schools. According to the ratio of 1 teacher to 30,6 pupils, the projection was that there ought to be 2,207 teachers trained to teach ML in KZN.
During the duration of the programme in KZN, 2,142 teachers were registered for the two programmes. Of these, 1,596 graduated with a 74,5% pass rate, but this was still woefully short of the total of trained ML teachers required at the time for the Province. In a previous study (Bansilal, Goba, Webb, James & Khuzwayo, 2012), focusing on one district in KZN, we looked at four phases of the joint project. The success rate of the joint project was defined as the percentage of teachers who passed and were teaching ML in terms of the total number of teachers needed. It was found that the joint undertaking was only 13% successful in ensuring that a sufficient number of teachers were trained to teach ML in that district. These figures suggest that there is a great shortage of trained ML teachers. However, presently there are no in-service programmes to reskill teachers, and there are no plans for further government funding for ML skills training.
The future
Although the DBE has indicated that they would prefer more Grade 12 students to take up mathematics instead of ML, the reality is that the numbers of learners opting to study ML has steadily increased from 267,236 or 47.1% of Grade 12 candidates in 2008, to 324,097 or 57.3% of the candidates in 2013 (DBE, 2014). This increase indicates that the education system requires an even larger number of ML teachers than those who were trained and are currently teaching ML. Considering that there are no pre-service ML teacher training initiatives run by the two HEIs in KZN, the situation is very serious indeed. HEIs and the DoE need to urgently work together to offer professional development programmes for practising teachers as well as to expand pre-service teacher programmes in ML. This study has presented some lessons that have been learnt in the delivery and follow up research component of two ACE programmes, which we hope can contribute to future programme developments for ML teachers.
The study shows that in terms of ML content knowledge, it is not sufficient for teachers to know only basic mathematics, but they need to develop competence in working with various contextual rules. In terms of PCK, many teachers appreciated the close alignment of the programme to the school curriculum, and future programmes may consider utilising some elements of the model employed in the first ACE. The teachers also identified further help that they required in terms of specific curriculum and assessment issues related to the interpretation of curriculum documents and assessment policies. These point to the need for regular departmental workshops with ML teachers, so that they are kept abreast of changes and revisions to policies. These workshops could also target PCK skills associated with the teaching of contextual attributes.
A change in the higher education landscape has narrowed down possibilities for those teachers who may have wanted to pursue formal post-graduate studies in areas linked to ML. The MRTEQ policy (Department of Higher Education and Training (DHET), 2011) has brought about changes in levels and purposes of qualifications in teacher education. The previous ACE, in addition to serving the purpose of retraining and upgrading, also opened up a pathway for teachers with only a three-year college diploma to higher postgraduate education qualifications. However, the new policy has replaced the ACE with an Advanced Certificate (FET teaching), which caters for teachers who "want to specialise in a new teaching subject not studied in a prior professional teaching qualification" (DHET, 2011:29). This certificate route is therefore only for retraining and if teachers wanted to study further, they would need to study for another qualification before entering the higher education pathway.
This qualification, at level 6, aims at retraining or upgrading teachers with an emphasis on the teaching specialisation, which in this instance would be ML. The knowledge mix of the qualification focuses on the field of specialisation: a minimum of 96 credits is set aside for "specialised disciplinary, pedagogical and practical learning" (DHET, 2011:31). Thus, content and PCK is catered for, and 16 credits could be allocated for "the study of education and its foundations, as well as general pedagogical learning and situational learning" (DHET, 2011:31), whereas eight credits are mandatory for work-integrated learning. Fundamental learning is not a prerequisite for the qualification; however teachers are expected to be computer literate before they enrol for the course.
A key contribution to teacher learning is reflection, and the study revealed that there was room for improvement with respect to teachers' reflective skills. In-service teachers need to be given structured opportunities to reflect on their own learning, so as to deepen their understanding of the content as indicated by T2 in Brijlal's study (2014). Structured opportunities for reflection on the learning of their learners, will also contribute to the development of PCK. The study has shown that teachers need more help with developing reflective competence. Reflection about the aims and purposes of ML helps teachers understand the nature of the subject. The interviews with participants in the two programmes indicate that they have clear conceptions about ML, its purpose and role in their own lives. Such conceptions about the nature of ML are more likely to influence their ML teaching approach in a manner that is aligned to the goals of ML with regards to life preparation and orientation.
Although reflective learning is not specifically mentioned in the MRTEQ framework, HEIs could utilise the opportunity offered by the work-integrated learning to focus on the development of teachers' reflective skills. We recommend that teacher development programmes have two components, one of which could be held at university campuses or off-campus sites, where teachers are taught topics in mathematics by means of the contexts which appear in the application topics. However, teachers need a second component, which works together with the first, but which focuses on their classrooms and is organised according to the development of reflective practice. This component is mentioned in the MRTEQ document as work-integrated learning (DHET, 2011) and this alludes to an important dimension of teacher learning, namely that of building up of teachers' own content knowledge and PCK by reflecting on what takes place in their classrooms. Mentoring should be used to support practicing teachers, who are struggling with the content they are teaching, so that teachers can build up their knowledge, while also developing reflective practice.
Conclusion
The introduction of ML in South African schools was intended to address the lack of access to mathematics for the larger part of the population. Reasons of social justice as well as economic justice underpinned this introduction. It is therefore imperative that teacher-training initiatives be aligned with the objectives of the subject. In this article we have analysed some of the demands of teaching the subject ML in order to identify what we consider to be essential elements of a teacher development programme for ML teachers. It is hoped that the study has shed some light on what future programmes should include in order to meet the demands of the subject.
The lessons from the two ACEs that have been offered in KZN suggest that HEIs need to align their qualifications with the framework and principles of ML knowledge for teaching, where there is a balance among the aspects suggested by Ball et al. (2008), while also taking into account the demands of the contextual attributes framework in a manner which is in line with the MRTEQ policy. The method of delivery should include rigorous content knowledge, with an emphasis on teacher reflection, which is supported by visits to the teachers. However, the curriculum of the qualifications should be comprehensive enough to span the vicissitudes of curriculum change in the classroom.
The dire need for trained ML teachers in every school needs to be addressed by further government-funded initiatives; however, HEIs need to be allowed to control access to the programmes so that the dropout rate is minimised. A further suggestion for the future could be for the Department of Higher Education to facilitate a vertical trajectory for motivated ML teachers so that they can access higher academic qualifications. The study also recommends that the pre-service ML teacher training be expanded to meet some of these demands.
References
Ball DL, Thames MH & Phelps G 2008. Content Knowledge for Teaching. What Makes It Special? Journal of Teacher Education, 59(5):389-407. [ Links ]
Bansilal S 2011. Unpacking Mathematical Literacy teachers' understanding of the concept of inflation. African Journal for Research in Science, Mathematics and Technology Education, 15(2):179-190. [ Links ]
Bansilal S 2013. Understanding the contextual resources necessary for engaging in mathematical literacy assessment tasks. Journal of Education, 58:45-66. [ Links ]
Bansilal S & Debba R 2012. Exploring the role of contextual attributes in a Mathematical Literacy assessment task. African Journal for Research in Mathematics, Science and Technology Education, 16(3):302-316. [ Links ]
Bansilal S, Goba B, Webb L, James A & Khuzwayo H 2012. Tracing the impact: A case of a professional development programme in Mathematical Literacy. Africa Education Review Special Issue: Quality Education for Social Development, 9(Supplement 1):S106-S120. [ Links ]
Bansilal S, Mkhwanazi T & Mahlabela P 2012. Mathematical literacy teachers' engagement with contextual tasks based on personal finance. Perspectives in Education, 30(3):98-109. [ Links ]
Bansilal S & Rosenberg T 2011. An exploration of teachers' reflections about their problems of practice. Progressio, 33(2):91-105. [ Links ]
Brijlal P 2014. An exploration of the contribution of the Advanced Certificate in Education in Mathematical Literacy programme towards the professional development of teachers in KwaZulu-Natal. Unpublished M.Ed dissertation. Durban: UKZN. [ Links ]
Brombacher A 2010. National Senior Certificate Mathematics and Mathematical Literacy: A Balance between Dreams and Realities. Report presented at The National Science and Technology Forum (NSTF). Proceedings of Workshop on Science, Technology, Engineering and Mathematics (STEM) Education, April 2010, KwaZulu-Natal. Available at http://www.nstf.org.za/ShowProperty?nodePath=/NSTF%20Repository/NS TF/files/Workshops/2010/proceedingsapril2010.pdf. Accessed 20 November 2014. [ Links ]
Brookfield SD 1995. Becoming a critically reflective teacher. San Francisco: Jossey-Bass. [ Links ]
Child K 2012. We need to heal wounds to move forward. The Times, 7 June. [ Links ]
Depaepe F, Verschaffel L & Kelchtermans G 2013. Pedagogical content knowledge: A systematic review of the way in which the concept has pervaded mathematics educational research. Teaching and Teacher Education, 34:12-25. [ Links ]
Department of Basic Education (DBE) 2011. Curriculum and assessment policy statement. Further Education and Training Phase Grades 10-12. Mathematical Literacy. Pretoria, SA: Government Printing Works. Available at http://www.education.gov.za/LinkClick.aspx?fileticket=jB/jGQ35UgI=. Accessed 20 November 2014. [ Links ]
DBE 2014. The Ministerial Task Team Report on the National Senior Certificate (NSC). Pretoria, SA: DBE. Available at http://www.education.gov.za/LinkClick.aspx?fileticket=YLrgfGldINU%3D&tabid=36. Accessed 20 November 2014. [ Links ]
Department of Education (DoE) 2003. National Curriculum Statement, Grades 10-12 (General): Mathematical Literacy. Pretoria, SA: DoE. [ Links ]
Department of Higher Education and Training (DHET) 2011. The minimum requirements for teacher education qualifications. Government Gazette, 553(34467). Available at http://www.dhet.gov.za/Teacher%20Education/Policy%20on%20Minimum%2 0Requirements%20for%20Teacher%20Education%20Qualifications%20%282 011%29,%2022%20July%202011.pdf. Accessed 20 November 2014. [ Links ]
Duranti A & Goodwin C (eds.) 1992. Rethinking context: Language as an interactive phenomenon. Cambridge: Cambridge University Press. [ Links ]
Gadebe T 2005. New Curriculum focuses on Africa. Bua News, 2 August. Available at http://www.southafrica.info/about/education/curriculum-190705.htm#.VG2fomd8eZQ. Accessed 20 November 2014. [ Links ]
Graven M & Venkat H 2007. Emerging pedagogic agendas in the teaching of mathematical literacy. African Journal of Research in Mathematics, Science and Technology Education, 11(2):67-84. [ Links ]
Hatton N & Smith D 1995. Reflection in teacher education: Towards definition and implementation. Teaching and Teacher Education, 11(1):33-49. [ Links ]
Jansen J 2011. Sinking deeper into mediocrity. Times LIVE, 23 February. Available at http://www.timeslive.co.za/opinion/columnists/2011/02/23/sinking-deeper-into-mediocrity. Accessed 20 November 2014. [ Links ]
KwaZulu-Natal Department of Education (KZNDoE) 2009. Grade 12 KZN Mathematical Literacy Grade 12 trial Examination Paper 2. [ Links ]
North M 2013. Dispelling the myths of mathematical literacy. In Z Davis & S Jaffer (eds). Proceedings of the 19th Annual Congress of the Association for Mathematics Education of South Africa (Vol. 1). Cape Town: Association for Mathematics Education of South Africa (AMESA). [ Links ]
Shulman LS 1986. Those who understand: knowledge growth in teaching. Educational Researcher, 15(2):4-14. [ Links ]
Steinbring H 1998. Elements of epistemological knowledge for mathematics teachers. Journal of Mathematics Teacher Education, 1(2):157-189. [ Links ]
Thembela TE 2013. An exploration of the role of the Advanced Certificate in Education on the professional development of Mathematical Literacy teachers. Unpublished M.Ed theses. Durban: UKZN. Available at http://researchspace.ukzn.ac.za/jspui/handle/10413/9662?mode=full. Accessed 20 November 2014. [ Links ]
Thompson AG & Thompson PW 1996. Talking about rates conceptually, Part II: mathematical knowledge for teaching. Journal for Research in Mathematics Education, 27(1):2-24. [ Links ]
Thompson PW & Thompson AG 1994. Talking about rates conceptually, Part I: A teacher's struggle. Journal for Research in Mathematics Education, 25(3):279-303. [ Links ]
Venkat H 2010. Exploring the nature and coherence of mathematical work in South African Mathematical Literacy classrooms. Research in Mathematics Education, 12(1):53-68. [ Links ]
Vithal R & Bishop AJ 2006. Mathematical Literacy: A new literacy or a new mathematics? Pythagoras, 64:2-5. [ Links ]
Webb L, Bansilal S, James A, Khuzwayo H & Goba B 2012. Some insights concerning mathematical literacy teacher training. Proceedings of 12th International Congress on Mathematical Education (ICME). Seoul, South Korea, 8-15 July [ Links ]
Zaslavsky O 2009. Mathematics educators' knowledge and development. In R Even & DL Ball (eds). The professional education and development of teacher of mathematics. New York: Springer Science & Business Media. [ Links ]














