The need for invariant assessments in South African education

 

 

Graham A Dampier

Department of Childhood Education, University of Johannesburg, South Africa gadampier@uj.ac.za

 

 

---

ABSTRACT

Presently, a plethora of instruments designed to assess a mathematical skill, disposition, or competence prevail in South Africa. Yet few of them adhere to the basic requirements of the unidimensionality and invariance of measures. The Marko-D is a mathematical instrument designed to test learners between the ages of 4 and 8. The instrument, thus far, appears to adhere to the central tenets of fundamental measurement, which hold that a test should be invariant across different groups of people and that it should measure a single variable to a level of precision that is useful practically and theoretically. The Marko-D was used to assess the mathematical competence of 249 foundation phase pupils. Even though we cannot conclude at this stage that the Marko-D satisfies the requirements of invariance and unidimensionality completely, this study provides an elucidation of the need for invariant assessments in South African education.

Keywords: foundation phase learners; invariance; mathematical competence; Rasch Model

---

 

 

Introduction

The scientific status of the social sciences, or the human sciences, has been called into question since its inception in the 19th century^I (Hollis, 1994; Winch, 1958; Wittgenstein, 1922; Benton & Craib, 2011). Fundamental measurementII seeks to address the scientific status of various disciplines in the social sciences by attempting to establish instruments of measurement and assessment that are consistent in time and for different cultures (Bond & Fox, 2007). Fundamental measurement is the commitment and endeavour, both within the social sciences and the natural sciences, to establish measures that are obtained directly from the object of study. Andrich (1988) argues that with the careful application of the Rasch model it is possible to attempt to produce fundamental measures of various phenomena in the social sciences. Measures that can be considered fundamental are by and large elusive and necessarily entail developing scales of measurement and instruments of assessment that produce a direct and stable quantification of phenomena that do not waver in consistency, or that have little variation between people of similar ability (Andrich, 1988; Rasch, 1960; Wright, 1994; Wright & Stone, 1979; Wright & Stone, 1999).

Currently, we do not have one test for basic mathematical skills that can be used in different cultures; yet scientific instruments of measurement, such as thermometers and barometers, produce consistent readings and results everywhere on earth. There is, at best, in the field of foundation phase mathematics, a loose collection of tests available in South Africa that are vaguely related by their interest in a particular phenomenon or subject area. We certainly do not lack readily available instruments to test various mathematical skills. We have the Trends in Mathematics and Science (TIMSS), the Annual National Assessments (ANAs), psychological tests such as the Wechsler Individual Achievement Test (WIAT), and many others with which to test the ability of our learners. What we lack is a single reliable measure of what children in the foundation phase can do with numbers. We lack an instrument to determine whether a particular pupil lacks a basic set of mathematical skills that are necessary for progress through the grades that constitute the foundation phase.

Fundamental measurement consists of a set of axioms that are designed to advance the endeavour of measuring phenomenon consistently in time and in different social and cultural contexts (Bond & Fox, 2007). Unidimensionality and invariance are its most important tenets. Unidimensionality holds that only the ability of persons and the difficulty of items should affect the outcome of a test or assessment (Andrich, 1988; DeMars, 2010; De Ayala, 2008; Bond & Fox, 2007). Anything else would be considered noise, hazardous to the accuracy of measurement, and ultimately unscientific (Linacre, 2002). A test that is unidimensional should measure a single variable "to a level of precision that is of some practical or theoretical use" (Andrich, 1988:10). Let us suppose that we have a unidimensional test that claims to measure a core mathematical ability. If this test is translated into three different languages and used to test participants from each, and if each version of the test measures a common latent trait, then the pattern of responses to the items of the test in the different languages should be consistent, given that the population of each language is representative, heterogeneous in terms of ability, and that sample error has been reduced as much as possible. The test should be invariant for those three groups of people and the respective languages should not obscure our ability to measure the latent trait.

Allalouf, Hambleton and Sireci (1999) explain that little research has been conducted on why translated tests produce different results in different languages. They argue that few studies have dealt with detecting the causes of variance across different languages, because few studies use translated tests. The linguistic diversity in South Africa requires that any attempt at large scale standardised assessment, in the vein of the TIMSS, Progress in International Reading Literacy Study (PIRLS), and the ANAs, engages in the process of translating tests into various language. The linguistic diversity of South Africa is potentially a rich source of data in cross-cultural test adaptation and the endeavour of producing invariant measures of people.

This article reports on the attempt to arrive at measures of mathematical competence that are invariant and unbiased across three different language groups. I proceed by elucidating, however briefly, unidimensionality and invariance from the perspective of Rasch measurement theory, before conducting tests of invariance and differential item functioning (Clauser & Mazor, 1998; Rudas & Zwick, 1997; Swan-son, Clauser, Case, Nungester & Featherman, 2002, Fidalgo, 2011). This is done to establish whether data gathered with the Marko-D adheres to the basic tenets of measurement, i.e. that an instrument should not be easier for one group of people as opposed to another, and that a test should produce measures that do not vary from one group of people to another. Lastly, I evaluate the implications that the invariance of measures has on assessing the mathematical competence of foundation phase learners in South Africa.

The Rasch Model

The pervasive tenet of the Rasch model, and other models of measurement that fall within the ambit of Item Response Theory (IRT), is that a single dimension is accessed when the items of a test measure one discrete construct or latent trait (DeMars, 2010: 38; De Ayala, 2008; Andrich, 1988). Unidimensionality maintains that a single continuous attribute, dimension or construct is the object of study when an instrument, which adheres to this assumption, is used to assess people who possess varying degrees of the construct being measured. Unidimensionality delimits the measurement of a latent trait to the ability of people, and the difficulty of items used to measure the latent trait and discriminate between people of different levels of ability. Instruments remain faithful to this tenet when they distinguish effectively between people of various levels of ability without discriminating at the same time between people of different genders, cultural groups, linguistic backgrounds or socio-economic status. Two variables, then, are used to describe the latent trait, the ability of people and the difficulty of items.

Another inherent requirement of the Rasch model is that a test should not be easier for one group of people than another. The Rasch model holds that items should only discriminate between people according to their ability and not according to their membership of a particular group of people (Bond & Fox, 2007; De Ayala, 2009; Zumbo, 1999; Rudas & Zwick, 1997). A particular item of a test should make a distinction between two people of differing abilities and should not distinguish between two people of the same ability who belong to two different genders or cultural groups, or who speak different languages. Stated differently, if various translations of a test are used to measure a latent trait consistently, then there should be no statistically significant difference in individual responses to the items of each version of the test (given that sample error has been contained as far as possible and that each population is heterogeneous in ability).

In order for a test that was developed in Germany and translated into English, isiZulu and Sesotho to maintain its validity, it must measure the latent trait without discriminating between people of the same ability who speak different languages. It must allow for the possibility that two people of the same ability, who belong to different language groups, will get an item correct. The likelihood of a person getting an item correct should depend only on their level of ability and not on the language they speak.

When a latent trait is measured consistently across different groups of people the difficulty of the items should remain invariant. There should be no fluctuation in the hierarchical ordering of items from one group of people to the next. When the difficulty of a given item varies from one group of people to the next, and when this variance exceeds model error, its unidimensionality is thereby violated (De Ayala, 2008). This would suggest that different responses would have been elicited not by varying degrees of ability, but by group membership (assuming there is no sampling error from group to group). Bond and Fox (2007:92) explain that the "principles underlying the plots of person and item invariance across testing situations is exactly that underlying the detection of Differential Item Functioning (DIF). When an item's difficulty estimate location varies across samples by more than the modelled error, then prima facie evidence of DIF exists".

In another sense, DIF will be present in the items of a test when the latent trait is measured differently in different languages. If the language of a test improves the likelihood of a person getting an item correct, or if language presents an added dimension of difficulty, one cannot argue that the test is unidimensional (Zumbo, 1999). In this instance the language of a test will either aid or impeded the ability of a person to respond correctly to an item. The test will be measuring two dimensions the latent trait and the language ability of persons being tested.

The property of invariance is essential to fundamental measurement and is intimately related to the reliability and validity of instruments. According to De Ayala (2008:3), instruments with high reliability will yield consistent results over a series of repeated measurements: "...If these repeated measurements varied wildly from one another [...] they would be considered to have low consistency or to have low reliability". The validity of measures are defined by the degree to which they "are actually manifestations of the latent variable" (De Ayala, 2008:3). Even though the invariance of an instrument does not prove that it is valid in the strictest sense, the consistent measurement of a latent trait over a series of testing sessions certainly strengthens the case that an instrument displays content and construct validity (Field, Miles & Field, 2012). De Ayala writes that (2008:3)

Thurstone noted that a measuring instrument must not be seriously affected in its measuring function by the object of measurement. In other words, we would like our measurement instrument to be independent of what it is we are measuring. If this is true, then the instrument possesses the property of invariance [italics in the original].

 

Method

Design

The study reported here is part of a larger panel research project, which is concerned with measuring the conceptual growth of learners between the ages of five and nine. The longitudinal development of mathematical, literacy and science concepts is studied over four years (Henning, 2012). An instrument developed, normed and standardised in Germany is used to assess the mathematical competence of individuals, and to capture their growth.

The authors of the test describe it as a process-orientated diagnostic instrument that can be used to measure an individual's mathematical abilities either repeatedly over time or cross-sectionally (Ricken, Fritz & Balzer, 2011). The "Mathematical and Arithmetic Competence Diagnostic" instrument (or MARKO-D the German acronym) measures ability with a stable "scale of mathematical achievement" that was "developed on the basis of theoretical suppositions and empirical data" (Ricken et al., 2011:256). The MARKO-D was designed and validated with the principles of the Rasch model in mind. Its developers were striving to arrive at a unidimensional test of mathematical competence. The test captures five incremental levels of mathematical ability, which begin with a basic assessment of the ability to use the counting sequence. Level two assesses understanding of the ordinal number line, level three the knowledge of cardinality, level four the use of the part-whole concept of number, and level five the understanding of congruent intervals, which refers to the ability to understand that any given number is constituted by intervals on the number line, for instance the number "9" can be analysed into "3" and "6" or "4" and "5" (Fritz, Ehlert & Balzer, 2013).

Subjects

The research is conducted at an urban South African public school where children receive home language instruction in one of two languages, either isiZulu or Sesotho. The learners at the school are representative of the surrounding community, which includes households that are spread across the socio-economic spectrum. This conveniently sampled population constitutes a heterogeneous testing sample in terms of ability and socio-economic status.

The dataset consists of 249 responses to 54 variables. Two home languages, isiZulu (129) and Sesotho (120), are represented in this data. Learners between the ages of five and seven are tested in their mother tongue (i.e. either in isiZulu or Sesotho), while learners of 8 and 9 years are tested in English. The reason is that at the end of grade 3 learners at this school will be required (in line with the South African curriculum) to switch to the first additional language (FAL), which in this instance is English. To assist with the transition to English, learners are taught mathematical concepts in both their particular home language and the FAL (Henning & Dampier, 2012) in a pedagogical model of translation that spurns the mixing of languages within sentences (Henning, 2012).

In addition, since the school follows the national public school curriculum strictly, grade R learners receive little, if any, guided instruction in mathematics. Our data can, then, be analysed according to (1) the home language of the participants, (2) the language in which they were tested, and (3) exposure to the formal instruction of mathematics.

Preliminary analysis

Before conducting the DIF analysis the Rasch model of measurement was used to determine whether the data fît the assumptions and parameters of a unidimensional model. An initial analysis of the data yielded a near to ideal value for infit (.99), but a high outfit value of 1.05, which indicates that 50% more variation was observed when unexpected responses were elicited by items. Table 1 contains the summary statistics of the MARKO-D before nine items were excluded for eliciting erratic responses from persons at extreme ends of the latent trait continuum. Even though the summary statistics suggest that the items of the instrument are effective in eliciting on target responses, it was decided to forward those items that were eliciting unexpected responses from persons to a panel of experts for review (Linacre, 2002).

 

 

The high measure of outfit has been reduced to 1.00 after excluding those items that were most underfitting. Nine underfitting items were excluded on the basis that they all had high outfit measures (>1.02) that were statistically significant (>2.00). When items display a large degree of underfit in the outfit column, it may suggest the presence of an element of noise in those items (Linacre, 2002). This can mean that something other than the latent trait is affected by the way in which people are responding to these items. It is important to note that these items are not excluded from the test entirely and interminably, but that they will be subject to review by a panel of experts (De Ayala, 2008). It is likely that the translation of the construct from the original German to English, and then into isiZulu and Sesotho may have obscured the accuracy of these items.

Data analysis

Invariance across the languages and grades

Even though we require more information to establish definitively what the norms and standards of the MARKO-D^III in South Africa are, its general validity as an instrument for testing mathematical competence is being reaffirmed. With the exception of a few, all the items of the MARKO-D fit the assumptions and parameters of the Rasch model. This bodes well for a test that was developed in Germany on the basis of cutting-edge theory and empirical research into the early development of mathematical competence. The theoretical basis of the instrument posits that certain mathematical abilities may be invariant across cultures (Ricken et al., 2011). The test measures mathematical competence according to five levels of ability, which are acquired sequentially over time (Fritz et al., 2013). Each level is embedded in the level(s) above it and an individual learner must acquire the skill associated with level one before they can move on to level two, and so on.

Our analysis of the (in)variance of responses across the different groups of people tested, proceeds with the assumption that the MARKO-D can be used to measure the mathematical competence of this sample at different points in time and arrive at similar results.

The invariance of a test is determined by comparing the responses of one group of people to another. This comparison is represented visually by a scatterplot and is measured statistically with a correlation coefficient. Figure 1.1 represents a comparison of people who speak isiZulu as a home language to people who speak Sesotho. The individual items are plotted between 95% confidence intervals (or bands), which indicate the extent to which individual items are invariant.

 

 

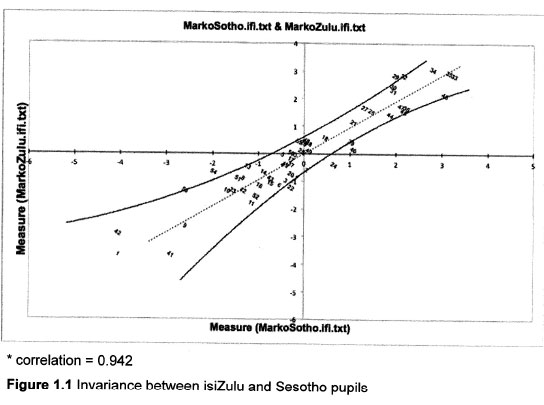
Since only four items fall outside of the confidence intervals (α = 0.942), we can argue that the MARKO-D does not violate the assumption of unidimensionality when it is used to measure mathematical competence in isiZulu and Sesotho speaking learners.

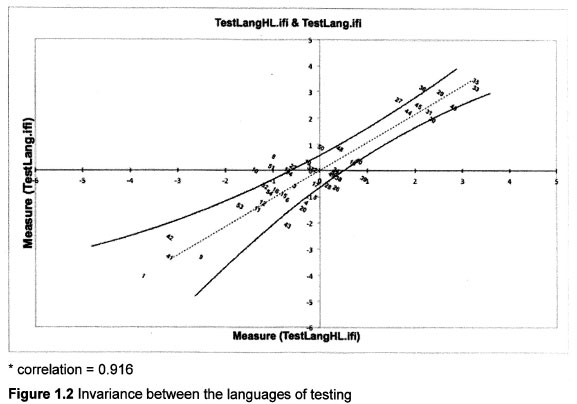
A similar picture emerges when we compare people who were tested in English to people who were tested in their home language. Figure 1.2 presents a visual representation of this comparison. Even though the variation between those learners tested in their home language and those tested in English is comparably higher than the juxtaposition of isiZulu and Sesotho speakers (regardless of the language of testing), the degree of variance is slight enough (α = 0.916) to argue that the test remains invariant when learners are tested in different languages.

 

 

 

 

 

 

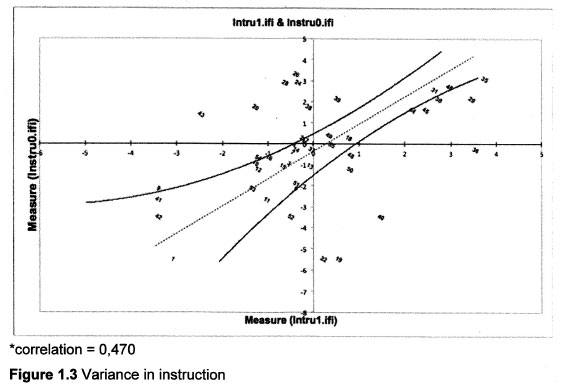
By contrast, when we compare participants who have not received formal instruction in mathematics (i.e. Grade R learners) to those who have (i.e. Grade one and two learners), the variance between these groups is too large and too significant. This represents the first indication that the MARKO-D is not measuring mathematical competence in a way that is consistent for learners who have received instruction in mathematics (grade ones and twos) and those who have not (grade Rs). There is notably little structure in the response patterns of these two groups to the items, since they are scattered all over the diagram (α = 0.470).

The degree of variance in this comparison is to be expected since Grade R learners have not been taught a formal syllabus of mathematical concepts and skills, while Grade one and two learners have been exposed to the national curriculum. The expectation is that Grade R learners will think differently about mathematics and are likely to react differently to mathematical problems.

To arrive at a more robust idea variance within our data, we conducted a DIF analysis for speakers of the different languages and the participants who belong to different categories of instruction (namely, those with exposure to a formal syllabus and those who have never been exposed to formal instruction in mathematics).

Differential item Functioning

Conventionally analyses of DIF are used to determine whether a test exhibits bias, which is normally assessed by comparing distinct groups of people defined by a common categorical characteristic, such as gender, culture, language, socio-economic status or even age. According to De Ayala (2008:324), item bias or test bias is defined statistically as "the systematic under- or overestimation of a parameter", which departs from the lay connotation of unjust a priori partiality. Even though bias can be assessed for individual items (DIF), or for a test as a whole (differential test functioning), the psychometric preference falls on analysing the bias of individual items (De Ayala, 2008). However, for practical significance it is useful to analyse the bias of a test more generally (Camilli & Penfield, 1997), since this will indicate the extent to which, in the main, a test is invariant across different groups of people. For the sake of rigour it is necessary to analyse the parts if one wants to have a complete idea of the whole.

We define DIF in terms of individual items. DIF refers to differences in responses to items garnered from people with the same ability who belong to different groups. Sinharay and Dorans (2010:474) define DIF as referring to "a psychometric difference in how an item functions for two groups," while Van den Noortgate and De Boeck (2005:443) write that, "Differential Item Functioning refers to the phenomenon that, conditionally on the latent ability, the probability of successfully answering a specific item may differ from group to group." The presence of an extraneous variable that causes people from different groups of the same ability to react differently to a single item, violates the tenet of unidimensionality, since it serves as a source of additional difficulty (Zumbo, 1999).

The aim of conducting a DIF analysis is to identify an item or a series of items that are likely to exhibit measurement bias, since these items cast doubt on the invariance of measures. Bond and Fox (2007:70) argue that invariance "remains the exception rather than the rule" in the human sciences. This state of affairs casts doubt on the scientific rigour of instruments used to arrive at context-independent measures of people across a range of latent traits (Bond & Fox, 2007:70): "[t]his context-dependent nature of estimates in human science research, both in terms of who was tested and what test was used, seems to be the complete antithesis of the invariance we expect across thermometers and temperatures".

When an item is identified as exhibiting DIF and for this reason obscuring the accuracy of measures, it is necessary to evaluate whether the variance in responses to the item warrants revision, or, in more drastic situations, omission from the test completely. De Ayala (2008:324) recommends that items exhibiting DIF be "reviewed by a panel of experts to determine whether the source of an item's differential performance is relevant or irrelevant to the construct being measured".

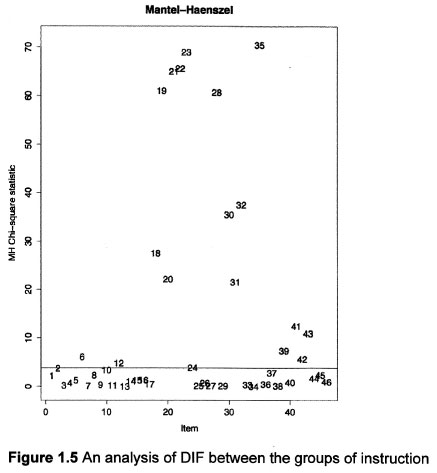
Using the difR 4.3 package (Magis, Beland & Raiche, 2012) we analysed our data according to the specifications of the General Mantel-Haenszel Chi-square statistic to determine which items display notable DIF in: firstly, a comparison of isiZulu and Sesotho speaking pupils; and, secondly, in a comparison of pupils who have not received formal instruction in maths (i.e. Grade R pupils) to pupils who have. We compared results from this analysis to output obtained from Randall Penfield's software package DIFAS 4.0 (Penfield, 2007), as well as output from Winsteps (Lin-acre, 2009). The results were consistent with the same items flagged for DIF in each software package. We prefer to report the output obtained from R. The reason for this is that R is famous for its visual representation of data. Figures 1.5 and 1.6 are simple, clear indications of the extent to which individual items display DIF.

 

 

Home language

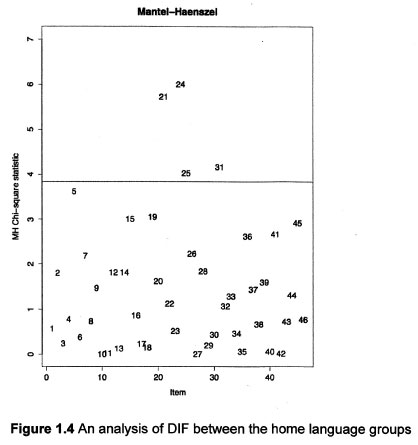
Table 3 presents the Mantel-Haenszel Chi-square statistics for an analysis of DIF between isiZulu and Sesotho responses to the items of the Marko-D.

 

 

 

 

The threshold for detecting items that were displaying DIF was found to be 3.8415 (with a significance level of 0.05 and below). Items display large DIF when they measure above this threshold, while at the same time obtaining a significant p value. It is evident that items v5 (marginally), v24, v29, v30 and v39 all measure above the threshold, and have statistically significant p-values to boot. These four items are individually more difficult for one language group as opposed to the other.

Figure 1.5 indicates that for the most part, the items of the MARKO-D remain invariant when they are used to measure the mathematical competence of isiZulu and Sesotho home language speakers, which considering the lexical, grammatical and syntactic differences of these languages is significant, as it suggests that the latent trait remains invariant when the home language of the pupil being tested varies. More data will show to what extent this is true for other home languages, including English, Afrikaans and perhaps even German.

Instruction

A comparison of learners who have received formal mathematics instruction with learners who have not, indicates that exposure to the "learning" of mathematics alters responses to the items of the test dramatically. Table 3 presents output of a DIF analysis conducted in R. At a glance, it is evident that many items display significant variation from one group to the next. As many as 18 items display patterns of response that differ significantly from one group to the next, which suggests that the property of invariance is violated when the status of a child's exposure to the formal teaching of mathematics changes.

The threshold of detection was again a measure of above 3.8415. Items were flagged for DIF when they exceeded this Mantel-Haenszel value and when they obtained a p value of 0.05 and below.

Figure 1.5 is a representation not only of significant variation between the different groups of instruction, but also an indication of the extent to which DIF is detected in particular items. In Figure 1.5 the greatest extent of DIF was detected in item 24 (or variable 29), which exhibited a Mantel-Haenszel value of 6.3193. Interestingly, items 5 (v5), 24 (v29) and 25 (v30) display less DIF when the two groups of instruction are compared than when the home languages are compared. This may negate the possibility that a common source of DIF is present in the two comparisons. We can argue then that the DIF detected in the two comparisons are independent and unique to the groups in question.

 

Discussion

The property of the invariance of instruments used in the social sciences to measure the ability of people or the presence of a latent trait (for example (e.g.) anxiety or stress) has become essential to ensuring that the study of human beings is as scientific and as accurate as the measurement of distance, temperature and weight in physics. This study has illustrated that the linguistic resources of a country, such as South Africa, can be valuable in the attempt to produce invariant measures across different languages, which will enhance our ability to produce invariant measures of unidimensional constructs in different cultures. The process of adapting tests to suit the cultural and linguistic context of a diverse South African society, if done rigorously, can contribute significantly to the process of attaining fundamental measures of people. At least, the work on translated tests that will stem naturally from test adaptation will assist researchers in other social contexts with detecting invariance across languages and in dealing with this productively.

While our findings are by no means conclusive, it appears that the Marko-D may well prove in the future to measure mathematical competence consistently in people who speak different languages and who hail from different cultures. As exciting as this prospect is, we do not claim at this very instant to possess a test that is invariant across different languages. The performance of grade Rs in this test suggests either that more work needs to be done to ensure that the instrument measures that latent trait consistently in people who have not entered school as yet, or it suggests that instruction fundamentally alters the way we do maths.

The jury, we argue, is still out on whether the current approach to instruction improves our ability to think mathematically or whether the language of mathematics we use somehow impedes the fluidity of thinking mathematically - a proclivity we are all born with (Carey, 2009; Dehaene, 2010; Dehaene & Brannon, 2011; Spelke, 2000). In a separate study we argue, in line with the theoretical framework that informs the Marko-D, that all children enter grade R with a more or less similar ability to do maths (Dampier & Mawila, 2012). Differences that are apparent can be addressed at this very early age, since at this point very little formal orientation into the discourse of mathematics, with its cumbersome and confusing terminology, would have taken place. This argument is well rehearsed in continental and American neuropsychology and in the works of various cognitive psychologists, such as Le Corre, Spelke and Carey.^IV What is more, the grade Rs in this study managed to get some of the more challenging items of this test right when their older counter parts struggled.

Future studies will confirm whether the property of invariance is something the Marko-D can lay a legitimate claim to and whether instruction in mathematics, as it is currently conceived and conceptualised in South Africa, does indeed impede the ability of children to reason clearly when they are tasked with solving mathematical problems. What is certain, however, is that instruments which are more scientific are required in a country such as South Africa, where ordinary children are given the extraordinary burden of being among the worst performing mathematicians in the world. With more scientific instruments of measurement and assessment we will be able to identify whether performance in our system is the same for all cultures and the various languages of instruction. Our instruments may be faulty, because we assume they assess the same phenomena in different people without exhibiting item bias.

The veritable absence of scientific rigour in the manner of assessment that prevails in South Africa, and elsewhere, is enough to cast sufficient doubt on the validity and reliability of standardised testing of foundation phase pupils. Standardised tests treat different people as being the same. The differences between people are overlooked, which from a statistical point of view amounts to committing a fatal analytic error. This error can only be remedied by following the strict principles of fundamental measurement and reconceptualising our approach to testing accordingly.

 

Acknowledgements

Funding for the project was derived from an NRF grant No. 78827 entitled "Language in the Foundation Phase", as well as from a Zenex Fund grant for a project entitled "Conceptual Development of Children in the Early Grades of School: How Language Features in the Learning of Mathematics".

 

Notes

I The various arguments levelled against the claims to scientific status made by the social sciences are perhaps best captured by Wittgenstein's (1922:89) seventh proposition: "What we cannot speak of we must pass over in silence". Hollis (1994:42) argues that the "driving idea of Logical Positivism was that, because claims to knowledge of the world can be justified only by experience, we are never entitled to assert the existence of anything beyond all possible experience. It can never be probable, let alone certain, that there are, for instance, unobservable structures, forces, instincts or dialectical processes".

II This refers to the process of obtaining direct measures or values of a phenomenon or latent trait that does not rely on previous measurements.

III A German acronym for Mathematical and Arithmetic Competence Diagnostic instrument.

IV Here it is worth mentioning the work of: Feigenson, Carey and Spelke (2002); Feigenson, Dehaene and Spelker (2004); Le Corre and Carey (2007); Le Corre, Van de Walle, Brannon and Carey (2006); Spelke (2003); Starkey (1990); Carey (2001); and Carey (2004).

 

References

Allalouf A, Hambleton RK & Sireci SG 1999. Identifying the causes of DIF in translated verbal items. Journal of Educational Measurement, 36(3):185-198. doi: 10.1111/j.1745-3984.1999.tb00553.x        [ Links ]

Andrich D 1988. Rasch Models for Measurement. London: SAGE Publications.         [ Links ]

Benton T & Craib I 2011. Philosophy of Social Science: The Philosophical Foundations of Social Thought. New York: Palgrave Macmillan.         [ Links ]

Bond TG & Fox CM 2007. Applying the Rasch Model: Fundamental Measurement in the Human Sciences (2nd ed). London: Routledge.         [ Links ]

Camilli G & Penfield DA 1997. Variance estimation for differential test functioning based on Mantel-Haenszel statistics. Journal of Educational Measurement, 34(2):123-139. doi: 10.1111/j.1745-3984.1997.tb00510.x        [ Links ]

Carey S 2009. The origin of concepts. London: Oxford University Press.         [ Links ]

Carey S 2004. Bootstrapping and the origin of concepts. Daedalus, 133(1):59-68. doi: 10.1162/001152604772746701        [ Links ]

Carey S 2001. Cognitive foundations of arithmetic: Evolution and ontogenesis. Mind and Language, 16(1):37-55. Available at http://postcog.ucd.ie/files/Susan%20Careyt.pdf. Accessed 13 April 2014.         [ Links ]

Clauser BE & Mazor KM 1998. Using statistical procedures to identify differentially functioning test items. Educational Measurement: Issues and Practice, 17(1):31-44. doi: 10.1111/j.1745-3992.1998.tb00619.x        [ Links ]

Dampier GA & Mawila D 2012. Test items and translation: Testing mathematical concepts reliably? South African Journal of Childhood Education, 2(2):35-57.         [ Links ]

De Ayala RJ 2008. The theory and practice of item response theory (methodology in the social sciences). London: The Guilford Press.         [ Links ]

Dehaene S 2010. The number sense: How the mind creates mathematics (2nd ed). New York: Oxford University Press.         [ Links ]

Dehaene S & Brannon E (eds.) 2011. Space, time and number in the brain: Searching for the foundations of mathematical thought. London: Academic Press.         [ Links ]

DeMars C 2010. Item response theory. Cape Town: Oxford University Press.         [ Links ]

Feigenson L, Carey S & Spelke E 2002. Infants' discrimination of number vs. continous extent. Cognitive Psychology, 44(1):33-66. http://dx.doi.org/10.1006/cogp.2001.0760        [ Links ]

Feigenson L, Dehaene S & Spelker E 2004. Core systems of number. Trends in Cognitive Sciences, 8(7):307-314. http://dx.doi.org/10.1016/j.tics.2004.05.002        [ Links ]

Fidalgo AM 2011. A new approach for differential item functioning detection using Mantel-Haenszel methods: The GMHDIF program. The Spanish Journal of Psychology, 14(2):1018-1022.         [ Links ]

Field A, Miles J and Field Z 2012. Discovering statistics using R. London: Sage Publications Ltd.         [ Links ]

Fritz A, Ehlert A & Balzer L 2013. Development of mathematical concepts as basis for an elaborated mathematical understanding. South African Journal of Childhood Education (Special Issue), 3(1):38-67.         [ Links ]

Henning E 2012. Learning concepts, language, literacy in hybrid linguistic codes: The multilingual maze of urban grade 1 classrooms in South Africa. Perspectives in Education, 30(3):70-79.         [ Links ]

Henning E & Dampier GA 2012. Linguistic liminality in the early years of school: Urban South African children 'betwixt and between' languages of learning. South African Journal of Childhood Education, 2(1):101-120.         [ Links ]

Hollis M 1994. The philosophy of social science: An introduction. Cape Town: Cambridge University Press.         [ Links ]

Le Corre M & Carey S 2007. One, two, three, four, nothing more: An investigation of the conceptual sources of the verbal counting principles. Cognition, 105(2):395-438. http://dx.doi.org/10.1016/j.cognition.2006.10.005        [ Links ]

Le Corre M, Van de Walle G, Brannon EM & Carey S 2006. Re-visiting the competence/performance debate in the acquisition of the counting principles. Cognitive Psychology, 52(2):130-169. http://dx.doi.org/10.1016/j.cogpsych.2005.07.002        [ Links ]

Linacre JM 2002. What do infit and outfit, mean-square, and standardized mean? Rasch Measurement Transactions, 16(2):878. Available at http://www.rasch.org/rmt/rmt162f.htm. Accessed 13 April 2014.         [ Links ]

Linacre JM 2009. Winsteps (Version 3.68) [Computer Software]. Beaverton, OR: Winsteps.com.         [ Links ]

Magis D, Beland S & Raiche G 2013. Collection of methods to detect dichotomous differential item functioning (DIF) in psychometrics. Package 'difR': version 4.5. Available at http://cran.r-project.org/web/packages/difR/difR.pdf. Accessed 26 February 2013.         [ Links ]

Penfield DR 2007. Differential item functioning analysis system (DIFAS 4.0). Available at http://www.education.miami.edu/facultysites/penfield/index.html. Accessed 26 February 2013.         [ Links ]

Rasch G 1960. Probabilistic models for some intelligence and attainment tests. Copenhagen: Nielsen and Lydiche.         [ Links ]

Ricken G, Fritz A & Balzer L 2011. MARKO-D: Mathematik und Rechnen - Test zur Erfassung von Kompetenzen im Vorschulalter. In M Hasselhorn & W Schneider (Hrsg). Tests & Trends 9. Jahrbuch der pädagogisch-psychologischen Diagnostik. Frühprognoseschulischer Kompetenzen. Göttingen. Hogrefe.         [ Links ]

Rudas T & Zwick R 1997. Estimating the important of differential item functioning. Journal of Educational and Behavioural Statistics, 22(1):31-45. doi: 10.3102/10769986022001031        [ Links ]

Sinharay S & Dorans NJ 2010. Two simple approaches to overcome a problem with the Mantel-Haenszel statistic: Comments on Wang, Bradlow, Wainer, and Muller. Journal of Educational and Behavioural Statistics, 35(4):474-488. doi: 10.3102/1076998609359789        [ Links ]

Spelke ES 2000. Core knowledge. American Psychologist, 55(11):1233-1243. doi: 10.1037/0003-066X.55.11.1233        [ Links ]

Spelke ES 2003. What makes us smart? Core knowledge and natural language. In D Gentner & S Goldin-Meadow (eds). Language in mind: Advances in the study of language and thought. Cambridge, MA: MIT Press.         [ Links ]

Starkey P 1990. Numerical abstraction by human infants. Cognition, 36(2):97-127. http://dx.doi.org/10.1016/0010-0277(90)90001-Z        [ Links ]

Swanson DB, Clauser BE, Case SM, Nungester RJ & Featherman C 2002. Analysis of differential item functioning (DIF) using hierarchical logistic regression models. Journal of Educational and Behavioural Statistics, 27(1):53-75. doi: 10.3102/10769986027001053        [ Links ]

Van den Noortgate W & De Boeck P 2005. Assessing and explaining differential item functioning using logistic mixed models. Journal of Educational and Behavioural Statistics, 30(4):443-464. Available at https://ppw.kuleuven.be/okp/_pdf/VandenNoortgate2005AAEDI.pdf. Accessed 13 April 2014.         [ Links ]

Winch P 1958. The idea of a social science and its relation to philosophy. London: Routledge and Keegan Paul.         [ Links ]

Wittgenstein L 1922. Tractatus logico-philosophicus. London: Routledge.         [ Links ]

Wright BD 1994. Where do dimensions come from? Rasch Measurement Transactions, 7(4):325. Available at http://www.rasch.org/rmt/rmt74j.htm. Accessed 13 April 2014.         [ Links ]

Wright BD & Stone MH 1979. Best test design. Chicago: MESA Press.         [ Links ]

Wright BD & Stone MH 1999. Measurement essentials (2nd ed). Wilmington, DE: Wide Range Inc.         [ Links ]

Zumbo BD 1999. A handbook on the theory and methods of differential item functioning (DIF): Logistic regression modelling as a unitary framework for binary and likert-type (ordinal) item scores. Ottawa, ON: Directorate of Human Resources Research and Evaluation, Department of National Defence.         [ Links ]