Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Education
On-line version ISSN 2076-3433
Print version ISSN 0256-0100
S. Afr. j. educ. vol.34 n.2 Pretoria Jun. 2014
A case study on the investigation of reasoning skills in geometry
Berna Canturk Gunhan
Department of Primary Mathematics Education, Dokuz Eylul University bernagunhan@gmail.com
ABSTRACT
The aim of this study is to evaluate the reasoning skills in geometry-related subjects of six 8th Grade students. The study data were obtained at the end of the 2011-2012 spring period in a public elementary school. The study uses a case study with qualitative research techniques to investigate how students use reasoning skills. In this study, six geometry problems were used to collect the study data. The students were asked to think aloud when solving the problems so as to be better able to explain their thoughts. From the data obtained, it was identified that the processes involved when demonstrating reasoning skills showed a number of differences.
Keywords: geometry, reasoning, reasoning skills, teaching geometry
Introduction
Reasoning is a skill that is demonstrated during the advanced stages of thought (Umay, 2003), in other words, during problem-solving processes (Yıldınm, 2000), and which represents high-order mathematical thinking (Kenney & Lindquist, 2000). Webster (1982) also defines reasoning as "the ability to think coherently and logically and draw inferences or conclusions from facts known or assumed" (cited in Mansi, 2003:9). Reasoning skills are an important component of education, and reasoning skills are necessary for understanding mathematics in particular, and they present an important means of developing ideas (National Council of Teachers of Mathematics [NCTM], 2000). Mathematical reasoning refers to the ability to formulate and represent a given mathematics problem, and to explain and justify the solution or argument (Kilpatrick, Swafford & Findell, 2001). According to the NCTM (2000), mathematical reasoning can be gained at the elementary school level. In order to acheive this, during elementary education students should be placed in situations in which they are able to make, refine, and test their own conjectures (Mansi, 2003). Secondary school students must be able to evaluate conjectures and assertions, to reason deductively and inductively by formulating mathematical assertions, and to develop and maintain their reasoning skills (Altıparmak & Öziş, 2005). If their reasoning skills remain underdeveloped, students will come to view mathematics as an aggregate of specific rules, and an ensemble of thoughtlessly executed calculations and drawings (Ross, 1998). In addition, studies indicate that good mathematical reasoning skills are imperative to proof-writing performance (Battista & Clements, 1995; Edwards, 1999; Fischbein & Kedem, 1982; Izen, 1998; Jones & Swafford, 1997; Mistretta, 2000). Toole (2001) and Kramarski, Mevarech and Lieberman (2001), have emphasised that a direct relation exists between reasoning skills and success in mathematics, where individuals who demonstrate better reasoning skills display good problem-solving profiles with the interrelations they are able to identify, while also having better communication skills.
Malloy (1999) described that individuals may use more than one reasoning approach in problem-solving situations. Moreover, their ability to use these approaches and reasoning skills is closely related to the depth of their conceptual knowledge and to their corresponding associative skills (Briscoe & Stout, 2001 ; Gerald, 2002 ; Lithner, 2000). In addition, reasoning is a process that provides depth to the existing body of knowledge (Duval, 1998). Battista (2007) described that educators need to understand students' thought processes in order to provide them with a meaningful education. In addition, Makina and Wessels (2009) stated that understanding students' minds during problem solving improves a teacher's understanding of his pupils. In this process, students can be encouraged to explain why they made certain errors and exhibited certain misconceptions (Molefe & Brodie, 2010). For example, students may sometimes choose the correct problem solving strategy, yet follow the wrong course of action when finding solutions by using information, by finishing reasoning processes before they have been finalized, or by becoming oriented towards familiar solution patterns due to conceptual shortcomings. These situations, commonly known as faulty reasoning, should be investigated closely, as they provide important clues for understanding students' thought processes (Umay & Kaf, 2005). In addition, students experience issues in problem solving due to poor reasoning. Poor reasoning involves unfounded and hasty reasoning processes resulting from insufficient understanding of the subject in question. Students who lack knowledge of what to do and how to solve the problem in these circumstances will add, subtract, multiply, or divide the numbers they see without giving much thought to their reasons for doing so (Russell, 1999 cited in Umay & Kaf, 2005). Işrksal, Koç and Osmanoğlu (2010) revealed that 8th Grade students showed difficulty in solving problems, in demanding a conceptual understanding of reasoning, and in measuring the surface area and volume of cylinders. Mukucha (2010) found in his study in South Africa that most students lacked conceptual understanding and reasoning skills. Similarly, Arslan (2007) noted that students in 6th, 7th and 8th Grades exhibited low-level reasoning skills. These studies have suggested that different methods and techniques are necessary for students to develop reasoning skills. For example, Pilten (2008) has described metacognition-based education to have led to the development of mathematical reasoning, and Maqsud (1998) found that metacognitive strategies influenced low-achieving South African students. Additionally, cooperative learning should be used to improve students' mathematical reasoning (NCTM, 2000; Kramarski et al., 2001). As described by researchers, communication skills are important for the development of students' reasoning skills (Lithner, 2000; Briscoe & Stout, 2001; Aineamani, 2011). For this reason, both teachers and students should be in the habit of asking 'why?', as this question is essential for students to develop their mathematical reasoning skills (Mansi, 2003). Information about a students' reasoning skills helps the teacher develop an opinion regarding the students' thoughts, based on which he or she can review the procedures and techniques used in learning processes, if necessary.
Geometry is an important branch of mathematics. It allows for people to understand the world by comparing shapes, objects and their connections. Goos, Stillman and Vale (2007) have indicated the processes of visualisation and reasoning to be part of in mathematical thinking. Moreover, Duval (1998) has stated that the geometric thinking involves the cognitive processes of visualization and reasoning. Visualization and reasoning are those essential mental skills required for mathematics (Battista, Wheatley & Talsma, 1989), and these cognitive processes are interconnected, promoting students' success in geometry (Duval, 1998). Visualization is a skill that helps students to recognise shapes, to create new shapes or objects, and to reveal relationships between them (Arcavi, 2003). Battista (2007:843) said that geometric reasoning refers to the act of "inventing and using formal conceptual systems to investigate shape and space". Many researchers claimed that visualization can be improved by training (Ben-Chaim, Lappan & Houang, 1988; Brinkmann, 1966) and by using materials (Werthessen,1999; Battista, Wheatley & Talsma, 1982; Ben-Chaim et al., 1988; Onyancha, Derov & Kinsey, 2009; Yıldız, 2009). In addition, visualization and reasoning skills can be improved through the instruction methods (Jones, 2000; Arıcı, 2012; Goos et al., 2007). Furthermore, the NCTM (2000) also recommends the use of Dynamic Geometry Software (DGS) to promote reasoning skills and geometric understanding. The relationships between visualisation and mathematical problem solving (Moses, 1977; Van Garderen & Montague, 2003), as well as between visualization and mathematics achievement (Fennema & Sherman, 1977; Ünal, Jakubowski & Corey, 2009), have been shown in many studies. Furthermore, Kospentaris, Spyrou and Lappas (2011) stated in their study that visualization is important factor that effects the choice of strategy when students undertake geometry tasks. Küchemann and Hoyles (2006) investigated students' mathematical reasoning in geometry and development in their reasoning, by an analyses of students' responses to three annual proof tests. They found that many students made little progress. Tierney, Boyd and Davis (1990) emphasised that three factors effected students' responses were "knowledge, visual perception, logical arguments". Carroll (1998) identified that students who acquired an effective experience in geometry during elementary school were better able to use their reasoning skills to solve geometry problems in secondary education. For this reason, it is important to investigate 8th Grade students' reasoning skills in geometry. As described by Duval (1998), in order to determine the difficulties encountered by students in geometry, it is necessary to identify the cognitive processes that underlie geometric processes. The reasoning skills demonstrated by a student whilst problem solving will allow us to observe the way in which the student associates geometric concepts and by what means they reach a solution. Trends in International Mathematics and Science Study (Acat, Şişman, Aypay & Karadağ, 2011) has stated that a student with reasoning skills must be able to perform the following: identify and use interrelations between variables in mathematical situations; dissociate geometric shapes in order to facilitate the resolution of a geometrical problem; draw the expansion of an object; visualise the transformation of three dimensional objects; and deduce valid results based on the provided information (Analyse); think mathematically and describe anew the results obtained through problem solving and expand on these solutions (Generalise); use mathematical operations in combination and combine the results in order to obtain more advanced solutions (Synthesise); use mathematical results or properties to provide evidence for the validity of an action or the truth of a mathematical expression (Justify); and solve non-routine problems by applying his/her geometrical knowledge and appropriate mathematical processes (Solve Non-routine Problems). In this context, when solving geometry problems, this study aims to investigate whether 8th Grade students display reasoning skills indicated by TIMSS. The results of this study are important for assessing the way in which the students think when solving geometry problems as well as for observing the way in which they demonstrate reasoning skills. Additionally, the study will help teachers to assess whether the students' performance is reflected their reasoning skills. The results also provide for the teachers' self-assessment, and encourage them to reconsider the current techniques used in learning processes. In addition, it is expected that the results of this study will contribute to improving the quality of geometry education in those developing countries with low mathematical performance (e.g. Botswana, Colombia, Ghana, Iran, Saudi Arabia, South Africa, and Turkey) in international exams (e.g. TIMSS).
Methodology
This study employed qualitative research methods. In qualitative studies, the goal is to provide an accurate description of a real situation. To this end, such studies attempt to directly present the opinions of individual participants and to collect data through detailed and in-depth methods (Yıldrım & Şimşek, 2008). As this study investigates the way in which students use reasoning skills, a case study with qualitative research techniques was produced.
Participants
The study was conducted at the end of the 2011-2012 spring terms with six 8th Grade students (3 female and 3 male) receiving their education at a public elementary school that was randomly selected from among schools of a moderate socioeconomic level. The participants were selected from a class with a mathematics teacher capable of effectively implementing the mathematics curriculum, based on his 23 years of experience. The participants were selected according to their level of achievement (high, medium, low) in the mathematics class and their willingness to voluntarily participate in the study. In this respect, the sampling technique used for sampling purposes in this study is the "exception sampling technique". This sampling technique envisages the study of a low number of cases that can be subject to evaluation, but which, at the same time, hold a wealth of information (Yıldrım & Şimşek, 2008). The actual names of the participants are provided in this study. The female participants, in decreasing order of academic performance (i.e. from the highest to lowest performer) were Ceren, Elif and Mine; the male students were Ege, Arda and Baha. They were 14 years old. The information regarding the students was obtained from their mathematics teachers by talking about math achievement levels of students in the previous period (autumn term) and by looking at their mathematics exam score for the spring term.
Data collection tool
The questions used for data collection in this study were multiple-choice examination questions for 8th Grade students, prepared by experts at the Student Selection and Placement Center (ÖSYM) and the Ministry of Education (MNE) and used within the context of an examination ["Level Determination Examinations (SBS)"] performed during the transition to secondary education. This examination was developed in accordance with the elementary school curriculum in order to assess students' higher level thinking skills (Güzeller, 2006). The examination questions allow for an assessment of the adequacy of the student's interpretation, analysis, critical thinking, result prediction, and problem-solving skills, based on his/her educational achievements in class (MNE, 2007). On the other hand, within the scope of the internationally conducted TIMSS examination, the TIMSS mathematics framework has two dimensions: Content Domain (numbers: 30%, algebra: 30%, geometry: 20%, and data and chance-probability: 20%) and Cognitive Domain (knowing: 35%, applying: 40%, and reasoning: 25%) (Acat et al., 2011). Also, in the examination results (especially in the latest reports of TIMSS, in which Turkey is also a participant and is ranked 30th among 49 countries in the TIMSS of 2007), Turkey not only figures below average in all fields of learning, but it also has the lowest average in geometry. This situation necessitates a revision of geometry education (Acat et al., 2011). In Turkey, the distribution of SBS questions applied to 8th Grade students with respect to the learning areas in mathematics is approximately as follows: 20% numbers; 25% geometry; 20% measurement; 15% probability and statistics; and 20% algebra. Within the context of this study, 2 mathematics educators and 1 mathematics teacher were asked to categorise, according to the cognitive processes described in Acat et al. (2011), 15 questions regarding geometry from SBS examination questions that were applied to 8th Grade students in 2009, 2010 and 2011. Prior to the categorisation, example questions were shown to the experts about how TIMSS categorises geometry questions, and about how information was provided regarding cognitive processes. Based on the categorisation they performed, the mathematics educators and mathematics teacher were asked to describe the reasoning skills reflected by the questions that were part of the reasoning cognitive processes. The working definition for reasoning skills provided by Acat et al. (2011), which includes "analysis, generalisation, synthesis, justification, and non-routine problem solving" was used. Table 1 shows the reasoning skills that were assessed.
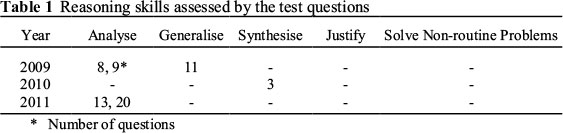
As can be seen in the table, the test questions used in each of the three years did not make use of reasoning skills pertaining to the justification or solving of non-routine problems. As a result of this evaluation, it was observed that the consistency was approximately 91%. The test questions are listed in an Appendix.
Process and data analysis
A clinical interview was performed, while the six students were solving the geometry questions. The clinical interview is a technique structured according to Piaget's clinical method and Vygotsky's educational experience; it aims to study information structures and thought processes (Clement, 2000; Hunting, 1997). The participants were told that their answers to the questions would not be considered as grades, and that the interview notes would only be used to understand their thoughts during problem-solving. The students were then asked to think aloud when solving the problems so as to be better able to explain their thoughts. The researcher also asked them questions when necessary. In addition, questions such as "How did you think of this?" and "How did you draw this?" were asked in order to reveal the students' thought processes. The clinical interviews were performed in a silent environment in the school library and recorded on video. The problem-solving process for each student lasted approximately 30 minutes. For the analysis of the study data, the video records were first transferred to the interview forms without any corrections being performed. An expert then evaluated the extent to which the transferred data and original data were consistent with one another. The data transferred to the interview forms were coded independently by two area experts. The codes that were created by each expert were converted into visual form and associated with one another by using a diagram. Converting the diagram into a visual form through the use of a diagram becomes important with regard to rendering the relations between the emerging concepts and themes more apparent and to reaching certain results based on these concepts, themes, and relations (Miles & Huberman, 1994; Yıldrım & Şimşek, 2008). To calculate the reliability of the data coded by the researcher and field experts, the
Reliability = Agreement / (Agreement + Divergence) formula of Miles and Huberman (1994) was used, and the reliability coefficient was determined as 89%. Among the different qualitative data analysis methods, the content analysis method was used to analyse the data from the video recording. The results obtained from these types of analyses are presented in an organised and interpreted form (Yıldrım & Şimşek, 2008). In order to enrich the data analysis and interpretation, the students who were interviewed were directly quoted, and their statements were compared with the study results. When examining the students' responses, the reasoning skills which TIMSS indicated such as "analysis, generalisation, synthesis" were emphasised.
Results
The questions the students were asked were to assess their skills in analysing, generalising, and synthesising among their different reasoning skills. Their answers are evaluated as follows within the context of these skills.
Among the different reasoning skills, results that are related to analyse
The first question assessed the students' analytical skill from among the reasoning skills indicated by TIMSS. The students were expected to select, from among the given choices, the triangle that satisfied this condition, and which had the largest perimeter. The results of the student responses to this question are shown in Figure 1. Also provided are an analysis of the student's answers, with the resulting sub-themes and categories formed within the context of identifying the relation between the triangle's edges, and finding the triangle with the largest perimeter. These results also include information regarding the students.
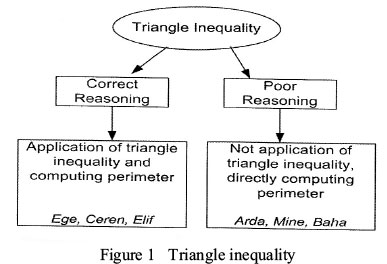
The students employed two different approaches when solving this question. Ege, Ceren, and Elif employed correct reasoning. These students found the triangle with the largest perimeter length by pointing out that the formation of a triangle is based on satisfying the triangle inequality theorem, and then identifying the triangles that satisfied this condition. Ege's interview statement is provided below as an example:
For there to be a triangle, one of the edges must be shorter than the total length of 2 edges and larger than their difference. Let's try this for all of the edges...if we think of L, it is larger than 2 and smaller than 10, so it satisfies this condition; M is bigger than 3 and smaller than 9, so it also satisfies it; N is bigger than 1 and smaller than 7; so it also satisfies it. [From amongst] L, M [and] N: The correct option is D. There is [the] option [of] B, but its perimeter is smaller.
However, Arda, Mine and Baha, demonstrated poor reasoning, by trying to determine the largest perimeter in a direct manner by adding the length of the strips that were given, without determining the relationship between the edges of the triangle. In this question then, these students were unable to associate the adding up the length of three strips with the triangle inequality theorem. They could not use interrelations between variables in mathematical situations. Below is an excerpt from Mine's interview:
Among the strips given in these options, the ones that are the longest will have the largest perimeter, and I will find the answer that way...[She reviews each option according to the length of the strips]...the longest one is option C.
The second test question also assessed the students' analytical skill. In this question, the students were asked to form a cube by using geometric objects. The students were expected to join three-dimensional geometric objects and visualise the transformation of three dimensional objects. Figure 2 shows the sub-themes and categories obtained from the analysis of the student responses.
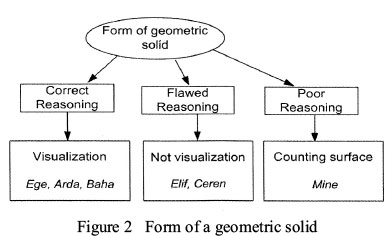
Students employed three different approaches when solving this question. Ege, Arda and Baha formed a cube by visualising the given structures using correct reasoning skills. Arda found the correct answer in a short period by visualising the structures in his mind, and then placing them on top of one another to form a cube. Ege and Baha formed a cube in a similar way. However, the other students did not. Being unable to fully visualise the structures when bringing them together, Elif and Ceren displayed inadequate, or in other words, flawed reasoning. Part of Ceren's clinical interview reads as follows:
If I look at option B...L, M, N... If I a place M here, it will close this location [shows that she is placing M vertically in a location suitable for the cube in the lower section of the N structure]. Empty spaces remain here and there [shows the empty spaces that are one cube in size in front of and behind the 2nd line of the N structure]. If I tip L sideways and place it here, I think it'll work. Yes, it might be the B option.
As can be seen from Ceren's interview, she was not able to perceive the excess in the structure she formed, which she assumed to be correct. Similar to Elif, she chose to place the structures on top of one another; however, she was not able to visualise the section that would form an excess. Mine, on the other hand, attempted to form the required cube by counting the surfaces. However, she was not able to find the right answer, due to poor reasoning. In her clinical interview, Mine stated the following:
I am trying to count the surfaces, but I can't because I am not good at imagining. I am having some difficulties with this question... Now let's try K, L, M...if we place K on top of L, and we place M in front...hmm...actually, the surface areas also match. In my opinion.I say that this option is correct.
The fifth question also assessed analytical skill. In this question, the students were asked to find the situation in which the surface areas did not change as a result of the separation of three dimensional geometric shapes. Figure 3 shows the sub-theme, along with categories obtained from the analysis of the student responses.
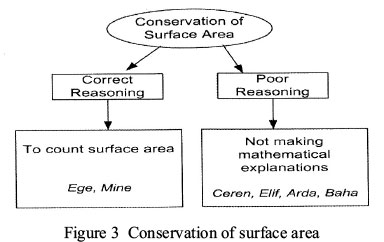
The students employed two different approaches when solving this question. Ege and Mine solved the question through correct reasoning. Both students were able to find the correct answer by calculating whether the same amount of surface area remained on the structure after subtracting the surface area provided by the unit cubes. During the clinical interview, Mine stated that she did not have any difficulties when solving this question, and she mentioned that "When solving this question, my brother's cubes came to my mind. When we played together, we would join the smaller cubes to build larger cubes. That's why I did not have any difficulties in solving this problem." So, Mine's previous experience of concrete materials helped her to visualise during the task. The other students couldn't dissociate geometric shapes. Among the other students, Ceren and Baha demonstrated poor reasoning by stating,"while unit cubes 1, 2 and 4 are located on the sides, unit cube 3 will not change the surface area because it is located in the center" and they did not indicate the correct answer. Elif also demonstrated poor reasoning by saying that "As unit cube 4 is under the large cube, nothing will change if it is removed." Although he provided the correct answer, Arda could not provide a mathematical argument for its validity. He said, "I cannot explain...teacher, I won't be able to [answer] this question" [sic]. For this reason, he was considered to have demonstrated poor reasoning.
The other question that assessed analytical skill was the sixth question, in which the students were asked to find which one of the edges would have the same length when the opened geometric shape is transformed into an enclosed form. Figure 4 shows the sub-theme along with categories obtained from the student interviews.

The students employed two different approaches when solving this question. Ege, Ceren, Elif, and Arda were able to see the edges that would join when creating the enclosed form of the prism, and also the edges of similar length when the edges that formed the bases of the prism were compared. When assessing this situation, the students expressed that among the edges that formed the base of the prism, the edges oriented in the same direction were also of the same length. Based on this observation, it can be said that Ege, Ceren, Elif and Arda were able to visualise the enclosed form of the object. In contrast, Mine and Baha were not able to find edges that would join. As they only considered the edges on the same base in order to find the edges of equal length, they demonstrated poor reasoning and were not able to find the correct answer. Their performance indicates that Mine and Baha hadn't formed the enclosed form of the prism by visualising.
Results related to generalisability skills
The third test question assessed generalisability skills. To solve this question, the students were expected to both identify the existing pattern using the rule of self-similarity and repetition of fractals, and to find a generalisation of the mathematical relation that existed within the pattern. Figure 5 shows the sub-themes and categories based on the analysis of the student interviews.

The students used two different approaches when solving this problem. All of the students were able to see the relation between the processes. However, Ege, Ceren, Elif and Arda were able to identify the pattern in the question and saw that the length of the edges decreased by half. They were then able to determine the generalisation of the mathematical relation to be found in the pattern of the question. This reveals that these four students had thought mathematically and expand on these solutions. Then, by describing the length of the edge of the square they formed in the 10th step, they demonstrated a balance between conceptual and procedural knowledge. Mine and Baha noticed the pattern; however, following flawed reasoning, they did not notice that their answers represented the edge length of the square that was formed in the 11th step instead of the 10th step. This demonstrates that Mine and Baha had not shown the truth of a mathematical expression. In this context, it was flawed reasoning.
Results related to synthesising skills
The fourth test question assessed the students' skill in synthesis. To solve this question, the students were expected to determine and use the relation between the length of the given triangle's edges and the size of the angles facing these edges. Figure 6 shows the sub-themes and categories based on the analysis of the student interviews.
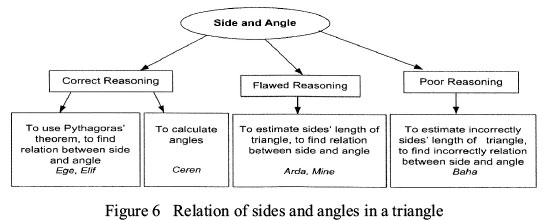
The students used three different approaches when solving this problem. Prior to determining the relation between the length of the triangle's edges and the size of the angles that faced these edges, Ege and Elif attempt to find the length of the edges of the triangle using the Pythagorean theorem. Then, based on the relation that sets the largest angle in front of the longest edge, they followed correct reasoning by comparing the size of the angles. Ceren, on the other hand, followed different reasoning. She attempted to estimate the size of the angles and length of the edges in the given triangle, and she followed correct reasoning when she described her claim regarding the situation in mathematical terms. Her reasoning, which followed a different course, was as follows:
Now, the points on the geometry board have been placed at equal distances... Now [draws an isosceles right triangle such that AC becomes its hypotenuse], there will be an isosceles right triangle here. The angles will be 45 o degrees [on the isosceles triangle, shows the base angles that consider AC edge as the base]. Here I can draw an isosceles right triangle [draws an isosceles right triangle such that the AB edge is the hypotenuse]. These angles will be 45o [on the isosceles triangle that she formed, shows the base angles that consider the AB edge as the base]. Here, angle A will be 90o [shows angle A of the ABC triangle]. For B, I can say this...if this edge [shows the BC edge] passed over the upper points, angle B would have been 45o, but instead it passes from below...and the angle is greater than 45o...as the total of internal angles of a triangle is 180o, angle C must be smaller than 45o. If I compare the angles in that case...the correct option would be D.
Arda and Mine also found the correct answers. However, they followed flawed reasoning by estimating the edge lengths and comparing the respective angles, and they could not confirm their explanations in mathematical terms. The example below is from Arda's clinical interview.
Arda: One of the reasons the geometry table was provided is to show points that are equally distant from each other, so I also considered that the distance between these points is 1 unit. The BC edge is 6 units; the AB edge is 3 units; and the AC edge is 4 units.
Researcher: But while the AB and AC edges pass over the points, The BC edge does not pass over these points. Could they be equal?
Arda: .but we can consider it so. For this reason, angle A is larger than B, which is larger than C.
By attempting to determine the sizes of the triangle's inner angles depending on how large or small they appear, Baha made visual estimations, displayed poor reasoning, and gave the wrong answer.
Discussion, conclusion, and recommendations
The aim of this study was to investigate 8th grade students' reasoning skills in solving geometry questions, and to determine when the students display reasoning skills which TIMSS indicated (analysis, generalization, synthesis). Various results were found. In this study. It was determined that the students' responses affected the geometrical knowledge, visual perception, personal logical arguments as Tierney et al. (1990) have said. Because the students sometimes have insufficient geometrical knowledge and visual perception, sometimes they are not able to provide a mathematical argument for its validity.
Based on the results of the question regarding triangle inequality, three of the students were observed to have followed correct reasoning and to have successfully used the triangle inequality theorem, whereas the other three students were not able to associate their operations with the triangle inequality theorem. This indicates that some students did not know the requirements for the formation of a triangle. Similarly, studies conducted with 8th Grade students and teachers regarding the triangle inequality also identified difficulties experienced with regard to this theorem (Türnüklü, 2009; Alatorre, Flores & Mendiola, 2012), and it was deduced that inadequate learning of the triangle inequality might be the underlying cause of these difficulties (Alatorre et al., 2012). To solve this problem, exploratory activities on triangle inequality can be conducted during the education period.
In the cube formation, the question requiring visualisation of structures, where three of the students successfully formed a cube by following correct reasoning. However, the other three students could not do so, following flawed reasoning instead. This performance demonstrates that the students were not able to visualise the joining of the geometric object. Similarly, in the question where the students were expected to visualise a closed geometric shape based on the open geometric shape that was provided, two of the students followed poor reasoning. In order to solve this problem, and given that visualisation is a form of reasoning (Gutiérrez, 1996), learning environments ought to allow students to visualise the assembly or separation of geometric shapes. Sarfaty and Patkin (2013) said that examples of solids in different positions and non-examples of the same concepts are an important stage in building children's conceptual comprehension. For this reason, the assembly or separation of geometric shapes ought to be in different positions.
The results obtained from the question regarding the preservation of surface area showed that the majority of the students followed poor reasoning. The underlying cause of their poor reasoning was their lack of conceptualisation regarding the instances in which surface area preservation was achieved, as well as their inability to visualise surface area preservation. If visual perception was considered an important component (Kospentaris et al., 2011), and if the visual perception of students had been supported during the educational process, then it may have been possible to obtain the desired results. For this reason, and as mentioned by Pitta-Pantazi and Christou (2009), the skills necessary for the development of student performance in area preservation ought to be further investigated and supported. In addition, Naidoo (2012) said that visual tools can facilitate the learning of mathematical concepts. Furthermore, one student stated that her previous experience with tangible objects helped her solve the problem. Therefore, future studies should investigate the effect of tangible materials on a student's understanding of area preservation.
In the question regarding the skill of generalisation, all of the students easily identified the existing pattern as well as the mathematical relationship within the pattern by using the self-similarity and repetition rules of fractals. However, even though two low-achieving students noticed the pattern, they were unable to balance conceptual and procedural information, using flawed reasoning instead. Because patterns contribute to a better understanding of the structure of mathematics and assist in making generalisations (Olkun & Toluk, 2007; Tamşlı & Özdaş, 2009), it is necessary to ensure that students use proper reasoning when reaching generalisations from patterns. In order to achieve this and to consolidate geometrical knowledge, educational environments should assist students. As Samson (2012) stated, it is difficult for students to transition from a visual expression to an algebraic expression, where this balance can be expected to help students.
In the question where the skill of synthesis was tested, three of the students easily established the relation between the edge lengths of the given triangles and the size of the angles facing these edges by following correct reasoning. In addition, one of these students used a different reasoning for solving the questions, focusing on problem solving by associating conceptual knowledge in a different way. Although they provided the correct answer, two students followed flawed reasoning in solving the question, and were unable to substantiate their answer with a rational explanation. This leads to the conclusion that the students did not achieve conceptual learning. Besides, Baha made visual estimations. He followed poor reasoning by attempting to estimate the angles of the triangle according to their appearances. The expressions based only on visual estimations seem to be unreliable, as Kospentaris et al. (2011) noted.
In conclusion, it appears that school curriculum should place more emphasis on reasoning skills. When it comes to geometrical concepts, students ought to be presented problems that allow them to use different reasoning skills. For this, the results suggest that the number of studies should increase in order to reflect their geometrical knowledge, visual perception, and logical arguments. Besides this, the results of this study have implications for teachers and educators. Specifically, the results can help teachers better understand the way in which their students think when they are solving geometry problems, and can help them see their students' reasoning skills. The results also encourage teachers to reconsider the techniques used in learning processes. Studies that explore methods for teaching and learning in geometry-related subjects will serve to assist teachers and students in developing their reasoning skills. In addition, for students to acquire geometric reasoning skills, research should first and foremost be conducted in relation to whether teachers have these necessary skills, and it would be appropriate to emphasise those topics that are important for teacher training.
References
Aineamani B 2011. Communicating mathematics reasoning in multilingual classrooms in South Africa. Unpublished Masters' dissertation. Johannesburg: University of the Witwatersrand. Available at http://wiredspace.wits.ac.za/bitstream/handle/10539/10133/COMMUNICATING%20MATHEMATICAL%20REASONING.pdf?sequence=1. Accessed 14 April 2014. [ Links ]
Alatorre S, Flores P & Mendiola E 2012. Primary teachers' reasoning and argumentation about the triangle inequality. In TY Tso (ed). Proceedings of the 36th Conference of the International Group for the Psychology of Mathematics Education. Taipei, Taiwan: PME. [ Links ]
Arcavi A 2003. The role of visual representation in the learning of mathematics. Educational Studies in Mathematics, 52(3):215-241. doi: 10.1023/A:1024312321077 [ Links ]
Arici S 2012. The effect of origami-based instruction on spatial visualization, geometry achievement and geometric reasoning of tenth-grade students. Unpublished Masters' dissertation. Istanbul, Turkey: Bogaziçi University. [ Links ]
Battista MT 2007. The development of geometric and spatial thinking. In F Lester (ed). Second Handbook of Research on Mathematics Teaching and Learning. Reston, VA/USA: National Council of Teachers of Mathematics. [ Links ]
Battista MT & Clements DH 1995. Geometry and proof. Mathematics Teacher, 88(1):48-54. Available at http://investigations.terc.edu^library/bookpapers/geometryand_proof.cfm. Accessed 14 April 2014. [ Links ]
Battista MT, Wheatley GW & Talsma G 1989. Spatial visualization, formal reasoning, and geometric problem-solving strategies of preservice elementary teachers. Focus on Learning Problems in Mathematics, 11(4):17-30. [ Links ]
Battista MT, Wheatley GW & Talsma G 1982. The importance of spatial visualization and cognitive development for geometry learning in pre-service elementary teachers. Journal for Research in Mathematics Education, 13(5):332-340. [ Links ]
Ben-Chaim D, Lappan G & Houang RT 1988. The effect of instruction on spatial visualization skills of middle school boys and girls. American Educational Research Journal, 25(1):51-71. doi: 10.3102/00028312025001051 [ Links ]
Brinkmann EH 1966. Programmed instruction as a technique for improving spatial visualization. Journal of Applied Psychology, 50(2):179-184. [ Links ]
Briscoe C & Stout D 2001. Prospective Elementary Teachers' Use of Mathematical Reasoning in Solving a Lever Mechanics Problem. School Science and Mathematics, 101(5):228-235. doi: 10.1111/j.1949-8594.2001.tb18025.x [ Links ]
Carroll WM 1998. Middle school students' reasoning about geometric situations. Mathematics Teaching in the Middle School, 3(6):398-403. [ Links ]
Clement J 2000. Analysis of clinical interviews: Foundations and model viability. In AE Kelly & RA Lesh (eds). Handbook of research design in mathematics and science education. London: Lawrence Erlbaum Asssociates Publishers. [ Links ]
Duval R 1998. Geometry from a cognitive point of view. In C Mammana & V Villani (eds). Perspectives on the Teaching of Geometry for the 21st Century: An ICMI Study. Dordrech: Kluwer. [ Links ]
Edwards LD 1999. Odds and evens: Mathematical reasoning and informal proof among high school students. Journal of Mathematical Behavior, 17(4):489-504. http://dx.doi.org/10.1016/S0732-3123(99)00002-4 [ Links ]
Fennema E & Sherman J 1977. Sex-related Differences in Mathematics Achievement, Spatial Visualization and Affective Factors. American Educational Research Journal, 14(1):51-71. doi: 10.3102/00028312014001051 [ Links ]
Fischbein E & Kedem I 1982. Proof and certitude in the development of mathematical thinking. In A Vermandel (ed). Proceedings of the Sixth International Conference for the Psychology of Mathematics Education. Antwerp, Belgium: Universitaire Instelling. [ Links ]
Gerald LM Jr 2002. An evolutionary theory of knowledge and conceptual evolution in science. Global Bioethics, 15(3):73-80. [ Links ]
Goos M, Stillman G & Vale C 2007. Teaching Secondary School Mathematics: Research and Practice for the 21st Century. Singapore: CMO Image Printing. [ Links ]
Gutiérrez A 1996. Visualization in 3-dimensional geometry in search of a framework. In L Puig & A Gutiérrez (eds). Proceedings of the 20th Conference of the International Group for the Psychology of Mathematics Education. Valencia, Spain: PME. (ERIC Number: ED453074). Available at http://files.eric.ed.gov/fulltext/ED453074.pdf. Accessed 14 April 2014. [ Links ]
Güzeller C 2006. Modelling the examination for secondary education in terms of language competency in Turkish. Kastamonu Education Journal, 14(2):403-412. [ Links ]
Hunting RP 1997. Clinical interview methods in mathematics education research and practice. Journal of Mathematical Behavior, 16(2):145-165. http://dx.doi.org/10.1016/S0732-3123(97)90023-7 [ Links ]
Işıksal M, Koç Y & Osmanoğlu A 2010. A study on investigating 8th grade students' reasoning skills on measurement: the case of cylinder. Education and Science, 35(156):61-70. [ Links ]
Izen SP 1998. Proof in modern geometry. Mathematics Teacher, 91(8):718-721. [ Links ]
Jones GA & Swafford JO 1997. Increased knowledge in geometry and instructional practice. Journal for Research in Mathematics Education, 28(4):467-484. [ Links ]
Jones K 2000. Critical Issues in the Design of the Geometry Curriculum. In B Barton (ed). Readings in Mathematics Education. Auckland: University of Auckland. [ Links ]
Kenney PA & Lindquist MM 2000. Students' performance on thematically related NAEP tasks. In EA Silver & PA Kenney (eds). Results from the seventh mathematics assessment of the National Assessment of Educational Progress. Reston, VA: NCTM. [ Links ]
Kilpatrick J, Swafford J & Findell B (eds.) 2001. Adding It Up: Helping Children Learn Mathematics. Washington, DC: National Academy Press. [ Links ]
Kospentaris G, Spyrou P & Lappas D 2011. Exploring students' strategies in area conservation geometrical tasks. Educational Studies in Mathematics, 77(1):105-127. doi: 10.1007/s10649-011-9303-8 [ Links ]
Kramarski B, Mevarech ZR & Lieberman A 2001. Effects of multilevel versus unilevel metacognitive training on mathematical reasoning. Journal Of Educational Research, 94(5):292-301. [ Links ]
Küchemann D & Hoyles C 2006. Influences on students' mathematical reasoning and patterns in its development: insights from a longitudinal study with particular reference to geometry. International Journal of Science and Mathematics Education, 4(4):581-608. doi: 10.1007/s10763-006-9039-6 [ Links ]
Lithner J 2000. Mathematical reasoning in task solving. Educational Studies in Mathematics, 41(2):165-190. [ Links ]
Makina A & Wessels D 2009. The role of visualisation in data handling in Grade 9 within a problem?centred context. Pythagoras, 69:56-68. Available at http://scholar.sun.ac.za/handle/10019.1/19525. Accessed 14 April 2014. [ Links ]
Malloy CE 1999. Developing mathematical reasoning in the middle grades: recognizing diversity. In LV Stiff & FR Curcio (eds). Developing mathematical reasoning in Grades K-12. Reston, VA: National Council of Teachers of Mathematics. [ Links ]
Mansi KE 2003. Reasoning and Geometric Proof in Mathematics Education: A Review of the Literature. Degree of Master of Science. USA: North Carolina State University. Available at http://repository.lib.ncsu.edu/ir/bitstream/1840.16/2692/1/etd.pdf. Accessed 14 April 2014. [ Links ]
Maqsud M 1998. Effects of metacognitive instruction on mathematics achievement and attitude towards mathematics of low mathematics achievers. Educational Research, 40(2):237-243. [ Links ]
Miles MB & Huberman AM 1994. An expanded sourcebook: qualitative data analysis (2nd ed). California: Sage Publications. [ Links ]
Mistretta R 2000. Enhancing geometric reasoning. Adolescence, 35(138):365-379. [ Links ]
Molefe N & Brodie K 2010. Teaching mathematics in the context of curriculum change. Pythagoras, 71:3-12. [ Links ]
Moses BE 1977. The nature of spatial ability and its relationship to mathematical problem solving. Unpublished Doctoral thesis. Indiana: Indiana University. [ Links ]
Mukucha J 2010. Mathematical reasoning in BODMAS. In Proceedings of the 16th Annual Congress of the Association for Mathematics Education of South Africa (AMESA). Durban: KwaZulu-Natal. 28 March-1 April. [ Links ]
Naidoo J 2012. Teacher reflection: The use of visual tools in mathematics classrooms. Pythagoras, 33(1): Art. #54, 9 pages. http://dx.doi.org/10.4102/pythagoras.v33i1.54 [ Links ]
National Council of Teachers of Mathematics (NCTM) 2000. Executive summary: Principles and standards for school mathematics. Reston, VA: NCTM. Available at http://www.nctm.org/uploadedFiles/Math_Standards/12752_exec_pssm.pdf. Accessed 16 April 2014. [ Links ]
Onyancha RM, Derov M & Kinsey BL 2009. Improvements in spatial ability as a result of targeted training and computer-aided design software use: Analyses of object geometries and rotation types. Journal of Engineering Education, 98(2):157-167. doi: 10.1002/j.2168-9830.2009.tb01014.x [ Links ]
Pitta-Pantazi D & Christou C 2009. Cognitive styles, dynamic geometry and measurement performance. Educational Studies in Mathematics, 70(1):5-26. doi: 10.1007/s10649-008-9139-z [ Links ]
Ross KA 1998. Doing and proving: the place of algorithms and proof in school mathematics. American Mathematical Monthly, 105(3):252-255. [ Links ]
Samson D 2012. Pictorial pattern generalisation: Tension between local and global visualisation. Pythagoras: Journal of The Association for Mathematics Education of South Africa, 33(3):Art. #172, 9 pages. http://dx.doi.org/10.4102/pythagoras.v33i3.172 [ Links ]
Sarfaty Y & Patkin D 2013. The ability of second graders to identify solids in different positions and to justify their answer. Pythagoras: Journal of The Association for Mathematics Education of South Africa, 34(1): Art. #212, 10 pages. http://dx.doi.org/10.4102/pythagoras.v34i1.212 [ Links ]
Tierney C, Boyd C & Davis D 1990. Prospective primary teachers' conception of area. In G Booker, P Cobb & TN Mendicuti (eds). Proceedings of the 14th PME international conference (Vol. 2). Oaxtepec, Mexico: PME. [ Links ]
Toole CM 2001. Explaining math achievement by examining its relationships to ethnic background, gender, and level of formal reasoning. Unpublished Doctoral Thesis. Greensboro: The University of North Carolina. [ Links ]
Türnüklü E 2009. Some Obstacles on the Way of Constructing Trianglur Inequality. Education and Science, 34(152):174-181. [ Links ]
Unal H, Jakubowski E & Corey D 2009. Differences in Learning Geometry among High and Low Spatial Ability Pre-service Mathematics Teachers. International Journal of Mathematical Education in Science and Technology, 40(8):997-1012. doi: 10.1080/00207390902912852 [ Links ]
Van Garderen D & Montague M 2003. Visual-spatial representation, mathematical problem solving, and students of varying abilities. Learning Disabilities Research & Practice, 18(4):246-254. [ Links ]
Werthessen H 1999. Instruction in spatial skills and its effect on self-efficacy and achievement in mental rotation and spatial visualization. Unpublished Doctoral thesis. Colombia: University of Colombia. [ Links ]
Yıldız B 2009. The effects of using three-dimensional virtual environments and concrete manipulatives on spatial visualization and mental rotation abilities Unpublished Masters' dissertation. Ankara, Turkey: Hacettepe University. [ Links ]
Appendix















