Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Education
versión On-line ISSN 2076-3433
versión impresa ISSN 0256-0100
S. Afr. j. educ. vol.33 no.2 Pretoria ene. 2013
The zone of proximal development in the learning of mathematics
Sibawu Siyepu
Fundani Centre for Higher Education Development, Cape Peninsula University of Technology, South Africa siyepus@cput.ac.za
ABSTRACT
South Africa has a huge shortage of skilled workers in various fields such as engineering, applied sciences, accountancy, architecture, medicine and law. Mathematics is a requirement for entry in these careers to enable learners to grasp the content of various subjects in these disciplines. Despite that, in South Africa, learners' performance in mathematics is shocking. This article highlights the high failure rate of mathematics in a South African context. It suggests possible causes of learners' poor performance based on the literature. The article brings a socio-cultural theory of learning focusing on the zone ofproximal development as a possible solution in the development of instructional practices. It makes recommendations on what should be done to tackle anticipated problems as suggested in the discussion.
Key words: activities; at risk learners; classroom discussions; exercises; high failure rate; more knowledgeable other; quality teaching; socio-cultural theory; understanding mathematics; zone of proximal development
Introduction and background
Globally there is a major concern about the poor performance of learners in mathematics. Van der Walt, Maree and Ellis (2008:490) state that "researchers agree that the subject matter knowledge of the majority of learners in South Africa is parlous". They further explain that South African learners experience problems relating to their limited technical vocabulary of mathematics. The South African Human Sciences Research Council (HSRC) conducted studies in 1995, 1999, and 2003 to test learners at the Grade 8 level in mathematics and science. Among the six African countries (Egypt, Tunisia, Morocco, Botswana, Ghana and South Africa) that participated in the Trends in International Mathematics and Science Study [TIMSS] (2003), South Africa had the lowest score in science and mathematics.
The results of the South African National Study in mathematics and science, Reddy (2004) reveals that there is a difference in performance among provinces, with the Western Cape, Northern Cape and Gauteng being the three highest performers. The three lowest performers were KwaZulu Natal, Eastern Cape and Limpopo. The top provinces had almost twice the scores of the lowest performing province.
Analysis of learners' performance reflects that learners in the former white schools have the highest scores whereas learners in the African schools have the lowest scores. Learners in the former white schools have a score just below the international mean.
Reddy (2004:1) stated that:
There is no single cause of South Africa's poor and diverse performance. Preliminary explanations could be linked to multiple, complex and connected sets of issues, including the following: issues of poverty, resources and infrastructure of schools, low teacher qualification, and poor learning cultures in schools. Language proficiency is a contributory factor but the issues of conceptual and cognitive demands placed on students in classrooms seem to be significant.
This is supported by researchers such as Van der Walt et al. (2008) and Ndlovu (2011) in their claim that the reasons for the poor performance of South African learners in mathematics include the poor socioeconomic background of learners (little incentive to study at home), lack of appropriate learner support materials, general poverty of school environment, general poor quality of teachers and teaching (including poor subject knowledge and poor motivation), language of instruction (often not the same as learners' mother tongue) and an inadequate study orientation.
At a media conference held on the 4th of January 2012 in Pretoria, the South African Minister of Basic Education announced that the pass rate for mathematics in matriculation examination ws 46.3% in 2011, a decline from 47.4% in 2010. This indicates that mathematics is still a problem in South Africa.
In spite of the poor pass rate at matriculation level, South African researchers such as Engelbrecht, Harding and Phiri (2010:4) assert that "several lecturers who taught first-year mathematics in 2009 reported under-preparedness of students". This is attributed to various reasons such as students who enter universities already at risk.
At 'risk' students are students who are experiencing poor achievement in their schooling system. They are usually low academic achievers who show low confidence. This is supported by Padayachee, Boshoff, Olivier and Harding (2011:1) as they explain that "from the experience of teaching first-year mathematics students, they observed that many first-year students are under prepared for mathematics. The identification of at risk students and the development of programmes to prevent their failure are necessary components of educational reform in universities (Donnelly, 1987). The following section discusses learners' understanding of mathematics.
Understanding Mathematics
The meaning of the word 'understanding' is controversial in teaching and learning of mathematics. Educators, researchers and mathematicians have different interpretations for the word 'understanding' in mathematics. Hiebert and Carpenter (1992:67) state that:
A mathematical idea or procedure or fact is understood if it is part of an internal network. More specifically, the mathematics is understood if its mental representation is part of a network of representations. The degree of understanding is determined by the number and the strength of the connections. A mathematical idea, procedure, or fact is understood thoroughly if it is linked to existing networks with stronger or more numerous connections.
Well-connected and conceptually grounded ideas enable their holders to remember, link, transfer and make connections among ideas to solve new problems that require solutions via previously learned strategies (Stylianides & Stylianides, 2007). They further emphasise that the merits of learners in developing conceptual understanding stress the importance of the powerful connections established between procedures and concepts in the learning of mathematics.
Mji and Makgato (2006:254) assert that "outdated teaching practices and lack of basic content knowledge have resulted in poor teaching standards." They emphasise that the poor standards have been exacerbated by a large number of under-qualified or unqualified teachers who teach in overcrowded and non-equipped classrooms.
This is a theoretical pap er emanated from Siyepu's (2009) paper published in 'The Association for Mathematics Education of South Africa (AMESA) conference proceedings. Siyepu (2009) used the zone of proximal development in the learning of differential calculus. The table below gives a summary of findings tabulated by Siyepu (2009).
Table 1 (see Page 4) shows the analysis of marks based on the four written tests. T1, T2, T3, and T4 are acronyms used for tests 1, 2, 3, and 4 and Avg is used for average.
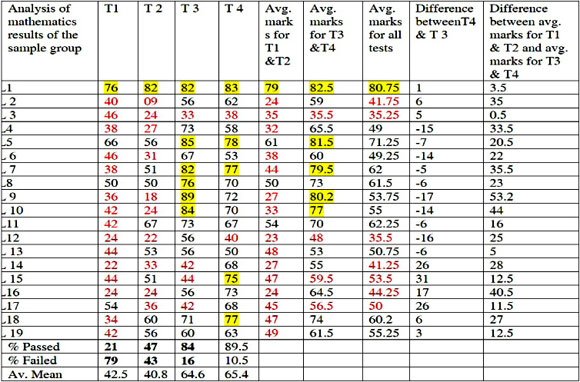
Siyepu (2009:140) shows students' performance before and after intervention (quantitative findings)
In test 1 only 4 students out of 19 passed, that is, students who obtained more than fifty percent but in that four, one student obtained a distinction. This reveals that only 21% of students in the sample group passed and 79% failed. In test 2, 9 students out of 19 passed with one student having a distinction. This reveals that 47.4% passed and 42.6% failed. The student who obtained distinction in test 1 also obtained a distinction in test 2. In test 3, 15 students out of 19 passed and 6 students obtained a distinction. This reveals that 84.2% passed and 15.8% failed. One may look at learner 9 who moved from 18% in test 2 to 89% in test 3 - see Table 1. In test 4, 17 students passed and 2 students failed. This indicates that the number of passes increased as the number of failures decreased. The essence of this paper is the use of the Zone of Proximal Development (ZPD) to assist learners who are at risk to develop understanding in their learning of mathematics not necessarily to a specific topic.
Zone of Proximal Development in the learning of mathematics
The ZPD is the difference between what a learner can do without help and what a learner can do with help. Vygotsky (1978:86) defines ZPD as "the distance between the actual developmental level as determined by independent problem solving and the level of potential development as determined through problem solving under adult guidance, or in collaboration with more capable peers"
Teachers may use the zone of proximal development (ZPD) to bridge the gap between what a learner can do without help and what a learner can do with assistance. Vygotsky (1978) argues that learner's thinking and problem solving ability fall into three categories: those that can be performed independently, those that can be performed with assistance and those that cannot be performed even with assistance. Those that cannot be performed even with assistance are those that lie beyond the ZPD.
Learners' understanding is facilitated by means of activities, classroom discussions and exercises that are done outside and inside classrooms. The learning activities are designed by the lecturer to start from what the learners can do independently based from prior knowledge to link the already existing knowledge with knowledge that they can perform with assistance. As learners continue to practice, they can do certain tasks independently in activities that were previously performed with assistance. The shifts the learners gain in understanding help them to find a way of attempting the problems that they were unable to solve even with assistance.
Gallimore and Tharp (1990:185) model the zone of proximal development by the diagram in Figure 1.
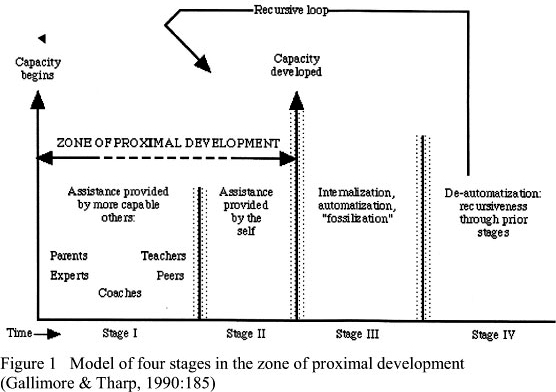
Stage I: The first stage demonstrates how learners develop an understanding of language that is appropriate to their study and the basics of the topic under study by relying on others such as instructors to perform the task.
Stage II: In the second stage learners use prior knowledge to carry out the task- without any guidance. The ZPD occurs between the first and second stages. Learners practice alone, which implies that they perform certain activities without assistance. However, they are not at a stage of perfect proficiency and require some assistance sometimes.
Stage III: In the third stage performance is developed, is happening without thinking and knowledge is fixed and it cannot be forgotten. This means that at this stage learners reach the stage of independence. In this stage a student does not need help from an adult, nor to practise more exercises to reinforce the already existing knowledge (Gallimore & Tharp, 1990).
Stage IV: In the fourth stage learners are at the de-automatisation of performance that leads to the process of repeating a function, each time applying it to the results of the previous stage through the ZPD.
Lifelong learning by any individual is made up of the same regulated ZPD sequences, from other-assistance to self-assistance recurring over and over again for the development of new capacities (Gallimore & Tharp, 1990).
The interpretation of Vygotsky's socio-cultural approach on cognitive development is that one should understand the two main principles of Vygotsky's work: More Knowledgeable Other (MKO) and ZPD. The MKO refers to someone who has a better understanding or a higher ability level than the learner with respect to a particular task, process, or concept (Galloway, 2001).
The ZPD implies that at a certain stage in development, learners can solve a certain range of problems only when they interact with teachers and cooperate with peers (Morris, n.d.). Morris (n.d.) further explains that once learner problem solving activities have been internalised, the problems initially solved under guidance and in cooperation with others can be tackled independently. Vygotsky (1978:87) highlights that "what is in the ZPD today will be the actual developmental level tomorrow, that is, what a learner can do with assistance today, she or he will be able to do it alone tomorrow".
Vygotsky believed that when a learner is at the ZPD for a particular task, providing the appropriate assistance will give the learner advancement to achieve the task (Galloway, 2001). Once the learner, with the benefit of assistance, masters the task, the assistance can then be removed and the learner will then be able to complete the task on his or her own.
Wertsch (1985:67) states that ZPD "is to deal with two practical problems in the learning situation: the assessment of learners' intellectual abilities and the evaluation of instructional practices". Learning activities challenge learners' thinking within the learning process.
Borchelt (2007:2) further asserts that "learning is determined by the interactions among learners' existing knowledge, established social context, and the problem to be solved". This supports Vygotsky's (1978) idea that higher order thinking developed first in action and then in thought. Borchelt (2007:2) argues that "the potential for- cognitive development is optimised within ZPD or an area of exploration for which a learner is cognitively prepared, but requires assistance through social interaction".
The process can be understood in a socio-cultural perspective with reference to Vygotsky's ZPD, which explains how to advance students' learning process. This approach is reinforced by Wertsch (1985:60-61) who asserts that:
Any function in the student's cultural development appears twice, or on two planes. First, it appears on the social plane, and then on the psychological plane.
First it appears between people as an inter-psychological category and then within the student as an intra-psychological category.
Wertsch (1990:114) states that "the fundamental claim is that human activity (on both the inter-psychological and the intra-psychological plane) can be understood only if we take into consideration the "technical tools" and "psychological tools" or "signs that mediate the activity". Technical tools are physical learning resources such as textbooks, teaching notes, calculators and classroom written activities.
Psychological tools are tools such as language, counting systems, mnemonic techniques, art, writing, diagrams, and maps. Psychological tools are created by society and are directed towards the control of behaviour (Quek & Alderson, 2002). Psychological tools alter the flow and structure of mental functions, just as physical tools alter the way our work processes evolve (Quek & Alderson, 2002). In the teaching of mathematics teachers might use learning activities and text books as physical tools to facilitate the learning process of mathematics.
Tools carry with them a historical background. They are instilled with the collective experience and skill that was involved to develop them (Quek & Alderson, 2002). Teachers use learners' prior knowledge and their experiences of learning mathematics in the previous levels. For example, in classroom discussions, students explain and justify their understanding and interpretations of the topic studied to other members of the class.
Socio-cultural theory emphasises that the most advantageous learning environment is one where a dynamic interaction between teachers, learners and tasks provides an opportunity for learners to create their own understanding during interaction with others (Atkinson, Derry, Renkl & Wortham, 2000). Atherton (2005) emphasises that in a socio-cultural classroom, learners are active makers of meanings and the role of the teacher is to guide learners to gain meaningful understanding of the learning material.
Semiotic mediation
The process of moving from elementary to higher mental functions is called semiotic mediation and an important mechanism in this transition is the use of tools and symbols (Wertsch, 1991). Semiotic activity is defined as the activity of investigating the relationship between sign and meaning, as well as improving the existing relationship between sign and meaning (Van Oers, 1997). Teachers focus on learners'- methods of making meaning through reading and interpreting learning activities to bring solutions in their mathematical problems.
Centrality of communicative practices
Vygotsky (1987:249-250) places communication at the centre of his theory of language and thought by arguing that "the thought is completed in word". This implies that in designing activities, teachers should pay attention to arranging interactions where the teacher and learners can pause to comment on their problem solving efforts in oral or written reflections (Brown & Cole, 2002).
Communication is important in developing mathematical understanding (Steele, 2001). Steele (2001) explains that within a socio-cultural perspective, students exchange ideas amongst one another and listen actively to one another's views. This creates mutual understanding based on culturally established mathematical practices. Vygotsky (1994) asserts that language is a cultural tool and a human instrument of communication.
Discussion, recommendations and conclusion
The discussion about the use of ZPD in the teaching of mathematics indicates importance of availing physical and psychological resources to both teachers and learners. The discussion of availability of physical and psychological resources might not be enough another aspect is the availability of human resources that is teachers of high calibre. Atebe (2011:110) states that "no curriculum prescription of the body of knowledge that students are expected to learn in mathematics can be said to be complete without specifying how best the students might be apprenticed into acquiring that knowledge". Firstly, let me briefly outline characteristics of physical resources needed to enable learners to gain understanding in the learning of mathematics.
In South Africa there is a widespread complaint about inappropriateness of textbooks in the field of mathematics, especially at school level. Department of Basic Education (2009:28) states that "the quality and quantity of learner and teacher support materials in South Africa are not adequate to support quality learning." Analysis of TIMSS results of 1998 (Johnson, 1998) claims that South African textbooks have very few activity-based exercises and almost no assessment suggestions. It further elaborates that South African textbooks encourage mainly lower order skills (such as recall), as opposed to the higher order skills (such as problem solving). This is supported by southern and eastern Africa consortium for Monitoring Educational Quality II and III [SACMEQ II] (Moloi & Strauss, 2005) and [SACMEQ III] (Moloi & Chetty, 2010) Mathematics achievement in South Africa as shown in Table 2.

In order for learners to link the levels tabulated in the table there should be learning materials that allow learners and teachers to shift within the zone of proximal development gaining relational understanding of the content studied in that particular topic understudy by that time. Right from the introduction of the Outcomes Based Education (OBE) system; the curriculum of South Africa (Department of Education,- 2002:1) proposed a shift from "teacher tells" to an investigative approach. Throughout the entire process of training teachers and implementation of OBE there were no appropriate textbooks that guided teachers on how to assist learners to create, invent, discover, and investigate knowledge on their own. This is substantiated by Moloi (2005:1) in research of mathematics achievement in South Africa in the claim that "analysis of local textbooks of mathematics showed significant gaps between what texts presented and what the official curriculum requires". He emphasises that the quality of textbooks seemed not to be supportive of the ideals of the curriculum.
Textbooks that were available continued giving readymade information. This means South African textbooks do not have appropriate activities that can assist learners to develop relational understanding of certain concepts in their learning of mathematics (Skemp, 1976). Relational understanding is not only knowing what to do but why as it includes rationalisation of the underlying mathematical relationship and properties (Choat, 1981).One level of understanding gained by learners in textbooks is instrumental understanding where learners and teachers think that they understand something if they are able to obtain correct answers to a given category of questions without knowing why the method works (Choat, 1981:18).
In many instances South African textbooks use a cookbook approach where teachers supply learners with formulae such as Area of a cylinder is
A = 2πr2 + 2πrh.
Learners are not given an opportunity to make inferences, conjectures and generalisation to understand strategies used to derive the formula.
This cookbook approach of providing formulae, where learners have no idea where the formulae come from, is an educational and mathematical sin (Freudenthal, 1991). There is a need of a dynamic approach to deal with concepts by deliberately guiding learners through a reinvention process (Freudenthal, 1991). This might be an approach that guides learners on how to reach mathematical rules, laws and formulae.
Coming to human resources, research dating back to 2005 demonstrates that of- the 16,581 mathematics teachers present in the Eastern Cape, only 7,090 were teaching the subject. In that 7,090 teachers teaching mathematics, 5,032 were not qualified to teach mathematics. Metcalfe (2008:10) concurs that:
Teacher quality is the "most significant factor affecting learner performance", and then citing findings from research, states:
... the conceptual knowledge of our teachers is low; teachers have a poor grasp of the subjects they teach; there is a high level of teacher error in the content and concepts presented in lessons; and teachers have low expectations of learners, who then achieve to these low expectations.
The ZPD requires that teachers should be more knowledgeable in order to assist learners to gain understanding of what they cannot do without assistance.
From the above quotation it is clear that teachers lack competence and commitment in the workplace. Department of Basic Education (2009:28) substantiates that "limited teacher knowledge, coupled with low levels of accountability is one of the challenges that impact learners' performance in a South African context. Teachers' competencies may be improved by means of in-service courses or advancing their knowledge by further studies such as Bachelor of Education (Honours) in Mathematics and Science degrees. This is where teachers can be advanced by means of subject content knowledge and pedagogical content knowledge of mathematics which can introduce different approaches in the teaching of mathematics. Teachers should also be encouraged to participate in local and national conferences to share teaching strategies and techniques with their colleagues. That might also raise their enthusiasm. The government should devise appropriate means to bring back the value of teaching in order for teachers to maximize their potential.
References
Atebe HU 2011. The van Hiele levels as correlate of students' ability to formulate conjectures in school geometry. In H Venkat & AA Essien (eds). Proceedings of the 17th National Congress of the Association for Mathematics Education of South Africa (AMESA): "Mathematics in a Globalised World" (Volume 1). 11-15 July, Johannesburg: Association for Mathematics Education of South Africa (AMESA). Available at http://www.amesa.org.za/AMESA2011/Volume1.pdf. Accessed 28 March 2013. [ Links ]
Atherton JS 2005. Learning and teaching: Constructivism in learning. Available at http://www.learningandteaching.info/learning/constructivism.htm. Accessed 23 August 2007. [ Links ]
Atkinson RK, Derry SJ, Renkl A & Wortham DW 2000. Learning from examples: Instructional principles from the worked examples research. Review of Educational Research, 70(2):181-214. doi: 10.3102/00346543070002181 [ Links ]
Borchelt N 2007. Cognitive computer tools in the teaching and learning of undergraduate calculus. International Journal for the Scholarship of Teaching and Learning, 1(2):1-17. Available at http://academics.georgiasouthern.edu/ijsotl/v1n2/articles/borchelt/Article_Borchelt.pdf.- Accessed 13 July 2009. [ Links ]
Brown K & Cole M 2002. Cultural historical activity theory and the expansion of opportunities for learning after school. In G Wells & G Claxton (eds). Learning for life in the 21st Century: Sociocultural perspectives on the future of education. Malden, MA: Blackwell. [ Links ]
Choat E 1981. Understanding in Young Children's Mathematics. Mathematics in school, 10(2):18-21. Available at http://www.jstor.org/stable/pdfplus/30213633.pdf?acceptTC=true. Accessed 28 March 2013. [ Links ]
Department of Education 2002. National mathematics standard grades 10-12 (schools). Mathematics draft. Pretoria: Government Printer. [ Links ]
Department of Basic Education 2012. Annual Report 2011/12. Pretoria: Department of Basic Education. Available at http://www.education.gov.za/LinkClick.aspx?fileticket=Yl%2BhMxe4mVU%3D&tabid=422&mid=1263. Accessed 28 March 2013. [ Links ]
Donnelly M 1987. At-risk students. ERIC digest series number 21. Available at http://www.ericdigests.org/pre-928/risk.htm. Accessed 08 October 2011. [ Links ]
Engelbrecht J, Harding A & Phiri P 2010. Are OBE-trained learners ready for university mathematics? Pythagoras, 72:3-13. Available at http://repository.up.ac.za/bitstream/handle/2263/17348/Engelbrecht_OBE-trained%282 011%29.pdf?sequence=1. Accessed 28 March 2013. [ Links ]
Freudenthal H 1991. Revisiting Mathematics Education: China Lectures. Dordrecht: Kluwer Academic Publishers. [ Links ]
Gallimore R & Tharp R 1990. Teaching mind in society: Teaching, schooling, and literate discourse. In LC Moll (ed). Vygotsky and Education: Instructional implications and applications of sociohistorical psychology. Cambridge: Cambridge University Press. [ Links ]
Galloway CM 2001. Vygotsky's constructionism. In M Orey (ed.). Emerging perspectives on learning, teaching, and technology. Available at http://projects.coe.uga.edu/epltt/index.php?title=Vygotsky%27s_constructivism. Accessed 13 May 2009. [ Links ]
Hiebert J & Carpenter TP 1992. Learning and teaching with understanding. In DA Grouws (ed.). Handbook of Research on Mathematics Teaching and Learning. New York: MPC. [ Links ]
Johnson EG 1998. Linking the national assessment of educational progress (NAEP) and The Third International Mathematics and Science Study (TIMSS): A Technical Report. Washington, DC: National Center for Education Statistics. Available at http://nces.ed.gov/pubs98/98499.pdf. Accessed 4 April 2013. [ Links ]
Mji A & Makgato M 2006. Factors associated with high school learners' poor performance: a spotlight on mathematics and physical science. South African Journal of Education, 26:253-266. [ Links ]
Metcalfe M 2008. Why our schools don't work.. .and 10 tips on how to fix them. Sunday Times, 13 January. [ Links ]
Moloi MQ 2005. Mathematics Achievement in South Africa: A Comparison of the Official Curriculum with Pupil Performance in the SACMEQIIProject. Paper to SACMEQ International Invitational Conference, 28 September - 2 October. Paris: International Institute for Educational Planning, Unesco. Available at-http://www.sacmeq.org/downloads/05conf/Moloi.pdf. Accessed 28 March 2013. [ Links ]
Moloi MQ & Strauss J 2005. The SACMEQ II Project in South Africa: A Study of the Conditions of Schooling and the Quality of Education. Pretoria, SA. [ Links ]
Moloi MQ & Chetty M 2010. The SACMEQ IIIProject in South Africa: A Study of the Conditions of Schooling and the Quality of Education. Pretoria, SA: Ministry of Basic Education. Available at http://www.info.gov.za/view/DownloadFileAction?id=172469. Accessed 4 April 2013. [ Links ]
Morris C (n.d.). Lev Semyonovich Vygotsky's Zone of Proximal Development. Available at http://www.igs.net/~cmorris/zpd.html. Accessed 17 June 2008. [ Links ]
Ndlovu MC 2011. University-school partnerships for social justice in mathematics and science education: the case of the SMILES project at IMSTUS. South African Journal of Education, 31:419-433. [ Links ]
Padayachee P, Boshoff M, Olivier W & Harding A 2011. A blended learning Grade 12 intervention using DVD technology to enhance the teaching and learning of mathematics. Pythagoras, 32(1), Art #24, 8 pages. doi:10.4102/pythagoras.v32.i1.24 [ Links ]
Quek A & Alderson A 2002. An activity theory approach to understanding the difficulty of applying web engineering in practice. Technical report. United Kingdom: Staffordshire University, School of Computing. [ Links ]
Reddy V (2004, December 14). TIMSS media briefing. Pretoria: Human Sciences Research Council. [ Links ]
Siyepu SW 2009. The zone of proximal development in the learning of differential calculus. In JH Meyer & A van Biljon (eds). Proceedings of the 15th Annual Congress of the Association for Mathematics Education of South Africa (AMESA): "Mathematical Knowledge for Teaching" (Volume 1). 29 June - 3 July. Bloemfontein: University of the Free State. Available at http://www.amesa.org.za/AMESA2009/Volume109.pdf. Accessed 28 March 2013. [ Links ]
Skemp RR 1976. The psychology of learning mathematics (2nd ed). London, UK: Penguin. [ Links ]
Steele DF 2001. Using sociocultural theory to teach mathematics: a Vygotskian perspective. School Science and Mathematics, 101:404-416. doi: 10.1111/j.1949-8594.2001.tb17876.x [ Links ]
Stylianides AJ & Stylianides GJ 2007. Learning mathematics with understanding: A critical consideration of the learning principle in the principles and standards for schools mathematics. The Montana Mathematics Enthusiast, 4:103-114. [ Links ]
TIMSS 2003. International mathematics report. In IVS Mullis, MO Martin, EJ Gonzalez & SJ Chrostowski (eds). Findings From IEA's Trends in International Mathematics and Science Study at the Fourth and Eighth Grades. Chestnut Hill, MA: TIMSS & PIRLS International Study Center, Boston College. [ Links ]
Van der Walt M, Maree K & Ellis S 2008. A mathematics vocabulary questionnaire for use in the intermediate phase. South African Journal of Education, 28:489-504. [ Links ]
Van Oers B 1997. On the narrative nature of young children's iconic representations: some evidence and implications. International Journal of Early Years Education, 5:237-245. Available at http://webpages.charter.net/schmolze1/vygotsky/vanoers.html. Accessed 5 October 2009. [ Links ]
Vygotsky LS 1978. Mind in Society: The development of higher psychological processes. In M Cole, V John-Steiner, S Scriber and E Souberman (eds). Cambridge, MA: Harvard University Press. [ Links ]
Vygotsky LS 1987. Thinking and speech. In RW Riber & AS Carton (eds). The collected works of LS Vygotsky (Volume1: Problems of general psychology). New York: Plenum. [ Links ]
Vygotsky LS 1994. Thought and language. Cambridge, MA: Harvard University Press. [ Links ]
Wertsch JV 1985. Vygotsky and the social formation of mind. Cambridge, MA: Harvard University Press. [ Links ]
Wertsch JV 1990. The voice of rationality in a socio-cultural approach to mind. In LC Moll (ed). Vygotsky and education: Instructional Implications and Applications of Sociohistorical Psychology. New York: Cambridge University Press. [ Links ]
Wertsch JV 1991. Voices of the mind. A socio-cultural approach to mediation action. Cambridge, MA: Harvard University Press. [ Links ]














