Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Education
On-line version ISSN 2076-3433
Print version ISSN 0256-0100
S. Afr. j. educ. vol.33 n.2 Pretoria Jan. 2013
Scale development for pre-service mathematics teachers' perceptions related to their pedagogical content knowledge
Esra Bukova-GüzelI; Berna Cantürk-GünhanI; Semiha KulaI; Zekiye ÖzgürII; Aysun Nüket ElçíIII
IBuca Education Faculty, Dokuz Eylül University, Izmir, Türkiye esra.bukova@gmail.com
IISchool of Education, University of Wisconsin-Madison, USA
IIIEducation Faculty, Bartin University, Bartin, Türkiye
ABSTRACT
The purpose of this study is to develop a scale to determine pre-service mathematics teachers' perceptions related to their pedagogical content knowledge. Firstly, a preliminary perception scale of pedagogical content knowledge was constructed and then administered to 112 pre-service mathematics teachers who were enrolled in a mathematics teacher education programme. Exploratory and confirmatory factor analysis, item analysis, correlation analysis, internal consistency and descriptive statistic techniques were used to analyse the data. Then validity and reliability of the scale were investigated. The analyses resulted in the development of a five-factor scale of 17 items that was proved valid and reliable. We contend that the scale developed has the merit to contribute to pre-service teachers' self-awareness by revealing their perceptions regarding their pedagogical content knowledge.
Keywords: pedagogical content knowledge, pre-service mathematics teachers, scale development
Introduction
The domains and categories of teacher knowledge that teachers ought to possess were first introduced and identified in detail by Shulman (1986, 1987). Shulman (1987:8) identified seven domains of teacher knowledge: "general pedagogical knowledge; knowledge of learners and their characteristics; knowledge of educational context; knowledge of educational ends, purposes, and values, and their philosophical and historical grounds; content knowledge; pedagogical content knowledge (PCK); and curriculum knowledge". Researchers such as Ball & McDiarmid (1990), Gess-Newsome (1999), Grossman (1990), Marks (1990), Verloop, Van Driel & Meijer (2001) have taken up this framework seriously since then and have conducted many studies in teacher education to date, with a particular emphasis on pedagogical content knowledge (PCK). In broad strokes, PCK consists of knowledge of ways to transform subject-matter knowledge into forms that are accessible to and comprehensible by students, and is a complex structure with multiple components. Ernest (1989) points out that two teachers with the same level of subject-matter knowledge of mathematics may present their knowledge in quite different ways when teaching mathematics. Thus, PCK plays an important role in teachers' instruction. Ball et al. (2001, cited in Bütün, 2005) point out that evaluating PCK of a teacher exclusive of observing their practices in classroom is often superficial and missing. Thus, it is essential to focus on pre-service and in-service teachers' instruction in order to properly assess their PCK. However, determining their perceptions regarding their PCK beforehand seems important.
Perception is a conscious awareness derived from the individual's sense-making or interpretation of the stimulus occurred in his mind when the individual is directed to a concept (Akarsu, 1975 cited in Acil, 2011). Perceptions are formed based on individuals' past experiences and knowledge (Binbasioglu & Binbasioglu, 1992), and since individuals' past experiences and knowledge vary from each other and so do their perceptions. Given that individuals learn through perception (Gökdag, 208), determining pre-service teachers' perceptions becomes important to support their learning. In this study, our goal was to develop a scale for determining pre-service teachers perceptions related to their PCK. In addition, such a scale would contribute to pre-service teachers' self-awareness by way of identifying their perceptions regarding to their PCK. Furthermore, such a scale could or may function as a tool to support pre-service teachers' development by identifying the PCK components that pre-service teachers perceive themselves weak and then targeting teacher preparation on those components. Therefore, the scale is valuable for teacher educators as well, since it can inform them about how to revise the courses in their teacher education program and how to better mentor their students in order to meet the needs of their students. In the next section, we present a brief literature review on PCK and its measurement, and then proceed with a detailed explanation regarding the development of the scale.
Literature review
Pedagogical Content Knowledge
The first four domains of the seven domains of teacher knowledge identified by Shulman can be conceived as generic knowledge - that is, all teachers no matter what subject they teach ought to possess. The last three domains of teacher knowledge are content-specific knowledge (Rowland, Turner, Thwaites & Huckstep, 2009). Although curriculum knowledge, one of the content-specific knowledge domains, was first introduced by Shulman (1987) as a separate domain, later on it has been defined as a component of PCK in almost all of the subsequent studies (e.g. An, Kulm & Wu, 2004; Chick, Baker, Pham & Cheng, 2006; Grossman, 1990; Hill, Ball & Schilling, 2008; Magnusson, Krajcik & Borko, 1999; Marks, 1990; Schoenfeld, 1998). For Shulman (1986), content knowledge refers to what a teacher knows, how much s/he knows and what s/he should know (Ball & McDiarmid, 1990; Leavit, 2008). In Shulman's words, PCK includes knowing:
"Most regularly taught topics in one's subject area, the most useful forms of representation of those ideas, the most powerful analogies, illustrations, examples, explanations, and demonstrations - in a word, the ways of representing and for- mulating the subject that make it comprehensible to other" (Shulman 1986:9).
PCK also contains knowing which approaches facilitate or complicate learning of particular subject areas along with knowing what students of different ages and backgrounds bring to the learning environment, including common misconceptions (Shulman, 1986). Curriculum knowledge is defined as being aware of all components of a curriculum designed for teaching a topic at a particular level or a specific subject area, the variety of instructional tools available for that curriculum and under what conditions using a particular curricular tool is applicable or not (Shulman, 1986). In addition, PCK indicates how a teacher uses his or her knowledge of subject matter in the course of instruction within the curriculum (Carter, 1990).
Content-specific knowledge domains for mathematics teachers can be named as mathematics subject-matter knowledge, mathematics curriculum knowledge and mathematical pedagogical content knowledge. The idea that knowing the subject is enough for teaching is well refuted by research (Ball & Bass, 2000; Ball, Thames & Phelps, 2008; Shulman, 1986, 1987) and what is more, the structure and type ofmathe-matical knowledge a mathematics teacher needs to posses has been shown to be quite different than what a mathematician would need to posses (Ball & Bass, 2000; Ball et al., 2008; Noss & Baki, 1996). Those arguments have led the mathematics education community to put emphasis on mathematical pedagogical content knowledge in addition to mathematics subject-matter knowledge. Rowland et al. (2009) describe that teachers' mathematical pedagogical content knowledge enables them to transform their own subject-matter knowledge into a form that is apprehensible to students, draw on resources and effectively use various representations and analogies, understand students' thinking, and explain mathematical concepts well. Ball & Bass (2000), furthermore, argue that mathematical pedagogical content knowledge includes knowing on which aspects of a concept to focus in order to make it interesting to a particular grade level and knowing where students may possibly experience difficulties when problem solving. In addition, it includes being able to modify problems according to students' levels and being able to lead mathematical discussions.
Tamir (1988) identified five components of PCK in his study towards developing a framework for teachers' knowledge: a) orientation to teaching, b) knowledge about students' understandings, c) curriculum knowledge, d) knowledge of assessment, and e) knowledge of teaching strategies. Along similar lines, Grossman (1990) suggested a more elaborated categorization for PCK: a) teachers' knowledge and beliefs about the purposes for teaching a subject to students of different levels, including their conceptions regarding the nature of the subject and what topics are important for students to learn, b) knowledge of students' prior knowledge, preconceptions, possible misconceptions and alternative conceptions, c) knowledge of curriculum and curricular materials, including knowing the relationships both within a subject and between subjects, and d) knowledge of different instructional strategies and representations. Yet Fernández-Balboa & Stiehl (1995) proposed another categorization of PCK as subject-- matter knowledge, knowledge of learners, knowledge of teaching strategies, and knowledge of content and goals of instruction. As it is clear from the above-mentioned studies, researchers have defined the components of PCK differently. After an extensive literature review, Bukova-Güzel (2010) has developed a comprehensive framework of PCK consisting of three main categories and their components as shown in Table 1.

While there is no consensus on how to determine PCK of mathematics teachers and pre-service mathematics teachers alike, we contend that focusing on as different components as possible can generate more comprehensive knowledge about teachers' PCK. We also argue that identifying pre-service mathematics teachers' perceptions related to their PCK will serve as a significant clue for them to improve their PCK by showing them in what areas they need further improvement.
Measuring teachers' perception of PCK
Instruments used in measuring affective characteristics (attitudes, perception, attention, value, etc.) have many benefits and are used to determine the differences between individuals in terms of their affective characteristics or the difference between the responses that the same person gives at different times and situations (Tekindal, 2009). For instance, the perception scale developed in this study can be helpful for identifying the presence, direction and level of the pre-service teachers' perceptions regarding their PCK as they begin to their coursework in the teacher education program. Thus, we also consider that it can be informative for decisions regarding how to improve the implementation of the current teacher education program for mathematics teachers.
When we examined the existing literature, we failed to find an example of perception scale regarding PCK, but found that there are many studies on teacher efficacy scales, instead. The construct of teacher efficacy has been measured in numerous ways during the past two decades. To name a few, Enochs, Smith & Huinker (2000) developed Mathematics Teaching Efficacy Belief Instrument (MTEBI) by adapting the Science Teaching Efficacy Belief Instrument (STEBI) developed by Enochs and Riggs (1990). Both of these instruments are based on Banduras' social learning theory and explore self-efficacy in two dimensions as self-efficacy beliefs and outcome expectancy beliefs. Similarly, Charalambos, Philippou & Kyriakides (2008) developed a scale for teachers' efficacy belief in teaching mathematics by adapting the teacher efficacy scale developed for pre-service teachers by Tschannen-Moran and Woolfolk Hoy's (2001). This scale is also based on Banduras' social learning theory and yielded a two-factor model: efficacy beliefs in mathematics instruction and classroom management.
Some scales are designed for pre-service teachers to evaluate their cooperating teachers in terms of their guidance in instruction during their student teaching. One of such scales is Mentoring for Effective Mathematics Teaching (MEMT), which is designed by Hudson and Skamp (2003) by adapting the Mentoring for Effective Primary Science Teaching (MEPST) scale to mathematics (Hudson & Peard, 2006). The only change made was to replace "science" by "mathematics" when MEPST was turned into MEMT to use with primary mathematics teachers. So, both scales are based on a five-factor model, namely, Personal Attributes, System Requirements, Pedagogical Knowledge, Modeling, and Feedback. Hudson and Ginns (2007) designed the pre-service teachers' pedagogical development scale, with an aim to measure pre-service science teachers' pedagogical development level for teaching science. The scale is composed of four factors: theory, child development, planning, and implementation.
While there are numerous studies on teacher quality such as Kennedy (2010) and Rice (2003), there is a lack of research on scale development measuring pre-service teachers' pedagogical content knowledge for mathematics. Hence, there is a need for research on scale development to that end. Consequently, the purpose of this study is to develop a scale to determine pre-service mathematics teachers' perceptions related to their pedagogical content knowledge. In what follows we present our scale development efforts.
Methods
In this study, a scale entitled "Scale for Pre-service Mathematics Teachers' Perceptions related to their Pedagogical Content Knowledge" was developed, and then its validity and reliability were investigated. The process of developing the scale included the following steps: constructing the scale's items, consulting for expert opinion for content validity, and running exploratory factor analysis, confirmatory factor analysis and reliability analysis for construct validity.
Participants
The participants of this study were 112 elementary and secondary pre-service mathematics teachers who were enrolled in a teacher education programme in a large state university in Turkey in the spring semester of 2010. The sample included final-year pre-service teachers. Of 112 participants, 45.5% of them (n = 51) were male and 54.5% (n = 61) were female.
Constructing the items of the scale
The scale development studies began with reviewing the literature on PCK. Based on an extensive literature review, the components of PCK were determined (e.g. Bukova-Güzel, 2010; Fernández-Balboa & Stiehl, 1995; Grossman, 1990; Tamir, 1988). Then, the sub-dimensions of the scale were formed as the result of the factor analysis. After constructing the preliminary scale, we consulted with two mathematics educators who are experts on PCK with respect to the appropriateness of the items in the preliminary scale to measure pre-service mathematics teachers' perceptions related to their pedagogical content knowledge. Following the suggestion of an assessment and evaluation expert, the instrument was structured as a Likert type five-choice scale, with choices being "1: Never", "2: Rarely", "3: Undecided", "4: Usually", "5: Always". Increase in the scale scores indicates that the individual perceives himself or herself as having a high level PCK, while decrease in the scale scores indicates the opposite.
Content validity
Content validity indicates whether the items constituting the scale are quantitatively and qualitatively adequate for measuring the property that is intended to be measured (Büyüköztürk, 2007). To ensure the content validity, three mathematics educators and two mathematics teachers were asked to express their opinions with regard to the items in the scale and the appropriateness of the scale for the subject to be measured. In the light of the suggestions received, the scale was given its final form by omitting and revising some items. Consequently, the preliminary scale initially included 31 items. The scale contained no negative items.
Data analysis
The data were analysed with the statistical software packages, SPSS 15.00 and Lisrel 8.51. Exploratory factor analysis, confirmatory factor analysis, and internal consistency techniques were used to analyse the data. Exploratory factor analysis is a method used to find factors based on the relationships among the variables. Depending on the relation between the variables, a variable can be correlated by a factor or take load from it. In exploratory factor analysis, the nature of the factor is identified based on factor loads without a priori hypotheses about factors (Sümer, 2000; Büyüköztürk, 2007). We conducted the exploratory factor analysis via SPSS. Confirmatory factor analysis, on the other hand, is used to test a hypothesis or theory identified earlier about the relationship between the variables (Büyüköztürk, 2007). This type of factor analysis is used to determine which measures comprise the predetermined factors. We conducted the confirmatory factor analysis via LISREL 8.51. Confirmatory factor analysis is an effective analysis method in the first stage of scale development process. The preliminary results of the confirmatory factor analysis inform the researcher about the problems in the scale and give hints about potential changes needing to be made to resolve the problems (& SimSek, 2007). Confirmatory factor analysis is also used to examine to what extent the observed variables underlie the predetermined latent factors (Sümer, 2000). Lastly, reliability analysis is used to determine to what extent the measurement results are free of random errors (Tekindal, 2009). In this study, the Cronbach's alpha reliability coefficient was used via SPSS for the reliability analysis.
Results
In this section, the findings of exploratory factor analysis related to the validity of the scale, confirmatory factor analysis and reliability studies are presented.
Exploratory factor analysis
The goal of factor analysis, the most powerful technique for investigating construct validity, is to reduce "the dimensionality of the original space and to give an interpretation to the new space, spanned by a reduced number of new dimensions which are supposed to underlie the old ones" (Rietveld & Van Hout, 1993:254). Therefore, exploratory factor analysis was conducted to determine the sub-constructs of the pre-service mathematics teachers' perceptions related to their pedagogical content knowledge and to ensure the construct validity. Before conducting factor analysis, we first examined whether or not the sample was appropriate for factor analysis. To determine this, we calculated the Kaiser-Meyer-Olkin (KMO) index. For the sample of this study, the KMO index was found to be 0.837, which suggests that the sample is sufficient for conducting factor analysis.
Additionally, the diagonal amounts of Anti-image Correlation Matrix were also calculated to check the sufficiency of the sample (Akgul & Cevik, 2003). Furthermore, Bartlett's Spherecity Test was run to check whether the data represent a multivariate normal distribution. The test resulted in Approx. Chi-square: 1600.837 and p < 0.01, which shows that the results are significant.
Exploratory factor analysis was initiated with 31 items, and the first analysis suggested that the items were grouped into 8 factors whose eigen value was higher than 1. However, on the Scree Plot graphic (see Figure 1), the line was clearly broken after the fifth point that, in turn, suggests that five factors exist above that point.
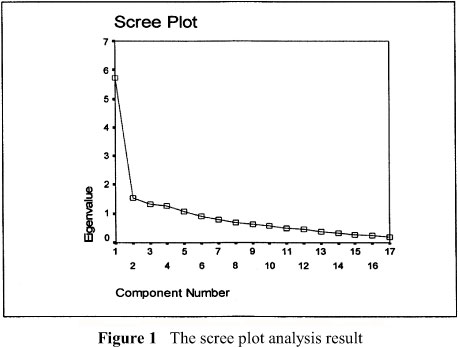
Investigation of the correlation between items showed that the items were correlated above 20% with each other. Therefore, Direct Oblimin rotation was conducted. The Direct Oblimin rotation also resulted in five factors. Two criteria were considered when deciding whether or not to keep an item in the scale after the rotation: a) an item must have at least 0.3 factor loading in only one factor, or b) an item partaking in more than one factor must have at least 0.1 higher factor loading in one of the factors than its factor loading in other factors. As a result, 14 items were eliminated from the scale because the analysis showed that those 14 items took part in more than one factor but did not satisfy the second criterion; that is, for those items the difference between factor loadings of the item in different factors was less than 0.1. Hence, in its final form, the scale includes 17 items. Table 2 presents the distribution of the items by factors, Factor 1 loadings of the items before the rotation and factor loadings and factor common variances after Direct Oblimin rotation.
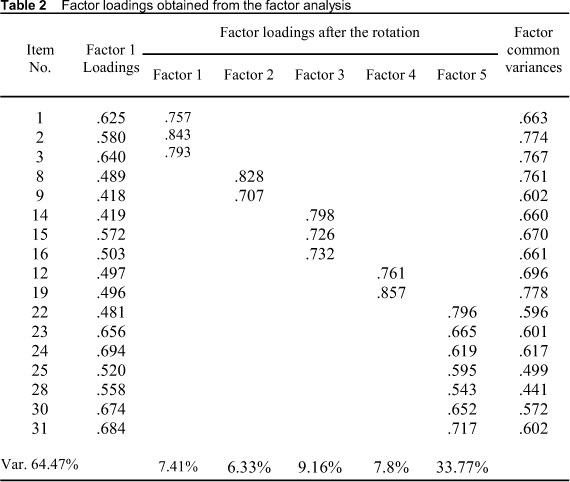
As seen in Table 2, the first factor explains 7.41% of total variance concerning the scale, the second does 6.33%, the third does 9.16%, the fourth does 7.8% and the fifth does 33.77%. In total, the five factors together explain 64.47% of the variability. By and large, the factor loadings of the items in the dimensions were found above the accepted limit and the total variance that the factors explain were found satisfactory. After the rotation, it was determined that the first factor consists of three items (1, 2, 3), the second factor consists of two items (8, 9), the third factor consists of three items (14, 15, 16), the fourth factor consists oftwo items (12, 19), and fifth factor consist of seven items (22, 23, 24, 25, 28, 30, 31).
Since the items in the first factor highlight pre-service teachers' perceptions related to their knowledge of teaching strategies to present mathematical concepts, the first factor was named "Knowledge of Teaching Strategies (KTS)". The second factor was called "Knowledge of Mathematical Language and Symbols (KMLS)" because the items in this factor stress participants' perceptions related to their knowledge of using mathematical language and symbols to present mathematical concepts. The third factor, "Knowledge of Misconceptions (KM)", includes items that highlight pre-service teachers' perceptions related to their knowledge about students' misconceptions in mathematics. The fourth factor was named "Knowledge of Learners (KL)" because the items in this factor emphasize pre-service teachers' perceptions related to their knowledge about students' developmental levels and prior knowledge. Lastly, the fifth factor, "Knowledge of Curriculum (KC)", includes items that highlight pre-service teachers' perceptions related to their knowledge of curriculum and curricular materials. The items of each factor are presented in Table 3.

To investigate the reliability of the determined dimensions, corrected item-total correlations were calculated first. Secondly, a t test was run to test the significance of the difference between the item scores of upper 27% and lower 27% groups of total score (see Table 4).
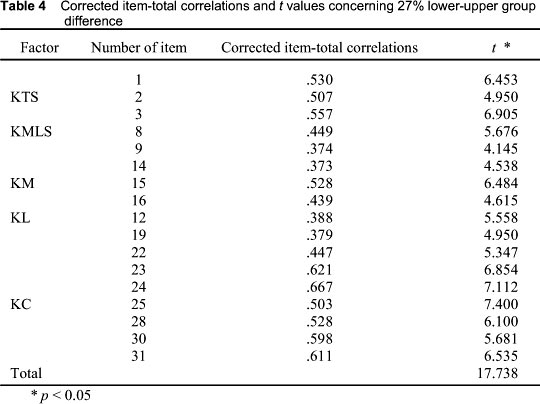
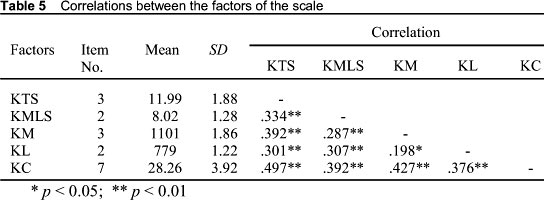
The corrected item-total correlations vary between 0.373 and 0.667, which, in turn, suggests that the scale has high internal consistency (see Table 4). Therefore, the scale has construct validity since the corrected item-total correlation coefficients are not negative, zero or close to zero (Tav°ancil, 2005). The results of the t test showed that for all items there was significant difference between the item scores of upper 27% and lower 27% groups of total score. This result suggested that all of the items in the scale were distinctive. Furthermore, we investigated the correlation between factors to determine the relationship between the factors of the scale. Correlation is often used to examine the construct validity (Tekindal, 2009). The results are presented in Table 5. There are positive and significant relationships between the scale's factors and between the factors and the total point (see Table 5). These correlations provide support for the multidimensionality of the scale.
Confirmatory factor analysis
We continued the study by modeling the relations between the factors identified through exploratory factor analysis and by considering the theoretical structure and their related items. To test the fit of the created model, confirmatory factor analysis was conducted by using Lisrel 8.51 program. For confirmatory factor analysis, various fit indexes are examined to evaluate the goodness of fit of the proposed factorial structure model. There are several criteria which considered as an indication of good fit of the factorial structure (Hooper, Coughlan & Mullen, 2008; Kelloway, 1998; Kline, 2005; Sümer, 2000, Simsek, 2007 cited in Cokluk, Sekercioglu & Büyüköztürk, 2010): (a) 2.5 or lower value for %2/df ratio, (b) higher than .90 value for Comparative Fit Index (CFI) and Goodness of Fit Index (GFI) and (c) .08 or less value for Root Mean Square Error of Approximation (RMSEA), Root Mean Square Residual (RMSR) and Standardized Root Mean Square Residual (SRMSR). However, GFI > . 85, RMSR and RMSEA < .10 are also considered acceptable criteria for evaluating the goodness of the fit of the model (Anderson & Gerbing, 1984; Cole, 1987).
With confirmatory factor analysis, we investigated the power of the items to represent and to what extend the sub-dimensions of the model relate to PCK, by examining the relations between the sub-dimensions and the relation of each sub-dimension to the PCK construct. Confirmatory factor analysis (CFA) is presented in two parts: a) examining first order and second order CFA and b) comparison of two models. We begin interpreting the results of the confirmatory factor analysis with the review of the five-factor model (first order CFA) as shown in Figure 2. In the figure, the circles represent the latent constructs, and the rectangles represent the measured variables. One-way arrows give information about how well each item represents its implicit variable (Simsek, 2007).
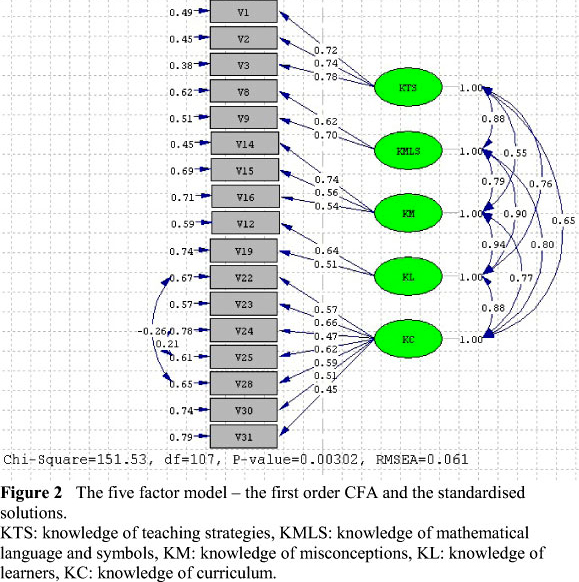
When Figure 2 is examined, it is seen that path coefficients (standardized regression coefficients) varies between .45 and .78. The range of path coefficients for each sub-dimension is as follows: .72-.78 for KTS dimension, .62-.70 for KMLS dimension, .54-.74 for KM dimension, .51-.64 for KL dimension, and .45-.66 for KC dimension. The goodness of fit indices of the model were found at an acceptable level (χ2 = 151.53, df = 107, x*/df = 1.42, CFI = 0.90, GFI = 0.86, RMSEA = 0.061, RMSR = 0.041 and SRMSR = 0.070). In addition, based on the modification indexes, item 24 (Iplan my lessons so as to relate the purposes of the mathematics curriculum with students' needs) and item 25 (When designing my lesson plans, I consider the goals of the topic), as well as item 22 (I have knowledge about the purposes of the mathematics curriculum) and item 28 (I can use the assessment tools presented in the mathematics curriculum) in Knowledge of Curriculum dimension were found more related to each other than the model predicted. Therefore, error covariance between those items was also included. It is natural for those items to be in the same factor and correlate with each other more than expected.
The proposed model was tested with second order confirmatory factor analysis. The model generated in this part illustrates a second-level model in which five sub-dimensions represent the PCK construct with significant relations. Confirmation of this model would indicate that the characteristics of pedagogical content knowledge can be measured in multiple ways and that the measured characteristics would be related to a higher-level factor (PCK). With this in mind, we ran the second order confirmatory factor analysis. The results are presented in Figure 3.
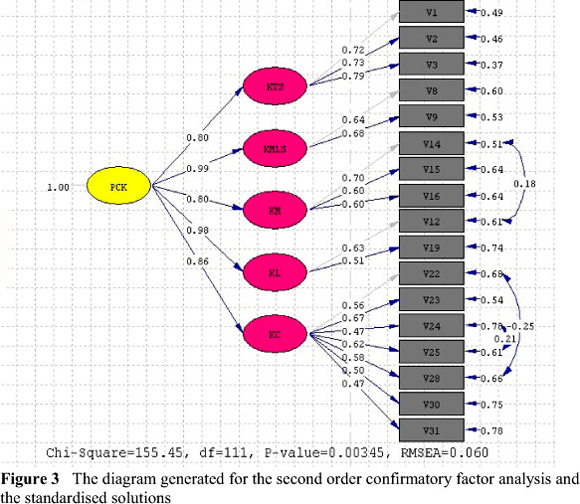
There are five first-level factors and one second-level factor in the last model. The path coefficients (standardized regression coefficients) for the first-level factors vary between .47 and .79 (see Figure 3). In addition, these five sub-dimensions found to represent the overall dimension of PCK at a high level (.80-.99). The goodness of fit indices of the model was found at an acceptable level (χ2 = 155.45, df = 111, x2/df =1.40, CFI = 0.90, GFI = 0.86, RMSEA = 0.060, RMSR = 0.040 and SRMSR = 0.070). In addition to the modifications in the first-order confirmatory factor analysis, item 12 (I know students' prior knowledge about a topic) and item 14 (I can anticipate students' possible difficulties about a topic) were found more related to each other than expected, and it was shown in the second order confirmatory factor analysis. The figure shows the relation between those items of different factors. Indeed, each item is about knowing students. For those items being correlated with each other more than expected is also supported by several studies in the literature. For instance, Bukova-Güzel (2010) defines knowing students' prior knowledge and possible student difficulties as knowledge of learners based on her literature review.
Although both the five-factor model and the second-order hierarchical model generated acceptable fit indices, there was a need to compare these two models in order to determine which model provided better fit to the data. Some procedures are recommended for comparing the models such as Akaike's informational criteria [AIC] (Akaike, 1987; Maruyama, 1998), consistent Akaike's informational criterion [CAIC] (Bozdogan, 1987), and expected cross-validation index [ECVI] (Browne & Cudeck, 1993). Lower values of AIC, CAIC and ECVI are generally associated with better model fit in comparing models (Maruyama, 1998). The five factor model yielded the following results: AIC = 243.53; CAIC = 414.59; ECVI = 2.19, and the second-order hierarchical model resulted in the following indices: AIC = 239.45; CAIC = 395.63; ECVI = 2.16. The second-order model generated lower values. Therefore, the second-order hierarchical model is considered a better model although both models are found to be acceptable. Consequently, the five-factor perception scale, composed of 17 items, on pedagogical content knowledge is confirmed as a model.
Reliability
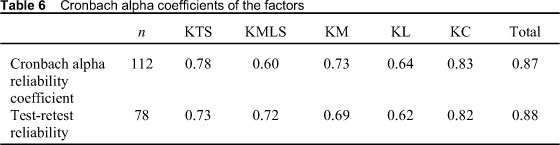
After exploratory and confirmative factor analysis, the reliability of the factors and the whole scale were examined by calculating the Cronbach alpha reliability coefficient. The results of the reliability test for each factor are presented in Table 6. The Cronbach alpha reliability coefficient of the whole scale was found to be .87. Furthermore, four weeks later the scale was re-administered to 78 of the participants in order to test the consistency of the scale. The Cronbach apha reliability coefficients of each factor and the whole scale were then calculated (see Table 6). Test-retest reliability of the scale was found to be .88. As seen in the table, the scale was found to be very consistent.
In addition to Cronbach's alpha reliability check, the reliability of the scale was also investigated with Split-Halves model. The scale was divided into two groups, and then the alpha value of each group was calculated. The alpha value of the first group with 9 items was found to be .78 while the alpha value of the second group with 8 items was found to be .83. The correlation between the halves was found to be .617, suggesting a positive linear relationship between the two groups of the scale. The reliability for the total scale was found to be .763 by using Spearman-Brown prophecy formula, and Guttmann's split-halve coefficient was found to be .763. These findings suggest that the validity and reliability of the scale are high.
Descriptive statistics
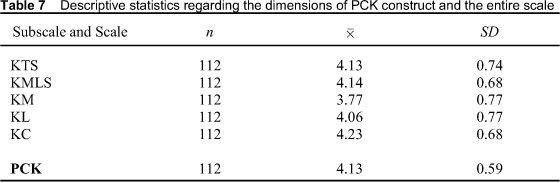
The pre-service teachers' responses to the scale items were interpreted by determining the width of the score interval in groups. Group interval coefficient value is obtained by "dividing the difference between the largest value and the smallest value in the measurement results by the determined number of groups" (Kan, 2009:407). In this study, group interval coefficient value is found to be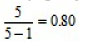 and thus the following intervals were used to evaluate the responses given to the scale items: 4.21-5.00 "Always", 3.41-4.20 "Usually", 2.61-3.40 "Undecided", 1.81-2.60 "Rarely", 1.00-1.80 "Never". In this scale, the highest possible score is 85 and the lowest possible score is 17.
and thus the following intervals were used to evaluate the responses given to the scale items: 4.21-5.00 "Always", 3.41-4.20 "Usually", 2.61-3.40 "Undecided", 1.81-2.60 "Rarely", 1.00-1.80 "Never". In this scale, the highest possible score is 85 and the lowest possible score is 17.
As seen in Table 7, while the pre-service teachers' perceptions regarding four dimensions of PCK (KTS, KMLS, KM, KL) correspond to "Usually" interval, their perceptions regarding KC dimension corresponds to "Always" interval. These findings suggest that the pre-service teachers have a positive perspective on their PCK and that they perceive themselves highly capable of fulfilling those skills outlined in the scale.
Discussion and Conclusion
In this paper, we present our efforts for developing a scale to determine prospective mathematics teachers' perceptions related to their pedagogical content knowledge. Following the statistical analyses, a five-factor scale composed of 17 items was developed. The factors of the scale are as follows: a) Knowledge of Teaching Strategies, b) Knowledge of Mathematical Language and Symbols, c) Knowledge of Misconceptions, d) Knowledge of Learners, and e) Knowledge of Curriculum. After constructing the scale, we proceeded to the validity and reliability analyses. As a result, the factors of the scale were found to be reliable with Cronbach's α value of 0.78, 0.60, 0.73, 0.64, and 0.83, respectively. The reliability of the whole scale was found to be .87. When the scale was re-administered to a subgroup of the sample, the scale was found to be reliable with α value of .88. In sum, the findings of the study showed that the generated scale is a valid and reliable instrument for determining the prospective mathematics teachers' perceptions related to their pedagogical content knowledge.
When the literature on this domain is reviewed, it is seen that the factors of the scale suggested in this study are compatible with other studies as well. For instance, Knowledge of Teaching Strategies, the first factor of the scale, has been addressed in various studies (e.g. Ball & Sleep, 2007; Bukova-Güzel, 2010; Fernández-Balboa & Stiehl, 1995; Grossman, 1990; Schoenfeld, 1998; Tamir, 1988; Toluk U?ar, 2010; Ye°ildere & Akko9, 2010; You, 2006). In several studies Knowledge of Mathematical Language and Symbols, the second factor of the scale, has been defined as a component of PCK (e.g. Ball, 2003; Ball & Sleep, 2007; Rowland et al., 2009). Similarly, there are a number of studies in which Knowledge of Misconceptions is defined as a component of PCK (e.g. Ball & Bass, 2000; Ball & McDiarmid, 1990; Bukova-Güzel, 2010; Grossman, 1990; Schoenfeld, 1998, 2000, 2005; Kovarik, 2008; You, 2006), as well as Knowledge of Learners is deemed as part of PCK (e.g. Fernández-Balboa & Stiehl, 1995; Grossman, 1990; Leavit, 2008; Schoenfeld, 1998; Tamir, 1988). Lastly, Knowledge of Curriculum is considered as an important component of PCK by many researchers (e.g. Bukova-Güzel, 2010; Grossman, 1990; Leavit, 2008; Schoenfeld, 1998; Tamir, 1988). It is clear that the factors of the scale encompass the components of PCK defined by relevant studies. In this sense, it is plausible to assert that the scale is very comprehensive.
The scale is considered as a useful tool for both pre-service and in-service mathematics teachers, as it provides them valuable information about their pedagogical content knowledge. It is a promising instrument to inform teachers about in which areas they need to improve. The scale can also be a useful tool for researchers in their- investigation of prospective mathematics teachers' perception of their pedagogical content knowledge and the related variables. Nevertheless, further studies in which the scale is administered to different samples and the dissemination of the related findings are recommended, as those would greatly contribute to the applicability of the scale. Taking different PCK frameworks into account, the scale can be elaborated further by increasing the number of items. Furthermore, given that assessing teachers' knowledge without observing their practices in class would be incomplete and superficial (Ball et al., 2001 cited in Bütün 2005), we strongly recommend that prospective teachers are given abundant opportunities to practice teaching in classrooms, particularly focusing on improvement-needed areas, once their perceptions related to their pedagogical content knowledge are ascertained with the scale. Consequently, we conceive that the scale can be used as a guide for studies aiming at determining pre-service teachers' perceptions related to their pedagogical content knowledge. It can also be used as a framework for qualitative studies to assist observations and interviews, as it gives ideas about what to focus on. In addition, this scale can be of use to studies aiming to determine in-service mathematics teachers' perceptions regarding their pedagogical content knowledge, and thus, to design professional development for teachers based on their needs.
References
Acil E 2011. Ilkogretim ogretmenlerinin etkinlik algisi ve uygulanisina iliskin gorusleri. Yayinlanmamis Yuksek Lisans Tezi, Gaziantep: Gaziantep Universitesi, Sosyal Bilimler Enstitusu. [ Links ]
Akaike H 1987. Factor analysis and AIC. Psychometrika, 52:317-332. [ Links ]
Akgul A & Cevik O 2003. Istatistiksel analiz teknikleri: SPSS'te Sletme yönetimi uygulamalari. Ankara: Emek Ofset Ltd. Sti. [ Links ]
An S, Kulm G & Wu Z 2004. The pedagogical content knowledge of middle school mathematics teachers in China and the U.S. Journal of Mathematics Teacher Education, 7:145-172. [ Links ]
Anderson JC & Gerbing DW 1984. The effect of sampling error on convergence, improper solutions, and goodness-of-fit indices for maximum likelihood confirmatory factor analysis. Psychometrika, 49:155-173. [ Links ]
Ball DL 2003. What mathematical knowledge is needed for teaching mathematics? Remarks prepared for the Secretary's Summit on Mathematics. Washington, D.C.: U.S. Department of Education. Available at http://www.erusd.k12.ca.us/ProjectALPHAweb/ indexfiles/MP/BallMathSummitFeb03.pdf. Accessed 26 November 2010. [ Links ]
Ball DL & Bass H 2000. Interweaving content and pedagogy in teaching and learning to teach: knowing and using mathematics. In J Boaler (ed). Multiple perspectives on mathematics teaching and learning. Westport, CT: Ablex Publishing. [ Links ]
Ball DL & McDiarmid GW 1990. The subject matter preparation of teachers. In R. Houston (ed). Handbook of research on teacher education. New York: Macmillan. [ Links ]
Ball DL & Sleep L 2007. What is knowledge for teaching, and what are features of tasks that can be used to develop MKT? Presentation Made at the Center for Proficiency in Teaching Mathematics (CPTM) Pre-session of The Annual Meeting of The Association- of Mathematics Teacher Educators (AMTE), Irvine, CA, January 25. [ Links ]
Ball DL, Thames MH & Phelps G 2008. Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59:389-407. [ Links ]
Binbaijioglu C & Binbasioglu E 1992. Endüstri psikolojisi. Ankara: Kadioglu Matbaa. [ Links ]
Bozdogan H 1987. Model selection and Akaike's information criterion (AIC): The general theory and its analytical extensions. Psychometrika, 52:345-370. [ Links ]
Browne MW & Cudeck R 1993. Alternative ways of assessing model fit. In KA Bollen & JS Long (Eds). Testing structural equations models. Newbury Park, CA: Sage. [ Links ]
Bukova-Güzel E 2010. An investigation of pre-service mathematics teachers' pedagogical content knowledge, using solid objects. Scientific Research and Essays, 5:1872-1880. [ Links ]
Bütün M 2005. Ukögretim matematik ögretmenlerinin alan egitimi bilgilerinin nitelikleri üzerine bir calis.ma. Yüksek Lisans Tezi: Karadeniz Teknik Üniversitesi. [ Links ]
Büyüköztürk S 2007. Sosyal bilimler igin veri analizi el kitabi. Ankara: Pegem Akademi Yayincilik. [ Links ]
Carter K 1990. Teachers' knowledge and learning to teach. In WR Houston & MHJ Sikula (eds). Handbook of research on teacher education. New York: Macmillan. [ Links ]
Charalambos CY, Philippou GN & Kyriakides L 2008. Tracing the development of preservice teachers' efficacy belief in teaching mathematics during fieldwork. Educational Studies in Mathematics, 67:125-142. [ Links ]
Chick H, Baker M, Pham T & Cheng H 2006. Aspects of teachers' pedagogical content knowledge for decimals. In J Novotná, H Moraová, M Krátká & N Stehlíková (eds). Proceedings of the 30th Conference of the International Group for the Psychology of Mathematics Education (Vol. 2). Prague: PME. [ Links ]
Cokluk Ö, Sekercioglu G & Büyüköztürk ? 2010. Sosyal Bilimler igin Cok Degiskenli Istatistik: SPSS ve Lisrel Uygulamalari. Ankara: Pegem Yayincilik. [ Links ]
Cole DA 1987. Utility of confirmatory factor analysis in test validation research. Journal of Consulting and Clinical Psychology, 55:1019-1031. [ Links ]
Enochs LG & Riggs IM 1990. Further development of an elementary science teaching efficacy belief instrument: A preservice elementary scale. School Science and Mathematics, 90:694-706. [ Links ]
Enochs LG, Smith PL & Huinker D 2000. Establishing factorial validity of the mathematics teaching efficacy beliefs instrument. School Science and Mathematics, 100:194-202. [ Links ]
Ernest P 1989. The knowledge, beliefs, and attitudes of the mathematics teacher: A model. Journal of Education for Teaching, 15:13-33. [ Links ]
Fernández-Balboa JM & Stiehl J 1995. The generic nature of pedagogical content knowledge among college professors. Teaching and Teacher Education, 11:293-306. [ Links ]
Gess-Newsome J 1999. Pedagogical content knowledge: an introduction and orientation. In J Gess-Newsome & NG Lederman (Eds). Examining Pedagogical Content Knowledge: The construct and its implications for science education. Netherlands: Kluwer Academic Publisher. [ Links ]
Gökdag D 2008. Etkili iletisim. In U Demiray (Ed). Etkili Iletisim. Ankara: Pegem Akademi Yayincilik. [ Links ]
Grossman PL 1990. The making of a teacher: teacher knowledge and teacher education. New York: Teachers College Press. [ Links ]
Hill H, Ball DL & Schilling S 2008. Unpacking 'pedagogical content knowledge': conceptualizing and measuring teachers' topic-specific knowledge of students. Journal for Research in Mathematics Education, 39:372-400. [ Links ]
Hooper D, Coughlan J & Mullen MR 2008. Structural equation modelling: guidelines for determining model fit. Electronic Journal of Business Research Methods, 6:53-60. [ Links ]
Hudson P & Ginns I 2007. Developing an instrument to examine preservice teachers' pedagogical development. Journal of Science Teacher Education, 18:885-899. [ Links ]
Hudson P & Peard R 2006. Mentoring Pre-Service Elementary Teachers in Mathematics Teaching. EDU-COM 2006. International Conference. Engagement and Empowerment: New Opportunities for Growth in Higher Education, Edith Cowan University, Perth Western Australia, 22-24 November. Available at http://ro.ecu.edu.au/cgi/viewcontent.cgi?article=1078&context=ceducom. Accessed 26 November 2010. [ Links ]
Hudson P & Skamp K 2003. Mentoring pre-service teachers of primary science. The Electronic Journal of Science Education, 7. Available at http://wolfweb.unr.edu/homepage/crowther/ejse/hudson1.pdf. Accessed 11 October 2009. [ Links ]
Kan A 2009. Ölçme somman üzerinde istatistiksel islemler (Statistical processes on the results of measurement). In H Atilgan (ed). Egitimde ölçme ve degerlendirme. Ankara: Ani Publications. [ Links ]
Kelloway KE 1998. Using LISREL for structural equation modeling: A researcher's guide. Thousand Oaks, CA: Sage. [ Links ]
Kennedy MM 2010. Attribution error and the quest for teacher quality. Educational Researcher, 39:591-598. [ Links ]
Kline RB 2005. Principles and practice of structural equation modeling (2nd ed). New York: The Guilford Press. [ Links ]
Kovarik K 2008. Mathematics educators' and teachers' perceptions of pedagogical content knowledge. Doctoral Dissertation. United States of America: Columbia University. [ Links ]
Leavit T 2008. German mathematics teachers' subject content and pedagogical content knowledge. Doctoral Dissertation. Las Vegas: University of Nevada. [ Links ]
Magnusson S, Krajcik J & Borko H 1999. Nature, sources, and development of pedagogical content knowledge for science teaching. In J Gess-Newsome & NG Lederman (eds). Examining pedagogical content knowledge. Dordrecht: Kluwer Academic Publishers. [ Links ]
Marks R 1990. Pedagogical content knowledge: from a mathematical case to a modified conception. Journal of Teacher Education, 41:3-11. [ Links ]
Maruyama GM 1998. Basics of structural equation modeling. Thousand Oaks, CA: SAGE Publications. [ Links ]
Noss R & Baki A 1996. Liberating school mathematics from procedural view. Hacettepe University Journal of Education, 12:179-182. [ Links ]
Rice JK 2003. Teacher quality: Understanding the effectiveness of teacher attributes. Washington, DC: Economic Policy Institute. [ Links ]
Rietveld T & Van Hout R 1993. Statistical techniques for the study of language and language behaviour. Berlin/New York: Mouton de Gruyter. [ Links ]
Rowland T, Turner F, Thwaites A & Huckstep P 2009. Developing primary mathematics teaching: reflecting on practice with the knowledge quartet. London: Sage. [ Links ]
Schoenfeld AH 1998. Toward a theory of teaching-in-context. Issues in Education, 4:1-94. [ Links ]
Schoenfeld AH 2000. Models of the teaching Process. Journal of Mathematical Behavior, 18:243-261. [ Links ]
Schoenfeld AH 2005. Problem solving from cradle to grave. Paper Presented at the Symposium 'Mathematical Learning from Early Childhood to Adulthood', July 7-9, Mons, Belgium. [ Links ]
Shulman LS 1986. Those who understand: Knowledge growth in teaching. Educational Researcher, 15:4-14. [ Links ]
Shulman LS 1987. Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57:1-21. [ Links ]
Simsek ÖF 2007. Yapisal esitlik modellemesine giris temel ilkeler ve lisrel uygulamalari. Ankara: Ekinoks Yayincilik. [ Links ]
Sümer N 2000. Yapisal esitlik modelleri: Temel kavramlar ve örnek uygulamalar. Türk Psikoloji Yazilari, 3:49-74. [ Links ]
Tamir P 1988. Subject matter and related pedagogical knowledge in teacher education. Teaching & Teacher Education, 4:99-110. [ Links ]
Tavsancil E 2005. Tutumlann ölgülmesi ve SPSS ile veri analizi. Ankara: Nobel Yayincilik [ Links ]
Tekindal S 2009. Duyussal özelliklerin ölçülmesi araç olusturma. Ankara: Pegem Akademi Yayincilik. [ Links ]
Toluk Uçar Z 2010. Sinif ögretmeni adaylarinin matematiksel bilgileri ve ögretimsel açiklamalari. In proceedings of 9 Ulusal Sinif Ögretmenligi Egitimi Sempozyumu, 20-22 Mayis, Elazig, 261-264. [ Links ]
Tschannen-Moran M & Woolfolk Hoy A 2001. Teacher efficacy: Capturing and elusive construct. Teaching and Teacher Education, 17:783-805. [ Links ]
Verloop N, Van Driel J & Meijer P 2001. Teacher knowledge and the knowledge base of teaching. International Journal of Educational Research, 35:441-461. [ Links ]
Yesildere S & Akkoç H 2010. Matematik ögretmen adaylarinin sayi örüntülerine iliskin pedagojik alan bilgilerinin konuya özel stratejiler baglaminda incelenmesi. Ondokuz Mayis ÜniversitesiEgitim Fakültesi Dergisi, 29:125-149. [ Links ]
You Z 2006. Pre-service teachers' knowledge of linear functions within multiple representation modes. Doctoral Dissertation. Texas: A&M University. [ Links ]














