Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Education
On-line version ISSN 2076-3433
Print version ISSN 0256-0100
S. Afr. j. educ. vol.33 n.2 Pretoria Jan. 2013
Consistencies far beyond chance: an analysis of learner preconceptions of reflective symmetry
Michael Kainose Mhlolo; Marc Schafer
Education Department, FRF Mathematics Education Chair, Rhodes University, South Africa M.Mhlolo@ru.ac.za
ABSTRACT
This article reports on regularities observed in learners' preconceptions of reflective symmetry. Literature suggests that the very existence of such regularities indicates a gap between what learners know and what they need to know. Such a gap inhibits further understanding and application, and hence needed to be investigated. A total of 235 Grade 11 learners, from 13 high schools that participate in the First Rand Foundation-funded Mathematics Education project in the Eastern Cape, responded to a task on reflective symmetry. Our framework for analysing the responses was based on the taxonomy of structure of the observed learning outcome. The results indicated that 85% of learner responses reflect a motion understanding of reflections, where learners considered geometric figures as physical motions on top of the plane. While this understanding is useful in some cases, it is not an essential aspect of mapping understanding, which is critical for application in function notations and other analytical geometry contexts. We suggest that if this gap is to be closed, learners need to construct these reflections physically so that they may think of reflections beyond motion.
Keywords: preconceptions, reflective symmetry, regularities, SOLO taxonomy, transformations
Introduction
Changes to assessment have always been recognised as an important means of achieving curriculum change in practice and in setting standards (Sieborger & Macintosh, 2004), yet in the past assessment was rarely integrated with the development process. In this article we analyse Grade 11 learners' responses to a benchmark task on reflective symmetry with the aim of understanding: (a) preconceptions that were common or typical in learners' responses; (b) how both practice and previous research findings have explained such regularities; and (c) some suggestions that Mathematics Education literature has put forward to mitigate similar challenges.
Statement of the problem
In our analyses of learner responses we observed a rather disturbing consistency in the way in which they conceptualised reflective symmetry. Berieter (1985:24) has previously pondered such regularities, which were usually not connected with any accepted mathematical definition, through the following question:
Out of the infinitude of correspondences that might be noticed between one event and another, how does it happen that ... different children, with consistency far beyond chance, tend to notice the same correspondences? With specific reference to reflective symmetry, Hoyles and Healy (1997) posited that the very existence of these regularities suggested that learners had constructed a socially shared understanding of reflection. Because these regularities were not connected with the wider mathematical community's ways of knowing; the problem of explaining how students make such constructions seemed intractable as long as 'we' failed to make them objects of 'our' analyses (Cobb, Yackel & Wood, 1992). Hence here we are making such learner constructions the objects of our analyses, and we do so by raising the following research questions:
What are the consistent preconceptions of reflective symmetry that are evident in learner responses?
How can we explain such regularities?
What strategies could be used by teachers to connect learner preconceptions with mathematically acceptable ways of reflective symmetry?
Background
A number of strategies have been put in place to mitigate the problem of poor performances in Mathematics. Our institution is privileged to host one of the four First Rand Foundation (FRF) Chairs that have been tasked with, among other things, the responsibility of researching and getting: (a) to understand the nature of the problem of poor performance in Mathematics; and (b) to suggest strategies for improving learner performances.
In pursuance of that objective, in January 2012 we did benchmark testing in all of the Grades 10-12 in the 13 high schools that participate in our FRF project, with the aim of establishing the nature and extent of learner backlog. In turn, this knowledge would enable the project to suggest possible intervention strategies.
Nature of the task
We analysed learner responses to a task (see Figure 1) where the questions were phrased as follows:
The diagram below shows a Cartesian plane with points A (- 3; 6), B (4;- 2) and C (-5; 1). Draw, on the grid below, A', B' and C, clearly labelling the coordinates of each point if:
(a) A' is the image of A reflected in they-axis.
(b) B' is the image of B reflected in the line y = 0.
(c) C is the image of C reflected in the line y = x.
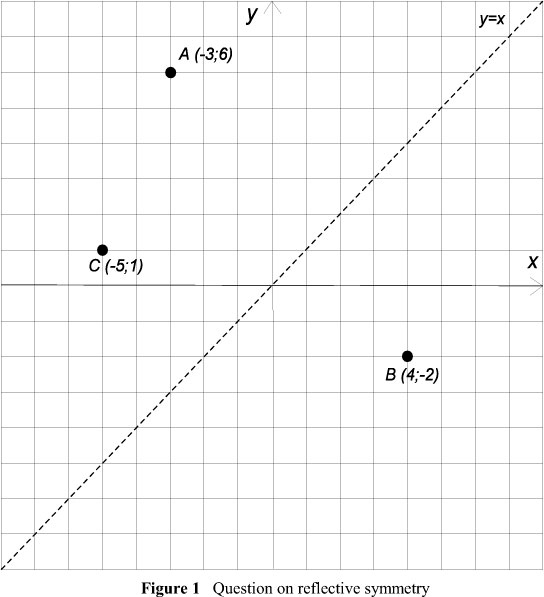
When we examined the characteristics of this task, our view was that it offered learners opportunities to answer the question from either a visual or an analytical approach, or by complementing both approaches. A visual approach advocates investigations and discovery of properties via concrete manipulations, models and diagrams (Bansilal & Naidoo, 2012). Literature suggests that visual communication in Mathematics Education is especially important to students with limited proficiency in English (Cummins, 1984; Dawe, 1983; Presmeg, 1989).
Because the FRF project in our institution targets learners in previously disadvantaged communities, where language problems have been documented, ensuring learners' development of their visual abilities is particularly critical for our project. Nevertheless, according to Bansilal and Naidoo (2012) a diagram provided on the Cartesian plane may elicit visualisation strategies, provided the learner is able to recognise what is given and what needs to be done. Therefore, the first question guiding our analyses was: 'What did the learners recognise as given in this diagram and do they show any understanding of what needs to be done?'
It was also possible for learners to tackle the task from a purely analytical ap- proach by applying algebraic rules for reflective symmetry. The analytical approach is characterised by algebraic formulae used to describe the results of transformations of figures situated within a Cartesian plane. Analytical abilities therefore suggest that learners understand a representation or a change between two representations because of the ready availability of algebraic formulae. This ability to imagine and reason about changes of objects and their spatial layout is important both for everyday cognition and for reasoning in many technical domains.
The algebraic formulae for dealing with reflections in the three different mirror lines is summarised in Table 1.

According to Maharaj (2008) Mathematics makes use of such symbolic notation, which serves a dual role as an instrument of communication and of thought. This special language makes it possible to represent mathematical concepts, structures and relationships in coded form. In order to successfully use analytical techniques in this task learners needed to know these symbolic notations and rules of reflective symmetry first, and to be able to apply the rules using the coordinates of the given points. In our analyses we were also interested to see how the learners applied such algebraic rules.
We also conjectured that in attempting to solve this task learners might also have followed a sequential and hierarchical order, starting from a visual perspective then complementing that with an analytical approach. Franco and Sperry (1977) posited that nonverbal visuospatial apprehension commonly seemed to precede and support the sequential deductive analysis involved in the solution of geometry problems. Even the well-known and widely applied van Hiele model of geometric thought also specifies visual reasoning as an initial level of geometric understanding (Bansilal & Naidoo, 2012).
The general consensus among researchers is that the analytical approach would be useful as a tool to verify the accuracy or correctness of the image positions. We argue that such verification ability was not only critical for learners in this particular task but that verification is, in its own right, an indispensable life-long mathematical skill. It is for that reason that we were also interested in our analyses to see whether learners were able to make such connections between the visual and the analytical approaches.
Importance of the study
As an entry point into the importance of our study, the reader may be interested to know why we opted to use the term 'preconceptions' as opposed to others (such as 'epistemological obstacles', 'didactic obstacles', 'misconceptions' or 'misunderstandings') that we often meet in the Mathematics Education literature. Our view follows that of McGowen and Tall (2010), who argued that such terminology was not helpful in a developmental agenda as it suggests a deficiency in the thinking of the child - yet learners cannot have a misconception without first having a conception. From our observations, learners had a conception of reflective symmetry which was useful in some cases but not applicable in more complicated contexts. From a developmental perspective:
It is surely more productive to accentuate the positive (what worked before) and consider how to look at new ideas in a different way that is more appropriate for the new situation rather than accuse learners of making errors when they need carefully directed support to help them attempt to make sense of complicated new ideas (McGowen & Tall, 2010:172).
McGowen and Tall (2010) therefore prefer the term 'preconceptions', in the sense that learners are reasoning based on aspects that were experienced before the need for a new conception and were helpful in the earlier context. It is this view that we also took in our work, and hence our use of the term preconceptions. Our concern about consistencies in learner responses followed literature which suggests that it is by capitalising on students' mathematical activity that the teacher initiates and guides the classroom community's development of taken-as-shared ways of mathematical knowing towards those of the wider mathematical community (Cobb et al., 1992). So we were interested in understanding the nature of the learners' shared understandings of reflective symmetry, and then to strategise as to how the gap between such understanding and the wider mathematical community's ways of knowing could be closed.
Why preconceptions in geometry, one might ask? Geometry was central to the debates that shaped the most recent Mathematics curriculum in South Africa, yet empirical evidence indicated that space and shape were problematic to both teachers and learners (Kotze, 2007). Literature also shows the importance of reflective symmetry in other areas of Mathematics. For example, when graphing quadratics learners might be asked to sketch the parabola, determine its axis of symmetry, use reflective symmetry to find points through which it passes, or to complete other related tasks where they are expected to use Cartesian coordinates to analyse geometric systems.
Outside Mathematics one can also notice the value and applicability of symmetry in design and technology. In the textile industry, for example, the shapes drawn from folding garment material when making garments provides models which actually serve as graphic explications of the concept of symmetry through its actual use. This same principle applies in sheet-metal industries, wood technology and many other related areas.
The importance of our analyses could also be seen in that they are not focused on transformation geometry per se but also on the visual and analytical skills that learners can also apply in other areas. Transformation geometry is only a subset of geometry in which learners learn to identify and illustrate movement of shapes in two and three dimensions, both qualitatively and quantitatively (Tartre, 1990). In fact, spatial intuition or spatial perception is an enormously powerful tool, not only for things that are obviously geometrical but even those that are not. Smith (1964:213-214) emphasised this more central role for spatial skills in problem solving:
... the conception of spatial ability ... is so all embracing that one is led to inquire whether the process of perceiving and assimilating general patterns or configurations is not in fact a process of abstraction.
Suydam (1985) shows how transformations play a role in developing such spatial abilities by arguing that the spatial visual aspect becomes as important as the logical-deductive aspect with the help of transformations. Yet we noticed a consistency of preconceptions in learners' visual and analytical abilities 'far beyond chance', which in our view would inhibit their abstraction of reflective symmetry.
Having given this background, we now show how we went about collecting data and which tools were used to provide possible explanations for such learner responses.
Methodology
Sampling process
We analysed all 235 Grade 11 learners' responses from all 13 high schools participating in the FRF Mathematics Education Chair project. After observing some regularity in the way learners were responding to the task across all the 13 high schools, consistent with our research questions, we were interested to explain why there were such regularities. We conjectured that it was possible that their conceptualisation of reflective symmetry might have been influenced by the way textbooks, and not teachers, presented the subject matter.
We argue that teachers alone could not have presented reflective symmetry uniformly across all 13 schools. Literature shows how textbooks set the style and order in which facts to be learnt are covered within the schools. So we designed a questionnaire for teachers to capture data on the textbooks that they were using. Analysis thereof revealed that 88% of the schools used one standard set of textbooks. We then analysed how reflective symmetry was presented in this particular set of textbooks from Grade 7 right through to Grade 11. Our observations are detailed in the discussion of results.
Analytical tool for learner responses
It is important for the reader to note that when we designed the benchmark tasks, we were not aiming at testing an a priori theory on learning Mathematics in general or geometrical transformations in particular. Our aim was to establish levels of content knowledge that Grade 11 learners had in different mathematical areas, and then to develop an ' a posteriori' framework for justifying our descriptions of learner responses that we observed in each of the areas tested. The phrases 'a priori' and 'a posteriori' are Latin for 'from what comes before' and 'from what comes later', respectively, and are used in research to distinguish two different types of knowledge. A priori knowledge is known independently of experience (conceptualised knowledge), and a posteriori knowledge, which guides this article, is proven through experience. Because 'a posteriori' justification or argument makes reference to experience, the issue then becomes how one knows the proposition or claim one makes, and what justifies or grounds one's belief in it. Consistent with that view, we will show how our experiences with learner responses together with literature guided our choice of the analytical tools, the initial propositions or claims that we made, our justifications of such claims, as well as our conclusions.
In deciding on the analytical tool for this analysis we took it that the purpose was to construct an understanding of the observed learning outcomes regarding line symmetry. We therefore needed to develop an evaluation model which took into consideration the learners' knowledge of and abilities for solving line symmetry tasks. Biggs and Collis (1989) and later Xistouri (2007) suggested that the taxonomy of structure of the observed learning outcome (SOLO) could be used as a means for evaluating learners' development of knowledge in symmetry. SOLO is a means of classifying learning outcomes in terms of their complexity, enabling researchers to assess students' work in terms of its quality as opposed to how many bits of this and of that they got right (Biggs & Collis, 1989). From the literature the SOLO taxonomy is considered as a hierarchical model that is suitable for measuring learning outcomes of different subjects, levels, and for all lengths of assignments (Chan, Tsui, Chan & Hong, 2002).
The taxonomy follows hierarchical levels where the very first level (prestructural) is marked by incompetence, an indication that learners missed the point. At the next level learners might pick up only one aspect of the task (unistructural), then they may pick up several aspects which are unrelated (multistructural), then they may show an ability to integrate them into a coherent whole (relational), and finally they may be able to generalise their coherent whole to as yet untaught applications (extended abstract). Figure 2 lists verbs typical of each of the above-mentioned levels.
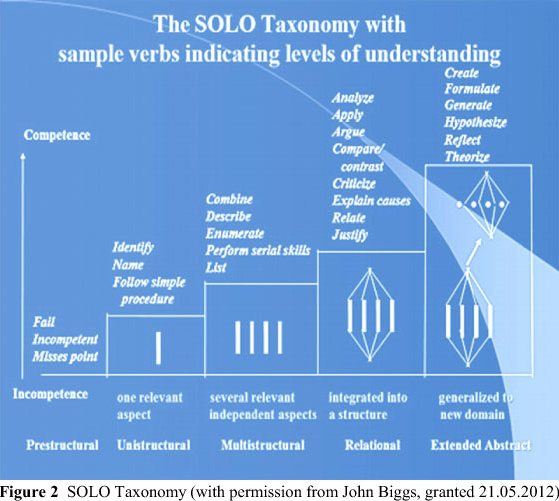
We did not decide on the SOLO taxonomy without taking into consideration other possible taxonomies like the popular van Hiele model. However, a number of researchers who have applied the SOLO taxonomy credit its comprehensiveness in application and its objective criteria for measuring students' cognitive attainment (Chick, 1998; Lake, 1999; Van Rossum & Schenk, 1984; Xistouri, 2007). All these factors compelled us to settle for the SOLO taxonomy.
Data presentation
In the next section we show how the SOLO taxonomy helped us to categorise and then analyse learners' responses within the different levels of attainment.
Prestructural stage
Our first observation was that what intuitively came to the majority of learners' minds was a 'shape'; hence they joined the three points A, B, and C to form a triangle, as shown in Figure 3.
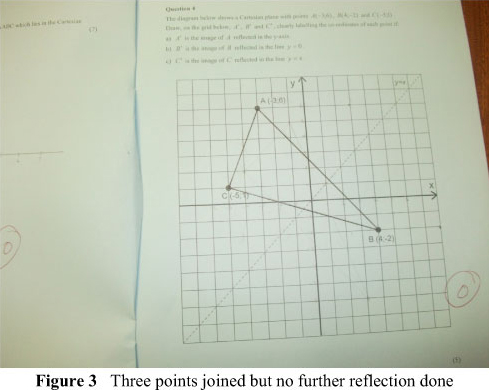
While some learners might have been able to move to the next stage of reflecting the intuitively formed triangle in either the y- or the x-axis, the majority of learners got stuck and were not able to do anything else after joining the three points. Consistent with the SOLO taxonomy, we argue that such learners were still at the prestructural stage - where the task is not attacked in an appropriate way and the student has not understood the point.
Unistructural stage
We observed that more learners were able to move a step further with some reflecting the triangle in the y-axis and others in the x-axis, as shown in Figures 4 and 5, respectively.
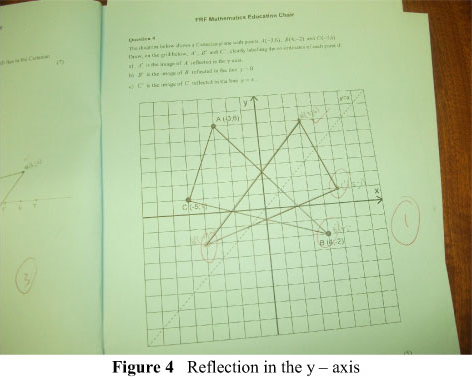

Consistent with the SOLO taxonomy we argue that such learners were at the unistructural stage - where one relevant aspect (one mirror line) of the task is picked up, but there is no relationship between facts or ideas. We argue that there was no relationship between ideas and facts, because nowhere in the task does it suggest that the three points A, B, and C were vertices of a triangle.
Multistructural stage
Our view was that learners would have reached this multistructural stage if they were able to visually reflect the three points in their respective lines of symmetry, but went on to fumble when naming the points. We argue that the visual approach did not require the application of special mathematical abilities other than conservation of two properties, i.e. the same distance from the mirror line, and that the image was vertically opposite, both of which could have been obtained by mere visualisation. Consistent with this argument, naming the coordinates of the images would therefore have been another independent skill. In accordance with the SOLO taxonomy the multistructural stage is where several (two or more) independent aspects are picked up or understood serially, but are not interrelated. From our analyses none of the learner responses fell into this category, although the taxonomy would have enabled us to capture such responses.
Relational stage
Consistent with the SOLO taxonomy and with reference to the task under review, we considered that learners would have reached this relational stage if they were able to integrate the relevant aspects. In this case, they would have been able to reflect all the three points in the different lines of symmetry and to label the coordinates of the images correctly. Such learners would have scored all the points allocated for this task and indeed a few were able to do so.
Extended abstract stage
The extended abstract stage is where the coherent whole is generalised or recon ceptualised to a higher level of abstraction and our view was that the task under review did not test learners at this level. We therefore had no responses coded under this extended abstract stage. Table 2 shows the summary of the findings in the three levels that we were able to code the learner responses.
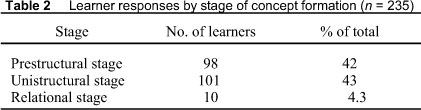
Summary of the findings
Table 2 shows that 42% of the learner responses were still at the prestructural stage, 43% were at the unistructural stage, and only 4.3% were at the relational stage.
Discussion
The first question that the research raised had to do with the consistencies that were evident in learner preconceptions of reflective symmetry. We have argued that ascertaining what students think and reasoning about the implications of those responses are critical elements of teaching, because children's thinking is seldom capricious. The very existence of these regularities suggested that learners had constructed a socially shared understanding of reflection, and we would not be able to alleviate such challenges if we failed to make such regularities the objects of our analyses. Three regularities were evident in the learners' responses, and we now discuss each in terms of how other researchers have explained similar observations and what strategies have been suggested to alleviate similar challenges.
Learners joining the three points to form a triangle
Our observations were that although 43% of the learners progressed from the pre-structural to the unistructural stage, while 42% remained stuck at the prestructural stage, the entry point for all 85% of these learners was through joining the three points A, B, and C to form a triangle, as shown in Figures 3, 4, and 5. To us this was typical of regularity 'far beyond chance', which could not be treated as a learner 'misconception' but as a 'preconception'.
We became intrigued to understand why most learners were starting by joining the points to form a triangle. We had earlier conjectured that textbooks could have contributed to the way learners conceptualised reflective symmetry. Fauvel (1991) has pointed to the dominant role of textbooks in teaching, and argued that for both students and teachers Mathematics is simply what is written in the textbooks. Fauvel (1991: 116) used a metaphor positing that "as teachers at a distance" textbooks often define the facts to be learnt within schools' curricula. They set the style and order in which the material is covered in the course, and teachers rely on them to organise lessons and structure the subject matter.
Our analyses of the standard set of textbooks (Grades 7-12) used by 88% of the FRF project teachers revealed that reflective symmetry is not introduced until Grade 8. Introduction of reflective symmetry at Grade 8 is done informally through looking at patterns and identifying 'geometrical shapes', which are then reflected (folded), mainly around a vertical and horizontal axis. In Grade 9 the formal definition of reflective symmetry is given as follows: "... the line about which a shape is folded to give a reflection is called a line of reflection or an axis of symmetry" (Laridon, Aird, Essack, Kitto, Pike, Sasman, Sigabi & Tebeila, 2001:223). The activities that follow this definition involve copying diagrams and drawing a line of reflection for each one. Even though in Grade 10 a few tasks specifically focus on the reflection of points, the textbook still defines reflective symmetry as ". when a figure has an axis of symmetry, it will reflect onto itself if it is reflected about such a line" (Laridon, Barnes, Jawurek, Kitto, Myburgh, Pike, Scheiber, Sigabi, Wilson & van Rooyen, 2008:192).
From the way both the definition and properties of reflective symmetry are presented in these textbooks, we argue that reflective symmetry suggests a 'shape/ diagram/figure' that is of the 'same size' or 'congruent' which is 'reversed' or 'flipped over' or ' laterally inverted' in the mirror line. This gives learners a 'motion understanding' of reflections which, we argue, is insufficient for conceptual understanding of reflective symmetry.
According to Yanik & Flores (2009) a person who has a motion understanding of transformations may conceive the plane as a background with geometrical objects able to be manipulated on it. In this motion understanding one may consider transformations as "physical motions of geometric figures on top of the plane" (Edwards, 2003:8), yet the plane consists of an infinite number of distinct points, and geometric figures are only subsets of points of the plane rather than separate entities.
When transforming a figure in the plane, all points in the plane need to be considered (Hollebrands, 2004), and from this viewpoint transformation is not limited to a figure or a point. This is referred to as the 'mapping understanding' of transformations, where one maps all points in the plane to other points in the plane rather than removing images/points from their original locations to different locations (Yanik & Flores, 2009). A mapping understanding of transformations allows us to think about transformations beyond motion.
From the way the learners in this study joined points A, B, and C, we argue that they have not yet fully conceptualised this mapping understanding of reflection -hence we are referring to such responses as preconceptions. They were conceiving of the plane as a background on which the triangle was placed, and therefore separate from the plane in which it was located. This is different from the perspective of contemporary Mathematics, in which points (or lines or figures) are located at particular places on the plane and are not separate from but actually subsets of the plane (Edwards, 2003).
We further argue that although the term 'shape' or 'object' is generally used when defining reflective symmetry, there are fundamental differences when compared with a point, as was the case in this task. A point, unlike a shape, has no 'size' - and neither does it have an 'orientation' which can be flipped over or reversed. This makes the process of reflection of points in this task rather complex compared to the motion understanding learners might have worked with earlier. However, we conjecture that this complexity was more productive, as it forced learners to abstract a reflection not as a static property of shapes but as a function with specific properties that transcended any particular configuration of object and mirror line. Our view is that this ability to visualise a reflection through mapping of points is fundamental to the understanding of reflective symmetry, as it enables learners to apply the concept in other areas.
Learners reflecting horizontally and vertically
The second regularity that we noticed was that after joining the three points to form a triangle, 43% of the learners then reflected their triangles, mainly in the y-axis and in the x-axis. Consistent with our second research question, we were interested to explain such regularities in learner responses. In a similar study by Hollebrands (2004), where learners were asked to draw an example of a reflection, the researchers noted that before performing the task almost all the learners implicitly used a vertical or horizontal line of reflection (although they may not have actually included the line in their examples).
Similar preferences for the horizontal and vertical reflections were observed in Hoyles and Healy's (1997) study. As to why learners could not call on the algebraic rules to verify their reflections, Hoyles and Healy (1997) also observed that all the learners in their study were resistant to checking their constructions, because their images 'looked like a reflection'. There was nothing to suggest otherwise, hence they saw no reason to check or verify.
These findings are also evident in the learner responses that we analyse in this article, as all the learners seemed to think about reflection as flipping over the horizontal or vertical axes. They also tried to draw the image congruent to their incorrect pre-image, without attending to the required lines of reflection and without using other methods such as the algebraic rules to verify or check the accuracy of their constructions - presumably because their constructions 'looked like reflections'. Such findings were also evident in the works of Burger and Shaughnessy (1986), Perham, Perham and Perham (1976), and Schultz and Austin (1983).
Learners avoiding the diagonal line
The third and last regularity that we noticed was that none of the learners tried to reflect in the line y = x. In similar studies Küchemann (1981), Schultz and Austin (1983), Hoyles and Healy (1997) and Hollebrands (2004) also found that learners had most difficulty with reflection over a diagonal line; the students were found often to ignore the angle or slope of the reflection line, and performed a horizontal or vertical reflection instead. From a visual perspective properties of equidistance and perpendicularity are not easy to notice in a slanting line of reflection, such as the lines y = x or y = -x, hence reflections in such slanting lines are likely to be 'impossible' to the learners and hence ignored. This might also explain why learners find reflections in the lines x = 0 and y = 0 relatively easier to work with, because perpendicularity is almost visible at a glance.
What recommendations have been suggested?
There are two complementary recommendations that we could make from such observations, both of which would move learners from a predominantly motion understanding to a mapping understanding of reflective symmetry. Firstly, we concur with Hollebrands (2004), who suggested that when students thought about reflections as the motion of flipping an object; tasks which used points rather than a single polygon as pre-images seemed appropriate. This is also consistent with the view that a point is the most fundamental object in geometry, and from a point concepts such as line segments and shapes are developed. Our view is that this ability to visualise a reflection through mapping of points would enable learners to identify those attributes of the pre-image which are variant (changed) and those which are invariant (unchanged) by the reflection. In this way learners might then conceptualise why size, shape and flipped over are not in fact fundamental properties of reflective symmetry, as they only become incidental once the image is placed vertically opposite the pre-image and equidistant from the line of reflection.
Another recommendation that we make is that learners have to draw or construct these reflections, especially on the Cartesian plane. Our contention is that most activities on reflective symmetry focus on defining the concept, showing examples of such symmetry, and identifying lines of symmetry in such images, but rarely do they require learners to perform such constructions. Yet constructions allow learners to measure lines and angles of geometrical objects, and when this is done on a Cartesian plane it might enable them to couple visualisation with its symbolic/analytical counterpart as they also work with the coordinates of points of both the pre-image and the image. This may allow students to move from reasoning about the drawing to reasoning about the properties of the pre-images and their images.
This back and forth movement is also critical for verification, yet we observed in this study that learners appeared to be unable to make such connections. This verification ability was not only critical for validating their visual manipulations, but verification/validation is an indispensable life-long mathematical skill in its own right. So unless visualisation is coupled with an appropriate symbolic/analytical counterpart, learners are unlikely to build reflections in a consistent way which connects visual intuition with mathematical structure. This underlines the problem with an approach to teaching which stresses visual appreciation disconnected from formalisation.
Conclusion
Although we analysed just one task for this article, the responses we got from learners reflect a fundamental gap between what learners know and what they need to know with regard to reflective symmetry. This gap would inhibit further conceptual understanding. We were firstly interested to know what learners recognised as given in this task and what they recognised as being required to do. Our analyses revealed that learners visualised a shape (triangle) which had to be reflected in the y- or x-axis, instead of three independent points located on the Cartesian plane. Following that observation, we were interested to know the likely cause of such visualisation. Our analyses of the textbooks together with previous research and literature suggest that learners are usually given a motion understanding of reflective symmetry, which tends to inhibit the mapping understanding. Our recommendation is that the transition from the level of a motion understanding to a mapping understanding requires a change of schema, which can be achieved through transforming points and drawing such transformations.
Acknowledgements
This study was carried out under the auspices of the Catch-up and Mathematics Teacher Enrichment Projects funded by the First Rand Foundation Mathematics Education Chair.
References
Bansilal S & Naidoo J 2012. Learners Engaging with Transformation Geometry. South African Journal of Education, 32:26-39. [ Links ] Berieter C 1985. Toward a solution of the learning paradox. Review of Educational Research, 55:201-226. [ Links ]
Biggs JB & Collis KF 1989. Towards a Model of School-Based Curriculum Development and Assessment using the SOLO Taxonomy. Australian Journal of Education, 33:151-163. [ Links ]
Burger WF & Shaughnessy JM 1986. Characterizing the van Hiele levels of development in geometry. Journal for Research in Mathematics Education, 17:31-48. [ Links ]
Chan CC, Tsui MS, Chan MYC & Hong JH 2002. Applying the Structure of the Observed Learning Outcomes (SOLO) Taxonomy on Student's Learning Outcomes: An Empirical Study. Assessment & Evaluation in Higher Education, 27:511-527. [ Links ]
Chick H 1998. Cognition in the formal modes: research mathematics and the SOLO taxonomy. Mathematics Education Research Journal, 10(2):4-26. [ Links ]
Cobb P, Yackel E & Wood T 1992. A Constructivist Alternative to the Representational View of Mind in Mathematics Education. Journal for Research in Mathematics Education, 23:2-33. [ Links ]
Cummins J 1984. Bilingualism and Special Education: Issues in Assessment and Pedagogy. San Diego, CA: College-Hill Press. [ Links ]
Dawe L 1983. Bilingualism and mathematical reasoning in English as a second language. Educational Studies in Mathematics, 14:32-53. [ Links ]
Edwards LD 2003. The Nature of Mathematics as viewed from cognitive science. Third Conference of European Research in Mathematics Education, Bellaria, Italy. [ Links ]
Fauvel J 1991. Tone and the teacher: Instruction and complicity in mathematics textbooks. In D Pimm & E Love (eds). Teaching and learning school mathematics. London: Hodder & Stoughton. [ Links ]
Franco L & Sperry RW 1977. Hemisphere Lateralization for Cognitive Processing of Geometry. Neuropsychologia, 15:107-114. [ Links ]
Hollebrands KF 2004. High School Students' Intuitive Understandings of Geometric Transformations. Mathematics Teacher, 97:207-214. [ Links ]
Hoyles C & Healy L 1997. Unfolding Meanings for Reflective Symmetry. International Journal of Computers for Mathematical Learning, 2:27-59. [ Links ]
Kotze G 2007. Investigating shape and space in mathematics: a case study. South African Journal of Education, 27:19-35. [ Links ]
Küchemann D 1981. Reflection and rotation. In K Hart (ed). Children's understanding of mathematics. London: John Murray. [ Links ]
Lake D 1999. Helping students to go SOLO: teaching critical numeracy in the biological sciences. Journal of Biological Education, 33:191-198. [ Links ]
Laridon PJ, Aird J, Essack R, Kitto A, Pike M, Sasman M, Sigabi M & Tebeila S 2001. Classroom Mathematics - Grade 9 Learners Book. Sandton: Heinemann. [ Links ]
Laridon PJ, Barnes H, Jawurek A, Kitto A, Myburgh M, Pike M, Scheiber J, Sigabi M, Wilson H & van Rooyen R 2008. Classroom Mathematics - Grade 10 Learners Book. Sandton: Heinemann. [ Links ]
Maharaj A 2008. Some insights from research literature for teaching and learning mathematics. South African Journal of Education, 28:401-414. [ Links ]
McGowen MA & Tall DO 2010. Metaphor or Met-before? The Effects of Previous Experience on the Practice and Theory of Learning Mathematics. Journal of Mathematical Behaviour, 29:169-179. [ Links ]
Perham AE, Perham BH & Perham FL 1997. Creating a learning environment for geometric reasoning. Mathematics Teacher, 90:521-542. [ Links ]
Presmeg NC 1989. Visualization in multicultural mathematics classrooms. Focus on Learning Problems in Mathematics, 11:17-24. [ Links ]
Schultz KA & Austin JD 1983. Directional Effects in Transformation Tasks. Journal for Research in Mathematics Education, 14:95-101. [ Links ]
Sieborger R & Macintosh H 2004. Transforming assessment: A guide for South African Teachers (2nd ed). Cape Town: Juta. [ Links ]
Smith IM 1964. Spatial ability: Its educational and social significance. London: University of London Press. [ Links ]
Suydam MN 1985. The Shape of Instruction in Geometry: Some Highlights from Research. Mathematics Teacher, 78:481-486. [ Links ]
Tartre LA 1990. Spatial orientation skill and mathematical problem solving. Journal for Research in Mathematics Education, 21:216-229. [ Links ]
Van Rossum EJ & Schenk SM 1984. The relationship between learning conception, study strategy and learning outcome. British Journal of Educational Psychology, 54:73-83. doi: 10.1111/j.2044-8279.1984.tb00846.x [ Links ]
Xistouri X 2007 Students' ability in solving line symmetry tasks. In D Pitta-Pantazi & GN Philippou (eds). Proceedings of the Fifth Congress of the European Society for Research in Mathematics Education. Lanarca, Cyprus: Department of Education, University of Cyprus. [ Links ]
Yanik HB & Flores A 2009. Understanding rigid geometric transformations: Jeffs learning path for translation. Journal of Mathematical Behaviour, 28:41-57. [ Links ]














