Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Education
versión On-line ISSN 2076-3433
versión impresa ISSN 0256-0100
S. Afr. j. educ. vol.33 no.2 Pretoria ene. 2013
High school learners' mental construction during solving optimisation problems in Calculus: a South African case study
Deonarain BrijlallI ; Zanele NdlovuII
IDepartment of Mathematics, Statistics and Physics, Durban University of Technology, South Africa deob@dut.ac.za; Brijlalld@ukzn.ac.za
IIDiscipline of Mathematics Education, School of Education, University of KwaZulu-Natal
ABSTRACT
This qualitative case study in a rural school in Umgungundlovu District in KwaZulu-Natal, South Africa, explored Grade 12 learners' mental constructions of mathematical knowledge during engagement with optimisation problems. Ten Grade 12 learners who do pure Mathematics participated, and data were collected through structured activity sheets and semi-structured interviews. Structured activity sheets with three tasks were given to learners; these tasks were done in groups, and the group leaders were interviewed. It was found that learners tended to do well with routine-type questions, implying that they were functioning at an action level. From the interviews it appeared that learners might have the correct answer, but lacked conceptual understanding. Exploring learners' mental constructions via their responses to activity sheets and interviews enabled common errors and misconceptions to be identified. Themes that emerged were that learners: 1) lacked the understanding of notation dy/dx, 2) had not constructed the derivative and minima/maxima schema, 3) had some difficulty in modelling problems, 4) preferred rules and formulas, and 5) applied algebraic notions incorrectly. Inferences are drawn for curriculum developers and teachers. This study also formulated itemised genetic decompositions for particular tasks, which contribute to APOS theory.
Keywords: APOS theory, Calculus, genetic decomposition, optimisation
Introduction
Calculus forms a major part of the Grade 12 South African Mathematics curriculum. In the National Curriculum Statement (Department of Education [DoE], 2007:51) it is clearly stated that "the purpose of mathematics is the establishment of proper connections between mathematics as a discipline and application of mathematics in real world contexts. Mathematical modelling provides learners with the means to analyse and describe their world mathematically, and so allows learners to deepen their understanding of mathematics while adding to their mathematical tools for solving real world problems". In the Grade 12 curriculum this is achieved through tasks in Calculus. In the South African school syllabus Calculus forms about 40% of Algebra, as seen in the Grade 12 paper one national examinations set by the Department of Basic Education in 2011. This forms about 20% of the overall assessment. At school level Calculus traditionally focuses on mastery of symbolic methods for differentiation and applying these to solve a range of problems (Tall, 2006). The application problems of maximising and minimising take this concept to a higher level where the tasks can be linked to real life.
Students' understanding of Calculus concepts lays the foundation for their future study of advanced Mathematics (Marrongele, n.d.). Learners who do Mathematics learn different algorithms to solve problems, but in many cases cannot solve application problems where no algorithms are provided. Marrongele (n.d.) asserts that learners can carry out methods of differentiation successfully but lack the conceptual underpinnings necessary to explain procedures and make connections between concepts. Over the past few years it has become evident that many learners find it difficult to understand Calculus as it is rich in abstraction and requires a high level of conceptual understanding (Parameswan, 2007). This is due to the fact that our learners rely mostly on isolated facts and procedures when learning Mathematics. This may be caused by the way teachers teach Calculus concepts, which puts an emphasis on procedural aspects and neglects a solid grounding in the understanding of conceptual underpinnings (Bezuidenhout, 2001). Also it might be that the resource materials that are used encourage an instrumental rather than a relational understanding of Calculus concepts.
This study does not introduce optimisation tasks via textbooks; it employs the idea of using structured activity sheets as described by Cangelosi (cited in Brijlall & Maharaj, 2009, 2010). Instrumental understanding refers to understanding rules without reasons, while relational understanding refers to knowing both what to do and why (Maharajh, Brijlall & Govender, 2008). In this study the design of the structured activity sheets considered the characteristic aspects of relational understanding of real-life problems involving maximising and minimising.
According to Bezuidenhout (2001), students' failure to express meaningful ideas on the optimisation concept's role in Calculus may to a large extent be due to inappropriate and weak mental links between knowledge of other Calculus concepts such as derivatives. Since many studies on the difficulties encountered in the learning of Calculus have been conducted with students at university level, this study explored how difficulties impact on learning of Calculus at school level. It was aimed at understanding not only the difficulties that learners are encountering when learning Calculus, but how learners mentally construct knowledge when learning the concepts of maximum and minimum. According to Tall (2006:29) there is a growing desire to "research the learning process to understand how individuals conceptualise calculus concepts".
Theoretical basis
Of late the focus on Mathematics is on the mental processes that an individual employs to understand the learnt concept. A number of learning theories, such as Piaget's theory on constructivism (Piaget, 1967), Vygotsky's theory of scaffolding (Vygotsky, 1962) and Skinner's theory of behavioural learning (Stones, 1970) focus on learning. These theories are general and do not specifically refer to the learning of mathematical concepts. This study mainly engages with APOS theory, which is a framework for the process of learning Mathematics that pertains specifically to learning more complex mathematical concepts (Weyer, 2010).
Constructivism forms the basis of how learners learn and this study is underpinned by APOS theory, which is fundamentally a constructivist one. The focus of the study is not only to understand how learners construct knowledge but also to explore the cognitive structures involved in the construction of knowledge. This theory clearly describes the cognitive structures used by learners to construct knowledge through action, process, object and schema, hence the acronym APOS. Based on APOS theory the construction of knowledge of the concepts of maximisation and minimisation were explored through identifying the relevant initial genetic decomposition.
APOS theory is premised on the hypothesis that mathematical knowledge consists of an individual's tendency to deal with perceived mathematical problem situations by constructing mental actions, processes, and objects and organising them in schemas to make sense of the situations and solve the problems (Dubinsky & McDonald, 2008). This theory builds on Piaget's notion of reflective abstraction (Piaget, 1967). According to Dubinsky (1991) reflective abstraction refers to construction of logicomathematical structures by an individual during the course of cognitive development. Piaget (1967) distinguished three types of abstraction: empirical abstraction, pseudo empirical and reflective abstraction. Cetin (2009) stated that in empirical abstraction the focus is on general characteristics of objects, and in reflective abstraction the focus is on the actions or operations done by a subject on mental objects. He further elaborated that action, process, object and schema are the mental structures that an individual builds by the mental mechanism of reflective abstraction. Therefore APOS allows for the development of ways of thinking about how abstract Mathematics can be assimilated and learned (Meagher, Cooley, Martin, Vidakovuc & Loch, 2006). In looking at Mathematics this theory is very applicable in understanding learners' learning of different concepts in Calculus, such as derivatives and optimisation problems.
According to Dubinsky (1991) there are five kinds of reflective abstractions: interiorisation, encapsulation, coordination, reversal and generalisation. These can be linked to the four stages of APOS. The following are the definitions as cited in Brijlall & Maharaj (2009, 2010) which we adopt:
Action is a repeatable physical or mental manipulation that transforms objects. Action is based on rules and algorithms, where a rule is practised repeatedly until it becomes routine; this takes place without adequate thinking. In the action stage the manipulation of entities is thought of as external, and the learner only knows how to perform an operation from memory or a clearly given instruction (Weyer, 2010).
A process is an action that takes place entirely in the mind. Once an individual becomes aware that actions or operations can be performed on a concept, then he/she might encapsulate a process into an object.
An object is a static entity which one transforms (Cetin, 2009). According to Weyer (2010) encapsulation refers to the mental construction of a process into a cognitive object that can be seen as a total entity, which is referred to as a schema.
In the schema stage the learner has a collection of actions, processes, objects and other schemas that he/she understands in relation to the concept.
These notions helped us to devise a linear model, shown in Figure 1, to depict an optimisation schema. When solving an optimisation problem a learner would be expected to relate the quantities in the boundary conditions with already assimilated schemas. This will involve mental actions interiorised as a process. These constraints then need to be encapsulated into an object generally represented by a mathematical expression. In the next step, to find the gradient function, the individual would be triggered by external stimuli like the power rule for differentiation. Equating the derivative to zero could be an action if a learner is prompted by the words 'find minimum/maximum', which automatically results in her/him equating to zero. However, a learner might realise the gradient of the tangent to be zero at the maximum/minimum point, and will have interiorised this notion and it can hence be seen as a process. The next step involves the solving of an equation. Depending on the type of the equation, the solution might require the learners to possess an action conception or a process conception. Hence this solution would lead to finding the minimum/maximum, that could be an action or a process.
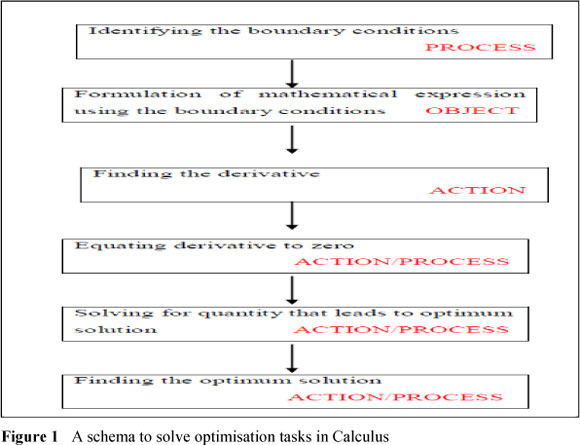
Preliminary genetic decomposition
The genetic epistemology of Jean Piaget was found to be useful for this study. At the centre of Piaget's work is a fundamental cognitive process, which he termed "equilibration" (Piaget, 1967). Based on this epistemology the initial genetic decomposition integrating modelling was designed for this study and involves an algebra schema, an area schema and a volume schema:
As part of his/her algebra schema the learner should: 1) model the given problem, 2) relate variables to formulate the equation, 3) be able to find the derivative, 4) be able to interpret the derivative to obtain minimum/maximum value, and 5) be able to find the minimum/ maximum value by substitution.
As part of his/her area schema the learner should: 1) realise the area of the rectangle as the product of two sides, 2) use the given information to construct the formula for an area function, 3) manipulate the symbols to find the derivative of the area function, and 4) relate the notion of a maximum value to a derivative to solve for x in the quadratic equation.
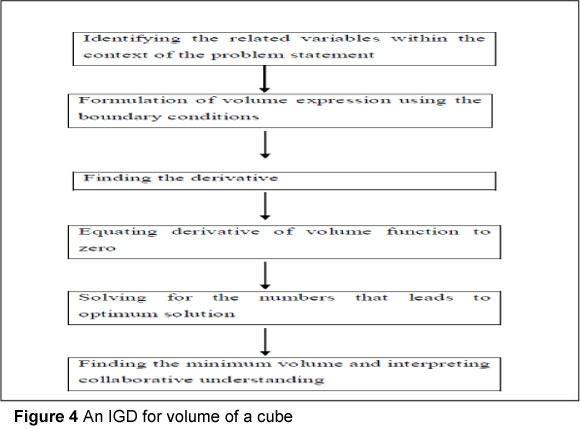
As part of his/her volume schema the learner should: 1) realise the volume as a product of three sides, 2) use the given information to construct the formula for the volume function, and 3) find the derivative and use it to find the minimum/maximum value. For the purposes of this study we introduced the notion of 'itemised genetic decomposition' (IGD), which we define as a genetic decomposition specific to an optimisation item that an individual is confronted with. For example, we will speak of IGD for rectangle area. This notion deals with a specific problem requiring learners to find the maximum/minimum area of a given rectangle.
Research question
The study aimed to explore learners' construction of knowledge in Mathematics in solving maximisation and minimisation problems in Calculus. This was done by exploring the research question: How do learners construct mathematical knowledge when solving tasks in optimisation?
In order to unpack this question we asked the following sub-questions:
What do learners' written responses reveal about their understanding of optimisation problems?
How do students' mental constructions of action, process and object derived from the learners' written responses coincide with the preliminary genetic decomposition of the study?
Research methodology
A qualitative approach provides multiple ways of understanding the inherent complexity and variability of human behaviour and experience (Cohen, Manion & Morrison, 2007; Higgs, Horsfall & Grace, 2009). Creswell (2007) maintains that researchers use a qualitative approach in order to understand the contexts in which the participants in a study address the issue in question. In this case study we administered questionnaires in the form of activity sheets and carried out interviews. The data extracted from these instruments were analysed descriptively and interpretively. Furthermore the variables were not controlled and the natural setting of the classroom involving the learning activities was observed.
This study was conducted in a school consisting of only black African learners and teachers. This school offers both Mathematical Literacy and Mathematics (which we refer to as pure Mathematics). In the school there were only 10 learners in Grade 12 who did pure Mathematics and participated in the study.
During the study learners worked collaboratively. Since there were only 10 learners who were doing pure Mathematics, we decided to have three groups: two groups had three members each and one had four members. These learners' Grade 11 Mathematics marks were used to rank them. Then it was ensured that each group had a learner from the different ranges in the examination scores in order to form groups on the basis of mixed abilities. The following codes were used: R for the researcher, and L1, L2 and L3 for the respective group leaders. The group leaders were those with the highest Grade 11 Mathematics scores within each group.
After discussing the solution to the tasks each group wrote down their responses. The written responses for each task were coded and categorised. Interviews were then held with the group leaders. The interview questions were designed to clarify themes observed from the written responses. Before the learners engaged in these activities they had been taught the following sections: 1) finding derivatives by first principles, 2) finding derivative by use of the rule, 3) finding equations of tangents to curves, and 4) sketching graphs of cubic functions. Hence the learners had come across the notion of local maximum/minimum when investigating the stationary points for the cubic function. However, the section on optimisation was not taught to them by the teacher; it was expected that the activity sheets would be self-explanatory and structured to guide the learners with least interference from the teacher.
Discussion of data for task one
We present an IGD for products of consecutive numbers in Figure 2, with an example of the task related to consecutive numbers provided in Extract 1.
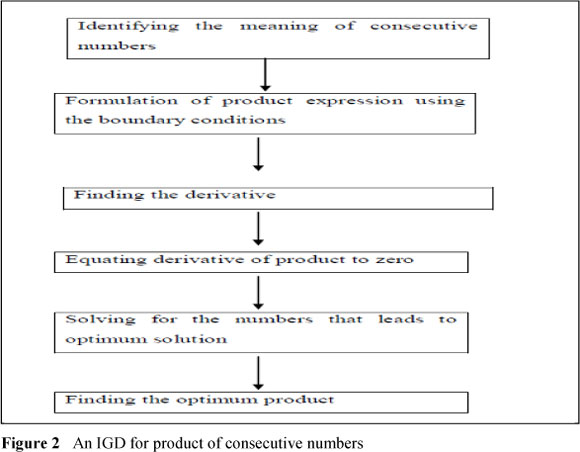
The written response of Group 1 is shown in this extract. The Group 1 members were able to give examples of consecutive numbers, which showed that they could illustrate what consecutive numbers were. They were able to use their understanding of consecutive numbers to express them algebraically. At this stage the learners were working at an action level of the APOS theory, because they wrote down the numbers "1 and 2" as a response to the meaning of 'consecutive', which became a stimulus for this action. Also this action, after being interiorised as a process, was encapsulated into an object, which they could easily translate into algebraic expressions. As Brijlall & Bansilal (2010) pointed out, an action is triggered by an external stimulus. At this point of the task the learners could easily write examples of two consecutive numbers without thinking too deeply. In the study by Cetin (2009) it was highlighted that when an individual encounters new mathematical concepts, concept formation begins with transformation of the existing mental objects. This was seen in Group 1 who used their existing mental objects of consecutive numbers to form new algebraic expressions.
Extract 1 Group 1 's written responses to task one
1. Write down two consecutive numbers. 1, 2
2. How can we represent any two consecutive numbers algebraically in terms of x? x;x =1
3. How can we write the product (P) of any two consecutive numbers? Ρ = χ2 +χ
4. Find the minimum value for this product. P' = 2x + 1
5. Comment on the following response that Nkanyiso provided to answer
Question 4. He provided two answers

Group discussion: P(x) = 2x + 1 is correct because the derivative of our pro-duct is the same as the one for Nkanyiso and P(x) is also correct, it is the consecutive in number, e.g. 1;2 the product is 2 and the derivative of 2 = 0 P(x) = 0
To clarify how Group 1 learners constructed their knowledge when they found the minimum value in task one, the following questions were asked during the interviews with the Group 1 representative (L1):
R: In question one you were asked to write down two consecutive numbers and then you wrote 1 and 2 which was correct. Can you explain what consecutive numbers are?
L1: Consecutive numbers is the numbers that you add to the previous number in order to get a new number. Like if I want like 1 and 2, if I want 2 I will add 1 to get 2, and if I want 3 I will say 2+1 to get 3.
We noticed that she could extend the concept of 'consecutive' to a generalised setting. This was promising as it would imply that if asked for two consecutive even numbers then 2x + 2 and (2x + 2) +2 would be provided, since 2 is added to obtain the first and then 2 should be 'added to the previous to get a new number'. However, she then resorted to consecutive numbers with a difference of 1. As they wrote χ;; χ + 1 they repeatedly worked out a pattern of getting successive consecutive numbers until the whole procedure was interiorised. By being able to generate and apply the rule they saw this whole entity as a process and thereafter encapsulated it in an object, viz. Ρ =χ2 +χ.
This indicated growth in their mental structures, as they started by focusing on an action level then interiorised the concept of consecutive numbers as a process. This is in line with reflective abstraction, as she derived her knowledge of representing numbers algebraically from her understanding of consecutive numbers. According to Dubinsky (1991) reflective abstraction is where the focus is on the physical entities, and it derives knowledge from the properties of such entities. Also, the learners could relate variables to formulate an equation which is within the algebra schema discussed in the preliminary genetic decomposition section of this paper.
Discussion of data for task two
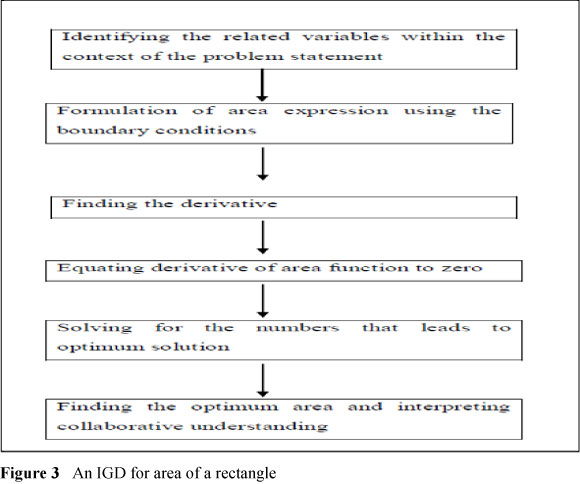
An IGD for finding the maximum value of an area plot is presented in Figure 3. We include a portion of the activity sheet to show task two in Extract 2. This task was used as an example to model the itemised genetic decomposition for the area of a rectangle. The response of Group 3 to question 6 is also shown in Extract 2. For question 1 of task two, Group 3 wrote: χ = 1 was acceptable. This meant that it was possible that Group 3 had not substituted their accepted value in the given dimensions. This we can conclude since x 2 = 1 for χ = 1. In this context this showed that they had no understanding of the importance of the dimensions in the problem. For question 2 they wrote:
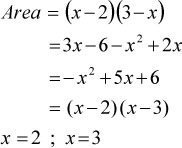
This showed that even though they knew how to calculate the area, they had not assimilated the relevant mental constructions to find the area, and relate the important characteristics to the dimensions thereof. They had memorised the formula for the area of a rectangle and could substitute in it without any formal understanding. This was apparent in this case as they did not bother to understand the question but just inserted the numbers and applied rules without any insight into the reality of the context provided by the task.
This seemed to show that the area schema was not completely in place. The first two steps in the area schema outlined in the preliminary genetic decomposition section were displayed. The third step, which involved application of the power rule for differentiation, was lacking. However, in question 6 they explained the meaning of Á (x) = 0 in terms of the gradient. In order to better understand what was implied in this written response it became necessary to probe further with more questions. Hence the following interview:
R: In question 1 you were asked to discuss the possible values of x, can χ = 1? In your explanation you wrote the product of (x - 2)(3 - x). Can you explain why you wrote this in your explanation? L3: So miss, we were trying to prove that can χ = 1 so that is why we substituted 3 instead of χ in this side of χ - 2.
R: Ya but for someone who will put 2 since you said χ = 2 or χ = 3 will say χ ≠ 1 because if someone put 2 there [pointing at the breadth] will get zero.
L3: Actually miss we did not look for those possible values, we were trying to prove that χ = 1, that is why we put 3 instead of x; we got 1 and this side we got 1 too.
Extract 2 Group 3 's written response to the item 6 of task two
We are asked by the Mpofana Municipality to find the dimensions of the rectangular plot of land below so that the area is a maximum.

1. Discuss the possible values of x. Can x = 1m? Explain.
2. Find the area of the land plot in terms of x. Call the area A(x)
3. Explain why the area will have a maximum value.
4. Find A'(x)
5. Solve for A'(x) = 0
6. In the context of the problem what meaning does A'(x ) = 0 afford? Explain clearly.
If we have an Á (x) than we find the derivative of Á (x) we will first equate it to "0" because the "m" gradient at the TP is equal to zero.
The extract from the interview reveals that she misinterpreted the question, and confused the side dimensions with the x-values. She pointed out that Group 3 thought that they were required to calculate one side with measure 1m (coincidently the answer x = 3 gave x  2 to be 1m). They also displayed a lack of understanding of algebraic expressions and algebraic equations. This was followed by a lack of cohesion as they could not relate question 2 to questions 4 and 5 of task two. This revealed that even though she knew formulas and rules, she had not interiorised the notion into a process. To interiorise this notion into a process, the context has to be taken into account. To clarify the written response to question 3 we had the following conversation:
R: What do you mean by the value of 'a' being negative?
L3: It means that if we draw this graph it will face downwards, which will give us the maximum value because... R: The value of 'a' where?
L3: Miss, on this χ2 + 5x 6 then our 'a' is negative. Miss, 'a' is the gradient of this; it has a negative gradient, so it will face downward, so it will have a maximum value.
The student was confident in dealing with the tasks where she needed to apply rules and algorithms, as she had done in question 2. She easily explained how they arrived at the answer A = -x2 + 5x - 6, but could not explain why the area had a maximum value. To probe the gradient concept we proceeded with the following dialogue:
R: In question 6 which gradient are you referring to?
L3: The gradient of the derivative.
R: Is the derivative not the gradient?
L3: It is, miss.
R: But you are saying the gradient of the derivative?
L3: Miss, we are referring to the gradient of the turning point of our derivative.
The above extract from the interview showed that the derivative and the gradient schema had partially developed in her cognitive structures. She was correct in claiming that the sign of the coefficient of x2 in the expression ax2 + bx + c indicated whether a maximum or minimum arose. However, she could not explain why. This implied that she did not have an object level of the maximum/minimum of a parabolic function. This also meant that step four of the area schema, which required equating the derivative of the area function to zero, was lacking.
Discussion of data for task three
In exploring how learners constructed their knowledge in dealing with the concept of minimisation of the volume of a cube, we analysed data from the written responses of Group 2. The part of the activity sheets showing the problem statement for task three is shown in Extract 3. The itemised genetic decomposition that was used to analyse this task is presented in Figure 4.
Extract 3 The problem statement for task three
A rectangular box has the following dimensions: Length 5x units Breath (9-2x) units Height x units
1. Write down the formula for finding the volume of the box.
2. Hence find the volume in terms of x.
3. Find the value of x for which the box will have a minimum value.
4. Explain all the steps you followed when finding the minimum value.
In question 1 of task three, Group 2 learners showed that they knew the formula for the volume of a box. Using length and breadth in their formula showed that they figured out that the base of this figure was a rectangle. In question 2, as they had already known the formula, they effectively substituted into the formula and worked out the volume of the box. In question 3 they had shown that they understood that to find the minimum value they needed to first find the derivative of a function. They did, however, confuse this with a quadratic function, where they could have used.
Also, they knew that for a minimum to occur the derivative should be zero, as they had equated their derivative to zero. This we concluded since the questionnaire items and interview questions asked the learners to clarify how equating to zero helped finding the solution to the tasks. In Extract 2, for instance, responses to item 6 made it possible for us to arrive at this conclusion.
They were now at the process stage in terms of APOS theory, because without actually writing all the steps, they displayed that the derivative was the same as the gradi- ent at the point, and where the gradient was zero the minimum value occurred. This showed that the gradient schema and derivative schema had developed, which now led to construction of the minima/maxima schema. We coded their attempt as partially correct, because after finding the two x values they did not state which one of the two gave the minimum value. It was possible that they had not known how to determine which χ value provided the minimum value. Also, it was possible that they considered the values of x as both minimum values.
By leaving their answer as they did, they implied that it could either be both of them, which was not true and which proved that they did not possess a complete volume schema. In order to verify what had been observed in the Group 2 learners' written responses to questions in task three and to explore their mental constructions related to the concept of minima/maxima, an extract of the interview with the Group 2 leader appears below:
R: If we look at this figure, would you say it is a 2D or a 3D shape?
L2: It's a 3D shape.
R: What is a 3D shape?
L2: It has eh...the dimensions, miss, it has like this, this side that are facing each other [pointing to the figure], it has three sides, miss. He knew that this figure was 3D even though he couldn't describe it properly. He attempted to describe it as he saw, without using mathematical terminology.
We decided to assess whether the members of Group 2 were operating at the object stage in their mental construction of the optimisation of a volume of a cube, and so proceeded with the following interview:
R: If you were to sketch this graph or any other graph, at which point will you find the minima/maxima values? L2: Maximum, miss, you will find it where it turns at the positive, like this [sketching], at the top, miss, and at the bottom you will find the minimum.
R: But what do we call those points where we will find the maxima and minima value? L2: Turning points. R: What is happening at those points?
L2: The gradient is...what happened, miss? We know that the gradient is equal to zero.
He had encapsulated the concept of a function into an object as he could, by looking at the equation given, to decide if the function will first have the maxima then minima or vice versa. The gradient and derivative schema had developed, as he understood that the derivative was the gradient of the tangent at that point, and for maxima and minima the derivative at that point was equal to zero. Since the gradient schema had developed, he could then assimilate the maxima/minima schema into his cognitive structures, and that was why he could explain his thinking and constructed the required knowledge about the concepts and showed knowledge of the procedures followed in calculating, and not just by memorising it.
Even though he had constructed the knowledge he still used the incorrect terminology when referring to the derivative, as he kept saying we 'derive'. The term derive, according to him, meant the same as differentiate (finding the derivative).
Findings
The main question focused on how learners construct mathematical knowledge when faced with solving tasks in optimisation. In unpacking the question it was discovered that learners frequently constructed their knowledge based on their previous mental assimilations. They relied mostly on procedural thinking rather than conceptual thinking when solving the given task. Hobden (2006) emphasised that to be successful in learning Mathematics, learners need to be competent in both conceptual understanding and procedural fluency. Some groups constructed their knowledge of the derivative with instrumental understanding of the notation To them this was the representation for the derivative in every context. It appeared that they constructed their mathematical knowledge as isolated facts, struggling to see an interrelationship between concepts, as in their responses they seemed to struggle to link the maxima/minima concept to different functions.
In some cases it appeared that they struggled to accommodate new learnt topics with the previous ones; in task one the concept of minima/maxima had been dealt with in Grade 11, but they couldn't apply that knowledge to the task at hand, as they were now doing Calculus. The equation they had was quadratic and to them a quadratic equation generated parabolas, and they knew how to find the turning point in such situations. It seemed that since they were doing Calculus, minima/maxima meant something different, and they needed other mechanisms to deal with it.
After analysis of the data, five themes emerged:, namely that learners: 1) lacked the understanding of notation, 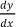 2) had not constructed the derivative and minima/maxima schema, 3) had some difficulty in modelling the problems, 4) preferred rules and formulas, and 5) applied algebraic notions incorrectly.
2) had not constructed the derivative and minima/maxima schema, 3) had some difficulty in modelling the problems, 4) preferred rules and formulas, and 5) applied algebraic notions incorrectly.
How do learners' responses coincide with genetic decomposition?
The four stages of APOS theory were used to explore the level at which learners constructed their knowledge to understand the concept of optimisation. Each level highlighted the stages of knowledge construction, and when learners had reached the schema stage we assumed that they fully understood the concept.
In this study the learners' responses revealed that most of them functioned at an action level, as in all three tasks they could effectively complete all the questions where rules were required which they repeatedly substituted into area and volume formulas and applied differentiation rules to find the derivative. Some learners, as in Group 3, interiorised certain concepts into a process. In task three they interiorised the volume formula into a process whereby internally they visualised the volume as a cubic function and encapsulated the derivative as an object which they could use to find the minima of the volume.
Looking at all the tasks it was apparent that the minima/maxima schema was partially assimilated into their cognitive structures, but at times they failed to coordinate it with other existing schemas, such as function and gradient, which were vital in solving optimisation problems.
Looking at the model depicting the optimisation schema (Figure 1), learners' construction of knowledge was centred around stages three to six. These general stages were linked with the IGD for each task, and learners revealed that they had instrumental understanding of optimisation which coincided with the action stage and partly with the process stage of APOS theory. It could be said that mostly their knowledge construction was limited to action conception of maxima/minima, as they could only complete the problems that required external cues. This might also be due to the stimulus created within the structured nature of the tasks: others could coordinate the respective objects as a complete totality, so that other actions or processes could act on these objects.
Conclusion
Although this was a small-scale study and the findings cannot be generalised, the formulation of IGD and the theory of APOS provided a valuable way of exploring the learning of maximising/minimising in Calculus in a Grade 12 Mathematics class. The study revealed that some aspects of APOS theory were not fully operational, because most of the learners were successful with the questions where they could use formulas and substitute when necessary. These manipulations took place externally, as they could follow the given instruction and apply rules that they had memorised.
Some of them had acquired the process stage of APOS theory, like Group 3, who interiorised the volume formula into a process where they showed understanding that for maxima/minima to occur, the gradient at that point is zero. Among the learners, L2 seemed to have the maxima/minima schema developed.
Based on the genetic decomposition presented at the beginning of each analysis, the study showed that learners were partially in line with the IGD, but the schema part was lacking in their attempt to construct knowledge of the learnt concept. The study showed that learners' construction of knowledge was mainly based upon isolated facts and procedures. This might be a result of the way in which teaching and learning occurred, which put more emphasis on procedural aspects in Calculus, neglecting conceptual understanding of the concept. The exercises that learners were doing in class encouraged the action stage of APOS theory and instrumental understanding.
Research has shown that learners need to be taken beyond the action stage of APOS. It must be mentioned that some items in the tasks encouraged the action stage of the various IGDs. However, the follow-up items in this study were designed to take these learners' conceptions into the process and object stages.
We found that learners extended their understanding into other facets of their learning indiscriminately. This occurred on two occasions: 1) when asked about the gradient of a curve defined by y = ax2 + bx + c learners referred to 'a' the coefficient of the first term. The learners contradicted that the coefficient of the first term in y = mx + c is used for the gradient of a straight line; and 2) to find the minima/maxima at the turning point for y = ax3 + bx2 + cx + d, learners used the formula to find 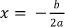 the χ value at the local maxima/minima. They obviously used what they learnt from the quadratic function.
the χ value at the local maxima/minima. They obviously used what they learnt from the quadratic function.
Teachers need to be aware of learners' learning conflicts so as to reinforce the new concepts they encounter. Also, teachers can devise IGDs for various tasks, as these IGDs would inform the teachers of the mental constructions of their learners. This feedback will help teachers to gauge whether effective teaching is taking place.
References
Bezuidenhout J 2001. Limits and continuity: some conceptions of first- year students. International Journal of Mathematical Education in Science and Technology, 32:487-500. [ Links ]
Brijlall D & Bansilal S (18-21 January 2010). A genetic decomposition of the Riemann Sum by students teachers. In V Mudaly (ed). Proceedings of the 18th annual meeting of the Southern African Association for Research in Mathematics, Science and Technology (Volume 2: Short Papers). Durban: University of KwaZulu-Natal. [ Links ]
Brijlall D & Maharaj A 2010. An APOS analysis of students' construction of the concept of continuity of a singled- valued function. In Proceeding of the 7th Southern Hemisphere Conference on Mathematics and Statistics Teaching and Learning. Stellenbosch, SAf. [ Links ]
Brijlall D & Maharaj A 2009. Using an inductive approach for definition making: Monotonicity and boundedness of sequences. Pythagoras, 70:68-79. [ Links ]
Cetin I 2009. Students' understanding of limit concept: An Apos perspective. Unpublished doctoral dissertation. Northern Cyprus: Middle East Technical University. [ Links ]
Cohen L, Manion L & Morrison K 2007. Research Methods in Education (6th ed.). London & New York: Routledge. [ Links ]
Creswell JW 2007. Qualitative Inquiry and Research Design: Choosing among five approaches (2nd ed). London: Sage Publications. [ Links ]
Department of Education 2007. National Curriculum Statement Grade 10-12. Pretoria: Department of Education. [ Links ]
Dubinsky E 1991. Reflective Abstraction in Advanced Mathematical Thinking. In DO Tall (Ed). Advanced Mathematical Thinking. Dordrecht: Kluwer. [ Links ]
Dubinsky E & McDonald MA 2001. APOS: A constructivist theory of learning in undergraduate mathematics education research. In D Holton (ed). The teaching and learning of mathematics at university level. Netherlands: Kluwer. [ Links ]
Higgs J, Horsfall D & Grace S 2009. Writing Qualitative Research on Practice. Atlanta, GA: Sense Publishers. [ Links ]
Hobden P 2006. Mathematical proficiency - a way of describing successful mathematics learning. Unpublished BEd Honours thesis. Durban: University of KwaZulu-Natal. [ Links ]
Maharajh N, Brijlall D & Govender N 2008. Preservice mathematics students' notion of the concept definition of continuity in calculus through collaborative instructional design worksheets. African Journal of Research in SMTEducation, 12:93-106. [ Links ]
Marrongele K (n.d.) The role ofphysics in students' conceptualization of calculus concepts: Implications of research on teaching practice. Portland: Portland State University. http://www.math.uoc.gr/~ictm2/Proceedings/pap153.pdf Accessed 23 March 2010. [ Links ]
Meagher M, Cooley L, Martin B, Vidakovuc D & Loch S 2006. The learning of linear algebra from an APOS perspective. In S Alatorre, JL Cortina, M Sáiz & A Méndez (eds). Proceedings of the 28th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. Mexico: Universidad Pedagógica Nacional. [ Links ]
Parameswan R 2007. On understanding the notion of limits and infinitesimal quantities. International Journal of Science and Mathematics Education, 5:193-216. [ Links ]
Piaget J 1967. Six Psychological Studies. New York: Vintage Press. [ Links ]
Stones E 1970. Readings in Educational Psychology. New York: Routledge. [ Links ]
Tall D 2006. A theory of mathematical growth through embodiment, symbolism and proof. Annels de Didactique et de Sciences Cognitives, 11:195-215. [ Links ]
Vygotsky LS 1962. Thought and language: Cambridge, MA: MIT Press. [ Links ]
Weyer RS 2010. APOS theory as a conceptualisation for understanding mathematics learning. Summation, 9-15. [ Links ]














