Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Education
On-line version ISSN 2076-3433
Print version ISSN 0256-0100
S. Afr. j. educ. vol.30 n.1 Pretoria Jan. 2010
Language diversity in the mathematics classroom: does a learner companion make a difference?
Hendrik Botes; Andile Mji*
ABSTRACT
Language and education are interrelated because all teaching is given through the medium of language. Language is considered to be both a precondition for thought and a bearer of thought and therefore influences the extent to which a child's intelligence is actualised. In the South African context linguistic diversity is a complex issue. It has increasingly become the task and responsibility of educators to develop strategies in an attempt to facilitate quality education for their learners. In this study, the researchers developed an 'aid' that would assist learners to relate mathematics terms and concepts in English with terms in their own languages. The study determined whether a visual multilingual learner companion brought change in learners' performance in mathematics. Also what the educators' views were about this. A combination of a quasiexperimental study and an interview schedule was conducted. The quasiexperimental study was conducted among learners while the interview schedule was with their educators. The sample comprised 2,348 learners in Grade 4, Grade 5 and Grade 6 from 20 schools as well as 20 educators from the treatment schools. The results indicated that the mathematics marks of the treatment group improved. Also, the educators were complimentary about the learner companion and indicated that they would utilise this going forward in their teaching. It is recommended that the multilingual visual explanatory mathematics learner companion be used and investigated on a larger scale to corroborate the efficacy reported here.
Introduction
Mathematics education begins in language, it advances and stumbles because of language, and its outcomes are often assessed in language (Durkin, 1991:3).
The critical period of language acquisition is when it takes place effortlessly in a natural setting (Brown, 1994). This acquisition inevitably influences the acquired language skills and vocabulary of monolingual children as compared to bilingual and multilingual children. The acquisition of language by a child is not only associated with the expansion of the child's world of meaning, but is also attuned to it. In the total learning event language is considered to be both a precondition for thought and a bearer of thought and therefore influences the extent to which the child's intelligence is actualised. Inadequate language acquisition then results in inefficient actualisation of intelligence (Vygotsky, 1989). On the other hand, it has been argued that learners who are taught in a non mother tongue language probably do not achieve academic excellence, not because they are less able, but due to an artificially created linguistic problem (Danesi, 1988). What is clear however is that irrespective of differences, children respond to different stimuli at school in virtually the same manner. For example, it has been argued that African children are as responsive to the principles of learning, motivation and success as much as any other children (Mwamwenda, 1995).
Language and mathematics
Language is critical for cognitive development as it provides the concepts for thinking and therefore a means for expressing ideas and asking questions (Vygotsky, 1989). In agreement with this view, it has been argued that we use words to construct our interpretation of experience; that our experiences shape our language; and in the culture of schools a concept does not exist until it has been named and its meaning shared with others (Davalos & Griffen, 1999). The enhancement of the learner's thought processes, as envisaged by the critical outcomes of Curriculum 2005 (DoE, 1997), should be the main objective of the school. This is a point that has been emphasised by researchers (e.g. Young, 1995:69) who indicated that the "... interplay of language and the development of thinking needs serious attention, not only in language education, but also in all learning-areas". Researchers are of the view that teachers can encourage learners to be aware of their own thought processes; and to engage actively in appropriate thinking by using precise terminology, through posing critical questions, clarifying ideas and processes, as well as withholding value judgements (Cole & Chan, 1994). Language also enables learners to interact with more capable peers and adults and later with written material which gives them a chance to share their accumulated knowledge (Parilla, 1995).
In order to achieve in-depth mathematical understanding, it has been suggested that effective communication of mathematical ideas is the key because language forms an integral part of this communication (Thurston, 1995). In a similar vein it has been pointed out that many of the learners' problems in mathematics originate from an inadequate knowledge of the basic vocabulary (McLean, 2000). Also, it has been argued, "It [language] is the medium by which teachers introduce and convey concepts and procedures, through which texts are read and problems are solved" (Bohlmann, 2001:6). It should be pointed out however that proficiency in conversational English for example is not the only requirement for learners to master mathematics. Learners also need to be familiar with scientific English. In fact, it has been argued that "... mastery of a specialized subject like science is in large part mastery of its specialized ... language" (Lemke, 1990:21). Further, Lemke (1990) has indicated that mathematical English entails the use of abstract generalisations and logical relationships that both first and second language learners have to master. In concurrence, it has been pointed out that the difference "... between everyday language and science or mathematics terminology also leads to first language speakers learning a new language when learning science" (Rollnick, 2000:100). Mastering mathematics is sometimes considered to be a two-step process: firstly, learners have to understand the mathematical concepts (Richards, 1982). Secondly, they have to be able to communicate their understanding of these concepts in written format (Brown, 1994). Initially the educator explains mathematical concepts by using two verbal languages: A commonly spoken, everyday language and a subjectspecific, mathematics language. Therefore learners have to be proficient in both these languages. However, competency in the former does not imply competency in the latter (Lemke, 1990). Thereafter learners have to familiarize themselves with the scientific manner of writing acquired mathematical concepts. This step is especially important if one considers that learners need to be able to (a) read and write mathematics when using textbooks and (b) complete various assessment activities in writing during a mathematics course.
Background
Learning and teaching mathematics in multilingual classrooms where the medium of instruction is not the learners' home language is a complicated matter. Learners have to deal with the new terminology of mathematics as well as the new language of instruction in which mathematics is taught (English). Educators therefore need to develop effective ways of teaching both the language of mathematics and the language of teaching and learning (Setati, 1998a). In support of this view it has been stated "Mathematics teachers face different kinds of challenges in their bi-/multilingual classrooms from English Language teachers" (Adler, 1997:17). English language teachers have as their goal fluency and accuracy in English. Mathematics teachers however have a dual task. They face the challenge of continuously needing to teach both mathematics and English at the same time (Adler, 1997). In fact, it has been opined that the challenge for many educators is helping learners to move from where they are unable to understand English to where they can communicate mathematics in English (Setati, 1998b).
A mathematics register does not only consist of terminology, but it also involves the social usage of particular words and expressions in mathematics. It is actually argued that knowing the mathematics register in one language, is probably not an indication of knowing it in another language (Khisty, 1995). Part of the process of learning mathematics is gaining control over the mathematics register. The learner should learn to speak, read and write like a mathematician because the register includes words, phrases, symbols, abbreviations and ways of speaking, reading, writing and arguing that are unique to the subject (Setati, 1998b). Further it has been argued that speaking like a mathematician does not only involve the use of technical terms but also using phrases and modes of arguing that are consistent with the mathematics register (Pimm, 1987). The reality though is that speaking or writing mathematics requires the use of the language in which it is taught and in South Africa that language in the majority of classrooms is English (Setati, 1998b).
In 2003 the first author analysed admission records of selected schools from one region of the North West province. The analysis revealed an exodus of learners from township schools to former Model C English medium schools. Further, it was found that the English speaking learners performed much better than their African counterparts. For example, 2005 mathematics marks for Grade 4, Grade 5 and Grade 6, revealed that a majority (95.8%) of the English speaking learners obtained a mark of 50% or more while 78.1% of the new African learners obtained a mark of 40% or less. A perusal of the English subject marks revealed a similar situation. This revelation led to the hypothesis that the African learners probably had inadequate English vocabulary and therefore needed some form of help that would bring them up to speed with their understanding of mathematics. Importantly, the researchers felt that such help should be integrated with their mathematics learning. The reasoning here was that the learners should not see the form of help as well as the teaching and learning of mathematics as separate components. Considering that in South Africa learners start Grade 1 when they are 7 years (cf. Fleisch & Shindler, 2007) most learners in Grade 4, Grade 5 and Grade 6 would be expected to be in the concrete operational stage in Piaget's cognitive developmental terms (Huitt & Hummel, 2003). An important aspect of the concrete operational stage is that if learners are given an opportunity to ask questions and explain situations then this allows them to mentally manipulate information. Mental manipulations may however be hampered by inadequate knowledge of English vocabulary or terminology in a mathematics classrooms. This argument was the forerunner to developing an 'aid of sorts' that would assist learners to relate mathematics terms and concepts in English with terms that they hopefully knew or they would make sense of, in their own language. In this regard we developed a multilingual and visual learner companion aimed at augmenting learners' mathematics understanding.
The learner companion
In the South African context linguistic diversity is a complex issue. It has increasingly become the task and responsibility of educators to develop strategies in an attempt to facilitate quality education for their learners. However, educators in especially former Model C English medium schools struggle to respond adequately to the increased linguistic diversity found in their classrooms. This is because in many instances the educators are themselves monolingual English speakers. This suggests that their explanations are only in English which may be to the detriment of the learners who speak different languages (observations of the first author as a teacher in this type of school). Monolingual teachers have been shown to allow learners to express their thoughts in their own language when speaking with their peers however they require them to use English in reporting back in class (Adler, 1995). This is an issue Adler (1995:271) identifies as a dilemma in pointing out "... the extent of English spoken by the teacher is not an issue for English-speaking monolingual teachers. These teachers, however, face other dilemmas as they confront the otherwise taken-for-granted in their particular settings". In recognition of this shortcoming, we developed the learner companion. The learner companion comprises mathematical terms or expressions, visual representations as well as translations of such terms in English and a selected number of other South African languages. The selected languages were Afrikaans, IsiZulu, IsiXhosa, Setswana and Sesotho. These particular languages were selected because they were spoken by a majority of learners who formed the sample of this study. The learner companion was developed in a 'dictionary like' manner in the sense that selected mathematical terms and expressions were arranged alphabetically. Typical examples involving all the components of the learner companion are shown in Figure 1.
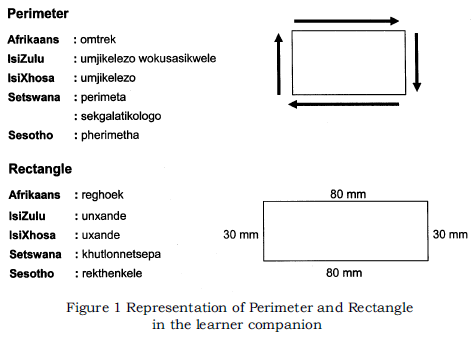
The target group for the companion were learners in Grade 4, Grade 5 and Grade 6. It should be pointed out that the intention was not to provide translations for the entire mathematics learning programme but to select terms and expressions most often used in these grades. The learning companion as presented in this study is not unique in that a glossary of mathematics terms for Grades R to Grade 6 presented in the 11 South African languages is available (cf. Department of Arts and Culture, n.d.). A novel element of the learner companion is that it enables learners to have a visual picture as well as to have an idea of what a concept is referred to in different languages. In essence our aim was to enhance the learners' mathematical literacy and understanding. This we felt was consistent with the argument that, if fluent reading and understanding of mathematical text and symbolism are essential then the importance of proper mathematical literacy becomes even more necessary (O'Toole, 1996). Also, we wanted to use the learner companion to address language diversity in the mathematics classroom. A comprehensive description of the development of the learner companion as well as the validation process of translations is described in Botes (2008).
Purpose
Learners who are taught in a language that is not their mother tongue probably do not achieve academic excellence mainly because of reasons they may not have control over. To this effect it has been argued that lack of academic excellence may be caused by an artificially created linguistic problem (Danesi, 1988). In most instances this is because there is no educator who understands the different languages that such learners bring to school. In fact it has been averred that "... educators face the challenge of coping with and finding solutions to culturally and linguistically diverse urban school contexts ..." (Du Plessis & Louw, 2008:53). The purpose was therefore to determine the efficacy of the learner companion in respect of overcoming what Danesi (1988) referred to as the linguistic barrier. In particular, we (a) investigated whether the learner companion had an effect on learners' achievement in mathematics and, (b) established the educators' views of the learner companion. The educators' views were in respect of the companion's usage and how it could be improved.
Method
Sampling
In order to retain the advantages of a quasi-experimental design as much as possible, it was crucial to ensure that the treatment and comparison groups were as similar as possible. From 43 schools that indicated their willingness to participate in the study we conveniently selected 20. The selection was based on the 2006 annual statistics survey that all schools have to submit to the North-West Education Department. The survey provides information regarding enrolment, gender, age, home language and medium of instruction. Analysis of the different schools' reports enabled us to identify and select 20 schools that were similar in composition and nature. We then provisionally allocated 10 schools to the treatment group and another 10 schools to the comparison group. Principals and educators were shown the provisional allocations and were asked to give input in selecting the two groups. Deliberations resulted in two schools being swapped from the treatment group to comparison group and vice versa. In essence inclusion in either group was by mutual consent wherein each school provided one class of Grade 4, Grade 5 and Grade 6 learners. Participating schools were assured that their names would not be revealed. It was agreed with the principals that letters of the alphabet would be used. In this regard, the treatment group comprised schools named School A, School C, School E, up to School S. Similarly for the comparison group the schools were named School B, School D, School F, up to School T. Typically the chosen classrooms had a variety of language speakers and except for a few instances a majority of learners spoke languages other than English (see Table 1).
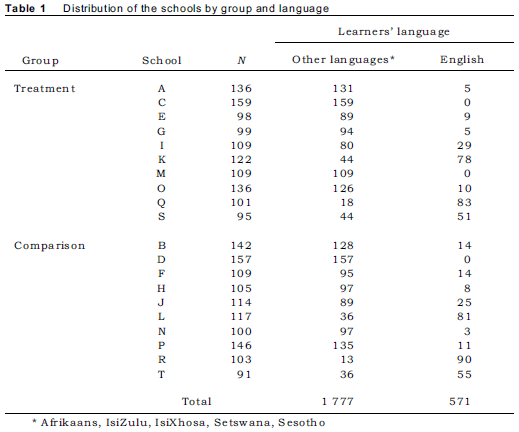
Participants were 2,348 learners in Grade 4, Grade 5 and Grade 6 made up of 1,189 (50.6%) girls and 1,159 (49.4%) boys. Their ages ranged between 9 and 15 years (M = 11.4; SD = 1.2). The comparison group comprised 1,184 learners made up of 399 Grade 4, 393 Grade 5 and 392 Grade 6. Among the comparison group 301 (25.4%) learners were receiving mother-tongue instruction while the rest were second language speakers of English (the language of instruction). The treatment group on the other hand had 1,164 learners made up of 396 Grade 4, 384 Grade 5 and 384 Grade 6. Among this group of learners 270 (23.2%) were receiving mother-tongue instruction.
Procedure
The sole medium of instruction from Grade 1 at all the sample schools was English. According to the educators all the learners were randomly assigned to their classes. That is learners were not assigned to different classes based on ability for example. We negotiated and agreed upon a number of arrangements that were to be followed by each of the two groups of learners and educators. Agreement on all the issues was critical for this study because consistency in the treatment of the participants would ensure the internal validity of the study. For example, the availability of the learner companion to the comparison groups would jeopardise the validity. Also, the negotiation allowed for minimal or no disruption in the daily planning and teaching of the participating educators. The agreements were:
1. During the treatment period learners in the treatment group would be encouraged to communicate in any form they chose until the post-test at the end of the research study;
2. learners in the comparison group would only use English in their mathematics lessons;
3. educators in the treatment group would use the interactive teaching model daily (constantly) for teaching and learning during the treatment period;
4. learners in the comparison groups will not receive the learner companion at any stage during the research project;
5. researcher will provide continuous guidance to the mathematics educators at the treatment schools during the research project regarding use of the learner companion; and
6. learners in the treatment group will be encouraged to use the learner companion freely and as often as possible for the completion of class work, worksheets, assignments and projects.
What the agreements mean in essence was that teaching would continue as usual in the comparison groups. On the other hand teaching in the treatment group would incorporate the use of the learner companion. In this regard educators were encouraged to utilise the learner companion in virtually all activities in the mathematics classroom. In doing this, educators were asked to introduce activities such as 'find the word'. In this activity the educator would for example ask a learner to find the concept 'area' in the learner companion and explain it in their mother tongue to the other learners.
Based on the assignment of the learners the quasi-experimental design was seen to be appropriate for the study. Specifically we used the non-equivalent groups design. In this design a pre-test and a post-test are administered to a treatment group and a comparison group (Gribbons & Herman 1997). As was agreed, both the pre-test question papers and post-test question papers were set by the first author. Setting the question papers was possible because this author had had twenty years of teaching mathematics at the general education phase. The educators requested that two senior mathematics educators should moderate the question papers prior to the administration. Two educators were duly nominated and they also offered to produce the memorandums for each test. In selecting the two educators it was indicated that they possessed the necessary mathematics teaching experience. In fact the researchers were told that the two had each been teaching the subject for an average of ten years. To ensure consistent marking among all the educators, the memorandums produced were all discussed and everybody had a common understanding of the allocation of marks for each question. In undertaking this inclusive consultation on the testing of the learners, we wanted all the educators to be happy and take ownership of the process. This was because in a sense such ownership of the process ensured the face and content validity of the tests. Both the comparison group and the treatment group wrote the pre-test during the last week of February 2007 with the educators invigilating. It is worth pointing out that each grade wrote a test based on work in that particular grade. The marking and the recording of marks was carried out by the educators who supplied these to the first author. The post-test was taken by both groups in November 2007 with similar procedures as in the pre-test followed.
Data collection and analysis
Quantitative data comprised scores obtained by the learners in each of the two tests. As the aim was to determine whether the learner companion had an effect on learners' achievement in mathematics, the two scores obtained were compared using the t test. This test was specifically used to find out whether significant differences could be established between the scores obtained in the pre-test and those of the post-test. This comparison was primarily based on the assumption that if all other variables were constant in the classrooms then any computed differences would be attributable to the intervention brought about by the learner companion. Qualitative data were obtained through interviews conducted with selected educators. Specifically the interviews were meant to find out what the educators' views were in respect of the learner companion and how it could be improved. In respect of the analysis, a sample of examples opined by individual educators is outlined.
Quantitative findings
The researchers acknowledge that it was not ethically correct, in a sense, to advantage one group of learners by providing them with a learner companion while another group had no access to this. However, it should be pointed out that the educators from the comparison schools were privy to the learner companion throughout the research period. For research purposes it was agreed that they would not use it. To address this ethical issue, we decided on a non-equivalent group pre-test post-test design (Gribbons & Herman 1997). That is, the researchers refrained from establishing differences between the comparison and the treatment group. Hence the findings presented here are mainly about differences within the treatment group. Further, the educators were supplied with copies of the learner companion for later use in their classrooms.
Comparison group
The two tests that the learners wrote had a total mark of 20. Figure 2 shows the distribution of marks obtained by learners in the comparison group for both the pre-test and the post-test. In the post-test, ten learners were absent and therefore their marks were not included in the analysis. It may be observed from this figure that in both tests, a majority of learners' marks were consistently between 8 and 12 marks. There were 601 (50.8%) learners in the pre-test and 598 (50.9%) in the post-test. The mean scores for both tests were not significantly different [t (1173) = .993, n.s.] M = 9.92; SD = 3.89 (pre-test) and M = 10.01; SD = 3.92 (post-test). In fact this finding indicates that there was no change in the marks from one test to the other.

Treatment group
Figure 3 shows the distribution of marks obtained by learners in the treatment group for both the pre-test and the post-test. Observation of Figure 3 reveals that the learners' marks of the post-test were generally higher than those of the pre-test. In fact, between one mark and seven marks, there were more learners in the pre-test than in the post-test. The mean scores for both tests in this instance were M = 9.89; SD = 4.24 (pre-test) and M = 10.88; SD = 3.61 (post-test).
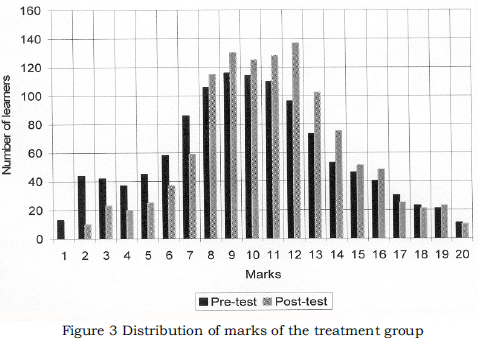
Since a number of t tests were computed, a Bonferroni adjustment (á = .05/6 = .0083) was applied. The adjustment was carried out to reduce the chance of making a type 1 error, that is, finding a false significance (Bland & Altman, 1995). These means were significantly different, [t (1173) = 42.41, p < .008.]. In this case the finding indicates that there was a positive change in the marks from the pre-test to the post-test.
When the analysis was conducted with respect to each grade, in each case a statistically significant difference for the treatment group was computed. Table 2 shows the statistically significantly different mean scores (p < 0.008) in respect of both the pre-test and the post-test of the treatment group by the grade. Observations of the means in each grade suggest that learners' marks were higher for the post-test compared to the pre-test.

We further investigated whether gender differences could be established and found that among girls there was a significant difference, t (600) = 28.45, p < .0008 between the pre-test marks (M = 10.20; SD = 4.36) and the post-test marks (M = 11.19; SD = 3.66). Similarly among the boys the difference was significant, t (562) = 32.06, p < .0008. Here the mean scores were (M = 9.55; SD = 4.09) for the pre-test and (M = 10.56; SD = 3.52) for the post-test. With respect to the grades, Table 3 shows that there were significant differences between girls and boys in Grade 4 and Grade 5. However this was not the case for the Grade 6 learners.

Qualitative findings
Interviews were conducted with all the 20 participating educators after the learners had written the post-test. This was possible because the comparison group educators knew about and had the learner companion, the difference is that they did not use it. Each interview session took approximately twenty minutes. During the interviews educators were asked to indicate what they felt about the learner companion. Jacques (pseudonym) from School K indicated that he was impressed with the multilingual visual explanatory mathematics learner companion. He pointed out "... this companion has brought me closer to my learners ...", asked how so, he said "I always knew the problem was with English - unquestionable ... but for me to try and understand what an expression means in my pupils' language ... I cannot express in words - that's what this has meant to me". Thapelo (pseudonym) an educator at School B expressed his unequivocal support for the use of the learner companion. On being asked why this was the case he indicated "... it is easier now to explain to my children what something means, ... think of for example, expanded notation I can now explain to the child what it means in Setswana, ... the good thing is he can also look it up any time he wants to". Karabo (pseudonym) from School D was complimentary and had high regard for the learner companion. She said "... the drawings definitely helped the learners to understand better. What makes it even more wonderful is that the child's home language is right there". In concurrence, Goitsemang (pseudonym) an educator at School S remarked "... this learner companion is very important for me because most of my learners struggle with English". When asked why the learner companion was very important for him, he replied "... I like the drawings because they help the learners to see and understand what I am trying to explain".
We also requested the educators to indicate what they would like to be added or removed from the learner companion. Regarding additions, Thapelo (School B) wanted the learner companion to be expanded to span Grade 4 mathematics to Grade 8. His basis for this call was continuity on the one hand and the fact that he teaches up to this grade in his school. This view was interesting to the researchers, first because it was mentioned by 18 (90%) of the educators yet none had taught mathematics beyond Grade 6. Second, because it intrinsically meant these teachers were indeed in favour of utilising the learner companion in teaching mathematics. Sam (pseudonym) from School A proposed that the official languages excluded from the learner companion be included as soon as possible. Sam (School A) continued by stating, "I have learners in my class whose home language is ChiVenda ... they were excluded in that their home language does not appear in the companion... they had to rely on the drawings only". Karabo (School D) suggested that instead of using the learner companion solely as a visual explanatory document, it could be used as a workbook as well. The way to achieve this, in her words, was to "... add say three perforated blank pages after each printed page. Learners will then also be able to practise what they see. When they make mistakes or the page becomes damaged, they simply remove the page". Julia (pseudonym) an educator at School Q indicated that the size of the learner companion should be reduced from A4 to A5. In motivating this she stated, "... the learner companion occupied a lot of space on the pupil's desks". Godfrey (pseudonym) from School 1 suggested that the learner companion be developed even further to eventually include more mathematical terms. This educator also proposed one or two improvements regarding the drawings in the companion.
Conclusions and discussion
Our aim was to establish whether learners' performance in mathematics would be positively impacted upon by the introduction of a multilingual visual explanatory mathematics learner companion. In doing this, we hypothesised that learners utilising the learner companion would perform better in the subject because they would subsequently understand what a mathematical term meant in their own language. In this regard we felt that backed by a better grasp of mathematical terms in their language, learners would understand classroom activities better. In general the results indicated that the marks of learners in the treatment group in particular, improved from the pre-test to the post-test. We felt that if all other factors were constant in the different classrooms then the impact of the learner companion was indeed positive. We concluded that the companion helped learners to understand mathematical vocabulary sufficiently enough for an improvement in marks by second language speakers. This conclusion was based on the fact that approximately one in four of the learners were English speaking, which was the language of instruction of mathematics at the participating schools. This meant that the usage of and the findings reported in respect of the learner companion could not have been influenced by these learners. What is undeniable in South Africa is that classrooms are largely multilingual. The challenge for educational practise is therefore to provide a sustained provision of education with appropriate learning and teaching resource materials. Researchers have argued that in learning mathematics, second language learners are at a disadvantage (Barton & Neville-Barton, 2003; Mestre, 1981). We introduced the learner companion specifically to help alleviate this disadvantage and to add to the teaching resource materials that may be used to teach mathematics in our schools. The preliminary results reported here seem to suggest that ours is a right direction to pursue. The positive reviews by educators also seem to be a positive endorsement of the learner companion. A pleasing finding was also the fact that the educators indicated that the learner companion brought them closer to their learners in terms of reducing the language barrier.
A limitation here was the fact that the first author could not be at the different schools at all times to monitor the frequency of use of the learner companion. For this, we could only rely on the word of the educators. For all practical purposes some of the educators were different language speakers (e.g. Afrikaans) compared to their learners (e.g. Setswana). This meant that educators could not ascertain that learners were learning the correct terms in their vernacular. Also, the learner companion may not have been useful for the first language speakers of English say, in respect of what it was meant for. However, a spin-off of its introduction to these learners is that it inherently made them aware of fellow learners' languages. This situation we hoped would help enhance mutual understanding on both sides. Understanding would be enhanced because one group during peer tutoring would invariably have to explain to the other the meaning as well as pronunciation of terms in the learner companion. A number of factors that were not easy to control may have had an influence on the study. For example, good teaching by the educators may have influenced the findings. The fact that the educators themselves were positive about the learner companion is however helpful in this regard. We also wish to acknowledge that the fact that 20 schools participated in the study does not in any way mean that the findings reported here may be generalised to all schools in the province. While the presented results are encouraging it is recommended that the learner companion should be used and investigated on a bigger scale to corroborate the efficacy reported in this study.
References
Adler J 1995. Dilemmas and a paradox-secondary mathematics teachers' knowledge of their teaching in multilingual classrooms. Teaching & Teacher Education, 11:263-274. [ Links ]
Adler J 1997. A participatory inquiry approach and the mediation of mathematical knowledge in multilingual classrooms. Educational Studies in Mathematics, 33:235-258. [ Links ]
Barton B & Neville-Barton P 2003. Language issues in undergraduate mathematics: A report of two studies. New Zealand Journal of Mathematics , 32:19-28. [ Links ]
Bland JM & Altman DG 1995. Multiple significance tests: Bonferroni method. BMJ, 310:170. [ Links ]
Botes HG 2008. The use of reinforced resources to overcome linguistic diversity in the mathematics classroom. DEd thesis. Pretoria: Tshwane University of Technology. [ Links ]
Brown T 1994. Towards a hermeneutical understanding of mathematics and mathematical learning. In: P Ernest (ed.). Studies in Mathematics Education. London: The Falmer Press. [ Links ]
Bohlmann C 2001. Reading skills and mathematics. Communications: Third Southern Hemisphere Symposium on Undergraduate Mathematics Teaching, 5-14). [ Links ]
Cole PG & Chan LKS 1994. Teaching principles and practice. New Jersey: Prentice Hall of Australia. [ Links ]
Danesi M 1988. Mother-tongue training in school as a determinant of global language proficiency: A Belgian case study. International Review of Education, 34:439-454. [ Links ]
Davalos RA & Griffen G 1999. Empowering teachers and students to change through shared language. Education (Chula Vista, CA), 119:542-550. [ Links ]
Department of Arts and Culture, Republic of South Africa n.d. Multilingual mathematics dictionary: Grade R - 6, English - Afrikaans - Isizulu - Isixhosa - Siswati - Isindebele - Setswana - Sepedi - Sesotho - Thsivenda - Xitsonga. Available at http://www.dac.gov.za/ [ Links ]
Department of Education 1997. Language in Education Policy. Pretoria: Government Printer. [ Links ]
Du Plessis S & Louw B 2008. Challenges to preschool teachers in learner's acquisition of English as Language of Learning and Teaching. South African Journal of Education, 28:53-75. [ Links ]
Durkin K 1991. Language in mathematical education: Research and practice. Buckingham: Open University Press. [ Links ]
Fleisch B & Shindler J 2007. School participation from 'Birth-to-Twenty': Patterns of schooling in an urban child cohort study in South Africa. Paper prepared for the UKFIET Conference, Oxford University, UK, 11-13 September 2007. Available at http://www.create-rpc.org/pdf_documents/fleisch.pdf. [ Links ]
Gribbons B & Herman J 1997. True and quasi-experimental designs. Practical Assessment, Research & Evaluation, 5. Available at http://PAREonline.net/getvn.asp?v=5&n=14. [ Links ]
Huitt W & Hummel J 2003. Piaget's theory of cognitive development. Educational Psychology Interactive. Valdosta, GA: Valdosta State University. Available at http://www.edpsycinteractive.org/topics/cogsys/piaget.html. [ Links ]
Khisty LL 1995. Making inequality: Issues of language and meanings in mathematics teaching with Hispanic students. In: WG Secada, E Fennema & LB Adajian (eds). New directions for equity in mathematics education. New York: Cambridge University Press. [ Links ]
Lemke JL 1990. Talking science: Language, learning and values. Norwood, NJ: Ablex Publishing Corporation [ Links ]
McLean A 2000. The predictive approach to teaching statistics. Journal of statistics education, 8. Available at www.amstat.org/publications/jse/secure/v8n3/mclean.cfm [ Links ]
Mestre JP 1981. Predicting academic achievement among bilingual Hispanic college technical students. Educational and Psychological Measurement, 41:1255-1264. [ Links ]
Mwamwenda TS 1995. Educational Psychology: An African Perspective. Durban: Butterworths. [ Links ]
O'Toole M 1996. Science, schools, children and books: Exploring the classroom interface between science and language. Studies in Science Education, 28:113-144. [ Links ]
Parilla RK 1995. Vygotskian Views on Language and Planning in Children. School Psychology International, 16:167-183. [ Links ]
Pimm D 1987. Speaking Mathematically. London: Routledge. [ Links ]
Richards P 1982. Difficulties in learning mathematics. In: M Cornelius (ed.). Teaching Mathematics. London: Nichols publishing company. [ Links ]
Rollnick M 2000. Current issues and perspectives on second language learning of science. Studies in Science Education, 35:93-121. [ Links ]
Setati M 1998a. Code-switching in a senior primary class of second language mathematics learners. For the Learning of Mathematics, 18:34-40. [ Links ]
Setati M 1998b. Innovative language practice in multilingual mathematics classrooms. Johannesburg: Joint Education Trust. [ Links ]
Thurston WP 1995. On proof and progress in mathematics. For the learning of Mathematics, 15:29-37. [ Links ]
Vygotsky L 1989. Thought and Language. Massachusetts Institute of Technology: Halliday Lithograph. [ Links ]
Young D 1995. The role and status of the first language in education in a multilingual society. Multilingual Education for South Africa, A Project for the Study of Alternative Education in South Africa. The National Language Project. Isando: Heinemann Publishers. [ Links ]
Authors
Hendrik Botes is a Senior Educator and has taught for 20 years. His research focuses on introduction and management of reinforced resources to negotiate language barriers in multicultural mathematics classes.
Andile Mji is responsible for research in the Faculty of Humanities at the Tshwane University of Technology. His research interests include the psychological aspects of learning mathematics and the psychometric properties of instruments used in mathematics education.














