Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Education
versión On-line ISSN 2076-3433
versión impresa ISSN 0256-0100
S. Afr. j. educ. vol.29 no.3 Pretoria ago. 2009
Incorporating the indigenous game of morabaraba in the learning of mathematics
Nkopodi NkopodiI; Mogege MosimegeII
ISenior Lecturer at the University of South Africa. His research interests include language, culture, and indigenous knowledge in mathematics and science education. E-mail: nkopon@unisa.ac.za
IIVice Rector: Academic at North-West University, Mafikeng Campus. His research interests are ethnomathematics, socio-cultural issues in mathematics education, access to mathematics, science and technology education, and Indigenous Knowledge Systems. E-mail: mogege.mosimege@nwu.ac.za
For many years, education in South Africa has been based mainly on western values. This has contributed to the fact that many learners from disadvantaged backgrounds cannot see the connection between the education they receive at school and their everyday experiences. This may well have contributed to the high failure rate amongst mathematics learners as well as the perceived difficulty of mathematics. It is believed that indigenous knowledge, in general, can be used to promote the teaching of mathematics in multicultural classes. We report on an enquiry into the use of the indigenous game of morabaraba in the mathematics class. Various mathematical concepts have been identified from the game. It was found that learners enjoy playing the game, and that it can be used in the mathematics classroom to promote the learning of mathematics. It was also found that the use of this game promotes spontaneous interaction amongst learners as they communicate their activities to fellow participants. The enjoyment of the game was found not to be restricted to a specific cultural group, which suggests that it can be used in a multicultural setting.
Keywords: culture and mathematics; ethnomathematics; Indigenous Knowledge Systems (IKS); mathematics education; traditional mathematics
Introduction
Since 1994, South Africa has made an effort to take into consideration various cultural groups in all spheres of life. It remains a challenge for educators to extend this in classrooms, particularly in science and mathematics classrooms. Anecdotal evidence shows that this challenge is usually explained through the statement that mathematics and science are seen as 'western' and are never associated with African culture.
Our aim in this article is to show that some cultural aspects related to indigenous games can be incorporated in the teaching and learning of mathematics. Examples used for illustration in this article have been trialled in South African mathematics classrooms. This has been done by incorporating mathematical activities identified from the analysis of the indigenous game of morabaraba, a game played in different communities in South Africa and other neighbouring countries, like Lesotho and Mozambique. The Mindsports Games in South Africa (formerly known as the South African War Games Union) has, over that past 10 years, promoted the game by organising clubs and competitions nationally and supporting international participation in related competitions.
Contexts in which mathematics is used in different cultures have already been documented by many authors, amongst others Mosimege (2005) and Vithal (1992). Various mathematics concepts that can be identified in different indigenous games can be related to both geometry and algebra and other points of focus in mathematics. We focus here on examples found in indigenous games, in particular morabaraba (also known as 'mmela' by some Sotho speakers and 'umlabalaba' by the Nguni speakers). Mosimege (2006) points out that the South Sotho name of morabaraba is the name most used for this game by South Africans. Zaslavsky (1999) uses the term 'mill' in referring to the game.
Our purpose is to show that the indigenous game of morabaraba has the potential of being used with success in the teaching and learning of mathematics. The use of indigenous games in general in mathematics classrooms provides the learners with an opportunity to relate their experiences outside the classroom to mathematical concepts and processes encountered in their mathematics classrooms. This, to a greater extent, creates familiarity between mathematics and indigenous games and in the process helps learners to overcome their fear of mathematics. The use of indigenous games in the classroom also creates a relationship between culturally specific activities and classroom activities (Laridon, Mosimege & Mogari, 2005:147).
Theoretical background
We will discuss some learning theories and how the game of morabaraba fits in with the theories.
Learning for understanding
According to Klafki's theory, there are five basic questions according to which learning content may be analysed (Fraser, Loubser & Van Rooy, 1994:19):
- What particular meanings (fundamental principles, basic structures) are basic to the learning content of the subject?
- What is the significance of the learning content with regard to the acquisition of knowledge, skills, proficiency and experience by the child?
- What is the significance of the learning content with regard to the child's future?
- What is the structure of the learning content?
- How can the child's interest in the learning content be stimulated, and how can the structure of the learning content be explained to the child?
This section elaborates on the first three aspects of Klafki's theory.
In the context of this study, 'child' should be understood to refer to a learner. The importance of taking into consideration what the learner already knows in creating a meaningful learning environment was documented as early as 40 years ago (Ausubel, 1968). According to constructivist theory, learners construct new knowledge based on what is already known to them. This is in line with Tobin and Tippins' (1993:4) view that "science is viewed as set of socially negotiated understanding of events and phenomena that comprises the experiences universe". It will therefore be important for learners to be exposed to learning opportunities that link mathematical concepts and principles with their applications encountered in everyday experience. Play is a relevant tool to help achieve this connection if it can be linked to school mathematics. Although play and games are generally similar, there are some situations where play becomes different from a game, since in play, the participants' objective may not be to determine a winner but merely to while away the time.
Van der Stoep and Louw (1981) describe play as an entertaining action or relaxation that takes place according to rules. Kirkby (1992) states that games can help learners to develop mathematical skills. Educators are challenged to find ways in which games can be used to develop and enhance mathematical skills. This may be motivating to learners when they enjoy playing the game.
In a game, participants have to follow the rules of the game or come to a consensus on how the rules can be amended. Each player wishes to win the game while simultaneously having the same interpretation of the rules as the opponent. This is in line with mathematical problem solving, as certain rules have to be followed in solving a mathematical problem. Each player plans the next move and strategies, while keeping all the rules in mind. At the same time the player considers what the opponent's next move will be, based on the move he is taking and the fact that the player must follow certain rules. The player in fact visualises these moves. These activities are similar to problem solving where one has to arrive at a solution according to proven rules. In some cases participants can form teams of two or more members to compete against a person or a team, also comprised of two or more members.
Vithal (1992) suggests that there may be both cognitive and affective advantages for the learners when games are used, and further points out that time and money could cause problems. The issue of a lack of time will need to be addressed alongside the general matters of teaching strategies. By using indigenous games, the problem of inadequate finances may partly be alleviated, because indigenous games can often be constructed simply without spending any money. In the South African context, some of these matters have been discussed by Nkopodi (2001) as well as by Mosimege (2000) and Vithal (1992). The important principle is that what is used from different cultures should be familiar to all cultures. If a game from one culture is to be used, then other learners who are unfamiliar with the game should first be taught how to play it.
Definition of games and their uses in the teaching and learning of mathematics
The word 'game' is usually associated with recreation, competition, sportsmanship, winning, losing, enjoyment, and many other similar and related notions. According to Ascher (1991:85), the term 'game' encompasses a variety of activities like children's street play, puzzles, board games, dice games, card games, word games, golf, team sports, and international competitions. She goes on to define a game as "an activity that has clearly defined goals towards which the players move while following agreed upon rules". Other definitions of games like those of Bright, Harvey and Wheeler (1985), Fletcher (1971), and Guy (1991) specify various criteria that define a game. These criteria concur with Ascher's definition.
Crump (1990:115) expresses the view that games, as a category of human activity, are easier to recognise than define. He identifies three properties which, if not sufficient to define the category unambiguously, are in practice common to almost all games. The second category is particularly important as it highlights the importance of context:
Games have a clearly defined context — generally both in time and space. The context is defined not so much by the rules of the game, but by the culture in which it is played, in which the game itself will have any number of well-recognised connotations.
It is this context that tends to be overlooked when games are played, especially as part of "formal" education. It is generally assumed that games can be used in a variety of circumstances without consideration of the culture in which such games were initiated or the social circumstances under which they are played.
More than a decade ago, Vithal (1992:178-179) pointed out that games have been used in the teaching and learning of mathematics over the years, and that this use has increased in the recent past. Since Vithal's statement, a number of reports on research into games and their uses in classrooms have been published (Coombe & Davis, 1994; Mapapa, 1995; Ismael 1997; Mosimege 1997; 1998; 1999). Some of the uses of games in mathematics education are to learn the language and vocabulary of mathematics, develop mathematical skills, develop ability with mental mathematics, and devise problem-solving strategies and to be the generator of mathematical activity at a variety of different levels. Games also contribute in stimulating investigational work in mathematics (Kirkby, 1992; Sobel & Maletsky, 1975). Studies that explore the use of games in problem-solving situations have been documented (Krulik, 1977; Williford, 1992), suggesting an important relation between games and problem-solving, one of the central aspects in mathematics learning. The use of games also leads to discovery of patterns (Harlos, 1995), decision making (Buckhiester, 1994), and logical reasoning, deduction and skills (Brumfiel, 1981).
The above uses of games suggest that games play a more profound role than just being recreational or pastime activities, which tends to be the focus most of the time when games are used. As people engage in any game, the language, vocabulary, mathematical skills and a variety of mathematical activities are generated. Although some of these aspects may be very basic, they serve as important components in the development of mathematical concepts.
Indigenous games, indigenous knowledge systems and ethnomathematics
On 24 February 2001 the Minister of Sports and Recreation launched the indigenous games of South Africa at the Basotho Cultural Village in the northern part of the Free State province. This was a culmination of one of the phases of the project by the South African Sports Commission (SASC) to revive indigenous games in South Africa. In this phase the project by the SASC had identified 23 indigenous games in the different regions of South Africa. These games are linked to "traditions of a cultural group, being of a local origin and requiring physical skill, strategy and/or chance" (SASC, 2001:3). The launch focused on seven games which were found to be generic in most regions of the country. These are dibeke, kho-kho, kgati, diketo, jukskei, moruba, and morabaraba. The SASC notes that these games were "grossly neglected in historical and anthropological accounts of indigenous peoples in South Africa" (SASC, 2001:3). The launch and focus of indigenous games has resulted in an annual celebration of indigenous games in the different provinces of South Africa.
The focus on Indigenous Knowledge Systems (IKS) worldwide and the associated debates have led to a variety of definitions of IKS. Most of these definitions have taken into account the importance and relevance of indigenous, traditional and local knowledge, as well as the subtle but important differences between these three concepts. One of the earlier definitions of IKS is that of Warren (1996) who defined it as
a systematic body of knowledge acquired by local people through the accumulation of experiences, informal experiments and intimate understanding of their environment in a given culture (Warren, 1996).
After exploring the extent of indigenous knowledge in Tanzania, Mascarenhas (2004:5) defined indigenous knowledge as
[t]he sum total of the knowledge and skills which people in a particular geographic area possess, and which enable them to get the most out of their natural environment. Most of this knowledge and these skills have been passed down from earlier generations, but individual men and women in each new generation adapt and add to this body of knowledge in a constant adjustment to changing circumstances and environmental conditions. They in turn pass on the body of knowledge intact to the next generation, in an effort to provide them with survival strategies.
According to Mosimege and Onwu (2004:2), indigenous knowledge is
an all inclusive knowledge that covers technologies and practices that have been and are still used by indigenous and local people for existence, survival and adaptation in a variety of environments. Such knowledge is not static but evolves and changes as it develops, influences and is influenced by both internal and external circumstances and interaction with other knowledge systems. Such knowledge covers contents and contexts such as agriculture, architecture, engineering, mathematics, governance and other social systems and activities, medicinal and indigenous plant varieties, etc.
The study and analysis of indigenous games has shown that they are a component of indigenous knowledge systems. Both indigenous games and indigenous knowledge systems deal with knowledge of local origin which is known largely by specific cultural groups. However, this knowledge is not strictly confined to the specific group, as evidenced by different cultural groups' knowledge of the morabaraba game. The knowledge of other cultural groups may be attributed to interrelations between cultures and studies on a variety of cultures and cultural activities which have been published. However, the fact that other cultural groups have knowledge of the game does not make the game less indigenous and less contextual.
IKS is a broad concept which incorporates ethnomathematics. This can be seen in the definitions given by D'Ambrosio (1984, 1985). Two of D'Ambrosio's earlier definitions of ethnomathematics show a close link between ethnomathematics and indigenous knowledge systems. D'Ambrosio's 1984 definition states that
[societies] have, as a result of the interaction of their individuals, developed practices, knowledge and in particular, jargons … and codes, which clearly encompass the way they mathematise, that is the way they count, measure, relate, and classify and the way they infer. This is different from the way all these things are done by other cultural groups. [We are] interested in the relationship … between ethno-mathematics and society, where 'ethnos' comes into the picture as the modern and very global concept of ethno both as race and/or culture, which includes language, codes, symbols, values and attitudes. This naturally implies science and mathematics practices.
Here D'Ambrosio looks at the cultural elements such as language, codes, symbols, values, and attitudes which characterise a particular practice. In a subsequent definition, he defines the cultural groups as national tribal societies, labour groups and children of a certain age bracket. D'Ambrosio (1985: 45) states that "we will call ethnomathematics the mathematics which is practised among identifiable cultural groups, such as national-tribal societies, labour groups, children of a certain age bracket and professional classes". On the basis of D'Ambrosio's two definitions, and other definitions of ethnomathematics not quoted here, it is appropriate that ethnomathematics is classified as one of the components of indigenous knowledge systems.
Ethnomathematical studies and the mathematics classrooms
Vithal and Skovsmose (1997:135) indicate that one of the main challenges of ethnomathematics is that there are relatively few detailed descriptions of the actual implementation and outcomes of such an approach within the formal school system. They further argue that this is still an under-researched area. Since their article was published in 1997, a number of studies have been undertaken to address this concern that they raised. The study reported here is an attempt to explore how ethnomathematical studies may be implemented in the context of the mathematics classroom and how related challenges may be dealt with. It follows on similar studies by Ismael (2002), Cherinda (2002), Mogari (2002), and Mosimege (2000), which outline how various ethnomathematical activities may be used in mathematics classrooms.
Indeed as pointed by Vithal and Skovsmose (1997:137), to South Africans the language of ethnomathematics — particularly its articulation of a concern with culture in education — may appear all too familiar and conceptually rather close to apartheid education. Our view however, is that this focus has contributed to a greater and deeper understanding of how various cultures can contribute and how they can be viewed and interpreted with respect to mathematical classroom challenges. Studies that focus on relations between mathematics and culture enable one to reflect on the different cultures and find ways in which classroom challenges may be explored in classroom settings.
Research design
Qualitative research was used in this study. This was considered appropriate since the researchers wished to obtain an in-depth understanding of how and what learners thought about the game of morabaraba as they played the game (De Vos & Fouche, 1998; Trochim 2001). In this regard, participant observation and teaching experiments were used. Learners were video recorded while playing the game. Their discussions were transcribed verbatim.
The research sites consisted of schools in Limpopo and the North-West Province, respectively. These schools were chosen because the learners and educators in the two provinces were familiar with the game as played in the provinces and were willing to participate freely in the study. In addition, the researchers had grown up in the two provinces and so were also familiar with the games in the context of the provinces.
Participant observation
Participant observation is one of the central ways of collecting data in qualitative studies (Overholt & Stallings, 1976; Booth, 1987; Jacobs, 1988). One of its key successes is fitting in, becoming part of the group i.e. establishing an accepted social role as a participant in the interaction being studied. Ellen (1984) argues that every kind of anthropological research requires a certain, if minimal, amount of participation on the part of the researcher. This is due to necessities like exchange of greetings, introductions, explanation of what is involved in the research and which tasks the subjects are expected to perform.
In classroom application, participant observation may mean joining the learners in the activities that they have been assigned to undertake and noting all pertinent aspects thereof. It may also mean creating an atmosphere for an in-depth investigation of a particular area or problem of concern by arranging the classroom activities. This depends on the circumstances of the work and the problem being researched. This is the participant observation approach used in this study. The game of morabaraba that was introduced was not part of the regular classroom activities that the learners were exposed to, and this resulted in the introduction of the game in the classroom and an intense observation of the learners' behaviours when they engaged in the game. The participant observation approach therefore took the form of a teaching experiment which is explained below.
Teaching experiment
The 'teaching experiment' is a generic term for a variety of pedagogical research forms in which the strictly statistical analysis of quantitative data is of less concern than the daily subjective analysis of qualitative data (Kantowski, 1979:3). Its aim is to "catch" processes in their development and to determine how instruction can optimally influence these processes. This Soviet research methodology grew out of a need to permit researchers to observe qualitative effects of various forms of instruction.
Lessons were presented to the learners by the researchers and not by the educators after their training on the use of ethnomathematical materials. This was decided after the realisation that most of the time, when the schools' educators had taken part in earlier workshops on ethnomathematical activities were visited, the educators still felt very uncomfortable in presenting ethnomathematical lessons, especially in the presence of the researchers. Using the 'teaching experiment' therefore allowed the researchers to introduce the game into the daily classroom activities at intervals for the duration of the study. Perhaps this study also fitted the 'teaching experiment' model owing to its longitudinal nature (another characteristic of the 'teaching experiment'), i.e. working with each of the schools over a period of about two years.
Preparation of using indigenous games in the classroom
Specific activities necessary before indigenous games can be used in the mathematics classroom will be discussed.
Identification of indigenous games according to the potential of their use in the curriculum
There are a variety of indigenous games in South Africa. If educators want to use these games in the classroom, they would have to select a particular game or number of games depending on the subject area of focus and the relevance of such games in terms of the curriculum focus. The following questions should be asked in selecting games:
- Is it possible to obtain or make the material?
- Is it possible to use the games inside the classroom?
- Can the games be played by both male and female learners?
- Do the games reveal a variety of embedded mathematical concepts (even at a superficial level of analysis)?
The last criterion would apply specifically when the games are to be used in the teaching and learning of mathematics.
Analysis of games
A mathematical analysis (applying mathematical concepts, principles and processes) of any game reveals the extent to which mathematical concepts are embedded in the game. The following mathematical concepts are found in the analysis of morabaraba:
- Identification of various quadrilaterals (squares) and the similarities and differences between them;
- Ratio and proportion between the lines and the squares making the complete morabaraba board;
- Symmetry: Symmetry is observed in at least three different instances, namely, (1) the various sides of the board; (2) within each side of the board; (3) the placement of tokens and repetitive movements of the tokens on the board;
- Logical deductions in the execution of the various steps of the game;
- Counting of the tokens;
- Addition and subtraction of the tokens until a game is won on the basis of the remaining number of tokens.
Application of indigenous games in the classroom
Our research revealed interesting observations in both schools despite their location in different provinces. These observations are discussed below.
As learners play together, most of them tend to be very quiet in order to concentrate on the moves they are going to make. Whenever any verbalisation takes place, it is in hushed tones, with verbal expressions few and far between. As a result, it is generally very difficult to follow the reasoning behind the learners' moves without asking them questions. The following episode illustrates that even when the researcher continuously requested the learners to speak loudly so that he could hear, the learners still struggled to do so.
Illustration of the game of morabaraba
Notations will be used for ease of identifying players, moves taken and positions of tokens.
| Notation used for players and moves | |
| R: | Researcher |
| ML: | Male learner |
| FL: | Female learner |
| ML1: | When there is more than one male learner they are specified by using ML1 for male learner 1, ML2 for male learner 2. The same applies for the female learners, i.e. FL1, FL2, etc. |
| P: | Placements of tokens are represented by P, where P1 represents the placement of the first token, P2 placement of the second token, etc. |
| M: | Movements of tokens are represented by M, where M1 represents the movement of the first token, M2 movement of the second token, etc. |
The discussion took place at School A in Limpopo province where all learners speak Sepedi (North Sotho) as home language. The school uses English as medium of instruction.
School A, Grade 10 B
Morabaraba game between two male players at the back of the classroom
| R: | Le boleleleng godimo, le boleleleng godimonyana because ke batla gore ke lekwe mo, akere? [Speak loudly, speak loudly because I need to hear you here, isn't it?] |
| L2: | Ja. [Yes.] {The second learner looks at me and nods his head slightly in agreement with the first learner.} |
| R: | Le boleleleng godimonyana. [Speak loudly.]. {The learners then continue to place the tokens on the board, 7 remaining tokens by each player. They still speak in hushed tones. They place most of the tokens without saying anything.} |
Despite the repeated request by the researcher that the learners should speak a bit louder and the agreement by both learners (one of them agreeing verbally and the other through nodding the head) the learners still continued to speak so softly that the researcher could not hear exactly what they said. This instance and many similar instances seem to indicate that morabaraba is a game which is not characterised by speaking loudly but is characterised by either quietness or some thinking as it relates to the tokens and the related movements. This is different from the indigenous game of moruba in which most of the activities are verbalised.
A few learners verbalised to express that a good move had been made and a token captured, or to express desperation on the part of the losing player, but not to explain why a particular move was made. The expressions were mostly made in the learners' home language. For instance, a learner would express the capturing of a token by saying "mamo", (short for "mamola") meaning either 'removing' or 'beating'.
Some of the learners made physical gestures to signify a particular activity (placement, movement, formation of three-in-a-row) in the game. For instance, after capturing a token, a learner would show this by making a hand-sign that signifies beating. When this action is signified physically, players move a pointing index finger downwards, such that at the end of the movement the finger makes a striking sound against the other fingers, particularly the third finger. This results in a striking sound made by the two fingers, giving a feeling that something has been beaten.
Within a period of 10 minutes the learners had played an average number of three games. This was dependent on whether learners who were playing together both understood the rules of the game. If both learners did not know the game they would spend a few minutes referring to the rules at the back of the morabaraba board. In instances where one of the learners knew the rules, this learner would explain the rules to the other learners. If one or both learners did not know how to play the game, they generally played only two games at the most. This shows that a lack of knowledge of the game caused the game to take longer than when the rules were known. If one of the learners knew the rules a Learning and Sharing Opportunity (LSO) was presented on the part of the knowledgeable learner. However, it also presented a difficulty in which the learner who did not know the game was to a greater extent dependent on the knowledgeable learner for some of the decisions, which in turn favoured the knowledgeable learner as he/she could exploit this situation to his/her advantage.
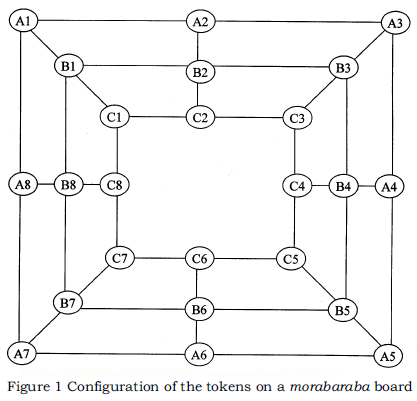
Notation on the morabaraba board
The morabaraba board is made up of three squares, with lines joining the corners of the squares and the middle of each square. These lines, including the lines forming the squares, indicate where the tokens can be moved after placement. Each square has 8 junctions at which tokens may be placed, numbered as follows:
Square 1 — Outer square: A1, A2, A3, A4, A5, A6, A7, A8
Three-in-a-row combinations of this square: A1A2A3; A3A4A5; A5A6A7; A7A8A1
Square 2 — Middle square: B1, B2, B3, B4, B5, B6, B7, B8
Three-in-a-row combinations of this square: B1B2B3; B3B4B5; B5B6B7; B7B8B1
Square 3 — Inner square: C1, C2, C3, C4, C5, C6, C7, C3
Three-in-a-row combinations on this square: C1C2C3; C3C4C5; C5C6C7; C7C8C1
Combinations may also be made that involve the three squares as follows:
Square cutting combinations: A1B1C1; A2B2C2; A3B3C3; A4B4C4; A5B5C5; A6B6C6; A7B7C7; A8B8C8.
The above possible combinations can be seen in Figure 1.
Below is a description of the game of morabaraba as played by learners, L1 and L2.
M1: L1 — C2 to C1 {Before making this move, L1 places the right palm on top of the left knuckles and then a few moments later moves the left hand over possible junctions, starting with the side of the board containing A7A8A1, followed by the side containing A1A2A3, and finally moving the token on C2}; L2 — B6 to C6 {Forming three-in-a-row on C1C2C3, captures the token on C1, hits the palm of the right hand against the flat part of clenched left fist. This move temporarily forms a free pathway ("seregerege") between the middle square and the inner square on the side facing L1};
M2: L1 — A6 to B6 {Blocking the "seregerege" by L2 between C1C2C3 and B1B2B3. Before L1 makes this move, he realises that L2 is paying attention to players in another group, so he draws his attention to the move he is about to make}; L2 — C3 to C2 {a move that does not seem to be aimed at anything specific for L2 and therefore inconsequential};
M3: L1 — B6 to A6 {Forming three-in-a-row on A5A6A7, captures the token on B5, destroying a possible three-in-a-row for L2 on B1B2B3. Before capturing this token, L1 moves his right hand as if to capture the token on C2, but then immediately realises that there is danger on B6 because of the free pathway. He uses his finger to point out the three-in-a-row on C5C6C7 and what could happen, then settles for the token on B5}; L2 — C6 to B6. {This move disrupts the three-in-a-row on C5C6C7 with the intention of closing it again. However, L2 does not seem to realise that L1 can move A5 to B5, thereby forming three-in-a-row on B3B4B5, which L2 could have prevented by moving C5 to B5 instead of C6 to B6};
M4: L1— A5 to B5 {forming three-in-a-row on B3B4B5, captures on B6 which destroys the possible formation of three-in-a-row for L2 on C5C6C7}.
The recording of the game ends after the fourth (M4) move by L1 in which he formed a three-in-a-row on B3B4B5. The recording shifts away to focus on another activity just after L1 has captured the token from the formation of a three-in-a-row on B3B4B5. Even though the video recording had shifted from this game before it was completed, the way in which the game was progressing gave a good indication that L1's tokens were so well placed that he was going to win. There are two three-in-a-rows for L1 who is using the blue tokens, and in his next movement he can just move B5 to C5 to form another three-in-a-row whereas L2 does not have that luxury. L1 does not even have to rush into forming the obvious three-in-a-row on A5A6A7 but can instead create other opportunities as L2 has only one option of creating a three-in-a-row by moving A1 to A8, which can be easily blocked by L1 who can then move B1 to A1, thus blocking the possibility for L2 and also creating another opportunity on B1B2B3. It is therefore safe to conclude that L1's token is placed such that he can win the game if he follows the strategy just suggested.
It was clear from the observation of the learners' activities and the comments they made amongst themselves that they were enjoying participating in the games. This enjoyment of the game can be used to enhance the learners' interest in mathematics. This can lead to the enjoyment of mathematics itself, minimise the fear of mathematics and encourage more learners to take mathematics as a subject.
Implications for mathematics education
As learners engage in a variety of games on morabaraba, they use a number of terms in the game. Here is an opportunity that educators can use to correct, introduce and highlight some of the mathematical concepts (such as geometric shapes, ratio and proportion, symmetry, logical reasoning and counting) that are part of the game being used. Learners should be encouraged to use the language of mathematics while playing the game so that the understanding of concepts can be noted.
An alternative approach of getting an idea of learners' understanding of concepts would be to video-record the play in action. The video can then be replayed and paused at intervals so that the game can be analysed. Moves taken can be discussed and the everyday language used translated into mathematical language. Gifted learners themselves can be asked to identify mathematical concepts in the applied during the game and in the construction of the game board itself. The teacher's role would be to ask appropriate questions for the level of learners.
This clearly shows an important role that educators can play in elevating games from being an activity for fun to be activities that can be related to a variety of mathematical concepts. There are many other mathematical concepts that may be identified in various games, such as has been done in games like chess (Rubin, 1981; Hayes, 1992), tic-tac-toe (Rosenholtz, 1984, 1993; Schram, 1986; Markowsky, 1990a; Markowsky 1990b), and mancala games (Broline & Loeb, 1985). It is the role of mathematics educators to continue analysing a variety of games for the mathematical concepts that are embedded in them or mathematical concepts that can be taught through the use of these games.
The analysis and identification of related mathematical concepts should not be done without the related and important socio-cultural context and implication of the games. Leaving the socio-cultural context out when indigenous games are used deprives the mathematics learners of the rich context that is necessary to fully understand and use such games in mathematics learning. Room should thus be given for bystanders to take sides with either player and encourage them. The teacher's role should also be to enable learners to relate concepts learned to their everyday life. This is in line with constructivism where learners construct new knowledge by linking their new knowledge with their prior knowledge.
In the South African context, the National Curriculum Statement encourages the incorporation of the Indigenous Knowledge Systems in the learning of mathematics. Using indigenous games such as morabaraba in this way is therefore important for putting government policy into practice.
References
Ascher M 1991. Ethnomathematics: A Multicultural View. California: Brooks/Cole Publishing Company. [ Links ]
Ausubel DP 1968. Educational Psychology: A Cognitive View. New York: Holt, Rinehart and Winston. [ Links ]
Bright GW, Harvey JG & Wheeler MM 1985. Learning and Mathematics Games. Journal for Research in Mathematics Education Monograph 1. Virginia: National Council of Teachers of Mathematics. [ Links ]
Broline DM & Loeb DE 1995. The Combinatorics of Mancala-Type Games: Ayo, Tchoukaillon, and 1/?. The UMAP Journal, 16:1. [ Links ]
Booth EO 1987. Researcher as Participant: Collaborative Evaluation in a Primary School. Education as Urban Society, 29:55-85. [ Links ]
Brumfiel C 1981. Using a Game as a Teaching Device. In: KE Easterday, LL Henry & M Simpson (eds). Activities for Junior High School and Middle School Mathematics: Readings From the Arithmetic Teacher and the Mathematics Teacher. Virginia: NCTM. [ Links ]
Buckhiester PG 1994. Probability, Problem Formulation and Two-Player Games. Mathematics Teacher, 87:154-159. [ Links ]
Cherinda M 2002. The use of a cultural activity in the teaching and learning of mathematics: exploring twill weaving with a weaving board in Mozambican classrooms. Unpublished PhD thesis, University of the Witwatersrand, Johannesburg. [ Links ]
Coombe J & Davis Z 1994. Games in the Mathematics Classroom. In: K Brodie & J Strauss (eds). Proceedings of AMESA First National Congress and Workshop,Johannesburg: University of the Witwatersrand. [ Links ]
Crump T 1990. The Anthropology of Numbers. Cambridge: Cambridge University Press. [ Links ]
D'Ambrosio U 1984. Socio-Cultural Bases for Mathematical Education. Proceedings of ICME 5, Adelaide. [ Links ]
D'Ambrosio U 1985. Ethnomathematics and its Place in the History and Pedagogy of Mathematics. For the Learning of Mathematics, 5:44-48. [ Links ]
De Vos AS & Fouche CB 1998. General introduction to research design. In: AS de Vos (ed.). Research at grass roots. Pretoria: JL van Schaik Publishers. [ Links ]
Ellen RF 1984. Ethnographic Research: A Guide to General Conduct. London: Academic Press. [ Links ]
Fletcher JL 1971. The Effectiveness of Simulation Games as Learning Environments. Simulation and Games, 2. [ Links ]
Fraser WJ, Loubser CP & Van Rooyen MP 1994. Didactics for the undergraduate student. Butterworth Publishers (Pty) Ltd. [ Links ]
Guy RK 1991. What is a Game? In: RK Guy (ed.). Combinatorial Games: Proceedings of Symposia in Applied Mathematics. Rhode Island: American Mathematical Society. [ Links ]
Hayes P 1992. A Problem of Chess Queens. Journal of Recreational Mathematics, 24:264-271. [ Links ]
Harlos CA 1995. And the Winner Is … Mathematics Teaching in the Middle School, 1:450-454. [ Links ]
Ismael A 1997. A Study on N'tchuva: An Ethnomathematical Approach. In: M Sanders (ed.). Proceedings of the 5th Annual Meeting of the Southern African Association for Research in Mathematics and Science Education. Johannesburg: University of the Witwatersrand. [ Links ]
Ismael A 2002 An Ethnomathematical Study of Tchadji — About a mancala type boardgame played in Mozambique and possibilities for its use in mathematics education. Unpublished doctoral thesis, University of the Witwatersrand, Johannesburg. [ Links ]
Jacobs E 1988. Clarifying Qualitative Research. Educational Researcher, 17:16-24. [ Links ]
Kantowski MG 1979. The Teaching Experiment and Soviet Studies of Problem Solving. In: L Hatfield & D Bradford (eds). Mathematical Problem Solving: Papers from a Research Workshop. Columbus, OH. [ Links ]
Kirkby D 1992. Games in the Teaching of Mathematics. Cambridge: Cambridge University Press. [ Links ]
Krulik S 1977. Problems, Problem Solving, and Strategy Games. Mathematics Teacher, 70:748-752. [ Links ]
Laridon P, Mosimege M & Mogari D 2005. Ethnomathematics Research in South Africa. In: R Vithal, J Adler & C Keitel (eds). Researching Mathematics Education in South Africa: Perspectives, Practices and Possibilities. Pretoria: HSRC Press. [ Links ]
Mapapa A 1995. Children's Games/Toys for Mathematics Education: The Case of Mozambique. In: T Kjaergard, A Kvamme & N Linden (eds). Proceedings of the Third International Conference of the Political Dimensions of Mathematics Education. Bergen: Caspar-Forlag. [ Links ]
Markowsky G 1990a. Numerical Tic-Tac-Toe — I. Journal of Recreational Mathematics, 22:114-123. [ Links ]
Markowsky G 1990b. Numerical Tic-Tac-Toe — II. Journal of Recreational Mathematics, 22:192-200. [ Links ]
Mascarenhas A 2004. Knowledge, Indigenous Knowledge, Peace and Development. Indilinga: African Journal of Indigenous Knowledge Systems, 3:1-15. [ Links ]
Mogari D 2002. An ethnomathematical approach to teaching and learning of some geometrical concepts. Unpublished doctoral thesis, University of Witwatersrand, Johannesburg. [ Links ]
Mosimege MD 1997. The Use of Games in Mathematics Classrooms. In: M Sanders (ed.). Proceedings of the 5th Annual Meeting of the Southern African Association for Research in Mathematics and Science Education. Johannesburg: University of the Witwatersrand. [ Links ]
Mosimege MD 1998. Culture, Games and Mathematics Education: An Exploration Based on String Games. In: A Olivier & K Newstead (eds). Proceedings of the 22nd Conference of the International Group for the Psychology of Mathematics Education. Stellenbosch: University of Stellenbosch. [ Links ]
Mosimege MD 1999. The Use of Cultural Games in Secondary School Mathematics Classrooms. Paper presented at the 77th Annual Meeting of the National Council of Teachers of Mathematics, San Francisco. [ Links ]
Mosimege MD 2000. Exploration of the Games of Malepa and Morabaraba in South African Secondary School Mathematics Education. Unpublished PhD thesis, University of the Western Cape, RSA. [ Links ]
Mosimege MD & Onwu G 2004. Indigenous Knowledge Systems and Science Education. Journal of the Southern African Association for Research in Mathematics, Science and Technology Education, 8:1-12. [ Links ]
Mosimege M 2006. Indigenous Knowledge Systems and Ethnomathematics. In: B Barton (ed.). Proceedings of the Third Ethnomathematics Conference, University of Auckland, New Zealand, 12-16 February. [ Links ]
Nkopodi N 2001. Using games to promote multicultural mathematics. In: A Rogerson (ed.). Proceedings of the International Conference on New Ideas in Mathematics Education, Palm Cove, Queensland, Australia. 19-24 August. [ Links ]
Overholt GE & Stallings WM 1976. Ethnographic and Experimental Hypothesis in Educational Research. Educational Researcher, 5:12-14. [ Links ]
Rosenholtz I 1984. Tackling a Ticklish Type of Tic-Tac-Toe (Or the Case of the [Almost] Total Tactics) II. Journal or Recreational Mathematics, 17:81-90. [ Links ]
Rosenholtz I 1993. Solving Some Variations on a Variant of Tic-Tac-Toe Using Invariant Subsets. Journal of Recreational Mathematics, 25:128-135. [ Links ]
Rubin SJ 1981. The Longest Game. Journal of Recreational Mathematics, 14:241-245. [ Links ]
Schram JM 1986. Boolean Tic-Tac-Toe. Journal of Recreational Mathematics, 18:118-124. [ Links ]
Sobel MA & Maletsky EM 1975. Teaching Mathematics: A Sourcebook of Aids,Activities, and Strategies. Englewood Cliffs, NJ: Prentice-Hall Inc. [ Links ]
South African Sports Commission (SASC) 2001. South African Indigenous Games. A Report on Indigenous Games in South Africa. [ Links ]
Topin K & Tippins D 1993. Constructivism as a referent for teaching and learning. In: KG Tobin (ed.). The practice of constructivism in education. Available at books.google.co.za/books. Accessed 4 February 2008. [ Links ]
Van der Stoep F & Louw WJ 1981. Inleiding tot Didaktiese Pedagogiek. Pretoria: Academica. [ Links ]
Vithal R 1992. Use of games in teaching mathematics. In: M Moodley, RA Njisane & NC Presmeg (eds). Mathematics education for in-service and pre-service teachers. Pietermaritzburg: Shuter & Shooter. [ Links ]
Warren MD 1996. Indigenous Knowledge in Education. Proceedings of a Regional Workshop on Integration of Indigenous Knowledge into Nigerian Education Curriculum. University of Ibadan. [ Links ]
Williford H 1992. Games for Developing Mathematical Strategy. Mathematics Teacher, 85:96-98. [ Links ]














