Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Education
On-line version ISSN 2076-3433
Print version ISSN 0256-0100
S. Afr. j. educ. vol.28 n.4 Pretoria Nov. 2008
CONTENTS
Conceptions on modelling processes in Italian high-school prospective mathematics and physics teachers
Claudio FazioI; Filippo SpagnoloII
IAssistant Professor of physics education in the Faculty of Education at Palermo University, Italy. His research interests focus on the pedagogical use of the new technologies of information and communication and the re-direction of pupils' cognitive resources to improve understanding of physics at all schooling levels
IIAssociate Professor of mathematics education in the Faculty of Education at Palermo University, Italy. His research interests focus on (a) the multicultural approach in mathematics education with contributions from history of mathematics, Epistemology, Natural Language, Semiotic approach in mathematics, and mathematics communication; and (b) statistical instruments of research in mathematics education. E-mail: spagnolo@math.unipa.it
ABSTRACT
We present a study on the conceptions of Italian prospective mathematics and physics teachers with respect to modelling activities. Common ground for both the mathematician and the physicist, these activities are a relevant aspect of the Graduate School for Mathematics and Physics Teacher Education curriculum at University of Palermo, Italy. The answers to a questionnaire on the processes of modelling are analysed, according to an a-priori analysis built by taking into account a general scheme of reference on the philosophy of mathematics and physics. The study was performed by using methods of quantitative data analysis: factorial analysis of the correspondences and Gras implicative analysis. The results showed that prospective teachers appear to use mostly a constructivist approach in the modelling processes.
Introduction
Modelling activities are very common both in mathematics and in physics and they also represent a popular subject in the teaching of these disciplines. One of the goals of education in scientific disciplines is, at every schooling level, to lead pupils to build models or, in other words, representations that can describe and explain real world phenomena. By means of models it is possible to obtain predictions about experimental trends, mechanisms and processes. The construction of models can be a very formative pedagogical activity (Andaloro et al., 1991; Berry et al., 1986). In fact, it allows students to see analogies and differences between many apparently different phenomena and may help them to better understand the unitary way science approaches real world problems.
It is easy to find in mathematics and physics education research literature different definitions of the process of model construction (Gilbert et al., 1998). We understand "modelling" of a phenomenon as the process by which one can,
1. identify the variables which can be relevant in the description of the phenomenon itself;
2. give a verbal and schematic description of the phenomenon;
3. determine the existing relationships between the variables; and
4. express such relationships through equations and/or rules that give the model a predictive value (Gilbert et al., 1998).
In a pedagogical approach to modelling a phenomenon, the habit of following the previously stated steps can lead to a more complete understanding of the phenomenon. It can be definitely considered an improvement with respect to the traditional school approach to the study of physics, that usually starts from the analysis of already well-formalised situations and simply involves pupils in discussing or solving equations and adapting a mathematical function to experimental data, when they are available.
It is important to note that the above indicated four steps do not necessarily have to be developed all together for every schooling level. They indicate the complete logical sequence that a mature student should perform in order to learn to correctly model an observed phenomenon. The experienced teacher will opportunely select and measure their treatment, adapting it to her/his pupils' age, to her/his own pedagogical goals, and to the level at which she/he wants to go deeper into the modelling idea.
In this article, we discuss a research study carried out with respect to the conceptions of future mathematics and physics teachers on modelling activities. Such activities are a common ground for both the mathematician and the physicist and they are a relevant aspect of the curriculum of the Mathematics and Physics section of the Graduate School for Secondary School Teacher Education (SSIS) at the University of Palermo. An aspect to take into consideration is the fact that the courses of SSIS are usually attended by mathematicians, physicists, and engineers. They have had a previous education in specific technical/scientific subjects at their university graduate courses (four years for mathematics and physics and five years for engineering). The SSIS courses consist of very intense theoretical preparation with respect to general pedagogy and psychology and also include theoretical and laboratory activity with respect to the teaching of mathematics and physics in upper secondary schools (high schools). Moreover, a relevant part of the curriculum is devoted to apprenticeship activities to be performed in real school classes, under the supervision of experienced school teachers.
The main work hypothesis is that mathematics and physics prospective teachers implicitly have their own philosophy with respect to construction of knowledge and to understanding the reality, which then becomes explicit in actual modelling processes. This "implicit philosophy" turns out to be the result of their past experience as students and of other implicit behaviours of their past teachers. Experiences of scientific literature reading and other cultural references, coming from parents and relatives and from the social context in which they live and work, can also play a relevant role.
Philosophy of mathematics and philosophy of physics: a reference framework
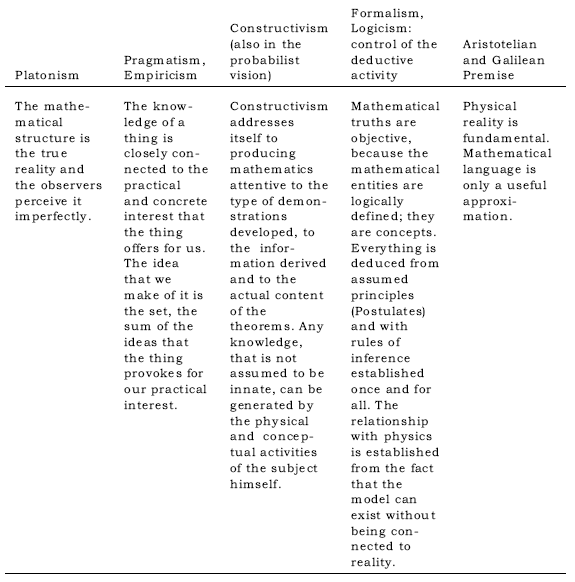
In literature it is possible to find many references on different philosophical approaches more or less explicitly linked to mathematics and physics and to their teaching. In Appendix 1 a description of some of these approaches is presented. In our research, we concentrated only on some of them, mainly because many philosophical approaches are not easily or commonly identifiable in future teacher behaviours. They are summarised in Table 1.
Sample and methodology
The research sample was chosen by looking at students enrolled at the mathematics and physics section of SSIS, at the University of Palermo, during the academic year 2002/2003. The number of students enrolled for their first year was 58; they were mainly graduates in mathematics and engineering, with only a few with a physics discipline degree. The two-year SSIS course included:
a. Head-on lessons on pedagogy, epistemology, pedagogy, psychology and anthropology;
b. widening head-on lessons on mathematics and physics subjects, from both a theoretical and an experimental point of view;
c. disciplinary pedagogical laboratories for both mathematics and physics (pedagogical laboratory of algebra, pedagogical laboratory of calculus, pedagogical laboratory of thermodynamics, etc.);
d. apprenticeship activities in high school real classes, under the supervision of experienced teachers.
At the beginning of the course, a questionnaire on the processes of modelling was administered and the answers were analysed without considering the differences in the students' cultural origin.
The questionnaire and its a-priori analysis
In this section we report on the six open-answer questions of the questionnaire, and the related a-priori analysis1 (Brousseau, 1997).
1. Are the models creations of human thought or do they already exist in nature?
A1 They are creations of human thought. They are idealisations of events that happen in nature.
A2 They are creations of human thought. They are used to outline phenomena in nature and they are only approximations of them.
A3 They are creations of human thought. Their creation comes from the continuous interaction with the 'real' external world.
A4 They are creations of human thought. They formalise the 'natural models'.
A6 They are creations of human thought.
A7 Some of them exist in nature and others are creations of human thought.2. Do the physical models play an explanatory and/or predictive role of the phenomena?
B1 Building, understanding and explaining how the various phenomena operate.
B2 They have both roles.
B3 The model represents the reality. When formalised, it can give new information about nature.
B4 They have both roles, but are understood better within a theory (formal laws).
B6 They explain phenomena.
B7 They foresee phenomena.3. Do the models serve to obtain information about nature?
C1 Understanding and explaining how the phenomena happen and operate.
C2 Yes.
C3 Yes, if theorised it can lead to new information about nature.
C4 Yes, if theorised it can lead to new information about nature and it can be used to make some predictions.
C5 Yes, but they do not completely exhaust the scientific research.
C6 Yes, it checks the evolution and the development of a well known phenomenon.
C7 No, they are only representations of natural phenomena.
C8 Not always.4. Are the terms model and theory synonymous?
D1 No
D2 No, because the model is a representation of a phenomenon and on this a theory is built.
D3 The model can be useful for explaining a theory.
D4 No, the theory includes the models.
D5 No, but they are dialectically connected.
D6 No, they are connectible but not synonymous.
D7 Yes.
D8 The model can be useful for building a theory.
D9 No, the model is the tool that makes a theory explicit.5. Are all models in physics representations of real things, existing objects structures or processes in nature? Give some examples and reasons for them.
E1 Yes. For example: kinetic theory of gases, atomic model, harmonic oscillator with/without friction, heat. … .
E2 Not always. For example: some electrical and magnetic phenomena, heat, …
E3 Yes, they are representations in continuous evolution for a better adaptation to the observed phenomena.
E4 No, because the model is always an abstraction.
E5 Yes, the model is a representation of how "things could be" for explaining a series of observed phenomena.
E6 Yes.6. What can be the usefulness of formalising a theory?
G1 It must allow a process of explanation, but above all it has to allow the prediction of a series of phenomena. To the 'Theory' concept is associated the idea of predicting what can happen.
G2 It must be able to describe the observed phenomena, generalising them into typical cases.
G4 Mathematical formalisation always allows explaining and predicting.
G5 Mathematical formalisation supplies the operative tools to allow the quantitative application of the theory.
G6 It allows communication and sharing of results. It represents a reference point for everyone.
Data analysis
Every experimental research project requires the researcher to collect some data that can be considered formed of a collection of elementary information. In the specific field of pedagogical research, each piece of elementary information reports, in general, a behaviour of a pupil in a situation. A statistical analysis of data will, therefore, take into account a set composed of: student, situation, and behaviours.
Let us consider that the student belongs to an observed sample E, assumed to be extracted from a larger population, either by chance or following a system of control situations (e.g. scholastic level, gender, previous personal knowledge). The situation is chosen in a set S (e.g. of questions, exercises) generated and structured by conditions and parameters of varying nature (e.g. the knowledge in play, material conditions, didactic conditions). The behaviours (typical of knowledge or of aimed knowledge) are taken in a set C of the student's possible responses in the conditions in which he is placed.
A class can be defined as a set of students E, a Mathematics/Physics course as a set of exercises S, the results of the students as a certain application of E in the set S × C, where C is the set of the behaviours of success or error, a note as an application of S × C in R.
Knowledge of a certain behaviour can be represented by a certain application of a set of questions in a set of behaviours.
With respect to historical and epistemological analysis, we have attempted to identify the groups of variables (behaviours of the pupils in a table of contingency) highlighted in the a-priori analysis. This made us able to identify a table (Table 2) of a-priori contingency that gave us the possibility to analyse the experimental data in an appropriate way.

We called these groups 'supplementary variables'. They represent different cognitive styles and they allow better analysis of the experimental data. The introduction of supplemental variables as ideal individuals has been used in many research papers of the GRIM (see, for example, Spagnolo, 1998; 2006; 2008). The results of these research projects allow us to validate this method both experimentally and theoretically. In this context, due to the high number of variables in play, such an investigative method allows better highlighting of the fundamental characteristics of the a-priori analysis.
Let us clarify the conceptions further:
1. Platonism:
a. Models are creations of human thought. They formalise the 'natural models'.
b. Some exist in nature, others are creations of human thought.
c. Understanding and explaining how the phenomena operate.
d. Yes (the models serve to obtain information about nature).
e. Yes, if theorised they can lead us new information about nature.
f. Yes, if theorised they can lead us to new information about nature and to make predictions.
g. No, they are only representations of natural phenomena.2. Pragmatism, Empiricism:
a. Yes. For example: kinetic theory of gases, atomic model, harmonic oscillator with/without friction, heat ...
b. Mathematical formalisation supplies the operative tools to allow the quantitative application of the theory.
c. It allows communication and sharing of results. It represents a reference point for everyone.3. Constructivism (also in the probabilist vision):
a. Models are creations of human thought. Their creation comes from the continuous interaction with the 'real' external world.
b. Building, understanding and explaining how the various phenomena operate.
c. They have both roles.
d. They foresee phenomena.
e. Yes, if theorised they can lead us to new information about nature and to make predictions.
f. Yes, but they do not completely exhaust the scientific research.
g. Yes, it checks the evolution and the development of a well-known phenomenon.
h. No (the terms model and theory are not synonymous).
i. No, because the model is a representation of a phenomenon and on this a theory is built.
j. The model can be useful for building a theory.
k. Yes, models are representations in continuous evolution for a better adaptation to the observed phenomena.
l. It must allow a process of explanation, but above all it has to allow the prediction of a series of phenomena. To the 'Theory' concept is associated the idea of predicting what can happen.
m. Mathematical formalisation supplies the operative tools to allow the quantitative application of the theory.
n. It allows communication and sharing of results. It represents a reference point for everyone.4. Formalism, Logicism: control of the deductive activity
a. The model represents reality; when formalised, it can give new information about nature.
b. They have both roles, but are understood better within a theory (formal laws).
c. Yes, if theorised they can lead us to new information about nature.
d. Yes, if theorised they can lead us to new information about nature and to make predictions.
e. The model can be useful for explaining a theory.
f. No, the theory includes the models.
g. No, but they are dialectically connected.
h. No, they are connectible, but not synonymous.
i. Yes, (the terms model and theory are synonymous).
j. No, the model is the tool that makes a theory explicit.
k. Not always, example: some electrical and magnetic phenomena and/or heat.
l. No, because the model is always an abstraction.
m. It must be able to describe the observed phenomena, generalising them into typical cases.
n. Mathematical formalisation always allows explaining and predicting.5. Aristotelian and Galilean Premise:
a. Models are creations of human thought; they are idealisations of events that happen in nature.
b. They are creations of human thought. They are used to outline phenomena in nature. They are approximations of the natural phenomenon.
c. They are creations of human thought.
d. Some of them exist in nature and others are creations of human thought.
e. Building, understanding and explaining how the various phenomena operate.
f. They explain phenomena.
g. Yes. For example: kinetic theory of gases, atomic model, harmonic oscillator with/without friction, heat …
h. Yes, the model is a representation of how 'things could be' for explaining a series of observed phenomena.
i. Yes (the models in physics are representations of real things …)
Statistical analysis with respect to the variables in play
The analysis of the similarities, the implicative and the hierarchical implicative analysis do not give results that can be compared in a clear-cut way. Five profiles of pupils who follow the table of a-priori contingencies have been introduced as supplementary variables. These profiles correspond to:
1. Platonist;
2. Pragmatist, Empiricist;
3. Constructivist;
4. Formalist, Logicist;
5. With Aristotelian-Galilean premise.
Similarity analysis and factorial analysis with supplementary variables.
Non-parametric statistics uses small samples and utilises specific analysis methods and software. In this research we used two different non-parametric statistical data analysis methods: the method of similarities between variables and factorial analysis. These two methods classify variables and group them according to hierarchical levels (similarities) and to variables of variable (factorial analysis) and supplement each other.
Lermann's similarity index classifies variables according to hierarchical levels. It follows the Poisson law and it is defined as follows:
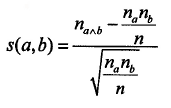
Where n a and n b are, respectively, the occurrences of A and B.
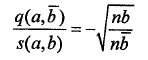
The Lermann's similarity index is related to the implication index 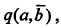 by the following formula:
by the following formula:
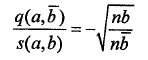
Data were analysed by using C.H.I.C.2 (Classification Hiérarchique Implicative et Cohésitive) software. The analysis of data with supplementary variables was done on the transposed matrix. Therefore, the number of variables, in the transposed matrix, is 58 plus 5. The matrix that we took into account is of the following form:

So, when taking into account the transposed matrix, it has the form:

The similarity graph, resulting from C.H.I.C. analysis, is reported in Figure 1.
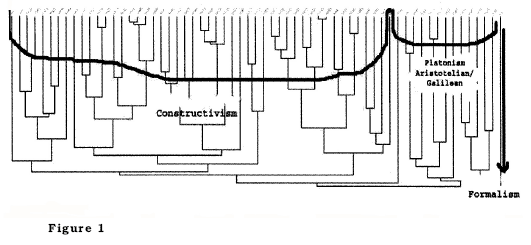
From this graph it can be seen that the similarity analysis classifies student groups with respect to the three supplementary variables 'Constructivism', 'Platonism Aristotelian/Galilean' , 'Formalism'. The closer the variables are with respect to the highest level, the stronger the similarity is, but the splitting between the three groups appears to be clear. The Formalist profile remains isolated, while the Platonist with the Aristotelian-Galilean form a significant group. The majority of students appears to be Constructivist, even if at a lower level of significance.
Factorial analysis of the correspondences
Data were also analysed with the SPSS 10.03 software. In using this software, we used only two factors4 as the information possible to obtain is still sufficient, while obtaining a significant simplification of analysis.
The resulting variance spread is 27.45. This value can be considered significant, due to the high number of variables in the transposed matrix (students plus supplementary variables). The rotated components graph, reporting results of the performed factorial analysis, is shown in Figure 2.
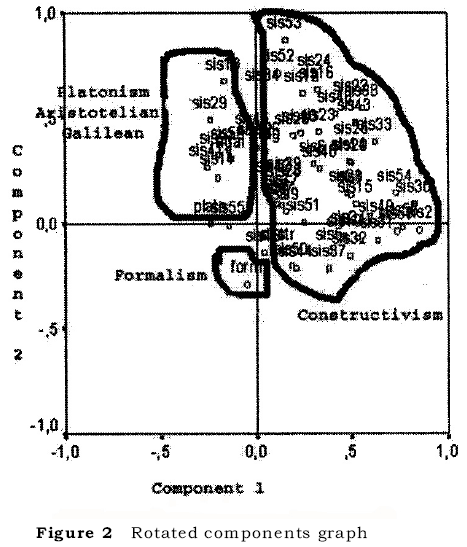
From the factorial analysis we can make a final consideration. One rather evident result is that there are two large groups of pupils with respect to the vertical factor. The bigger group is composed by 'Constructivist', while the other one is composed by 'Aristotelian-Galilean' and 'Platonist'.
This allows us to conclude that a relevant number of future mathematics and physics teachers appear to adopt constructivist reasoning schemes, but other reasoning schemes appear to be present too.
Conclusions
In this article, we have reported a research study regarding the conceptions on modelling activities of future upper secondary school mathematics and physics teachers. The research sample was composed of prospective teachers attending the mathematics and physics section of the Graduate School for Secondary School Teacher Education (SSIS) at University of Palermo, Italy. In analysing the data, we used two different quantitative analysis methods, obtaining very similar results.
From our data the 'constructivist' conception seems to be the most common in our sample. This confirms our main work hypothesis: we can suppose that previous experience as a student of the secondary schools and subsequent university instruction can have induced some, maybe unconscious, disposition toward Constructivism in prospective teachers.
This is apparently a common trend in future teacher conceptions about modelling in several industrialised countries. The 20th century tendencies with respect to scientific education have still be studied in their entirety, but we think that experimental considerations of this type can supply useful indications for deeper theoretical-experimental knowledge about epistemology, history of science, and the conceptions of future teachers with respect to the discipline they are going to teach.
Notes
1. Given a situation/problem, one defines a-priori analysis of a given situation/problem the set of the: a) epistemological representations; b) historical-epistemological representations; c) possible behaviours.
a. By 'epistemological representations' we understand the representations of the possible cognitive paths with respect to a particular concept. Such representations can be prepared by a student or by a scientific community in a particular historic period.
b. By 'historical-epistemological representations' we understand the representations of the cognitive paths (syntactic, semantic, pragmatic) with respect to a particular concept.
c. By 'possible behaviours' of the pupil when confronting the situation/problem, we mean all the possible solution strategies both correct and not. Amongst the incorrect strategies, those that can devolve into correct strategies will be taken into consideration.
The study of the epistemological and historical-epistemological representations is a priori an element of diversification with respect to the paradigm of the theory of situations. This study allows us a more exact analysis of the possible behaviours also in relation to the erroneous strategies on the part of the pupils.
2. Information regarding the software can be found at the following site of the A.R.D.M. (Association de Recherche en Didactique des Mathématiques): http://www.ardm.asso.fr/CHIC.html
3. Widely used professional statistical software.
4. Factors represent the meaning given to experimental variables that are near to x and y axes. They help to discriminate between the remaining variable groups.
References
Andaloro G, Donzelli V & Sperandeo-Mineo RM 1991. "Modelling in Physics Teaching: the Role of Computers Simulation". International Journal of Science Education, 13, 243-254. [ Links ]
Berry JS, Burghes DN, Huntley ID, James DJG & Moscardini AO (eds). 1986. "Mathematical Modelling. Methodology, Models and Micros". New York: John Wiley & Sons. [ Links ]
Brousseau G 1997. Theory of Didactical situations in mathematics. 1970-1990. English traduction: Cooper M, Balacheff N, Sutherland R & Warfield V. Kluwer Academic Publishers. [ Links ]
Changeux JP & Connes A 1989. Matière à pensée, Editions Odile Jacob, Paris. (Pensiero e Materia, Bollati Boringhieri Editore). [ Links ]
Dalla Chiara Scabia ML 1968. Modelli sintattici e semantici delle teorie elementari. Milano: Feltrinelli. [ Links ]
Dedekind R 1963. Essays on the Theory of Numbers, "Continuity and Irrational Numbers". New York: Dover. [ Links ]
Enriques F 1984. Problemi della scienza. Bologna: Zanichelli. [ Links ]
Frege G 2007. The Foundations of Arithmetic: A Logical-Mathematical Investigation into the Concept of Number. Translation and Introduction With Critical Commentary by Dale Jacquette (Die Grundlagen der Arithmetik: eine logisch mathematische Untersuchungen über den Begriff der Zahl, 1884. New York: Longman. [ Links ]
Gilbert JK, Boulter C & Rutherford M 1998. "Models in explanations: part 1, horses for courses?". International Journal of Science Education, 20, 83-97. [ Links ]
Gras R 2000. Les fondements de l'analyse implicative statistique. Quaderni di Ricerca in Didattica, Palermo. Available at http://dipmat.math.unipa.it/~grim/quaderno9.htm [ Links ]
Gras R, Diday E, Kuntz P & Couturier R 2001. Variables sur intervalles et variables-intervalles en analyse implicative. Actes du 8ème Congrès de la Société Francophone de Classification de Pointe à Pitre, 166-173. [ Links ]
Gras R, Couturier R, Guillet F, Spagnolo F 2005. Extraction de règles en incertain par la méthode statistique implicative. Comptes rendus des 12èmes Rencontres de la Société Francophone de Classification, Montréal, 30 May - 1 June, UQAM, 148-151. [ Links ]
Gras R, Suzuki E, Guillet F & Spagnolo F (eds) 2008. Statistical Implicative Analysis: theory and applications. Springer. [ Links ]
Lakatos I 1976. Proofs and Refutations. Cambridge: Cambridge University Press. (Lakatos I. Dimostrazioni e Confutazioni, Feltrinelli, Milano, 1979). [ Links ]
Le Lionnais F 1948. Les Grandes courantes de la pensée mathématique. , Paris: Cahiers du Sud. [ Links ]
Lerman IC 1981. Classification et analyse ordinale des données. Paris: Dunod. [ Links ]
Lerman IC, Gras R & Rostam H 1981. Elaboration et évaluation d'un indice d'implication pour des données binaires. I et II, Mathématiques et Sciences Humaines, 74:5-35; 75:5-47. [ Links ]
Lolli G 2002. Filosofia della matematica. Bologna: Il Mulino. [ Links ]
Mangione C 1993. Storia della Logica, da Boole ai nostri giorni. Garzanti, Italy. [ Links ]
Maturana HR & Varela FJ 1980. Autopoiesis and Cognition. The Realization of the Living. (Autopoiesi e cognizione. La realizzazione del vivente. Venezia, Marsilio, 1985). [ Links ]
Popper KR 1934. The Logic of Scientific Discovery. London: Routledge. (Logica della scoperta scientifica. Torino: Einaudi, 1970). [ Links ]
Popper KR 1969. Conjectures and Refutations: The Growth of Scientific Knowledge. London: Routledge. (Congetture e confutazioni. Bologna: Il Mulino, 1972). [ Links ]
Putnam H 1967. Mathematics without Foundations. Journal of Philosophy, 64. [ Links ]
Quine WVO 1959. Methods of logic. New York: Henry Holt and Co. [ Links ]
Spagnolo F 1998. Insegnare le matematiche nella scuola secondaria. Firenze: La Nuova Italia. [ Links ]
Spagnolo F & Toscano E 2002. Un percorso interpretativo della Logica del '900. Quaderni di Ricerca in Didattica, 11. Available at http://math.unipa.it/~grim/quaderno11.htm [ Links ]
Spagnolo F, Bagni G & Furinghetti F 2004. History and epistemology in mathematics education. Italian Research and Teacher Training in Mathematics Education in Italy 2000-2003. Presented to ICMI-10, Copenhagen, UMI-CIIM. Milano: Ghisetti & Corvi. [ Links ]
Spagnolo F & Gras R 2004. Fuzzy implication through statistic implication: a new approach in Zadeh's framework. 23rd International Conference of the North American Fuzzy Information Processing Society, NAFIPS (IEEE), Vol I. Banff, Canada. Scott Dick-Lukasz, Kurgan-Petr, Musilek-Witold, Pedrycz-Mark Reformat (eds). [ Links ]
Spagnolo F 2005. L'Analisi Statistica Implicativa: uno dei metodi di analisi dei dati nella ricerca in didattica delle Matematiche. Troisième Rencontre Internazionale A.S.I. (Analyse Statistique Implicative). Supplement 2-15, "Quaderni di Ricerca in Didattica". Available at http://math.unipa.it/~grim/asi/suppl-quad_15_2.htm. [ Links ]
Spagnolo F 2006. 'La modélisation dans la recherche en didactiques des mathématiques: les obstacles épistémologiques'. Recherches en Didactiques des Mathématiques, 26:337-379. [ Links ]
Tarski A 1965. Introduction to logic and to the methodology of deductive science. London: Oxford University Press. (Introduzione alla Logica. Milano, Italia: Bompiani, 1969). [ Links ]
Wang H 1974. From Mathematics to Philosophy. London: Routledge & Kegan Paul. [ Links ]
Appendix 1
In this appendix, we take into account some approaches to the philosophy of mathematics and physics, without certainly claiming to completely describe the philosophical analysis of the two disciplines. Here we will refer to some exemplifications of each philosophical framework, referring to the specialised literature for possible wider investigations.
Nominalists
They negate the existence of abstract elements of mathematics, but also those of other contexts. They accept finite sets. They reject the infinite as an analysable and changeable object. Classical analysis is not essential for physics, but only useful. In mathematical practice, nominalist reconstruction utilises constructive methods (algorithms for example). Amongst the nominalists one can encounter both constructivists and formalists (Wang, 1984).
Formalists
They hold a nominalist position but they are nominalists who don't draw on mathematics. For example: Robinson and non-standard analysis, Hilbert and the deductive hypothetical system without any relationship to real objects. (Wang, 1984).
Constructivists
They are also nominalists, above all in the re-construction phases.
Theory of knowledge and cybernetic constructivism
The concept of self-regulation had its origin in the attempts to construct mechanical devices ('servomechanisms') able to substitute human activity which had the aim of controlling a specific aspect of a given situation and controlling it, or governing it, as would a human agent. The refrigerator thermostat is perhaps the most notable example. A specific temperature limit is set and, if everything works (including the cooling system), the thermostat then makes sure that, in the controlled environment, the temperature does not exceed the indicated value. It isn't, however, the thermostat that chooses the aspect to control nor the value to maintain. This choice comes from an external agent. This fact, obvious and almost insignificant in the engineering environment, assumed central importance when applying cybernetic concepts to the field of cognition was attempted. Actually, it led to a distinction between that which, in retrospect was defined as "first cybernetics" and that which was then defined as 'cybernetics of the second order'. Meanwhile, some psychologists and neurophysiologists, appropriating some of the concepts of cybernetic technique, began explaining certain behaviours of living organisms in terms of servomechanisms and homeostasis (always maintaining absolute separation between the scientist-observer and the object observed, the object to explain. Others posed for themselves as a problem their own perceiving, observing and thinking. Thus, one passed from the study of the systems observed to the study of the observers.
If one is convinced that a living organism can be distinguished from mechanical devices by the ability to choose, at least within certain limits, the aspects to be conceived (because also perception presupposes the existence of concepts) and to keep them more or less in balance amongst themselves, then one very quickly realises that what is called 'Knowing' is something something the organism cannot find prefabricated. One realises that 'Knowledge' cannot be a 'representation' of the external world made up of little pieces or 'information' taken away of the 'real' world, but must be an internal construction made with internal material. Starting from neurophysiologic research in the field of visible perception of amphibians, Maturana & Varela (1985) reached the same conclusions. On the basis of a series of very refined experiments, they showed that what the observer categorises, for example, as 'the insect that gets eaten by a frog in one jump', is nothing for the frog but a combination of electrical impulses of whose origin the frog can know nothing.
A second factor brought to light by cybernetics regards communications. It isn't necessary to dwell on the mathematical theory of Shannon who for the first time supplied a useful and precise definition of the notion of information. It suffices to remember what the analysis of the communication process shows in a very clear way: it is the physical signals that, one can say, 'travel' from the sender to the receiver, not their meanings. Therefore, these signals, and this also stands for the words of natural language, do not transmit contents but instructions of choice, and this choice regards the repertoire of concepts and of conceptual structures that each of the communicants has built during his experience of social interaction. Cybernetics, therefore, with these two factors has supplied two important elements to the theory of knowledge.
In Psychology …
In 1936 Piaget published 'La construction du réel chez l'enfant' (The Construction of Reality in the Child). At first glance, despite the unsettling title and some argumentative sentences in the introduction, the text could seem nothing other than a chronicle of the conceptual development of Piaget's children during the first two years of their lives. Therefore, it does not surprise us that professional philosophers and others interested in the epistemology of adults have relegated this work to infantile psychology. Instead, the work is not only complex but profound; such that even today it constitutes a cornerstone of constructivism.
The complexity of the text derives from the fact that Piaget presents a model of construction of more than one concept: 'object', 'space', 'randomness' and 'time', and then suggests how the four elements are integrated to form the background of experience, that is, the external world. Given that it has to do with a composite model, the author must of course explain the construction of the parts, one after the other, although in the child their generation is simultaneous. In this way, it is up to the reader to consider the play of the interactions that is realised up to the end of the constructive process towards the age of two years. A notable effort and, seeing the inappropriate judgments that are heard from various parts, I have the impression that few readers have carried it through to the end.
Piaget introduces the term 'constructivism' as descriptive of his 'Genetic Epistemology'. In short, in cognitive psychology, constructivism begins just as soon as one realises that any knowledge, that is not assumed to be innate, can only be generated by the physical and conceptual activities of the subject himself. Setting aside the question of whether knowledge is or is not a representation of an independent reality, if one doesn't want to imagine a newborn child who has in his head everything he will know in his life, it is necessary to explain the way in which he knows. Such an explanation, however one looks at it, will have to highlight a process of construction. And, it is exactly the way in which the conceptual construction is analysed that generates a distinction between the contemporary versions of constructivism.
Setting aside the construction of conceptual structures, there is another indispensable idea for completing the concept of radical constructivism; an idea that comes from the Darwinian theory of evolution and was used independently by various scholars around the beginning of the last century. It has to do with the idea of negative selection; therefore, the elimination of that which is not necessary or does not work, so that everything that remains is "suitable" or, as I prefer to say, viable, that is, usable, practicable. It seems that William James was the first to suggest, in 1880, the use of this principal in epistemology.
In mathematics and physics …
Intuitionism of the 1900s, Constructivism is a way of doing mathematics and physics. There exist different types of constructivists: liberals, fundamentalists, etc. …
Constructivism addresses itself to producing mathematics/physics attentive to the type of demonstrations developed, to the information derived and to the actual content of the theorems. Every theorem must state something that can be done, not that exists. It generally uses weak logic. It accepts the potential infinite. It rejects classical mathematics (of the 1900s), the continuous set theory, the "pathological" functions, the management of the infinite carried out with Cantor's methodologies.
"Mathematics is a mix of the real and the ideal", the real part supplies the check, the ideal part allows simplifications and opens new possibilities. The balance must be reasonable and the pragmatic considerations must be the final guide. (Wang, 1985; Mangione, 1993).
Realists and Structuralists
Mathematics (theory of sets) is the study of an objective universe, the universe of sets; that which renders the mathematical structure semantically meaningful. In Greek mathematics: the distinction between geometry and land surveying.
Bourbakism and the architecture of mathematics:
1. The entities of which the mathematical theories speak exist;
2. The theories that have to do with them (in large measure) are true;
3. Their truth is independent of our knowledge and of our way of knowing them.
And finally:
1. The terms of the theory are either true or false;
2. That which makes them true or false is external (the semantic base of the concept of truth) (Tarski, 1965; Mangione, 1993). Quine: scientific realism. (Quine, 1969; Wang, 1985).
Pragmatists
They belong to a philosophical current that presents itself as a reaction to the intellectualism of the 1800s, taking on, in the face of the failure of reason in relation to metaphysical problems, practice as the criterion of evaluation. Pragmatism developed between the end of the 19th century and the first twenty years of the 20th, specifically in the American and Anglo-Saxon cultural area, but it had vast influence also on continental European thought and especially in Italy. The fundamental theses of pragmatism — as the term itself — were introduced by the American philosopher, CS Peirce, one of its greatest representatives. He attributed the gnoseological problem to a pragmatic behaviour that is the true font of every cognitive activity. For Peirce, the knowledge of a thing is closely connected to the practical and concrete interest that the thing offers for us and the idea that we make of it is the set, the sum of the ideas that the thing provokes for our practical interest.
This cognitive behaviour would be the only unique genuine way to gather the sense of things and objects, leaving aside all those theoretical and abstract formulations that such sense ends up losing. The main worry of the Peirce pragmatists, therefore, is the establishing of a theory of meaning.
Platonists
They champion Ontological Realism. The mathematical entities exist outside of us with the same character necessary for objective reality and we can then encounter, discover, study them …
Connes: 'I believe myself to be rather close to the realist point of view. For me the list of the prime numbers, just to give an example, has a more stable reality than the material reality that surrounds us. We can compare the work of a mathematician to that of an explorer exploring the world'. (Changeux & Connes, 1991).
Separation between mathematics and the physical world (Galileo and the scientific revolution). The mathematical structure is the true reality and the observers perceive it imperfectly.
Logicists
Mathematical truths are objective because the mathematical entities are logically defined; they are concepts. Maximum control of the deductive activity. (Dedekind, 1967; Frege, 2003).
Semiotics Interpreters
Mathematics can be classified semiotically: syntax, semantics, pragmatic. There exist, then, the operative tools of semiotics; icon, indicator, symbol, metaphors, etc. ...
Deductivists
Mathematics is the set of assertions: 'If … then …' that are logically valid. Logic of the first order. Its role is only deductive. Formalisation is not requested. Weak logic is used. (Enriques, 1984).
Fallibilists
Conjectures and Confutations (Lakatos, 1976; Popper, 1934).
Empiricists
Mathematical knowledge is like empirical knowledge (Putnam, 1967).
Aristotelians
There are three main interpretations of Aristoteliansim: Alexandrist, Averroist and Thomist.
a. The first comes from the ancient commentator on Aristotle, Alexander of Aphrodisias. Alexander maintained that in man the Intellect Potential is present, but that the Intellect Agent is the same supreme Cause (God) who, illuminating the intellect potential, makes knowledge possible. Being so, there is no place for an immortal soul, given that it should coincide with the Intellect Agent.
b. In the 11th century, Averroës commented on the works of Aristotle. Characteristic of his interpretation was the thesis according to which there existed an Intellect, unique for all men and separate from them. Thus, every possibility of speaking of the immortality of man collapsed, the only immortal being the unique Intellect.
Typical of this current was, then, the so-called doctrine of the 'double truth', which distinguished the truth accessible through the force of reason from that accessible only through faith.c. The third interpretation is the Thomistic one, which attempted a grand conciliation between Aristotelian thought and Christian doctrine.
In the Renaissance ...
In the age of the Renaissance all of these interpretations were posed again. Today, one tends to contest the validity of this outline, noting how reality is very complex and how there is not a single Aristotelian who can claim to be a follower of one of these tendencies on all points and how, on the individual problems, the various thinkers mutate ideas with great variety of combination.
As concerns the themes, we recall that, because of the structure of university teaching, the Aristotelians of the Renaissance period were overall involved with logical-gnoseological problems and with physics problems (the politics, the ethics and the poetry remained the heritage of the humanistic philologists).
With respect to the sources of knowing, the Aristotelians distinguish: (a) the authority of Aristotle, (b) reason applied to the facts, (c) direct experience. However, little by little they began to prefer the last one, to the point that scholars believe they can be defined (at least tendentially) as "empiricists".
All the concepts of Aristotelian physics were analytically discussed, but, on this ground, the general set up of the cosmology of the Stagirian, that distinguished the celestial world made up of incorruptible ethers from the terrestrial one constituted of corruptible elements, did not allow for notable progress, imposing this rigorous separation of astronomy from physics. Moreover, the theory of the four qualitatively determined elements and of the "forms" made the qualification of physics and the application of mathematics impossible.
Physical reality is fundamental. Mathematical language is only a useful approximation.














