Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
Koedoe
On-line version ISSN 2071-0771
Print version ISSN 0075-6458
Koedoe vol.53 n.2 Pretoria Jan. 2011
ESSAY
A framework for deriving and triggering thresholds for management intervention in uncertain, varying and time-lagged systems
Robert J. ScholesI; Judith M. KrugerII
INatural Resources and Environment, CSIR, Pretoria, South Africa
IISouth African National Parks, Skukuza, South Africa
ABSTRACT
Ecosystems are characterised by complexity: high connectivity, the presence of positive and negative feedback loops, non-linear, abrupt and sometimes irreversible changes, delays between cause and effects, and uncertainties in observations, understanding and prediction. 'Adaptive management' is the preferred approach for the rational management of such systems. Where the management objective is to allow natural feedbacks and adaptive processes to operate as much as possible - as it is in many areas set aside for biodiversity conservation - a key issue is defining the thresholds that will trigger management intervention. This paper outlines and illustrates a logical process for doing so, taking into account the characteristics of complex, continuously changing ecosystems and the reality of information that is partial and understanding that is always provisional. After identifying a key ecological process that is believed to have an element of irreversibility beyond a certain point, the process has several steps, (1) define an indicator of the system state, (2) set a limit of acceptable change and add a safety margin, (3) project the indicator forward using a model, including uncertainty, (4) note the time when the indicator might transgress the safety-buffered limit and (5) subtract ecosystem and management response times. If the resultant time is at hand, an action is indicated - if not, the action is to continue to monitor the situation and refine the observations and models.
CONSERVATION IMPLICATIONS: Ecosystems are characterized by abrupt and sometimes irreversible changes. The challenge that face conservationists and managers are to identify which of these changes are likely to be irreversible and at what levels this will occur. This paper describes a logical process that enable mangers to determine which ecological processes have levels of irreversibility and monitor their status at all times. Once these processes are nearing the levels that are undesirable management actions can be invoked to prevent this from happening.
Introduction
The formal and informal management philosophy that has guided ecosystem management in state-owned, protected areas in South Africa has evolved through various phases over the past century (Carruthers 1995). The approach adapted in the early years (up to the mid-1950s) has been characterised as 'command and control'. The first conservation officers were military men - decisive, action-orientated and used to being in charge. They assumed that the desired state was known, unchanging and achievable using the tools at hand. The desired state usually amounted to 'preservation': a perpetuation of the status quo or a return to some pre-existing, Eden-like ideal. The underlying world view was the notion that nature is intrinsically in balance, but perturbed by human activities. Therefore, self-regulation can be achieved by simply eliminating the human impacts, or, where this is impossible, by intervening to restore the balance.
This first generation of conservators was replaced by a generation of technocrats, many trained as biological scientists, and backed up by a powerful, but not very consultative state apparatus (mid-1950s to about 1990). They were increasingly able to implement 'grand schemes' such as fencing, water provision, game translocation, culling and fire control. Nevertheless, the ecological outcomes were often not what was anticipated or desired. These experiences, which were not unique to South Africa, eventually taught a degree of humility regarding both our state of relative ignorance towards ecosystem functioning and in relation to how ineffective our interventions can be (Holling & Meffe 1996).
The past three decades have seen a fundamental shift, worldwide, in the scientific perspective regarding ecosystem dynamics (a key paper in the African savanna context is Ellis and Swift 1988). It is now generally accepted that 'natural' ecosystems may be intrinsically variable due to their internal dynamics and as a result of the variability of external drivers, such as climate. Thus, although the ecosystem may have a theoretical point of balance or equilibrium, it is seldom actually at that point, and it is neither desirable nor possible in the long term to suppress the variability. It is now thought to be necessary for ecosystems to vary in time and space in order to maintain their diversity and resilience in light of future challenges (Folke et al. 2004). Furthermore, many ecosystems may exhibit more than one equilibrium state, with transitions between them that may be somewhat abrupt and irreversible, and that very often are unanticipated. Since both human and ecological systems are self-organising, the position of the threshold itself may change over time. Finally, the distinction between 'human' and 'natural' disturbances is often spurious. For instance, people have been important shapers of ecosystem structure and function in Africa for millennia and are internal to the system, rather than external forces impinging on it. These considerations, and a realisation of how expensive (and often unintentionally injurious) ongoing interventions on multiple fronts can be, have led to a much greater reluctance on the part of conservation managers to intervene in ecosystems.
Furthermore, the conservation authorities themselves, and interested parties outside the agencies, began to ask questions regarding what the desired state is, and who decides it. This trend started in the 1980s, and in South Africa, accelerated after 1994 as a broader and more participatory style of governance took root in many facets of South African society.
In this paper, we start from a position that there is probably no universally 'right' style of ecosystem management (although it is likely that there are some that are clearly 'wrong' in a given situation). There are circumstances in which one style is more likely to achieve the desired ends, at lower financial and ecological cost, than others. Command and control is a reasonable approach when the level of understanding and the capacity to effect change are both high. Where the understanding of how the system works is essentially no better than blind guesswork and the capacity to take directed action is very low, a non-interventionist stance (sometimes called a 'laissez faire' approach) is both theoretically defensible and practically unavoidable. In the case where understanding is high but the capacity or desire to intervene is low, 'watchful tolerance' might be a sensible philosophy.
South African National Parks (SANParks) are generally neither completely powerless nor completely ignorant. Furthermore, there is a societal and legislated expectation that the conservation authorities act to meet various explicit and implicit objectives, including the avoiding of ecosystem degradation and the prevention of species extinction. The park managers have demonstrated a capacity to influence certain ecosystem outcomes, even on a large scale, and are relatively well resourced to do so. After more than half a century of research, some things are relatively well understood, and at least reasonable hypotheses as to what might be going on can be posed on most topics. Under these circumstances, we argue that the most reasonable management philosophy is 'adaptive management' (Biggs & Rogers 2003). In this style of management, objectives are stated provisionally but explicitly - in other words, they are equivalent to 'hypotheses' in experimental research. Management actions are treated as experiments from which learning can take place, even if the outcome is not the expected one. This requires that the interventions are designed and implemented with enough scientific rigour for the outcomes to be attributed to causes. The interventions are undertaken on a scale and with an intensity that permits the consequences to be distinguished against the background noise of inherent variation. The actions are documented and the outcomes are monitored. It is an axiom of this style of management that the actions and, if necessary, the objectives are subject to change on the basis of evidence provided by the experiment itself, or because changing societal expectations require it.
Gregory, Ohlson and Arvai (2006) highlight four criteria that must be met for adaptive management to be valid; (1) it must be able to cope with the spatial and temporal scale of the issue, (2) it must deal explicitly with the uncertainty associated with observing and making predictions, (3) it must evaluate costs, benefits and risks and (4) it must have stakeholder support.
This is the context in which SANParks, starting in the Kruger National Park, began to define their management plan, based on the 'thresholds of potential concern' (TPC) (Biggs & Rogers 2003). The approach is summarised briefly as follows: a set of high-level goals is defined and then translated into more specific objectives. A threshold or thresholds are then set in relation to selected indicators of each objective. The thresholds are often expressed in the form of a traffic light analogy: an 'amber light' warns of an impending problem, and a 'red light' triggers an intervention. Initially the TPCs were determined by expert judgement, following a debate among specialists and a review of the evidence that was available. The TPCs have subsequently been refined and reviewed in several iterations. Problems have surfaced as the system has been implemented. For instance, the number of TPCs and indicators has proliferated, which makes the system burdensome and open to internal contradictions. Secondly, in the cases where TPCs have been transgressed, the reaction has most often been to simply redefine the acceptable level of change, rather than to embark on an expensive and far-reaching intervention. This underscores the often arbitrary nature of the 'thresholds' that have been set.
This paper suggests a conceptual framework for setting trigger points for management action, such as the SANParks TPCs, in time-varying ecosystems, taking into account uncertainty and the time lags inherent in both ecosystem processes and intervention actions.
A general approach to the problem
The approach outlined below is analogous to a control-theory problem (Brogan 1985), such as guiding a missile to a moving target or steering a vehicle down a twisty road. The control system consists of a sensor, which provides information (including a degree of error) about the position and motion of the object relative to the current location. This information is used to activate course adjustments, taking into account the time lag in the response of the system.
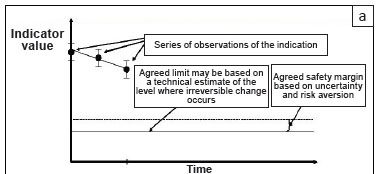
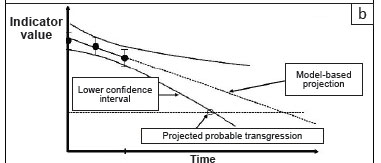
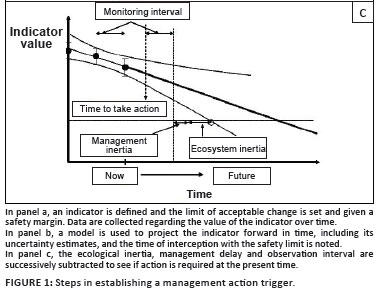
In this paper, we assume that the highest-level objective has been set, that is, there is clear guidance regarding what the area is managed for. In the missile analogy, the target has been selected. In our view, the top-level goal is not principally a technical decision, but a societal one. A 'political' process - in other words, a legitimate, values-driven consensus-based process - must be followed to decide on the desired state, taking into account the various tradeoffs, perceptions and power relations between the stakeholders. Once the overarching purpose has been agreed upon (accepting that this social consensus process is non-trivial and will always be provisional and dynamic), the following, more 'technical' (i.e. expert-based) analysis can follow. The way in which the approach is developed is illustrated in Figure 1 (panels [a] to [c]).
Define a sensitive, relevant and measurable indicator of the issue at hand
Although it typically is a system that is being managed, with many component parts, we need to settle on a single measure of system performance for tracking purposes, otherwise potentially contradictory signals will result. 'Indicator' is a term that also embraces proxy measures, but the preferred indicators are the ones most closely linked to the actual factor of concern. For instance, if soil loss is the issue, a direct measure of soil export in tonnes per hectare is unambiguous; an indirect observation such as the area of bare ground is less preferred, while an index such as a calculation based on the Universal Soil Loss Equation (USLE, see Risse et al. 1993) is only indirectly based on observations. If complex indices are chosen, then those with physical units and a clear and established underlying logic (such as USLE) are by far preferable to arbitrary combinations of indicators, such as averages of a number of variables that are thought to be related to the state of the system in some way.
Set a limit of acceptable change in the indicator
In this paper, we avoid calling the limit of acceptable change a 'threshold' in order to prevent it from becoming confused with the notion of a system threshold separating one state from another; in other words, a boundary in system state-space at which negative feedbacks are overwhelmed by positive feedbacks, and thus, when crossed, causes the system to accelerate into a new domain of attraction under its own dynamics. Many of the limits that are typically set for ecosystem management do not have this property of discontinuous change, but are simply agreed levels along a continuum, beyond which you do not wish to proceed, for whatever reason. Nonetheless, it is very helpful to the identification of limits if they are true system thresholds, since this introduces a much stronger element of causality and non-arbitrariness into the definition, which usually cuts out a lot of unproductive debate. Furthermore, we argue that these 'true' thresholds of relative irreversibility (very few things are truly irreversible, if you have enough time and money to fix them) are the ones that the managers of protected areas really need to worry about. Therefore, selecting system thresholds as the limits, even if they are relatively rare, has the advantageous effect of reducing the number of criteria that have to be monitored. (See Martin et al. [2009] for a discussion of the differences between ecological thresholds, utility thresholds and decision thresholds.) Here we are concerned with decision thresholds, but it is helpful if they are founded on ecological thresholds. Note that ecological thresholds are themselves dynamic, so the process of defining the limit needs to be revisited periodically.
Add a safety margin based on societal risk tolerance and technical certainty
It is very rare that ecologists know the position of a threshold or limit exactly. Neither is the present state of the system known with absolute precision. Faced with a situation of risk, most people prefer to stay well away from the edge - especially if they are not too sure where the edge lies. Our willingness to stay near to the limit depends on what is at stake. For instance, if a population were allowed to drop below some minimum viable level, would the result be a global extinction, or just a local extirpation? The level of risk taken also depends on the appetite for risk among the stakeholders. For example, people struggling to meet basic human needs are thought to be willing to take greater local environmental risks in meeting those needs than populations that are more comfortably off (Goklany 2001). The central point is that the magnitude of the safety margin is not simply a technical or statistical issue, but a decision that is taken within a particular ecological and social context. Figure 1(a) illustrates the steps so far.
Project the indicator into the future using a model, including an uncertainty range
Knowing that you have crossed a limit after the fact is not very helpful. It is much more useful to be able to predict well ahead of time that you are likely to cross the line, so that corrective action can be taken. Therefore, decisions should generally be made on the basis of some sort of predictive 'model'. Models can range in sophistication from a simple extension of a trend line to a complex, multi-variable, non-linear systems model. Expert judgement and experience are also 'models', but not very transparent ones. Any model, regardless of its sophistication, has uncertainty associated with it. For instance, the 95% confidence interval can be calculated for a linear trend, as is suggested in Figure 1(b). In the case of a complex systems model with many variables, each of which has some uncertainty, the joint uncertainty distribution is quite complex. This uncertainty is often approximated by running an ensemble of different models incorporating different assumptions, or else by running the same model but varying the key parameters in a statistically realistic way within their likely ranges ('Monte Carlo simulation', Vose 1996).
Note the time at which the relevant uncertainty limit intercepts the safety margin
The approach we describe aims to be conservative. Therefore the key point is not where the mean of the forward projections breaches the safety-buffered limit that you have set, but the earliest moment when there is a reasonable probability of such a limit being exceeded. Note that for 'upper limits' being approached from below, it is the higher uncertainty range that matters, whereas for 'lower limits' being approached from above it is the lower uncertainty range. What is 'reasonable' must be considered against the risk tolerance of the stakeholders, and it should be consistent with the implied risk tolerance used when setting the safety buffer, described above. In many cases, the default is the widely accepted scientific norm of the 95% confidence limit - in other words, there is a less than one in 20 chance that the safety margin will be breached earlier than the time projected.
Subtract the system response time
From the time when the limit is crossed by the lower 95th percentile confidence limit, we subtract a period that reflects the inertia in the ecosystem - in other words, the response time following an intervention. In our car analogy, think of it as how responsive the vehicle is to a touch on the steering wheel. If the car is fast and heavy, the turning circle will be large and the response sluggish, but if the car is light and agile, last-minute course corrections are possible. Ecosystem inertia can have many causes. One of the most common sources of ecosystem inertia is the longevity of the organisms involved. For example, if you try to alter the population dynamics of an elephant herd through contraception, you need to start a decade ahead of time, since that is more or less the period between birth and sexual maturity. If you are similarly intervening in an impala population, 2 years would be sufficient. Sources of ecosystem inertia that are short-lived (weeks) are probably virtually irrelevant in this context, as are exceedingly slow processes - for instance, land-forming processes that take millennia. The most critical issues for management lie inbetween - processes where you need to act years to decades before the threshold of non-return is reached if you wish to materially affect the outcome.
Multiple runs of the projection model, starting at progressively earlier times and simulating the appropriate corrective action in the model until a starting moment is reached, that does not result in the safety limit being transgressed, is a way of assessing the inertial delay. Bear in mind that the models are invariably imperfect - so an informed judgement based on a consideration of the key lags in the ecosystem may be nearly as good.
Subtract the management response time
It is not only the natural world that has delays built into it - the human side of the system does as well. For instance, you may need to wait until the next management meeting, or the next budgetary cycle, to commence an action. Or you may need to initiate a protracted stakeholder engagement process. While it is tempting to think that we have a bit more control over human delays than we have over the time lags in the ecosystem, experience teaches us that big decisions take time to implement. The uncertainties in the magnitude of the management response time underscore the futility of trying to be too precise in estimating the ecosystem response time, since the two numbers are added together.
Subtract the monitoring interval
A further time lag must be subtracted to allow for the fact that observations of the system take place only occasionally. Sometimes the period is very short - for instance, satellite-derived images of fire extent are obtained weekly. In other cases, the interval may be long: for example, full census data for large mammals in the Kruger National Park are only obtained once every 3 to 5 years because of the effort and expense of doing so. On average, you are only half a monitoring interval away from the next estimate, but in order to be conservative, this lag should be set as equal to the monitoring interval.
Is an action triggered?
Since the point at which we identified when the conservative limit of projected trend intercepts the safety-buffered threshold of concern we have been working in time units, backwards from that moment. The final steps in the procedure are illustrated in Figure 1(c). We first subtracted the ecosystem response time, then the management response time, then the monitoring interval. If the result is a date that is at or before the current date, then an intervention is triggered. If the result is after the current date, then, in theory, you can safely wait until the next monitoring date, assuming that reanalysis will occur at that time on the basis of the updated data. If the indicated trigger date is between the current date and the next monitoring date, it is appropriate to indicate an 'amber' (caution) light, which would set off various actions aimed at increasing your confidence or proactively decreasing the various delays in the system. For instance, you could shorten the monitoring period or intensify the monitoring effort for the key variable involved; you could commission research to improve the confidence in the projection model; you could take actions to reduce the delays in the decision cycle; or you could take actions to reduce the ecological lag - for instance, you could proactively administer immuno-contraception primers to reduce population response delays to contraception. Often you would undertake some combination of these actions.
The practical application of these steps is illustrated in a worked example below.
Example: Elephants and big trees in the Kruger National Park
The elephant population in what is now the Kruger National Park and surrounding private and state-owned wildlife areas had been reduced to close to zero at the beginning of the 20th century. Small groups of elephant began to wander into the region from Mozambique after the first reserves were established. By 1967, the elephant population had reached an estimated 6600 through a combination of in-migration and natural increase. At this time, on the basis of expert consideration of the elephant densities in a range of protected areas in Africa, it was decided to limit the number of elephants in Kruger Park to a total of 7000 (which corresponded to 'one per square mile', the threshold above which several experienced persons at the time considered unacceptable damage to the vegetation to occur). The Kruger Park elephant population was kept near this level through annual culling until 1994, when a moratorium on culling was imposed in response to pressure from animal rights advocates. Since then, the population has grown at a rate of approximately 6% per annum, and an intense debate is underway about what action to take (if any) in the future, and what the trigger points might be (Carruthers et al. 2008, and other chapters in Scholes & Mennell 2008).
We have chosen this example because it nicely illustrates several points made in the preceding section. Our analysis of the topic is solely for the purposes of illustrating the procedure we propose for setting action thresholds. It does not represent the policy of the South African government, SANParks or the authorities in the Kruger National Park. While the worked example is broadly grounded in observed data, in some respects it involves our informed judgement (as will be the case in almost any real-life situation). If a management trigger were to be set in practice for the elephant-tree system using an approach based on the one we describe, it would need to be based on a process somewhat more inclusive than the opinion of these two authors alone.
Choosing the indicator
The first thing that can be learned from the elephant-and-tree example is that taking an overly simple and purely technocratic view is likely to lead to implementation problems sooner or later. The culling moratorium was motivated partly by the arbitrariness of the 'one elephant per square mile' rule, the origin and validity of which was never properly researched or documented. As the Scientific Assessment of Elephant Management in South Africa (Scholes & Mennell 2008) points out, elephant population density per se is not the problem. Elephants are part of a system, which involves, at a minimum, elephants and the plants that they consume or damage. An even wider view would also consider indirect ecosystem effects (for instance, other species that are in competition with elephants for food, or are affected by the habitat changes elephants bring about). A yet wider view contextualises elephants within human society and the choices this society collectively makes regarding the desired appearance of landscapes and the relative importance of different species.
Therefore, the indicator variable on which the intervention trigger is set in this case should not be the size of the elephant population, but some variable that reflects our underlying concern for the effects the elephants have on the ecosystem. The issue that usually surfaces in consultation with a range of stakeholders in the context of the Kruger Park ecosystem is damage to trees (and, specifically, large and old trees) caused by elephants. This often has an aesthetic component - visitors have grown accustomed to seeing the Kruger Park landscape in a certain way, with scattered large trees and dense riparian forests, and do not wish to see a landscape consisting of bushy coppice and downed trees, regardless of whether the latter situation supports the same productivity or biodiversity. This is a legitimate stance, but raises difficult questions in terms of setting an operational limit - whose opinion counts in the poorly defined trade-off between the appearance of a landscape and the desire not to interfere with the lives of elephants? How much landscape transformation is acceptable, and to whom?
Setting a safety-buffered limit
Further unpacking of the 'large tree issue' reveals that a whole guild of species - the large raptors - are almost totally dependent on large trees for nesting opportunities. Since there is well-established literature on the importance of maintaining top predators and scavengers in functional ecosystems (e.g. Terborgh et al. 1999), conserving large raptors by providing nesting opportunities provides a somewhat more robust ecological basis for setting a limit. Large raptors and vultures occur relatively sparsely and, in some cases, are rare outside large protected areas such as the greater Kruger National Park. Some are arguably dependent for their regional population viability on having a core breeding population in the Kruger Park. The lower limit for a minimum viable population could therefore conceivably be reached if the breeding habitat was restricted. Population viability analysis (Shaffer 1990) could be applied to determining what the safe lower limit of breeding pairs might be. Since the birds nest in the crown of live trees, typically at a height of 12 m or more above the ground, this minimum population level can be translated into a number of nesting sites, and, in turn, into a minimum density of large trees. We do not intend to do this full analysis here, but simply assume that it works out at about one tree per square kilometre, including a generous safety margin. (In practice, because the decline in large trees accelerates as they become rarer, the exact value of the threshold hardly matters in setting the trigger. This is a very desirable property in an indicator.) This can be considered a 'threshold of irreversibility', since the regional or global extinction of some species could result if the large tree population falls below this threshold.
Projecting the dynamics forward
Reasonably reliable data exist to build simple models of both elephant population dynamics and tree demography. The two models can then be coupled to create a model of the elephant-tree system (for example, Duffy et al. 1999; Owen-Smith 2002). A simple implementation of such a model is applied here, again for illustrative purposes only. Because important time lags are introduced by both elephant maturation and the growth of large trees, the minimal model needs to include an age structure. Our discrete-timestep elephant model has annual cohorts of female elephants (the number of bulls is simply assumed to equal the number of females) that reach sexual maturity at age 12, and thereafter produce one calf every 2.5 years until death at age 60. The basic rate of mortality is 3% per year for all size classes, and increases as food becomes scarce. The values are chosen to reproduce the observed 6% per annum growth rate in the elephant population, as well as the extensive research on elephant population dynamics in the Kruger Park system (Van Aarde et al. 2008). No direct effect on population growth rate resulting from food shortage or other density-dependent phenomena has been observed at the densities experienced to date in the Kruger Park ecosystem, but there are data from elsewhere in southern Africa to suggest that the inter-calf interval extends when forage becomes scarce (Van Aarde et al. 2008) and, at some degree of forage inadequacy, mortality must occur. These effects should be included in the model if it is to be realistic when projected forward sufficiently to take into account the inertia of tree and elephant populations. Forage is produced by both trees and grasses, in an inverse relationship, and a portion of it (set nominally at half) is consumed by other species of herbivores.
The tree model is based on discrete size classes of stem diameter, in 5 cm increments up to a maximum diameter of 80 cm. All species are combined. There is a rough relationship between stem diameter (d, cm) and height (H, in m):
H = -0.011 d2 + 0.2162 d+1.336
derived from a database of several thousand stems measured in the Kruger National Park (Scholes, unpublished data). Trees taller than 12 m have a diameter at breast height of 80 cm or more on average. The same database was used to calculate the size-based mortality rates for trees. On average, the number of trees in each size class is 32.3% fewer than the number in the next smallest diameter class, for all classes with a diameter greater than 5 cm.
In order to allow the size-structured tree model to run on a common basis with the age-structured elephant model, it is necessary to know the stem diameter growth rate. Based on multi-year repeated measurements on savanna trees throughout South Africa (Shackleton 1998), the percentage annual growth rate in stem cross-sectional area (ΔA) is a function of both the diameter of the stem and the degree of competition to which it is exposed:
ΔA = (1.0 + 19.0 e-0.2d )*(1-B/Bmax)
where B is the basal area of woody plants (m2/ha) and Bmax is the maximum basal area that can be attained given the rainfall (converted from the data used by Sankaran et al. 2005 into basal area terms, Bmax= 0.03 [MAP-100]), which in this example is about 12 m2/ha for the average Kruger Park rainfall of 500 mm/year. Seed production was made proportional to stem cross-section, and began when the trees reached a third of their maximum height. A combined germination and survival rate for seedlings up to the 5-cm diameter class was estimated on the basis of the assumption that the tree population was initially in a steady state.
Coupling of the two models was achieved by assuming that elephants have two main impacts on trees. For trees larger than 15 cm in diameter but smaller than 40 cm, the stem is snapped or uprooted as a result of being pushed over by elephants in order to browse on the canopy foliage. For trees smaller than 15 cm in diameter, the canopy is entirely within reach and, although browsed, the main stem (if one exists) is not broken. Trees larger than the upper limit are harder to break or uproot, but are subject to debarking. The resulting mortality is complex, depending on the fraction of bark circumference lost and the presence of other agents, such as wood-boring insects and pathogens. We assumed that tree death occurred when the equivalent of a full circumference was debarked. In the absence of data, we assumed that each elephant strips 1 m of bark circumference per day, distributed over the size classes in proportion to their circumference. The fraction of a size class that dies per year (Fi) through this mechanism is thus:
Fmortality = [ni πdi /S(ni πdi )] [365 Σ/niπdi ]
where ni is the number of trees in size class i (km-1), πdi is the midpoint circumference of size class i, Σni πdi is the sum over all size classes of the stem circumferences, and E is the number of elephants (km-1).
Pushed-over trees do not die, but revert to the smallest size class as coppice resprouts. Female elephants push over an average of one tree a day and bulls, four times as many.
When is the limit likely to be transgressed?
Starting this model with the observed tree size distribution and the observed elephant age distribution for the Kruger Park shows the trajectories illustrated in Figure 2. Note that our model projects a slow decline in the number of large trees even in the absence of elephants, suggesting that the observed tree size distributions are not in a steady state. The ensemble results presented in the same figure are the year in which the threshold is crossed in a hundred independent model runs, when both a key 'tree' parameter (the mortality due to elephant damage) and a key elephant parameters (mortality and its dependence on density) were systematically and independently varied according to a normal distribution using the mean and standard deviation reported in the literature. More of the assumptions in the model could be tested in this way, but this scheme is sufficient to demonstrate the principle of creating an uncertainty range.
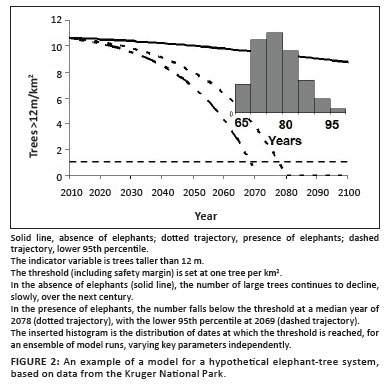
The lower 95th percentile of the predicted number of trees taller than 12 m intersects the chosen threshold of one tall tree per km2 at a time 60 years from the simulation start (which nominally represents year 2009). This is the starting date from which we begin the intervention calculation.
Subtracting the response times
In this example, we have assumed that the chosen management intervention is to reduce the fertility of elephant cows using immuno-suppressant contraception. A 75% success rate is assumed (Bertshinger et al. 2008). Running the model using just the 'best estimate' values for the parameters but reducing the fertility of the cows by this fraction results in the response trajectories illustrated in Figure 3, depending on when the intervention begins. By plotting the years of pre-emptive management against the extra years of non-transgression of the threshold thereby gained, we can deduce that the 'inertia' of the elephant-tree system as defined above is in the order of 30 years.
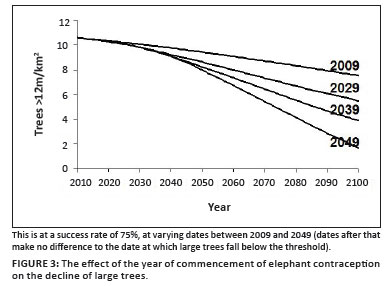
We further estimate that it would take about 3 years to launch a contraception programme of this magnitude, including making the decision, getting approval in terms of an elephant management plan approved by the minister concerned, consulting with stakeholders, manufacturing the vaccines, and conducting field operations to vaccinate all sexually mature elephant cows. Finally, we added a monitoring interval for the key elements in the system (trees taller than 12 m, and elephant population) of one year.
Is an action triggered?
The indicated time to trigger a decision regarding elephant contraception in order to prevent the limit of one tall tree per km2 being exceeded, thus, is the year in which more than 5% of the model runs indicate the limit being breeched (2069), minus the sum of the system response time (30 years), the management delay (3 years) and the monitoring interval (1 year). This suggests that a decision would need to have been made, at the latest, by 2035. We stress once again that this is a theoretical example only.
Discussion and conclusion
This paper has outlined a logical procedure for triggering management interventions in systems that are dynamic and prone to measurement error and theoretical uncertainty. The steps seem complicated, but we would argue that they are necessary and that the level of detail aimed for in any one of them needs to be matched to the uncertainty inherent in the full logical chain, which is determined by the data that are available or readily accessible. The effort involved should be guided by the consequences of getting the signal wrong, either as a result of initiating an action where no action was needed, or by failing to do so when intervention was necessary. The process we have described reveals where the key uncertainties lie and what can be done to address them. Finally, it is clear that several of the steps (selecting the overall objective, setting the level of risk aversion) are not purely technocratic, but require input from stakeholders in a legitimate fashion. On the other hand, there are elements (particularly the forward projection of system trajectories) that do require specialised technical input, and the quality of those technical inputs can be increased through investment in monitoring and research.
Acknowledgements
Two anonymous reviewers made useful comments that improved the paper.
References
Bertshinger, H., Delsink, A., Van Altena, J.J., Kirkpatrick, J., Killian, H., Ganswindt, A., et al., 2008, 'Reproductive control of elephant', in R.J. Scholes & K.G. Mennell (eds.), Elephant management: a scientific assessment for South Africa, pp. 257-327, Witwatersrand University Press, Johannesburg. [ Links ]
Biggs, H.C. & Rogers, K.H., 2003, 'An adaptive system to link science, monitoring and management in practice', in J.T. du Toit, K.H. Rogers & H.C. Biggs (eds.), The Kruger experience, pp. 59-80, Island Press, Washington DC. [ Links ]
Brogan, W.L., 1985, Modern control theory, Prentice-Hall, New York. [ Links ]
Carruthers, J., 1995, The Kruger National Park: A social and political history, University of Natal Press, Pietermaritzburg. [ Links ]
Carruthers, J., Boshoff, A., Slotow, R., Biggs, H.C., Avery, G. & Matthews, W., 2008, 'The elephant in South Africa: history and distribution', in R.J. Scholes & K.G. Mennell (eds.), Elephant management: a scientific assessment for South Africa, pp. 23-83, Witwatersrand University Press, Johannesburg. [ Links ]
Duffy, K.A., Page, B.R., Swart, J.H. & Baji, V., 1999, 'Realistic parameter assessment for a well known elephant-tree ecosystem model reveals that limit cycles are unlikely', Ecological Modelling 121, 115-125. doi:10.1016/S0304-3800(99)00091-5 [ Links ]
Ellis, J.E. & Swift, D.M., 1988, 'Stability of African pastoral ecosystems: alternate paradigms and implications for development', Journal of Range Management 41, 450-459. doi:10.2307/3899515 [ Links ]
Folke, C., Carpenter, S., Walker, B., Scheffer, M., Elmqvist, T., Gunderson, L., et al., 2004, 'Regime shifts, resilience and biodiversity in ecosystem management', Annual Review of Ecology and Systematics 35, 557-581. doi:10.1146/annurev.ecolsys.35.021103.105711 [ Links ]
Goklany, I.M., 2001, The Precautionary Principle: a critical appraisal of environmental risk, Cato Institute, Washington DC. [ Links ]
Gregory, R., Ohlson, D. & Arvai, J., 2006, 'Deconstructing adaptive management: criteria for application to environmental management', Ecological Applications 16, 2411-2425. doi:10.1890/1051-0761(2006)016[2411:DAMCFA]2.0.CO;2 [ Links ]
Holling, C.S. & Meffe, G.K., 1996, 'Command and control and the pathology of natural resource management', Conservation Biology 10, 328-337. doi:10.1046/j.1523-1739.1996.10020328.x [ Links ]
Martin, J., Runge, M.C., Nichols, J.D., Lubow, B.C. & Kendall, W.L., 2009, 'Structured decision making as a conceptual framework to identify thresholds for conservation and management', Ecological Applications 19(5), 1079-1090. doi:10.1890/08-0255.1, PMid:19688917 [ Links ]
Owen-Smith, N., 2002, 'Credible models for herbivore-vegetation systems: towards an ecology of equations', South African Journal of Science 98, 445-449. [ Links ]
Risse, L.M., Nearing, M.A., Laflen, J.M. & Nicks, A.D., 1993, 'Error estimation in the Universal Soil Loss Equation', Soil Science Society of America Journal 57, 825-833. doi:10.2136/sssaj1993.03615995005700030032x [ Links ]
Sankaran, M., Hanan, N.P., Scholes, R.J., Ratnam, D.J., Augustine, B.S. Cade, J., et al., 2005, 'Determinants of woody cover in African savannas', Nature 438(7069), 846-849. doi:10.1038/nature04070, PMid:16341012 [ Links ]
Shackleton, C.M., 1998, 'Annual production of harvestable deadwood in semi-arid savannas, South Africa', Forest Ecology and Management 112, 139-144. doi:10.1016/S0378-1127(98)00321-1 [ Links ]
Shaffer, M.L., 1990, 'Population viability analysis', Conservation Biology 4, 39-40. doi:10.1111/j.1523-1739.1990.tb00265.x [ Links ]
Scholes, R.J. & Mennell, K.G. (eds.), 2008, Elephant management: A scientific assessment for South Africa, Witwatersrand University Press, Johannesburg. [ Links ]
Terborgh, J., Estes, J., Paquet, P., Ralls, K., Boyd-Heger, D., Miller, B., et al., 1999, 'The role of top carnivores in regulating terrestrial ecosystems', Wild Earth 9, 42-56. [ Links ]
Van Aarde, R., Ferreira, S.M., Jackson, T.P., Page, B., De Beer, Y., Junker, J., et al., 2008, 'Population biology and ecology', in R.J Scholes & K.G. Mennell (eds.), Elephant Management: A scientific assessment for South Africa, pp. 84-l45, Wits University Press, Johannesburg. [ Links ]
Vose, D., 1996, Quantitative risk analysis: a guide to Monte Carlo simulation modelling, John Wiley & Sons, New York. [ Links ]
 Correspondence to:
Correspondence to:
Judith Kruger
Postal address: Private Bag X402
Skukuza 1350, South Africa
Email: Judith.kruger@sanparks.org
Received: 20 Jan. 2010
Accepted: 19 May 2010
Published: 13 May 2011
© 2011. The Authors. Licensee: OpenJournals Publishing. This work is licensed under the Creative Commons Attribution License.