RESEARCH ARTICLE

 

Students' ability to correctly apply differentiation rules to structurally different functions

 

 

Aneshkumar Maharaj; Mthobisi Ntuli

School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Durban, South Africa

Correspondence

 

 

---

ABSTRACT

The derivative concept is studied in first-year university mathematics. In this study, we focused on students' ability to correctly apply the rules for derivatives of functions with the different structures that they encounter in their university studies. This was done by investigating the online responses of first-year students at the University of KwaZulu-Natal to online quizzes that contributed to their assessment. Based on this investigation, we then interviewed eight students to gain an insight into the thinking behind their responses. We report on the analysis of students' responses to five items on the online quizzes based on the derivative concept. The categories in which those items were based are: condition for existence of derivative at a point; rules for derivatives of standard functions; application of chain rule to different function structures; the application of multiple rules; and application of derivatives to optimise a function. Our findings indicate that students had difficulty in detecting that multiple rules for derivatives were required to differentiate certain types of functions represented in symbolic form. Furthermore, students had difficulty in finding the derivative of a function when more than one application of the chain rule was required. However, there were students who had the ability to apply the rules for derivatives of functions without difficulty. In particular, most of the students were able to correctly recall the differentiation rules for functions with standard structures f(x)=xⁿ, h(x)=e^kx and y=[g(x)]ⁿ, n = 0 and k is a non-zero constant. Students were also able to correctly apply the chain rule to an exponential function with base e, raised to 4x. The majority of students were able to correctly apply the chain rule together with differentiation rules for logarithmic and exponential (with bases a >1) function structures, and function structures that required the application of the product rule together with the chain rule. Most of the students were able to apply derivatives to optimise a function.
Significance: A significant percentage of students who took online quizzes experienced difficulties with applying multiple differentiation rules in the context of a single function. The difficulties stemmed from their inability to detect from the structure of the function which rules should be applied and also the order in which those relevant rules should be applied

Keywords: calculus; derivatives; diagnostics; online quizzes; student difficulties

---

 

 

Introduction

One of the most important concepts in university mathematics is the concept of the derivative. In fact, it is one of the fundamental concepts of calculus. In the South African education system, this concept is introduced to learners during their high school studies in mathematics. According to Maharaj¹, first-year university students should already have the knowledge of the concept of the derivative of a function f(x) or f. They are exposed to the following two interpretations of the derivative f'(x) during their schooling years: (1) the gradient of the tangent to the curve f at any point (x, f(x)); and (2) the instantaneous rate of change of f with respect to x. While students are introduced to these concepts as early as Grade 12, many first-year university mathematics students have difficulty with the derivative concept.¹ Earlier studies by Orton² and Uygur et al.³ also found that the derivative is a difficult concept for many students. Maharaj¹ carried out a study which used the APOS (action-process-object schema) theoretical framework to investigate university students' understanding of derivatives and their applications in the context of multiple-choice items. A similar approach was used in this study, but the focus here is on students' ability to correctly apply the rules for finding derivatives of functions that they encounter at university level and the application of those rules to find the derivatives of such functions. According to Stewart⁴, rules of differentiation help us to calculate with relative ease the derivatives of polynomials, rational functions, algebraic functions, exponential and algorithmic functions, and trigonometric functions. If students have difficulty with these types of calculations, which are regarded as basic, then they are unlikely to correctly apply the concepts that are related to the derivative. Concepts related to the derivative are, for example, increasing or decreasing functions and the concavity of a function, over different intervals. For example, applying the first derivative test to a function M(x) will result in obtaining the increase and decrease intervals of the function where M(x) increases if M'(x)>0 and M(x) decreases if M'(x)<0. It is our opinion that the students' success in answering a question on the increase or decrease of a function given in symbolic form depends on their ability to interpret the structure of the given function M(x). For this reason we focused on students' ability to correctly apply the rules for differentiation to functions with different structures.

 

Research question

Are students able to correctly apply the rules for finding the derivatives of functions which have different structures? To help answer this question the following sub-questions were formulated: Which rule(s) can students apply with a high degree of success? To which function structures can they apply those rule(s) successfully? Which rule(s) gave the students difficulty? To which function structures did the students not apply the/those rule(s) successfully?

 

Literature review

A number of past studies^2,3,5-8 have focused on students' understanding of the derivative concept and how this understanding could be improved. Some of these studies indicated that the derivative is a difficult concept to understand for many students.^2,3 In particular, students experienced difficulty when applying the rules of derivatives to composite functions.⁵ The concept of derivatives forms an important topic of analysis at university level.⁷ Hence Maharaj⁸ focused on the development of diagnostic testing items for derivatives of functions. The paper by Maharaj⁸ was motivated by the need to help first-year mathematics students to improve their performance. That study formulated sample diagnostic questions that could be used to enable students to detect their strengths and or weaknesses. All the questions elaborated on in the results and discussion section of this paper were based on the sample diagnostics questions for calculus that were proposed in the paper by Maharaj⁸. Those sample questions were modified to true/false or multiple-choice questions (MCQs) that were suitable for an online format. For this paper, we analysed the responses of students to five of those modified questions.

Hähkiöniemi⁹ stated that exposing students to different kinds of representations can help improve students understanding of the derivative. Zandieh⁶ observed that graphical representation is preferred by students when it comes to tasks and explanations about derivatives. The focus in the present study was on the students' ability to correctly apply the rules for differentiation to differentiate functions with different symbolic structures. In this study, in comparison with previous studies in the literature, we assessed whether students were able to correctly detect from the different symbolic structures of functions the rules that were required to differentiate the functions and then apply those rules correctly.

Tall¹⁰ argues that there is a direct link between visualisation and symbolisation when teaching the derivative concept. In this study, we focused on the basic rules for derivatives of functions represented in symbolic form: for example, the basic forms xⁿ, e^kx, [g(x)]ⁿ; the derivative of [g(x)]ⁿ is n[g(x)]^n-1.g'(x). We further focused on the ability of students to identify the application of such basic rules in the context of particular functions that are also represented in symbolic form [for example f(x)=3e^4x + (5x-1)^e ]; identifying that (5x-1)^e is similar to the structure [g(x)]ⁿ which requires the application of the chain rule. The focus of the investigation was on the students' ability to correctly apply the rules for finding the derivatives of functions which have different structures. Before finding the derivative of a function represented in symbolic form one needs to study the structure of this symbolic form and then make a decision on the rule(s) for differentiation that need(s) to be used. Studying the structure of the function given in symbolic form involves visualisation in the sense that different aspects of the structure have to be seen and noted. For example, when finding the derivative of the function h(x)=(x²-x)(1-3x)¹⁰⁰ a student should first study the structure of the function and then decide which rules apply. This function appears as Question 3 in the results and discussion section. Note that the students should recognise from the structure that they need to apply the product rule and the chain rule. Application of the chain rule here is imbedded in the structures of the power rule; for example, in (x²-x) and (1-3x)¹⁰⁰. If the student visualises the structure of h(x), detects and notes these different aspects together with the rules for differentiation that are required to be applied, then he or she should arrive at the following:

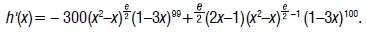
For students to be able to apply derivatives with a high degree of success, they need to understand the basics of derivatives; this includes unpacking the structure of functions represented in the symbolic form for which the derivatives are required. Rules for finding derivatives of functions help us to calculate with relative ease the derivatives of functions with different structures.⁴ It is our view that if students have a high level of understanding of the rules for finding derivatives which are represented in symbolic form, it could be easier for them to apply these rules with a high degree of success to functions of different structures and to concepts related to derivatives.

 

Conceptual framework

This study was guided by the literature review and the following principles:

1.There is a conceptual hierarchy in the body of mathematics.¹¹ This principle informed the formulation of the student expected learning outcomes and the development of sample diagnostic questions proposed by Maharaj¹¹.

2.Students' responses to the items on finding the derivatives of functions given in symbolic form give an insight into their understanding of the rules for derivatives and their applications to finding derivatives of such functions.

3.The quantitative data collected from the relevant online quizzes which focused on students' responses to finding the derivatives of functions represented in symbolic form would reveal trends that could be used to inform teaching with the aim of improving students' understanding of the rules for finding the derivatives of functions.

 

Methodology and participants

For the 'Introduction to Calculus' module at the University of KwaZulu-Natal, online diagnostics were set up based on the rationale and sample problems outlined in the paper by Maharaj⁸. The problems indicated there were transformed to the format of true/false statements or MCQs that were suitable for online quizzes. These quizzes were a subset of quizzes students were required to take online that contributed to the calculation of their class marks for the module.

A total of 293 first-year undergraduate students were registered for the Introduction to Calculus module at the University of KwaZulu-Natal in 2017. This module is compulsory for those wanting to pursue studies in mathematics. As part of the module assessment, students must undertake online quizzes which assess the material covered in class. The online quizzes were designed in such a way that students could do them anywhere and at anytime within the time frame set for each quiz by the module coordinator or lecturer. The University has numerous computer labs, some of which are open 24 hours a day, so the students had access to computers to take each quiz. Students could also access the quizzes using their own devices, even from outside university premises. The online quizzes were administered by the Moodle platform that was used at the University of KwaZulu-Natal.

The online system provided instantaneous feedback from which the students could determine their strengths and weaknesses when answering a particular question type. The system allowed a student a maximum of five attempts per MCQ but there were penalties for multiple attempts. Each question had a maximum of 2 marks. If a student submitted the correct answer on their first attempt, they were awarded 2 marks; however, only 1 mark was awarded for a correct answer on the second or third attempts. A correct answer on the fourth or fifth attempts scored zero. An incorrect answer on the fifth attempt also scored zero.

The rationale was that, after the students were exposed to formal lectures on a particular section, by taking these online quizzes they could determine their strengths and weaknesses on a topic before sitting for formal written tests. If weaknesses were determined, students were expected to take appropriate remedial actions, for example, revise a section or seek help from a hot seat tutor who was available for individual student consultations at specified times each weekday. The term 'hot seat tutor' refers to a tutor who is available to assist students for particular first-year modules, outside the designated tutorial times. Students who require assistance can access the hot seat tutors during the specified times and meet with them on a one-to-one basis.

At the end of the first semester in 2017, the data for those quizzes were obtained from the Moodle site and the statistics obtained were used in the analysis.

In this paper we focus on five quizzes which covered the section on rules for derivatives and their applications. For this study, only those students who completed all the quiz questions were regarded as having taken the quiz. Students who submitted their responses to only some of the questions were not considered. In the results and discussion section, the focus is on only five quiz items selected from those five quizzes. Those five items were chosen because they give an overall insight into student responses. For each of those five items, statistics were retrieved from the Moodle site on the following: facility index; discrimination index; and discriminative efficiency. The meanings of these are briefly outlined below as they were used in the results and discussion section for the structure analysis of each of the five quiz items that were chosen. We also give the meanings of intended weight and effective weight, as the latter is used in the description of discrimination index. The reader is referred to https://docs.moodle.org/dev/Quiz_statistics_calculations for further clarity on these terms.

Facility index: Obtained from the mean score of students for an item. The mean score over 2 is expressed as a percentage; the higher the facility index, the easier the question. For a true or false type question the facility index was calculated by using the students' first attempt, and for MCQs, all attempts were used in the calculation. Interpretation of the results is given in Table 1.

 

 

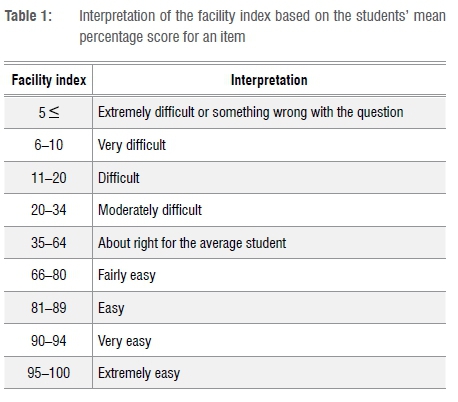
Intended weight (IW): The question weight expressed as a percentage of the overall quiz score. Because each item had a maximum score of 2, IW=100 . So, for a quiz with four items, the intended weight for each item is 25%.

Effective weight: An estimate of the weight the question actually has in contributing to the overall spread of scores for a given quiz. The effective weights should add to 100%. Note that in the results and discussion section, the five quiz items selected were extracted from five different quizzes.

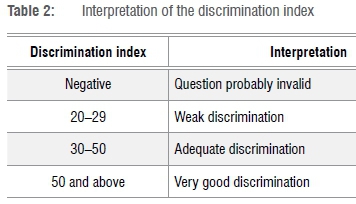
Discrimination index: The correlation between the effective weight of an item from a quiz and the rest of the items in the quiz, expressed as a percentage. It indicates how effective the item is at sorting out able students from those who are less able. The results were interpreted as indicated in Table 2.

 

 

Discrimination efficiency: This statistic is expressed as a percentage of attempts to estimate how good the discrimination index is relative to the difficulty of the question. An item which is very easy or very difficult cannot be used to discriminate students' because most students are likely to get the same score for that item. Maximum discrimination requires a facility index in the range 30-70% (although such a value is no guarantee of a high discrimination index). The discrimination efficiency will very rarely approach 100%, but values in excess of 50% should be achievable. Lower values indicate that the question is not nearly as effective at discriminating between students of different ability as it might be and therefore is not a particularly good question.

After analyses of the data, we emailed 14 students who were selected based on their attempts to correctly answer the five items. The selected students did not submit the correct response on their first attempt. Those who did not submit a correct response even after five attempts were also included in the selection to gain insight into why they were unable to answer correctly. After repeated requests for interviews via email and at tutorial sessions, eight students agreed to be interviewed. During the interview, we accessed that student's online record of submissions to determine which items they answered incorrectly. The student was given a printed copy of the five quiz items. For some items we indicated the student's response. In such cases, the students were asked to explain their responses. The student was allowed to do the relevant working on the print copy or to think aloud. Based on the student's verbal and/or written responses, we probed further to get a deeper insight into the student's reasoning.

The student participants completed an online consent form. Ethical clearance for the study was obtained from the Research Office of the University of KwaZulu-Natal (protocol reference HSS/1058/014CA).

 

Results and discussion

The results are presented under the following sub-headings:

Question 1: condition for existence of derivative at a point

Question 2: rules for derivatives of standard functions

Question 3: application of chain rule to different function structures

Question 4: application of multiple rules

Question 5: application of derivatives to optimise a function

In each case, the relevant question is given, followed by the question structure analysis and the analysis of student responses to that question. The latter includes relevant extracts from the interviews while question structure analysis focuses on the facility index, discrimination index and discrimination efficiency of the relevant question.

Question 1: Condition for existence of derivative at a point

This question focused on the defining condition for the derivative of a function to exist at a specific value in the domain of the function; finding the derivative from first principles. Basically, one needs to use the formal definition of the derivative based on first principles and use algebra to find a general expression for the gradient of the tangent to the curve f at any point (x, f(x)). This question reviews the importance of the formal concept definition.⁸

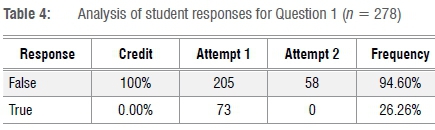
The facility index indicated that Question 1 was fairly easy while the discrimination index suggested that this question was adequate in discriminating able students from those who were less able (Table 3).

 

 

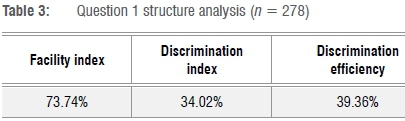
The students demonstrated a high level of understanding of the derivative from first principles. The facility index of 73.74% gives a clear indication that most of the students did not experience difficulty in responding correctly to the question. It should be noted that this is a definition question and students are expected to answer correctly on their first attempt. That 205 students answered correctly on their first attempt (Table 4) implies that about 26% of the students had difficulty with the defining condition for the derivative of a function at a point. Note that the frequency column in Table 4 indicates, as a percentage for each response to the item, the ratio of the total number of attempts for this response over the number of students who submitted an attempt to this item. For example, for Question 1, the number of 'false' responses is 263, over the number of attempts which is 278, which gives a frequency of 94.60%. The same interpretation applies to the frequency column in the tables that follow. For students who responded 'true', it seems that they did not properly observe and detect the salient feature in the expression for f'(a). This assumption seemed to be confirmed during a think-aloud interview with Student S5 who gave the response 'false' during the interview. When asked why, she responded as follows:

 

 

S5: If it is f'(a) why did this [pointing to the x in f(x)] not change to a?

This student observed the given expression and detected that the f(x) within the given expression for the derivative at a point should be f(a). That was the reason for the response 'false' during the interview. In our opinion, looking at an expression does not imply that one observes the salient features of the expression. If one accepts this, then the ability to actually observe is an aspect that could be focused on and developed among students during the teaching process. So the teaching implication here is that students need to be taught how to observe/see features within the structure of expressions and also within equations that define functions. This focus on observing features within the structure of expressions and also within equations that define functions could be done by framing suitable questions of the type given in Question 1, followed by asking for a reason for the response.

We now focus on the different rules for finding the derivatives of functions which have different structures.

Question 2: Rules for derivatives of standard functions

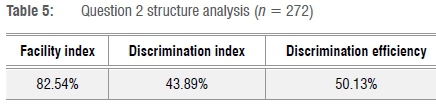
This question was designed to focus on students' understanding of the power rule and chain rule. Table 5 summarises the structure analysis of Question 2 while Table 6 indicates the student responses.

 

 

 

 

 

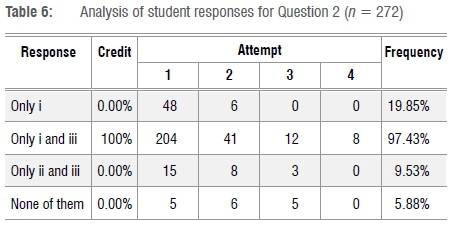
The analysis of student responses indicated that students could apply the power rule on the algebraic and exponential functions with high levels of success. This ability was evident by the fact that about 75% of students chose the correct answer on their first attempt. Note that 54 students chose the first option as their correct answer. This suggested that those students failed to visualise that the exponential function h(x)=e^kx was not the standard exponential function e^x, so that the derivative is different from the latter standard function. This was confirmed during the interview when Student S1 was asked why he indicated as his response 'only i'. The relevant extract from the interview follows:

S1: I didn't fully grasp the concept of derivative of e^kx…..

R: What do you mean by that?

S1: Because in my understanding it stays the same for e^x … there it is different [pointing to the kx in the context of e^kxon the sheet].

When asked why he regarded ii as incorrect, the student wrote: y'=n[g(x)]^n-1.g'(x). This implies that he was able to detect that the given structure required the application of the chain rule, although he did not see that when finding the derivative of the structure e^kx. This implies that it is crucial in the teaching and learning situation to have interactions based on the subtle features of functions represented in symbolic form, in particular when finding the derivative of exponential functions. These interactions should focus on the base and the exponent of the exponential function.

The facility index (82.54%) suggested that the question was easy but the discrimination index (43.89%) and discrimination efficiency (50.13%) indicated that even though the question was easy it was still effective at discriminating between students of different abilities. In the following question we look closely at the composite function y=[g(x)]ⁿ and see how students who chose the third option for Question 2 found difficulty in the context of finding the derivative of composite functions.

Question 3: Application of chain rule to different function structures

The students were required to differentiate the function f(x)=3e^4x+(5x-1)^e and their responses are indicated in Table 7. Table 8 summarises the structure analysis for Question 3.

 

 

 

 

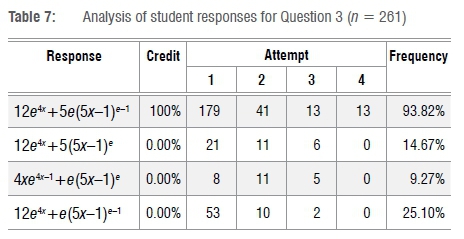
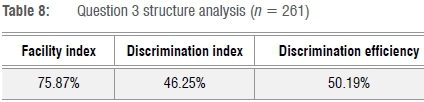
Table 7 indicates that students were able to differentiate the exponential function structure 3e^4x with ease. This ease can be concluded by the low number of students who chose the third option. It is interesting to note that those students just used the power rule without seemingly understanding that it does not apply to exponential function structures. This was confirmed during the interview with Student S1; for further details see discussion under Question 4.

The visualisation of the composite function structure and the detection that the chain rule was required in this question was the discriminating factor. Students who were able to unpack the function structure and detect that the application of the chain rule was required were successful in correctly answering. Table 8 indicates that this question had a discrimination index of 46.25% and discrimination efficiency of 50.19%, hence it was a good discriminator. To arrive at the correct answer, students had to apply the chain rule on the composite function structure (5x-1)^e. The first likely difficulty was realising that the exponent e was a constant and that the power rule could easily be applied to this composite function structure. These difficulties could be concluded from Table 7 which indicates that 38 students chose the second option and that 24 students chose the third option during their first three attempts. Those options also indicate that the second difficulty was in applying the chain rule to the composite function structure (5x-1)^e. Both these difficulties were detected during the interview with Student S5. The student was asked to differentiate (5x-1)^e. Relevant extracts from that think-aloud interview follow:

S5: I don't know what to do.

R: What do you see? [pointing to (5x-1)^e]

S5: 5x-1 in brackets raised to e.

R: What is e?

S5: e is a number … so I think we should use the chain rule to find the derivative.

[When asked to do it the student successfully found the derivative of (5x-1)^e .]

R: What did you learn from this exercise?

S5: See what is given … don't assume.

This once again implies that it is crucial in the teaching and learning context that students are taught how to see what is given in a symbolic representation of a function.

The above suggests that the correct detection and application of the chain rule was the determining factor on whether a student could or could not arrive at the correct answer. If we look at the first and fourth options note that they differ in the 5 outside the bracket. Students could only arrive at the 5 if they had correctly applied the chain rule.

A suggestion follows on how these particular aspects might be better taught to students. For example, one could give as responses those in Table 7 for the derivative of the function f(x)=3e^4x+(5x-1)^e. The requirement from students could then be to determine why each response is incorrect or correct. The following illustrative question is framed to set up the teaching activity.

Consider the following four student responses for the derivative of the function f(x)=3e^4x+(5x-1)^e:

12e^4x+5e(5x-1)^e-1

12e^4x+5(5x-1)^e

4xe^4x-1+e(5x-1)^e

12e^4x+e(5x-1)^e-1

Required: Determine whether each of the above responses is correct or incorrect. In each case motivate your answer.

This student activity should be followed by a suitable class discussion based on the answers of students to each given response.

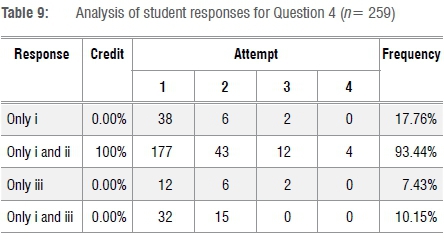
Question 4: Application of multiple rules

This question focused on the students' ability to apply differentiation techniques based on different rules to different function structures. It also exposed them to the application of the chain rule in the context of various mathematical representations.⁸

This question focused on the application of multiple rules for differentiation in the context of the three functions. The analysis in Table 9 indicates that 46 students chose the first option while 47 students chose the fourth option. This implies that the majority of the students who attempted this question later in the semester were comfortable with applying differentiation rules in the context of exponential and logarithmic functions.

 

 

Student S1 was one of the students who answered 'only i and iii'. In the context of the function g(x)=(3)^-x+log(91-x) we were interested to know how he obtained the derivative of (3)^-x. The following is an extract from the interview.

S1: Using the power rule … [and writes x(3)^-x-1].

R: What is the power rule?

[The student wrote y=xⁿ followed by y'=nx^n-1. This was followed by drawing his attention to where the variable x was in the structure xⁿ]:

S1: In the base.

R: Where is the x in the structure (3)^-x?

S1: [pointing to the x in (3)^-x] … can't use the power rule … I need to go and learn this …

This example reinforces the need in the teaching and learning situation to have interactions based on the subtle features of functions represented in symbolic form; in context of the power and exponential functions this should be with regard to where the variable appears. In particular, differentiation of functions with the following structures should be focused on: (3)^-x; (-x)³.

A more in-depth analysis of the data relating to those students who chose the second option for their second or later attempts (Table 9) revealed that they had difficulty in differentiating the function h(x). A possible reason for this difficulty could be that the function h(x) has a structure which requires the application of the product and chain rules for differentiation, and more than one application of the chain rule. Our interviews with students indicated that any one of these three - product rule, chain rule or more than one application of the chain rule - could be the reason for their difficulties. For example, students S2 and S3 did not see that the product rule had to be used and Student S7 did not detect the need for the chain rule. Students S4, S5 and S6 detected that both the rules had to be applied, but they applied the rules in the incorrect order: the chain rule was applied first to both functions in the context of h(x). The following is an extract from the think-aloud interview with Student S5, after the student was asked to differentiate h(x)=(x²-x)(1-3x)¹⁰⁰:

R: What do you see?

S5: (x²-x)and (1-3x)¹⁰⁰ are multiplied.

R: To differentiate h(x) which rules would you apply?

S5: The chain rule and the product rule.

R: Which of these rules would you apply first?

S5: The chain rule.

When asked to apply the rule, the student wrote down (x²-x)^-1(2x)x100(1-3x)⁹⁹ (3). We note that the application of the chain rule to both the functions that comprise h(x) is incorrect.

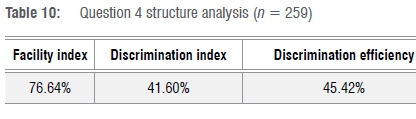
The above, as well as the fact that some students answered incorrectly on their fourth attempt (Table 9), indicated that Question 4 was effective at discriminating able students from those who were less able (discrimination index of 41.60% and discrimination efficiency of 45.42%; see Table 10).

 

 

Question 5: Application of derivatives to optimise a function

This question focused on the application of derivatives in the context of optimisation of a function.

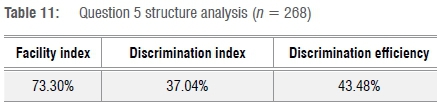
From Table 11, the discrimination index (37.04%) and the discrimination efficiency imply that the question was not a good discriminator in effectively sorting the able students from those less able. In the context of the data that were available, we could not detect which part of the question contributed to the relatively weak discrimination effect.

 

 

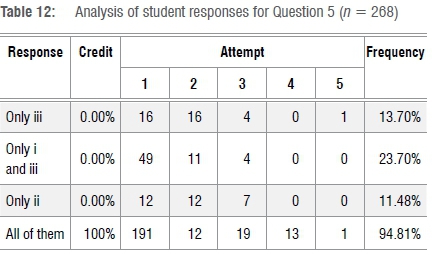
Question 5 was based on derivative-related concepts for a function given in symbolic form, for example: determining the interval(s) for which the function is increasing or decreasing; optimising a function. The question required a student to detect the relevant derivative-related concept within each statement and to do the necessary working to determine if the statement was correct or not. Table 12 indicates that 191 of 268 students (about 71%) correctly answered on the first attempt. This finding implies that a large number of the students were able to detect the relevant derivative concept on which each given statement focused, do the necessary working and make relevant conclusions. What was concerning, is the number of attempts required for some students to obtain the correct answer. This conclusion can be drawn by looking at the first three incorrect options; the students made up to five attempts. In our opinion, such students do not have the necessary derivative-related concepts for a function given in symbolic form, to answer a question of this type. This opinion is supported by the following that transpired during the interview with Student S8:

 

 

R: How can you use M(x) to find out where the function is increasing or decreasing?

S8: Take the derivative of M(x), equate it to zero, then solve for x …….

[Student S8 then correctly did the working and arrived at x=45, which indicated that the student was able to do a routine procedure, by following an algorithm.]

However, the extracts that follow indicate the student did not know what x=45 represented, in the context of the relevant derivative-related concept.

R: Look at x=45 in the context of the interval 30x65. What can you conclude?

S8: x=45 lies within the given interval, then the function M(x) is an increasing function.

This response clearly suggests that the student could not interpret that x=45 represented the value at which the derivative is 0, although this was part of the working that this student correctly did when following the algorithm. This was confirmed by the silence that followed when the researcher posed the following question: M'(x), what does this represent? Upon further probing, the student was able to interpret x=45 as confirmed by the following interview extract:

R: What type of function is M(x)?

[Student S8 was able to correctly identify the function and draw a rough sketch.]

R: Where is the turning point?

[Student S8 correctly pointed out the turning point on the sketch.]

R: What is the value of M'(x) at the turning point?

S8: zero.

R: So, what does x=45 represent?

S8: The x value of the turning point.

From the above, one could conclude that even if students correctly apply the rules for differentiation together with relevant related algorithms, they do not necessarily understand the deeper derivative-related concepts. The implication is that the teaching and learning of the derivative-related concepts should focus on understanding why certain steps in an algorithm are followed. This means that before the algorithms are stated there needs to be understanding of why certain steps are included in the algorithm. In our opinion, this reinforces the need in the teaching and learning situation to have interactions based on the subtle features of functions or equations that result from them, represented in symbolic form.

 

Conclusions and recommendations

This paper was based on sample diagnostic questions for the concept of derivatives with the aim of improving students' ability to correctly apply the rules for finding derivatives of functions. The study has confirmed that the derivative is one of the concepts students have difficulty with, as indicated in the literature.^2,3 More specifically, students experienced difficulties with applying multiple differentiation rules in the context of a single function (a composite function or imbedded function). These functions required application of the chain rule and it was found that, especially when more than one application of this rule was required, in the context where the applications of multiple differentiation rules were required, students experienced difficulties. It seems that the difficulty stemmed from the inability of students to detect from the structure of the function which rules should be applied. In particular, during teaching, we recommend that there should be a deliberate focus on the different rules that are required to differentiate functions with symbolic forms in the context of exponential and power functions. For example, correct interpretation of the symbolic structure and rules that are required to differentiate each of 3^x and x³. This should be followed by 3^-x and (-x)³ when focusing on application of the chain rule. Although this teaching implication was suspected from the analyses of online responses of students, it was confirmed during the interviews with selected students. In cases in which students detected the rules that were required, some had difficulty in detecting that more than one application of the rule was required. Any one of the three rules - product rule, chain rule or more than one application of the chain rule - could be the reason for students experiencing difficulties. In the context of a function that required the application of the product and chain rules, some students only detected the chain rule and did not see that the product rule was required. Further, students who saw that both rules were required tried to first apply the chain rule to both the functions that comprised the given function, h(x)=(x²-x)(1-3x)¹⁰⁰. In the teaching and learning situation the implication is that there should be interactions based on the subtle features of functions represented in symbolic form. If this is accepted, then our recommendation is that lecturers should during formal lectures focus on the importance of studying and visualising the structure of a function. In particular, students need to be taught how to observe/see features within the structure of expressions and also within equations that define functions.

It seems that if students could first study and visualise the given structure of the function, then detecting and noting the structural representation could help them to decide which rule(s) to apply when finding the derivative of the relevant function. We recommend that research be conducted to further investigate this hypothesis.

 

Acknowledgements

We thank the University of KwaZulu-Natal for allowing us to use the data on Moodle and also the students' results for research purposes. M.N. acknowledges A.M. and Dr D. Varghese. We also acknowledge the NRF for making available grants for the project, 'Online diagnostics for undergraduate mathematics'. The Tertiary Education Support Programme of Eskom is acknowledged for making funds available for the UKZN-Eskom Mathematics Project.

 

Authors' contributions

A.M.: conceptualisation, critically reviewing the writing, and project leadership; M.N.: writing the initial draft.

 

References

4.Maharaj A. An APOS analysis of natural science students' understanding of derivatives. S Afr J Educ. 2013;33(1), Art. #458, 19 pages. https://doi.org/10.15700/saje.v33n1a458        [ Links ]

5.Orton N. Students' understanding of differentiation. Educ Stud Math. 1983;14(3):235-250. https://doi.org/10.1007/BF00410540        [ Links ]

6.Uygur T, Özdaş A. Misconceptions and difficulties with the chain rule. In: Rogerson A, editor. The Mathematics Education into the 21st Century project. Proceedings of the Eighth International Conference; 2005 November 25 - December 01; Skudai, Johor, Malaysia. Malaysia: RIC Publications; 2005. p. 209-213.         [ Links ]

7.Stewart J. Calculus. 6th ed. Toronto: Thomson Brooks/Cole; 2009.         [ Links ]

8.Tall D. Students' difficulties in calculus. In: Proceedings of Working Group 3 on Students' Difficulties in Calculus, ICME-7; 1992 August 17-23; Québec, Canada. Québec: Les Presses de l'Université Laval; 1993. p. 13-28. Available from: http://homepages.warwick.ac.uk/staff/David.Tall/pdfs/dot1993k-calculus-wg3-icme.pdf        [ Links ]

9.Zandieh M. A theoretical framework for analysing student understanding of the concept. CBMS Issues Math Ed. 2000;8:103-122. https://doi.org/10.1090/cbmath/008/06PMid:25265997        [ Links ]

10.Orhun N. Graphical understanding in mathematics education: Derivative functions and students' difficulties. Procedia Soc Behav Sci. 2012;55:679-684. https://doi.org/10.1016/j.sbspro.2012.09.551        [ Links ]

11.Maharaj A. An outline of possible in-course diagnostics for derivatives and integrals of functions. Int J Sci Educ. 2015;11(1):78-90. https://doi.org/10.1080/09751122.2015.11890377        [ Links ]

12.Hähkiöniemi M. Perceptual and symbolic representations as a starting point of the acquisition of the derivative. In: Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education. 2004(3):73-80. http://emis.ams.org/proceedings/PME28/RR/RR168_Hahkioniemi.pdf        [ Links ]

13.Tall D. A sensible approach to the calculus. Presented at: The National and International Meeting on the Teaching of Calculus; 2010 September 23-25; Puebla, Mexico. Available from: http://homepages.warwick.ac.uk/staff/David.Tall/pdfs/dot2010a-sensible-calculus.pdf        [ Links ]

14.Maharaj A, Wagh V. An outline of possible pre-course diagnostics. S Afr J Sci. 2014;110(7/8), Art. #2013-0244, 7 pages. https://doi.org/10.1590/sajs.2014/20130244        [ Links ]

 

 

Correspondence:
Aneshkumar Maharaj
Maharaja32@ukzn.ac.za

Received: 28 Nov. 2017
Revised: 24 Apr. 2018
Accepted: 24 July 2018
Published: 27 Nov. 2018