Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Science
versión On-line ISSN 1996-7489
versión impresa ISSN 0038-2353
S. Afr. j. sci. vol.114 no.9-10 Pretoria sep./oct. 2018
http://dx.doi.org/10.17159/sajs.2018/4452
RESEARCH ARTICLE
Monthly average daily solar radiation simulation in northern KwaZulu-Natal: A physical approach
Betty Kibirige
Department of Physics and Engineering, University of Zululand, KwaDlangezwa, South Africa
ABSTRACT
Solar energy is a poorly tapped energy source in northern KwaZulu-Natal (South Africa) and many locations in the region have no available measured solar radiation data. Unfortunately, these areas are among the rural, non-commercial farming areas in South Africa that need to harness solar radiation as an alternative energy source for their needs. These communities are mostly disadvantaged and unable to access the currently sophisticated approaches available for the prediction of such data. For this reason, a modelling tool accessible to these communities has been created using data from the South African Sugarcane Research Institute at eight stations in the region. This article presents the physical approach which can be used within readily available resources such as Microsoft Excel to develop a simulation environment that can predict monthly daily average solar radiation at locations. A preliminary model was later customised by considering the physical condition at each individual location. The validated tool provides estimations with a percentage root mean square error (%RMSE) of less than 1% for all locations except for Nkwaleni which had 1.645%. This is an extremely promising estimation process as compared to other methods that achieve estimations with %RMSE of above 10%. The simulation environment developed here is being extended to predict the performance of solar photovoltaic systems in the region. Using data from other sources, the approach is also being extended to other regions in South Africa.
Significance:
• The study modifies the physical approach that is deemed complicated to something that can be accessible to many communities.
• The accuracies achieved with this approach (<0.9%RMSE) in the considered region are commendable.
• The approach can be extended to other regions in South Africa.
Keywords: Zululand; simulation; Microsoft Excel; model; estimates
Introduction
Northern KwaZulu-Natal is mostly rural with weather data collection stations widely spread apart. The South African Sugarcane Research Institute has data collecting points that leave most areas of interest with no measured records. South African universities have initiated a community that collects weather data and publishes it on the Internet1 but still these areas are not covered. Some researchers use satellite data to estimate the data at a location. However, these approaches are rather sophisticated and expensive, making them inaccessible for rural communities.
Weather data are used by many disciplines and solar energy conversion is one such field. This field involves engineers, economists, meteorologists, peasant farmers and rural communities to mention a few. Many researchers have estimated solar radiation in areas that have some data collecting stations but these methods are mostly abstract and not easily explicable. Other researchers use satellites to estimate the required data - an approach that is rather sophisticated and expensive for rural communities. This article presents a physical approach using readily available resources like Microsoft Excel to develop an environment that can be used to predict monthly daily average solar radiation and eventually assist in photovoltaic system performance analysis. This approach is a consolidation of various reports on the intensity of solar radiation on the earth's horizontal surface in an effort to come up with a non-abstract prediction of the same in northern KwaZulu-Natal. The model is part of a larger model designed to predict the performance of solar photovoltaic systems in the region. Only the equations deemed to be effective towards the prediction were extracted from the literature. Weather data from eight stations in northern KwaZulu-Natal were used in the analysis of solar radiation trends in the region. Two of the stations with latitudes at the centre of the investigated region were used to generate a preliminary model. Four other stations were used to refine the preliminary model and the final two (with the lowest and the highest latitude) were used to validate the model.
Photovoltaic system designers need to have an estimation of daily monthly average solar radiation for locations where no data collecting stations are present in order to size photovoltaic electrical generating systems appropriately. One of the widely used methods of estimation is a correlation between solar radiation and sunshine hours introduced by Angstrom2, and later modified by Prescott3, and the original form of the formula is:

where  is the ratio of the total solar radiation to the available solar radiation at the top of the atmosphere and
is the ratio of the total solar radiation to the available solar radiation at the top of the atmosphere and  is the ratio of the measured sunshine duration to the theoretically available sunshine hours. The coefficients a and b are calibrated to suit the various location. It is observed from Equation 1 that the total solar radiation G is proportional to the actual effective sunshine hours S of a given location.
is the ratio of the measured sunshine duration to the theoretically available sunshine hours. The coefficients a and b are calibrated to suit the various location. It is observed from Equation 1 that the total solar radiation G is proportional to the actual effective sunshine hours S of a given location.
Others have estimated mean monthly solar global radiation as a function of temperature.4 Here the difference between the maximum and minimum temperatures has been used. These methods include the Bristow-Campbell model5 and the Allen model6. Rainfall and temperature measurements have also been used to make the estimation.7 Artificial neural networks have been used as an alternative computational approach to estimating daily monthly average global irradiation.8,9
The ethos of these methods is to offer a way of estimating solar radiation without delving into what has been perceived as the more complicated physical approach.10 These methods are abstract and are not easily explained practically. This study falls back on the more realistic physical approach. With this approach, the prediction of monthly daily average solar radiation averages is done starting with the value of the solar constant, I0.11 A simulation environment was developed in Microsoft Excel to assist in the prediction of solar radiation at locations in Northern KwaZulu-Natal, a subtropical region in South Africa. Microsoft Excel is an environment commonly used for computation by many fields and is mostly easily accessible to disadvantaged communities. This tool and other similar open-source tools can be used effectively to make informed decisions on solar energy availability at specified locations. This makes the estimation process open to the user and corrections to the estimations can be made readily if necessary - a welcome advantage that is masked by commercially available software.
Earth's atmosphere and solar irradiance: A review
Photovoltaic cells react to the photo energy incident on their top surfaces to generate a current or voltage that can be harnessed as a source of electrical energy. Photo energy passing through a medium is attenuated according to the properties of the medium. Therefore, photo energy from the sun is scattered by clouds and atmospheric particles, absorbed by atmospheric particles, gases and clouds, diffused and or reflected as it traverses the earth's atmosphere before it makes its way to the surface of the earth. Although most of the radiation received at the surface of the earth is directly radiated from the sun, a substantial amount of it is received from diffused radiation. This is radiation that has been scattered by particles in the atmosphere but still makes its way to the surface of the earth. A conservative estimation is an average of about 10% of the direct radiation, although this varies from dawn up to about 40% at sunset.
The solar irradiance from the sun that is perpendicular to the virtual atmospheric surface of the earth is known as the solar constant I0 and has a value of approximately 1367 W/m2. The optical path through the earth's atmosphere is known as air mass (AM).12 This mass indicates the path length of the rays of the sun relative to the zenith at sea level. The sea level air mass at the zenith is 1 and increases to 38 as the angle between the rays and the zenith increases to that at the horizon. AM decreases as the altitude above sea level increases and can be less than 1 at some altitudes. AM is simply defined as the ratio of the path length, L, of the rays of the sun through the atmosphere to the surface of the earth to the length, L0, if the rays of the sun were directly perpendicular to the surface of the earth (the zenith). Using the zenith angle θZ between the two lengths, AM is given by the expression:

Photovoltaic modules are normally rated using an AM of 1.5 (AM1.5).13
An approximation of the effects of AM on the global solar irradiance G0 as suggested by Forero et al.14, Meinel and Meinel15 quoting Laue16 and PVEducation17 for clear skies is:

modified to include altitude h in km17:
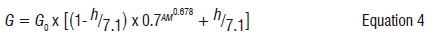
Equation 4 signifies the solar radiation intensity at the surface of the earth taking into consideration the effects of the earth's atmosphere. For clear weather, especially during the winter solstice in the southern hemisphere, it can be assumed that most of the radiation received at the earth surface is a result of direct solar radiation. Equation 4 is used as the base equation in the modelling process for this study. Effects of diffusion scatter, absorption and albedo are considered as varying parameters dependent on the time of year and the physical conditions of a location.
Global latitude, longitude and solar irradiance
The equator of the earth is tilted at an angle of 23.45° to the plane of the orbit of the earth around the sun leading to a solar declination angle (δ), defined as the angle between a sun's ray (extended form the centre of the sun to the centre of the earth) and the earth's equatorial plane. This angle varies between 23.45° and -23.45° as the earth orbits the sun and can be expressed as:
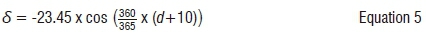
or
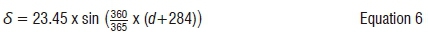
The irradiance at the surface of the earth is also affected by the solar elevation angle α. This is defined as the angle between the sun's ray from the centre of the sun to the centre of the earth and the earth's horizontal plane. Daily averages are considered in this study; and the elevation angle is a function of the solar declination δ, and the latitude φ of the location. At noon, in the southern hemisphere, the elevation angle is expressed as:

The longitude of the location gives an hour shift every 15° longitude and will not affect the solar elevation if daily averages are considered. With the assumption that the earth is spherical, solar radiation intensity at the surface of the earth should vary in a sinusoidal manner to the elevation angle α leading to Equation 8:

Therefore, apart from diffusion, solar radiation intensity at the surface of the earth varies with the day of the year d, the air mass AM, the altitude of a location h, declination angle δ, the latitude φ and the elevation angle α. The expression is consolidated using Equation 4 and Equation 8 to arrive at Equation 9:
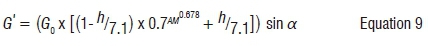
In the following sections, Equation 9 is translated to read solar radiation intensity I. Factors including the solar constant Io, the effective sunshine hours SAve, and the atmospheric effects (scatter, absorption, diffusion, albedo etc.) are used to estimate the available monthly daily solar radiation.
Sunshine hours
The day length in hours is calculated by considering the theoretical sunrise/sunset angle, ωs, which is expressed as:

At the equator when φ=0°, the sunrise/sunset angle is 180° and the day length in hours is observed to be 12 h.
The day length in hours S0 at the equator is derived from Equation 10 by considering that the longitude of the location gives an hour shift every 15° longitude:

S0 depicts the maximum possible sunshine hours which differ from the effective sunshine hours. The sunshine hours are important in determining the amount of solar energy available in an area during a typical day in a month. Peak sun hours, which are hours during which the intensity of the sun is 1 kW/m2, are observed to average about only half of the maximum possible sunshine hours in the region under consideration. An expression derived from Equation 11 above gives these hours, referred to as sunshine hours S, as:

A yearly average of the calculated effective sunshine hours SAve was then used to calculate a solar constant I'0 in MJ/m2/day using the expression below:

where 24 is indicative of the hours available in a 24-h day (and could be represented by S0) and 11.574 is a conversion factor from watts (W) to megajoules (MJ). Equation 13 like Equation 1 makes the proportionality of global solar radiation to the actual effective sunshine hours apparent and hence provides a possible explanation of the possible validity of the Angstrom-Prescott equations. That is:  for Equation 13 and
for Equation 13 and 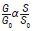 for Equation 1.
for Equation 1.
Absorbed global solar radiation
Clouds and atmospheric particles absorb global solar radiation, which results in a low radiation received at the surface of the earth. Rainy and misty seasons will have higher solar radiation absorption. The effect will be a reduction in the solar radiation, making it necessary to modify Equation 10 with an attenuation factor that is determined in the model development process.
Earth's surface topography and global solar radiation
The study of the shape and features of the surface of the earth - earth's topography - indicates that these features affect the weather of a location.18 In mountainous terrain, solar radiation measurements may be lower or higher than expected depending on the locality of the measuring site within the terrain. Mountain shadows lower sunshine hours of a location when compared with another location with similar latitude but with a flat terrain.
In essence, the simulated radiation, RadSim, can be summarised as in Equation 14:
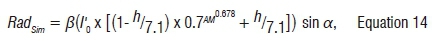
where β represents the absorption/diffusion factor depending on the physical implications. This factor takes on a value of 1 if these effects are deemed to be absent at a location.
Methods
Development of the simulation environment
Monthly average daily solar radiation data, collected over long periods of up to 20 years from eight weather stations in the KwaZulu-Natal Province of South Africa,19 were used for the study.
Figure 1 shows the regional map of the area under study and Table 1 presents the latitudes, longitudes and altitudes together with the period of observation of the chosen sites. In order to establish a way of making estimations for sites without measured data, six of the eight sites were used in the modelling process and the data from the other two sites were used for model validation.
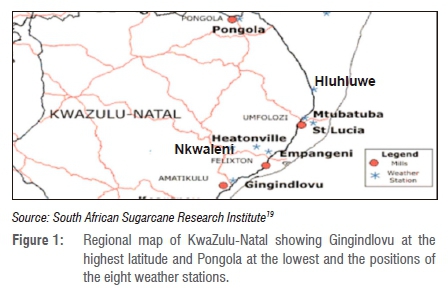
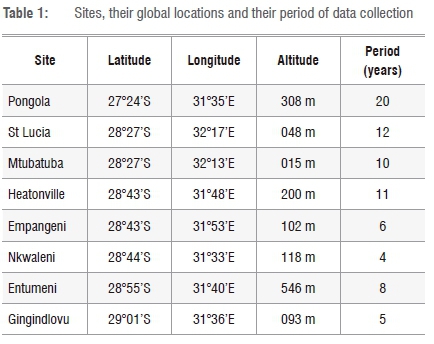
Two sites - Heatonville and Empangeni - are at the same latitude (28°43'S) and are positioned at a latitude central to that of all the chosen weather stations. These two sites were used to make a preliminary development of the simulation environment. The other four sites (St Lucia, Mtubatuba, Nkwaleni and Entumeni) were used to refine the model further. Pongola and Gingindlovu were chosen for the validation of the simulation environment. These stations are positioned at the lowest (27°24'S) and the highest (29°01'S) latitudes of the region under study, respectively.
The development of the simulation environment was carried out in Microsoft Excel. A field labelled d was created as the variable for each mid-month day (about the 15th of each month). Then other fields including latitude (φ), declination angle (δ) (Equation 7); solar constant (I'0) (Equation 13); a factor caused by air mass and altitude (AM & h) (Equation 15); simulated radiation (RadSim) and collected radiation data (Raddata) were created as shown in Table 2. Table 2 represents the proposed simulation environment that can be developed for any location if latitude, longitude, altitude and other geographical variables are known for the location.
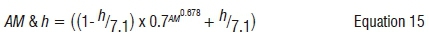
In calculating the solar constant in MJ/m2/day from 1367 W/m2, an average value of 6 sunshine hours per day was used as is appropriate for the region. This was determined by using Equation 12 for each middle day of the month to determine Sm and then a yearly average SAve calculated in Excel, for 12 months of the year. The subscript m stands for month.

Graphical representations of simulated and collected data of monthly average daily solar radiation for each site were plotted and the process of fitting simulated data to collected data was carried out.
Analysis
Analysis of results was done using statistical methods. The percentage mean bias error (%MBE), the %RMSE and the coefficient of determination (R2) were used. Where:
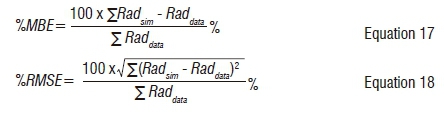
The %RMSE method in Equation 18 gives a true reflection of the data fit. By squaring the differences between simulated and collected data, and then determining the square root of the squared differences, negative differences and positive differences are allowed to contribute to the solution without one cancelling out the other, hence giving a realistic fit.
The %RMSE and %MBE show the best fit when the values tend towards zero while an R2 is indicative of a good fit when its value tends towards 1.
Results and discussion
Figure 2 shows simulated and collected data before and after including the diffusion factor. The fitted linear regression is shown, together with the corresponding coefficient of determination, R2, for Heatonville and Empangeni. Data from Heatonville and Empangeni weather stations were used to start the process of fitting simulated data to collected data.
It is observed from the preliminary data (Figure 2a), that on days on which simulated and collected data did not agree, the simulated data had a lower value than the collected data. The days on which this happens are representatives of the summer solstice months (December to March) in the southern hemisphere.
Seasonal changes carry with them varying atmospheric conditions. The summer months in the studied region are prone to have many particles in the atmosphere that scatter the direct radiation. This scattered radiation still makes its way to the surface of the earth, resulting in diffusion. By including the diffusion factor introduced in Equation 4, a 1.1 factor estimated by Meniel and Meniel15 and Laue16, fitted simulated data to collected data for the months of January and March; but a factor of 1.2 was needed to fit the data for the months of December and February at both stations.
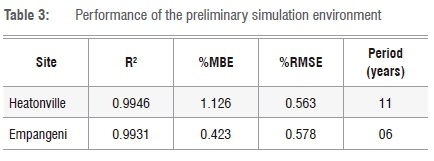
As discussed, clouds and atmospheric particles scatter but also absorb global solar radiation. The value of the simulated data in the months of June and October is higher than that of the collected data. As recorded by the South African Sugarcane Research Institute19, October and June are rainy months but also colder than the summer months, leading to absorption rather than diffusion. A factor of 0.95 was needed to fit the two sets of data. After including these changes, the simulated and collected data were as shown in Figure 2b. Figure 2c shows a comparison between collected data and simulated data. The fitted linear regression and the corresponding R2 are 0.9946 and 0.9931 for Heatonville and Empangeni, respectively. The %MBE and the %RMSE are shown in Table 3. The preliminary simulation environment showed a very good correlation between the two data sets and was further used on the four other locations.
Results for simulations carried out for the four other stations using the preliminary model developed for Heatonville and Empangeni are presented in Figure 3 and Table 4.
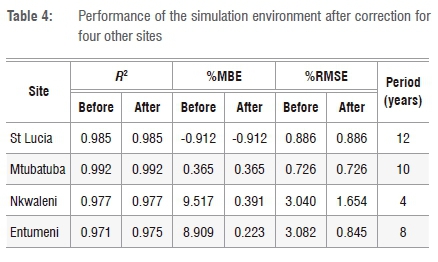
A summary of the results of the stations after using the preliminary Heatonville/Empangeni model is given in the before column given in Table 4. Although the simulations for St Lucia and Mtubatuba showed good correlation with %RMSEs as low as 0.886% and 0.726%, respectively, those for Nkwaleni and Entumeni did not. For both of these stations, the %RMSE was as high as 3%.
Better data fitting at Nkwaleni was achieved by changing the value of the sunshine hours from the 6 h used as the average for the region to 5.5 h. Figure 4 shows the graph after changing the value of the sunshine hours.
Further investigations reveal that Nkwaleni is surrounded by mountainous terrain resulting in shadows over the station and hence reduced sunshine hours at the station. Therefore, mountainous terrain could lead to more exposure to the sun, necessitating an increase in the averaged sunshine hours; or, the same physical feature could lead to shadows, necessitating a decrease in sunshine hours.
Data captured from Entumeni weather station did not agree with the simulated data for the months of November, December, January and March. The data simulated using the Heatonville/Empangeni model, for the location, were found to be higher than the collected data at the location. Entumeni is a misty area, especially in the summer months, which leads to a reduction in the received solar radiation in those months. Including an absorption factor of 0.95 for these months, fitted the data within a desirable range. Figure 4a shows the corrected simulation data.
The results of the analysis of the four stations are summarised in Table 4.
Further validation, results and discussions
This study showed that the daily monthly average radiation received at any location will be affected by: latitude, altitude, day of the year, the earth terrain at the location and AM. Pongola and Gingindlovu were used to validate the model further. Data at these stations were estimated by considering the physical condition and the global data given in Table 1. An estimation of the expected solar radiation was made starting with the Heatonville/Empangeni model.
Gingindlovu
At a latitude of 29°01'S and an altitude of 93 m, Gingindlovu is 7 km from the coast and has a relatively flat terrain with no extreme weather patterns. It was therefore deemed sufficient to rely on the Heatonville /Empangeni model without any further correction.
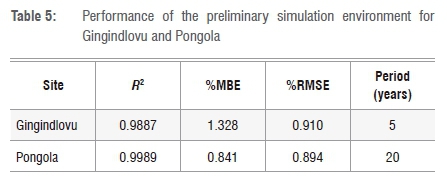
The simulated and collected weather data were plotted on the same graph and a comparison made between the two sets of data. Results are shown in Figure 5. A summary of the model performance is given in Table 5. The model performed well with a %RMSE of 0.91.
Pongola
At a latitude of 27°24'S and an altitude of 308 m, Pongola is situated on a mountainous slope prone to receive more sunshine in the day. As the sunshine hours of Nkwaleni, a location situated in a shadow, were reduced from 6 h to 5.5 h, the sunshine hours for Pongola were increased from the averaged 6 h to 6.5 h to account for perceived extra sunshine hours.
The simulated and collected radiation data are presented in Figure 5. Table 5 gives a summary of the results for Gingindlovu and Pongola. A model performance and a %RMSE of 0.894 was achieved for Pongola.
Summary and conclusion
A physical approach has been used to estimate the monthly average daily solar radiation of a demarcated region in northern KwaZulu-Natal, South Africa. Starting with the solar constant, various mathematical expressions that represent the physical processes that the solar radiation encounters on its way to the earth's surface were drawn upon to consolidate a complete model that provides an estimation of the daily monthly average solar radiation at a location within a region. This approach reduces the complications of the physical approach by including only equations that are significant to the modelling process. Latitude, altitude, day of the year, and the location's geographical features were used to develop a simulation environment in Microsoft Excel that gave a prediction of radiation for eight locations, two of which (Gingindlovu and Pongola) were used in validating the model. A preliminary model was developed using two of the locations and the other four locations were used to establish ways of customising the preliminary model to suit a given location. It is noted that mountainous regions could either lead to an increase or a reduction in sunshine hours. This trend was brought out clearly using the developed model to predict sunshine radiation at two of the stations (Nkwaleni and Pongola). Entumeni is a misty place and the solar intensity at the station was observed to be lower than the preliminary estimations, implying a reduction as a result of absorption by the particles in the atmosphere. A factor that compensated for diffused radiation was added in the summer months which confirms that diffused radiation is most prevalent in the summer solstice.
The model gave good results for most months at the considered stations. Solar radiation at Gingindlovu and Pongola was predicted at less than 1%RMSE for both locations and for all other locations except for Nkwaleni which was 1.645%RMSE. This is a very good fit and this approach could therefore be used, with minimal customisation, to estimate energy yields from solar systems around northern KwaZulu-Natal region. The Microsoft Excel program used to carry out the estimations is readily available and can be used easily by many communities. This approach could be used for other regions that have similar needs.
Future work
The simulation environment developed here is being extended to include the prediction of a system's performance for the same region in South Africa. While assisting communities in rural Zululand has been a major motivation for this paper, working with overseas collaborators has highlighted the need for location-specific simulations in order to minimise discrepancies in systems' predictions.
Other data sources like the South African Universities Radiometric Network (SAURAN) do exist. Therefore, as a future project, the approach will be extended to other regions in the country using other data sources.
Acknowledgements
The University of Zululand Research Office is acknowledged for providing funding.
References
1. Southern African Universities Radiometric Network. Solar radiometric data for the public [webpage on the Internet]. No date [cited 2018 Feb 14]. Available from: http://www.sauran.net [ Links ]
2. Angstrom A. Solar and terrestrial radiation. Q J Roy Met Soc. 1924;4:121-126. [ Links ]
3. Prescott JA. Evaporation from a water surface in relation to solar radiation. Trans Roy Soc S Aus. 1940;64:114-125. [ Links ]
4. Meza F, Varas E. Estimation of mean monthly solar global radiation as a function of temperature. Agric For Meteorol. 2000;100:231-241. https://doi.org/10.1016/S0168-1923(99)00090-8 [ Links ]
5. Bristow K, Campbell G. On the relationship between incoming solar radiation and daily maximum and minimum temperature. Agric For Meteorol. 1984;31:159-166. https://doi.org/10.1016/0168-1923(84)90017-0 [ Links ]
6. Allen R. Self-calibrating method for estimating solar radiation from air temperature. J Hydrol Eng. 1997;2:56-67. https://doi.org/10.1061/(ASCE)1084-0699(1997)2:2(56) [ Links ]
7. Liu DL, Scott BJ. Estimation of solar radiation in Australia from rainfall and temperature observations. Agric For Meteorol. 2001;106:41-59. https://doi.org/10.1016/S0168-1923(00)00173-8 [ Links ]
8. Mubiru J, Banda EJKB. Estimation of monthly average daily global solar irradiation using artificial neural networks. Sol Energy. 2008;82:181-187. https://doi.org/10.1016/j.solener.2007.06.003 [ Links ]
9. Tymvios FS, Jacovides CP, Michaelides SC, Scouteli C. Comparative study of Angstrom's and artificial neural networks methodologies in estimating global solar radiation. Sol Energy. 2005;78:752-762. https://doi.org/10.1016/j.solener.2004.09.007 [ Links ]
10. Dewitte S, Crommelynck D, Mekaoui S, Joukoff A. Measurement and uncertainty of the long term total solar irradiance trend [document on the Internet]. c2004 [cited 2018 Feb 14]. Available from: www.kmi.be/meteo/download/de/519987/pdf/rmi_scpub-898.pdf [ Links ]
11. Willett HC. American air mass properties. Cambridge, MA: Massachusetts Institute of Technology and Woods Hole Oceanographic Institution; 1933. https://doi.org/10.1575/1912/1142 [ Links ]
12. American Society for Testing and Materials (ASTM). Terrestrial reference spectra for photovoltaic performance evaluation. ASTM G173-03. West Conshohocken, PA: ASTM; 2012. [ Links ]
13. Salazar GA, Hernández AL, Saravia LR. Practical models to estimate horizontal irradiance in clear sky conditions: Preliminary results. Renew Energy. 2010;35:2452-2460. https://doi.org/10.1016/j.renene.2010.01.033 [ Links ]
14. Forero N, Caicedo LM, Gordillo G. Correlation of global solar radiation values estimated and measured on an inclined surface for clear days in Bogota. Renew Energy. 2007;32:2590-2602. https://doi.org/10.1016/j.renene.2006.12.012 [ Links ]
15. Meinel AB, Meinel MP. Applied solar energy, an introduction. Reading, MA: Addison-Wesley;1976. [ Links ]
16. Laue EG. The measurement of solar spectral irradiance at different terrestrial elevations. Sol Energy. 1970;13:43-50. https://doi.org/10.1016/0038-092X(70)90006-X [ Links ]
17. PVEducation.org. Welcome to the Photovoltaic Education Network [webpage on the Internet]. No date [cited 2017 Jul 10]. Available from: http://www.pveducation.org/pvcdrom/2-properties-sunlight/air-mass [ Links ]
18. Aguilar C, Herrero J, Polo MJ. Topographic effects on solar radiation distribution in mountainous watersheds and their influence on reference evapotranspiration estimates at watershed scale. Hydrol Earth Syst Sci. 2010;14:2479-2494. https://doi.org/10.5194/hess-14-2479-2010 [ Links ]
19. South African Sugarcane Research Institute. Unlocking the potential of sugarcane [webpage on the Internet]. No date [cited 2016 Dec]. Available from: http://www.sasa.org.za/sasri.aspx [ Links ]
 Correspondence:
Correspondence:
Betty Kibirige
Email: kibirigeb@unizulu.ac.za
Received: 19 Oct. 2017
Revised: 14 Feb. 2018
Accepted: 22 Feb. 2018
Published: 11 Sep. 2018
FUNDING: University of Zululand














