Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Science
versión On-line ISSN 1996-7489
versión impresa ISSN 0038-2353
S. Afr. j. sci. vol.114 no.5-6 Pretoria may./jun. 2018
http://dx.doi.org/10.17159/sajs.2018/20170255
RESEARCH ARTICLE
Power laws, demography and entrepreneurship in selected South African regions
Daan Toerien
Centre for Environmental Management, University of the Free State, Bloemfontein, South Africa
ABSTRACT
Statistically significant Pareto-like log-log rank-size distributions were recorded for population and enterprise agglomeration in the towns of three different regions of South Africa, and are indicative of skewed distributions of population and enterprise numbers in regional towns. There were no distinct differences between groups of towns of regions from different parts of the country. However, the regional agglomerations differed from those of groups of towns randomly selected from a database. Regions, therefore, appear to have some uniqueness regarding such agglomerations. The identification of Zipf-like links between population and enterprise growth in regional towns still does not fully explain why some towns grow large and others stay small and there is a need to further explore these issues. The extreme skewness in population and enterprise numbers of different towns' distributions should, however, be considered in local economic development planning and execution.
SIGNIFICANCE:
• This contribution illustrates that the populations and enterprises of South African regional towns are distributed in orderly ways (called Pareto distributions) that result in some being large/many and others small/few.
Keywords: power laws; Zipf's law; demography; entrepreneurship; agglomeration patterns
Introduction
Accounting for the way populations are distributed over different geographical locations and their evolution over time is important. The distribution of populations across geographical areas is not random1: there is a strong tendency toward agglomeration, i.e. populations are concentrated within common restricted areas such as cities, which results in a few large cities and many smaller cities. This striking pattern of geographical agglomeration is called Zipf's law for cities.2 For instance, the size distribution of cities in the USA is startlingly well described by a simple power law,3 which essentially states that the probability that the size of a city is greater than some S is proportional to 1/S. Zipf's law is a special case of a Pareto distribution.4
Although normal (Gaussian) distributions and related quantitative methods are still relevant for a significant portion of organisational research, the increasing discovery of power laws signifies that Pareto rank-frequency distributions are pervasive and indicative of non-linear organisational dynamics.4 Researchers ignoring Pareto distributions risk drawing false conclusions and promulgating useless advice to practitioners. Most managers face extremes, not averages.4 Morudu and du Plessis5 reported Pareto rank-frequency distributions for population, employment and gross economic value addition data of municipalities in South Africa. Their results hint of a limited impact of national policies such as GEAR (the Growth, Employment and Redistribution), ASGISA (Accelerated and Shared Growth Initiative for South Africa) and NGP (the New Growth Path) plans since 2001, and the marginal spatial impact of local economic development plans on economic variables at municipal level.
Patterns of a few large towns and many smaller ones have also been observed in regional studies of South African towns.6-12 It is unknown if these patterns adhere to a rank-size distribution consistent with Zipf's law. Considering the above warning4 and the implications reported for municipalities5, it is necessary to investigate the possible presence of Pareto (Zipf-like) population and/or enterprise distributions in the towns of South African regions. The presence of linear regularities (proportionalities) in the form of statistically significant correlations between the demographic and entrepreneurial characteristics of South African towns7-19 could signal the possible presence of Pareto rank-size distributions in regions.
Knudsen20 examined the size distribution of cities in Denmark by way of three questions: (1) Does Zipf's law apply to the population distribution of Danish cities? (2) What are the implications of Zipf's law for models of local growth? (3) Is there a Zipf's law for firms? Knudsen found that Zipf's law applies to Danish cities and that the size pattern of more than 14 000 Danish production companies follows a rank-size distribution consistent with Zipf's law. He did not examine the distribution patterns of the number of enterprises in Danish cities.
Knudsen's approach20 provided guidance to this investigation about possible Pareto population and/or enterprise distributions in the towns of South African regions, i.e. the use of questions to examine the distribution patterns. The following questions were examined: (1) Does Zipf's law or Pareto rank-size distributions apply to the population distribution of towns in different regions of South Africa? (2) If Zipf's law (or a Pareto rank-size distribution) applies to town populations, does it also apply to the number of enterprises in these towns? (3) If Zipf's law (or a Pareto rank-size distribution) applies to populations and/or enterprises, do different regions differ from one another (in other words, do they have uniqueness)? (4) Should such distributions, if they exist, be considered in local economic development planning and support? The purpose of this contribution is to provide answers to these questions.
Approach used in this contribution
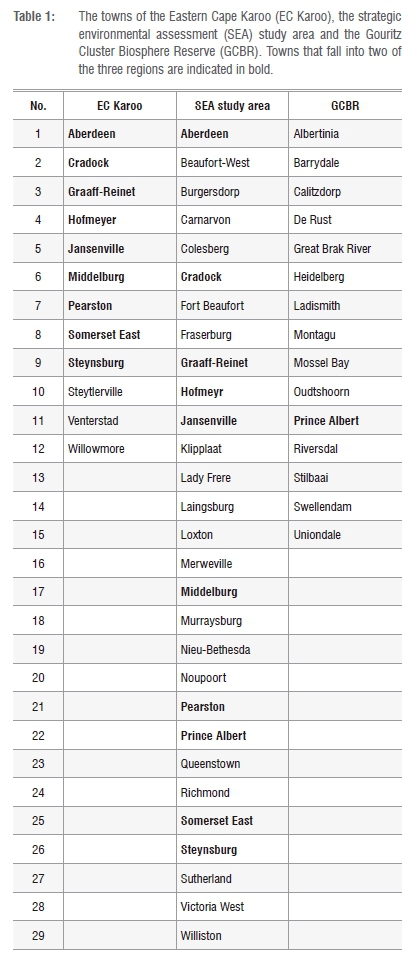
Previously studied towns of three different regions of South Africa were selected for this analysis (Table 1). The first group includes 12 towns of the Eastern Cape Karoo (EC Karoo) that have previously been extensively studied.6,9 These studies included an analysis of data covering almost a century (1911 to 2006).11 The second group includes 29 Karoo towns included in a recent Shale Gas Strategic Environmental Assessment of the Karoo.21 Further study of these towns could provide information essential for decision-making about shale gas production. The third group includes the towns of the Gouritz Cluster Biosphere Reserve (GCBR) in the southern Cape.22
Population and enterprise distribution in cities
Why do cities exist, and why do they vary in size? These fundamental questions have received a considerable amount of attention from regional and urban economists in recent years.23 Cities are thought to arise to give consumers easy access to a large variety of goods or because of the 'external' effects of consumer location or because of the advantages of proximity of consumers to their workplaces. Although these reasons are probably important, Brakman et al.23 believe they do not explain why cities are spread out unevenly across space or explain why systems of cities exist.
Already in 1682, Alexandre Le Maitre remarked on a systematic pattern in the size distribution of French cities.1 Power laws were discovered more than a hundred years ago by Vilifredo Pareto.24 Felix Auerbach, in 1913, and George Kingsley Zipf, in 1949, formally established an empirical regularity: the sizes of the large cities are inversely proportional to their ranks.1 The proportionality of rank and size implies a power distribution with exponent equal to one - a phenomenon that became known as Zipf's law for cities, a special case of a Pareto distribution. It is a striking pattern of agglomeration that may well be the most accurate regularity in economics and it holds for many countries and dates.2 If a sample of cities is ranked according to population size and presented as a graph of log population size (independent variable) and log rank (dependent variable), a straight line with slope -1 indicates a Zipf distribution.23 If the slope is higher than one, cities are more dispersed than predicted by Zipf's law, and if the slope is less than one, cities are more even-sized than the prediction.23
The reason for the existence of Zipf's law for population distribution is still rather obscure and Krugman3 remarked: 'At this point we are in the frustrating position of having a striking empirical regularity with no good theory to account for it.' However, Gabaix2 stated that the reason why cities become large is essentially because of inertia in the creation of jobs: the number of new jobs is roughly proportional to the number of existing jobs. Eeckhout1 remarked that once population mobility is understood, the underlying economic mechanisms can be examined. Agglomeration and residential mobility of the population between different geographical locations are tightly connected to economic activity; the evolution of the population across geographical locations is an extremely complex amalgam of incentives and actions taken by many individuals, enterprises and organisations.
A pattern of some large towns combined with a number of smaller towns is also present in the three regions under consideration here. However, it is not known if there are Pareto rank-size regularities as far as populations are concerned, and, if present, whether they adhere to Zipf's law or differ from one another.
What about enterprise development? Axtell25 mentioned that Gibrat reported a lognormal distribution of the sizes of French industrial firms in 1931. Such a distribution was later also recorded in the UK.26 Axtell27reported that the distribution of US firm sizes closely followed the Pareto distribution with an exponent near unity, i.e. the Zipf distribution. Knudsen20 reported that the size distribution of Danish production companies had a strong fit with a Pareto rank-size distribution with an exponent of 0.741.
No record was found that the distribution patterns of the number of enterprises in countries or regions have received research attention. Given the statistically significant relationships between population sizes and enterprise numbers frequently recorded for South African towns,7-19 it is clear that town size (measured by the population number), the creation of jobs, and thus enterprise numbers and entrepreneurial decisions, have similar variance patterns. It is, therefore, also necessary to examine if the enterprise numbers of regions have Pareto rank-size distributions. If they do, such regularities could be used in development decisions and support as suggested by Andriani and McKelvey4 and used by Morudu and du Plessis5.
EC Karoo towns
The EC Karoo and its 12 towns (Table 1) provided the focus of a number of studies.6,9,11 This area is a sub-region of the Karoo, wholly included in the Eastern Cape Province. Its selection for study by Nel and Hill6was based on the availability of comparable and continuous census data records over an extended period. They identified the following trends based on nearly 100 years of continuous records: shifts in agricultural production, small town and rural population change, and evolving small town economies. The 12 towns were also used in a study of enterprise proportionality phenomena in small towns of the EC Karoo.9 The towns' enterprises were identified, enumerated and classified into different business sectors. Statistical analyses were used to examine the enterprise dynamics. Regional proportionalities, i.e. fairly constant ratios between business sector enterprise numbers and total enterprise numbers in the towns, were used to construct a 'regional enterprise structure'.
The 12 towns have also been used to address the question of whether the proportionality between population numbers and enterprise numbers in South African towns was present at earlier times. Access to the century-long database of Nel and Hill6 enabled such a study.11 Ten data sets were extracted in which the years of the population estimates and enterprise counts in a specific data set differed by at most 2 years. Proportionalities were present over the century and a detailed picture of the relationship between population dynamics and enterprise dynamics was developed.11 The Nel and Hill6 data sets also lend themselves to examination of the time-dependence of rank-size distributions of the population and enterprise numbers of the EC Karoo. This region was chosen as the first region in the present study.
Karoo towns
The Karoo, which occupies some 40% of the surface area of South Africa, has a continuous census record and a network of small towns of differing sizes, which made it a suitable area to research aspects of small town development.28 In addition, shale gas development in the Karoo is being considered by the South African government. An area of 171 811 km2 of the Central Karoo, delimited by the applications for exploration rights for shale gas lodged by different companies, plus a 20-km buffer, constituted the study area of a strategic environmental assessment that considered shale gas development in the Karoo.21 The study area includes 29 towns (Table 1).
The Karoo was slowly urbanised after 1785 when its first town, Graaff-Reinet, was founded.29 By 1850 only 10 of the selected 29 towns had been founded, but, with a couple of exceptions, all had been founded by 1900. These towns exhibit a spread of population and enterprise sizes that raises a question about the possible presence of rank-size distributions.
There is an overlap of nine towns between the groups of the EC Karoo and the strategic environmental assessment study area (Table 1). This overlap was considered acceptable because comparison of the results for the two groups would help to determine if specific rank-size distributions, if present, are typical of a specific region. The shale gas development strategic environmental assessment study area, with its 29 towns, was selected as the second region in this study.
The Gouritz Cluster Biosphere Reserve
The GCBR is located in the southern Cape area of South Africa. It is globally unique as it is the only area in the world where three recognised biodiversity hotspots converge: the Fynbos, Succulent Karoo and Maputaland-Tongoland-Albany hotspots.22 Two mountain ranges (the Swartberg Mountains in the north and the Langeberg/ Outeniqua Mountains in the south) separate the GCBR into two separate geographical sub-regions. To the north and nestled between the Swartberg and the Langeberg/Outeniqua/Tsitsikamma mountain ranges lies a semi-arid to arid valley, the Little Karoo.30 In the south lies a more verdant coastal plain bordered by the Langeberg mountains in the north and the Indian Ocean in the south.
Urbanisation of the GCBR was also slow. Only one town, Swellendam, had been founded by 1800 for administrative purposes.29 By 1850 there were only five towns but thereafter the pace of urbanisation increased to the extent that all 15 of the GCBR towns (Table 1) had been founded by 1900. Most of these towns were founded to cater for a rural population's needs of religious services and not for commercial reasons.29 The GCBR was selected as the third region of this study.
Methods
Population size rank-size analyses
Population numbers for 1946 were obtained from a government report which provides information from 1904 to 1970.31 Population numbers for 2001 and 2011 of the towns were sourced from a German website.32Population estimates for 2014 or 2016 were based on 2011 data extended by the growth rate between 2001 and 2011.
The towns of each of the regions for a specific year were ranked from highest to lowest according to their population numbers. The following regression was then calculated for each time period and region:
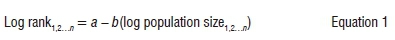
where a is the intercept, b is the regression coefficient and n is the number of towns in a region. Microsoft Excel software was used for the calculations.
Enterprise numbers rank-size analyses
Enterprise numbers for 1946/1947 and 2013/2014 or 2015/2016 of towns of all three regions were determined according to the methods of Toerien and Seaman7, using telephone directories for the specific year.
The towns of the different regions for a specific year were ranked from highest to lowest according to their enterprise numbers. The following regression was then calculated for each time period and region:

where a is the intercept, b is the regression coefficient and n is the number of towns in a region. Microsoft Excel software was used for the calculations.
Time dependence of rank-size distributions
Once statistically significant Pareto rank-size distributions were recorded, it became necessary to test the time dependence of such distributions. The database of Nel and Hill6 was used to extract population and enterprise data for the 12 EC Karoo towns and their associated rural areas for selected years during 1911 to 2004. Twelve of the years were selected for the population analyses and ten years were selected for the enterprise analyses.
Are regions unique?
Once statistically significant Pareto rank-size distributions were recorded, it also became necessary to test the uniqueness of a region's population and enterprise distribution. It is possible that the towns in a region are analogous to a random selection of towns from a database. To test this possibility, six random selections were made of towns from a database of 206 South African towns that contains, among others, 2011 population and recent enterprise data for each town. The selected towns and their population and enterprise numbers are presented in Table 2. The rank-size distributions of population and enterprise numbers of each selection were analysed as described earlier.
It was hypothesised that if there are links between the towns of a region resulting in unique rank-size distributions, the same would not be observed for random selections of towns. The null hypothesis was that a random selection of towns from the database would not result in statistically significant rank-size distributions and/or dissimilar regression coefficients.
Results
Population rank-size distributions
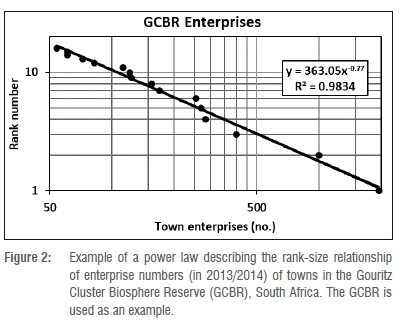
Pareto power laws describe the rank-size relationships of populations of the towns of the three regions for the respective years (Table 3). Figure 1 illustrates this relationship for the towns of the GCBR in 2013/2014. In all cases, except the GCBR towns in 1946, more than 90% of the variation was explained (see R2 in Table 3). There is clearly significant orderliness in the population agglomeration patterns of the South African regions investigated.
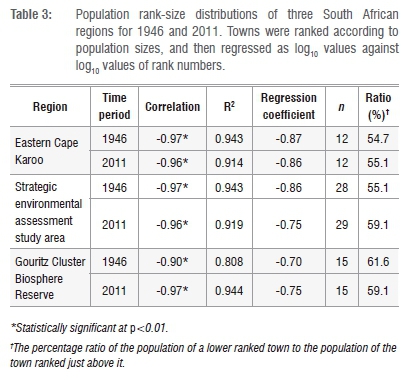
The exponent of Zipf's law for the population distribution of cities is normally -1 or close to it.23 The regions investigated here do not rigidly exhibit Zipf's law because their coefficients are lower than -1 (Table 3). Their Pareto rank-size distributions are nevertheless reasonably close to Zipf's law and predict that a lower-ranked town in the three regions investigated here would have from 55% to 62% of the population of a town just above it in the rank (Table 3).
To examine the time dependence of the population rank-size distribution, use was made of the database for the 12 EC Karoo towns of Nel and Hill.6Urban and rural population data recorded by Nel and Hill6 of 12 different years between 1911 and 2004 for the 12 towns were subjected to the same rank-size analyses described earlier. The results are presented in Table 4.
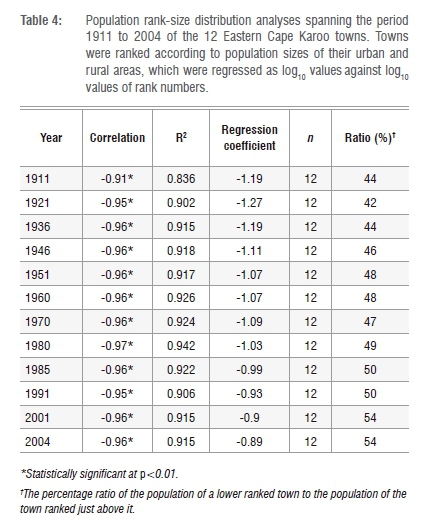
With the exception of 1911, more than 90% of the variation for every year was explained (see R2 in Table 4). The results substantiate the finding that the population rank-size distribution follows a Pareto power law (Table 4) and indicate that the relationship holds true over time. Changes in the regression coefficient show a definite pattern. It changed from -1.2 in the early 1900s to about -0.9 by the early 2000s. As a consequence, the population ratio of a lower-ranked town to a town ranked just above it has changed from about 40% in the early 1900s to just over 50% by the early 2000s (Table 4).
Enterprise number rank-size distributions
The rank-size relationships of enterprise numbers in 1946/1947 and 2013/2014 of the towns of the three regions and the ranks of their enterprise numbers are also described by power laws (Table 5). Figure 2 shows the relationship for the GCBR towns in 2013/2014. Except for the GCBR towns in 1946/1947, more than 90% of the variation was explained for both time periods (see R2 in Table 5). This result is not unexpected given the often-observed linear relationship between population sizes and enterprise numbers of South African towns.7-19 If the rank-size population distribution of towns in a region is described by a power law, the enterprise number rank-size distribution of the region should exhibit the same pattern.
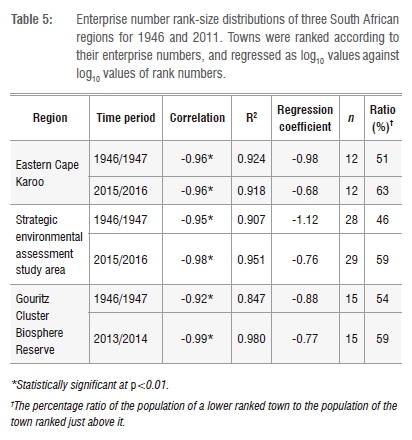
The ratios observed for the enterprise distribution of the three regions indicate that lower-ranked towns in the three regions have from 50% to over 60% of the enterprises of the towns ranked just above them (Table 5). The ratios of all towns in 2015/2016 were higher than those of 1946/1947, suggesting a shift over time. Based on these ratios there is no clear distinction between the different regions (Table 3).
To examine the time dependence of the enterprise number Pareto rank-size distributions of the EC Karoo towns, use was also made of the database for the 12 EC Karoo towns of Nel and Hill6. Enterprise numbers recorded by Nel and Hill6 of 10 years between 1904 and 2000 for the 12 towns were subjected to the same rank-size analyses described earlier. The results are presented in Table 6.
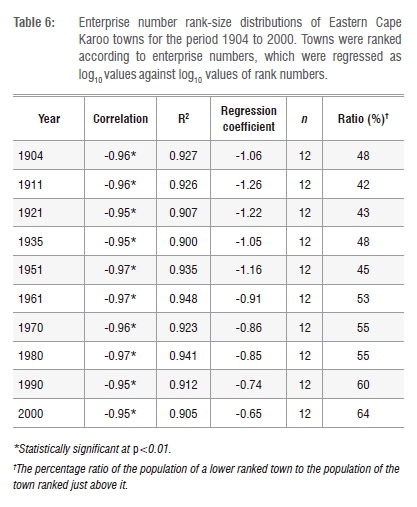
Pareto-like rank-size distributions of enterprises in the EC Karoo towns were observed between 1904 and 2000. Pareto rank-size distributions appear to be enduring and time-independent characteristics. The ratios observed for the enterprise distributions indicate that lower-ranked towns in the region varied from 42% to over 64% of the enterprises of the towns ranked just above them (Table 6). A definite shift in the ratio was observed after 1951: lower-ranked towns progressively had more enterprises relative to higher-ranked towns. This shift could be because lower-ranked towns had over time increased populations relative to higher-ranked towns (Table 3).
are statistically significant (Table 7). The regression coefficients varied from -0.48 to -0.70 with an average of -0.58±0.073, which is clearly lower than the regression coefficients of the three selected regions (Table 3). The average is also much lower than the century-long coefficients of the towns of the EC Karoo (Table 4). The ratios of more than 60% of lower-ranked towns to towns ranked just above them are consequently higher than those of the three regions (compare Table 7 with Tables 3 and 4). In randomly selected groups of towns, population numbers tend to be more evenly distributed.
The rank-size enterprise distributions of the selected groups also exhibited Pareto-like properties and the correlations are statistically significant (Table 7). The regression coefficients of the randomly selected groups varied from -0.56 to -0.71 with an average of -0.64±0.0059, which is somewhat lower than the regression coefficients of the three selected regions (Table 5). These coefficients are also lower than the century-long coefficients of the EC Karoo towns except for the year 2000. As a consequence, the ratios of lower-ranked towns to towns ranked just above them are higher (compare Tables 5 and 7). The enterprise numbers of randomly selected groups of towns were more evenly distributed than those of the three regions.
Because the database of more than 200 towns contains large as well as small towns, the random selection of 15 towns from it should yield a group that has a spread of town sizes (measured in terms of populations or enterprise numbers). This spread could lead to the recording of statistically significant log-log rank-size distributions, as was observed (Table 7). The coefficients of the randomly selected groups were, however, lower and their ratios higher than those of the three regions, which suggests that population agglomeration and enterprise development patterns of regions do have uniqueness. Expressed differently: what happens in one town of a specific region influences what happens in other towns of that region. Regions, however, do not appear to differ from one another.
Returning to the questions initially raised in this contribution, the following can be concluded:
-
Statistically significant log-log rank-size distributions apply to population agglomerations of towns in different regions of South Africa.
-
Such rank-size distributions also apply to the number of enterprises in these towns.
-
Based on the relationships observed, there is no clear distinction between different regions. However, the regional agglomerations differed from those of groups of towns randomly selected from a database (compare Tables 5 and 7). Regions, therefore, appear to have some uniqueness regarding such agglomerations.
Discussion
Population distribution across geographical areas is not random: there is a strong tendency toward agglomeration.1 Why then are there large and small towns? This question led Christaller to theorise about the centrality of towns, based on the services that towns deliver to their hinterlands.33 Christaller argued about a system of central places that exhibits a hierarchical principle: any goods supplied in a central place of order i is also supplied in all central places of order j>i. Centrality became an important issue in studies of South African towns.34
However, Eaton and Lipsey35 argued that Christaller's theory of central places is simultaneously a theory of the location and agglomeration of economic activity in which there is no force creating agglomeration, in which agglomeration serves no purpose, and in which no firm ever chooses a location. Despite this criticism, economic geographers and regional economists remain interested in the reasons for uneven regional development. They still ask why economic growth does not lead to similar levels of prosperity, employment and welfare across space (for example see Gardiner et al.36); a question of relevance also about South African regions.
A number of questions were posed in this study that can now be answered. Whereas population agglomeration patterns in many countries are subject to Zipf's law, a power law with Pareto-like characteristics1,2, this study has demonstrated that Pareto-like population and enterprise distributions close to Zipf's law are present in the towns of different South African regions (Tables 3 and 5) - a fact hitherto unknown. Morudu and du Plessis5 reported Zipf-like distribution of the population, employment and economic value addition characteristics of South African municipalities. The latter are organisations that are man-made constructs, often containing more than one town, which do not necessarily reflect the 'natural' way in which agglomeration phenomena evolve in towns of a region.
The Pareto distribution types encountered in this study have endured over a long time even when the regression coefficients progressively changed (Tables 3 and 6). The patterns recorded in regions differ from that of randomly selected groups of towns, suggesting that there is some uniqueness in the orderly way in which regions give rise to population and enterprise agglomeration patterns.
This study has revealed an additional dimension of the regularities observed between population and/or enterprise characteristics in South African towns.7-19 Previously, linear relationships between population and enterprise numbers and enduring power law relationships between total enterprise numbers and the enterprise richness (total number of enterprise types) of South African towns15,19 were recorded. This study recorded log-log agglomeration patterns for the population and enterprise numbers of regional towns. Population growth and distribution, and enterprise development and distribution, are clearly highly orderly processes. This fact should be factored into local economic development planning and support, as was also suggested by Morudu and du Plessis5.
The similarities in the variance patterns for population and enterprise distributions observed in this study, raise a 'chicken or egg' scenario, that is, does population growth precede enterprise development, or does enterprise development precede population growth? Fujita and Thisse37 argue that consumer behaviour predicts agglomeration because consumers face search costs and have incomplete information about the retail landscape, so they find it efficient to patronise larger centres. Firms cluster because of consumer behaviour and benefit from demand externalities by locating in the larger centres. Their thinking, therefore, implies that population growth precedes enterprise development. Eaton and Lipsey35 also commented that because the clustering of heterogeneous firms facilitates multipurpose shopping, it allows consumers to economise on shopping costs.
However, the contrary - that enterprise development could precede population growth - should also be considered. Gabaix2 stated that the creation of jobs is important and people are attracted to where there are jobs. This implies that enterprise growth has to take place before population growth results from immigration of people seeking employment. Eeckhout1 remarked that agglomeration and residential mobility of the population between different geographical locations are tightly connected to economic activity and that the evolution of populations across geographical locations is an extremely complex amalgam of incentives and actions taken by many individuals, enterprises and organisations.
Fransen29 remarked that most towns in the former Cape Colony in South Africa were not founded for commercial reasons. So-called 'church towns' developed around churches that were built to satisfy the needs of farming communities for religious services. In many cases following the building of a church, members of a congregation built 'town houses' for use when the rural families attended church services. Regular gathering of people in these settings created informal markets where goods were exchanged or bartered. These markets attracted entrepreneurs and the establishment of enterprises followed. In this case, population growth preceded enterprise growth. However, over time, the presence of enterprises and the possibility of finding employment, attracted more people to the fledgling towns, thereby growing the local market.
Population growth and enterprise development, therefore, seem to proceed hand in hand. On the one side, an entrepreneur might start a new business and if it is successful, it contributes to employment, which enhances the image of the town as a place to find employment. On the other side, a new immigrant attracted to the town enhances its total disposable income, thereby increasing the ability of the town to 'carry' more enterprises. This interdependence probably causes the similarities of the population and enterprise distribution patterns. This fits in with Eeckhout's suggestion that agglomeration and residential mobility of the population between different geographical locations are tightly connected to economic activity.1
However, a better understanding of the links between population and enterprise growth in regional towns still does not explain fully why some towns grow large and others stay small. Krugman's3 lament that there is not a good theory to account for the striking empirical regularities in population agglomeration patterns observed, which is now also the case for enterprise agglomeration patterns, still applies. There is a need to further explore these issues. The extreme skewness in population and enterprise numbers of different towns' distributions should, however, be considered in local economic development planning and execution.
Acknowledgements
Funding and support for this study was received from the Board of the Gouritz Cluster Biosphere Reserve and the Centre for Environmental Management, University of the Free State. Etienne Nel, Trevor Hill and Doreen Atkinson allowed access to their database on the towns of the Eastern Cape Karoo.
References
1. Eeckhout J. Gibrat's law for (all) cities. Am Econ Rev. 2004;94(5):1429-1451. https://doi.org/10.1257/0002828043052303 [ Links ]
2. Gabaix X. Zipf's law for cities: An explanation. Q J Econ. 1999;114(3):739-767. https://doi.org/10.1162/003355399556133 [ Links ]
3. Krugman P. Confronting the mystery of urban hierarchy. J Japan Int Econ. 1996;10(4):399-418. https://doi.org/10.1006/jjie.1996.0023 [ Links ]
4. Andriani P McKelvey B. From Gaussian to Paretian thinking: Causes and implications of power laws in organizations. Organ Sci. 2009;20(6):1053-1071. https://doi.org/10.1287/orsc.1090.0481 [ Links ]
5. Morudu H, Du Plessis D. Economic and demographic trends of municipalities in South Africa: An application of Zipf's rule. Town and Regional Planning. 2013;63:24-36. http://dx.doi.org/10.13140/2.1.2587.7125 [ Links ]
6. Nel E, Hill T. Marginalisation and demographic change in the semi-arid Karoo, South Africa. J Arid Env. 2008;72:2264-2274. https://doi.org/10.1016/j.jaridenv.2008.07.015 [ Links ]
7. Toerien DF, Seaman MT. The enterprise ecology of towns in the Karoo, South Africa. S Afr J Sci. 2010;106(5/6):24-33. http://dx.doi.org/10.4102/sajs.v106i5/6.182 [ Links ]
8. Toerien DF, Seaman MT. Proportionality in enterprise development of South African towns. S Afr J Sci. 2012;108(5/6):38-47. http://dx.doi.org/10.4102/sajs.v108i5/6.588 [ Links ]
9. Toerien DF, Seaman MT. Regional order in the enterprise structures of selected EC Karoo towns. S Afr Geogr J. 2012;94(2):1-15. http://dx.doi.org/10.1080/03736245.2012.742782 [ Links ]
10. Toerien DF, Seaman MT. Evidence of island effects in South African enterprise ecosystems. In: Mahamane A, editor. The functioning of ecosystems. Rijeka: Intech; 2012. p. 229-248. http://dx.doi.org/10.5772/36641 [ Links ]
11. Toerien DF. 'n Eeu van orde in sakeondernemings in dorpe van die Oos-Kaapse Karoo [A century of order in the enterprises of towns of the Eastern Cape Karoo]. LitNet Akad. 2014;11(1):330-371. Afrikaans. [ Links ]
12. Toerien DF. The enterprise architecture of Free State towns. Technical report 2014 DTK [document on the Internet]. c2014 [cited 2017 Jun 28]. Available from: https://www.researchgate.net/profile/Daan_Toerien/publications [ Links ]
13. Toerien DF, Seaman MT. Ecology, water and enterprise development in selected rural South African towns. Water SA. 2011;37(1):47-56. https://doi.org/10.4314/wsa.v37i1.64106 [ Links ]
14. Toerien DF, Seaman MT. Paradoxes, the tyranny of structures and enterprise development in South African towns. Paper presented at: Strategies to overcome poverty and inequality: Towards Carnegie3; 2012 September 3-7; Cape Town, South Africa. Available from: http://carnegie3.org.za/docs/papers/269_Toerien_Paradoxes,%20the %20tyranny%20of%20structures%20 and%20enterprise%20development%20in%20SA%20towns.pdf [ Links ]
15. Toerien DF, Seaman MT. Enterprise richness as an important characteristic of South African towns. S Afr J Sci. 2014;110(11/12), Art. #2014-0018, 9 pages. http://dx.doi.org/10.1590/sajs.2014/20140018 [ Links ]
16. Toerien DF. Enterprise proportionalities in the tourism sector of South African towns. In: Kasimoglu M, editor. Visions of global tourism industry: Creating and sustaining competitive strategies. Rijeka: Intech; 2012. p. 113-138. http://dx.doi.org/10.5772/37319 [ Links ]
17. Toerien DF. Economic value addition, employment, and enterprise profiles of local authorities in the Free State, South Africa. Cogent Soc Sc. 2015;1, Art. #1054610, 21 pages http://dx.doi.org/10.1080/23311886.2015.1054610 [ Links ]
18. Toerien DF. New utilization/conservation dilemmas in the Karoo, South Africa: Potential economic, demographic and entrepreneurial consequences. In: Ferguson G, editor. Arid and semi-arid environments: biogeodiversity, impacts and environmental challenges. New York: Nova Science Publishers; 2015. p. 79-123. [ Links ]
19. Toerien DF. The enduring and spatial nature of the enterprise richness of South African towns. S Afr J Sci. 2017;113(3/4), Art. #2016-0190, 8 pages. https://doi.org/10.17159/sajs.2017/20160190 [ Links ]
20. Knudsen T. Zipf's law for cities and beyond: The case of Denmark. Am J Econ Sociol. 2001;60(1):124-146. https://doi.org/10.1111/1536-7150.00057 [ Links ]
21. Scholes R, Lochner P Schreiner G, Snyman-Van der Walt L, De Jager M, editors. Shale gas development in the Central Karoo: A scientific assessment of the opportunities and risks. Stellenbosch: Council for Scientific and Industrial Research; 2016. Available from: http://seasgd.csir.co.za/wp-content/uploads/2016/12/SGD-Scientific-Assessment-Binder1_LOW-RES_INCL-ADDENDA_21Nov2016.pdf [ Links ]
22. Toerien D. Enterprise development and dynamics in the Gouritz Cluster Biosphere Reserve. Special Report (undated): Gouritz Cluster Biosphere Reserve [document on the Internet]. No date [cited 2017 Jun 25]. Available from: http://www.gouritz.com/enterprise-development-and-dynamics-ingcbr-%20towns-hot-off-the-press-repor%20t-available-a-quantitative-study-ofenterprise-%20development-and-dyna#.WuwqdIiFOUl [ Links ]
23. Brakman S, Garretsen H, Van Marrewijk C, Van den Berg M. The return of Zipf: Towards a further understanding of the rank-size distribution. J Regional Sci. 1999;39(1):183-213. https://doi.org/10.1111/1467-9787.00129 [ Links ]
24. Blank A, Solomon S. Power laws in cities population, financial markets and internet sites (scaling in systems with a variable number of components). Physica A. 2000;287:279-288. https://doi.org/10.1016/S0378-4371(00)00464-7 [ Links ]
25. Axtell RL. Zipf distribution of U.S. firm sizes. Science. 2001;293(5536):1818-1820. https://doi.org/10.1126/science.1062081 [ Links ]
26. Florence PS. The logic of British and American industry: A realistic analysis of economic structure and government. Chapel Hill, NC: University of North Carolina Press; 1953. [ Links ]
27. Axtell RL. Firm sizes: Facts, formulae, fables and fantasies. SSRN Electr J. 2006, working paper #44, 23 pages. https://doi.org/10.2139/ssrn.1024813 [ Links ]
28. Nel E, Taylor B, Hill T, Atkinson D. Demographic and economic changes in small towns in South Africa's Karoo: Looking from the inside out. Urban Forum. 2011;22:395-410. https://doi.org/10.1007/s12132-011-9131-z [ Links ]
29. Fransen H. Old towns and villages of the Cape. A survey of the origin and development of towns, villages and hamlets at the Cape of Good Hope. Johannesburg: Jonathan Ball Publishers; 2006. [ Links ]
30. Burman J. The Little Karoo. Cape Town: Human & Rousseau; 1981. [ Links ]
31. Population of South Africa: 1904-1970. Pretoria: Government Printing Works; 1976. [ Links ]
32. City population: South Africa [webpage on the Internet]. No date [cited 2017 May 25]. Available from: https://www.citypopulation.de/php/southafrica [ Links ]
33. Baskin CW. Central places in southern Germany. Translation of Christaller W: Die Zentralen Orte in Süddeutschland. Englewood: Prentice-Hall; 1966. [ Links ]
34. Van der Merwe IJ, Nel E. Die stad en sy omgewing: 'n studie in nedersettingsgeografie [The city and its environment: A study of settlement geography]. Stellenbosch: Universiteits-uitgewers; 1975. Afrikaans. [ Links ]
35. Eaton C, Lipsey RG. An economic theory of central places. Econ J. 1982;92(365):56-72. https://doi.org/10.2307/2232256 [ Links ]
36. Gardiner B, Martin R, Tyler P. Does spatial agglomeration increase national growth? Some evidence from Europe. J Econ Geogr. 2011;11(6):979-1006. https://doi.org/10.1093/jeg/lbq047 [ Links ]
37. Fujita M, Thisse J. Economics of agglomeration: Cities, industrial location, and regional growth. New York: Cambridge University Press; 2002. https://doi.org/10.1017/CBO9780511805660 [ Links ]
 Correspondence:
Correspondence:
Daan Toerien
Email: dtoerien@gonet.co.za
Received: 01 Aug. 2017
Revised: 26 Oct. 2017
Accepted: 15 Jan. 2018
Published: 30 May 2018
FUNDING: Gouritz Cluster Biosphere Reserve; University of the Free State














