Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Science
versión On-line ISSN 1996-7489
versión impresa ISSN 0038-2353
S. Afr. j. sci. vol.114 no.5-6 Pretoria may./jun. 2018
http://dx.doi.org/10.17159/sajs.2018/20170078
RESEARCH ARTICLE
Revelations from an online diagnostic arithmetic and algebra quiz for incoming students
Aneshkumar Maharaj; Thokozani Dlomo
School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Durban, South Africa
ABSTRACT
A review of relevant literature revealed that research indicates an alarming number of secondary school students who enter tertiary institutions display a serious lack of mathematical basics required for the study of university mathematics. This so-called change from the secondary school to tertiary study of mathematics has become an important field of mathematical learning research. In this context, at the University of KwaZulu-Natal, online diagnostics for pre-calculus knowledge and skills were made available to first-year mathematics students. We report here on some findings from an analysis of the provision of diagnostic questions for basic arithmetic and algebra. The results show that the diagnostic questions which were in the form of an online quiz assisted students to cope with their mathematics module in the sense that it positively impacted on the final results of students who attempted the quiz.
SIGNIFICANCE:
• Students who completed an online quiz on basic arithmetic and algebra to identify their strengths and weaknesses indicated that the quiz prepared them for the material they had to study for their mathematics module.
Keywords: preparedness; diagnostics; pre-calculus; performance; examinations
Introduction
The increase in the number of students entering university has revealed a greater inconsistency in the background levels of those students enrolled for first-year mathematics modules.1 This transition from secondary to tertiary education in mathematics creates a complex phenomenon covering a huge range of problems and issues.2Although it is believed that there is evidence of similar transitional issues in other disciplines in science, it seems that the transition in mathematics is by far the most serious and the most problematic.3,4 A possible reason for this discrepancy is the many changes that take place in the transition from secondary to tertiary education. These include changes in teaching and learning styles, the type of mathematics that is taught, conceptual understanding, procedural knowledge that is required to advance through and the changes in the level of advanced mathematical thinking needed.5 News24, a local online newspaper, reported that, according to Umalusi (a South African council for quality assurance in general and further education and training), matric (Grade 12) mathematics results were worse in 2014 than in the previous years.6 This news report supports the perception that there is a very serious decline in core mathematical skills. Because a percentage of those matric students enrol for tertiary studies in mathematics in subsequent years, this issue should be of concern to those who lecture to such students, especially in first-year mathematics modules.
Jennings2 is of the opinion that it has now become even more important to understand a student's prior knowledge of mathematics before they study tertiary mathematics. The main reasons for this need are: (1) to find out whether a student would benefit from additional support on basic arithmetic and algebra, offered in an online format and (2) to produce suitable first-year students who are going to be competent throughout their course of study. These are not the only reasons, but we have chosen in this paper to focus on these two given reasons. For students to be competent throughout their course of study, necessary steps need be taken to improve their performance, which implies that all possible assistance should be available to students to reach the ultimate goal of succeeding in their mathematics course. For this reason, at the University of KwaZulu-Natal (UKZN), the provision of online diagnostic questions for basic mathematical knowledge and skills for incoming students was rolled out at the beginning of February 2015. Keeping in mind the fact that not all the students attempted the online quiz, for this paper the final performance of students who completed the quiz was considered for the analysis and compared with the performance of those students who did not take the quiz.
Research question
The main research question was: What does an investigation into completion of the online diagnostic basic arithmetic and algebra quiz by incoming university students reveal? To answer this question the following sub-questions were formulated for the provision that was in place for 2015: (1) What was the participation level of students with regard to the online diagnostic quiz? (2) What was the performance level of students with regard to the online diagnostic quiz? (3) How did students' participation in the quiz affect their performance in the final examination? (4) What are the views of students on the impact of this online diagnostic quiz?
Literature review
There has been a huge concern about the inflow of students to tertiary level institutions who are lacking the fundamentals in mathematics. It is perceived that the majority of students have difficulties with mathematical basics in arithmetic and algebra. Breiteig and Grevholm7 noted that the abstractness of algebra is one reason for students' problems. This problem impacts on the study of calculus because algebra is a pre-requisite for such studies. This lack of student preparedness has consequences for student and staff satisfaction, student self-esteem, retention and progression of students, and financial costs to universities and to students arising through failure to progress or complete a course.3 According to Kaput8, algebra is a route to higher mathematics, but at the same time a barrier for many students which forces them to take another educational direction. On the transition from arithmetic to algebra, Moseley and Brenner9 noted that ' ...moving from arithmetic problems to working with more symbolic representations of relationships with variables in algebra is an area of persistent difficulty for many' (p. 4). The provision of diagnostic questions for basic arithmetic and algebra focused on in this paper was intended to assist the students to develop the ability to see variables as representations of unknown quantities that, despite their abstract nature, can still be altered by the arithmetic operations.9 Looking at the challenges that students have concerning mathematics and also considering the importance of mathematics in our modern society, it is not surprising that learning support in mathematics is becoming ever more important.10
To address the under-preparedness of incoming students to study mathematics, many universities offer mathematical support services such as tutors, online resources and individual consultations in order to improve the results of the students.11 The majority of institutions in Ireland and internationally now make use of diagnostic testing for incoming first-year students.11 This kind of support gives students an opportunity to revise some basic concepts in mathematics. It is believed that, generally, diagnostic testing has helped to indicate the level of preparedness of students who are entering tertiary level and has also contributed to some level of improvement in their final results.11 Thus it bridges the gap between the level of preparedness expected or required upon entry level and the mathematical capabilities acquired by new students. At UKZN, such online support was put in place. Students attempt the quizzes online to improve their knowledge or to practise a particular topic. Online quizzes can be attempted an unlimited number of times and there is no time limit to complete the quiz questions. Thus, a student has the opportunity to work on the quiz questions and improve on their basic knowledge and skills considered relevant for the study of calculus. The article by Maharaj and Wagh12 provides detailed information on how the quiz questions were formulated based on the identified expected learning outcomes for basic arithmetic and algebra. Those identified outcomes were used to frame suitable online diagnostic questions. In this paper, we focus on the provision of those diagnostics to students.
Conceptual framework
Our conceptual framework was informed by the literature review and was guided by the following:
1. The study of mathematics is hierarchical in nature.13
2. To study university calculus, students need to have adequate knowledge and skills relating to basic arithmetic and algebra.4
3. The provision of suitable online diagnostic questions on basic arithmetic and algebra could improve the level of student competencies with regard to these.11,12
4. There was a need to research the impact of the provision of online diagnostics for pre-calculus as offered at UKZN before a decision could be arrived at as to whether the quizzes should be made compulsory for all incoming students who want to study first-year calculus.
Methodology and participants
The UKZN learning MOODLE site for Diagnostics for Pre-calculus was used for data collection. On this site, students had access to five pre-calculus quizzes that were designed to focus on relevant knowledge and skills for the study of calculus. The students had to first complete an online consent letter, as required by the research office at UKZN for ethical clearance (protocol reference number HSS/1058/014CA). The Basic Arithmetic and Algebra quiz was used to gather data on the participants who completed the quiz. The quiz consisted of 24 questions which involved purely basic mathematical knowledge in arithmetic and algebra. Each question carried a maximum of 2 marks. The system awarded 2 marks if a student submitted the correct answer for their first attempt. If the first attempt was incorrect, the system awarded 1 mark for a correct second or third attempt. A final mark of zero was awarded for a question if the first three or more attempts were incorrect. For the study, only those students who completed all the quiz questions were regarded as having taken the quiz. Students who submitted their responses to only some of the questions were considered as having not attempted the quiz.
The quiz was attempted by students from different first-semester mathematics modules offered at UKZN: Introduction to Calculus (Math130), Mathematics for Natural Sciences (Math150), Mathematics 1A Engineering (Math131) and Quantitative Methods (Math134). In total, there were 1888 attempts for the quiz, which indicated the overall number of attempts. That number was reduced to 997 based on the criteria that only students who completed the quiz were considered for the study. For the purpose of this study, it was decided to investigate the impact of the quiz on the final results of students enrolled for the Math130 and Math150 modules. The reason for this choice was that Math130 is a core module for students who want to continue with further studies in mathematics, while Math150 is a compulsory module for other students who want to study science.
A total of 250 students enrolled for Math130, and out of those, 95 students attempted the quiz, so 155 students did not attempt the quiz. A total of 872 students enrolled for Math150, and out of those, 392 students attempted the quiz, so 480 did not attempt the quiz. For the students who attempted the quiz more than once, only their highest-graded complete attempt was considered. Students' responses for the quiz were used to gather information to answer the research question. On the system, each question was allocated a maximum of 2 points. As indicated earlier, if the first attempt submitted was incorrect then there was a penalty for subsequent attempts. After studying the students' performances, it was decided to use the following interval mark ranges for each question: 1.70 and below; 1.70 to 1.89; 1.90 and above.
A questionnaire was also formulated to obtain students' views on the diagnostic quiz and how it could be improved. Participants were chosen based on the criteria that they used the learning site to attempt the quiz questions. An email was sent to such students indicating that research was being conducted to gauge the effectiveness of the provision of the online diagnostics in which they participated and that they were invited to complete the online questionnaire. Also, the final examination results for all the students registered for the two modules were obtained from the UKZN Student Management System website. Those final results were used to determine if there were differences in the final scores between the students who attempted the quiz and those who did not.
The final examination results lists were obtained for Math130 and Math150. Each list was used to separate the students into two groups: students who completed the quiz and students who did not complete the quiz. Because we were comparing the two population means within a large data set, the two-sample z-statistical test was used, which follows a normal distribution and the population samples are independent.14 The Z-test formula used was:
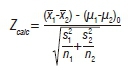
where Zcalc is a calculated Z value; and x, s, μ and n represent the sample mean, standard deviation, population mean and the number of students who attempted the quiz, respectively, for both groups. Setting up the hypothesis test, we wanted to determine if there is a difference in the final examination results of the students who attempted the quiz compared to those who did not. Thus our null hypothesis was: attempting the quiz had no effect on final examination results. That is:
H0 : μ1 - μ2 =0 or H0 : μ1 - μ2
Against the alternative hypothesis:
H1 : μ1 > μ2
According to the null hypothesis, our population mean difference is zero. In the formula, this is represented as (μ1-μ2)0.
Not all students wrote the final examinations. Possible reasons for not writing the final examination include that students dropped out of the module or did not obtain Duly Performed (DP) Certificates. The data for such students were excluded from the study. For the testing of this hypothesis, only student attempts for Math130 and Math150 were considered. As indicated before, the former is a mainstream module undertaken by students who want to continue with studies in mathematics, while the latter is a compulsory service module offered to science students.
Entry requirements for the mathematics modules
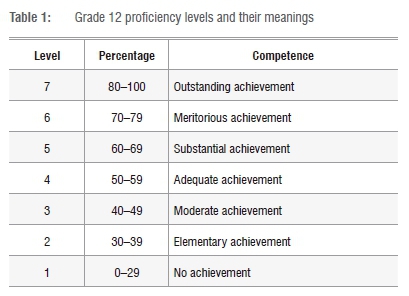
The following entry requirements were obtained from the UKZN College of Agriculture, Engineering and Science handbook.15 For Math130 (Introduction to Calculus), the pre-requisite requirement was: Higher Grade D or Standard Grade A for matric Mathematics, or NSC Level 5 Maths. For Math150 (Mathematics for Natural Sciences), the prerequisite requirement was: Higher Grade E or Standard Grade B for matric or NSC Level 4 Maths. The minimum pre-requisite requirements for each of those two modules are regarded as being equivalent by the College of Agriculture, Engineering and Science. For each of those two modules, the students who were enrolled satisfied the minimum requirements. In a case in which a student did not meet the minimum requirements, the student was required to enrol for a foundation mathematics module, called Math199. After a student passed Math199 with a specified minimum percentage, then they qualified to enrol for Math130 or Math150. The purpose of Math199 is to equip students with mathematical tools that are needed for their chosen mathematics module. Table 1 indicates the percentage ranges for the different levels and their meaning, which were in operation from 2008 onwards for the National Senior Certificate examinations (NSC). Because some participants completed their Grade 12 examinations before the year 2008, during which period symbols were used, the necessary conversions were done to match the old Grade 12 symbols with the new levels.
Participants' Grade 12 mathematics and English proficiency levels
In this section we focus on the mathematics and English proficiencies of the Math130 and Math150 students as determined by the NSC examinations. For each module, bar graphs represent visually the spread of the NSC levels and the frequency for each of those levels.
Figure 1 indicates that the majority of students in both the groups had proficiency levels from 5 to 7, with regard to their senior certificate mathematics and English results. Also note that from the Math130 entry requirements it was required that students who wanted to be enrolled for Math130 had to have obtained at least a level 5 in their senior certificate mathematics. There was also a small number of students who achieved less than level 5. Those students were the ones who did foundation mathematics (Math199), and after passing with at least 60% were enrolled for Math130.
Figure 2 indicates that the majority of students attained levels from 4 to 6 with regard to their results for senior certificate mathematics and English. Note that for Math150, the entry requirement was a pass at at least a level 4 for mathematics. There was also a small number of students who achieved less than level 4. Those students were the ones who did foundation mathematics (Math199), and after passing with at least 50% were enrolled for Math150.
With the above focus on the Grade 12 entry requirements and their frequencies, it was revealed that for each module the two student groups considered were not of different ability levels with regard to their school achievement for mathematics and English. For mathematics, they could be grouped into one category because of the entry requirements for each module. The implication here is that in testing the hypothesis for each module, the participants who completed and those who did not complete the quiz could be regarded as being of similar ability levels with regard to their mathematics and English proficiency when they were enrolled for their university mathematics modules.
Analysis, findings and discussion
The analyses and findings are presented under the following subheadings: Average student scores per question; student participation and performance levels; and student views on impact of quiz.
Average student scores per question
These results are for all the students across the different modules who attempted and completed the quiz on Basic Arithmetic and Algebra.
Looking at Figure 3, which gives the average student scores for each question, we observe that the questions could be placed into one of three categories, for which the students: (1) scored an average of 1.70 and below, (2) between 1.70 to 1.89 and (3) an average of 1.90 and above. A high average shows that most students scored full marks on the particular question, that is, they correctly answered the question. Likewise, when the average is low it shows that on that question students did not perform well.
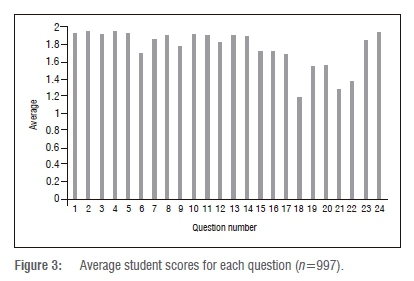
Scores of 1.70 and below
Looking at Figure 3, student performance in Questions 17 to 22 was below the average of 1.70. This score indicates that students had difficulty in answering these questions. The following are the types of questions for which students scored 1.70 and below:
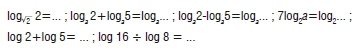
The finding is that questions on the application of basic properties for logarithms were not adequately understood by students. The implication is that first-year mathematics lecturers should be aware of and plan to address this shortcoming. If one accepts the principle of moving from the known to the unknown, then it is important to determine and address this shortcoming before the students are exposed to the natural logarithm and its notation, that is lnx.
Scores of 1.70 to 1.89
As can be seen in Figure 3, students performed in this intermediate range for Questions 6, 7, 9, 12, 15, 16 and 23. The following are the types of questions for which students scored marks in this interval:
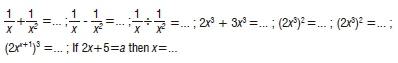
The finding here is that, although students performed better, these types of questions could become stumbling blocks to their success when faced with calculus-related questions that require knowledge and skills based on the following: (1) addition, subtraction and division of algebraic fractions, (2) adding like terms, (3) applying the raising a power to a power law for exponents and (4) solving a linear equation in which a constant is represented by a letter. The implication is that measures need to be put in place to improve the proficiency of students with regard to these fundamentals.
Scores of 1.90 and above
It is evident from Figure 3 that average student performance was the highest for Questions 1-5, 8, 10, 11, 13, 14 and 24. This gives the impression that these questions were simple and easy to answer for the participants. The following are the types of questions for which students scored in this interval range:
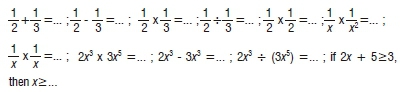
The finding here is that students displayed adequate proficiency for knowledge and skills based on: (1) addition, subtraction, multiplication and division of arithmetic fractions, (2) multiplication of simple algebraic fractions of the type indicated, (3) applying the multiplication and division laws of exponents for which base is the same, (4) subtracting like terms and (5) solving simple linear inequalities. The average student scores suggest that students were more proficient in subtracting like terms than they were at adding like terms, which seems strange; the question on the subtraction of like terms seems to be more difficult because it requires the calculation 2 - 3 compared with the easier calculation of 2 + 3.
Student participation and performance levels
These results are presented under the following sub-headings: Students enrolled for Math130 and students enrolled for Math150.
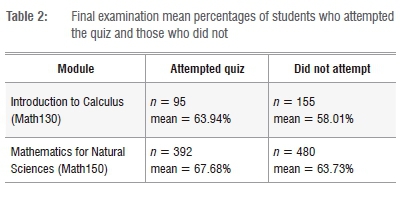
Table 2 indicates that of 250 students who wrote the Math130 examinations, 95 students completed the quiz and 155 did not. For Math150, 872 students wrote the exam, 392 completed the quiz and 480 did not. We note that average examination marks for both modules were higher for students who completed the quiz compared with students who did not. For both modules, there was a large number of students who did not attempt the quiz, because participation was voluntary.
Students enrolled for Math130
Here we present our findings on the impact of the quiz on the average final examination marks of students who completed the quiz (n=95) and those who did not (n=155).
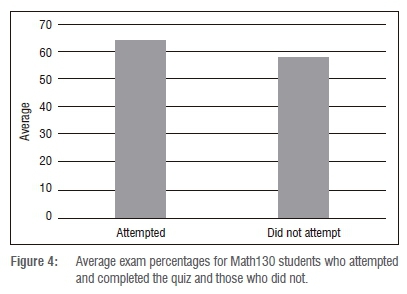
Figure 4 shows the overall performance in the Math130 final examinations for students who completed the quiz and those who did not. From Figure 4 and Table 2, we observe that students who completed the quiz scored an average examination mark of 63.94% and those who did not scored an average mark of 58.01%. So the students who completed the quiz scored on average about 6% higher in their final examination compared with students who did not take the quiz. The implication here seems to be that completing the quiz impacted positively on the final examination results of the students. However, before any conclusions can be reached, we need to determine if the difference is statistically significant.
A 99% level of significance (α=0.01) was used. We tested the null hypothesis:
H0 : μ1 - μ2 = 0
Versus the alternative hypothesis:
H1 : μ1 > μ2.
The test statistic Zcalc=3.128 and H0 is rejected if Za< Zcalc where Za was obtained from a Normal Z table. As Za=Z0.01 and Zcalc=3.128, it follows that Za < Zcalc so we conclude that H0 is rejected. Thus, the results verify that the difference is statistically significant at a 99% confidence level, that is, that the students who completed the quiz performed better in their examinations than those who did not.
Students enrolled for Math150
We present our findings on the impact of the quiz on the average final examination marks of students who completed the quiz (n=392) and those who did not (n=480).
Figure 5 illustrates the overall average performance of Math150 students who completed the quiz and those who did not. From Figure 5 and Table 2, we observe that students who completed the quiz scored an average final exam mark of 67.68% and those who did not scored 63.73%. So students who took the quiz scored on average about 4% higher in their final examination than students who did not take the quiz. The implication seems to be that attempting the quiz improved the final examination results of the students. However, once again, before any conclusions can be reached, we need to determine whether the difference is statistically significant.
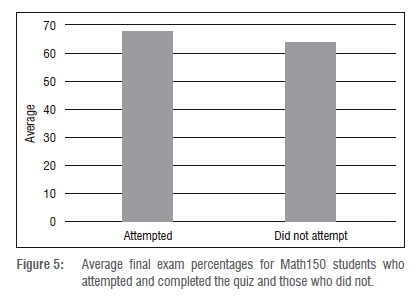
A 99% level of significance (α=0.01) was used. We tested the null hypothesis:
H0 : μ1 - μ2 = 0.
Versus the alternative hypothesis:
H1 : μ1 > μ2
The test statistic arrived at was Zcalc= 4.142. Za was obtained from a Normal Z table. As Za=Z0.01=2.58 and Zcalc= 4.142, the implication is that Za < Zcalc so we conclude that H0 should be rejected. Thus the results verify that the difference is statistically significant at a 99% confidence level, that is, that the students who completed the quiz performed on average better in their final examinations than those who did not.
Student views on impact of quiz
A questionnaire consisting of 10 multiple-choice and open-ended questions was completed by 60 students from both Math130 and Math150. The questions and student responses are indicated in Table 3.
Table 3 indicates that the majority of the respondents felt that the online diagnostic quiz was helpful to them, it was easy to access the diagnostic quiz online and that they were likely to continue attempting diagnostic quizzes online. Furthermore, students felt that the online diagnostic quiz related well to the course topics and that the online diagnostic quiz on Basic Arithmetic and Algebra helped them to understand key concepts in the relevant university mathematics module for which they were registered. This response is quite significant because the diagnostic quiz focused on identified knowledge and skills for basic arithmetic and algebra which are prerequisites for the modules for which the respondents were enrolled. The response to Question 6 indicates that the majority of the respondents were satisfied with the online diagnostic quiz. Note that at least 15% indicated that they were extremely satisfied. This response is worth noting as extremely satisfied was not indicated as a possible option in the framing of the question. The finding from the data was that the majority of the respondents rated the importance of attempting the online quiz towards the higher end of the scale, that is 7 or more. The responses for Questions 5 to 9 indicate that the majority of the students rated highly that taking the quiz was of benefit to them. The second and third responses that are indicated as common responses to Question 10 could be used to improve on the online diagnostic quiz. It is clear that some students want more challenging quiz items. Also, for students who do not answer correctly, there is a need to give more feedback that could help them. Perhaps the idea of building in pop-ups to further assist such students, as was suggested by a previous study16, should be considered.
Conclusions and recommendations
Although participation in the quiz was voluntary, it was found that a satisfactory number of students registered for each of the modules on which the study focused completed the quiz. For the Introduction to Calculus (Math130) module, the participation from registered students was 38% while for the Mathematics for the Natural Sciences (Math150) module it was 45%. Quiz items that were based on the application of basic laws for logarithms gave the students the most difficulty. Further, it was found that the students who completed the quiz performed better in their examinations than those who did not attempt or complete the quiz. This was determined at a 99% confidence level for each of the two modules, Math130 and Math150. For those modules it was found that the majority of students in both groups (those who completed and those who did not complete the quiz) had similar proficiency levels with regard to their senior certificate mathematics and English results.
Thus the quiz should be made compulsory for incoming students who want to study calculus, because the research shows that there was a positive correlation between completing the quiz and final examination results. This positive correlation was for both the modules. Also from the questionnaire responses it was noted that the majority of those students who responded felt that the online diagnostic quiz benefitted them and contributed to their understanding of key concepts in the mathematics module for which they were enrolled. These responses suggest that those students appreciated that the basic concepts and skills for arithmetic and algebra formed the foundation for their university calculus modules.
We recommend that the quiz should be made compulsory because the research shows that it had a positive impact on students' final examination results. It is also recommended that the lecturing staff should analyse the results of quiz items to determine which pre-calculus knowledge and skills require attention and address these areas so that subsequent teaching of the relevant calculus concepts is likely to be beneficial to their students.
Acknowledgements
We acknowledge the National Research Foundation (South Africa) for supporting T.D. to be part of their internship programme for 2015/2016 and for making available grants for the project 'Online diagnostics for undergraduate mathematics'. We thank UKZN for allowing us to use the data on MOODLE and also the students' results for research purposes. Eskom is acknowledged for providing grants for the UKZN-Eskom Mathematics Project, which laid the groundwork for assisting students to cope with their university mathematics studies.
Authors' contributions
A.M. was responsible for the conceptualisation of the study and proofreading the paper. T.D undertook the data collection. Both authors analysed the data and wrote the paper.
References
1. Hoyles C, Newman K, Noss R. Changing patterns of transition from school to university mathematics. Int J Math Educ Sci Technol. 2001;32(6):829-845. https://doi.org/10.1080/00207390110067635 [ Links ]
2. Jennings M. Issues in bridging between senior secondary and first year university mathematics. In: Hunter R, Bicknell B, Burgess T, editors. Crossing divides: Proceedings of the 32nd Annual Conference of the Mathematics Education Research Group of Australasia. Volume 1. Palmerston North, NZ: MERGA; 2009. p. 273-280. [ Links ]
3. Croft AC, Harrison MC, Robinson CL. Recruitment and retention of students - An integrated and holistic vision of mathematics support. Int J Math Educ Sci Technol. 2009;40(1):109-125. https://doi.org/10.1080/00207390802542395 [ Links ]
4. Kajander A, Lovric M. Transition from secondary to tertiary mathematics: McMaster University experience. Int J Math Educ Sci Technol. 2005;36:149-116. https://doi.org/10.1080/00207340412317040 [ Links ]
5. Hong YY Kerr S, Klymchuk S, McHardy J, Murphy P Thomas M, et al. Teacher's perspective on the transition from secondary to tertiary mathematics education. In: Hunter R, Bicknell B, Burgess T, editors. Crossing divides: Proceedings of the 32nd Annual Conference of the Mathematics Education Research Group of Australasia. Volume 1. Palmerston North, NZ: MERGA; 2009. p. 241-248. https://doi.org/10.1080/00207390903223754 [ Links ]
6. Maths, physics results worse than 2013 - Umalusi. News24. 2014 December 30. Available from: http://www.news24.com/SouthAfrica/News/Maths-physics-results-worse-than-2013-Umalusi-20141230 (reference) [ Links ]
7. Breiteig T, Grevholm B. The transition from arithmetic to algebra: To reason, explain, argue, generalize and justify. In: Novotná J, Morová H, Krátká M, Stehlíková NA, editors. Proceedings of the 30th Conference for the International Group for the Psychology of Mathematics Education. Prague: Charles University Prague; 2006. p. 2-225-2-232. [ Links ]
8. Kaput J. A research base supporting long term algebra reform. In: Owens DT Reed K, Millsops GM, editors. Proceedings of the 17th Annual Meeting of the North America Chapter of PME. Volume 2. Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education; 1995. p. 71-108. [ Links ]
9. Moseley B, Brenner ME. A comparison of curricular effects on the integration of arithmetic and algebraic schemata in pre-algebra students. Instr Sci. 2009;37:1-20. https://doi.org/10.1007/s11251-008-9057-6 [ Links ]
10. Carroll C. Evaluation of the University of Limerick Mathematics Learning Centre [BSc report]. Limerick: University of Limerick; 2011. [ Links ]
11. Sheridan B. How much do our incoming first year students know?: diagnostic testing in Mathematics at third level. Ir J Acad Pract. 2013;2(1), Art. #3, 19 pages. Available from: https://arrow.dit.ie/cgi/viewcontent.cgi?referer=https://www.google.co.za/ &httpsredir=1&article=1010&context=ijap [ Links ]
12. Maharaj A, Wagh V. An outline of possible pre-course diagnostics for differential calculus. S Afr J Sci. 2014:110(7/8), Art. #2013-0244, 7 pages. http://dx.doi.org/10.1590/sajs.2014/20130244 [ Links ]
13. Makuuchi M, Bahlmann J, Friederici AD. An approach to separating the levels of hierarchical structure building in language and mathematics. Phil Trans R Soc B. 2012;367:2033-2045. https://doi.org/10.1098/rstb.2012.0095 [ Links ]
14. Groebner DF, Shannon PW, Fry PC, Smith KD. Business statistics: A decision making approach. 6th ed. Upper Saddle River, NJ: Pearson Education Inc.; 2005. [ Links ]
15. University of KwaZulu-Natal (UKZN). College of Agriculture, Engineering and Science handbook. Pietermaritzburg: College of Agriculture, Engineering and Science, UKZN; 2015. [ Links ]
16. Maharaj A, Brijlall D, Narain O. Designing website-based tasks to improve proficiency in mathematics: A case of basic algebra. Int J Educ Sci. 2015;8(2):369-386. https://doi.org/10.1080/09751122.2015.11890259 [ Links ]
 Correspondence:
Correspondence:
Aneshkumar Maharaj
Email: maharaja32@ukzn.ac.za
Received: 16 May 2017
Revised: 24 Oct. 2017
Accepted: 11 Dec. 2017
Published: 30 May 2018
FUNDING: Eskom; National Research Foundation: South African Agency for Science and Technology Advancement














