Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.113 n.9-10 Pretoria Sep./Oct. 2017
http://dx.doi.org/10.17159/sajs.2017/20160345
RESEARCH ARTICLE
The benefits of segmentation: Evidence from a South African bank and other studies
Douw G. Breed; Tanja Verster
Centre for Business Mathematics and Informatics, North-West University, Potchefstroom, South Africa
ABSTRACT
We applied different modelling techniques to six data sets from different disciplines in the industry, on which predictive models can be developed, to demonstrate the benefit of segmentation in linear predictive modelling. We compared the model performance achieved on the data sets to the performance of popular non-linear modelling techniques, by first segmenting the data (using unsupervised, semi-supervised, as well as supervised methods) and then fitting a linear modelling technique. A total of eight modelling techniques was compared. We show that there is no one single modelling technique that always outperforms on the data sets. Specifically considering the direct marketing data set from a local South African bank, it is observed that gradient boosting performed the best. Depending on the characteristics of the data set, one technique may outperform another. We also show that segmenting the data benefits the performance of the linear modelling technique in the predictive modelling context on all data sets considered. Specifically, of the three segmentation methods considered, the semi-supervised segmentation appears the most promising.
SIGNIFICANCE:
• The use of non-linear modelling techniques may not necessarily increase model performance when data sets are first segmented.
• No single modelling technique always performed the best.
• Applications of predictive modelling are unlimited; some examples of areas of application include database marketing applications; financial risk management models; fraud detection methods; medical and environmental predictive models.
Keywords: predictive models; case studies; logistic regression; linear modelling; semi-supervised segmentation
Introduction
Predictive modelling is the general concept of building a model that is capable of making predictions by predicting a target variable based on various explanatory variables. Specifically in this paper, the target variable will be binary, i.e. there are only two possible outcomes.
The number of modelling techniques available in predictive modelling is extensive.1 These techniques can be split into linear and non-linear modelling techniques. Linear modelling techniques assume a linear relationship between the target variable and each explanatory variable. Linear modelling techniques are typically easier to understand and very transparent. For these reasons, linear modelling techniques are the most used techniques in industry. However, linear modelling techniques may in some cases perform worse in terms of model performance and may be less robust as a result of the linearity assumption made. In this paper, we show that, by first segmenting the data, linear modelling techniques can perform just as well (and sometimes better) than popular non-linear modelling techniques.
Non-linear modelling techniques, on the other hand, are typically more complex and do not assume a linear relationship between the target variable and each explanatory variable. Non-linear modelling techniques are not as transparent but usually more robust and sometimes perform better in terms of model performance.2
In the process of determining how well a predictive modelling technique performs, the lift of the model is considered, where lift is defined as the ability of a model to distinguish between the two outcomes of the target variable.3 There are several ways to measure model lift and in this paper Gini coefficient was chosen.
Segmentation of the data that are used for predictive modelling is a well-established practice in the industry.4-6 The ultimate goal of any segmentation (in the predictive modelling context) is to achieve more accurate, robust and transparent models.6 Segmentation is defined as the practice of classifying (or partitioning) data observations into distinct groups or subsets with the aim of developing predictive models on each of the groups separately, in order to improve the overall predictive power.
Two main streams of statistical segmentation exist in the industry, namely unsupervised and supervised segmentation.7,8 Unsupervised segmentation7 focuses on the explanatory variables in the models, whereas supervised segmentation8 focuses on the target variable. We also used a third stream, combining both aspects, called semi-supervised segmentation, as developed in a recent PhD thesis.9
The main objective of this paper was to compare the model performance when first segmenting the data before fitting a linear modelling technique to the model performance of popular non-linear modelling techniques that may not require segmentation. Of the three methods of segmentation that were compared, semi-supervised segmentation looks the most promising overall.
Modelling techniques
Linear modelling technique
The most common linear modelling technique is linear regression; however, when modelling a binary target variable using linear regression, two problems arise.2 The first problem is that one of the assumptions underlying the linear regression model does not hold, namely normally distributed error terms. The second problem is that in linear regression, no bounds are on the target variable, whereas with a binary target variable, the target variable is restricted to two outcomes. To overcome these problems, logistic regression is used (by combining linear regression with a specific bounding function), which is sometimes referred to as the logit transformation10, i.e. the log of the odds of the probability of the target variable.
Technical specifications
SAS software's Proc Logistic was used with default settings with the addition of using stepwise selection as a subset selection criterion. Note that this means that the final regression analysis does not use all of the explanatory variables, but selects a subset of variables that explains the target variable in the most efficient way.
Three methods of segmentation
We first segmented the data before fitting a logistic regression to the data. As mentioned, two main streams of statistical segmentation exist in the industry: unsupervised and supervised segmentation.7,8 Unsupervised segmentation7 focuses on the explanatory variables in the models to be developed and does not take the target variable into account; a popular example of unsupervised segmentation is clustering. Supervised segmentation focuses on the target variable; a popular example of supervised segmentation is the decision tree.
Both these streams make intuitive sense depending on the application and the requirements of the models developed11 and many examples exist in which the use of either technique has improved model performance12. However, both these streams focus on a single aspect (i.e. either target separation or independent variable distribution) and combining both aspects might better deliver. This approach is explored in Breed et al.13 and described in more detail in a recent PhD thesis9 and was used as the third segmentation method. This specific technique uses k-means clustering to measure the independent variable distribution and uses information value to measure target separation. A supervised weight is defined to measure the balance between the two aspects.13 This algorithm is thus called SSSKMIV to indicate semi-supervised segmentation as applied to k-means using information value. The implementation of this algorithm is quite complex and the detail can be found in Breed9.
Technical specifications
All three segmentation methods were implemented in SAS. The detail of the technical specifications (e.g. the optimal number of segments, the weight parameters in SSSKMIV, the optimal value of k in the k-mean algorithm, heuristic example) can be found in Breed9.
Non-linear modelling techniques
For the non-linear modelling techniques, we used: neural networks; support vector machines; memory-based reasoning; decision trees (used here as the final model, not as segmentation) and gradient boosting (which is a boosting variation of random forests).
Technical specifications
The results of the non-linear modelling techniques were obtained through SAS Enterprise Miner software using specific nodes. Nodes are tools in SAS Enterprise Miner that implement, for example, different modelling techniques.14 By using the default settings in SAS Enterprise Miner, the benefits of most techniques were utilised (e.g. subset selection is automatically done and complexity is automatically optimised).
Neural networks (also known as multilayer perceptrons) are often regarded as mysterious and powerful predictive tools, but on closer inspection the most typical form of a neural network is just a regression model with a flexible addition. The power of this addition must not be underestimated and enables the neural network to model virtually any relationship between the explanatory variable and the target variable.14 Neural networks have been researched since the early 1940s15 and are very well known in the predictive modelling field today.
Technical specifications
The AutoNeural Node of SAS Enterprise Miner software was used with default settings.
Support vector machines were introduced in the 1990s and are considered to be relatively new (compared to other well-known modelling techniques).16 Support vector machines have been researched quite extensively over the last number of years.17-19. They predict a binary target by maximising the margin between the two outcomes through hyperplanes; more detail can be found in Meyer and Wien19.
Technical specifications
The Enterprise Miner SVM (support vector machine) node was used with default settings, with one exception: the estimation method was set to least squares support vector machine as opposed to decomposed quadratic programming, as this setting failed to find a conclusive result on one of the six data sets (the claim prediction data set).
Memory-based reasoning uses k-nearest-neighbour principles to classify observations in a data set. When a new observation is evaluated, the algorithm allows the k-nearest observations of the development set to 'vote' regarding that observation's classification (their votes are based on the values of their target variables). These votes then represent the probabilities of the new observation belonging to that specific target value.
Technical specifications
The memory-based reasoning node was used with the default settings provided by the SAS Enterprise Miner software.
Decision trees are simple classifiers that produce prediction rules that are easy to interpret and apply and are commonly referred to as CART (classification and regression trees). For this reason they are also quite popular in the industry.4 Note that usually decision trees are used to segment data as an example of supervised segmentation, but here decision trees are used for predictive modelling.
Technical specifications
The decision tree node in SAS Enterprise Miner was used. Two changes were made to the default settings. The splitting criterion for nominal input variables was changed from chi-squared probability to Gini, as the Gini is the measure we used for model performance in this paper. In addition, the number of branches or subsets that a splitting rule can produce was increased to six, which allows results that are more granular.
Gradient boosting draws its concept from the greedy decision tree approach proposed by Friedman20. The algorithm creates a number of small decision trees on the development set, and these trees are combined to produce the model's output. The technique can be linked to the techniques used in random forests21 in that a number of different trees are developed7.
Technical specifications
The gradient boosting node was used with its default setting in Enterprise Miner.
Model performance
In order to compare the model performance, each data set was first divided into two equal sets to form a development and a validation set. The development set, sometimes referred to as the training data, is used to develop the predictive models, whilst the validation set, alternatively known as the holdout data, is used to test the lift in model performance as measured by the Gini coefficient (hereafter lift).5 The Gini coefficient therefore quantifies the ability of the model to differentiate between the two outcomes of the target variable.3 Obviously many other performance measures could have been used. The Gini coefficient is one of the most popular measures to use in retail credit scoring4-6 and has the added advantage that it is a single number3.
The development set and validation set were randomly sampled with even sizes (i.e. 50% each). Although the norm is to usually use larger samples for the development set (70-80%, resulting in a 20-30% validation set), the validation Gini is used in this paper as the ultimate measure of success, and the larger validation set size of 50% was therefore preferred to ensure the Gini coefficients are not affected by low sample size.
In order to measure the combined Gini of the segmented models on the validation set, the predicted probabilities of all segments were combined, and the Gini was calculated on the overall, combined set.
In summary, the eight modelling techniques are shown in Table 1.
Data sets
The modelling techniques described above were compared on six different data sets. All explanatory variables were standardised (i.e. by subtracting the mean and dividing by the standard deviation). Standardising data is a data pre-processing step applied to variables with the aim of scaling variables to a similar range.
The first data set ('direct marketing') analysed was obtained from one of South Africa's largest banks. The data set contains information about the bank's customers, the products they have with the bank, and their utilisation of and behaviour regarding those products. The target variable was binary: whether or not the customer responded to a direct marketing campaign for a personal loan. This data set contains 24 explanatory variables and 4720 observations.
The second data set ('protein structure') was obtained from the UCI Machine Learning Repository22 and contains results of experiments performed by the Protein Structure Prediction Centre23 on the latest protein structure prediction algorithms. These experiments were labelled the 'Critical Assessment of Protein Structure Prediction' experiments.24 In computational biology, a persistent challenge is the prediction of tertiary structures of proteins.25-29 Proteins assume three-dimensional tertiary structures and are therefore complex in nature. Structures are further influenced by a number of physico-chemical properties which further complicates the task of accurate prediction.30 Protein structure prediction algorithms are algorithms that attempt to predict the tertiary structure of proteins.26 These prediction algorithms have been refined over a number of years31-34, but will still deviate when compared to samples of actual, experimentally determined structures. One way of measuring such deviations is through the root-mean-square-deviation.26,27,35 Note that the protein structure prediction algorithms are in no way related to predictive modelling as defined in this paper, as they are specific to the field of protein assessment. The protein structure data set contains various physico-chemical properties of proteins, and the target variable is based on the root-mean-square-deviation measurement, indicating how much the predicted protein structures deviate from experimentally determined structures. The binary target used was whether or not the root-mean-square-deviation had exceeded a certain value (7.5). Our goal was therefore to determine what physico-chemical properties cause protein structure prediction algorithms to deviate more than the norm from experimentally determined protein structures. This data set contains nine explanatory variables and 45 730 observations.
The third data set ('credit application') was obtained from the Kaggle website (www.kaggle.com).36 The data set is publicly available, and was used in a competition called 'Give me some credit', which ran from September to December 2011. The data set contains 10 characteristics of customers who applied for credit, and the target variable is binary, indicating whether or not the customer experienced a 90-day or longer delinquency. The data set is used in a number of studies covering various areas of predictive modelling.37-40 All missing values (indicated by a 'NA' value) were substituted with a value of zero.
The fourth data set ('wine quality') was obtained from the UCI Machine Learning Repository.22 The data comprise physico-chemical properties of wines that are extracted through analytical tests that can be easily performed on most wines. The data set was collected between May 2004 and February 2007.41 The target variable was derived from a score between 0 and 10 which indicates the quality of the wine as scored by tasting experts. The binary target variable used for this analysis was whether or not the score was greater than 6, thereby indicating a great quality wine (only 20% of the wines scored greater than 6). The repository consisted of two data sets - one for white wines and one for red wines. For the purposes of this exercise, the two data sets were combined. The data set has 11 explanatory variables and 6497 observations.
The fifth data set ('chess king-rook vs king') is based on game theory and was obtained from the UCI Machine Learning Repository.22 The data set is an 'Endgame database', which is a table of stored game theoretic values for the legal positions of the pieces on a chessboard. In this endgame, first described by Clarke42, the white player has both its king and its rook left, whilst the black player only has its king left - it is widely known as the 'KRK endgame' and is still the focus of many studies43-45. The database stores the positions of each piece as well as the number of moves taken to finish the game from those positions assuming minimax-optimal play (black to move first). The target variable is binary, and indicates whether the game will be completed within 12 moves or less. Minimax-optimal play is an algorithm often used by computers to obtain the best combination of moves in a chess game and is based on the minimax game theory introduced by Neumann46. More information on this can be found in a number of texts, for example see Casti and Casti47 and Russell and Norvig48. To the 6 explanatory variables another 12 derived variables were added (row distances, column distances, total distances and diagonal indicators). This data set contains 28 056 observations.
The sixth data set ('insurance claim'), also obtained from the Kaggle website36, contains information about bodily injury liability insurance. The competition was named 'Claim Prediction Challenge (Allstate)' and concluded in 2011. The binary target was whether or not a claim payment was made. The independent variables have been hidden, but according to the website, the data set contains information about the vehicle to which the insurance applies as well as some particulars about the policy itself. The data set itself has many observations (7.75 million), but events are rare (probability of occurrence around 1%). In order to reduce unnecessary computation time, the data set was therefore oversampled, which increased the event rate to around 33% (total observations on 14 782) with 12 explanatory variables. Oversampling in cases in which events are rare is a common technique applied in the industry.4951
Results
Eight modelling techniques were compared using all six data sets. We compared the model performance achieved on linear modelling techniques (when first segmenting the data) to the accuracy of popular non-linear modelling techniques.
Table 2 summarises the performance of the modelling techniques when applied to the 'direct marketing' data set (as measured by the Gini coefficient calculated on the validation set). The gradient boosting technique achieved the best result on this data set, with decision tree segmentation running a close second. Neural networks could not converge to a model without overfitting, and the resulting Gini on the validation set is therefore effectively equal to zero. What can be seen additionally from Table 2 is that segmentation-based techniques take in positions two through to four as ranked by the Gini coefficient on the validation set.
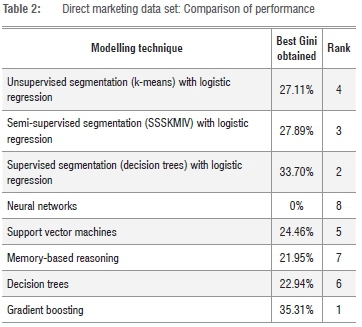
Table 3 summarises the Gini results of the various techniques as applied to the data set on 'protein tertiary structures'. As evidenced by the table, the ranking order of the techniques is completely different from the order seen in Table 2. As a start, gradient boosting ranks third from the bottom, at number six. The technique that achieves the best results in this case is memory-based reasoning. In Table 2, memory-based reasoning was ranked at position seven. The best-ranked segmentation-based technique for this data set is SSSKMIV in position two.
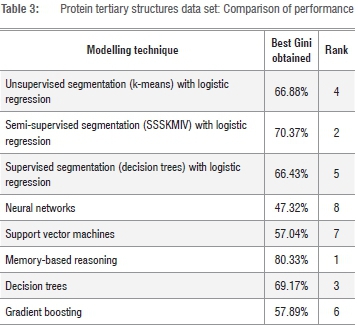
Table 4 shows that, for the 'credit application' data set, neural networks outperform all other techniques. In Tables 2 and 3, neural networks ranked last each time. However, in this case the structure of the data set evidently suited the technique well.
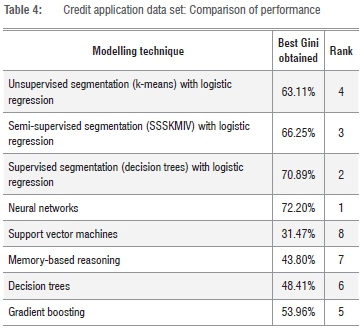
Similar to what was seen in Table 2, segmentation-based techniques take up positions two to four for this data set, with supervised segmentation (decision trees) performing best. At this point, a trend is emerging that segmentation-based techniques may not always render the best results, but seem to deliver results that are consistently amongst the top.
Table 5 shows that for the 'wine quality' data set, segmentation-based techniques occupy the top two positions, with supervised segmentation (decision trees) in position four. The results are generally very close, with only decision trees and support vector machines not doing particularly well.
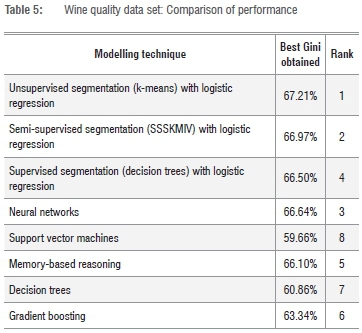
Table 6 shows that decision trees are best suited for the non-linear nature of the chess king-rook vs. king data set. This data set is the first for which segmentation-based techniques fail to be among the top two techniques, with supervised segmentation (decision trees) in third place.
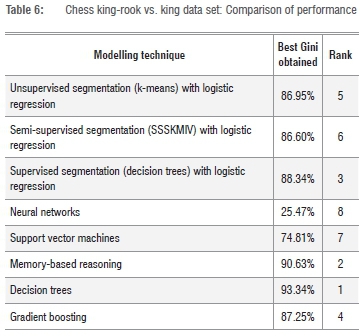
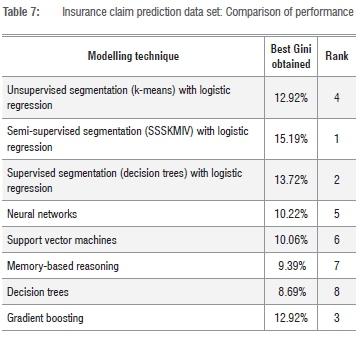
Table 7 shows the results of the last data set to be analysed - the 'insurance claim prediction' data set. It can be seen from the table that the first two positions are again held by segmentation-based techniques, with SSSKMIV achieving the best results. The best non-segmentation-based technique is gradient boosting in position three followed by unsupervised k-means segmentation. The Gini coefficients for this application are low, so the relative difference between the 15.18% obtained by SSSKMIV and the 12.92% of gradient boosting is quite high.
Conclusions
Although it was not the focus of this paper to do an exhaustive comparison of modelling techniques, we provide an overview of how some of the more popular non-linear techniques perform when compared to segmented linear regression. Perhaps because of the diverse nature of the data sets used in this paper, it was interesting to see that no single technique dominated the top position. The Gini coefficients on the validation set of eight modelling techniques were compared. Specifically when considering the data from a local South African bank, gradient boosting performed the best. What was also clear was that the three segmentation-based techniques explored always performed well on all six data sets, even though other techniques demonstrated some significant inconsistency. Table 8 summarises the best performing technique for each data set. In addition, the table also shows the position, or rank, of the best performing segmentation-based technique. The consistency is clear from the fact that these three segmentation-based techniques usually take either position one or two, with only a single third place.
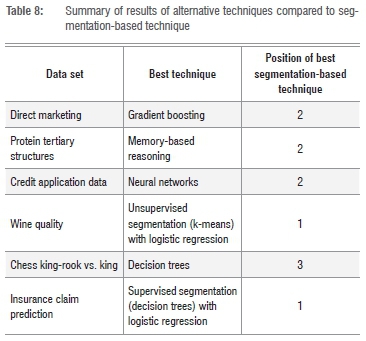
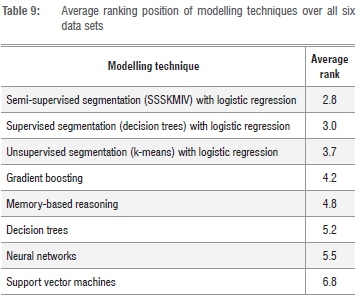
Table 9 provides another view on the consistency of the segmentation-based techniques. The table provides the average rank of each technique (calculated over all six data sets). The table was sorted from lowest average rank to highest average rank. As expected, the segmentation-based techniques do very well, taking the first three positions. SSSKMIV is rated first with an average rank of 2.8.
We conclude that the SSSKMMIV algorithm (semi-supervised segmentation method), although not always outperforming unsupervised and supervised methods, can be a valuable tool to improve segmentation for predictive linear modelling, and does in many cases provide better segmentation than the traditional segmentation methods. The benefit of segmentation was also clearly illustrated in the six data sets used. We showed that the use of non-linear models might not be necessary to increase model performance when data sets are first segmented.
Acknowledgements
This work is based on research supported in part by the Department of Science and Technology (DST) of South Africa. The grantholder acknowledges that opinions, findings and conclusions or recommendations expressed in any publication generated by DST-supported research are those of the authors and that the DST accepts no liability whatsoever in this regard.
Authors' contributions
D.G.B. was responsible for conceptualisation; methodology; data collection; data analysis; validation; data curation; writing revisions; and project leadership. T.V. was responsible for conceptualisation; sample analysis; data analysis; writing the initial draft; revisions; student supervision; and project management.
References
1. Hand DJ. What you get is what you want? - Some dangers of black box data mining. In: M2005 Conference Proceedings. Cary, NC: SAS Institute Inc.; 2005. [ Links ]
2. Baesens B, Roesch D, Scheule H. Credit risk analytics: Measurement Techniques, Applications, and Examples in SAS. New Jersey: Wiley; 2016. [ Links ]
3. Tevet D. Exploring model lift: Is your model worth implementing? Actuarial Rev. 2013;40(2):10-13. [ Links ]
4. Anderson R. The credit scoring toolkit: Theory and practice for retail credit risk management and decision automation. New York: Oxford University Press; 2007. [ Links ]
5. Siddiqi N. Credit risk scorecards. Hoboken, NJ: John Wiley & Sons; 2006. [ Links ]
6. Thomas LC. Consumer credit models. New York: Oxford University Press; 2009. http://dx.doi.org/10.1093/acprof:oso/9780199232130.001.1 [ Links ]
7. Friedman J, Hastie T, Tibshirani R. The elements of statistical learning. Berlin: Springer; 2001. https://doi.org/10.1007/978-0-387-21606-5_14 [ Links ]
8. Hand DJ. Construction and assessment of classification rules. West Sussex: John Wiley & Sons; 1997. [ Links ]
9. Breed DG. Semi-supervised segmentation within a predictive modelling context. Potchefstroom: North-West University: 2017. [ Links ]
10. SAS Institute Inc. Predictive modelling using logistic regression (SAS Institute course notes). Cary, NC: SAS Institute Inc.; 2010. [ Links ]
11. Cross G. Understanding your customer: Segmentation techniques for gaining customer insight and predicting risk in the telecom industry. Paper 154-2008. Paper presented at: SAS Global Forum 2008. Available from: http://www2.sas.com/proceedings/forum2008/154-2008.pdf [ Links ]
12. Fico. Using segmented models for better decisions [document on the Internet]. c2014 [cited 2015 Jan 05]. Available from: http://www.fico.com/en/node/8140?file=9737 [ Links ]
13. Breed DG, De La Rey T, Terblanche SE. The use of different clustering algorithms and distortion functions in semi supervised segmentation. In: Proceedings of the 42nd Operations Research Society of South Africa Annual Conference; 2013 September 15-18; Stellenbosch, South Africa. Available from: http://www.orssa.org.za/wiki/uploads/Conf/ORSSA2013_Proceedings.pdf [ Links ]
14. SAS Institute Inc. Applied analytics using SAS Enterprise Miner (SAS Institute Course Notes). Cary, NC: SAS Institute Inc.; 2015. [ Links ]
15. McCulloch WS, Pitts W. A logical calculus of the ideas immanent in nervous activity. B Math Biophys. 1943;5(4):115-133. http://dx.doi.org/10.1007/BF02478259 [ Links ]
16. Cortes C, Vapnik V Support-vector networks. Mach Learn. 1995;20(3):273-297. [ Links ]
17. Cristianini N, Shawe-Taylor J. An introduction to support vector machines and other kernel-based learning methods. Cambridge: Cambridge University Press; 2000. http://dx.doi.org/10.1017/CBO9780511801389 [ Links ]
18. Li L. Support vector machines. In: Selected applications of convex optimization. New York: Springer; 2015. p. 17-52. http://dx.doi.org/10.1007/978-3-662-46356-7_2 [ Links ]
19. Meyer D, Wien FHT. Support vector machines. Technical report. Boston: R Foundation for Statistical Computing; 2014. [ Links ]
20. Friedman JH. Greedy function approximation: A gradient boosting machine. Ann Statist. 2001;29(5):1189-1232. http://dx.doi.org/10.1214/aos/1013203451 [ Links ]
21. Breiman L. Random forests. Mach Learn. 2001;45(1):5-32. http://dx.doi.org/10.1023/A:1010933404324 [ Links ]
22. Lichman M. UCI Machine Learning Repository datasets [data sets on the Internet]. c2013 [cited 2016 May 06]. Available from: http://archive.ics.uci.edu/ml. [ Links ]
23. Protein Structure Prediction Center [homepage on the Internet]. c2015 [cited 2016 Jun 04]. Available from: http://predictioncenter.org/. [ Links ]
24. Kryshtafovych A, Monastyrskyy B, Fidelis K. CASP prediction center infrastructure and evaluation measures in CASP10 and CASP ROLL. Proteins: Struct Funct Bioinf. 2014;82(Suppl 2):7-13. [ Links ]
25. Fraenkel A. Complexity of protein folding. Bull Math Biol. 1993;55(6):1199-1210. http://dx.doi.org/10.1007/BF02460704 [ Links ]
26. Mishra A, Rana PS, Mittal A, Jayaram B. D2N: Distance to the native. BBA-Proteins Proteom. 2014;1844(10):1798-1807. [ Links ]
27. Rana PS, Sharma H, Bhattacharya M, Shukla A. Quality assessment of modeled protein structure using physicochemical properties. J Bioinform Comput Biol. 2015;13(2), Art. #1550005, 19 pages. http://dx.doi.org/10.1142/S0219720015500055 [ Links ]
28. Searls D. Grand challenges in computational biology. In: Salzberg S, Searls D, Kasif S, editors. Computational methods in molecular biology. Amsterdam: Elsevier; 1998. p. 3-10. [ Links ]
29. Unger R, Moult J. Finding the lowest free energy conformation of a protein is an NP-hard problem: Proof and implications. Bull Math Biol. 1993;55(6):1183-1198. http://dx.doi.org/10.1007/BF02460703 [ Links ]
30. Anfinsen CB. Principles that govern the folding of protein chains. Science. 1973;181(4096):223-230. http://dx.doi.org/10.1126/science.181.4096.223 [ Links ]
31. Dhingra P, Jayaram B. A homology/ab initio hybrid algorithm for sampling near-native protein conformations. J Comput Chem. 2013;34(22):1925-1936. http://dx.doi.org/10.1002/jcc.23339 [ Links ]
32. Jayaram B, Dhingra P, Lakhani B, Shekhar S. Targeting the near impossible: Pushing the frontiers of atomic models for protein tertiary structure prediction. J Chem Sci. 2012;124(1):83-91. http://dx.doi.org/10.1007/s12039-011-0189-x [ Links ]
33. Kim DE, Chivian D, Baker D. Protein structure prediction and analysis using the Robetta server. Nucleic Acids Res. 2004;32(2):W526-W531. http://dx.doi.org/10.1093/nar/gkh468 [ Links ]
34. Lambert C, Leonard N, De Bolle X, Depiereux E. ESyPred3D: Prediction of proteins 3D structures. Bioinformatics. 2002;18(9):1250-1256. http://dx.doi.org/10.1093/bioinformatics/18.9.1250 [ Links ]
35. Cozzetto D, Kryshtafovych A, Fidelis K, Moult J, Rost B, Tramontano A. Evaluation of template-based models in CASP8 with standard measures. Proteins. 2009;77(S9):18-28. http://dx.doi.org/10.1002/prot.22561 [ Links ]
36. Kaggle [homepage on the Internet]. c2016 [cited 2016 Sep 23]. Available from: http://www.kaggle.com. [ Links ]
37. Bahnsen AC, Aouada D, Ottersten B. Example-dependent cost-sensitive logistic regression for credit scoring. In: Proceedings of the 13th International Conference on Machine Learning and Applications (ICMLA); 2014 December 3-5; Detroit, MI, USA. Available from: https://doi.org/10.1109/ICMLA.2014.48 [ Links ]
38. Sharma D. Elements of Optimal Predictive Modeling Success in Data Science: An Analysis of Survey Data for the 'Give Me Some Credit' Competition Hosted on Kaggle. Available at SSRN 2227333. 2013. https://doi.org/10.2139/ssrn.2227333 [ Links ]
39. Sitar M, Raseta J, Klescek A. Implementation of data mining techniques in credit scoring. In: Markovic A, Rakocevic SB, editors. Proceedings of the XIV International Symposium Symorg 2014: New business models and sustainable competitiveness; 2014 June 6-10; Zlatibor, Serbia. FON; 2014. p. 130. [ Links ]
40. Zhou L, Wang H. Loan default prediction on large imbalanced data using random forests. TELKOMNIKA Indones J Electr Eng. 2012;10(6):1519-1525. http://dx.doi.org/10.11591/telkomnika.v10i6.1323 [ Links ]
41. Cortez P Cerdeira A, Almeida F, Matos T, Reis J. Modeling wine preferences by data mining from physicochemical properties. Decis Support Syst. 2009;47(4):547-553. http://dx.doi.org/10.1016/j.dss.2009.05.016 [ Links ]
42. Clarke M. A quantitative study of king and pawn against king. In: Clarke MRB, editor. Advances in computer chess. Edinburgh: Edinburgh University Press; 1977. p. 108-118. [ Links ]
43. Bain M. Experiments in non-monotonic learning. Paper presented at: The Eighth International Workshop on Machine Learning; 2014 September 6-7; Strasbourg, France. p. 380-384. [ Links ]
44. Bramer MA. Machine-aided refinement of correct strategies for the endgame in chess. Adv Comp Chess. 2014;3:93-112. [ Links ]
45. Cohen WW. Compiling prior knowledge into an explicit bias. In: Proceedings of the Ninth International Conference on Machine Learning. Burlington, MA: Morgan Kaufmann; 1992. p. 102-110. [ Links ]
46. Neumann Jv. Zur theorie der gesellschaftsspiele [On the theory of social games]. Mathematische Annalen. 1928;100(1):295-320. German. http://dx.doi.org/10.1007/BF01448847 [ Links ]
47. Casti JL, Casti JL. Five golden rules: Great theories of 20th-century mathematics and why they matter. New York: John Wiley & Sons; 1996. [ Links ]
48. Russell SJ, Norvig P Artificial Intelligence: A modern approach. 2nd ed. New Delhi: Pearson Education; 2003. [ Links ]
49. Chang CY, Hsu MT, Esposito EX, Tseng YJ. Oversampling to overcome overfitting: Exploring the relationship between data set composition, molecular descriptors, and predictive modeling methods. J Chem Inform Modeling. 2013;53:958-971. https://doi.org/10.1021/ci4000536 [ Links ]
50. Taft LM, Evans RS, Shyu CR, Egger MJ, Chawla N, Mitchell JA, et al. Countering imbalanced datasets to improve adverse drug event predictive models in labor and delivery. J Biomed Inform. 2009;42:356-364. https://doi.org/10.1016/j.jbi.2008.09.001 [ Links ]
51. Yap BW, Rani KA, Rahman HAA, Fong S, Khairudin Z, Abdullah NN. An application of oversampling, undersampling, bagging and boosting in handling imbalanced datasets. In: Herawan T, Deris M, Abawajy J, editors. Proceedings of the First International Conference on Advanced Data and Information Engineering (DaEng-2013); Lecture Notes in Electrical Engineering, vol 285. Singapore: Springer; 2014. p. 13-22. https://doi.org/10.1007/978-981-4585-18-7_2 [ Links ]
 Correspondence:
Correspondence:
Tanja Verster
Tanja.Verster@nwu.ac.za
Received: 10 Nov. 2016
Revised: 09 May 2017
Accepted: 15 May 2017














