Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.112 n.11-12 Pretoria Nov./Dec. 2016
http://dx.doi.org/10.17159/sajs.2016/20160139
RESEARCH ARTICLES
Formulating tasks to develop HOTS for first-year calculus based on Brookhart abilities
Aneshkumar Maharaj; Vivek Wagh
School of Mathematics, Statistics and Computer Science University of KwaZulu-Natal, Durban, South Africa
ABSTRACT
We describe an approach to develop higher-order thinking skills (HOTS) among first-year calculus students. The ideas formulated by Brookhart to develop HOTS were used to identify from the literature three core abilities that should be targeted. Then eight expected learning outcomes for the development of HOTS were documented, in the context of the study of first-year university calculus. Those expected outcomes were used to formulate sample tasks that were designed to target the development of the eight abilities. A pilot study was done to determine whether the tasks had the high mathematical demand envisaged. It was found that about 37% of the participants did not give any response to the tasks. Further it was found that about 31% of the participants were able to critically evaluate a given possible solution to a problem and make a value judgement. It is recommended that to promote HOTS among students, the formulation of tasks should focus on developing the following abilities: interpreting a general definition or statement in the context of a given model; translating a worded or graphically represented situation to relevant mathematical formalisms; identifying possible applications of mathematics in their surroundings; identifying linkages between groups of concepts and interpreting these linkages in the context of a model; working systematically through cases in an exhaustive way; critically evaluating one's and others' presented solutions to a problem; interpreting and extending solutions of problems; and using with reasonable skill available tools for mathematical exploration.
SIGNIFICANCE:
• A large proportion of the student intake at university level is unable to answer mathematics questions that focus on HOTS. There is therefore a need to deliberately focus on and promote HOTS amongst the average students in the context of calculus.
Keywords: outcomes; tasks; higher-order thinking skills; university performance
Introduction and motivation
During the past few years we have had informal discussions with colleagues who lecture first-year university calculus. Those discussions gave the impression that much of their energy was and still is consumed in getting students to become comfortable with the prerequisites for calculus and the basics (skills and concepts) of calculus. The former is a result of an increasing number of students gaining entry to study university calculus. A large proportion of the student intake significantly lacks the required basic knowledge and skills to study university mathematics. The situation is so serious that some of the universities in South Africa require qualifying prospective first-year students to take a National Benchmarking Test for mathematics. However, there are some universities that refuse to implement this requirement and go strictly by the matric results. The University of KwaZulu-Natal is one such institution. This situation has resulted in a lack of focus on higher-order thinking skills (HOTS) in the context of the study of calculus. It is for these reasons that we decided to do a study on the formulation of tasks to develop among our students HOTS in the context of first-year calculus.
Research question
Our main research question was: What types of tasks could be formulated to target the development of HOTS among students enrolled for first-year university calculus? To answer this question we need to be clear on the answer to the following question: What are the possible outcomes with regard to HOTS in the context of first-year university calculus?
Review of literature
We review the literature on HOTS; expected learning outcomes; mathematical understanding; and calculus. Higher-order thinking skills
There are a number of writings on HOTS.1-6 Heong et al.3 defined higher-order thinking as the expanded use of the mind to meet new challenges and noted that thinking skills are associated with the learning process. It should be noted here that the challenges should be new to the student. Karaali4 argued that higher-order thinking behaviour is the creative formation of new knowledge based on old knowledge and the ability to apply owned knowledge to new situations. Polly and Ausband5 noted that applying, analysing, generating, integrating and evaluating could be considered as HOTS. The study by Thompson6 found that teachers who defined higher-order thinking as involving problem solving, discovering patterns, interpreting information, and conceptual understanding were much more likely to formulate higher-order thinking items than teachers who did not use those terms. We note that the Department of Education of Newfoundland and Labrador2 gave a detailed document indicating the general outcomes, specific outcomes and achievement indicators for their calculus curriculum. Their examples of assessment items made use of the terms indicated above that were used to describe HOTS by the various authors mentioned. We unpack the ideas given by Brookhart1 which we feel adequately summarises the abilities to be targeted in order to develop HOTS. HOTS involve the attainment of the following three abilities: transfer, critical thinking and problem solving. Transfer is conceptualised as a student's ability to relate their learning to other elements beyond those with which they were taught to associate it. In the study of calculus, basic concepts (e.g. increasing, decreasing and concavity) related to the concept of derivatives are applied to various functions which model different situations. Critical thinking refers to a student being able to decide what to believe, reason, reflect and make sound decisions on their own and produce a reasoned argument. We believe that these attributes of critical thinking have subject-specific meanings and hence we will try to unpack these in the context of the expected outcomes for HOTS, in the context of calculus. Problem solving refers to the use of the above abilities to solve problems in different familiar and new contexts - which implies that the focus on questions in the context of calculus should include contexts that are familiar and new to the student.
Expected learning outcomes
Maharaj and Wagh7 discussed the importance of documenting expected learning outcomes to guide the focus. We note for the reader the key issues here as relevant to this paper. Use of the term 'learning outcome' refers to a clear and detailed statement of what a student should be able to do if they have learnt the content of a particular topic. The Council of Regional Accrediting Commissions8 (CRAC) in its discussion of student learning principles emphasised the importance of learning outcomes. With regard to learning outcomes towards which students are expected to aspire, CRAC pointed out that (1) these should be clear and easily available (made public) and (2) there should be reflection on such outcomes for a commitment to educational improvement. If one accepts these points then it follows that it is important for the learning outcomes relevant to the development of HOTS for calculus to be clearly documented, reflected on periodically and improved on if necessary, and also be made available at the outset to students. Those documented learning outcomes should guide the formulation of tasks which focus on the development of HOTS among students.
Next we looked at how some institutions addressed the issues of course outcomes and assessment for calculus. For example, a study of the University of New England9 (UNE) course site revealed that they gave a general description of the unit and assessment tasks. Each of their assessment tasks related to a particular unit stated learning outcomes in the context of the content and graduate attributes. The latter is interesting as it gives an additional dimension to what would be required of university students. UNE listed the following five graduate attributes: (1) knowledge of a discipline, (2) communication skills, (3) information literacy, (4) problem solving and (5) team work. UNE also clearly indicated the expectation of a student for each of those attributes. For example, problem solving was unpacked as follows:
The student will encounter in this unit a field of knowledge that is intensely problem based, and will acquire skills in connecting ideas within a network of logical relationships. A high emphasis will be placed on the development of analytical and deductive reasoning.9(p.4)
We note that for each of these five graduate attributes there was the intention for teaching, assessment and practise. In the context of the study of mathematics, we believe that a clear perception of the attributes of HOTS will contribute to the development of problem solving skills.
Mathematical understanding
A focus on mathematical understanding requires that one first answer the question: What is mathematics? In answering this question we found the view of Godino10 to be useful. This view - which is also discussed by Maharaj11 - is based on the following four assumptions which we summarise for the reader: (1) Mathematics is a human activity involving the solution of problematic situations. The problem situations could be external or internal. As responses or solutions to such problems are found and reflected on, mathematics emerges and evolves. (2) Mathematical problems and their solutions are shared in specific institutions or collectives involved in studying such problems. An example of such an institution is a university at which modules are offered that focus on the study of mathematics. (3) Mathematics is a symbolic language in which problem situations and the solutions found are expressed. It is this symbolic language which represents coded information that allows for the communication of problems and possible solutions among those who study mathematics. This implies that the teaching and learning of mathematics should also focus on the study of this symbolic language. (4) Mathematics is a logically organised conceptual system. When a mathematical concept is accepted as a part of this system, it is considered as a textual reality and a component of the global structure. The implication here is that those who teach and want to study mathematics should adhere to the logically organised conceptual system. Suppose that one is required to analyse a function to provide a graphical representation. Then, to indicate the logic or thinking involved in deducing the key characteristics, explanations should be given and use made of connectives to link symbolic representations of mathematical concepts with mathematical symbols such as '.·.' (therefore), '=>' (implies) and '<=>' (implies and is implied by).
We now focus on what is meant by mathematical understanding. Skemp12 identified two types of understanding: (1) relational understanding which he described as knowing what to do and why and (2) instrumental understanding which he described as rules without understanding. He noted that the process of learning relational mathematics leads to the building of a conceptual structure in mathematics. This is included in the logically organised conceptual system to which Godino10 referred. Our opinion is that the focus in the teaching and learning of mathematics should be on relational understanding. The development of relational understanding requires that the focus should be on the three HOTS abilities identified by Brookhart1: transfer, critical thinking and problem solving.2 Suppose one is required to sketch the graph of the function  . A focus on the structure represented by the symbolic language implies that one should consider cases based on the structure of the denominator |x-4|, which requires an understanding of the absolute value concept. Because the denominator cannot be 0, the following cases need to be considered: x - 4>0 and x - 4<0. Each of these cases results in different implications. In the context of the Brookhart1 abilities for HOTS one could view the sketching of the graph of f as targeting problem solving as this would include the abilities of: (1) transfer of learning on the absolute value concept to other elements beyond which students were taught to associate it with; and (2) critical thinking as the students would be required to reason, reflect, make sound decisions and produce a reasoned argument to arrive at the required graph of
. A focus on the structure represented by the symbolic language implies that one should consider cases based on the structure of the denominator |x-4|, which requires an understanding of the absolute value concept. Because the denominator cannot be 0, the following cases need to be considered: x - 4>0 and x - 4<0. Each of these cases results in different implications. In the context of the Brookhart1 abilities for HOTS one could view the sketching of the graph of f as targeting problem solving as this would include the abilities of: (1) transfer of learning on the absolute value concept to other elements beyond which students were taught to associate it with; and (2) critical thinking as the students would be required to reason, reflect, make sound decisions and produce a reasoned argument to arrive at the required graph of 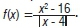
Calculus
A prerequisite to study calculus is adequate knowledge and skills relating to algebra. This knowledge should include algebraic aspects of functions and their standard forms. The derivative of a function and integral of a function are both key concepts in the study of calculus. For details on some studies on students' understanding of the concept of a derivative of a function the reader could refer to Maharaj13. The review of relevant literature revealed that some of the main points that relate to teaching and learning of calculus, in particular the derivative of a function, could be summarised in five points. Firstly, understanding the concept of the derivative of a function is difficult for many students.14,15 Secondly, one should be careful when distinguishing between a description of this concept (which specifies some properties of that concept) and the formal concept definition16 of the derivative of a function. For example, a description of the derivative of a function, say f'(x), could be:
the gradient of the function f(x) at x0 is the slope of the tangent line to the curve f at the point (x0,f(x0)).
The formal definition could be represented as:

Thirdly, the understanding of students could be improved if one exposes them to several representations of the derivative.17 Growth in understanding can be promoted by a variety of connections, both between and within representations, and also between a physical application and mathematical representations.18 The teaching implication here is that there should be a focus on representations and their relevant connections, as part of understanding derivatives. Fourthly, students seem to prefer graphical representation in tasks and explanations about derivatives.19 This finding was supported by Tall20 who argued that direct links between visualisation and symbolisation should be emphasised when teaching the concept of a derivative. Lastly, students' difficulties with the derivative increase in number and extent when the function they are confronted with is a composite function.21 Difficulties in dealing with composition and decomposition of functions could be the reason the chain rule is one of the most difficult ideas in calculus to convey to students.22,23
A number of studies have focused on student understanding of the concept integration of functions and also on what could be done to improve student understanding.24-29 It could be concluded from those studies that difficulties encountered by students in their understanding of the integration concept relate to two principle causes. Firstly, differentiation (finding the derivative of a function) could be viewed as a forward process in contrast to the reverse or backward process of integration. So any difficulties that students have with differentiation could compound their understanding of integration. Further the difficulties faced by students with regard to the concept of derivatives are not as complicated as those for the process of integration. Secondly, integration has a dual nature because it is both the inverse process of differentiation and a tool for calculation, for example, when required to determine the area or volume in the context of problem situations. The first teaching and learning implication from the above studies is that when introducing the antiderivative (improper integral) of a function this should be related to the concept of the derivative. This means that if fg(x)dx represents the general antiderivative of g(x) then ∫g(x)dx=G(x)+C provided G'(x)=g(x). Further, for the concept of the definite integral of a function, teaching should focus on the development of the spatial visualisation ability among students. The development of this ability could influence and strengthen the relationship between the graphical and the symbolic integral representation. Sevimli and Delice27 noted that such an approach increases the performance of students when solving definite integral problems. So problems based on the visualisation of what a particular definite integral represents, could develop among students a useful strategy to conceptualise different definite integral contexts with which they are confronted. It should be noted that only when a student has a deeper understanding of the structure of the definite integral then the use of 'area under a curve' is helpful in problem solving.30 This reinforces the assumption by Godino10 that mathematics is the study of a symbolic language. These ideas influenced the formulation of the tasks that appear later in this paper.
Conceptual framework
The literature review1-19 as well as our experience in teaching calculus to students and assessing their abilities in the context of calculus, guided the formulation of principles which give an overview of the conceptual framework for this study. In particular, the formulation of the following four principles were informed by the work of Brookhart1, Maharaj and Wagh7, the Council of Regional Accrediting Commissions8, Godino9 and Skemp12. (1) It is necessary to formulate and document expected HOTS outcomes on which teaching and learning should focus.1,7 Those outcomes should be easily available to lecturers/teachers and students.8 (2) The identified learning outcomes should inform the development of tasks7 that help in the development of abilities related to HOTS1. (3) The key abilities relate to the transfer of knowledge and skills, critical thinking and problem solving1 across sections in mathematics relevant to the context of studying calculus. The attainment of these should foster the development of relational understanding in students.12 (4) HOTS are acquired and refined by practising them in the context of several different representations of the same calculus related concept.17-20 So students need to be exposed to tasks that could help them develop the abilities related to HOTS. This implies that lecturers/tutors should plan and implement tasks that focus on those relevant abilities.
We now focus on the planning stage of sample tasks that could lead to the development of HOTS among students in the context of their study of calculus. We undertook a brief pilot study to determine whether the sample tasks had the high mathematical demand that we envisaged.
Methodology
The general literature review led us to focus on abilities required for the development of HOTS identified by Brookhart1. We then unpacked those abilities in the context of HOTS required for the study of calculus, keeping in mind the main conclusions of past studies on the teaching and learning of calculus, especially those abilities that could foster relational understanding. A tabulation of those abilities and their relationship with the abilities of transfer, critical thinking and problem solving is given in Table 1. In our opinion, the abilities identified in column two of Table 1 are generic to mathematics. We then used those generic abilities to document the expected outcomes for HOTS in the context of calculus that we felt should be developed among our first-year students. Those expected outcomes then guided the framing of sample tasks that we felt could develop the identified HOTS among students.

We then did an empirical pilot study on student responses to the tasks developed. That pilot study was conducted (in the month of August 2015) at a representative college, where average students seek admission to an undergraduate mathematics course, in the city of Nagpur in India. The institution also runs a postgraduate programme in mathematics. Permission to conduct the pilot study was obtained from the Principal of the college. The pilot study was part of the work required for the project 'Online diagnostics for undergraduate mathematics'. Ethical clearance for that project was provided by the Humanities and Social Sciences Research Ethics Committee of the University of KwaZulu-Natal (reference number HSS/1058/014CA).
The participants were 48 students, all of whom had exposure to the concepts that were covered by the tasks in the pilot study. There were 26 female students and 22 male students. The participants volunteered and were selected on the basis of their availability. Every question was explained before the students attempted the tasks for which an hour was given. The seven tasks are indicated in the sub-section 'Sample tasks for HOTS' below. We indicate for the reader what was clarified with the students before they attempted these seven tasks:
• Tasks 1 and 2: The concepts input and output were illustrated using the function of p(x)=x2
• Task 3: The meaning of second derivative was made clear
• Task 4: What is meant by relevant mathematical formalism was demonstrated by focusing on 'two distinct numbers are added'
• Task 5: It was pointed out to the students how knowledge of trigonometry is used for finding height of a building
• Task 6: The fractional part of a number was demonstrated by discussing the example {1.123}=0.123
• Task 7: It was explained that the students need to identify if the given solution is correct or not and they should provide a reason for their judgement.
All of the participants submitted their attempts within 50 min. Their written responses were then looked at and sorted into the following categories: no response for all seven tasks; some written response for a task; correct responses; partially correct responses. The latter category was used to denote responses in which it was clear that the student reasoned correctly but the response was either incomplete or had a mathematical error.
Findings and discussion
Possible outcomes for HOTS
Our formulation of expected learning outcomes is that students should be able to: interpret a general definition or statement in the context of a given model (given concrete situation); work systematically through cases in an exhaustive way; identify linkages between groups of concepts and interpret these linkages in the context of a model (given concrete situation); translate a worded situation to relevant mathematical formalisms; translate a graphically represented situation to relevant mathematical formalisms; identify possible applications of mathematics in their surroundings; critically evaluate one's and others' presented solutions to a problem/question by identifying errors, redundancies, alternative solutions and how a solution could be improved; interpret and extend solutions of problems; and use with reasonable skill available tools for mathematical exploration (as a general consensus expected from the student). These tools include algebraic and trigonometric identities; standard limits and laws of limits; standard derivatives and their laws; and standard anti-derivatives and their laws.
Sample tasks for HOTS
The questions that we formulated to target the development of HOTS abilities indicated in the above outcomes are documented in the following sample tasks. We indicate next to each of these sample tasks the identified HOTS expected outcome that the task was designed to develop.
Task 1: Ability to work systematically through cases in an exhaustive way
How many polynomial functions are there whose coefficients are natural numbers and in which the output of their derivative is less than 10 on the restricted domain [0,1]? Justify your answer.
Task 2: Ability to interpret and systematically extend solutions to problems
How many polynomial functions are there whose coefficients are natural numbers and in which the output of their derivative is less than 20 on the restricted domain [0,10]? Justify your answer.
Task 3: Ability to interpret a general definition or statement in the context of a given model
Statement: If f"(x)>0 ∀ x € I then the graph of f is concave upwards on the interval I.
Is the graph of the function defined by f(x)=1+x2+x3 concave upwards on the interval [-1,1]? Justify your answer.
Task 4: Ability to translate a worded situation to relevant mathematical formalisms
Find a function with domain the entire set of real numbers which satisfies the condition: the output at the sum of any two inputs is the sum of the outputs at those respective inputs.
Task 5: Ability to identify possible applications of mathematics in their surroundings
Identify at least five applications of the derivative in the context of your body. Explain how each is an application of the derivative.
Task 6: Ability to identify linkages between groups of concepts and interpret these linkages in the context of a model
Let x be a non-negative real number and {x} denote the fractional part of x . For natural number n find the integral 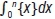 .
.
Task 7: Ability to critically evaluate a presented solution to a problem/question
Examine critically the following question and a solution presented by a student. Indicate clearly with justification your comments on the presented solution. Also present your alternative solution to the question.
Question: Evaluate the integral ƒ x sin x dx
Solution: ∫ x sin x dx = ∫ x dx ∫ sin x dx = 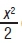 cosx+c
cosx+c
Most (if not all) of the above tasks should be a challenge to the average student studying first-year calculus. Additional sample tasks that we formulated to target the development of the identified HOTS expected outcomes are presented in Appendix 1 of the supplementary material. Note that the seven sample tasks and the additional sample tasks given in Appendix 1 illustrate how the eighth expected outcome could be achieved. Those sample tasks illustrate how available tools could be used to develop reasonable skill in the context of mathematical exploration.
Pilot study on sample HOTS tasks
In Table 2 a summary of the students' responses to the seven tasks is given. It was noted that 18 students gave a blank sheet; meaning there were no responses from those students for any of the seven tasks. An informal chat with those students indicated that they were unable to respond to a task. When probed further, students gave the following as the main reasons for their lack of responses: they were never given a method to solve such questions and they had forgotten some of the things that they had studied. The first reason suggests that many of those participants were comfortable only when they were exposed to some sort of a method to deal with problems. It seemed that these students were exposed to only routine problems on which they worked according to the method they were exposed to. Note that Task 4 was not a calculus task, but focused on mathematical symbolisms relating to the concept of a function - which is a prerequisite to study calculus.
Table 2 indicates that all 48 participants lacked five of the seven HOTS abilities on which the tasks focused. These five HOTS abilities were: working systematically through cases in an exhaustive way; interpreting and systematically extending solutions to problems; interpreting a general definition or statement in the context of a given model; translating a worded situation to relevant mathematical formalisms; and identifying linkages between groups of concepts and interpreting identified linkages in the context of a model. It is also evident from Table 2 that only about 31% of the participants was able to critically evaluate and make a value judgement on a possible solution to a problem. Furthermore, only about 8% of the respondents was able to identify possible applications of mathematics in their surroundings; in this case, applications of the derivative in the context of their body. The implication from the pilot study is that the formulated tasks had the high mathematical demand in calculus that we envisaged.
Conclusions
We identified from the literature review the following three abilities that are central to the development of HOTS among first-year calculus students: transfer of knowledge and skills across sections, critical thinking, and problem solving. Based on the general literature review on critical thinking and a review of literature on the teaching and learning of calculus, we were able to document expected learning outcomes for the development of HOTS in the context of the study of first-year university calculus. Those expected outcomes were used to formulate sample tasks. The sample tasks were designed to target the development of abilities identified in the documented expected outcomes for HOTS, in the context of calculus. The pilot study indicated that the HOTS abilities that we identified for calculus, which are also generic to mathematics, were seriously lacking among the participants who were average students who had been previously exposed to the concepts on which the tasks were based.
Our next investigation will focus on using the sample tasks formulated to further research the development of HOTS among our students. These students could be South African as all first-year university calculus courses cover the same content, namely the derivatives and integrals of standard functions and their applications. In particular, we want to explore the use of technology to promote the identified HOTS abilities that the study indicates should be developed among students. We encourage others who may be interested to feel free to use or adapt the sample tasks to conduct research. We recommend that the formulation of tasks should focus on developing the following HOTS abilities: interpreting a general definition or statement in the context of a given model; translating a worded or graphically represented situation to relevant mathematical formalisms; identifying possible applications of mathematics in their surroundings; identifying linkages between groups of concepts and interpreting these linkages in the context of a model; working systematically through cases in an exhaustive way; critically evaluating one's and others' presented solutions to a problem; interpreting and extending solutions of problems; using these abilities in both familiar and unfamiliar problem-solving contexts; and using with reasonable skill the tools available for mathematical exploration.
Acknowledgements
Professor Sanjay Wagh of the Central India Research Institute in Nagpur (India) is acknowledged for facilitating this collaboration. We also acknowledge the Society for Action Research in Education and Livelihood (Nagpur, India). This study was funded by grants from Eskom's Tertiary Education Support Programme (TESP) for the UKZN-Eskom Mathematics Project, and the International Society for Technology Education for the HP Catalyst Multiversity Consortium Project at UKZN, entitled 'Mathematics e-Learning and Assessment: A South African Context'. The National Research Foundation (South Africa) is acknowledged for the grant received for the project 'Online diagnostics for undergraduate mathematics' (ERSA13101856509).
Authors' contributions
This paper was conceptualised by both authors. All sections were formulated and drafted jointly. A.M. wrote the manuscript.
References
1. Brookhart SM. How to assess higher order thinking skills in your classroom. Alexandria, VA: ASCD; 2010. [ Links ]
2. Department of Education of Newfoundland and Labrador. Mathematics calculus 3208: Curriculum guide 2013 [document on the Internet]. c2013 [cited 2014 Jan 19]. Available from: http://www.ed.gov.nl.ca/edu/k12/curriculum/guides/mathematics/Calculus/Calculus_3208_ curriculum_guide.pdf [ Links ]
3. Heong YM, Yunos JBM, Hassan RB, Othman WB, Kiong TT. The perception of the level of higher order thinking skills among technical education students. In: Proceedings of the 2011 International Conference on Social Science and Humanity; 2011 February 26-28; Singapore. Singapore: IACSIT Press; 2011. p. 281-285. Available from: http://www.ipedr.com/vol5/no2/62-H10167.pdf [ Links ]
4. Karaali G. An evaluative calculus project: Applying Bloom's taxonomy to the calculus classroom. PRIMUS. 2011;21(8):721-733. http://dx.doi.org/10.1080/10511971003663971 [ Links ]
5. Polly D, Ausband L. Developing higher-order thinking skills through webQuests. J Comput Teach Educ. 2009;26(1):29-34. Available from: http://files.eric.ed.gov/fulltext/EJ856114.pdf [ Links ]
6. Thompson T. Mathematics teachers' interpretation of higher-order thinking in Bloom's taxonomy. Int Elect J Math Educ. 2008;3(2):96-109. Available from: http://www.iejme.com/022008/d2.pdf [ Links ]
7. Maharaj A, Wagh V. An outline of possible pre-course diagnostics for differential calculus. S Afr J Sci; 2014;110(7/8):27-33. http://dx.doi.org/10.1590/sajs.2014/20130244 [ Links ]
8. Council of Regional Accrediting Commissions. Regional accreditation and student learning: A guide for institutions and evaluators. Atlanta, GA: Southern Association of Colleges & Schools; 2004. Available from: http://www.sacscoc.org/pdf/handbooks/GuideForInstitutions.PDF [ Links ]
9. University of New England. MATH101 Algebra and differential calculus [homepage on the Internet]. c2013 [cited 2013 Feb 02]. Available from: http://www.une.edu.au/courses/units/MATH101 [ Links ]
10. Godino JD. Mathematical concepts, their meanings, and understanding [document on the Internet]. c1996 [cited 2013 Aug 02]. Available from: http://www.ugr.es/~jgodino/articulos_ingles/meaning_understanding.pdf [ Links ]
11. Maharaj A. A framework to gauge mathematical understanding: A case study on linear algebra concepts. Int J Educ Sci. 2015;11(2):144-153. [ Links ]
12. Skemp R. Relational understanding and instrumental understanding. Math Teach. 1976;77:20-26. [ Links ]
13. Maharaj A. An APOS analysis of natural science students' understanding of derivatives. S Afr J Educ. 2013;33(1):146-164. http://dx.doi.org/10.15700/saje.v33n1a458 [ Links ]
14. Orton A. Students' understanding of differentiation. Educ Stud Math. 1983;14:235-250. http://dx.doi.org/10.1007/BF00410540 [ Links ]
15. Uygur T, Özdas, A. Misconceptions and difficulties with the chain rule. In: Proceedings of the Mathematics Education into the 21st Century Project: Reform, Revolution and Paradigm Shifts in Mathematics Education; 2005 Nov 25- Dec 01; Johor Bahru, Malaysia. Johor Bahru: Malaysia University of Technology; 2005. Available from: http://math.unipa.it/~grim/21_project/21_malasya_Uygur209-213_05.pdf [ Links ]
16. Giraldo V Carvalho LM, Tall DO. Descriptions and definitions in the teaching of elementary calculus. In: Pateman NA, Dougherty BJ, Zilliox J, editors. Proceedings of the 27th Conference of the International Group for the Psychology of Mathematics Education; 2003 July 13-18; Honolulu, HI, USA. Honolulu, HI: Center for Research and Development Group, University of Hawaii; 2003. p. 445-452. Available from: http://www.warwick.ac.uk/staff/David.Tall/pdfs/dot2003d-giraldo-carv-pme.pdf [ Links ]
17. Hähkiöniemi M. Perceptual and symbolic representations as a starting point of the acquisition of the derivative. In: Hoines MJ, Fuglestad AB, editors. Proceedings of the 28th Conference of the International Group for the Psychology of Mathematics Education; 2004 July14-18; Bergen, Norway; 2004. p. 73-80. Available from: https://www.emis.de/proceedings/PME28/ [ Links ]
18. Roorda G, Vos P Goedhart M. Derivatives and applications: Development of one student's understanding. In: Durand-Guerrier V Soury-Lavergne S, Arzarello F, editors. Proceedings of CERME 6; 2009 Jan 28-Feb 01; Lyon, France. Lyon: Institut National de Recherche Pédagogique; 2010. p. 22962305. Available from: www.inrp.fr/editions/cerme6 [ Links ]
19. Zandieh MJ. A theoretical framework for analyzing student understanding of the concept of derivative. CBMS Issues in Mathematics Education. 2000;8:103-122. http://dx.doi.org/10.1090/cbmath/008/06 [ Links ]
20. Tall D. A sensible approach to the calculus. Plenary presented at: The National and International Meeting on the Teaching of Calculus; 2010 September 2325; Puebla, Mexico. Available from: http://homepages.warwick.ac.uk/staff/David.Tall/downloads.html [ Links ]
21. Tall D. Students' difficulties in calculus. Plenary presented at: ICME-7: Proceedings of Working Group 3 on students' difficulties in calculus; 1992 August 17-23; Québec, Canada. Quebec: ICME; 1993. p. 13-28. Available from: http://homepages.warwick.ac.uk/staff/David.Tall/downloads.html [ Links ]
22. Clark JM, Cordero F, Cottrill J, Czarnocha B, DeVries DJ, St. John D, et al. Constructing a schema: The case of the chain rule. J Math Behav. 1997;1:345-364. http://dx.doi.org/10.1016/S0732-3123(97)90012-2 [ Links ]
23. Gordon SP. Discovering the chain rule graphically. Math Comput Educ. 2005;39:195-197. [ Links ]
24. Abdul-Rahman S. Learning with examples and students' understanding of Integration. In: Proceedings of the Mathematics Education into the 21st Century Project: Reform, Revolution and Paradigm Shifts in Mathematics Education; 2005 Nov 25-Dec 01; Johor Bahru, Malaysia. Johor Bahru: Malaysia University of Technology; 2005. Available from: http://math.unipa.it/~grim/21_project/21_malasya_AbdulRahman24-28_05.pdf [ Links ]
25. Ubuz B. Students' understanding of differentiation and integration [document on the Internet]. c1993 [cited 2011 Oct 25]. Available from: http://www.bsrlm.org.uk/IPs/ip13-3/BSRLM-IP-13-3-12.pdf [ Links ]
26. Orton A. Students' understanding of integration. Educ Stud Math. 1983;14:1-18. http://dx.doi.org/10.1007/BF00704699 [ Links ]
27. Sevimli E, Delice A. The influence of teacher candidates' spatial visualization ability on the use of multiple representations in problem solving of definite integrals: A qualitative analysis [document on the Internet]. c2010 [cited 2011 Oct 25]. Available from: http://www.bsrlm.org.uk/IPs/ip30-2/BSRLM-IP-30-2-10.pdf [ Links ]
28. Haciomeroglu ES, Aspinwall L, Presmeg N. The role of reversibility in the learning of the calculus derivative and antiderivative graphs. In: Swars SL, Stinson DW, Lemons-Smith S, editors. Proceedings of the 31st annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education; 2009 Sep 23-26; Atlanta, GA, USA. Atlanta, GA: Georgia State University; 2009. p. 81-88. [ Links ]
29. Maharaj A. An APOS Analysis of natural science students' understanding of integration. REDIMAT. 2014;3(1):54-73. [ Links ]
30. Sealey V. Definite integrals, Riemann sums, and area under a curve: What is necessary and sufficient? In: Alatorre S, Cortina JL, Sáiz M, Méndez A, editors. Proceedings of the 28th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education; 2006 Nov 9-12; Mérida, Yucatán, México. Mérida: Universidad Pedagógica Nacional; 2006. p. 46-53. [ Links ]
 Correspondence:
Correspondence:
Aneshkumar Maharaj
maharaja32@ukzn.ac.za
Received: 12 May 2016
Accepted: 04 Aug. 2016
FUNDING: Eskom's Tertiary Education Support Programme; International Society for Technology Education; National Research Foundation (South Africa)














