Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.111 n.3-4 Pretoria Mar./Apr. 2015
http://dx.doi.org/10.17159/sajs.2015/20130193
REVIEW ARTICLE
Satellite laser ranging measurements in South Africa: contributions to earth system sciences
Christina M. BotaiI; Ludwig CombrinckII, III; Joel O. BotaiIII
ISouth African Weather Service, Pretoria, South Africa
IISpace Geodesy, Hartebeesthoek Radio Astronomy Observatory, Krugersdorp, South Africa
IIIDepartment of Geography, Geoinformatics and Meteorology, University of Pretoria, Pretoria, South Africa
ABSTRACT
This contribution reassesses progress in the development of satellite laser ranging (SLR) technology and its scientific and societal applications in South Africa. We first highlight the current global SLR tracking stations within the framework of the International Laser Ranging Service (ILRS) and the artificial satellites currently being tracked by these stations. In particular, the present work focuses on analysing SLR measurements at Hartebeesthoek Radio Astronomy Observatory (HartRAO), South Africa, based on the MOBLAS-6 SLR configuration. Generally, there is a weak geometry of ILRS stations in the southern hemisphere and the SLR tracking station at HartRAO is the only active ILRS station operating on the African continent. The SLR-derived products - such as station positions and velocities, satellite orbits, components of earth's gravity field and their temporal variations, earth orientation parameters - are collected, merged, achieved and distributed by the ILRS under the Crustal Dynamic Data Information System. These products are used in various research fields such as detection and monitoring of tectonic plate motion, crustal deformation, earth rotation, polar motion, and the establishment and monitoring of International Terrestrial Reference Frames, as well as modelling of the spatio-temporal variations of the earth's gravity field. The MOBLAS-6 tracking station is collocated with other geodetic techniques such as very long baseline interferometry and Global Navigation Satellite Systems, thus making this observatory a fiducial geodetic location. Some applications of the SLR data products are described within the context of earth system science.
Keywords: space geodesy; satellite laser ranging; precise orbit determination; International Laser Ranging Service; earth sciences
Introduction
The study of the gravity field, size, shape and rotation of the earth constitute the three main scientific pillars of space geodesy. Recently, Combrinck1 proposed the inclusion of the geometry of space-time as a fourth pillar, as the other pillars are dependent on highly accurate knowledge of spacetime geometry. Geodesy can be defined as the science that determines the size and shape of the earth, the precise positions and elevations of reference points, lengths and directions of lines on the earth's surface, and variations of terrestrial gravity.2 The three conventional pillars of space geodesy are realised through the use of space geodetic techniques such as Global Navigation of Satellite Systems (GNSS), very long baseline interferometry (VLBI), Doppler Orbitography and Radio-positioning Integrated by Satellite (DORIS), lunar laser ranging (LLR) and satellite laser ranging (SLR) and support from terrestrial measurements.3 In order to achieve high accuracy, all space geodetic techniques incorporate general theory of relativity corrections as a fourth geodetic pillar.1 These corrections are performed in both the observational as well as in data reduction components.
While each of these techniques has different observational strategies (and inherent strengths and weaknesses), most of the products derived from these techniques have common scientific applications in atmospheric research, gravity field modelling, and determination of site coordinates and velocities, geocentre motion and earth rotation parameters. For example, SLR utilises signal propagation between earth observing stations and satellites to derive station positions, earth orientation parameters (EOPs) and terrestrial reference frames (TRFs), among others. In VLBI technique, the radio propagation between distance celestial objects (quasars) and telescopes on earth or in space is used to derive station positions, EOPs and celestial reference frames. Furthermore, VLBI operates at radio frequencies while LLR and sLr operate at optical frequencies. Most of the geodetic sites are co-located with multiple geodetic instruments, allowing them to contribute towards derivation of combined geodetic products. These combined products are unique in terms of accuracy because of the utilisation of individual technique strengths as well as mitigated technique weaknesses.
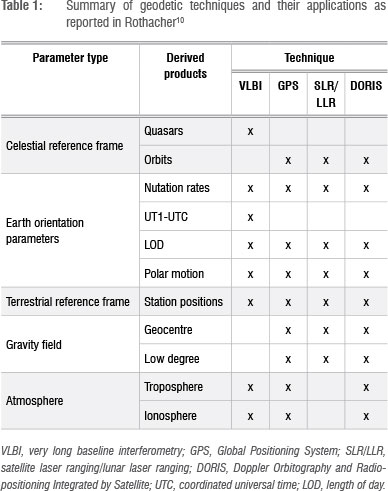
A summary of geodetic techniques and their applications is presented in Table 1. In this contribution, we particularly review milestones of the SLR technique, including its inception in South Africa as well as its role for the African geodetic research community. The reader is referred to various published literature for detailed information on other geodetic techniques, e.g. GNSS4, VLBI5, DORIS6-8 and LLR9.
Basic principle of satellite laser ranging
The SLR technique measures the two-way travel time of a short laser pulse which is reflected by an orbiting satellite. This method of measurement is possible for orbiting satellites equipped with corner cube retro-reflector mirrors made from glass prisms. A schematic diagram illustrating the operation of a typical SLR system is presented in Figure 1.
In a typical SLR system, a transmitting telescope emits short laser pulses with energy of between 10 mJ and 100 mJ at a pulse repetition frequency ranging between 5 Hz and 20 Hz. Some modern systems have lower power levels and higher firing rates of up to 2 kHz. The emitted laser pulse has a typical duration of 200 ps or less, most often specified by the full width at half maximum of the pulse. Laser pulses propagate through the atmosphere to the orbiting satellite, and those which illuminate any of the retro-reflectors are reflected back through the atmosphere to the ground station where they are collected via the receiving telescope. The receiving telescope collects and focuses the reflected pulse energy onto a transmission photocathode (a radiation sensor located inside the vacuum envelope of a photomultiplier tube). Some systems use a single-photon avalanche diode; the LLR system being developed at Hartebeesthoek Radio Astronomy Observatory (HartRAO) in South Africa will utilise such a diode.
In the case of a photomultiplier tube, photons entering the glass vacuum tube are directed to the photocathode where electrons are generated as the photons impinge on the photocathode. The electron yield from the photocathode is dependent on the material of the cathode and this electron yield is quantified by the quantum efficiency, ε (the ratio of emitted electrons to the number of incident photons). Typical SLR systems have efficiencies in the order of 10-15%.11 The emitted photoelectrons are directed by an appropriate electric field to an adjacent electrode or dynode within the envelope. As a result of the acceleration between the dynodes, the number of emitted electrons multiplies in a cascading process. For each primary photoelectron interacting with a dynode, secondary electrons are emitted. These secondary electrons in turn are directed to a second dynode and this process repeats between the first and second dynode until a final gain of the order 106 is achieved. The electrons from the last dynode are collected by an anode which provides the round-trip time-of-flight (TOF) of the pulse. The measured TOF can then be used to compute the distance (d) travelled by the pulse when the speed of light of propagation in free space is known. This range is approximately given by Equation 1:

In Equation 1, the speed of light, c, is the signal propagation speed and a factor of two is included to reduce the round trip distance to the one-way range. Various factors contribute to the accuracy with which the TOF is measured by the SLR tracking systems. These factors include:
- calibration (performed before and after each satellite pass) and drifts or stability of the laser ranging system during target calibration
- the noise of the instrument or uncertainty in computing the exact position of the pulse
- maintenance of time system synchronisation
- atmospheric conditions
For a more in-depth discussion the reader can refer to Combrinck12. Apart from the accuracy capability of a typical SLR system, the success of the laser ranging process (receiving photons back from the orbiting satellite) is also governed by its maximum range. Most SLR systems accomplish such high accuracy by operating at higher signal levels (e.g. a received signal level of five photoelectrons per shot). In such cases, the success of receiving any returns is governed by the standard radar link equation (see Equation 2). The radar link equation gives the average number of detected photoelectrons, Npe, for each transmitted laser pulse and is described as per Equation 2 found in Degnan13:
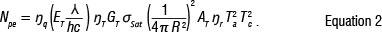
Here, ηq is the detector quantum efficiency, ET is the energy of the laser pulse, λ is the wavelength of the laser, h is Planck's constant, c is the speed of light in a vacuum, ητ and η tare the transmit and receive part efficiency, respectively, and GT is the gain of the transmitter. The satellite at slant range R has optical cross-section given by σSat. A typical spherical geodetic satellite has σSatin the order of 107 m2 and for the small arrays on modern altimetry satellites, σSatis an order of magnitude less.13 Furthermore, in Equation 2, ATis the area of the receiver aperture, and Taand Tc are the one-way atmospheric transmission and one-way transmissivity, respectively, of cirrus clouds (when present). The slant range can be calculated using Equation 3:
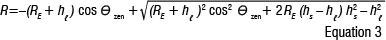
where RE is the radius of the earth, hℓ and hs are the heights of the station and satellite above sea level, respectively, and θ zen is the zenith angle of the satellite as observed from the SLR station and is the complement of the elevation angle. A general expression of transmitter gain for a Gaussian beam is given as per Equation 4:

where At = π2 a21 is the transmitting aperture and gt (αt, β, yt, X) is a geometric factor dependent on whether the collimating telescope is perfectly focused and whether the target is in the far field of the transmitter. Equation 4 accounts for the radial truncation of the Gaussian beam and central obscuration in a Cassegrain telescope. The effective receiver area is computed as per Equation 5, in which the radiation lost to the blockage by a secondary mirror and spillover at the spatial filter and/or detector is taken into account.13

Here Aris the effective area of the telescope receiver aperture, Ap = πα2) is the area of the receiver primary, y = b/aris the receiver obscuration ratio, (1 - y2) is the fraction lost as a result of blockage by the receiver secondary, Fsis the F-number of the receiving telescope and k = 2π/λ where λis the wavelength and lastly, ηΒ is the fraction of the incoming light intercepted by a detector of radius RD.
Various ILRS tracking stations operate with an observation rate of approximately one measurement per second.14 In such a case, a pass over an SLR station may contain more than 2000 data points, depending on the quality of the station and the atmospheric conditions. These data points are often cleaned up and compressed into normal points (NP), resulting in about 10-15 NP over a pass. During data compression, data points are first converted into a NP range (NPR, in metres) by using Equation 6:

where NPj (m) is the normal point range, NPlTOFI\s the normal point TOF in picoseconds at a given epoch and c is the speed of light in a vacuum (299792458.0 m/s). The normal point range as determined by Equation 6 requires certain corrections corresponding to atmospheric effects, centre of mass of the satellite and biases which are related to the tracking and relativistic effects. Taking such corrections into account, Equation 6 can be re-written as:
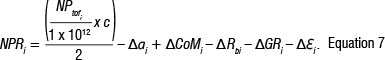
In Equation 7, Δαj denotes the error by the atmospheric delay, ΔCoMj the correction to the position and centre of mass of the orbiting satellite, Δ Rbj the system delay error, ΔGRj the error from relativistic theory and ΔEjis for un-modelled observational errors. Currently, the precision of the NP data (as averaged from a number of observations per satellite pass) is between 10 mm and 15 mm.15
Historical development of satellite laser ranging
The photographic tracking method pioneered in the late 1950s was arguably one of the first techniques used to measure angular positions of artificial satellites. This method was carried out using the Baker-Nunn satellite cameras developed by the Smithsonian Astrophysical Observatory (SAO). Using photographic satellite tracking, the Baker-Nunn camera (a Schmidt telescope with refinements designed to improve its optical performance) photographed satellites against a reference star field. Light entered the camera via a three element lens assembly (this was corrected for spherical and chromatic deviations) and was reflected from a spherical pyrex mirror onto the photographic film. Exact directions of the artificial satellite were commonly found by measuring the satellite's distance from the reference stars on the photographic film. This method of satellite tracking involved a global network of 12 Baker-Nunn cameras. One of the results from photographic satellite observations was the development by SAO of the first gravitational field model, Standard Earth (SE) - a set of spherical harmonic coefficients that described the gravity field of the earth and consistent station coordinates.16 The accuracy of the measurements obtained via photographic satellite tracking was limited to about 2 arc seconds. In addition to photographic observations using the Baker-Nunn cameras, smaller cameras were also used to track satellites such as ECHO or PAGEOS.16 These cameras included the Wild BC4 camera of the Coast and Geodetic Survey in the USA and the IGN (Institut Géographique National) camera in France. Furthermore, Schmidt telescopes were also used for observing satellites such as ANNA-IB, GEOS-A and B launched by the USA.17
By the early 1960s, progress in laser technology had advanced and slowly replaced the photographic observations. The SLR technique was developed to measure the range to an orbiting satellite equipped with corner cube reflectors. The first laser ranging experiment was reported in 1964 and involved the tracking of the Beacon Explorer-B (also known as Explorer-22) satellite using a telescope mounted with a dye-cell Q-switch ruby laser.17 During this campaign, the Goddard Space Flight Center (GSFC) team in the USA was the first to record laser returns in December 1964, followed by the French team from CNRS (Centre National de la Recherche Scientifique) at the Haute Provence Observatory in January 1965. Using a telescope mounted with a dye-cell Q-switch ruby laser, the reported precision based on the root mean square (rms) of the measurements was about 1.0-1.5 m. Because of the success of the first experiment, laser corner cube reflectors were also placed on other satellites, e.g. BEC, GEOS A, GEOS B and GEOS C.
As laser technology continued to progress, laser ranging became the most accurate technique for determining precise satellite orbits for geodetic applications.18 During the 1970s, the Baker-Nunn cameras were completely replaced and SLR tracking stations were established and participated in a laser network to track eight satellites. These tracking stations provided new and improved data sets that were used to generate new gravity field models, e.g. SE and SE III developed at SAO, GEM (Goddard Earth Model) series at GFSC and GRIM (GRgs/IMunich) series at Toulouse and Munich. By the mid-1970s, two dedicated satellites were launched to fully optimise the use of laser tracking. These satellites were: (1) STARLETTE, launched in 1975 in a low altitude orbit (to achieve high sensitivity of gravity field and its temporal variations) and (2) LAGEOS 1, launched in 1976 in a very high altitude orbit (to be as insensitive as possible to the gravity field and to the atmospheric drag effects). Later, other dedicated satellites similar to STARLETTE and LAGEOS were launched: STELLA, LAGEOS 2, AJISAI, ETALON and GFZ-1. Each of these satellites have different but comparable characteristics: for instance, they are all compact and dense, and are used in gravity field solutions, in determining polar motion and the earth's rotation, and are sensitive to the tidal potential, which can be used to determine the tidal potential parameters.
The SLR technique has continued to improve in terms of range precision. For example, orbital laser residuals computed over 10-day periods from normal points acquired on LAGEOS 1 varied from 500 mm (rms) in 1976, 100 mm in 1980, 50 mm between 1985 and 1986, and 30 mm in 2000 to 10-20 mm currently. Such improvements are attributed to the following improved laser technology:
- the replacement of a ruby laser with a neodymium-doped yttrium aluminum garnet (Nd:YAG) laser,
- lower energy laser beams (10-250 mJ),
- pulse widths of 30-200 ps,
- higher emission frequency rates (5 Hz - 2 kHz),
- faster and more sensitive detectors,
- improved timers (<10 ps) and
- improved clocks (<100 ns).
Today, the number of SLR tracking stations has increased globally, as depicted in Figure 2. These stations are coordinated by the iLRS, which was established in September 1998 as a service within the International Geodetic Association. The objectives of the ILRS are to support programmes in geodetic, geophysical and lunar research activities and to provide data products to the International Earth Rotation and Reference Systems Service (IERS) in support of its prime objectives.19
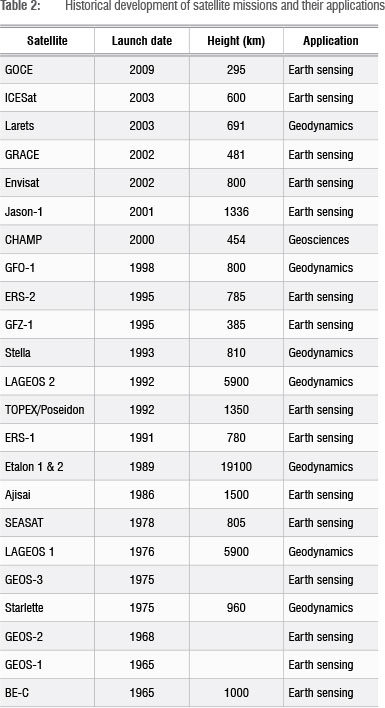
The current ILRS tracking stations involved in artificial satellite tracking consist of over 30 stations. As depicted in Figure 2, most of the SLR tracking stations are located in the northern hemisphere, leaving the southern hemisphere with weak coverage. Over the past years, the majority of these stations has undergone several upgrades to enhance SLR operations. These stations include the TLR-3 system at Arequipa, the Mt. Haleakala station, McDonald, MOBLAS-7 (GSFC), MOBLAS-4 (Monument Peak), Mt. Stromlo and MOBLAS-6. In Africa there are two stations - Helwan in Egypt (inactive) and MOBLAS-6 located at HartRAO in South Africa. Similarly to ILRS tracking stations, the number of artificial satellite missions has also increased from a mere 8 in the 1970s to more than 50. These satellites include passive geodetic (geodynamics), earth sensing, navigation and engineering missions and they all are tracked by the ILRS systems. Table 2 summarises the historical development of some of the satellite missions. Satellites listed in Table 2 include both past and currently tracked satellite missions.
South African satellite laser ranging observations: MOBLAS-6
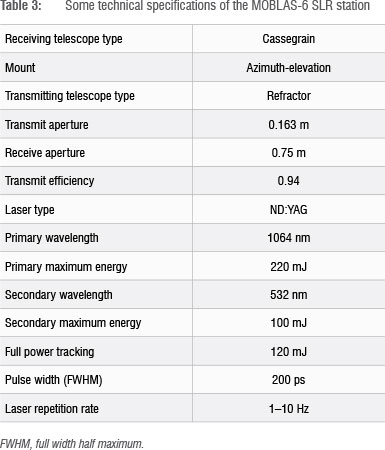
The MOBLAS-6 SLR system is located in a natural bowl of hills at Hartebeesthoek just south of the Magaliesberg mountain range in the Gauteng Province of South Africa, about 50 km west of Johannesburg. The area is an ideal remote site with limited frequency communications and clear weather conditions and hence meets the primary requirements for artificial satellite tracking. The MOBLAS-6 station is operated by HartRAO; a national research facility of the National Research Foundation in South Africa and the only major radio astronomy observatory in Africa. Its operation is an ongoing collaboration between the National Aeronautics and Space Administration (NASA) and HartRAO. Initiatives for this collaboration began in 1992 with discussions between the South African government and NASA. A final agreement was reached in February 1999, which was followed by the signing of a memorandum of understanding between NASA and the National Research Foundation. MOBLAS-6 arrived at HartRAO in June 2000 and its installation and collocation tests took place between June and August 2000, followed by training of on-site staff. Two staff members went to NASA Goddard Space Flight Center for advanced training. The HartRAO SLR station was formally inaugurated and commenced with operations on 20 November 2000. It uses a 0.75-m Cassegrain telescope built in a 12-m mobile trailer. The trailer also contains a 100-mJ, 532-nm, 200-ps pulse length laser and peripheral equipment. Some of the MOBLAS-6 technical specifications are summarised in Table 3.
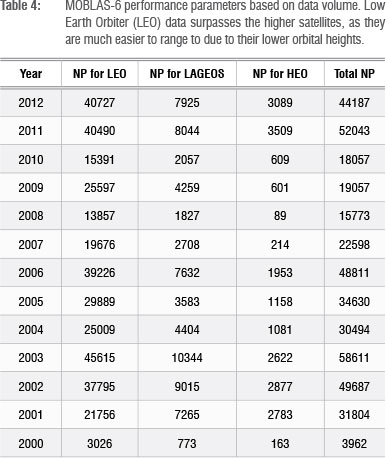
The MOBLAS-6 SLR station has been operational at HartRAO for over a decade now and is the major contributor of SLR data from Africa and an important node of the ILRS network in the southern hemisphere. Table 4 provides a summary of the station's performance in terms of averaged NP data volume since its inception in 2000. Based on the information given in Table 4, MOBLAS-6 meets the performance standards as set by the ILRS. These standards include yearly data quantity (1000 for LEO, 400 for LAGEOS and 100 for HEO), data quality (10 mm LAGEOS NP precision, Figure 3) and operational compliance (e.g. data delivery within 12 h).
At HartRAO, the MOBLAS-6 SLR station has been collocated with other space geodetic techniques - the Global Positioning System (GPS), VLBI, DORIS and the soon to be developed LLR (the first LLR system to be operated in the southern hemisphere) - forming a multi-technique fundamental station as depicted in Figure 4. Differential coordinates (local ties) between the measuring reference points of the collocated instruments play an essential role in the computation and combination of the International Terrestrial Reference Frames (ITRFs). The quality and accuracy of the ITRFs depend on the availability and quality of the local ties computed in co-location sites as well as on the number and distribution of these sites over the globe. As the distribution of most of the space geodetic techniques is sparse in the southern hemisphere, particularly in Africa, the HartRAO collocated site and the derived local ties therefore play an important role in providing combined products (such as site co-ordinates and velocities, earth rotation parameters, atmospheric correction and geocentre motion), which are central for computing quality and reliable ITRFs, gravity field modelling as well as for defining geodetic data for South Africa. The HartRAO site forms part of the Global Geodetic Observing System (GGOS). The GGOS system was conceived by the geodetic community to provide the observational basis for maintaining a stable, accurate global reference system. The global reference system has practical applications related to monitoring the earth system and for global change research, in addition to providing observations in support of the three fundamental pillars of geodesy and their variations. Furthermore, the SLR tracking station at HartRAO, together with other collocated geodetic systems, supports the ongoing development of the African Geodetic Reference Frame Project (AFREF)20 and the African geoid.

The data collected from the MOBLAS-6 station and the other geodetic systems are sent to NASA's data centre, the Crustal Dynamic Information System, and are freely available to the space geodesy and geodynamics community for research purposes. Numerous products are derived from the SLR data and these include the earth's gravity field, ocean tide models, EOPs, precession and nutation parameters which are necessary for satellite positioning applications, mapping, geographical information systems, monitoring of global change and the global hydrological cycle, the dynamics of the atmosphere, oceans and natural hazards and disasters. At HartRAO, various research studies are being undertaken which use LAGEOS data collected from MOBLAS-6. The research studies include testing the general relativity theory (see for example Combrinck1,21) and assessment of global gravity field models, research work published by Botai and Combrinck22.
As part of strengthening its operations, the MOBLAS-6 station underwent major repairs and upgrades between 8 October and 7 November 2008. The repairs and upgrades performed to the system included the replacement of the old Q-switched dye with a CR4 saturable absorber (a special doped crystal manufactured for ND:YAG 1032 nm Q-switched mode locking) and a new laser table. Since the time of the upgrade, MOBLAS-6 is believed to perform much better in terms of laser beam quality and stability and has since required less maintenance.
Today the MOBLAS-6 station continues to be involved with both the ILRS activities and the other services of the International Geodetic Association. In particular, the station continues to track all priority satellites as assigned by the ILRS. Some of the artificial satellites (and their properties) tracked by the MOBLAS-6 station and other ILRS stations are depicted in Table 5. Recently, MOBLAS-6 has increased its laser ranging activities to include tracking of the NASA Lunar Reconnaissance Orbiter (LRO) spacecraft in polar orbit around the moon. The laser tracking of LRO involves recording of one-way range measurements made by the use of laser pulse TOF from the ground station to the LRO spacecraft whenever the spacecraft is in view of the ground station. The LRO's high altitude (~400 000 km) allows the distance from MOBLAS-6 station to the LRO to be measured with an accuracy of about 200 mm.
Geodetic applications of satellite laser ranging observations
The global terrestrial reference frame
A terrestrial reference system is mainly concerned with connecting and comparing measurements over space, time and evolving technologies. This capability is realised through a reference frame - a set of geocentric coordinates and velocities for a network of stations.19 Such coordinates are derived from SLR and other geodetic observation techniques (VLBI, LLR, GPS, DORIS), and are then combined to form products such as the International Terrestrial Reference Frame (currently ITRF2008). In this way, each space geodetic technique provides unique data sets used in the realisation of the ITRF.19 The ITRF forms the fundamental reference system for accurately solving geodetic and geodynamical problems. In particular, the ITRF represents the most precise global terrestrial reference system and is the source for the realisation of other world reference systems, such as WGS84, and of continental and regional reference systems.19 The regional reference systems have various applications such as mapping, agriculture and environmental planning, engineering (road, rail and civil), surveying, tracking- and location-based services, and navigation. The ITRF is monitored, maintained and constantly updated by the IERS. Within this system, each TRF is either directly or after transformation expressed as a realisation of the ITRS.
Earth's gravity field models
Satellite laser ranging tracking data have been used to determine the earth's gravity field both at global and regional scales.23 Because the orbital motion of artificial satellites is influenced by gravitational forces, precise satellite tracking measurements provide orbit solutions which can be inverted to derive the gravity field. For instance, the long wavelength gravity information can be derived through SLR range measurements by high-altitude satellites such as LAGEOS.24,25 In contrast, the short wavelength components of the gravity field often decay rapidly with distance above the earth's surface.26,27 Hence their accurate detection requires low-altitude satellites (e.g. CHAMP, GRACE and GOCE). These satellites have on-board GPS receivers and dual frequency K-band microwave ranging systems (e.g. GRACE) allowing for accurate kinematic positioning, spatial-temporal coverage and continuous monitoring of the changing gravity field of the earth.28 Temporal variations of the earth's gravity field are caused by geological and geophysical processes associated with mass redistribution at the earth's surface and mass distribution in its interior. The seasonal variations in the earth's gravity field result from surface mass changes in the atmosphere, oceans, hydrosphere and lithosphere. Processes associated with isostatic glacial recovery and sea-level changes are manifested in long-term quasi-secular variations. In particular, data collected from CHAMP and GRACE missions have been used to compute various gravity field models including EIGEN-229, GGM0230, EIGEN-GL04C31 and EGM200832. The operational compliance of most ILRS tracking stations and availability of high-quality data greatly contribute to the ongoing computation of gravity field models. With the availability of new and high-quality data, developments in gravity field modelling include both the derivation of new models and upgrading and updating of some of the old models to a higher degree and order (e.g. EGM96 has been upgraded to EGM2008 with degree and order up to 2160). The derived models allow for continuous monitoring of changes in the geoid (the equipotential surface of the earth's gravity field that corresponds closely with mean sea level in the open oceans, ignoring oceanographic effects) and the geoidal height (the separation between the geoid and the ellipsoid) on both global and regional scales as well as on basin scales.33
Precise orbit determination and verification
Satellite tracking operations involve identifying the operational status of equipment on board a satellite in orbit and appropriately controlling and maintaining the satellite's specified orbit. To achieve this function, it is important to accurately determine the satellite's location and establish a link between a ground tracking station and the satellite. Here, the most important parameter is the precise orbit ephemerides of the satellite which are derived by precise orbit determination (POD) (the precise identification of the movement of a satellite in terms of its position and velocity using technology such as SLR). Results from complementary POD are needed to support the planning and scheduling of operations of other satellite missions.19 For these purposes, SLR data play an important role in POD for satellites. The accuracy of the computed satellite orbits depends on the quality and number of SLR data sets available. This determination often imposes certain challenges as SLR is weather dependent. For example, in most areas, approximately 50% of the time, weather conditions such as cloud cover and rain do not allow for laser ranging. In such cases, terrestrial and altimetry data are combined with SLR data to improve the precision of the computed satellite orbits. The technique is also applied as a tool for verification of POD results or for independent calibrations of observations from other tracking systems such as GPS.19
Geophysical applications
Changing mass distribution within system earth causes variations in the earth's gravity field. Time variations in gravity as quantified from SLR data, particularly from CHAMP and GRACE satellite missions, can be used to compute fluctuations in the earth's mass distribution. In particular, gravity variations computed from CHAMP and GRACE data are transformed into time series of global maps of surface mass anomalies. Mass variations on and near the earth's surface, as derived from CHAMP and GRACE data, often provide information about geophysical processes taking place within the earth's systems and/or subsystems. Such information is vital in our understanding and modelling of geophysical mass transfer within the earth. In addition, because mass variations (caused by the continental water cycle) are believed to be the dominant signal component after the removal of contributions from the solid earth tides, atmosphere and ocean, SLR data, particularly from CHAMP and GRACE missions, also have application in hydrological research.34
The role of MOBLAS-6 tracking station on the African continent
The earth system we live in is not constant; earth is a restless planet affected by various dynamic processes occurring on a wide range of spatio-temporal scales. As a result of these unsettling dynamic processes (driven by interior and exterior forces within the earth system as well as by anthropogenic effects), various regions of the earth are exposed to a variety of natural hazards. These hazards include earthquakes, tsunamis, volcanic eruptions, tectonic deformations, deglaciation, sea level rise, floods, desertification, storms, storm surges and global warming, particularly in the solid earth, the atmosphere and the ocean. In addition, resources such as clean water, arable land, minerals, energy, access to food and the capacity of the earth system to maintain a delicate equilibrium under increasing anthropogenic pressure are limited, adding additional stress on the finite resources of our planet. The lack of understanding of earth systems and processes, whether natural or modified by humans (anthropogenic), affects our lives and the lives of future generations. Any application, service or product to be used to tackle the challenges of the restless earth and its dynamic processes, requires a uniform coordinate reference system (geo-spatial reference or geo-reference) and other geographic information. The geo-reference defining position is often given as a set of coordinates (e.g. latitude, longitude and height above mean sea level) referenced to a well-defined origin. Previously, each country used to select its own origin and reference points for its national coordinate system for mapping, surveying and positioning. Such reference points were useful when working within the borders of a single country but tended to create difficulties when undertaking regional development projects that crossed the borders of neighbouring countries.
In order to overcome the cross-border heterogeneous reference frames, most continents around the world have established their own geodetic reference systems (e.g. EUREF for Europe, NAREF for North America, APREF for Asia Pacific) that are used for national surveying, mapping, remote sensing, geographical information systems, development of training programmes that enhance earth system science, and hazard mitigation (such as earthquake studies, fault motion detection, volcano monitoring, and severe storms detection and monitoring). To avoid inconsistent and ambiguous maps and geographical information in large projects (e.g. environmental management, transportation and trading) across the African continent, certain objectives were set out by African heads of government in the New Partnership for Africa's Development (NEPAD). These objectives include the establishment of a unified reference frame across each country and, ultimately, Africa. For this purpose, a network of continuous permanent GPS stations is being established to support a unified geodetic reference frame (AFREF), across more than 50 African countries. AFREF forms the fundamental basis of the national and regional three-dimensional reference networks and is consistent and homogeneous with the standard reference frame, ITRF. Implementation of AFREF (including a unified vertical datum and establishment of a precise African geoid) will allow users anywhere in Africa to have consistent access to GPS data collected from the installed permanent GPS stations. In this regard, the contribution of MOBLAS-6 tracking station to support AFREF is critical because it is one of the most accurate space geodetic techniques. Overall, the accuracy requirements of AFREF ought to meet those of the GGOS of 1 mm TRF origin at an epoch and 0.1 mm/year scale stability. This constraint can be met only by a combination of SLR (used for TRF origin definition) and VLBI (for absolute scale) measurements.
Conclusions
Satellite laser ranging plays an important role in the definition, monitoring and realisation of the TRFs as well as in the computation of long- to medium-wavelength spherical harmonic coefficients of gravity fields. The SLR tracking technique is also vital for precise satellite orbit determination - a key requirement for navigation, geo-location and communication. Weather dependency and poor geometry of ground stations (especially in the southern hemisphere) are some of the drawbacks associated with the SLR space-based technique and often lead to non-uniform SLR data. To widen the applications of SLR geodetic products, the SLR instrument is collocated with other space-based techniques (e.g. GNSS, VLBI and DORIS). Overall, the MOBLAS-6 SLR station at HartRAO plays an important role in the ILRS network as far as data coverage is concerned; in particular, it fills a gap in an area under-represented by SLR equipment and therefore strengthens the geometry of the global network. MOBLAS-6 is the only SLR station on the African continent involved in ILRS activities. In this way, HartRAO provides geodetic measurements that support the development and implementation of a unified geodetic reference frame, AFREF, in the southern hemisphere as well as general support to various earth system science studies. Hence the HartRAO SLR station plays a significant role in terms of network geometry in the southern hemisphere and is an important component of the only geodetic fiducial station in Africa (HartRAO), featuring collocation of SLR (MOBLAS-6), GNSS, VLBI and DORIS instruments.
Acknowledgements
We thank the anonymous reviewers for their constructive and detailed comments that helped to improve the quality of the manuscript.
Authors' contributions
M.C.B. conceptualised, designed and wrote the manuscript; J.O.B. conceptualised, designed and edited the manuscript; L.C. conceptualised, designed, edited and approved the manuscript.
References
1. Combrinck L. A comparison of general relativity theory evaluations using VLBI and SLR: Will GGOS improve these results? In: Behrend D, Baver K, editors. IVS 2012 General Meeting Proceedings; 2012 March 4-9; Madrid, Spain. International VLBI Service for Geodesy and Astrometry; 2012. p. 357-361. [ Links ]
2. Rummel R, Rothacher M, Beutler G. Integrated Global Geodetic Observing System (IGGOS) - Science rationale. J Geodyn. 2005;40(4-5):357-362. http://dx.doi.org/10.1016/j.jog.2005.06.003 [ Links ]
3. KoyamaY Kurihara N, Kondo T, Sekido M, Takahashi Y Kiuchi H, et al. Automated geodetic Very Long Baseline Interferometry observation and data analysis system. Earth Planets Space. 1998;50:709-722. http://dx.doi.org/10.1186/BF03352164 [ Links ]
4. Chang X-W, Paige CC. An algorithm for combined code and carrier phase based GPS positioning. BIT Numerical Mathematics. 2003;43:915-927. http://dx.doi.org/10.1023/B:BITN.0000014566.23457.85 [ Links ]
5. Tanir E, Tornatore V, Boehm J, Felsenstein K, Schuh H. The combinations of Kalman filter and least-squares solutions of different VLBI analysis centers. Geophys Res Abstracts. 2007;9:1-2. [ Links ]
6. Gambis D. Monitoring Earth orientation using space-geodetic techniques: State-of-the-art and prospective. J Geodesy. 2004;78:295-303. http://dx.doi.org/10.1007/s00190-004-0394-1 [ Links ]
7. Coulot D, Berio P, Biancale R, Loyer S, Soudarin L, Gontier A-M. Toward a direct combination of space-geodetic techniques at the measurement level: Methodology and main issues. J Geophys Res. 2007;112:1-21. http://dx.doi.org/10.1029/2006JB004336 [ Links ]
8. Willis P Jayles C, Barsever Y DORIS: From orbit determination for altimeter missions to geodesy. Cr Geosci. 2006;338(14-15):968-979. http://dx.doi.org/10.1016/j.crte.2005.11.013 [ Links ]
9. Bender PL, Currie DG, Dicke RH, Eckhardt DH, Faller JE, Kaula WM, et al. The Lunar laaser ranging experiment. Science. 1973;182(4109):229-238. http://dx.doi.org/10.1126/science.182.4109.229 [ Links ]
10. Rothacher M. Towards a rigorous combination of space-geodetic techniques.In: Richter B, Schwegmann W, Dick WR, editors. Proceedings of the IERS Workshop on Combination Research and Global Geophysical Fluids; 2002 Nov 18-21; Munich, Germany. Frankfurt: Verlag des Bundesamts für Kartographie und Geodãsie; 2003. p. 7-18. [ Links ]
11. Degnan JJ. Satellite Laser Ranging: Current status and future prospects. IEEE T Geosci Remote. 1985;GE-23(4):398-413. http://dx.doi.org/10.1109/TGRS.1985.289430 [ Links ]
12. Combrinck L. Satellite laser ranging. In: Xu G, editor. Sciences of geodesy I. Berlin: Springer-Verlag; 2010. p. 301-338. http://dx.doi.org/10.1007/978-3-642-11741-1_9 [ Links ]
13. Degnan JJ. Millimeter accuracy satellite laser ranging: A review. In: Smith DE, Turcotte DL, editors. Contributions of space geodesy to geodynamics: Technology. AGU Geodynamics Series. 1993;25:133-162. [ Links ]
14. Gambis D. Satellite laser tracking, construction of normal points. Proceedings of the 4th International Workshop on Laser Ranging Instrumentation. Austin, tX: Geodetic institute, University of Bonn; 1981. p. 80-93. [ Links ]
15. Montenbruck O, Gill E. Satellite orbits: Models, methods and applications. New York: Springer; 2000. http://dx.doi.org/10.1007/978-3-642-58351-3 [ Links ]
16. Lundquist CA. Geodetic satellite results during 1967. Smithsonian Astrophysical Observatory special report 264. Cambridge, MA: Smithsonian Astrophysical Observatory; 1967. p. 1-98. [ Links ]
17. Barlier F, Lefebvre M. A new look at planet earth: Satellite geodesy and geosciences. In: Bleeker JAM, Geiss J, Huber MCE, editors. The century of space science. Netherlands: Springer; 2001. p. 1623-1651. http://dx.doi.org/10.1007/978-94-010-0320-9_66 [ Links ]
18. Osorio JP. Satellite laser ranging. SPIE 1524 Bioptics: Optics in biomedicine and environmental sciences. Proc SPIE. 1991;1524:345-371. http://dx.doi.org/10.1117/12.57731 [ Links ]
19. Pearlman M, Noll C, McGarry J, Gurtner W, Pavlis E. The International Laser Ranging Service. Adv Geosci. 2008;13:1-21. [ Links ]
20. Botai OJ, Combrinck L, Rautenbach CJ. On the global geodetic observing system: Africa's preparedness and challenges. Acta Astronautica. 2013;83:119-124. http://dx.doi.org/10.1016/j.actaastro.2012.09.002 [ Links ]
21. Combrinck L. Evaluation of PPN parameter Gamma as a test of general relativity using SLR data. In: Proceedings of the 16th international Workshop on Laser Ranging; 2008 October 13-17; Poznan, Poland. p. 137-142. [ Links ]
22. Botai MC, Combrinck L. Investigating the accuracy of gravity field models using Satellite Laser Ranging data. S Afr J Geol. 2011;114(3-4):539-544. http://dx.doi.org/10.2113/gssajg.114.3-4.535 [ Links ]
23. Forsberg R, Sideris MG, Shum CK. The gravity field and IGGOS. J Geodyn. 2005;40:387-393. http://dx.doi.org/10.1016/j.jog.2005.06.014 [ Links ]
24. Lemoine FG, Kenyon SC, Factor JK, Trimmer RG, Pavlis NK, Chinn DS, et al. The development of the joint NASA GSFC and the National Imagery and Mapping Agency (NIMA) geopotential model EGM96. NASA Technical Paper. Greenbelt, MD: Goddard Space Flight Center; 1998. p. 1-98. [ Links ]
25. Tapley B, Watkins M, Ries J, Davis GW, Eanes RJ, Poole SR, et al. The joint gravity model 3. J Geophys Res. 1996;101(B12):28029-28049. http://dx.doi. org/10.1029/96JB01645 [ Links ]
26. Wahr J, Molenaar M, Bryan F. Time variability of the earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J Geophys Res. 1998;103:30205-30230. http://dx.doi.org/10.1029/98JB02844 [ Links ]
27. Wahr J, Swenson S, Zlotnicki V Vfelicogna I. Time-variable gravity from GRACE: First results. Geophys Res Lett. 2004;31:1-4. http://dx.doi.org/10.1029/2004GL019779 [ Links ]
28. Tapley BD, Bettadpur S, Watkins M, Reigber C. The Gravity Recovery and Climate Experiment: Mission overview and early results. Geophys Res Lett. 2004;31, L09607. [ Links ] Pavlis NK, Holmes SA, Kenyon SC, Factor JK. An earth gravitational model to degree 2160: EGM2008. Vienna: EGU; 2008. [ Links ]
29. Reigber CH, Schwintzer P, Neumayer K-H, Barthelmes F, Koenig R, Foerste CH, et al. The CHAMP-only earth gravity field model EIGEN-2. Adv Space Res. 2003;31(8):1883-1888. http://dx.doi.org/10.1016/S0273-1177(03)00162-5 [ Links ]
30. Tapley B, Ries J, Bettadpur S, Chambers D, Cheng M, Condi F, et al. GGM02 - An improved earth gravity field model from GRACE. J Geodesy. 2005;79:467-478. http://dx.doi.org/10.1007/s00190-005-0480-z [ Links ]
31. Foerste CH, Schmidt R, Stubenvoll R, Flechtner F, Meyer U, Koenig R, et al. The GeoForschungsZentrum Potsdam / Groupe de Recherche de Géodésie Spatiale satellite-only and combined gravity field models: EIGEN-GL04S1 and EIGEN-GL04C. J Geodesy. 2006;82(6):331-346. http://dx.doi.org/10.1007/s00190-007-0183-8 [ Links ]
32. Pavlis NK, Holmes SA, Kenyon SC, Factor JK. An earth gravitational model to degree 2160: EGM2008. Vienna: EGU; 2008. [ Links ]
33. Eckman M. What is the geoid? In: Vermeer M, editor. Coordinate systems, GPS, and the geoid. Report 95:5. Masala: Finnish Geodetic Institute; 1998. p. 49-51. [ Links ]
34. Peltier WR. Closure of the budget of global sea level rise over the GRACE era: The importance and magnitudes of the required corrections for global isostatic adjustment. Quart Sci Rev. 2009;28:1658-1674. http://dx.doi.org/10.1016/j.quascirev.2009.04.004 [ Links ]
35. International Laser Ranging Service. SLR map of stations [image on the Internet]. c2009 [updated 2013 Jun 19; cited 2013 Jun 20]. Available from: http://ilrs.gsfc.nasa.gov/images/ilrsmap.jpg [ Links ]
36. International Laser Ranging Service. Hartebeesthoek: Station Performance [homepage on the Internet]. c2009 [updated 2009 Feb 26; cited 2013 Jun 20]. Available from: http://ilrs.gsfc.nasa.gov/network/stations/active/HARL_ performance.html [ Links ]
37. Hartebeesthoek Radio Astronomy Observatory [homepage on Internet]. c2000 [updated 2005 May 27; cited 2013 Jun 20]. Available from: http://www.hartrao.ac.za/gallery [ Links ]
 Correspondence:
Correspondence:
Christina Botai
South African Weather Service
Private Bag X097, Pretoria 0001
South Africa
Email: Christina.Botai@weathersa.co.za
Received: 20 June 2013
Revised: 06 June 2014
Accepted: 09 July 2014














