Servicios Personalizados
Articulo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en Google
Similares en Google
Compartir
South African Journal of Science
versión On-line ISSN 1996-7489
versión impresa ISSN 0038-2353
S. Afr. j. sci. vol.111 no.1-2 Pretoria ene./feb. 2015
http://dx.doi.org/10.17159/sajs.2015/20130322
REVIEW ARTICLE
Realising high-dimensional quantum entanglement with orbital angular momentum
Melanie G. McLarenI; Filippus S. RouxII; Andrew ForbesI, II
ISchool of Physics, University of the Witwatersrand, Johannesburg, South Africa
IINational Laser Centre, Council for Scientific and Industrial Research, Pretoria, South Africa
ABSTRACT
We report the first quantum entanglement experiment in South Africa. The spatial modes of the entangled photon pair were investigated with their potential for high-dimensional entanglement. The generation, measurement and characterisation of the entangled states were examined in detail and we show high-dimensional entanglement in a Hilbert space of dimension 25. High-dimensional entanglement introduces the possibility for more secure communication and more efficient computations. We highlight the experimental challenges contained within each step and provide practical techniques for future experiments in the quantum regime.
Keywords: quantum entanglement; orbital angular momentum; spatial light modulators; quantum communication; quantum optics
Introduction
One of the most astonishing features of quantum mechanics is that of the entanglement of particles. First introduced as an objection to quantum mechanics by the famous Einstein, Podolsky and Rosen (EPR) thought experiment,1 entanglement represents the notion of non-local quantum correlations between two or more quantum-mechanical systems. That is, for an entangled pair of particles the measurement of an observable for one particle immediately determines the corresponding value for the other particle, regardless of the distance between the two particles.
This property of entangled systems led to a number of implications that disturbed many scientists and resulted in the emergence of hidden variable theories. Local hidden variable theory assumes that nature can be described by local processes, in which information and correlations propagate at most at the speed of light and in which the observables of a physical system are determined by some unknown (hidden) variables.
It was not until the 1960s when Bell's inequality (and Clauser-Horne-Shimony-Holt (CHSH) Bell's inequality2) demonstrated the possibility of practical experiments to test the validity of quantum theory with respect to local hidden variable theories. A slew of experiments followed to test Bell's inequality, each of which violated the inequality and in turn verified quantum mechanical predictions of entanglement.3-6 These results encouraged the search for a method of producing maximally entangled states. Spontaneous parametric down-conversion (SPDC) has proved to be the most efficient technique in generating two-photon entanglement, in which a single photon is split into a pair of lower frequency photons. Shih and Alley7 were the first to demonstrate a violation of Bell's inequality using SPDC-generated photon pairs. This demonstration was the start of various polarisation-entanglement experiments; however, in 2001, it was shown that the orbital angular momentum (OAM) of light could also be used as a basis for entanglement. The spatial modes associated with different OAM states also demonstrated a distinct advantage over polarisation with regard to the number of states available.8 Spatial modes possessing OAM have been studied often in recent years because of the infinite-dimensional alphabets they can possibly provide. In particular, the OAM modes of a photon are a very good avenue for exploring higher dimensions.9 Quantum mechanics in higher dimensional systems has the potential of revolutionising quantum communication and computation protocols. As an example, quantum cryptography using qudits (systems in which there are d orthogonal states) has been shown to be more secure and robust in the presence of noise.10-12
Quantum entanglement has sparked an interest in a number of scientific fields, such as quantum information processing13, quantum cryptography14 and quantum teleportation15.
In this paper we report on the first entanglement experiment in South Africa, where quantum correlations were observed for the first time in Africa in 2011. We create a bi-photon pair entangled in their spatial modes, allowing quantum states of high dimension. The paper should serve as a useful guide to encourage further quantum experiments in the region.
Theory
Entangled states
An entangled state can be simply viewed as two states which are inseparable. If the state cannot be separated into a product of the two systems - A and B - it is entangled. For example, the following superposition state is entangled:

where {|i} and {||i>} are orthonormal bases of A and B, respectively. In demonstrating quantum entanglement, a measurement must be made of one of the properties of single photons. It is possible to measure the position, momentum, energy and time of arrival of single photons.16-18 However, the most well-documented entanglement measurements have been demonstrated using angular momentum: both spin angular momentum (SAM) and OAM.
Spin angular momentum
Angular momentum associated with circularly polarised light is known as SAM and is quantified by h per photon. The direction of the electric field oscillation of light as it propagates, specifies the type of polarisation. For linearly polarised light, the field oscillates in a single plane, whereas the field rotates about the propagation axis for circularly polarised light. The direction of the rotation specifies the handedness of the circular polarisation: clockwise specifies right-handed, anti-clockwise specifies left-handed. Polarisation has offered an efficient way in which to demonstrate photon entanglement and much has been learnt in terms of optimising the efficiency of generating and detecting entangled photons.19'20 However, the limit on the amount of SAM carried per photon has prevented measurements of high-dimensional entanglement.
Orbital angular momentum
The OAM of light is associated with the spatial distribution of the light wave. In 1992, Allen et al.21 demonstrated that laser beams with OAm have helical phase fronts and possess an azimuthal phase dependence of exp(iℓθ), where ℓ (the azimuthal phase index of integer value) represents the number of azimuthal phase rotations in one full cycle from 0 to 2π. Interestingly, like SAM, the OAM of helically phased beams is in units of h; that is ℓh per photon. A light beam propagating along the z-axis with an ℓ-dependent azimuthal phase has a field amplitude described by:
 Equation 2
Equation 2
where ψ0is an amplitude distribution, ℓ is an integer and θ is the azimuthal angle. A common example of such beams is the Laguerre-Gaussian (LG) modes. The intensity distribution of an LG mode with ℓ>0 consists of a zero on-axis intensity surrounded by ρ+1 concentric rings (p represents the radial modes). This non-zero OAM results from the helical phase front of LG beams. This property is not unique to LG beams and is found in both higher-order Bessel beams22 and Ince-Gaussian beams23. It is therefore possible to study OAM entanglement using modes other than those in the LG basis.24 Figure 1 shows the intensity distributions for different superpositions of OAM modes in two different bases: the LG basis and the Bessel-Gauss (BG) basis. We can write these superposition states as:

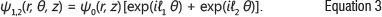
Here ℓ1and ℓ2represent two different azimuthal phase indices.
Entangled states in orbital angular momentum
The simplest method of generating entangled photons is via SPDC, where a single photon incident on a non-linear crystal produces two photons of half the original wavelength, which are entangled. Historically, the two entangled photons have been given the names signal and idler. These down-converted photons also possess the property of OAM; and the seminal paper by Mair et al.8 was the first experiment to demonstrate OAM as a property of single photons produced by SPDC. They showed that OAM is conserved in the SPDC process and consequently showed entanglement involving these modes.25 That is, the OAM of the entangled photon pair must sum to the OAM of the pump photon. The two-photon state for OAM can be written as

where |aℓ -ℓ|2 is the probability of finding one photon in state |ℓ> and the other in state |- ℓ>, where the pump beam has zero OAM. As l can assume any integer value, Equation 4 is true for d-dimensional two-photon states, where ℓ ranges over d different values. Here, the radial component of the LG basis is ignored for simplicity; however, there have been studies that examine the effect of the radial modes on entanglement.26,27
The conjugate variable of OAM is angular position and the Fourier relationship between them can be written as


where Aℓ is the amplitude of the OAM state and ψ(φ) is the azimuthal dependence of the corresponding complex beam amplitude.28
OAM entanglement became a priority for many groups as a result of its potential for increased information capacity per photon. In 2011, high-dimensional entanglement was demonstrated through violations of Bell-type inequalities up to dimension d=12.9 A violation of Bell's inequality is commonly used to test for quantum correlations and is one of many techniques we describe in this paper.
Experimental set-up
The most commonly used and most efficient method of producing entangled photon pairs is that of SPDC.29 This non-linear optical process decays a pump photon into two photons (signal and idler) in a crystal of optical non-linearity, X2. Both energy and momentum are conserved in this decay process, also known as the phase matching conditions:


Here, ωp , ωs , ωiare the frequencies and  the wave vectors of the pump, signal and idler photon, respectively. Because of these conditions, the measurement of one photon in a particular direction and energy, forces the existence of the other correlated photon pair of definite energy and direction. There are two types of SPDC - type I and type II. In type I, the down-converted photons are produced with the same polarisation, orthogonal to that of the pump. Photons of the same wavelength are emitted on concentric cones centred around the pump axis of propagation. The diameter of the cone depends on the angle between the pump beam and the optical axis of the crystal. Type II SPDC emits one photon with the same polarisation as the pump and the other with orthogonal polarisation. In both cases, the process is said to be degenerate if the down-converted photon pair has the same wavelength (i.e. λs = λi. = 2λρ) and non-degenerate otherwise.
the wave vectors of the pump, signal and idler photon, respectively. Because of these conditions, the measurement of one photon in a particular direction and energy, forces the existence of the other correlated photon pair of definite energy and direction. There are two types of SPDC - type I and type II. In type I, the down-converted photons are produced with the same polarisation, orthogonal to that of the pump. Photons of the same wavelength are emitted on concentric cones centred around the pump axis of propagation. The diameter of the cone depends on the angle between the pump beam and the optical axis of the crystal. Type II SPDC emits one photon with the same polarisation as the pump and the other with orthogonal polarisation. In both cases, the process is said to be degenerate if the down-converted photon pair has the same wavelength (i.e. λs = λi. = 2λρ) and non-degenerate otherwise.
Figure 2 shows our experimental set-up. A mode-locked ultraviolet pump source (fundamental Gaussian mode) with a wavelength of 355 nm and average power of 350 mW was used to pump a 3-mm thick type I barium borate (BBO) crystal to produce collinear, degenerate entangled photon pairs via SPDC. The laser produces pulses at 80 MHz; each pulse is made up of ~109 photons. The SPDC process produces on average 1 photon pair in every ~105 pulses, or 800 per second. This relates to an efficiency of ~10-12. An interference filter was placed after the crystal to reflect the pump beam and transmit the 710-nm down-converted light.
Depending on the tilt of the crystal, one can transit between non-collinear and collinear down-converted light, as shown in Figure 3.

It has been shown30 that positioning the crystal to produce near-collinear down-converted photons, potentially allows access to more OAM states. The front plane of the crystal was then imaged (f1 = 200 mm, f2 = 400 mm) onto two separate phase-only spatial light modulators (SLMs). Just as polarisers are used to 'select' a particular polarisation state, the SLMs allow a specific state to be chosen into which the photon will be projected. Initially, the LG basis set was chosen to measure the OAM states; however, any orthogonal basis set can be chosen, such as the BG basis24. The SLM planes were then re-imaged (f3 = 500 mm, f4 = 2 mm) and coupled into single-mode fibres (SMFs) (mode-field diameter = 4.6 μm) so as to extract only the Gaussian modal components. Interference filters centred at 710 nm were placed in front of each fibre coupler to prevent any scattered pump light from entering the fibres. Table 1 provides additional details of the equipment used in the experimental set-up.
An SLM enables the phase of an incoming beam to be shaped according to the encoded hologram. That is, a Gaussian beam illuminating a phase-only forked hologram of particular azimuthal index, ℓ, produces a helically phased beam in the first diffraction order. This process also operates in reverse, such that a beam with OAM ℓ incident on a forked hologram with an azimuthal index -ℓ, will produce a Gaussian beam as shown in Figure 4.
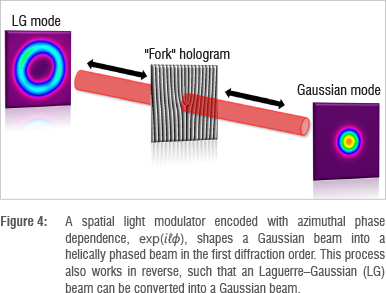
Only the fundamental mode (a Gaussian beam) can propagate through SMFs. The hologram on the SLM, together with the SMF, act as a 'match-filter'31 such that an incoming beam with OAM ℓ will only couple into the SMF if the hologram is encoded with the same azimuthal phase index, ℓ.
The inefficient down-conversion process makes the optical system difficult to align. We therefore used a method of 'back projection' or 'retrodiction', first proposed by Klyshko32, to align the system, by replacing the two detectors in Figure 2 with light from a 710-nm diode laser beam and passing it through each SMF so as to pass through the system in reverse. When the system is correctly aligned, the pump beam and both back-projected beams overlap at the plane of the crystal. Next, detector B was reconnected to the SMF and a 'pop-up' mirror was placed in the crystal plane. The back-projected light was then directed from fibre A to SLM A, which was imaged to the 'pop-up' mirror, reflected back to SLM B and coupled into detector B. By measuring the single count rate at detector B, the classical back-projection method provides a tool with which to predict the behaviour of the correlated down-converted photons in our entanglement set-up.33 Back-projection also allows us to view the modes that we generate on the SLMs, which guarantees that we are indeed measuring in the correct basis. We placed a flip-up mirror between the BBO crystal and lens L1 so as to reflect the back-projected light onto a charge-coupled device (CCD) camera (placed 200 mm from L1). The alignment of the beam with the centre of the hologram is very important, because a misaligned beam results in an uneven intensity distribution. The measurements of OAM are sensitive to lateral position alignment, while the angular position measurements are sensitive to the axial positions of the image planes. Observing the back-projected beam on the CCD allowed us to ensure both SLMs were placed in the correct image plane. Both lenses - L1 and L2 - were placed upon micrometre translation stages to allow for small adjustments along the axis of propagation to find the correct image plane. The size of variable aperture between lenses L1 and L2 was decreased until a clear image of the 'slice' was seen.
Quantum measurements
Following the rigorous alignment procedure, a number of fundamental tests were then performed, the first of which was to demonstrate the conservation of OAM. Each SLM was encoded with holograms ranging in ℓ from -20 to 20, one after another. Figure 5 shows the measured coincidence counts known commonly as the spiral bandwidth.
The anti-correlated diagonal is consistent with OAM conservation, that is ℓp = ℓs + ℓi, where the OAM of the pump, ℓp, must equal the sum of the generated signal, ℓs, and idler, ℓi photons. While the coefficients in the OAM spectrum demonstrate a decreasing trend from ℓ = 0, the size of the mode is another contributing factor as the mode size increases with the azimuthal index, which results in a loss in the detection efficiency, resulting in a decreasing trend from ℓ = 0. Another important feature obtained from Figure 5f is the values of the off-diagonal elements. Theoretically, these should be zero, but experimentally, this is often impossible to achieve as the spiral bandwidth is highly sensitive to misalignment. We measured the off-diagonal elements to be less than 5% of their corresponding diagonal element. From Figure 5g, we measured the full-width-half-maximum (FWHM) value to be 15.
The spiral bandwidth experiment offers an effective method to test whether the set-up is correctly aligned. Similarly, the angular position (the conjugate variable to OAM) can be used to ensure the optics are positioned in the correct image planes. An angular sector hologram was encoded onto each SLM; one hologram fixed at a particular orientation while the other hologram rotated in small increments through 2π. In a ghost imaging experiment,34 an aperture is placed in one arm and the detector in the other arm is scanned through its transverse position, resulting in the reconstruction of the aperture shape. Similarly, the width of the angular hologram was determined from the measured coincidence counts. A sharp coincidence peak was recorded when the holograms were both orientated at the same angle, see Figure 6, where the width of the peak gives the width of the angular 'slice'.
Einstein-Podolsky-Rosen paradox
The 1935 EPR thought experiment concluded that quantum mechanics was incomplete by highlighting the uncertainty principle of quantum mechanics, that is, the knowledge of one conjugate quantity precludes the knowledge of the other.1 In this thought experiment, two assumptions were made - the first being that of locality. This theory implies that measurements made on a subsystem that is spatially separated from another subsystem cannot influence the results of the measurement on the other subsystem. The second assumption of realism stated that a physical quantity has a corresponding element of physical reality if the value of that physical quantity can be predicted with certainty without disturbing the system. Howell et al.35 demonstrated the EPR paradox for position and momentum by measuring the correlations of position and momentum on separate photons. That is, by measuring either the position (x) or momentum (p) of one of the photons, either the position or momentum of the other photon could be inferred with certainty. EPR argued, on the assumption that spatially separated particles do not interact, that the possibility of making such inferences meant that the position and the momentum of the unmeasured particle were simultaneous realities, in violation of Heisenberg's uncertainty relation, (Δχ)2 (Δρ)2 > h2/4. This paradox can be extended to other conjugate variables such as angular position and OAM. The product of the uncertainty in OAM and in angular position is always larger than a minimum value, expressed as36:

A violation of the inequality in Equation 9 satisfies the EPR-Reid criterion37, which is analogous to the original EPR paradox, and thus demonstrates an incompatibility with local realism. These correlations demonstrate entanglement, not only for discrete variables such as OAM, but for continuous variables like angular position as well.
From the data recorded for both the spiral and angular bandwidths, we calculated the uncertainty relationship between the two. A profile from the centre of each spectrum was plotted and fitted with a Gaussian distribution (Figure 7), which gave the following widths: [Δℓ]2 = 0.128 ± 0.023 and [Δø]2= 0.056 ± 0.006. Therefore, by taking the product of the two [Δℓ]2 [Δø]2= 0.007 ± 0.001, the EPR-Reid criterion is satisfied as the product is clearly smaller than the uncertainty relation of 0.25 in Equation 9.

Bell inequalities
The EPR paradox does not eliminate the possibility of hidden variables. To do this, a violation of Bell's inequality must be shown. In 1964, Bell proposed a theorem in which a limit is placed on the correlations achievable by any local hidden-variable theory.38,39 This theorem provided a means to test for local hidden variables. In a polarisation-based experiment, a polariser is rotated to vary from vertical to horizontal polarisation, allowing access to the superposition states. Similarly, holograms are used to access the superposition states of an OAM subspace and are subsequently rotated. The first demonstration of a violation of a Bell inequality in the OAM basis was shown by Leach et al.40 in 2009. We follow their methodology in demonstrating a violation of Bell's inequality for our entangled system.
The holograms used to measure the superposition states are described by:
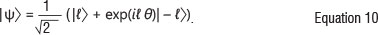
Here θ denotes the degree of rotation of the hologram around its centre in the plane of the SLM. By choosing a particular value for ℓ, we generated superposition holograms for a range of angles θ. The holograms were varied on both SLMs, by fixing one at orientation θΑand rotating the other θβ, and the coincidence count rates were measured. Bell showed that the sinusoidal behaviour seen in Figure 8 cannot be simulated by classical correlations and the deviation from classical theory can be calculated using Bell's inequality or a variation thereof derived by Clauser et al.2
The Bell parameter S can be defined as40:
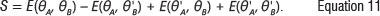
Where θ' is a different orientation from θ. Ε(θΑ, θβ) is calculated directly from the measured coincidence counts C(θΑ, θΒ) at particular orientations. The inequality is violated when |S|>2 . For the CHSH inequality, the upper limit for an entangled system is 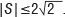
For |ℓ |=2, we observed a violation of the inequality by 26 standard deviations, S = 2.78 ± 0.03, indicating an entangled system.
State tomography
Lastly, it is important to form a characterisation of the entangled states by measuring the degree of entanglement. This characterisation is attained by performing a state tomography41 on the system. We chose to study OAM entanglement with the objective of measuring entanglement in higher dimensions. The density matrix, 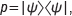 was reconstructed using two bits of information per photon, that is |ℓ> =±1 and its superpositions. However, in high-dimensional entanglement we encode multiple bits of information per photon. For example, for dimension d=3, we could use |ℓ>=0,±1 and for dimension d=5, we could use |ℓ>=-2,-1,0,1,2 (other combinations of OAM modes are also acceptable). We therefore reconstructed the density matrix for dimensions from d=2 to d=5. A detailed description on the tomography measurements can be found in Agnew et al.42 The linear entropy,43 St, defines the purity of the system, where the linear entropy of a pure entangled state is zero. The fidelity, F, is a measure of how close our reconstructed state is to the target state, which is the (pure) maximally entangled state with fidelity of 1. Figure 9 shows the measured values for both the fidelity and linear entropy.
was reconstructed using two bits of information per photon, that is |ℓ> =±1 and its superpositions. However, in high-dimensional entanglement we encode multiple bits of information per photon. For example, for dimension d=3, we could use |ℓ>=0,±1 and for dimension d=5, we could use |ℓ>=-2,-1,0,1,2 (other combinations of OAM modes are also acceptable). We therefore reconstructed the density matrix for dimensions from d=2 to d=5. A detailed description on the tomography measurements can be found in Agnew et al.42 The linear entropy,43 St, defines the purity of the system, where the linear entropy of a pure entangled state is zero. The fidelity, F, is a measure of how close our reconstructed state is to the target state, which is the (pure) maximally entangled state with fidelity of 1. Figure 9 shows the measured values for both the fidelity and linear entropy.

The results indicate that the degree of entanglement decreases as the dimensionality increases; however, the results do not fall below the threshold states, which lie on the threshold of the high-dimensional Bell inequality.44 The generalised Bell inequalities test whether or not the observed correlations, which are predicted by quantum mechanics, can be explained by local hidden variable theories. The quantum state at the threshold of the high-dimensional Bell inequality can be denoted as44:
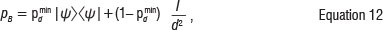
where pdmin is the probability above which the Bell inequality is violated, | ψ> is the maximally entangled state of two d-dimensional systems and I is the identity matrix of dimension d2. A state with a linear entropy below that of pBor a fidelity above that of pBwill violate the high-dimensional Bell inequality, and all of our measured states satisfy these conditions.
Discussion
We have introduced the techniques and equipment required to demonstrate quantum entanglement in the OAM basis. We have presented a set-up together with procedures to measure and quantify the entangled system (a more detailed description is presented in McLaren et al.45). We used SLMs encoded with specific 'forked' holograms together with SMFs to measure the OAM states of each photon and found that OAM is conserved in the down-conversion process. The alignment of single photons is made easier using the method of back-projection, such that classical light is passed through the set-up from one fibre to the other. By using the OAM basis we can choose to perform measurements of two-dimensional entangled states, or extend the set-up to higher dimensions by altering the phase holograms used in the measurement scheme.42 We first satisfied the EPR-Reid criterion by measuring both the angular position and OAM correlations. This result confirms the idea that local realism is incorrect; a measurement made on one entangled particle does in fact affect the properties of the other particle. We then built upon this idea of non-locality by demonstrating a violation of Bell's inequality. This result clarifies that the coincidence measurements are quantum in nature as Bell's theorem shows that the predictions of quantum mechanics and local hidden variable theories are inconsistent. For example, we have shown a violation of a Bell-type inequality for dimension two within the OAM subspace |ℓ=2>. Any subspace could be chosen to demonstrate a violation of Bell's inequality - we simply chose one in which we had a sufficient count rate. We then quantified our entangled states by showing high fidelity states up to dimension five, which equates to a Hilbert space of dimension 25 for a two-particle system (DHllberl = (dparitle)No of particles = 52). It is possible to measure the fidelity of even higher dimensions; however, the number of measurements required to perform a full-state tomography increases significantly as the dimension increases, thus becoming highly time consuming. Nonetheless, the high fidelity results indicate that our quantum states up to dimension 5 are very close to being maximally entangled, while the low linear entropy values confirm that we have very pure high-dimensional quantum states. Our results are consistent with those found in the literature; that is, as we increase the dimensionality of our entangled state, both the fidelity and linear entropy are affected negatively, suggesting that there is an upper bound on the dimensionality in which we can measure. In order to access higher dimensions, we require access to higher-order OAM modes. Theoretically, these modes are attainable; however, there are many experimental elements which have a considerable effect on the number of accessible OAM modes. These include both the length46 and orientation30 of the non-linear crystal, as well as the mode sizes of the pump, signal and idler photons47. Alternative methods to increase the number of measurable OAM modes include altering the pump beam incident on the non-linear crystal from a Gaussian to a Hermite-Gaussian mode,48 as well as changing the projective measurement basis from the LG to the BG basis. The latter technique not only demonstrated a wider OAM spectrum but also showed that entanglement lost as a result of an obstruction in the path, can be recovered but only if measured in the BG basis.49 High-dimensional entanglement is a requirement for a number of quantum processes. One such application is quantum key distribution, which establishes a secure key between two parties, allowing secret messages to be encoded. By implementing high-dimensional entangled states, higher generation rates of the secure key bits, as well as increased information capacity, were demonstrated.50
Authors' contributions
All authors contributed equally to this manuscript.
References
1. Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physical reality be considered complete? Phys Rev. 1935;47:777-780. http://dx.doi.org/10.1103/PhysRev.47.777 [ Links ]
2. Clauser J, Horne M, Shimony A, Holt R. Proposed experiment to test local hidden-variable theories. Phys Rev Lett. 1969;23:880-884. http://dx.doi.org/10.1103/PhysRevLett.23.880 [ Links ]
3. Freedman S, Clauser J. Experimental test of local hidden-variable theories. Phys Rev Lett. 1972;28:938-941. http://dx.doi.org/10.1103/PhysRevLett.28.938 [ Links ]
4. Clauser J. Experimental investigation of a polarization correlation anomaly. Phys Rev Lett. 1976;36:1223-1226. http://dx.doi.org/10.1103/PhysRevLett.36.1223 [ Links ]
5. Aspect A, Grangier P Roger G. Experimental tests of realistic local theories via bell's theorem. Phys Rev Lett. 1981;47:460-463. http://dx.doi.org/10.1103/PhysRevLett.47.460 [ Links ]
6. Aspect A, Grangier P, Roger G. Experimental realization of Einstein-Podolsky-Rosen-Bohm gedanken experiment: A new violation of Bell's inequalities. Phys Rev Lett. 1982;49:91-94. http://dx.doi.org/10.1103/PhysRevLett.49.91 [ Links ]
7. Shih Y Alley C. New type of Einstein-Podolsky-Rosen-Bohm experiment using pairs of light quanta produced by optical parametric down conversion. Phys Rev Lett. 1988;61:2921-2924. http://dx.doi.org/10.1103/PhysRevLett.61.2921 [ Links ]
8. Mair A, Vaziri A, Weihs G, Zeilinger A. Entanglement of the orbital angular momentum states of photons. Nature. 2001;412:313-316. http://dx.doi.org/10.1038/35085529 [ Links ]
9. Dada A, Leach J, Buller G, Padgett M, Andersson E. Experimental high-dimensional two-photon entanglement and violations of the generalized Bell inequalities. Nat Phys. 2011;7:677-680. http://dx.doi.org/10.1038/nphys1996 [ Links ]
10. Bechmann-Pasquinucci H, Tittel W. Quantum cryptography using larger alphabets. Phys Rev A. 2000;61:62308. http://dx.doi.org/10.1103/PhysRevA.61.062308 [ Links ]
11. Walborn S, Lemelle D, Almeida M, Souto Ribeiro P. Quantum key distribution with higher-order alphabets using spatially encoded qudits. Phys Rev Lett. 2006;96:090501. http://dx.doi.org/10.1103/PhysRevLett.96.090501 [ Links ]
12. Langford N, Dalton R, Harvey M, O'Brien J, Pryde G, Gilchrist A, et al. Measuring entangled qutrits and their use for quantum bit commitment. Phys Rev Lett. 2004;93:53601. http://dx.doi.org/10.1103/PhysRevLett.93.053601 [ Links ]
13. Bennett C, Di Vincenzo D. Quantum information and computation. Nature. 2000;404:247-255. http://dx.doi.org/10.1038/35005001 [ Links ]
14. Jennewein T, Simon C, Weihs G, Weinfurter H, Zeilinger A. Quantum cryptography with entangled photons. Phys Rev Lett. 2000;84:4729-4732. http://dx.doi.org/10.1103/PhysRevLett.84.4729 [ Links ]
15. Bouwmeester D, Pan J, Mattle K, Eibl M, Weinfurter H, Zeilinger A. Experimental quantum teleportation. Nature. 1997;390:575-579. http://dx.doi.org/10.1038/37539 [ Links ]
16. Kwiat PG, Steinberg AM, Chiao RY High-visibility interference in a Bell-inequality experiment for energy and time. Phys Rev A. 1993;47:R2472-R2475. http://dx.doi.org/10.1103/PhysRevA.47.R2472 [ Links ]
17. Rarity JG, Tapster PR. Experimental violation of Bells inequality based on phase and momentum. Phys Rev Lett. 1990;64:2495-2498. http://dx.doi.org/10.1103/PhysRevLett.64.2495 [ Links ]
18. Howell JC, Bennink RS, Bentley SJ, Boyd RW. Realization of the Einstein-Podolsky-Rosen paradox using momentum- and position-entangled photons from spontaneous parametric down conversion. Phys Rev Lett. 2004;92:210403. http://dx.doi.org/10.1103/PhysRevLett.92.210403 [ Links ]
19. Shih Y Entangled biphoton source - property and preparation. Rep Prog Phys. 2003;66:1009-1044. http://dx.doi.org/10.1088/0034-4885/66/6/203 [ Links ]
20. Rangarajan R, Goggin M, Kwiat P. Optimizing type-I polarization-entangled photons. 2009;17:18920-18933. [ Links ]
21. Allen L, Beijersbergen M, Spreeuw R, Woerdman J. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A. 1992;45:8185-8189. http://dx.doi.org/10.1103/PhysRevA.45.8185 [ Links ]
22. Volke-Sepulveda K, Garcés-Chávez V Chávez-Cerda S, Arlt J, Dholakia K. Orbital angular momentum of a high-order Bessel light beam. J Opt B Quantum Semiclass Opt. 2002;4:S82-S89. http://dx.doi.org/10.1088/1464-4266/4/2/373 [ Links ]
23. Bandres MA, Gutiérrez-Vega JC. Ince Gaussian beams. Opt Lett. 2004;29(2):144-146. http://dx.doi.org/10.1364/OL.29.000144 [ Links ]
24. McLaren M, Agnew M, Leach J, Roux FS, Padgett MJ, Boyd RW, et al. Entangled Bessel-Gaussian beams. Opt. Express. 2012; 20: 23589-23597. http://dx.doi.org/10.1364/OE.20.023589 [ Links ]
25. Vaziri A, Weihs G, Zeilinger A. Experimental two-photon, three dimensional entanglement for quantum communication. Phys Rev Lett. 2002;89:240401. http://dx.doi.org/10.1103/PhysRevLett.89.240401 [ Links ]
26. Salakhutdinov VD, Eliel ER, Loffler W. Full-field quantum correlations of spatially entangled photons. Phys Rev Lett. 2012;108:173604. http://dx.doi.org/10.1103/PhysRevLett.108.173604 [ Links ]
27. Zhang Y Roux FS, McLaren M, Forbes A. Radial modal dependence of the azimuthal spectrum after parametric down-conversion. Phys Rev A. 2014;89:043820. http://dx.doi.org/10.1103/PhysRevA.89.043820 [ Links ]
28. Yao E, Franke-Arnold S, Courtial J, Barnett S, Padgett M. Fourier relationship between angular position and optical orbital angular momentum. Opt Express. 2006;14:9071-9076. http://dx.doi.org/10.1364/OE.14.009071 [ Links ]
29. Ou ZY, Mandel L. Violation of Bell's inequality and classical probability in a two-photon correlation experiment. Phys Rev Lett. 1988;61:50-53. http://dx.doi.org/10.1103/PhysRevLett.61.50 [ Links ]
30. Romero J, Giovannini D, Franke-Arnold S, Barnett SM, Padgett MJ. Increasing the dimension in high-dimensional two-photon orbital angular momentum entanglement. Phys Rev A. 2012;86:012334(6). [ Links ]
31. Litvin IA, Dudley A, Roux FS, Forbes A. Azimuthal decomposition with digital holograms. Opt Express. 2012;20:10996-11004. http://dx.doi.org/10.1364/OE.20.010996 [ Links ]
32. Klyshko D. A simple method of preparing pure states of an optical field, of implementing the Einstein-Podolsky-Rosen experiment, and of demonstrating the complementarity principle. Soviet Physics Uspekhi. 1988;31:74-85. http://dx.doi.org/10.1070/PU1988v031n01ABEH002537 [ Links ]
33. McLaren M, Romero J, Padgett MJ, Roux FS, Forbes A. Two-photon optics of Bessel-Gaussian modes. Phys Rev A. 2013;88:033818. http://dx.doi.org/10.1103/PhysRevA.88.033818 [ Links ]
34. Pittman TB, Shih YH, Strekalov DV Sergienko AV. Optical imaging by means of two-photon quantum entanglement. Phys Rev A. 1995;52:R3429-R3432. http://dx.doi.org/10.1103/PhysRevA.52.R3429 [ Links ]
35. Howell J, Bennink R, Bentley S, Boyd R. Realization of the Einstein-Podolsky-Rosen paradox using momentum- and position-entangled photons from spontaneous parametric down conversion. Phys Rev Lett. 2004;92:210403. http://dx.doi.org/10.1103/PhysRevLett.92.210403 [ Links ]
36. Franke-Arnold S, Barnett SM, Yao E, Leach J, Courtial J, Padgett MJ. Uncertainty principle for angular position and angular momentum. New J Phys. 2004;6(103):8. [ Links ]
37. Reid MD. Demonstration of the Einstein-Podolsky-Rosen paradox using nondegenerate parametric amplification. Phys Rev A. 1989;40:913-923. http://dx.doi.org/10.1103/PhysRevA.40.913 [ Links ]
38. Bell JS. On the Einstein-Rosen-Podolsky paradox. Physics. 1964;1:195-200. [ Links ]
39. Bell JS. On the problem of hidden variables in quantum mechanics. Rev Mod Phys. 1966;38:447-452. http://dx.doi.org/10.1103/RevModPhys.38.447 [ Links ]
40. Leach J, Jack B, Romero J, Ritsch-Marte M, Boyd RW, Jha AK, et al. Violation of a Bell inequality in two-dimensional orbital angular momentum state-spaces. Opt Express. 2002;17:8287-8293. http://dx.doi.org/10.1364/OE.17.008287 [ Links ]
41. Jack B, Leach J, Ritsch H, Barnett S, Padgett MJ. Precise quantum tomography of photon pairs with entangled orbital angular momentum. New J Phys. 2009;811:103024. http://dx.doi.org/10.1088/1367-2630/11/10/103024 [ Links ]
42. Agnew M, Leach J, McLaren M, Roux FS, Boyd RW. Tomography of the quantum state of photons entangled in higher dimensions. Phys Rev A. 2011;84:062101. http://dx.doi.org/10.1103/PhysRevA.84.062101 [ Links ]
43. White AG, James DFV Munro WJ, Kwiat PG. Exploring Hilbert space: Accurate characterization of quantum information. Phys Rev A. 2001;65:012301. http://dx.doi.org/10.1103/PhysRevA.65.012301 [ Links ]
44. Collins D, Gisin N, Linden N, Massar S, Popescu S. Bell inequalities for arbitrarily high-dimensional systems. Phys Rev Lett. 2002;88:040404. http://dx.doi.org/10.1103/PhysRevLett.88.040404 [ Links ]
45. McLaren M, Roux FS, Forbes A. Realising high-dimensional quantum entanglement with orbital angular momentum. ArXiv:1305.7102[quant-ph]; [ Links ] 2013.
46. Torres JP Alexandrescu A, Torner L. Quantum spiral bandwidth of entangled two-photon states. Phys Rev A. 2003;68:050301. http://dx.doi.org/10.1103/PhysRevA.68.050301 [ Links ]
47. Miatto FM, Yao AM, Barnett SM. Full characterization of the quantum spiral bandwidth of entangled biphotons. Phys Rev A. 2011;83:033816. http://dx.doi.org/10.1103/PhysRevA.83.033816 [ Links ]
48. Romero J, Giovannini D, McLaren MG, Galvez EJ, Forbes A, Padgett MJ. Orbital angular momentum correlations with a phase-flipped Gaussian mode pump beam. J Optics. 2012;14:085401. http://dx.doi.org/10.1088/2040-8978/14/8/085401 [ Links ]
49. McLaren M, Mhlanga T, Padgett MJ, Roux FS, Forbes A. Self-healing of quantum entanglement after an obstruction. Nat Commun. 2014;5:3248. http://dx.doi.org/10.1038/ncomms4248 [ Links ]
50. Mafu M, Dudley A, Goyal S, Giovannini D, McLaren M, Padgett MJ, et al. Higher-dimensional orbital-angular-momentum-based quantum key distribution with mutually unbiased bases. Phys Rev A. 2013;88:032305. http://dx.doi.org/10.1103/PhysRevA.88.032305 [ Links ]
 Correspondence:
Correspondence:
Melanie McLaren
School of Physics, University of the Witwatersrand
Wits 2000, South Africa
Email:melanie.mclaren@wits.ac.za
Received: 11 Oct. 2013
Revised: 05 May 2014
Accepted: 02 July 2014














