Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.110 n.11-12 Pretoria Nov./Dec. 2014
http://dx.doi.org/10.1590/sajs.2014/20140008
RESEARCH ARTICLE
http://dx.doi.org/10.1590/sajs.2014/20140008
Factors affecting graduation and student dropout rates at the University of KwaZulu-Natal
Mike Murray
Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Durban, South Africa
ABSTRACT
This paper aims to introduce into the literature a competing risks methodology that can be used to help identify some student-specific and/or institutional factors which may be influencing the type of outcome experienced by a student when they leave the university system. Focusing on the length of time that it takes students to graduate or drop out from their studies, this new methodology was applied to a database comprising all students enrolled for a degree at the University of KwaZulu-Natal between the years 2004 and 2012. Financial aid and residence-based accommodation were found to help students who will eventually graduate to do so quicker in terms of the number of credit points that they have to repeat. These same factors, however, also cause someone who will eventually be excluded on academic grounds to linger longer in the system. By focusing on the number of extra credit points that it takes to reach a particular exit point, this paper introduces into the literature a new measure whose use will help to overcome some of the more obvious problems that can occur when one uses calendar time to measure the length of time that it takes to reach a particular exit point.
Keywords: competing risks; graduation rates; dropout rates; university; survival analysis
Introduction
The effects of race, gender and poverty, among other socio-economic variables, on student dropout or graduation from a higher education institution have been well documented in the literature.12 However, in almost all of these studies, a standard survival analysis based approach was used to analyse the problem. An assumption of stochastic independence amongst the possible outcomes that can occur is made, with these factors then fed into a hazard function which in turn generates a probability distribution for determining the time to dropout or graduation of that particular student. Such an assumption of stochastic independence is often questionable, particularly in our setting, in which a variety of individual and university-specific forces may be interacting with each other and pulling a student towards one or other type of exit point from the university system. The main purpose of this paper is to introduce into the literature a new competing risks based methodology which can then be used to compare the time that it takes to graduate with that of two other types of exit: a voluntary dropout where a student with a good academic record has decided possibly to change universities or an involuntary dropout where the student has been excluded on academic grounds from further study because of poor performance.
There is potentially a large number of factors that may have a causative effect on the length of time that it takes students to graduate or dropout from university-based studies. Some of these factors - such as a student's age, gender, race and financial status - may be more easy to measure than others, such as a student's level of motivation for studying, the level of academic integration and the type of living conditions that exist at the university where they want to study. With suitable proxies for some of these unobservable constructs already developed, most of the research work that appears in the literature attempts to feed these covariates into a predictive model with a statistical procedure then being used to determine the significance (or validity) of any relationship that one observes. Being essentially data-driven, one may argue that each one of the above approaches lacks a foundation that can be fully supported by an underlying socio-economic based theory. In order to bridge this gap, Tinto3 developed an approach for modelling student dropout behaviour that focuses on the quality of interaction that exists between a student and the higher education institution at which they enrol. More specifically, the individual attributes of each student (such as their underlying ability, race and gender), together with some family background characteristics (such as their parent's level of education) and pre-university schooling experiences (such as the grades that they have achieved), help to form a level of initial motivation that is then forced to interact with a set of institutional experiences within the university. Tinto3 divided these institutional experiences into two distinct components: (1) an academic component comprising the academic performance of the student and their interaction with faculty or staff members within the university and (2) a social component comprising their extracurricular activities and peer group interactions. The extent to which these forces can successfully integrate with each other helps to determine whether students persist with their studies or leave the university, whether leaving is on a voluntary basis (because they want to enrol at another institution) or an involuntary basis (because their poor results have led to them being permanently excluded on academic grounds from the university). When interpreted in this manner, one deals with a decision-making process that fits more comfortably into a competing risks paradigm in which a variety of socioeconomic forces are pulling the student towards one or other mutually exclusive set of possible outcomes.
Why study this problem?
The poor performance of students entering South Africa's higher education system has been well documented in the literature. A 2007 study by Scott et al.4 found that 25% of all students drop out in their first year of study, with only 21% being able to graduate within the minimum amount of time that has been allocated for the degree. A study by Letseka and Maile1 placed South Africa's overall graduation rate amongst the lowest in the world (15% across all South African based universities). In particular, their report suggested that a lack of available financing and the existence of a significant articulation gap between secondary education and higher education were the main causes for such a high dropout rate. The report also highlighted another fact that has been well established - that African students are generally under-represented at all universities, with nearly 70% of these students indicating that they were the first of their generation to be afforded an opportunity to attend university.
In a 2013 report released by the Council for Higher Education2, it was found that only one in four students was able to graduate from a contact-based institution within the minimum prescribed period set aside for that degree. A total of 58% of students attending a contact-based institution needed an extra 2 years to complete a 3-year degree, with this figure increasing to an alarming 91% for a non-contact based institution. When looking at race, the report stated that the completion rate for white students was on average 50% higher than that for non-white students. It was also found that the performance of students in the Engineering, Commerce and Business Management disciplines had declined sharply when compared with that of a 2000 study. Students enrolling in the Health Sciences, Education and Social Sciences, however, had shown a small improvement when compared with that of the 2000 intake. With this context in mind, it is important that we try and identify an appropriate set of socio-economic and academic factors that may be exacerbating what has become a 'revolving door' for many students who gain access to a higher education institution but then fail to succeed in their studies.5 However, almost all these studies focused on linking one or more of the above factors to dropout using a standard survival analysis based approach that feeds these factors into a hazard function which in turn generates a probability distribution for predicting the time to dropout of that particular student. No cognisance is taken of the fact that external socio-economic and institutional forces may exert an influence on the type of exit from a university that a student experiences.
The competing risks methodology
The competing risks methodology that has been developed in the statistical literature is ideally suited for modelling a decision-making process where we have a set of underlying but possibly different socio-demographic forces pulling a student towards one or other particular outcome. Given a medical setting, for example, one may be concerned with identifying potential factors that affect the length of time that it takes for someone to die from one of a mutually exclusive set of possible causes; for example, death from a stroke, death from cancer or death from a liver-related disease. The occurrence of one type of death will obviously prevent any one of the other events from occurring. Environmental and genetic factors may, however, be pushing the individual towards one or more possible causes of death. By incorporating this information into one's analysis, one is separating a competing risks problem from that of a more typical survival analysis based problem in which the focus rests solely on a primary cause of death with the other potential causes of death (and their effect on the primary cause) not being explicitly modelled (as potential competitors for the final outcome on an individual) in the model-building process.
Although the language and application of the competing risks idea was originally developed for applications in the health, medical and actuarial sciences, some applications have appeared in the social science literature. These applications include that of De Graaf and Kalmijn6 who used the idea to study what happens to couples after they have divorced - whether they stay single, remarry or enter into a cohabiting relationship can be viewed as being determined by a set of socioeconomic forces that are competing amongst each other for the final outcome of that individual. Diermeier and Stevenson7 used the theory to determine how long a government tenure will last and whether this end point will result in a reshuffling of ministers in the cabinet or the calling of a new election. Gordon8 used the theory to determine how long a criminal investigation will last, noting that the end point in this investigation may result in a decision to prosecute or to abandon the case. Researchers in labour markets have used the theory to determine how long people stay in their jobs - noting that one could leave a particular job because of a promotion or demotion within that organisation, a dismissal or even a retirement date being reached. Social scientists studying international conflicts have used the theory to determine how long a conflict will last, particularly for determining whether the conflict will end in a negotiated peace process, a conquest or a stalemate.
Given our education-based setting, let T denote a 'survival time' representing the number of extra credit points that are taken (repeated) by a student before leaving the university. Calendar time has generally been used to measure the length of time that it takes for a student to graduate or drop out from their studies. Attempting to use this measure becomes a difficult bookkeeping exercise when, for example, a student is forced to temporarily suspend their studies because of some family obligation and then returns at a later stage to complete their studies. Let x be a vector containing student-specific covariates, such as their age, gender, race and financial status, which hopefully has an effect on the outcome of T observed. The objectives of this paper can now be summarised as:
1. To compare the time that it takes to graduate from a particular university with that of two other types of exit, namely (1) a voluntary dropout, that is, a student with a good academic record decides, for example, to change universities and (2) an involuntary dropout, that is, a student who is excluded on academic grounds from further study at that university because of poor performance.
2. To ensure that the analysis incorporates the idea that a set of underlying socio-economic and university-based factors are pushing the student towards one or another particular outcome.
3. To determine if any socio-economic, student-specific or university-specific factors can be identified that affect the type of exit that a particular student will experience. In particular, this determination will be done by estimating cumulative incidence functions for each one of the above exit types (eventual graduation, a voluntary dropout or a forced academic exclusion).
A detailed discussion of the competing risks methodology can be found in Beyersmann et al.9 and Kalbfleisch and Prentice10 or in introductory articles11-14. More formally,
CIF1 (t, x) =P(T<t, student graduates|x)
defines a cumulative incidence function (CIF) that one can associate with a student who will eventually graduate from their studies. Setting t=35, an outcome of the form
P(T< 35, student graduates|x) = 0.40
implies that a student with an associated set of covariate values x has a probability 0.4 of eventually graduating and achieving this outcome without doing more than 35 extra credit points before completing their degree. Plotting CIF1 (t, x) against t will produce a CIF plot for graduation that forms the focus of much of the discussion in the results section of this paper.
A CIF for those students who are forced to drop out of university (on an involuntary basis) because they have a poor academic record is given by
CIF2 (t, x) =P(T<t, student is excluded |x)
Similarly, a CIF for those who will eventually drop out on a voluntary basis from their studies can be given by
CIF3 (t,x) = P(T<t, student drops out voluntarily|x)
Because each student comes with a very specific set of student-based covariates such as their age, gender and race, which we have coded in the vector x, their effect on each of the above CIFs can now be explicitly modelled by introducing the concept of a yth - a cause-specific subdistribution hazard function into the model:
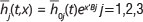
and allowing this hazard function to be fed into CIFj (t,x) in the following parametric manner:
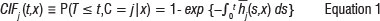
Having obtained a suitable set of estimates 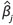 for the parameter vector ßj that appears in
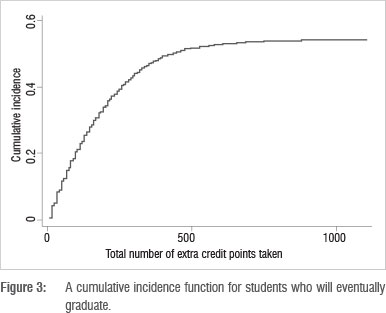
for the parameter vector ßj that appears in 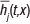 , whether or not the k'th factor variable in x significantly affects the CIF associated with exit-type /, requires the computation of what is called a sub-distribution hazard ratio (SHR) for this factor k and exit type j, namely
, whether or not the k'th factor variable in x significantly affects the CIF associated with exit-type /, requires the computation of what is called a sub-distribution hazard ratio (SHR) for this factor k and exit type j, namely
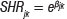
with the following interpretation then given to the result that one observes: if SHRjk is significantly greater than one, then any increase in the value of this kth factor variable will produce a higher CIF value for that exit type j. To illustrate this concept further, assume that the kth factor variable refers to gender, with males coded 1 and females coded 0. If the data set on which this analysis is based produces an estimated SHR value for exit type 1 of 2.34, then, because this value is greater than one, males in this data set have a higher CIF value associated with exit type 1 than females - this result is true regardless of the number of credit points t that they have to repeat. Stating this result in another way, males experience exit type 1 more quickly (on average) than females. If this SHR value is less than 1, then females experience exit type 1 more quickly (on average) than their male counterparts.
A case study
At the University of KwaZulu-Natal (UKZN), each course is assigned a value of 16 credit points, such that on completion of a 3-year degree a total of 384 credits have been awarded. As a response variable T for this paper, the total number of credit points that a student had to repeat before leaving UKZN was recorded together with another response variable for the type of exit. In particular, it was noted whether students had graduated when the data collection period ended in 2012, had been excluded on academic grounds or had dropped out on a voluntary basis (possibly to transfer to another university). Students who were still busy with their studies when the period of observation was completed were treated as being right censored in the analysis that was done.
Dropping out on a voluntary basis may also be associated with a poor academic record (i.e. a student may choose to leave before being excluded on academic grounds). Therefore, to identify only true voluntary dropouts in our data set, any person who had chosen to drop out but who had an academic record reflecting that they had not failed more than 64 credit points was regarded as a voluntary dropout. Students who had dropped out and who had an academic record reflecting that they had failed more than 64 credit points were removed from the data set, primarily because it could not be determined with absolute certainty whether the cause of the dropout was non-academic in nature, such as a funding- or family-related problem, or whether dropping out was a precursor to exclusion for academic reasons. A total of 324 students fell into this category. Ideally one would have liked to ask each student their reason for dropping out from their studies but the logistics behind such a data collection process made such an approach impossible to implement.
Given that different socio-economic and institutional forces may be exerting an influence on those students who drop out on a voluntary basis and those that are excluded on academic grounds, it was important to make a distinction in the analysis between these two types of dropout.
The data collection period
Over the period 2004-2012, the progress of all students entering UKZN was monitored from their date of registration until they had either completed their degree or left the university because of academic exclusion or as a voluntary dropout. A total of 56 079 enrollment records were collected; 17 602 students were still busy with their studies when the period of observation ended in December 2012. The four students who graduated from the 2011 first-time entry cohort would have entered UKZN as second-year students, which would have allowed them enough time to have graduated when the study period ended in December 2012.
The following covariates were also collected: the year in which each student first registered; a 0/1 indicator variable indicating whether (or not) the student was male (male=1); a collection of four 0/1 indicator variables indicating whether the student was African (or not), a student from the Coloured community (or not), an Indian student (or not) or a student from the white community (or not); a 0/1 indicator variable indicating whether the student was in residence during their first year of study; a 0/1 indicator variable indicating whether the student had received some form of financial aid in their first year of study; and a matric point score measuring the quality of pass that a student obtained for all their school-leaving subjects.
A breakdown of the student demographics at UKZN based on race and gender is given in Table 2. The total number of students that received some form of financial aid in their first year of study and/or some form of residence-based accommodation is given in Table 3.
Results
In a competing risks based methodology one needs to look at the CIFs that are generated by each competing event type - in this case, eventual graduation, voluntary dropout and academic exclusion. The SHRs values associated with each factor (and each event type) then help one to determine whether this factor affects the occurrence of the event type that is being considered in a statistically significant way.
Students who eventually graduate
Figure 1 is a plot of the number of credit points repeated by those 23 654 students in our data set who were able to eventually graduate from UKZN. As one would expect, the curve is sharply skewed to the left because these students generally did not need to repeat a large number of credit bearing courses.
Treating academic exclusion and voluntary dropout as competing risks for this event type, the results that appear in the second column of Table 4 were obtained using the Stata version 13 package. The column labelled 'SHR for eventual graduation' contains the estimated sub-distribution based hazard ratios for each covariate-based factor which can be interpreted in the following manner: if the SHR value is significantly greater than one, then any increase in the value of that covariate will produce a higher incidence of eventual graduation for students in that group of students who will eventually graduate. Noting that a student in residence would have been coded a 1 in our data set and those not in residence would have been coded a 0, the statistically significant SHR value of 1.2349 that we have obtained for the residence-based covariate indicates that those who have some form of residence-based accommodation are graduating (on average) more quickly (i.e. repeating fewer credit points) than students who have no form of residence-based accommodation. The stress associated with finding accommodation, or the benefit of being able to associate more easily with one's peers because one has residence-based accommodation, may provide an explanation for this result.
Having some form of financial aid and having a higher matric point score are also helping students in this cohort to graduate on average more quickly in terms of the number of credit points that they are having to repeat. Gender and race also seem to play a significant role - African males take longer on average to graduate than any other race or gender group. Although the above results are well known in the literature, the analysis allows us to study the effects of these factors in a modelling framework in which a set of mutually exclusive events compete for the final outcome.
Students who are excluded on academic grounds
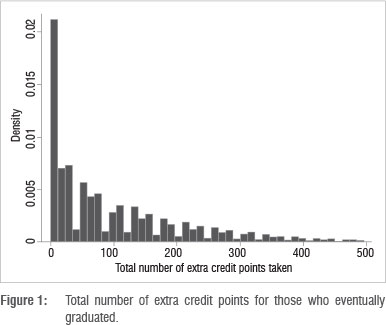
Treating voluntary dropout and eventual graduation as competing risks for this event type, produced the results that appear in the fourth column of Table 4. As one would expect, because students are academically excluded because of a poor academic record, the histogram that appears in Figure 2 has a mean and interquartile range that are much higher than those for graduating students (Figure 1).
Using a 5% level of significance, being of African origin and/or male seems to shorten the length of time - in terms of extra credit points - that students linger in the system before dropping out as an academic exclusion. Having some form of financial aid and staying in residence increases the length of time that students linger in the system before dropping out as an academic exclusion. An interesting anomaly is therefore observed: financial aid helps a student who will eventually graduate to do so quicker in terms of the number of credit points that they have to repeat, but also helps someone who will eventually be excluded on academic grounds to linger longer in the system. A similar argument could be made for students who receive some form of residence-based accommodation at UKZN.
Students who drop out but with a good academic record
Treating academic exclusion and eventual graduation as competing risks for this event produced the results that appear in the sixth column of Table 4. Using a 5% level of significance, white students seem to drop out more quickly, in terms of the number of credit points that they repeat, than a baseline Indian student. However, access to some form of financial aid and being in a residence helps to prevent these students with a good record from choosing to complete their studies at another university.
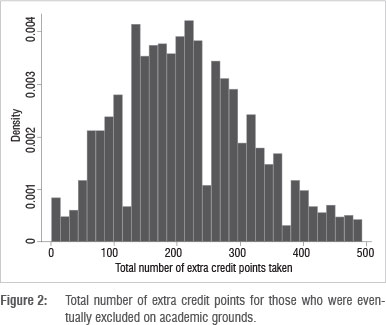
Figures 3 contains a CIF that one can associate with a student who will eventually graduate from their studies. In keeping with the national figures recorded in the Council for Higher Education report of 2013 - in which graduation rates within a 5-year period for a 3-year degree ranged between 48% and 58% - Figure 3 indicates that UKZN has an eventual graduation rate that is of a very similar order. Figures 4a and 4b provide an illustration of how easily this methodology can be used to compare one type of student with another. More specifically, the CIF associated with an African male student who will eventually graduate (Figure 4a) is compared with that of a white female student who will also eventually graduate (Figure 4b). From these curves one can see that white female students have a much higher graduation incidence rate, which means that white female students need (on average) fewer extra credit points to graduate than their African male counterparts.
Conclusions
The main purpose of this paper was to introduce into the literature a new methodology for comparing the graduation and dropout rates of students at a university. By changing one's point of focus from a calendar time based survival measure to one that looks at the number of credit points that are repeated before a student can graduate (or drop out), one is able to circumvent the type of problem that can occur when a student has been forced to interrupt their studies, because of a domestic or financial problem, and then returns at a later stage to complete their studies, or when a student is given a lighter load in a given semester to help them cope better with their studies.
References
1. Letseka M, Maile S. High university dropout rates: A threat to South Africa's future. Pretoria: Human Science Research Council; 2008. p. 1-7. [ Links ]
2. Council on Higher Education (CHE). A proposal for undergraduate curriculum reform in South Africa: The case for a flexible curriculum structure. Pretoria: CHE; 2013 [ Links ]
3. Tinto V. Dropout from higher education: A theoretical synthesis of recent research. Rev Educ Res. 1975;45:89-125. http://dx.doi.org/10.3102/00346543045001089 [ Links ]
4. Scott I, Yeld N, Hendry J. A case for improving teaching and learning in South African higher education. Higher Education Monitor No. 6. Pretoria: Council on Higher Education; 2007. Available from: http://www.che.ac.za/documents/d000155/index.php [ Links ]
5. Fisher G, Scott I. The role of higher education in closing the skills gap in South Africa. Background Paper 3 for 'Closing the skills and technology gap in South Africa'. Washington DC: The World Bank; 2011. [ Links ]
6. De Graaf P Kalmijn M. Alternative routes in the remarriage market: Competing-risk analyses of union formation after divorce. Soc Forces. 2003;81(4):1459-1498. http://dx.doi.org/10.1353/sof.2003.0052 [ Links ]
7. Diermeier D, Stevenson RT. Cabinet survival and competing risks. Am J Polit Sci. 1999;43(4):1051-1068. http://dx.doi.org/10.2307/2991817 [ Links ]
8. Gordon S. Stochastic dependence in competing risks. Am J Polit Sci. 2002;46(1):200-217. http://dx.doi.org/10.2307/3088423 [ Links ]
9. Beyersmann J, Schumacher M, Allignol A. Competing risks and multistate models with R. New York: Springer; 2012. [ Links ]
10. Kalbfleisch JD, Prentice RL. The statistical analysis of failure time data. Hoboken, NJ: Wiley; 2002. http://dx.doi.org/10.1002/9781118032985 [ Links ]
11. Putter H, Fiocco M, Geskus RB. Tutorial in biostatistics: Competing risks and multi-state models. Stat Med. 2007;26(11):2389-2430. http://dx.doi.org/10.1002/sim.2712 [ Links ]
12. Klein JP Competing risks. WIREs Comput Stat. 2010;2:333-339. http://dx.doi.org/10.1002/wics.83 [ Links ]
13. Lau B, Cole SR, Gange SJ. Competing risk regression models for epidemiologic data. Am J Epidemiology. 2009;170:244-256. http://dx.doi.org/10.1093/aje/kwp107 [ Links ]
14. Bakoyannis G, Touloumi G. Practical methods for competing risks data: A review. Stat Methods Med Res. 2012;21 (3):257-272. http://dx.doi.org/10.1177/0962280210394479 [ Links ]
 Correspondence:
Correspondence:
Mike Murray
Mathematics, Statistics and Computer Science
University of KwaZulu-Natal
Westville Campus
Private Bag X54001
Durban 4000
South Africa
EMAIL: murraym@ukzn.ac.za
Received: 08 Jan. 2014
Revised: 12 Feb. 2014
Accepted: 11 Mar. 2014














