Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Science
versão On-line ISSN 1996-7489
versão impressa ISSN 0038-2353
S. Afr. j. sci. vol.110 no.7-8 Pretoria Ago. 2014
RESEARCH ARTICLE
An outline of possible pre-course diagnostics for differential calculus
Aneshkumar Maharaj; Vivek Wagh
School of Mathematics,Statistics and Computer Science,University of KwaZulu-Natal,Durban, South Africa
ABSTRACT
There is a view that many first-year students lack the basic knowledge and skills expected of them to study at university level. We examined the expected work habits and pre-course diagnostics for students who choose to take a course on differential calculus. We focused on the lecturer pre-course expectations of a student in the context of work habits, knowledge and technical skills. In particular, we formulated outcomes and then sample diagnostic questions to test whether the identified learning outcomes on expected work habits and learning are in place. If students are made aware of the expected learning outcomes and if they take the diagnostic test, they should be able to achieve greater success in their studies. The validity of this assumption will be the subject of a future paper which will report on the implementation of the learning outcomes and diagnostic questions that we formulated for pre-course diagnostics in differential calculus.
Keywords: work habits of students; pre-course outcomes; diagnostics; differential calculus; technical knowledge
Introduction
Informal interviews with students across disciplines from a sample of institutions within South Africa indicated generally that students do not know what the precise outcomes of their courses or modules are. They stated the outcomes very vaguely, if at all. Without knowledge of the outcomes, students do not know what is expected of them. The process of thinking and the questions that lead to proper observations are rarely stated. We attempted to bridge such gaps in the context of the Math130 module (differential calculus) offered at the University of KwaZulu-Natal (UKZN).
Outcomes-based education (OBE) has been implemented at secondary-school level in South Africa.1 There is a general feeling that OBE at school level has not been successful. We believe that merely stating outcomes is not enough to ensure improvement in student understanding and performance. In the case of OBE the outcomes were mostly known to the teachers, but not the learners. We believe that it is important to document the outcomes for a course or module, and to make these outcomes available to students. In our opinion, students also need support in the form of diagnostics and skills to be acquired over a substantial period of time, which is generally absent. It is unrealistic to assume that students will have a long-term mastery of concepts and skills relevant to differential calculus, when exposed over only a 13-week period, as disuse degrades these skills. We are not disputing that students could attain a significant level of mastery for a limited period. The challenge is for students to be able to recall and use their skills and knowledge over a sustained period of their studies (while at university) and beyond (in their work and social contexts). Based on our experience, as well as from informal discussions with colleagues, a significant number of students are underprepared for university studies in mathematics. Our hope is that by providing clear pre-course diagnostics for expectations on work habits, background knowledge and means for self-assessment of the required background, there will be an improvement in the achievement of course outcomes. In another paper we focus on the course diagnostic component which is to help focus attention on crucial possible gaps in learning that could lead to underachievement by students. In this paper we attempt to answer the following research questions: What are the views of lecturers on pre-course expectations of a Math130 student in the context of work habits, knowledge and technical skills necessary for effective mathematics learning? And how do we test work habits, knowledge and technical skills?
Review of relevant literature
We use the term 'learning outcome' to refer to a clear and detailed statement of what students should be able to do when they have learnt the content of a particular topic. In its discussion of student learning principles, the Council of Regional Accrediting Commissions2 flagged the importance of learning outcomes. With regard to learning outcomes towards which students are expected to aspire, the Council noted that (1) these should be clear and easily available (made public) and (2) there should be reflection on such outcomes for a commitment to educational improvement. If these points are accepted then it follows that it is important for the learning outcomes of courses and modules offered by a tertiary education institution to be clearly documented, assessed regularly and improved upon if necessary, and to be made available at the outset to students. These learning outcomes should guide the type and level of assessment.
Discussing the characteristics of effective outcomes assessment, Banta3 noted that (1) there should be a recognition that assessment is essential to learning, (2) assessment should begin when the need is recognised and should allow sufficient time for development, (3) faculty development is required to prepare individuals to implement assessment and use the findings, and (4) an environment which is receptive, supportive and enabling should be available to students continually. The American Association for Higher Education4 gave the following principles of good practice for assessing student learning: (1) assessment requires attention to outcomes and to the experiences that lead to those outcomes; (2) assessment is most likely to lead to improvement in learning when it is part of a larger set of conditions that promote change; and (3) through assessment, educators meet their responsibilities to students and the public. We agree with all of these points. The challenge we face in developing countries is that an increasing number of underprepared students are admitted for university studies in mathematics. With this in mind we believe that diagnostic testing based on clear pre-course outcomes could help many students achieve success in their studies. Our view is that diagnostic testing should form an integral part of assessment, because the assessment should also promote student learning. By a diagnostic test, we mean a test that is designed to evaluate the precise strengths and shortcomings of a student with reference to a given context, such as preparedness for a particular course.
We looked at how some institutions addressed the issues of course outcomes and diagnostic testing. Florida International University5 gives a comprehensive list of learning objectives or outcomes for their calculus module. This list includes the general course objective and desired learning outcomes for their major topics in calculus. The calculus course outline of the University of Manchester6 stipulates under learning outcomes: 'On successful completion of this module students will have acquired an active knowledge and understanding of some basic concepts and results in calculus.' The required concepts and results were not clearly indicated, but the major topics and sub-topics were listed under the syllabus section.
The Stevens Institute of Technology7 gives the overall course objective and lists the expected learning outcomes under each of their topics in calculus. The website of the University of New England's8 calculus course gives a general description of the unit and assessment tasks. Each assessment task relates to stated learning outcomes in the context of the content as well as graduate attributes. We found the latter to be interesting because it gives a new dimension of what could be required of students. The following five graduate attributes were listed: knowledge of a discipline, communication skills, information literacy, problemsolving and team work. The expectation of a student for each of these attributes is clearly indicated. For example, communication skills are unpacked as follows:
The student will be encouraged to participate actively in discussion during lectures and tutorials. Written communication skills, particularly with regard to construction and presentation of logical expositions and arguments, will be taught and assessed.8(p.3)
For each of these five graduate attributes, the intention was for it to be taught, assessed and practised.
The Mathematics Diagnostic Testing Project (MDTP) of California State University9 provides free online student tests which can be taken more than once. There is a calculus readiness (CR) test which is designed to help individual students review their readiness to study calculus. Students are advised to take the test without the aid of a calculator. The recommended time for taking the test is approximately 1 h, but no time limit is enforced. The online test includes a diagnostic scoring report to help students identify their strengths and weaknesses in different topics. Students are expected to use these tests and reports to identify their weaknesses to study those topics more and overcome the identified weaknesses. Our review of the diagnostic test questions gave us the impression that they were too difficult for the majority of underprepared students who now gain access to universities in developing countries.
The California Mathematics Diagnostic Testing Project10 tests cover similar topics as those of the MDTP CR test and pre-calculus (PC) diagnostic tests administered by many Californian schools. This web-based test is intended to provide students with feedback on how well prepared they are for any of those tests. The only purpose of this test is to indicate the extent of a student's understanding of and facility for some important concepts and skills. Students are given a total score as well as a score for each of the topics covered by the test. It is stated that these results could help a student focus on additional study to be better prepared for a calculus course. This test is intended to give students an indication of their level of preparedness for the MDTP CR test. The prerequisites to study differential calculus, in terms of technical knowledge and skills, are indicated in the above diagnostic tests.
We have observed that our students often understand the calculus concepts but that their algebra tools fail them when they are solving problems. The University of British Columbia11 reported that data from their past final examinations showed that 75% of students' mistakes were related to basic high-school knowledge and skills. In order to address such underpreparedness, pre-course diagnostic tests for calculus are used in a number of institutions.11-14 A study of those diagnostic tests revealed that: (1) in many cases, for example Acadia University14, diagnostic tests are compulsory for all students taking a differential calculus course, (2) the tests cover high-school mathematics skills that are essential for the passing of a university-level calculus course, (3) the pre-calculus questions for such tests should be developed by using errors actually made by previous students, (4) such tests show a student where his/her basic weaknesses are, and provide him/her with means to improve, and (5) the main purpose of the tests is as an early warning system for those students with a weak mathematical background. Some institutions, for example the University of California15, use diagnostic tests as a placement tool to help students choose between the various mathematics modules that are offered.
We used the above findings and our experience to develop pre-course diagnostics that we consider to be more appropriate for the students we encounter. We note that most of the institutions referred to above place the responsibility of remedial measures on the student.
Conceptual framework
The literature review and our experience guided the formulation of principles which give an overview of the conceptual framework for this study. These principles are:
1. There is a conceptual hierarchy in the body of mathematics.
2. To study mathematics students should understand and possess good work habits.
3. It is important for the outcomes on prerequisites for the module to be clearly documented.
4. For effective learning, it is not enough for only the instructor (teacher, lecturer, tutor) to be aware of the prerequisite work habits and technical knowledge outcomes of a course or module.
5. Students should know explicitly at the outset what the expected outcomes for these prerequisites are.
6. Instructors should use the documented prerequisite outcomes to formulate suitable diagnostic questions for students.
7. When students attempt the diagnostic questions there should be provisions for remedial activity, in order to overcome their identified shortcomings.
Methodology
We first looked at the aim and the content for the Math130 module as indicated in the handbook of the UKZN's Faculty of Science and Agriculture,16 which is in the public domain. The aim is given as: 'To introduce and develop differential calculus as well as the fundamentals of proof technique and rudimentary logic.' The content includes: 'Fundamental Concepts - Elementary logic, proof techniques. Differential Calculus - Functions, graphs and inverse functions, limits and continuity, the derivative, techniques of differentiation, applications of derivatives, antiderivatives.'
Based on our experience with respect to teaching at secondary and tertiary education institutions, we documented outcomes and diagnostics on:
1. Expected student work habits. Students should be aware of the work habits that their instructors (lecturers, tutors) expect of them. We documented such outcomes that in our opinion give the characteristics of the work habits of successful students.
2. Pre-course (prerequisite) outcomes. We formulated these outcomes based on the conceptual hierarchy of mathematics and common errors of past students.
3. In-course outcomes. We formulated such outcomes for the Math130 module by studying the aim and the content, as indicated above.
4. Work habits. Firstly, work habits were classified into different areas, for example, be responsible for your own learning, be critical of your thinking, and be able to work constructively in group situations. We also formulated questions to focus students' attention on these aspects. Our thinking here was that we should help students improve their work habits to the level of that expected of them.
5. Pre-course diagnostics. Based on the outcomes identified, we formulated sample diagnostic questions on compulsory background and essential mathematical vocabulary. The compulsory background check focused on basic arithmetic and algebra, while the vocabulary check focused on mathematical syntax and precise knowledge of elementary mathematical terms. These diagnostic questions were discussed at meetings of interested role players (relevant lecturers, experienced members of staff and certain students). Feedback was encouraged with regard to the suitability of the diagnostic questions, their framing and the answers. A three-member editing team then looked at the feedback, considered the suggestions and revised the questions accordingly.
6. In-course diagnostics. We used the outcomes identified to formulate questions on course content for logic, functions, limit of a function, continuity of a function, derivative of a function, antiderivative and integral of a function, and specifically on creative thinking (for example, application to cooking).
Findings and discussion
We present the findings in four sub-sections: (1) outcomes for the expected work habits and questions to focus the students' attention on these, (2) compulsory background check, (3) essential mathematical vocabulary check and (4) exposure of students to outcomes, ways of diagnostic testing and remedial measures.
Outcomes for expected work habits and
diagnostic questions
We expect students to acquire the following work habits:
1. Be able to take responsibility for your own learning
- Read in advance and make a note of concepts that are not clear
- Participate actively in classroom discussions
- Attempt the homework problems seriously
- Recall basic knowledge quickly and correctly and also practise basic skills regularly
- Be self-motivated to work
- Seek help when required
2. Be able to unpack what is required to answer a question
3. Be able to identify gaps in your knowledge or skill set that hinder question solving
4. Be able to take appropriate measures to overcome the identified gaps
5. Be able to ask appropriate questions in class to improve understanding
6. Be able to learn what constitutes understanding
7. Be able to recall correctly the relevant knowledge and skills for a section
8. Be able to see connections within and across sections
9. Be able to formulate questions and then explore these in a manner that will promote your understanding
10. Be able to write down solutions to problems in a manner that enables others to follow the solution. Includes appropriate use of connectives, reasons and explanations
11. Be critical of your thinking
- Look for invalid assumptions
- Think of alternative strategies
- Check the flow of the logic, in particular for unnecessary sidetracks
12. Be able to critically examine solutions to problems
- Look for invalid assumptions
- Detect errors in your written solutions
- Check the flow of the logic, in particular for unnecessary sidetracks
- Check your written attempts to problems against given answers and do the necessary corrections from the point of breakdown
- Think of alternative solutions
13. Be able to take appropriate notes, including making notes during lectures, from appropriate material and from critical examination of your own work
- For a lecture and reading of appropriate materials this refers to a framework that enables one to reconstruct (within an appropriate time) the essentials that include definitions, statements of theorems, illustrative examples or counterexamples, observations and remarks
- For critical examination of your work, this outcome ref ers to observations, strategies, alternative strategies, misconceptions and common errors
14. Be able to constructively work in group situations
- Prepare for group sessions
- Read and work through the identified required materials
- Formulate questions and observations
- Identify points that you feel need further elaboration
- Participate actively
- Allow others to participate actively
- Make relevant notes or recordings
- Learn from others and allow others to learn from you
- Plan for everyone to have a share of the collective time
- Be polite
15. Be able to plan for your work
16. Be able to implement the work plan effectively
17. Be able to handle stress, including stress from examinations, tests, assignments and interviews
18. Be able to analyse a definition or statement of a theorem or relevant principles and use them appropriately in a given context
- Detect the conditions under which the definition or statement of the theorem applies
- Check that the conditions of the definition or of the statement of the theorem are satisfied in the given context.
The reference to homework in Point 1 refers to what is normally referred to as tutorial problems at university. We used the concept 'homework' because first-year students may be more familiar with this concept than the concept 'tutorial'. Our interactions with mathematics students have indicated that the above work habits lead them to take responsibility for their own learning, to develop a deep understanding for the subject matter and to be critical of their own thinking and the work of others. In formulation of the above outcomes on expected student work habits we tried to unpack for our context some of the graduate attributes focused on by the University of New England8. To make students aware of these attributes we formulated two diagnostic questions on work habits: (1) What do you need to do to take responsibility for your own learning? and (2) What is required of you to work constructively in group situations?
Question 1: What do you need to do to take responsibility for your own learning?
In our opinion, students are taking responsibility for their own learning if they comply with Points 1-13 and Points 15-17 above.
Question 2: What is required to work constructively in group situations?
In our opinion, students are able to constructively work in group situations (e.g. during tutorial sessions) if they comply with Point 14 above.
We believe it is important to expose students to these questions as a catalyst for them to reflect on pertinent points regarding responsibility for their own learning and working in group situations. Often new students coming to university do not know what is expected of them. Our experience in mentoring students who repeat modules suggests that these students could have succeeded in their first attempt. For example, when mentoring such a student on the work habits expected of students at a university, the student remarked, 'If only I knew this last year ... I would have passed!' Another such student asked 'Why was I not made aware of this last year?' Such responses indicate to us the need to expose students to diagnostic questions on work habits.
Compulsory background check
The background check consists of operations on numerical fractions, operations on algebraic functions, laws of exponents and laws of logarithms. Sample questions and answers for this part are given in Table 1. In our opinion a time limit of 40 min should be given to answer the sample questions in Table 1.
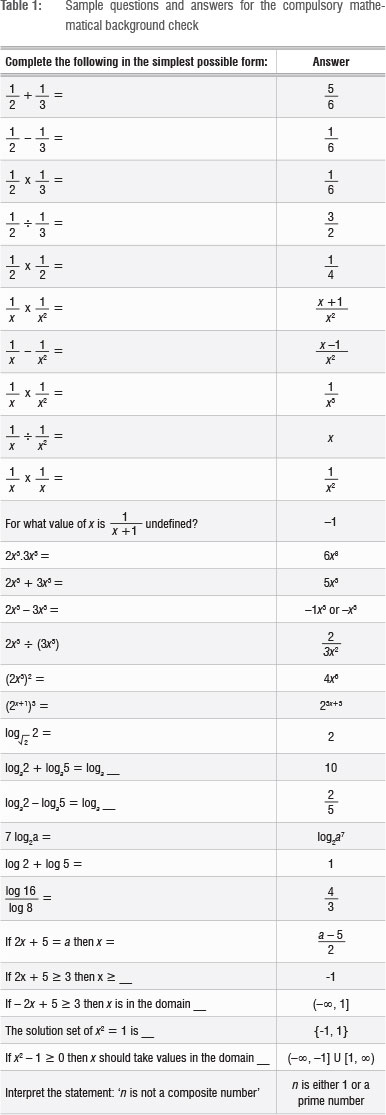
In our opinion, every first-year student who wants to study first-year mathematics should be given such a test. This assertion is supported by the literature review.10,14 Tests should be re-administered weekly for students who perform poorly (below 80%) and there should be increasingly less time for completion with each test. Candidates should know in advance that this process will be followed. One can formulate similar tests for each week until the student is able to score full marks. Note that the computations should be simple.
Essential mathematical vocabulary check
The background check tests familiarity with synonyms for commonly used mathematical syntax and precise knowledge of elementary mathematical terms. We present our sample questions and answers for arithmetic, algebra and mathematical syntax in Tables 2, 3 and 4, respectively.
Note that all of the above categories are pre-course diagnostics. Many of our students have English as their second language. It is for this reason that we included simple translations from English phrases to mathematical symbolism (see Table 3). Because mathematics has its own language we felt that it was important to expose students to the subtleties of mathematical syntax (see Table 4) and to check on their preparedness for this.
One could argue that the outcomes of expected work habits, compulsory background check and essential mathematical vocabulary check are general mathematics expectations. However, it is important for students to know exactly what work habits their lecturers expect of them so that if required a student could rectify their work habits timeously. Our experience is that first-year students who find it difficult to cope with their studies on differential calculus lack what could be termed good work habits. Often the case is that students know the work taught at university for differential calculus but find it difficult to solve problems based on differential calculus correctly because of a lack of the basic knowledge and technical skills necessary for success. This premise was the rationale for formulating the outcomes and then the sample diagnostic questions for the compulsory background and essential vocabulary checks.
Exposure of students to outcomes, diagnostic testing and remedial measures
In this section we focus on ways to expose students to the pre-course outcomes, the diagnostic testing of these outcomes and the remedial measures thereof.
Exposure to pre-course outcomes
Outcomes could be given to students as part of the welcome kit for the course, if costs permit. They could also be made available on the website of the course. Regardless of how they are made available, it is important that students have access to the pre-course outcomes at the outset of the course.
Ways of diagnostic testing
The diagnostic questions on work habits and those for the compulsory background and essential vocabulary checks could be administered as formal pre-course tests. We suggest that as much as is possible be done during the orientation programme for students. Tests could be completed by students either in hard copy or online. The tutors of the groups to which the students belong should look at their students' responses and prepare suitable feedback for the students.
Remedial measures
It is important that students be given qualitative feedback with regard to areas in which they have difficulties. Suitable feedback by tutors to students could also be one of the remedial measures. Similar diagnostic tests should be planned and administered on a regular basis to students who perform poorly. A student could also approach his or her tutor to discuss relevant difficulties. Students could also form self-help groups with the intention of overcoming identified shortcomings. The course coordinator or lecturer could also upload to the website additional notes with examples to address common shortcomings.
Conclusions
We were able to detect and document the views of lecturers on pre-course expectations of a Math130 (differential calculus) student in the context of relevant work habits, knowledge and technical skills necessary for effective mathematics learning. Our formulations of outcomes relating to the above context and sample diagnostic questions were an eye-opener for us. The outcomes and sample diagnostic questions indicated to us that there was much that we as lecturers at academic institutions assumed, often incorrectly. We detect an urgent need for addressing this issue across disciplines, particularly in the context of developing nations for which, in general, continuously falling educational standards are a major concern. Depending on the availability of resources, the implementation of diagnostic tests could be hard copy or electronic form. In another study we will look at the correlation of the pre-course results of the diagnostic tests with that of student performance in their differential calculus course at UKZN. Those results will inform the evaluation of the pre-course outcomes and diagnostic material that we have formulated and developed.
Acknowledgements
We acknowledge the University of KwaZulu-Natal (UKZN) for granting a sabbatical to Aneshkumar Maharaj, which made this collaboration possible. Professor Sanjay Wagh from the Central India Research Institute in Nagpur (India) is acknowledged for facilitating this collaboration. We also acknowledge the Society for Action Research in Education and Livelihood (Nagpur, India). This study was funded by grants from ESKOM's Tertiary Education Support Programme (TESP) for the UKZN-ESKOM Mathematics Project, and the International Society for Technology Education for the HP Catalyst Multiversity Consortium project at UKZn, entitled Mathematics e-Learning and Assessment: A South African Context. Members of the Mathematics Education Research Unit at UKZN, in particular Dr Paddy Ewer, are also acknowledged for their inputs towards the editing of the diagnostic tests.
Authors' contributions
V.W. came up with the idea of including expected work habits of students who want to study at university. The learning outcomes and the pre-course diagnostics were jointly formulated by both authors. All sections of the paper were jointly written by both authors. A.M. typed the manuscript and did most of the proofreading.
References
1. Department of Education. Revised national curriculum statements Grades 1012 (schools) mathematics. Pretoria: National Department of Education; 2003. [ Links ]
2. Council of Regional Accrediting Commissions. Regional accreditation and student learning: A guide for institutions and evaluators. Atlanta: Southern Association of Colleges & Schools; 2004. Available from: http://www.sacscoc.org/pdf/handbooks/GuideForInstitutions.PDF [ Links ]
3. Banta TW. Characteristics of effective outcomes assessment: Foundations and examples. In: T.W. Banta & Associates. Building a scholarship of assessment. San Francisco, CA: Jossey-Bass; 2002. [ Links ]
4. American Association for Higher Education. Nine principles of good practice for assessing student learning. Sterling, VA: Stylus; 1991. [ Links ]
5. Florida International University. Syllabus for Calculus I [document on the Internet]. c2009 [cited 2013 Feb 02]. Available from: http://www2.fiu.edu/~ritterd/cal-tran/c1syl9al.pdf [ Links ]
6. The University of Manchester. Math10131 - calculus and vectors [document on the Internet]. c2010 [cited 2013 Feb 02]. Available from: http://www.maths.manchester.ac.uk/undergraduate/ugstudies/units/2010-11/level1/MATH10131/ [ Links ]
7. Stevens Institute of Technology. MA 115 - Calculus 1 [document on the Internet]. c2007 [cited 2013 Feb 02]. Available from: http://archive.stevens.edu/ses/math/courses/ma115/ [ Links ]
8. University of New England. MATH101 - Algebra and differential calculus [document on the Internet]. c2013 [cited 2013 Feb 02]. Available from: http://www.une.edu.au/courses/units/MATH101 [ Links ]
9. The California State University. Mathematics Diagnostic Testing Project [homepage on the Internet]. c2012 [cited 2013 Feb 02]. Available from: http://mdtp.ucsd.edu/OnLineTests.shtml [ Links ]
10. California Mathematics Diagnostic Testing Project. Web-based calculus readiness test [homepage on the Internet]. c2013 [cited 2013 Feb 02]. Available from: http://mdtp.ucsd.edu/crtest/intro2.htm [ Links ]
11. University of British Columbia. Basic skills test [homepage on the Internet]. c2012 [cited 2013 Feb 06]. Available from: http://www.math.ubc.ca/Ugrad/bst.shtm [ Links ]
12. Simon Fraser University. Diagnostic test [homepage on the Internet]. c2013 [cited 2013 Feb 06]. Available from: http://www.math.sfu.ca/lecturers/tab [ Links ]
13. Dalhousie University. Diagnostic test [homepage on the Internet]. c2013 [cited 2013 Feb 06]. Available from: http://www.mathstat.dal.ca/~brown/diagnostic.htm [ Links ]
14. Acadia University. Math diagnostic test [homepage on the Internet]. c2004 [cited 2013 Feb 02]. Available from: http://math.acadiau.ca/diagnostic.htm [ Links ]
15. University of California. Calculus diagnostic placement exam [homepage on the Internet]. c2011 [cited 2013 Feb 06]. Available from: http://math.berkeley.edu/courses/choosing/placement-exam [ Links ]
16. Faculty of Science and Agriculture. Handbook for 2010. Durban: University of KwaZulu-Natal; 2010. [ Links ]
 Correspondence:
Correspondence:
Aneshkumar Maharaj
School of Mathematics Statistics and Computer Science
University of KwaZulu-Natal
Private Bag X54001
Durban 4000, South Africa
Maharaja32@ukzn.ac.za
Received: 07 Aug. 2013
Revised: 15 Nov. 2013
Accepted: 05 Dec. 2013





![Dichloro(bis[diphenylthiourea])cadmium complex as a precursor for HDA-capped CdS nanoparticles and their solubility in water](/img/pt/next.gif)








