COMMENTARY

 

On taking the transformation discourse for a ride: Rejoinder to a response (Govinder et al. 2014)

 

 

Tim Dunne

Department of Statistical Sciences, University of Cape Town, Cape Town, South Africa

Correspondence

 

 

---

Keywords: demographic divergence; measurement; percentages

---

 

 

This submission explicitly clarifies the fundamental mathematical and logical errors and conceptual inadequacies of three recent contributions by Govinder et al.^1-3, published in the South African Journal of Science.

 

Scientific foundations

Ordination is an act of aggregating pairwise comparisons on a set of elements (objects, persons, events, phenomena) in such a way that the ordering of the elements becomes meaningful. The comparisons are made on the basis of some single composite characteristic of each element. For example, we may specify a notion of extent or size, and then impose a linear ordering on any relevant set of objects which admit comparisons with respect to that characteristic.

The ordering guarantees to the observer that each object (by our chosen criterion) is larger than every object , say to its right, but smaller than every object to its left. We rank elements or objects, but permit tied ranks. This simple device of ranking is profoundly important, and has huge advantages in every sphere of human activity.

The familiar versions of size and extent are counts and measures. These versions are, however, profoundly different in nature and in consequentiality.

For any collection of elements, we may specify a binary property which is either present or absent in each element, and count the number of times the property is present. Effectively, we assign each element a zero for absence and one for presence, and then add all the digits. Count is a form of number that is relevant in handling categorical information.

Measurements are very different from counts, and far more complex, even though we perform measurements routinely in many aspects of everyday life. Measurements address quantity, while counts address multiplicity.

All measurements are fundamentally comparisons, but of a particular kind. We construct measurements by first defining a suitable convenient unit of extent for a particular characteristic of the elements under consideration. For example, we may use grams for mass, metres for lengths and seconds for time. Alternative choices of units are available, such as tonnes, kilometres, hours.

Then we establish or construct a mechanism or device by which a comparison of the extent of an element (e.g. its mass) with the unit of extent of mass (e.g. a kilogram) can be made. This comparison is multiplicative and is represented as a fixed ratio between the two masses. The ratio is fixed in the sense that repeated applications of the mechanism on a particular element will preserve the ratio. The mechanism also has to be reliable, and often we are able to construct an instrument which is able to reproduce the ratio virtually unchanged on repeated applications to the same object or element.

The achievement of science is that such mechanisms have been discovered, and suitable devices have been invented and brought into everyday use. In these discoveries and inventions science has had to read and mimic the architecture of the physical universe and copy the choreography of its intimate laws of cause and effect.

Measuring a characteristic is the result of allowing a mechanism and a unit to operate on an element with that characteristic (inter alia), in order to obtain a value for the fixed ratio, attributable to the element. The number we obtain, coupled with an explicit reference to the unit involved in the mechanism, is the measurement. Thus we might report measurements as 2.59 kg or 4.257 metres.

The ratio is a pure number, expressed to a convenient number of decimal places. For example, a beam of wood, if correctly labelled as having a length of 2 centimetres, should be twice as long as the unit 1 centimetre. Our gauges of the beam width should register 2.0 on any centimetre ruler and 20 on any millimetre ruler, applied to the appropriate part of the beam.

The ratio can only be consistent to a degree determined by the limitations of the instrument we have constructed as the mechanism for obtaining measurements. Thus we allow rounding conventions to limit the number of decimal places to which an instrument is required to preserve the ratio. The desired number of places required is a matter of context and then convenience. The bathroom scale reporting personal body mass in kilograms to one decimal place is adequate for that purpose, but we do not use the same scale for laboratory purposes.

 

Derived units

We note that besides fundamental units of length, mass, time and arc, we construct derived units for properties such as rate, acceleration, density, momentum and force. Derived units are composite quantities that involve further ratio and product relationships between two or more of the fundamental quantifiable characteristics. The corresponding derived measurements are ratios and products of the observable measurements of distinct fundamental features of the elements or objects in question. A multiplicative arithmetic underlies derived units and measurements of derived variables.

Derived measurements generally involve some degree of decimal fraction. Again, context and convenience give rise to choices of number of decimal places required and of rounding conventions. The decimal place has no independent utility or power. It arises from measurement but it does not in any way constitute measurement.

This remarkable architecture is not an outcome of arithmetic. The spectacular fact is that science has discovered and explored this architecture. Science confirms that the physical universe and its multifold processes are all governed by these elegant regularities. Consequently, our simple arithmetic permits us to harness these regularities into artefacts, machines, processes and constructions that make life more predictable and more comfortable.

The power of measurement lies in the fact that, when combined with insights into the physical world, it permits us to use the laws of cause and effect to reliably predict and engineer desirable outcomes. This benefit is seductive, and it accounts for the pervasive compulsive urge to measure in the social sciences.

 

Social sciences

The quest for measurement in the social sciences is, however, an illusion. The uncountable variables of social science, whether latent or manifest, whether notional, constructed or real, do not admit units and ratio comparisons. They do not have meaningful zero origins. They permit pairwise orderings of objective and subjective kinds, both of which can be meaningful.

These limitations are not faults in the fabric of the social sciences. They constitute admissions of the complexity of social sciences, where regularity of any kind is necessarily encased and pierced by the confining and transcending effects of human perception and agency, by belief, hope, will, endurance, insight, creativity and ethical imperatives. This list of roots of actions and outcomes in human society is only illustrative, and not intended to be exhaustive.

Nonetheless, in the various social sciences, it is now possible to create subjective instruments that pass peer scrutiny for validity as fit for purpose, but also have some measurement-like characteristics. These instruments involve a designed set of items and associated item scoring systems, for which the total score is a sufficient summary of a proficiency or a degree of attribute.

These test scores have stochastic rather than deterministic interpretations, and are inherently relative orderings rather than absolute measurements. The interpretations have complex relationships with percentages of observations, under specifiable conditions.

In the current debate, the conditions for measurement-like interpretations are not satisfied by the demographic percentages of any population, nor by any mathematical formulae derived from any versions of Govinder et al.'s demographic divergence index (DDI) or its possible generalisations.

 

Percentage

Percentage is a relational construct characterised by the comparison of the sizes of two objects or elements of interest. One element is declared to be the referent object. Effectively, a ratio comparison is invoked, a number with a decimal fraction is obtained, and then this number is converted to a new type of number called a percentage, through multiplication by 100. To the observer, it will appear that the decimal place in a ratio has been moved two places to the right in the string of digits, and the sign % appended. Note that the ratio is not a unit, but is just a number. Its conversion to percentage and the appending of % does not mean that there is now a unit called % in operation.

It is crucial also to note that the comparison is relative to a particular choice of referent in each context, and not to any specific absolute unit across contexts. The presence of decimal places does not warrant regarding percentage and measurement as equivalent.

Percentage notions are often invoked to describe part-whole relationships. In these cases, the whole is the referent and all the percentages of parts will be reported as between 0% and 100%. This operation may always be applied to part-whole ratio comparisons of measurements, but the result is just a number, not a measurement.

In contrast, in everyday life, percentage is most familiar in the reporting of counts relative to an overall total count. For simplicity of report and communication, a convention of using only distinct or disjoint or mutually exclusive parts of the referent whole, ensures that percentages associated with the parts sum to 100%. This convention avoids double and multiple inclusion induced by any overlapping parts of the whole.

Comparisons of percentages within a common referent context are validly and easily made. It is also admissible to define desired percentages and assess the profile of differences between sets of observed and desired percentages, part by part. The pertinence and utility of any desired percentages is matter for debate. Desired percentages of total counts do not always generate desired integer counts, but often imply desired counts with decimal fractions. The so-called chi-square statistic is recommended for assessing the goodness-of-fit between desired and observed profiles. It takes the decimal fractions and the total count into account. This divergence from perfect fit is obtained by the formula

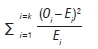
The formula first squares the differences between observed counts (O_i) and expected counts (E_i), and divides each square by the corresponding expected count, for each of k parts. It then sums all k of those relative terms to give an overall divergence value. This divergence index is available in any first-year statistics text.

For perfect agreement between observed and expected count values, the divergence statistic will be zero. When observed and expected count values are relatively close to one another the divergence statistic value is a small positive number. However, the divergence value will be dramatically large when the observed and expected counts differ substantially. Tables exist to inform judgements about the size of the goodness-of-fit statistics.

A large value serves to signal that the observed count differs from the expected count, which may require explanation, understanding and decision-making. The subsequent enquiry should involve both the beliefs which generated the expected counts, and the adequacy with which they can be associated with the context.

It is admissible, but not necessarily relevant or important, to contrast observed counts with any set of expectations. One such set of expected values might be derived from a population profile. We may note that the chi-square statistic is a pure counting number for the objects in the population under observation.

 

Divergence indices

A whole family of divergence indices for pairs of k-dimensional vectors of numerical values is offered by the Lp-norms:

where p is a positive real number. This family has been widely studied in the literature. The index has clear meanings for particular values, specifically p = 0, 1, 2 or ∞.

The special case of p=2 includes the divergence index that Govinder et al. advance for percentages and proportions. This application implies the index has to operate on a specific hyperplane on which proportions sum to 1 or, equivalently, percentages sum to 100%.

However, Govinder et al. prefer, advise and fiercely defend one logically flawed special case with k=6, for four ethnic or historical race categories and two genders. They purport to be unconcerned that the percentages sum to 200%. The approach of Moultrie and Dorrington⁴ is marginalised as an exercise of preference for k=8, rather than acknowledged as the only correct approach for race and gender.

 

Incoherence of approach

To exemplify Govinder et al.'s fallacy, we may approximate a South African population into groups B, C, W and I, with corresponding percentages 76%, 10%, 10% and 4% and gender groups M and F of percentages equal at 50% and 50%. These values are chosen only for simplicity, and more exact census count percentages can be invoked with the same general outcome.

In the intended Govinder et al. policy, any university with a matching profile to the population will be declared to have attained the ideal and constitutional transformation, by virtue of zero differences on these six percentages.

In Table 1, the desired Govinder et al.'s structure is indicated by the two common row and four common column percentages in all six tables. We may demonstrate the fallacy of Govinder et al.'s approach by exhibiting that amongst its immediate outcomes and implications, there are absurdities which defeat the misnamed purpose for which their DDI is intended.

The body of the table is unspecified in Table 1a. The letters a, b and c in Table 1b indicate three areas of arbitrariness in percentages associated with Govinder et al.'s specification. Here we may have three choices satisfying inequalities 0 < a < 10, 0 < b < 10 and 0 < c < 4.

Table 1c to 1f present four possible scenarios, each of which generates a Govinder et al. DDI index value of zero, and hence the Govinder et al. transformation 'jackpot' is attained. Technically there would be an infinite number of distinct race by gender profiles for universities, all of which would be compliant with Govinder et al.'s race criterion and gender criterion for perfect transformation. Only four of these perfect profiles are presented here (Table 1c-1f).

Closer inspection will show that only Table 1f satisfies a condition of independence of race and gender in the pseudo-university population. Race and gender would be mutually uninformative characteristics for a randomly chosen member of the pseudo-university associated with Table 1f. We may note that this possibly attractive inference about internal composition of pseudo-university profile is distinct from notions that the eight percentages in the body of the table mirror underlying South African population percentage realities for race and gender composition.

We now venture to construe the body of any table solely to university selection procedures based on race and gender alone, as per the parody of selection bias offered or imputed by Govinder et al. Then to which of the four universities would a black woman believe her chance of selection would be best, and where would she presume her selection is least likely? Clearly her first inferences would be for 1c as her highest and 1e as her least chance.

Ironically, a white man will interpret and make the same first qualitative inference for his own chances. Neither of these two selection candidates will perceive these four pseudo-universities as equivalent in their equity characteristics. If they have to choose only one university, they might apply to 1c.

In these apparently rational choices there are hidden assumptions: all other things being equal. We may render explicit several pieces of unknown information which have the potential to affect their decisions radically.

Such emerging facts include the size of the universities, the race and gender composition of the applicant cohorts at each university and the rationale offered for the varied forms of glaring inequity apparent despite Govinder et al.'s DDI perfect zero values. Knowing that the university in 1e was 10 times larger than its counterpart in 1c might lead both the applicants to reverse their preferences and prefer 1e over 1c, to maximise the probability of success in selection.

Likewise, information about the underlying composition of the applicant groups from which the pseudo-university admission processes selected to yield these profiles, will affect the interpretation of the two persons exploring their options from the various perfect equity universities of Govinder et al.

The question is simple: will any of these scenarios of perfect Govinder et al. compliance stand up to any rational tests of desirability under the Constitution to which Govinder et al. have made appeal. Universities have many simultaneous obligations and purposes for service to society which require many specificities beyond only race and gender.

 

Subspaces

The sense in which the Govinder et al. index decomposes into subspace indices of any kind, as claimed in the extract below, is simply mathematically false. Deeming race or gender as spaces or subspaces violates mathematical convention. It is therefore also erroneous to claim that (squared) distances are additive across subspaces.

The advantage of our approach is that one can actually determine a race EI (using data points with only four (race) components), EIr a gender EI (using data points with only two (gender) components), EIg, and an overall EI which is a combination of these two previous EIs via EI = sqrt(EIr² + EIg²). It was this aggregate combination possibility that led us to use n = 6. Importantly, the EIr and EIg both form subspaces of the EI space using this approach. For n = 8, we do not have this mathematical structure - one cannot find EI_rand EIg directly in that space.³

 

Constitution

The Constitution of the Republic of South Africa, Act No. 108 of 1996, as amended up to 2003, has a Bill of Rights at Chapter 2, sections 7 through 37. This set of rights sets out at section 9(3) obligations of the state to ensure no unfair discrimination, directly or indirectly against any person on the basis of any one or more grounds including race, gender, sex, pregnancy, marital status, ethnic or social origin, colour, sexual orientation, age, disability, religion, conscience, belief, culture, language and birth. A caveat of fair discrimination is provided at section 9(5).

Govinder et al. offer no rationalisation for the suppression of all but two of the outlawed grounds of discrimination in their index.

Their insistence on the entire South African population of all ages takes no account of the narrower age ranges associated with university student attendance and university staff employment.

Moreover Govinder et al. do not allow other relevant criteria for plausibly fair discrimination, such as an appropriate National Senior Certificate outcome, any entry or placement requirements for students, and qualifications or experience for employees.

The adamant position of Govinder et al. is that they have measured inequity, and, on these grounds, have advocated a misnamed DDI as the basis for teaching the universities a lesson or two in policy compliance and budget implications.

Ironically, the word 'equity' appears only twice in the Constitution (section 29.2(a) in respect of basic education and section 29.3(e) in respect of powers of municipalities). The word 'transformation' does not appear, although progressive realisation is addressed. Nowhere does the Constitution invoke the population profile or demographics as criteria or artefacts of its law. This note does not imply that the Constitution abjures use of these terms.

The Constitution and its Bill of Rights are certainly admissible as warrants for imperatives within South African society. It is important to note that the Constitution demands much more than redress of past injustice and deprivation. It advocates a journey to a just society, and progressive realisation as one mode of the journey.

The Constitution does much more than advocate and require transformation. It is as much or even more concerned with the delivery of fundamental rights and efficient delivery of service within the public sector. Included in these imperatives is the preservation of existence and function of institutions for the public good, and their responsibility to keep engaging with transformation.

The Constitution permits error, but it does not require error in the apparent pursuit of its imperatives. The Constitution is fairly understood as requiring our best intentions as citizens in the service of the common agenda that it represents. In requiring good intentions, the Constitution does not advocate good intentions as a sufficient condition for suspending debate on matters of error.

The Constitution demands that we address inequality. It does not require us to presume we can measure inequality. Inequity is explored by making comparisons and answering probing and difficult questions.

It is an ethically fragile and morally dubious strategy to invoke a misguided claim of measurement as the final criterion of debate and decision-making.

 

Context

Govinder et al. argue that their index has been unfairly misinterpreted by Dunne⁵ and debated out of the context into which their DDI was proposed as salient. The second claim is partly true, in a very weak sense.

The context they selected for its justification is such a narrow playing field that their index is virtually context free. Their approach advocates and requires race and perhaps gender as the only determinants of various university outcomes. Simultaneously, in contrast, the context selected by Govinder et al. for the application of their index is an entire gamut of social justice objectives of transformation, universally.

In particular, Govinder et al.'s DDI is proposed for policy monitoring and steering of universities towards claimed public imperatives. For this reason its logical and mathematical structure, its hidden assumptions, its claimed purpose and its fitness for purpose are all the proper focus of scientific enquiry and debate. Effectively, the various critiques have located Govinder et al.'s index in precisely the context to which its inventors seek to have it applied, and exhibited that it is hopelessly flawed.

 

References

1. Govinder KS, Makgoba MW. An Equity Index for South Africa. S Afr J Sci. 2013;109(5/6), Art. #a0020, 2 pages. http://dx.doi.org/10.1590/sajs.2013/a0020        [ Links ]

2. Govinder KS, Zondo NP Makgoba MW. A new look at demographic transformation for universities in South Africa. S Afr J Sci. 2013;109(11/12), Art. #2013-0163, 11 pages. http://dx.doi.org/10.1590/sajs.2013/20130163        [ Links ]

3. Govinder KS, Zondo NP, Makgoba MW. Taking the transformation discourse forward: A response to Cloete, Dunne and Moultrie and Dorrington. S Afr J Sci. 2014;110(3/4), Art. #a0060, 8 pages. http://dx.doi.org/10.1590/sajs.2014/a0060        [ Links ]

4. Moultrie TA, Dorrington RE. Flaws in the approach and application of the Equity Index: Comments on Govinder et al. (2013). S Afr J Sci. 2014;110(1/2), Art. #a0049, 5 pages. http://dx.doi.org/10.1590/sajs.2014/a0049        [ Links ]

5. Dunne T. Mathematical errors, smoke and mirrors in pursuit of an illusion: Comments on Govinder et al. (2013). S Afr J Sci. 2014;110(1/2), Art. #a0047, 6 pages. http://dx.doi.org/10.1590/sajs.2014/a0047        [ Links ]

 

 

Correspondence:
Tim Dunne
Department of Statistical Sciences, PD Hahn Building, Upper Campus
University of Cape Town
Rhodes Gift 7707, South Africa
tim.dunne@uct.ac.za