Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.109 n.5-6 Pretoria Jan. 2013
RESEARCH ARTICLE
Numerical investigation into the existence of limit cycles in two-dimensional predator-prey systems
Quay van der HoffI, II; Johanna C. GreeffI; P Hendrik KloppersI
IDepartment of Mathematics and Statistics, Tshwane University of Technology, Pretoria, South Africa
IIDepartment of Mathematics and Applied Mathematics, University of Pretoria, Pretoria, South Africa
ABSTRACT
There has been a surge of interest in developing and analysing models of interacting species in ecosystems, with specific interest in investigating the existence of limit cycles in systems describing the dynamics of these species. The original Lotka-Volterra model does not possess any limit cycles. In recent years this model has been modified to take disturbances into consideration and allow populations to return to their original numbers. By introducing logistic growth and a Holling Type II functional response to the traditional Lotka-Volterra-type models, it has been proven analytically that a unique, stable limit cycle exists. These proofs make use of Dulac functions, Liénard equations and invariant regions, relying on theory developed by Poincaré, Poincaré-Bendixson, Dulac and Liénard, and are generally perceived as difficult. Computer algebra systems are ideally suited to apply numerical methods to confirm or refute the analytical findings with respect to the existence of limit cycles in non-linear systems. In this paper a class of predator-prey models of a Gause type is used as the vehicle to illustrate the use of a simple, yet novel numerical algorithm. This algorithm confirms graphically the existence of at least one limit cycle that has analytically been proven to exist. Furthermore, adapted versions of the proposed algorithm may be applied to dynamic systems where it is difficult, if not impossible, to prove analytically the existence of limit cycles.
Keywords: Lotka-Volterra models; predator-prey systems; stable limit cycle; Poincaré mapping; numerical method
Introduction
The analytical methods used to prove the existence or non-existence of limit cycles are complex and mathematically challenging and may not be accessible to all scientists working in the field of ecological modelling. Such methods involve proving that all solutions of a system are positively and eventually uniformly bounded, that is, that an invariant region exists.1 In addition, it needs to be proven that the equilibrium point enclosed by the invariant region is unstable.2,3 Once these criteria have been established, Poincaré-Bendixson theory ensures the existence of at least one periodic solution. Uniqueness and stability of this periodic solution are more difficult to prove and most authors follow the method proposed by Zhang4, transforming the system to a Liénard system where the results concerning uniqueness of the limit cycle are well known.2,5-11
Various reports in the literature confirm the existence of a unique, stable limit cycle in a class of predator-prey models that include logistic growth and a Holling Type II functional response. One such a system is given by

For System 1, x denotes the number of prey, y denotes the number of predators and the parameters r K, a, b, c and D are all positive. The model represented by System 1 is biologically well described. The parameter c represents the death rate of the predator in the absence of prey, while D is the rate of the conversion of consumed prey to predator. The term  represents the standard assumption of logistic growth introduced by Verhulst in 1845, which accounts for competition amongst individuals of the prey species as their numbers increase. The carrying capacity of the environment is K while r is the intrinsic growth rate of prey in the absence of predators. The term
represents the standard assumption of logistic growth introduced by Verhulst in 1845, which accounts for competition amongst individuals of the prey species as their numbers increase. The carrying capacity of the environment is K while r is the intrinsic growth rate of prey in the absence of predators. The term 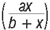 represents a Holling Type II functional response, describing the expected number of prey devoured by a predator per unit of time. See Wang and Sun11 and Kuznetsov et al.12 for detailed discussions.
represents a Holling Type II functional response, describing the expected number of prey devoured by a predator per unit of time. See Wang and Sun11 and Kuznetsov et al.12 for detailed discussions.
System 1 has three equilibrium points:

The latter, E*, is the only equilibrium point that could possibly lead to co-existence of both species. It has been proven analytically3,9-11,13 that E* exists and is unstable and that a unique, stable limit cycle will exist under the conditions

In 1899 Henri Poincaré introduced the analytical concept of Poincaré sections and Poincaré maps in a quest to define limit cycles, using hand-drawn sketches to illustrate his findings. In this paper we suggest a numerical approach, based on Poincaré theory, to investigate the behaviour of solution trajectories associated with E*, and propose an algorithm that graphically illustrates the existence of a limit cycle as proven analytically, subjected to the analytical conditions stated in Condition 2.
In the next section, the numerical application of Poincaré sections and Poincaré maps, in order to investigate the periodic behaviour of trajectories in System 1, is discussed. In the two-dimensional model the Poincaré map is represented by a sequence of discrete points where the Poincaré section intersects the solution trajectories of the nonlinear system.
In the section following, the application of the proposed numerical procedure is illustrated, using an example where the chosen parameter values satisfy Condition 2. The example visually illustrates a Hopf bifurcation when the parameter value of K is varied, and when the equilibrium point E* changes from an attracting spiral point to an unstable point surrounded by a unique, stable limit cycle. It is then possible to approximate coordinates on the limit cycle and the period of the limit cycle associated with the value of K,confirming analytical calculations suggested by Kuznetsov et al.12
Numerical method
An interesting numerical approach using the homotopy method to generate initial conditions that will produce periodic solutions was developed by Fay and Lott14. As is true for all numerical methods, their method does not prove the existence of a limit cycle. Similarly, the algorithm proposed in this paper does not claim to prove the existence of a limit cycle, but rather attempts to present a useful tool to illustrate the existence of proven limit cycles and investigate the nature thereof. The method involves determining the discrete points of intersection of a periodic trajectory initiated at (x(t0); y(t0)), associated with an unstable equilibrium point of a system, and a Poincaré section defined by a straight line L :y = mx + c passing through the equilibrium point. Possible convergence of the resulting sequence {qk} consisting of the x-values of the intersection points over an evenly spaced limiting time period, [t0= 0,tn = N], is investigated.
The Poincaré section L : y = mx + c should be chosen to intersect the trajectories transversely, that is, no trajectory is tangential to L. Any straight line passing through the equilibrium point will ensure this. A Poincaré map is a function P : L - L defined by pk+1 = P(pk) where pk, K=0,1,2,...(/7 - 1), consists of the sequence of points located on L, where the line and a trajectory of the system of differential equations intersect.15 To find an explicit analytical function P in continuous time is seldom possible, therefore we propose a numerical approach, using Mathematica®,16 to generate a sequence of discrete points located on L and to observe the behaviour of the sequence in order to illustrate the possible existence of a limit cycle.
The numerical procedure suggested in this paper involves several steps. Firstly, System 1 is solved over an evenly spaced time interval, resulting in a sequence of discrete coordinate pairs {(x(tk), y(tk))}. Each of these coordinate pairs is then substituted into the Poincaré section L : y = mx + c. If y(tk) - mx(tk) - c = 0, then (x(tk), y(tk)) is a simultaneous solution of the system and the straight line equation. As a result of the discrete nature of the solutions and the step size chosen, we may find only a few, or perhaps even no points satisfying both the system and the line equation, and closer observation in the regions where intersections 'almost' occur is necessitated. In order to identify such regions, it is convenient to observe the function

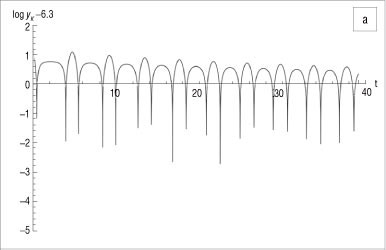
Because log|y(tk) - mx(tk) - c | - -∞ if y(tk) - mx(tk) - c -> 0, the graph of S(tk) forms downward spikes whenever an intersection of the solution to System 1 and the straight line may occur.17 This scenario is depicted in Figure 1.

To refine the search in the time sub-intervals containing a downward spike, select those coordinate pairs (x(t), y(t)) e {(x(tk), y(tk))} for which both S(t¡ _ 1) - S(t) > 0 and S(t¡ ) - S(t¡+1) < 0, and construct the sequence {q;.} = {x(t})}. We are only interested in the sequence of x-values, as the y-values will all tend towards the chosen mx + c. Because of the periodic nature of the solution trajectories, the elements of {q}} will alternate between intersection points on the first return and- the second return of the discrete Poincaré map. Separating {q} into two sub-sequences, {u} containing intersection points on the first return and {v} intersection points on the second return, the nature of each sequence is then investigated.
With regard to the sub-sequences {u} and {v}, there are three possible outcomes:
1. lim {uj} = lirn {vj}, which implies that the system has an asymptotically stable equilibrium point.
2. u1 = u2 =...= un and v1= v2 =...= vn , which indicates that the equilibrium point is a centre surrounded by an infinite number of periodic solutions, each depending only on its unique initial value.
3. u* and v* are fixed points such that lim {u } = u* and lim {v} = v*, u* φ v*. The system then possesses a limit cycle passing through u* and v*on the first and second return of the Poincaré map, respectively.
Example
The algorithm proposed in the previous section is applied to System 1 to graphically illustrate the existence of a stable limit cycle. Note that the choice of values used to substitute the numerical parameters is purely theoretical and is not intended to reflect any ecological situation.
Let r = 1.5, a = 5, b = 18, c = 4 and D = 2, so that System 1 becomes
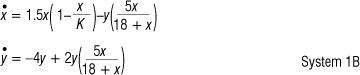
Referring to Condition 2, this choice of parameter values results in K = 42 and aD >c, where K represents the carrying capacity for prey in System 1B. In agreement with what is usually experienced in ecological dynamic systems, K should have a direct influence on the nature of the stability of the system. According to analytical findings, the equilibrium point E* of System 1B is asymptotically stable for K < 42 and unstable for K > 42, resulting in a stable limit cycle. Kuznetsov et al.12 found that for models such as System 1 and
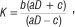
a Hopf bifurcation occurs as K is increased through the bifurcation value because the real parts of the complex eigenvalues become zero, forcing the stable equilibrium point E* to instability. Note that for each K > 42 the real parts of the complex eigenvalues are positive, resulting in an unstable equilibrium point surrounded by a limit cycle. Furthermore, Kuznetsov et al.12 state that the Hopf bifurcation is supercritical, which means that the limit cycle will always be stable with a period given by
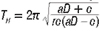
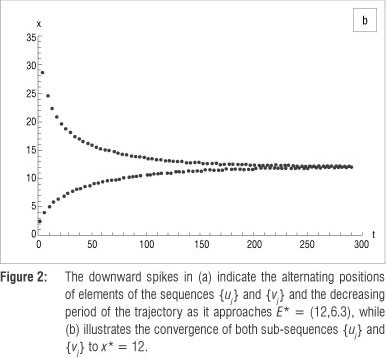
As an example, let K = 40, which results in the equilibrium point E* = (12,6.3). Therefore, define the Poincaré section as the horizontal line L : y = 6.3 to transversely intersect the trajectory initiated at, say, (5,20). Let t e [0;4000] and, using a step size 0.01, create a sequence {q} consisting of discrete values x(t}). Figure 2a illustrates the graph of S(t) = log|y(f.) - 6.3|, spiking downwards every time the straight line and the trajectory intersect. Separating {q} into sub-sequences {u} and {v}, and plotting the results against time (t) clearly shows that both sequences converge to E* = (12,6.3), as illustrated in Figure 2b. The phase plane in Figure 3 depicts the above properties of the system, illustrating an attracting spiral moving into the globally stable spiral point (12, 6.3)

Case 2: K> 42
Now suppose K = 45. The corresponding equilibrium point is (12 , 6.6) and, should a unique stable limit cycle exist, all trajectories, whether initiated on the inside or the outside of the expected limit cycle, should be attracted to this limit cycle. Choose the straight line L : y = 6.6 as a Poincaré section and, initiating a solution to System 1B at, say, (5, 20), generates the results shown in Table 1.

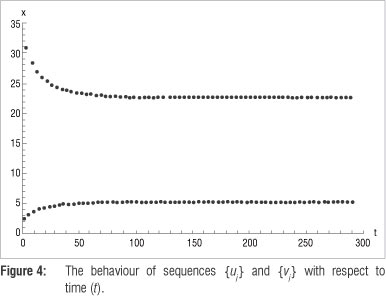
{uj} = {2.526299, 3.262434, .5.389401, 5.390238...} and {vj} ={30.804864, 28.416644, .22.580221, 22.567945...}, which indicate that lim {uj} ≈ 5.39 j?n and lim {vj} ≈ 22.57 j?n . Figure 4 shows the graphs of these two sequences plotted against time.
These limits of the respective sequences are only accurate to two decimals. To increase accuracy the search can be refined by decreasing the step size over smaller sub-intervals. Referring to Table 1 and using a step size of 0.000001 over the interval [287, 288] and again over [288, 289], results in Table 2, and an accuracy up to six decimals.

This option allows the deduction that u* ≈ 5.389374 and v* ≈ 22.573625 are fixed points of the sequences {u} and {v}}, respectively, accurate to six decimals, as y(t) -> 6.600000. In Figure 5 the sequences {u} and {v}} are shown on the xy-plane.
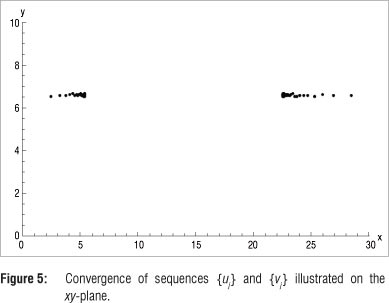
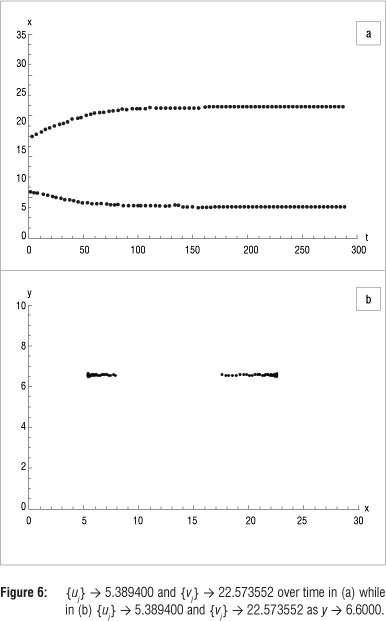
Again using K = 45, but now with initial value (15, 10), presumably located on the inside of the limit cycle and repeating the procedure above, generates the results in Table 3. The resulting figures of the sequences {u}} - 5.389400 and {v}} - 22.573552 as y(t}) -> 6.600000 are shown in Figure 6.

Proving the uniqueness of a limit cycle analytically is an outstanding and very challenging problem4,5,8,13 and remains unsolved for generalised predator-prey models.2 However, following the numerical approach discussed, Figure 7 depicts a phase plane representation suggesting that trajectories are attracted by a stable limit cycle in the invariant region, whether initiated from inside or outside the limit cycle, regardless of the chosen initial values.
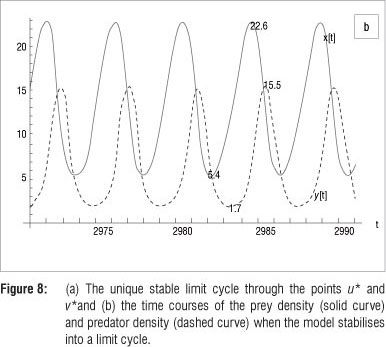
In Figure 8a, the isolated limit cycle passing through fixed points u* = 5.3894 and v* = 22.5736 (rounded to four decimals) is shown. Figure 8b shows time courses of the x and y populations when the model stabilises to its oscillatory dynamics, allowing graphical estimates of the period of the solution and amplitudes of the population densities of the steady state.
Case 3: K = 42
Using the same approach as before, a Hopf bifurcation is observed because a stable attracting spiral point bifurcates into an unstable equilibrium point as the value of K is increased from K < 42 through to K > 42. If K = 42 the equilibrium point is (12,6.428571) and a limit cycle passing through the points (12.928445,6.428571) and (11.117510,6.428572) is observed. This bifurcation is illustrated in Figure 9.
Note that each value of K > 42 is associated with its unique equilibrium point and at least one limit cycle, of which the period can be estimated from the population-time graphs, confirming calculations using Table 4.
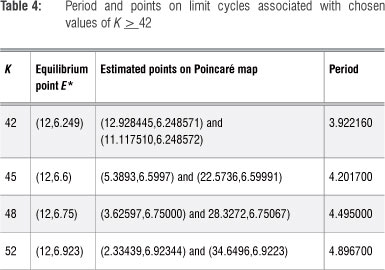
The limit cycles for these values of K are shown in Figure 10, but should not be confused with the typical periodic solutions of the traditional predator-prey model.

Conclusion
Although there are many ways in which to prove that System 1 possesses a stable limit cycle, the analytical methods at our disposal rely on transformations to Liénard systems, finding Dulac functions and proving the existence of an invariant region, which is mathematically cumbersome. Proving the uniqueness of a limit cycle analytically is an outstanding and very challenging problem4,5,18 and remains unsolved for generalised predator-prey models2.
The numerical method proposed, using Poincaré sections is accessible to scientists working in the field of ecological modelling and proves to be useful to illustrate the existence of at least one stable limit cycle. The Poincaré section recommended is y = y* where E* = (x*, y*), because this section does not miss and is not tangential to the limit cycle, should it exist. The method demonstrates accuracy up to six decimals where the Hopf bifurcation occurs and can be applied to determine coordinates of random points on the limit cycles for any value of K.It is possible to determine the periods of these limit cycles, confirming the analytical results when the Hopf bifurcation occurs.
The proposed algorithm provides a visual representation and an instant test to confirm or refute the existence of a limit cycle. It can be applied to the analysis of models appearing in the ecological literature where the existence of one or more limit cycles has not yet been proven analytically, and to investigate graphically the nature of these limit cycles, should they exist.
Acknowledgements
We thank the National Research Foundation, South Africa (grant no. 2054454), Tshwane University of Technology and the University of Pretoria for financial support.
Authors' contributions
Q.v.d.H. conceptualised the proposed numerical method; P.H.K. assisted with the development of the programmes in Mathematica®; and J.C.G. supervised the work and wrote the manuscript.
References
1. Zill DG, Cullen MR. Advanced engineering mathematics. 2nd ed. Sudbury, MA: Jones and Bartlett Publishers; 2000. [ Links ]
2. Morgadas SM, Corbett BD. Limit cycles in a generalized Gause-type predator-prey model. Chaos, Solutions and Fractals. 2008;37:1343-1355. http://dx.doi.org/10.1016/j.chaos.2006.10.017
3. Waltman P. Competition models in population biology. Philadelphia: Society for Industrial and Applied Mathematics; 1983. [ Links ]
4. Zhang ZF. Proof of the uniqueness theorem of limit cycles of generalized Liénard equations. Appl Anal. 1986;23:63-76. http://dx.doi.org/10.1080/00036818608839631
5. Cheng KS. Uniqueness of a limit cycle for a predator-prey system. SIAM J Math Anal. 1981;12:541-548. http://dx.doi.org/10.1137/0512047
6. Cherkas LA, Zhilevich LI. Some tests for the absence or uniqueness of limit cycles. Differential Equations. 1970;6:891-897.
7. Freedman HI. Deterministic mathematical models in population ecology. Edmonton: Marcel Dekker Inc.; 1980. [ Links ]
8. Hasík K. Uniqueness of limit cycles in predator-prey systems: The role of weight functions. J Math Anal Appl. 2003;277:130-141. http://dx.doi.org/10.1016/S0022-247X(02)00515-2 [ Links ]
9. Huang XC, Zhu L. Limit cycles in a general Kolmogorov model. Nonlinear Analysis. 2004;60:1393-1414. http://dx.doi.org/10.1016/j.na.2004.11.003
10. Kuang Y Freedman HI. Uniqueness of limit cycles in Gause-type models of predator-prey systems. Mathematical Biosciences. 1988;88:67-84. http://dx.doi.org/10.1016/0025-5564(88)90049-1
11. Wang W, Sun JH. On the predator-prey system with Holling(n+1) functional response. Acta Mathematica Sinica. 2003;23(1):1-6. http://dx.doi.org/10.1007/s10114-005-0603-8
12. Kuznetsov YA, Muratori S, Rinaldi S. Bifurcations and chaos in a periodic predator-prey model. International Journal of Bifurcation and Chaos. 1992;2(1):117-128. http://dx.doi.org/10.1142/S0218127492000112
13. Hasík K. On a predator-prey system of the Gause type. J Math Anal Appl. 2010;60:59-74.
14. Fay TH, Lott PA. Using the homotopy method to find periodic solutions of forced nonlinear differential equations. International Journal for Mathematics, Education in Science and Technology. 2002;33:701-714. http://dx.doi. org/10.1080/00207390210162430
15. Lynch S. Dynamical systems with applications using Mathematica. Boston: Birkhãuser; 2007. [ Links ]
16. Wolfram S. The Mathematica® book. 3rd ed. New York: Wolfram Media and Cambridge University Press; 1996. [ Links ]
17. Fedotov I, Shatalov M, Mwambakana JN. Roots of transcendental algebraic equations: A method of bracketing roots and selecting initial estimations. TIME Conference Proceedings; 2008 Sep 22-26; Buffelspoort, South Africa. Pretoria: Tshwane University of Technology; 2008. p.163-172. [ Links ]
18. Albrecht F, Gatzke H, Wax N. Stable limit cycles in predator-prey populations. Science. 2004;181:1073-1074. http://dx.doi.org/10.1126/science.181.4104.1073
 Correspondence:
Correspondence:
Johanna Greeff
Department of Mathematics and Statistics
Tshwane University of Technology
Private Bag X680, Pretoria 0001, South Africa
Email: greeffjc@tut.ac.za
Received: 20 Feb. 2012
Accepted: 16 Nov. 2012