Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Science
versão On-line ISSN 1996-7489
versão impressa ISSN 0038-2353
S. Afr. j. sci. vol.109 no.1-2 Pretoria Jan. 2013
RESEARCH ARTICLE
Soft-input iterative channel estimation for bit-interleaved turbo-coded MIMO-OFDM systems
Olutayo O. Oyerinde; Stanley H. Mneney
School of Engineering, Electrical, Electronic and Computer Engineering, University of KwaZulu-Natal, Durban, South Africa
ABSTRACT
Bit-interleaved coded modulation (BICM) is a robust multiplexing technique for achieving multiplexing gain in multiple-input multiple-output (MIMO)-orthogonal frequency division multiplexing (OFDM) systems. However, in order to benefit maximally from the various advantages offered by BICM-based MIMO-OFDM systems, availability of accurate MIMO channel state information (CSI) at the receiver end of the system is essential. Without accurate MIMO CSI, accurate MIMO demapping and coherent detection and decoding of the transmitted message symbols at the system's receiver would be impossible. In such cases, the multiplexing gain offered by the BICM technique, as well as the higher data rate made possible by the MIMO-OFDM system, is not benefitted from in full. In this paper, we propose a soft input based decision-directed channel estimation scheme for the provision of MIMO CSI for coherent detection of signals in MIMO-OFDM systems. The proposed channel estimator works in iterative mode with a MIMO demapper and a turbo decoder, and is based on the fast data projection method (FDPM) and the variable step size normalised least mean square (VSSNLMS) algorithm. Simulation results of the proposed estimator based on the FDPM and VSSNLMS algorithms indicate better performance in comparison with the same estimator employing minimum mean square error criteria and deflated projection approximation subspace tracking algorithms for both slow- and fast-fading channel scenarios. The proposed estimator would be suitable for use at the receiver end of MIMO-OFDM wireless communication systems operating in either slow- or fast-fading channels.
Keywords: BICM; channel transfer function estimator; channel impulse response estimator; adaptive predictor; fading channel
Introduction
The extension of bit-interleaved coded modulation (BICM)1 to a multiple-input multiple-output (MIMO) system2,3 is regarded as an effective spatial multiplexing technique for achieving multiplexing gain in MimO systems. In this technique, streams of data symbols are independently transmitted on different transmit antennas simultaneously. Consequently, multiplexing gain, which is the increase of data rate, is obtained at no additional power consumption or bandwidth expenditure. The achievable high data rate, in turn, leads to wideband communication. However, the MIMO channels involved exhibit strong frequency selectivity. The combination of an orthogonal frequency division multiplexing (OFDM) transmission technique with MIMO to form a MIMO-OFDM system provides an attractive way of transforming the frequency-selective MIMO channels to a set of frequency-flat sub-channels, thus reducing the receiver complexity. The joint use of MIMO and OFDM, referred to as MlMO-OFDM, is, without doubt, a promising approach for achieving a higher data rate for future wireless communication systems.
Despite the attractive advantages offered by MIMO-OFDM systems, reliable coherent signal detection would be elusive without the availability of accurate channel state information (CSI). Different approaches abound in the literature for obtaining CSI for communication systems. These approaches generally fall in three major categories: purely pilot-assisted channel estimation techniques, blind and semi-blind channel estimation methods and decision-directed channel estimation (DDCE) schemes. Despite various improvements gained through different research investigations, a major setback in the deployment of the pilot-assisted channel estimation technique is wastage in the scarce communication bandwidth. Another drawback of the pilot-assisted channel estimation scheme is that estimates are based on pilot symbols alone. Consequently, interpolation techniques are employed for channel estimation corresponding to the data points. This technique could result in errors in the estimation, especially in fast-fading channel scenarios. Unresolved errors would thereby be introduced into the estimation process. The blind and semi-blind channel estimation methods seek to circumvent these shortcomings associated with their pilot-assisted counterpart. However, blind and semi-blind channel estimation methods suffer from several deficiencies: a slow convergence rate because of the requirement of long data records, a tendency to become heavier from a computational complexity point of view,4 and a sensitivity to channel order overestimation.
In DDCE techniques, both the pilot symbols and the re-modulated detected message symbols are employed for channel estimation.5 As a result, DDCE schemes provide a more reliable channel estimate than their pilot-assisted channel estimation counterparts and are less complex than their blind and semi-blind counterparts.6,7,8,9 In an error-free transmission scenario, the DDCE scheme could be viewed as a pilot-assisted channel estimation scheme employing up to 100% pilot information symbols for channel estimation.7,10 In contrast, a purely pilot-assisted scheme uses few pilot symbols for the same estimation. By using DDCE techniques, the number of pilot symbols used for channel estimation is drastically reduced. This fact is our motivation in proposing an extension of the iterative version of the DDCE technique6,7 proposed previously for a single antenna OFDM system: a MIMO-OFDM system. It has been confirmed that the DDCE scheme outperforms its non-iterative counterpart for single antenna OFDM systems.7,8 It is worth mentioning that a DDCE scheme based on space-alternating generalised expectation-maximisation (SAGE) in combination with a least squares (LS) algorithm has also been proposed.9 However, this DDCE scheme only exchanges soft information with the decoder.
The iterative DDCE scheme proposed in this paper exchanges soft information with both the turbo decoder and the MIMO demapper for further enhancement in the system's performance. The proposed scheme comprises a temporary channel transfer function (CTF) estimator which employs an adaptive variable step size normalised least mean square (VSSNLMS) algorithm, a fast data projection method (FDPM)-based channel impulse response estimator,6 and an adaptive predictor based on the VSSNLMS algorithm. The proposed FDPM algorithm and deflated projection approximation subspace tracking (PASTd) algorithm employed previously for similar DDCe schemes10 belong to the same group of estimator - parametric subspace-based estimators.11 However, the SAGE algorithm belongs to another group of estimator - deterministic parametric estimators.11 In this paper, we show, using computer simulation, that the proposed adaptive VSSNLMS CTF estimator-aided iterative DDCE scheme performs better than the one based on linear minimum mean square error (MMSE).7,8,12 The results presented in terms of mean square error (MSE) and bit error rate (BER) indicate that the iterative DDCE scheme using the proposed FDPM-based CIR estimator outperforms its counterpart based on the PASTd algorithm.10
MIMO-OFDM system model
Block diagrams of the bit-interleaved turbo-coded MIMO-OFDM system model considered here are shown in Figure 1.
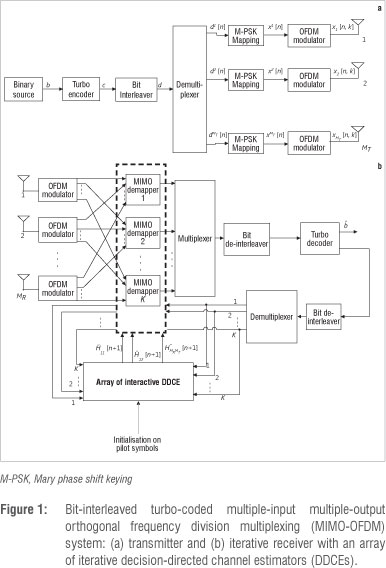
Transmitter
At the transmitter end of the system model, binary source bits 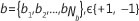 are encoded by a turbo encoder with code rate Rc. The encoder output sequence c=[c1,c2...,
are encoded by a turbo encoder with code rate Rc. The encoder output sequence c=[c1,c2...,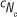 }, є{+1, -1}, where Nc =
}, є{+1, -1}, where Nc = 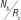 , is interleaved to d=[d1,d2,...,
, is interleaved to d=[d1,d2,...,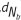 }, є {+1, -1} by employing a random interleaver of length N . The interleaved code bit stream d is demultiplexed to MT transmit antenna as di=[n], i = 1,...MT , at a time instant n. Each mt parallel stream is then mapped to complex symbol, x[n]=|x1 [n], x2 [n],...,xMT [n]}, chosen from M-ary signal constellation x. The outputs of the mapper are modulated by the OFDM modulator to each subcarrier as x[n, k]={x1 [n, k], x2 [n, k],...,x
}, є {+1, -1} by employing a random interleaver of length N . The interleaved code bit stream d is demultiplexed to MT transmit antenna as di=[n], i = 1,...MT , at a time instant n. Each mt parallel stream is then mapped to complex symbol, x[n]=|x1 [n], x2 [n],...,xMT [n]}, chosen from M-ary signal constellation x. The outputs of the mapper are modulated by the OFDM modulator to each subcarrier as x[n, k]={x1 [n, k], x2 [n, k],...,x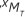 [n, k]}, and transmitted through MT antennas.
[n, k]}, and transmitted through MT antennas.
Channel statistics
By extending the complex baseband representation of the continuous-time channel impulse response (CIR) of a mobile wireless system13 to a MIMO channel, the time domain MIMO CIR from the ith transmit antenna to the jth receive antenna can be described as:

Equation 1 where γm (t) and τm are the time-variant complex amplitude and the delay of the mth path, respectively, and c(T) is the aggregate impulse response of the transmitter-receiver pair that corresponds to the square-root raised-cosine Nyquist filter. However, with the presence of an OFDM transmission scheme and the introduction of proper cyclic extension and adequate synchronisation, the discrete subcarrier-related CTF can be expressed as:
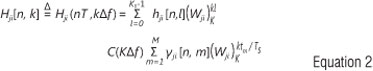
where
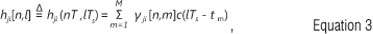
is the sample-spaced channel impulse response (SS-CIR) and each of the WK corresponding to ith transmit and jth receive is given as WK=exp(-j2π / K). The realistic channel condition associated with non-sample-spaced time-variant path-delays, τm considered in this article is the fractionally spaced (FS)-CIR with 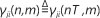 .10 This FS-CIR model is constituted by a low number of M < K0< K statistically independent non-zero taps associated with distinctive propagation paths. In matrix form, Equation 2 can be written as:
.10 This FS-CIR model is constituted by a low number of M < K0< K statistically independent non-zero taps associated with distinctive propagation paths. In matrix form, Equation 2 can be written as:

where Ηji =diag(C[k])WjÍ is defined as a (K x M)-dimensional matrix in which diag(C[k]) is a (K x K)-dimensional diagonal matrix with the corresponding elements of the vector C(f) on the main diagonal.10 Symbol wjt is the Fourier Transform matrix defined by wjt ( km )=( wji)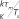 : of each propagation link between the ith transmit and jth receive antenna, for all k's and m's.
: of each propagation link between the ith transmit and jth receive antenna, for all k's and m's.
Receiver
At the receiver of the bit-interleaved turbo-coded MIMO-OFDM system, by assuming perfect time and frequency synchronisation, after the cyclic prefix has been discarded and OFDM demodulation has been carried out, the received signal at the jth receive antenna is the superposition of MT distorted transmitted signals. Consequently, the received signal at the jth receive antenna associated with the kth subcarrier of the nth OFDM block can be written as:
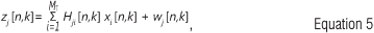
where zj [n,k], xi [n,k] and wj [n,k] denote the received symbol at the jth antenna, the transmitted symbol from the ith transmit antenna, and the complex zero-mean white Gaussian noise sample encountered at the jth receive antenna, respectively.
In vector form, the received signal of Equation 5 is given as:
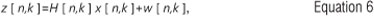
where

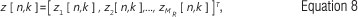
and
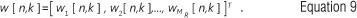
Iterative DDCE scheme
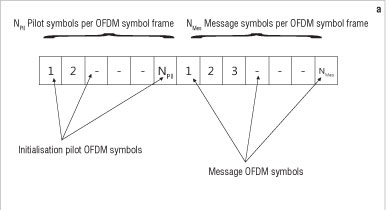
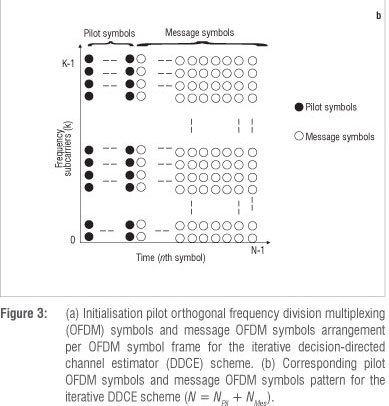
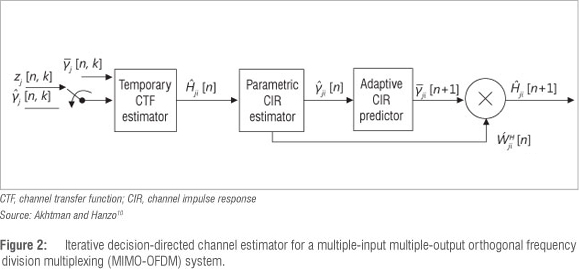
Figure 2 depicts the block diagram of the proposed iterative DDCE that constitutes the MT x MR array of the iterative DDCE scheme in Figure 1b. The array comprises a temporary CTF estimator, a parametric CIR estimator and an adaptive CIR predictor. These three components of the iterative DDCE work together to make estimates of the CSI. The estimates are fed to the soft MIMO demapper that uses the CSI in combination with the received message symbols to compute the soft information on each of the transmitted bits. In this case, the iterative DDCE and the soft MIMO demapper exchange information at every OFDM symbol time (index n. In order to ensure error-free estimation, the first Npil-th OFDM symbols comprise the known pilot symbol out of the total (Npil + Nmes) OFDM symbols per frame, as shown in Figure 3a. Figure 3b depicts the corresponding pilot messages OFDM symbols pattern. Both the iterative DDCE and the soft MIMO demapper work in an iterative mode with the turbo decoder to exchange soft information with the turbo decoder in a bid to refine the various outputs over a number of iterations. During the last iteration, the hard decision about the transmitted bits  is made by the turbo decoder. Details of each of the three components of the iterative DDCE follow.
is made by the turbo decoder. Details of each of the three components of the iterative DDCE follow.
Adaptive algorithm-based temporary CTF estimator
The linear MMSE-based CTF estimator7,8,12 for estimating the frequency domain (FD)-CTF coefficients was initially extended to estimate the CTF coefficient of the MIMO channel. However, it was observed that its performance in the context of a MIMO-OFDM system was very poor in comparison with its performance in the case of a single antenna OFDM system.7,8,12 To circumvent this poor performance, we proposed the use of an adaptive algorithm-based CTF estimator to recursively estimate the CTF coefficient, Hji [n], of the MIMO channel instead of the linear MMSE-based CTF estimator. The adaptive estimator is based on the VSSNLMS algorithm proposed previously for the channel estimator for a turbo equaliser-based communications receiver.14,15 The choice of the VSSNLMS algorithm as opposed to the well-known recursive least squares (RLS) algorithm was based on it being less computationally complex. In addition, the VSSNLMS-based estimator has been confirmed to exhibit a performance close to its RLS-based estimator counterpart.14,15
If indices i and j are omitted for simplicity, the VSSNLMS-based CTF estimate recursively estimates Hji [n] as follows:
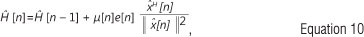
where superscript 'H' is an Hermitian conjugate,

and 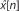 are the soft values of the detected symbols. The variable step size µ[η] is updated as12,13:
are the soft values of the detected symbols. The variable step size µ[η] is updated as12,13:
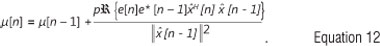
The values of µ[n] are restricted within the range 0< µ[n] <2 for stable operation of the algorithm.14,15
Time-domain CIR estimator employing FDPM algorithm
The time-domain MIMO CIR estimator is based on the FDPM algorithm,6 which was also used for the single antenna CIR estimator.7,8,12 If the symmetric, non-negative, definite, covariance matrix of the observation vector  [n] of size K is represented as
[n] of size K is represented as 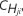 its singular vector corresponding to the M dominant singular values can be computed with the aid of an iterative procedure, referred to as orthogonal iteration,16 that has the following variants6:
its singular vector corresponding to the M dominant singular values can be computed with the aid of an iterative procedure, referred to as orthogonal iteration,16 that has the following variants6:
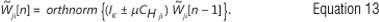
Replacing Cji with adaptive estimate Cjji[n], Equation 13 results in an adaptive orthogonal iterative algorithm:
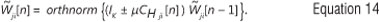
If Chji[n] is replaced with an instantaneous estimate of the covariance matrix Cjji[n] = Η [n] 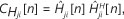 Equation 14 results in the data projection method algorithm given as:
Equation 14 results in the data projection method algorithm given as:
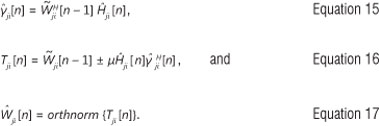
By applying a faster orthonormalisation procedure, Householder Transformation, to the DPM algorithm, we obtain the FDPM algorithm,6 which is then employed to track the time-domain MIMO CIR. The application of the faster orthonormalisation procedure to obtain the FDPM algorithm is the basis for its better performance in comparison with other subspace tracking algorithms with the same order of computational complexity.
In summary, the time-domain CIR estimate 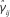 [n] of length M is tracked based on the temporary FD-CTF observation,
[n] of length M is tracked based on the temporary FD-CTF observation, 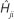 [n], using the subspace FDPM tracking algorithm as follows:
[n], using the subspace FDPM tracking algorithm as follows:
At time index n=0, the 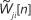 is initialised to orthonormal matrix (typically the first M columns of the identity matrix) with K rows for faster convergence.
is initialised to orthonormal matrix (typically the first M columns of the identity matrix) with K rows for faster convergence.
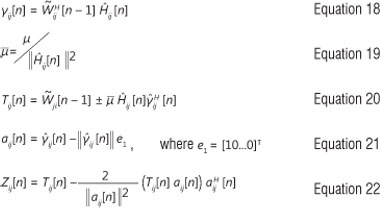

The performance FDPM subspace tracking algorithm in terms of MSE criteria is as follows:

where e(n) is given as:

Adaptive CIR predictor based on VSSNLMS algorithm
The adaptive VSSNLMS-based predictor8,9 is herein extended to the case of MIMO channels. The choice of the VSSNLMS-based predictor over its counterpart, the RLS-based adaptive predictor, is based on the same reason for employing a VSSNLMS-based CTF estimator instead of a RLS-based CTF estimator, namely computation complexity issues.8
The VSSNLMS algorithm updates the mth CIR tap's predictor coefficients PJ [n][m] of length Lpdd as89:
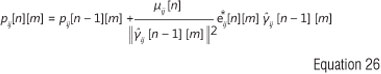
where
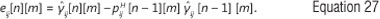
The MIMO CIR is then predicted for the next time index (n+1) as

and the variable step size of Equation 26 is obtained as
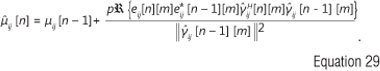
In order to restrict the variable step size µij [n] to the range 0< µij [n] <2 for the stable operation of the NLMS algorithm, the variable step size µij [n] in Equation 26 is restricted within the range given as:
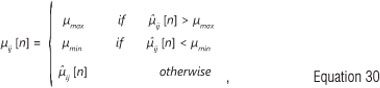
where 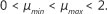
At time index n = 0, the prediction filters are initialised as pij[m][n] = [1 0 0 ...0]T.17
Soft MIMO demapper
The soft MIMO demapper is fed with the outputs of the OFDM demodulators, the estimated CTF, and the extrinsic (soft) information returns by the turbo decoder. The demapper computes the a posteriori likelihood ratios of the transmitted coded and interleaved bits for the ith antenna branch mapped at the kth subcarrier into the qth bit position (i = 1,...MT; and q = 1, . . . Q from the 2Q-ary signal constellation) as

Soft MIMO demapper formulation
If the qth bit corresponding to the symbol x. [n, k], transmitted from the ith transmit antenna and on the kth subcarrier, at time instant n, is represented as di,q [n, k], then its log-likelihood ratio can be denoted as L(di,q [n, k]), where i = 1,...MT; and q = 1,...Q. The log-likelihood ratio L(di,q [n, k]) of Equation 31, conditioned on the estimated channel state information 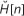 , made available by the proposed iterative DDCE scheme, is given as3:
, made available by the proposed iterative DDCE scheme, is given as3:
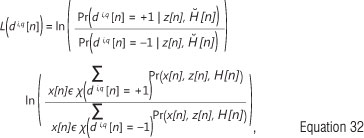
where x(di,q [n] = b; b є +1) is the set of all possible vectors having bit di,q [n] =+1 or -1). The number of elements in such a set is 2mtQ-13 The subcarrier index k is dropped for ease of exposition. The joint probability density of Equation 32, obtained from the product of the conditioned channel probability density function, and the a priori probability of the symbol vector, under additive white Gaussian noise (AWGN) assumption, is given as3:
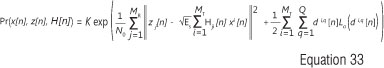
where K is a constant, and the elements of the symbol vector x [n] and the bits that are mapped to such a vector are denoted xi [n] and di,q [n] respectively. The a priori log-likelihood ratio La (d i,q [n]) is set to zero at the first pass in the iterative process, because there is no a priori information on the coded bit at this stage. During the subsequent iterations, the a priori ratios of the bits of each transmit antenna branch are derived from the output of the map turbo decoder. The a priori log-likelihood ratios from the decoder are also employed by a soft mapper to compute soft symbols that are fed into the proposed iterative DDCE scheme for the estimation of the CSI in the second iteration and beyond.
Soft MIMO mapper
The soft MIMO mapper follows after the mapper employed in the case of the single antenna OFDM system.7,8,12,14 In order to ensure effective performance of the soft MIMO mapper, different Mary phase shift keying (M-PSK) constellation arrangements, ranging from Gray to anti-Gray mapping arrangements, are used at the transmitter end of the MIMO-OFDM system.
Simulation results and discussion
In order to validate the performance of the proposed soft-input iterative DDCE scheme, computer simulations are conducted for the bit-interleaved turbo-coded MTx MR MIMO-OFDM system. The time-variant six-path COST 207 typical urban channel model18 with normalised Doppler frequencies of 0.005, 0.02 and 0.01 is employed, while the channel parameter associated with transmit and receive antenna pairs is independent but with the same statistical properties. A total channel bandwidth of 800 kHz divided into K = 64 subcarriers is assumed. In order to make the subcarriers orthogonal to each other, the symbol duration (7s) is set to 80 µs, while the cyclic prefix length is 16 samples (1/4 of the symbol period); an additional guard interval (Tg) of 20 is used to provide protection from intersymbol interference occasioned by channel multipath delay spread. Consequently, the total block period (T) sums to 100 µs. The turbo encoder of rate 1/3 and octal generator polynomial of (7, 5) are serially concatenated with a random interleaver in order to achieve the BICM technique. A realistic non-sample-spaced CIR of length M = 6 is assumed in all the simulations. The step size µ for a FDPM-based CIR estimator is set to 0.98, while η, the so-called 'forgetting factor' for the PASTd algorithm is set to 0.95. The length of the CIR predictor (Lprd) is set to 10, while initialisation values of µ[n] and µij[n] are set to 0.5, and ρ is set to 0.002 for the VSSNLMS-based CTF estimator and predictor, respectively.
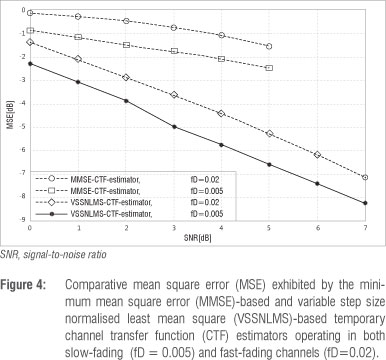
The simulation procedure begins by extending the linear MMSE CTF estimator employed for a single antenna system2,3 to the MIMO-OFDM system, followed by the adoption of the proposed VSSNLMS-based CTF estimator. At the initial stage, the OFDM frame length N is set to 25 while Npll = 1 and Nmes = 24 resulting in a 4% 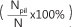 pilot message overhead. The number of the transmit and receive antennas is set to MT = MR = 2. The comparative results exhibited by the two estimators for both slow-and fast-fading channels are presented in Figure 4. It is observed that the performance of the linear MMSE CTF estimator in comparison with the adaptive VSSNLMS-based CTF estimator is very poor and worsens, for both fading channel scenarios, as the signal-to-noise (SNR) increases. The reason for the poor performance of the linear estimator is apparently as a result of the rank-deficient nature of the MIMO channel (whereby the number of channel taps to be estimated are greater than the number of known parameters for their estimation) associated with CTF estimation. It is difficult for a linear estimator like MMSE to accurately estimate the rank-deficient MIMO CTF. This problem is also alluded to by Akhtman and Hanzo10, who employed the RLS-based CTF estimator to mitigate the problem. However, it has been confirmed by Otnes and Tuchler19 that the complexity cost associated with a RLS algorithm does not predispose the algorithm to real-time implementation. In addition, linear estimators, such as the MMSE-based CTF estimator, require a prior knowledge of channel statistics not available in this scenario for their optimum performance.17 However, adaptive algorithm-based channel estimators do not require prior information of the channel and noise statistic for optimum performance.17 These algorithms enable the VSSNLMS-based CTF estimator to outperform the MMSE-based CTF estimator, as depicted in Figure 4. It is to this end, seeking good system performance together with low computational complexity of the system, that we put forward the use of the VSSNLMS-based CTF estimator for simulation of the first module of the iterative DDCE scheme for a MIMO-OFDM system.
pilot message overhead. The number of the transmit and receive antennas is set to MT = MR = 2. The comparative results exhibited by the two estimators for both slow-and fast-fading channels are presented in Figure 4. It is observed that the performance of the linear MMSE CTF estimator in comparison with the adaptive VSSNLMS-based CTF estimator is very poor and worsens, for both fading channel scenarios, as the signal-to-noise (SNR) increases. The reason for the poor performance of the linear estimator is apparently as a result of the rank-deficient nature of the MIMO channel (whereby the number of channel taps to be estimated are greater than the number of known parameters for their estimation) associated with CTF estimation. It is difficult for a linear estimator like MMSE to accurately estimate the rank-deficient MIMO CTF. This problem is also alluded to by Akhtman and Hanzo10, who employed the RLS-based CTF estimator to mitigate the problem. However, it has been confirmed by Otnes and Tuchler19 that the complexity cost associated with a RLS algorithm does not predispose the algorithm to real-time implementation. In addition, linear estimators, such as the MMSE-based CTF estimator, require a prior knowledge of channel statistics not available in this scenario for their optimum performance.17 However, adaptive algorithm-based channel estimators do not require prior information of the channel and noise statistic for optimum performance.17 These algorithms enable the VSSNLMS-based CTF estimator to outperform the MMSE-based CTF estimator, as depicted in Figure 4. It is to this end, seeking good system performance together with low computational complexity of the system, that we put forward the use of the VSSNLMS-based CTF estimator for simulation of the first module of the iterative DDCE scheme for a MIMO-OFDM system.
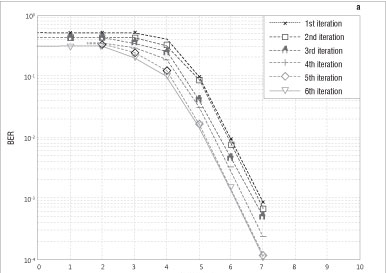
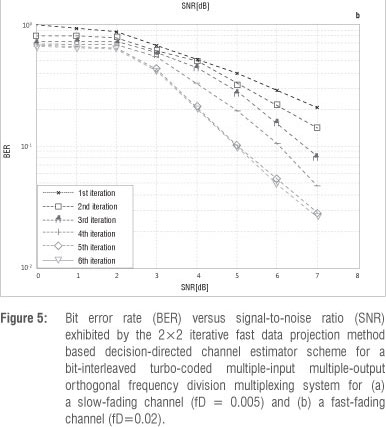
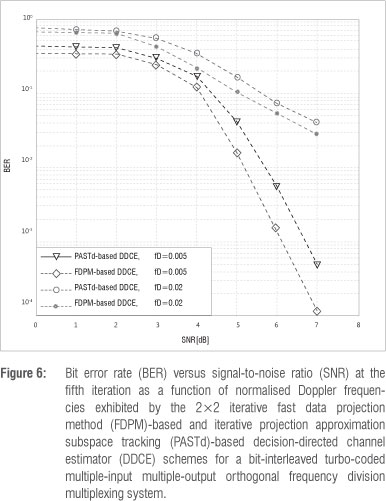
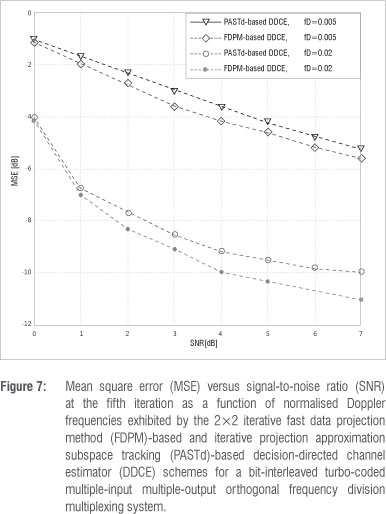
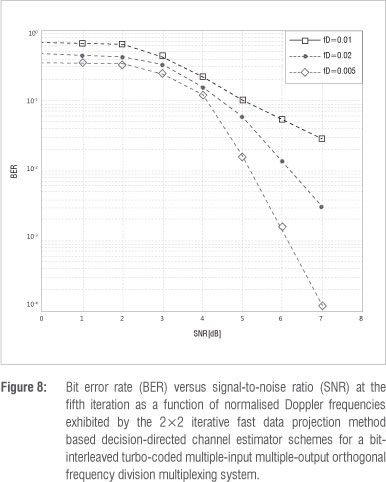
The effect of iteration between the three modules - the soft MIMO demapper, the turbo decoder and the proposed iterative DDCE - was examined over a number of iterations. The iterative DDCE is made up of the VSSNLMS-based CTF estimator, the FDPM-based parametric CIR estimator and the adaptive VSSNLMS-based predictor. The achievable bit error rate (BER) over six iterations is displayed in Figure 5a and 5b for slow- and fast-fading channels, respectively. The results show a significant improvement for both fading channels up until the fifth iteration. This improvement in the results is more noticeable for the fast-fading channel scenario. The simulation was run further for the PASTd-based CIR estimator for the DDCE proposed earlier10 for the MIMO-OFDM system. The BER and MSE performances of the FDPM-based iterative DDCE and the PASTd-based DDCE schemes after the fifth iteration are shown in Figure 6 and Figure 7, respectively. The proposed FDPM-based iterative DDCE exhibits better performance in comparison with its PASTd counterpart, especially at higher SNRs. It should be noted that the PASTd-based CIR estimator estimates each of the vector components in Equation 23 sequentially.20 However, these components are estimated simultaneously by FDPM-based CIR estimators.6 This difference certainly leads to faster convergence and improved performance of the FDPM-based CIR estimator in comparison with the PASTd-based CIR estimator, as shown in Figure 6 and Figure 7. Figure 8 shows the achievable BER performance of the proposed FDPM-based iterative DDCE as a function of the normalised Doppler frequencies 0.005, 0.02 and 0.01. The results indicate a poor performance at a very high normalised Doppler frequency of 0.01. This result suggests that it may be difficult for the proposed estimator to track a very rapidly fading channel. However, this scenario is not likely to occur in real life.
The effect of the pilot overhead 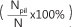 per OFDM frame in the proposed iterative DDCE was also investigated. The BER performances after the fifth iteration for the FDPM-based iterative DDCE, while varying the percentage overhead of the initialisation pilot symbols from 4% to 16% and 16% to 28% per OFDM symbol frame, are illustrated in Figure 9a and 9b for slow- and fast-fading channels, respectively. The results indicate that there is a more significant improvement in the obtainable channel estimate when the pilot overhead is increased from 4% to 16% than when it is increased from 16% to 28% in both slow- and fast-fading channels.
per OFDM frame in the proposed iterative DDCE was also investigated. The BER performances after the fifth iteration for the FDPM-based iterative DDCE, while varying the percentage overhead of the initialisation pilot symbols from 4% to 16% and 16% to 28% per OFDM symbol frame, are illustrated in Figure 9a and 9b for slow- and fast-fading channels, respectively. The results indicate that there is a more significant improvement in the obtainable channel estimate when the pilot overhead is increased from 4% to 16% than when it is increased from 16% to 28% in both slow- and fast-fading channels.
Lastly, the effect of the antenna diversity on the proposed iterative DDCE for the bit-interleaved turbo-coded MIMO-OFDM system was investigated. Figure 10a and 10b portray the achievable result with 1x1, 2x2 and 4x4 MIMO-OFDM systems for slow- and fast-fading channels. It was observed that the increment of MT and MR from MT = MR =1 to MT = MR = 4 results in a significant improvement in the BER performance of the estimator for both slow- and fast-fading channels. This improvement is largely as a result of the increased spatial diversity advantage associated with a higher number of antennas at both ends of the MIMO communication system. However, it was also noted that there is degradation in the performance of the proposed scheme for a MIMO system in relation to the single antenna system at the lower SNR for the fast-fading channel. The simple explanation for this finding is that it is difficult for the high complexity based DDCE scheme of the MIMO system, in the order of MT x MR compared with that of a single antenna system, to track the channel estimate accurately during the fast-fading channel scenario in comparison with the low complexity based DDCE scheme for a single antenna system at low SNR.
Comparative computational complexity of the scheme
In terms of complexity of the proposed iterative DDCE scheme, computational complexities of the adaptive VSSNLMS-based CTF estimator consist of M (6K+2) for multiplication or division operations and M (5K+2) for addition or subtraction operations,8 while the computational complexities of the RLS-based CTF estimator10 are 4M (K2+K) for multiplication or division operations and M (4K2+5K+2) for addition or subtraction operations, in each of the arrays of the proposed iterative DDCE scheme. The computational complexities of the adaptive VSSNLMS-based predictor algorithm are M (6Lprd+2) for multiplication or division operations and M (5Lprd+2) for addition or subtraction operations,8 while the computational complexities of the RLS-based predictor10 are 4M (L2prd+ Lprd) for multiplication or division operations and M (4L2prd+5Lprd+2) for addition or subtraction operations, in each of the arrays of the proposed iterative DDCE scheme. The FDPM subspace tracking algorithm-based CIR estimator exhibits computational complexity of the order 6KM+O(M)~O(7KM) - equal to that of the PASTd-based CIR estimator10 in each of the arrays of the proposed iterative DDCE scheme. The computational complexities of the decision-directed estimator employing a combination of LS and SAGE algorithms9 are MK for initialisation-based LS algorithms, and It(M3 +KM2+M2+3KM+K) + (MK+K) for multiplication operations and It M2 for addition operations of the SAGE algorithm. The symbol It represents the number of iterations within the SAGE algorithm. These comparative computational complexities of the estimators are tabulated in Table 1. Regarding computational complexity, it is obvious that the proposed DDCE scheme exhibited the lowest overall computational complexity, as indicated in Table 1, in comparison with its counterparts.9,10
Conclusion
We proposed a soft-input iterative DDCE scheme based on adaptive VSSNLMS and subspace tracking FDPM algorithms for the bit-interleaved turbo-coded MIMO-OFDM systems. The VSSNLMS-based temporary CTF estimator, the FDPM-based parametric CIR estimator and the adaptive VSSNLMS-based CIR predictor were derived in the context of MIMO channels for the proposed iterative DDCE scheme. We have presented and discussed simulation results portraying the performance trends of the proposed iterative DDCE for both slow- and fast-fading channels. In conclusion, the proposed estimator for MIMO-OFDM systems employing the proposed VSSNLMS and FDPM algorithms outperforms its counterpart based on the MMSE criterion and PASTd subspace algorithm. In terms of computational complexity, the proposed scheme exhibits a lower computational complexity in comparison with its counterparts9,10 described in the literature.
Acknowledgements
O.O.O. acknowledges financial support from the University of KwaZulu-Natal in the form of a postdoctoral research grant.
Authors' contributions
O.O.O. implemented the model and obtained the results. S.H.M. supervised the research. Both authors were involved with the preparation of the manuscript.
References
1. Caire G, Taricco G, Biglieri E. Bit-interleaved coded modulation. IEEE Trans Inf Theory.1998;44(3):927-946. http://dx.doi.org/10.1109/18.669123 [ Links ]
2. Ariyavisitakul SL. Turbo space-time processing to improve wireless channel capacity. IEEE Trans Commun. 2000;48(8):1347-1359. http://dx.doi.org/10.1109/26.864172 [ Links ]
3. Tonello AM. Space-time bit-interleaved coded modulation with an iterative decoding strategy. IEEE Vehicular Technology Conference; 2000 Sep 24-28; Boston, MA, USA. New York: IBM; 2000. p. 473-478. [ Links ]
4. Barhumi I, Leus G, Moonen M. Optimal training design for MIMO OFDM systems in mobile wireless channels. IEEE Trans Signal Process. 2003;51(6):1615-1624. http://dx.doi.org/10.1109/TSP.2003.811243 [ Links ]
5. Hanzo L, Munster M, Choi BJ, Keller T. OFDM and MC-CDMA for broadband multi-user communications, WLANs and broadcasting. West Sussex: John Wiley and IEEE Press; 2003. http://dx.doi.org/10.1002/9780470861813 [ Links ]
6. Doukopoulos XG, Moustakides GV. Fast and stable subspace tracking. IEEE Trans Signal Process. 2008;56(4):1452-1465. http://dx.doi.org/10.1109/TSP.2007.909335 [ Links ]
7. Oyerinde OO, Mneney SH. Decision directed channel estimation for OFDM systems employing fast data projection method algorithm. IEEE International Conference on Communications; 2009 June 14-18; Dresden, Germany. New York: IBM; 2009. p. 1-5. [ Links ]
8. Oyerinde OO, Mneney SH. FDPM aided decision directed channel estimation with VSSNLMS-based predictor for OFDM systems. IEEE International Symposium on Broadband Multimedia System and Broadcasting; 2010 March 24-26; Shanghai, China. New York: IBM; 2009. p. 1-6. [ Links ]
9. Ylioinas J, Juntti M. Iterative joint detection, decoding and channel estimation in turbo-coded MIMO-OFDM. IEEE Trans Vehicular Technol. 2009;58(4):1784-1796. http://dx.doi.org/10.1109/TVT.2008.2005724 [ Links ]
10. Akhtman J, Hanzo L. Advance channel estimation for MIMO-OFDM in realistic channel conditions. IEEE International Conference on Communications; 2007 June 24-28; Glasgow, Scotland. New York: IBM; 2009. p. 2528-2533. [ Links ]
11. Fleury BH, Tschudin M, Heddergott R. Channel parameter estimation in mobile radio environment using the SAGE algorithm. IEEE J Sel Areas Commun. 1999;17(3):434-450. http://dx.doi.org/10.1109/49.753729 [ Links ]
12. Oyerinde OO, Mneney SH. Soft iterative decision directed channel estimation for OFDM systems employing adaptive predictor. IEEE First International Conference on Wireless VITAE; 2009 May 17-20; Aalborg, Denmark. New York: IBM; 2009. p. 857-861. [ Links ]
13. Li Y Cimini L, Sollenberger N. Robust channel estimation for OFDM systems with rapid dispersive fading channels. IEEE Trans Commun. 1998;46(7):902-915. http://dx.doi.org/10.1109/26.701317 [ Links ]
14. Oyerinde OO, Mneney SH. Soft input iterative channel estimation for turbo equalization over time frequency selective fading channel. South Africa Telecommunication Networks and Applications Conference (SATNAC); 2008 Sep 7-10; Wild Coast Sun, Eastern Cape Coast, South Africa. Pretoria: SATNAC; 2008. p 77-82. [ Links ]
15. Oyerinde OO, Mneney SH. Improved soft iterative channel estimation for turbo equalization of time varying frequency selective channels. Wireless Pers Commun. 2010;52(2):325-340. http://dx.doi.org/10.1007/s11277-008-9650-7 [ Links ]
16. Golub GH, Van Loan CF. Matrix computation. Baltimore, MD: John Hopkins University Press; 1993. [ Links ]
17. Schafhuber D, Matz G. MMSE and adaptive prediction of time varying channels for OFDM systems. IEEE Trans Wireless Commun. 2005;4(2):593-602. http://dx.doi.org/10.1109/TWC.2004.843055 [ Links ]
18. Failli M. Digital land mobile radio communications COST 207. Project report. Brussels: European Commission; 1989. [ Links ]
19. Otnes R, Tuchler M. Iterative channel estimation for turbo equalization of time varying frequency selective channel. IEEE Trans Commun 2004;3(6):1918-1923. [ Links ]
20. Yang B. Projection approximation subspace tracking. IEEE Trans Signal Process. 1995;43(1):95-107. http://dx.doi.org/10.1109/78.365290 [ Links ]
 Correspondence to:
Correspondence to:
Olutayo Oyerinde
School of Engineering, Electrical, Electronic and Computer Engineering
University of KwaZulu-Natal
Howard College campus
King George V Avenue
Durban 4041, South Africa
Email: oyerinde@ukzn.ac.za
Received: 24 May 2011
Revised: 11 May 2012
Accepted: 19 July 2012