Services on Demand
Article
Indicators
Related links
-
 Cited by Google
Cited by Google -
 Similars in Google
Similars in Google
Share
South African Journal of Science
On-line version ISSN 1996-7489
Print version ISSN 0038-2353
S. Afr. j. sci. vol.108 n.7-8 Pretoria Jan. 2012
RESEARCH ARTICLE
Effect of National Senior Certificate maths on the pass rate of first-year Engineering physics
Jagathesan Govender; Mervlyn Moodley
School of Chemistry and Physics, University of KwaZulu-Natal, Durban, South Africa
ABSTRACT
There has been much controversy about the mathematics results of the 2008 National Senior Certificate examinations - the first to be written by pupils following the outcomes-based curriculum. This article examines the impact of the new high school mathematics curriculum on the performance in physics by first-year Engineering students at the University of KwaZulu-Natal. The first-year physics results of the Engineering students who wrote the 2008 National Senior Certificate (NSC) examinations were compared with the physics results of the Engineering students of the previous 4 years who wrote the Senior Certificate Examinations (SCE). Analysis of variance was used to compare the average physics marks of the NSC and SCE groups. Correlation analysis was performed to determine the relationship between performance in high school mathematics with performance in first-year physics in Engineering for both the 2008 NSC group and the 2007 SCE group. The results showed a lower physics pass rate for the NSC students compared with that of the SCE students. There was also a significant difference in the average marks obtained in physics between the NSC students and the SCE students. The new high school mathematics curriculum has fallen short in providing essential skills and techniques for students who wish to study physics at university. Furthermore, the high school mathematics results of the NSC students are an indication of considerable grade inflation.
Introduction
Prior to 2008, the Senior Certificate Examination (SCE) was the culmination of South African high school education, the results of which were used for entrance into tertiary institutions. In 1998, a new outcomes-based curriculum was introduced and the first National Senior Certificate (NSC) examination set on this curriculum was written in 2008. Unlike in the past, when subjects were offered at both higher and standard grades, all the subjects in the NSC are offered at one level. Even though the Department of Education has put considerable effort into its implementation, the outcomes-based curriculum has had its fair share of criticism. A major concern amongst tertiary educators in the mathematics and science fields has been the relegation of Euclidean geometry to an optional section of the NSC mathematics syllabus. When the results of the first 2008 NSC examination were released, they were, not surprisingly, greeted with much scepticism. A newspaper article titled 'New maths curriculum does not add up'1 laments the fact that the new mathematics curriculum denies pupils a satisfactory grounding to enable them to pursue post-matriculation studies in mathematics-dominated degrees such as Engineering and Natural Sciences. Taylor, in a newspaper article titled 'It's OBE, but not as it should be',2 argues that although contextualisation (such as calculating the height of a tree) is useful, in order for learners to learn enough trigonometry to study for an Engineering degree, they need to focus on the concepts, equations and graphs that make up the discipline. Smetherham3, in a newspaper article titled 'Varsity students lack essential skills', mentions that of the students who wrote the mathematics tests of the National Benchmarks Tests Project in February 2009, only 7% were found to be academically proficient.
The impact of the NSC curriculum on student performance at universities has been the feature of some recent research articles. Wolmarans et al.4 studied the effect of NSC mathematics on student performance in mathematics in first-year Engineering programmes, whilst Nel and Kistner5 researched the implications of the NSC on access to higher education. In this study, we investigated the influence of the 2008 outcomes-based mathematics curriculum on the physics pass rates of first-year Engineering students at the University of KwaZulu-Natal (UKZN). We first outline the reason for choosing mathematics as a predictor for success in first-year university physics.
The minimum requirements for entry into the BSc Engineering Programme (except Chemical Engineering) offered by UKZN are a C-symbol in both higher-grade mathematics and higher-grade physical science with a total of 33 matriculation points for SCE students, and a Level 6 pass in both mathematics and physical science with a total of 35 matriculation points for NSC students. Physics is a compulsory module in each semester of the first-year curriculum of the BSc Engineering degrees. All Engineering students, except those registered for Chemical Engineering, register for PHYS151, a 16-credit calculus-based physics module in the first semester. The topics studied in this module are: motion in one and two dimensions, Newton's Laws, work and energy, momentum, rotation of rigid bodies, elasticity, fluid mechanics, periodic motion, mechanical waves, sound, temperature and heat, and the thermal properties of matter. As with all modules in physics, a good grasp of mathematics is essential for students to succeed in this module. Landau, the Nobel prize winning physicist, often expressed the following sentiment when he advised students wishing to study physics: [acquire good] 'mathematical techniques, that is, the ability to solve concrete mathematical problems'6.
All South African tertiary institutions require a pass in high school mathematics as a prerequisite for entrance into their Science and Engineering faculties. Various studies have been made on the use of mathematics as a predictor of success in first-year university science courses. Eiselen et al.7 undertook a study amongst a set of bridging programme students at the University of Johannesburg to determine how basic mathematical skills acquired at high school can serve as predictors of success in first-semester mathematics. They found that the probability of being successful in first-semester mathematics increased with increasing performance in high school mathematics. Leopold and Edgar8 designed a calculator-free mathematics assessment for second-semester chemistry students at the University of Minnesota. This test consisted of 20 multiple choice questions on logarithms, scientific notation, graphs and algebra, and was administered as a surprise test. The chemistry course grades obtained by the students showed significant correlation with the scores obtained in a subset of the mathematics assessment test. Hudson and Liberman9 used a pretest of computational skills in algebra and trigonometry in an algebra-based introductory physics course at the University of Houston, Texas. This test, together with an instrument to measure abstract reasoning, was used to predict more than 25% of the variance in the final physics grade. Cohen et al.10 randomly chose students from four introductory physics courses at the University of Vermont to correlate their verbal and mathematics scores in the Scholastic Aptitude Tests to their performance in Piagetian tasks with their final course grades. They found that the mathematics score was the most successful in predicting success.
We will show in this article that the mark for mathematics obtained by the 2009 cohort of NSC students enrolled for first-year Engineering at UKZN is not a true representation of their mathematical skills. Whether the NSC students' high mathematics marks are as a result of an overly simplified school mathematics syllabus or 'grade inflation' will also be addressed.
Method
Students' performances in the first-semester Engineering physics module, PHYS151, were analysed for the period 2005 to 2009. Only students who had registered for this module for the first time and had written the final examination for this module were included in the sample. In other words, students repeating the module and those coming from access programmes were excluded. The sample of the 2009 cohort of new students included only those who had written their matriculation examination in 2008 (the NSC students). The annual sample size ranged between 250 and 300 students. A comparison was made of the pass rates of these students in the PHYS151 module for the years 2005 to 2009. The average physics marks for the years 2005 to 2009 were compared using analysis of variance (ANOVA, Microsoft Excel). The mathematics marks obtained in the matriculation examinations (hereafter referred to as matric maths mark) by the students in the 2009 sample were correlated with their physics marks obtained in PHYS151.
The 2008 and 2009 cohorts of students were further categorised into four bands according to the quality of their matric maths marks. The number of students in each band for both 2008 and 2009 are shown in Table 1. It must be noted that Band 4 did not apply to 2009 students, because the entrance qualification for entry into the Engineering Faculty is now a minimum of a Level 6 pass in maths (70% to 79%) compared to a minimum of a C-symbol (60% to 69%) for the years prior to 2009.
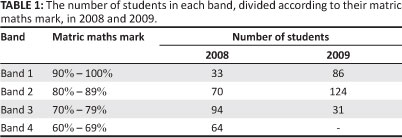
A comparison of the pass rates for each of these bands was made for the years 2009 and 2008. The average marks obtained by each band were compared using ANOVA. Finally, the results of the students from the 2009 sample who had written the second-semester physics module, PHYS152, were then analysed and compared with their matric maths marks. The numbers of students in each band for PHYS152 were: 82 students in Band 1, 74 students in Band 2 and 8 students in Band 3.
Results
Comparison of physics pass rates for the period 2005-2009
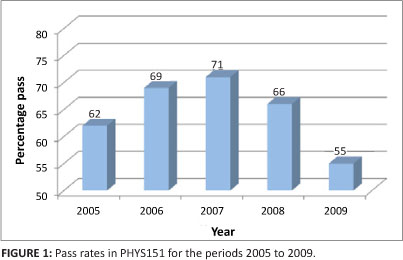
The pass rates for first-time students who qualified to write the final examination for the Engineering physics module PHYS151 for the years 2005 to 2009 are illustrated in Figure 1. These pass rates include students who passed after writing the supplementary examinations. Students qualify for the supplementary exam if they obtain a mark between 39% and 50% in the main examination. The average physics pass rate for the years 2005 to 2008 was 67%, whereas the pass rate for 2009 was 55%. It is evident that the physics pass rate of the NSC students (2009) was dramatically lower than those of the SCE students in 2005 to 2008.
Comparison of average physics marks for the period 2005-2009
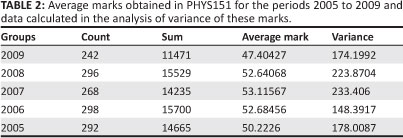
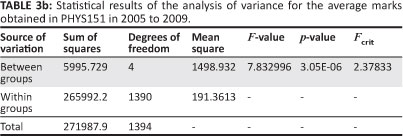
Data used in the ANOVA of the average mark (expressed as a percentage) in PHYS151 obtained by the cohorts of the years from 2005 to 2008 (SCE students) and 2009 (NSC students) are shown in Table 2. The statistical results of these analyses are shown in Table 3.
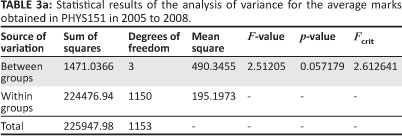
Because the F-value (2.51205) is less than the critical value Fcrit (2.612641), we concluded that there was no significant difference in the average marks obtained by PHYS151 students during the years 2005 to 2008 (Table 3a). This finding implies that the quality of the SCE students did not change over this period.
When the cohort of 2009 (NSC) students was included in the analysis, the results were somewhat different, as shown in Table 3b. Because the F-value (7.832996) is greater than the critical value Fcrit (2.37833), we concluded that there was a significant difference between the marks obtained by PHYS151 students during 2009 and those obtained in the previous years, 2005 to 2008.
First-semester pass rates compared with matric maths mark
The scatter plot in Figure 2 shows the correlation between the matric maths mark and the marks obtained in PHYS151 for the 2009 cohort of students. For illustration purposes, the graph was drawn by binning the average of the PHYS151 marks of all the students who had the same matric maths mark (ranging from 2 to 16 students per point).
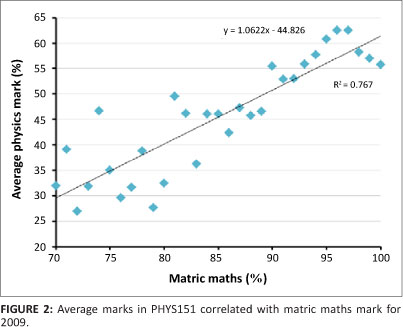
The analysis shows that there is a strong statistical correlation between the matric maths mark and the average physics marks obtained by the students (r = 0.875). When a similar analysis was done for the 2008 cohort, the correlation coefficient was 0.865. The first-semester (PHYS151) pass rates for each band (banded according to matric maths mark) for the years 2008 and 2009 are illustrated in Figure 3.
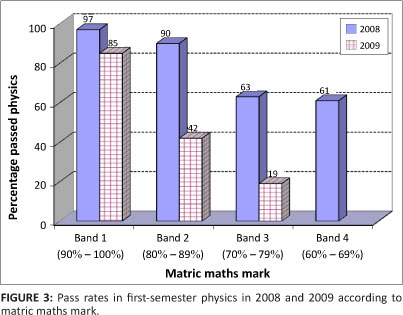
It is evident that the most successful students in the 2009 physics examinations, with a pass rate of 85%, were the ones who had obtained matric maths passes of 90% and above. Only 42% of the students who had matric maths passes of between 80% and 89% passed physics in 2009, whilst the physics pass rate for those with matric maths passes between 70% and 79% was a very low 19%. This trend is also evident with the 2008 students, but with significantly higher pass rates in each band. The 2008 students in Bands 1 and 2 had pass rates above 90%, whilst those in Bands 3 and 4 had pass rates above 60%.
Second-semester physics pass rates compared with matric maths mark
Of the 242 NSC students who wrote PHYS151 in the first semester, 168 sat for the examination for the second-semester physics module (PHYS152). These 168 students included those who had failed PHYS151, but who had achieved above 40%, which is the minimum requirement for entry into the second-semester module. The pass rate for the PHYS152 module was 86%. Figure 4 shows the pass rates in PHYS152 for the different bands of matric maths for the 2009 cohort.
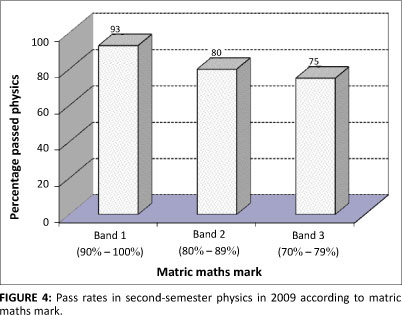
The disparities in the pass rates for the three bands in the PHYS152 module were not as great as in the PHYS151 module. This trend is consistent with that seen historically for students doing a second semester of physics after successfully passing the first semester of physics. The number of students in each band who passed first-semester (PHYS151) or second-semester (PHYS152) physics are summarised in Table 4. Band 1 (consisting of 82 students) had 10 students who failed PHYS151 in June and of these 7 passed PHYS152. This result means that 70% of the students failing in June passed at the end of the year. Band 1 also included three students who passed PHYS151 in June but who failed PHYS152. Band 2 (74 students) included 25 students who failed PHYS151 in June, of whom 14 passed at the end of the year (a pass rate of 56%). Band 2 also included four students who passed PHYS151 in June but who failed the second physics module. Band 3 (12 students) included two students who failed PHYS151 in June, one of whom passed at the end of the year (a pass rate of 50%). Band 3 also included one student who passed PHYS151 in June but who failed the second physics module.
Discussion and concluding remarks
In the 4-year period studied, our results show that the pass rate for PHYS151 prior to 2009 averaged 67%, with the average mark being fairly consistent. However, in 2009 - the first year to be undertaken by students who wrote the new NSC examination - there was a dramatic decrease in both the pass rate and the average module mark for PHYS151. As the core of the lecturing staff of PHYS151 has remained fairly stable for the period 2005 to 2009 and the teaching and examining of this module has been reasonably consistent, we can conclude that the new NSC curriculum produced students less prepared for university study than the previous SCE curriculum. This result is also supported by the studies made by Nel and Kistner5 and Wolmarans et al.4 Despite the noble intentions of outcomes-based education to make knowledge more accessible and more relevant to the lives of learners, the NSC mathematics curriculum does not seem to have equipped students with the fundamental skills and techniques necessary for success in post-matriculation studies in the sciences.
The 2008 NSC mathematics results also reinforce the notion of grade inflation - in which the matric marks obtained by the students are not matched by their actual performance. Grade inflation was particularly noticeable in the performance of the 2009 cohort of students who had obtained between 69% and 89% in their NSC mathematics. Only 38% of these students passed PHYS151, whereas 74% of the students of the 2008 cohort in this range passed PHYS151.
Umalusi's 2008 Maintaining Standards Report11 reveals that the 2008 NSC mathematics examinations comprised 72% of questions based on factual knowledge and routine calculations whilst the remaining 28% were on performing complex procedures and solving problems. By comparison, the report reveals that the 2005 to 2007 SCE mathematics examinations had 52% of questions based on factual knowledge and routine calculations and 48% based on performing complex procedures and solving problems. Based on this finding, a student writing the 2008 NSC mathematics examination would get 80% by correctly answering all the questions based on factual knowledge and routine calculations and only correctly answering 8% of the questions based on complex procedures and solving problems. Students who wrote the 2005, 2006 or 2007 SCE mathematics examinations would have needed to get 28% of the questions based on complex procedures and solving problems correct in addition to answering all the factual knowledge and routine calculation questions correctly to get 80%.
Grade inflation is not unique to this country, and is a phenomenon that is under much discussion in the USA and UK. In 2003, the Programme for International Assessment found that 15-year-old students from the USA ranked 23 out of 43 countries in mathematics,12 although they were performing quite well in their own national standardised tests. In the UK, Smithers13 found that the percentage of A-symbols in A-level examinations had increased from under 10% in 1995 to over 20% in 2005. Grade inflation is normally associated with falling standards, but can also be explained by any number of factors such as a change in curriculum, improvements in the manner of examining (for example, greater structuring of questions in examinations) and increased use of continuous assessment.
Our results showed a strong correlation between the matric maths mark and the physics mark obtained in PHYS151. This correlation has not diminished in the changeover from SCE to NSC, as can be seen by the correlation coefficients of 0.58 in 2008 and 0.55 in 2009. The matric maths mark continues to be a fairly good predictor of success in first-year Engineering physics.
The students' performance in the second-semester physics module PHYS152 in 2009 showed an improvement from that of the first semester. Although the PHYS152 pass rate for the NSC students was 86%, because only 168 of the original 242 wrote this module, the pass rate based on the initial enrolment was 60% (compared to 55% for PHYS151). Although students generally perform better in the second semester of their first year, having adapted to the rigours of university life, the 2009 cohort's improved performance in physics can be partly attributed to their increased mathematics fluency. The deficiencies in their mathematics knowledge would have been eliminated by their study of the first-semester and second-semester mathematics modules, which are taken as part of the Engineering curriculum.
The findings of this study do not necessarily mean that the new NSC mathematics curriculum is inherently flawed and should be completely overhauled. It is evident that in 2008, the year of the first NSC examinations and the first year in which mathematics was examined as a single grade, the examiners set a much easier paper than those of previous years. However, another factor which could have led to the inflated marks was the exemplar papers. These sample papers were set by the Department of Education to prepare teachers and learners for the new examinations of 2008, and Umalusi's 2008 Maintaining Standards Report11 found that the cognitive levels of the exemplar mathematics papers were similar to those of the final papers. Further studies over a longer period of time need to be conducted to determine the validity and reliability of the NSC mathematics curriculum. It must also be noted that at the time of this publication, the NSC mathematics curriculum was undergoing some changes, with some topics such as Euclidean geometry, exponents and logarithms being reintroduced into the curriculum.
Acknowledgements
Competing interests
We declare that we have no financial or personal relationships which may have inappropriately influenced us in writing this article.
Authors' contributions
J.G. was the project leader. J.G. and M.M. were both responsible for the compilation of the statistics and graphs. J.G. wrote the manuscript with assistance from M.M. M.M. made conceptual contributions, and was responsible for the editing and referencing of the manuscript.
References
1. Taylor N. It's OBE, but not as it should be. Mail and Guardian 2008 April 15. [ Links ]
2. Blaine S. New maths curriculum does not add up. Business Day 2010 May 24. [ Links ]
3. Smetherham J. Varsity students lack essential skills. The Star 2009 Aug 11. [ Links ]
4. Wolmarans N, Smit R, Collier-Reed B, Leather H. Addressing concerns with the NSC: An analysis of first-year student performance in Mathematics and Physics. Paper presented at: SAARMSTE 2010. Proceedings of the 18th Conference of the Southern African Association for Research in Mathematics, Science and Technology Education: Crossing the boundaries; 2010 January 18-21; Pinetown, KwaZulu-Natal, South Africa. Durban: University of KwaZulu-Natal; 2010. 274-284. [ Links ]
5. Nel C, Kistner L. The National Senior Certificate: Implications for access to higher education. S Afr J High Educ. 2009;23(5):953-973. [ Links ]
6. Lifshitz EM. L.D. Landau's plain talk to students of physics. Am J Phys. 1977;45(5):415-422. http://dx.doi.org/10.1119/1.10828 [ Links ]
7. Eiselen R, Strauss J, Jonck B. A basic mathematical skills test as predictor of performance at tertiary level. S Afr J High Educ. 2007;21(1):38-39. [ Links ]
8. Leopold DG, Edgar B. Degree of mathematics fluency and success in second-semester introductory chemistry. J Chem Educ. 2008;85(5):724-731. http://dx.doi.org/10.1021/ed085p724 [ Links ]
9. Hudson T, Liberman D. The combined effect of mathematics skills and formal operational reasoning on student performance in the general physics course. Am J Phys. 1982;50(12):1117-1119. http://dx.doi.org/10.1119/1.12895 [ Links ]
10. Cohen HD, Hillman DF, Agne RM. Cognitive level and college physics achievement. Am J Phys. 1978;46(10):1026-1029. http://dx.doi.org/10.1119/1.11422 [ Links ]
11. 2008 Maintaining Standards Report: Part 3: Exam Paper Analysis. Pretoria: UMALUSI; 2009. [ Links ]
12. Mathematics Teaching and learning strategies in PISA. Paris: Organisation for Economic Co-operation and Development; 2010. [ Links ]
13. Smithers A. Do school exams need reforming? Buckingham: University of Buckingham; 2005. [ Links ]
 Correspondence to:
Correspondence to:
Jagathesan Govender
Private Bag X 54001, Durban 4000, South Africa
Email: govenderj@ukzn.ac.za
Received: 05 July 2011
Accepted: 02 Feb. 2012
Published: 2 July 2012
© 2012. The Authors. Licensee: AOSIS OpenJournals. This work is licensed under the Creative Commons Attribution License.














