Serviços Personalizados
Artigo
Indicadores
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em Google
Similares em Google
Compartilhar
South African Journal of Science
versão On-line ISSN 1996-7489
versão impressa ISSN 0038-2353
S. Afr. j. sci. vol.107 no.9-10 Pretoria Out. 2011
RESEARCH LETTER
Effects of internal heat generation, thermal radiation and buoyancy force on a boundary layer over a vertical plate with a convective surface boundary condition
Philip O. OlanrewajuI; Jacob A. GbadeyanI; Tasawar HayatII; Awatif A. HendiIII
IDepartment of Mathematics, Covenant University, Ota, Ogun State, Nigeria
IIDepartment of Mathematics, Quaid-I-Azam University, Islamabad, Pakistan
IIIDepartment of Physics, Faculty of Science, King Saud University, Riyadh, Saudi Arabia
ABSTRACT
In this paper we analyse the effects of internal heat generation, thermal radiation and buoyancy force on the laminar boundary layer about a vertical plate in a uniform stream of fluid under a convective surface boundary condition. In the analysis, we assumed that the left surface of the plate is in contact with a hot fluid whilst a stream of cold fluid flows steadily over the right surface; the heat source decays exponentially outwards from the surface of the plate. The similarity variable method was applied to the steady state governing non-linear partial differential equations, which were transformed into a set of coupled non-linear ordinary differential equations and were solved numerically by applying a shooting iteration technique together with a sixth-order Runge-Kutta integration scheme for better accuracy. The effects of the Prandtl number, the local Biot number, the internal heat generation parameter, thermal radiation and the local Grashof number on the velocity and temperature profiles are illustrated and interpreted in physical terms. A comparison with previously published results on similar special cases showed excellent agreement.
Introduction
Boundary-layer flows over a moving or stretching plate are of great importance in view of their relevance to a wide variety of technical applications, particularly in the manufacture of fibres in glass and polymer industries. The first and foremost work regarding boundary-layer behaviour in moving surfaces in a quiescent fluid was performed by Sakiadis.1
Subsequently, many researchers2,3,4,5,6,7,8,9 worked on the problem of moving or stretching plates under different situations. In the boundary-layer theory, similarity solutions were found to be useful in the interpretation of certain fluid motions at large Reynolds numbers. Similarity solutions often exist for the flow over semi-infinite plates and stagnation point flow for two-dimensional, axisymmetrical and three-dimensional bodies. In special cases, when there is no similarity solution, one has to solve a system of non-linear partial differential equations. For similarity boundary-layer flows, velocity profiles are similar. But this kind of similarity is lost for non-similarity flows.10,11,12,13,14 Obviously, the non-similarity boundary-layer flows are more general in nature and are more important, not only in theory but also in application.
The heat-transfer analysis of boundary-layer flows with radiation is also important in electrical power generation, astrophysical flows, solar power technology, space vehicle re-entry and other industrial areas. Extensive literature that deals with flows in the presence of radiation effects is now available. Raptis et al.15 studied the effect of thermal radiation on the magnetohydrodynamic flow of a viscous fluid past a semi-infinite stationary plate. Hayat et al.16 extended the analysis of reference15 for a second-grade fluid.
Convective heat transfer studies are very important in processes involving high temperatures, such as gas turbines, nuclear plants and thermal energy storage. Recently, Ishak17 examined the similarity solutions for flow and heat transfer over a permeable surface with convective boundary condition. Moreover, Aziz18,19 studied a similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition and also studied hydrodynamic and thermal slip flow boundary layers over a flat plate with a constant heat flux boundary condition. Very recently, Makinde and Olanrewaju20 investigated the buoyancy effects on a thermal boundary layer over a vertical plate with a convective surface boundary condition.
In this study, the recent work of Ishak17, Aziz18 and Makinde and Olanrewaju20 was extended to include the effect of thermal radiation and internal heat generation. The numerical solutions of the resulting momentum and the thermal similarity equations are reported for representative values of the thermophysical parameters embedded in the fluid-convection process. The objective of this paper was to explore the effects of thermal radiation and internal heat generation on the fluid under a convective surface boundary condition. The non-linear equations governing the flow were solved numerically using a shooting technique together with a sixth-order Runge-Kutta integration scheme, which gives better accuracy than a fourth-order Runge-Kutta method. Graphical results are first reported for emerging parameters and then discussed.
Mathematical formulation
We considered a two-dimensional steady incompressible fluid flow coupled with heat transfer by convection over a vertical plate. A stream of cold fluid at temperature T∞ moved over the right surface of the plate with a uniform velocity U∞ whilst the left surface of the plate was heated by convection from a hot fluid at temperature Tf , which provided a heat transfer coefficient hf . The density variation as a result of buoyancy force effects was taken into account in the momentum equation and the thermal radiation and the internal heat generation effects were taken into account in the energy equation (the Boussinesq approximation). The continuity, momentum and energy equations describing the flow are, respectively:
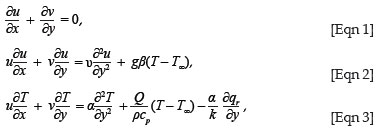
where u and v are the x (along the plate) and the y (normal to the plate) components of the velocities, respectively. T is the temperature, υ is the kinematics viscosity of the fluid, α is the thermal diffusivity of the fluid, β is the thermal expansion coefficient, Q is the heat released per unit per mass, g is the gravitational acceleration, qr is the radiative heat flux and k is the thermal conductivity. The velocity boundary conditions can be expressed as

and

The boundary conditions at the plate surface and far into the cold fluid may be written as

and

The radiative heat flux qr is described by the Rosseland approximation such that

where σ* and K are the Stefan-Boltzmann constant and the mean absorption coefficient, respectively. Following Chamkha21, we assume that the temperature differences within the flow are sufficiently small such that T 4 can be expressed as a linear function after using the Taylor series to expand T 4 about the free stream temperature T∞ and neglecting higher-order terms. This result is the following approximation:

Using [Eqn 8] and [Eqn 9] in [Eqn 3], we obtain

We then introduce a similarity variable η and a dimensionless stream function f(η) and temperature θ(η) as
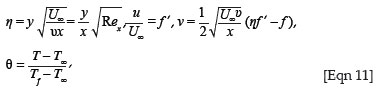
where the prime symbol denotes differentiation with respect to η and Rex = U∞x/υ is the local Reynolds number. [Eqn 1] to [Eqn 7] reduce to:
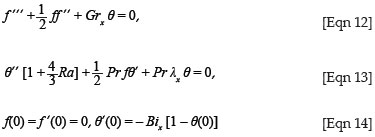
and

where
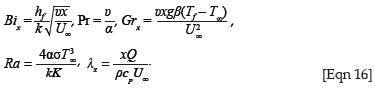
Bix is the local Biot number, Pr is the Prandtl number, Grx is the local Grashof number, Ra is the radiation parameter and λx is the internal heat generation parameter. For the momentum and energy equations to have a similarity solution, the parameters Grx, λx and Bix must be constants and not functions of x as in [Eqn 16]. This condition can be met if the heat-transfer coefficient hf is proportional to x-½ , the thermal expansion coefficient β is proportional to x-1 and the heat-release coefficient Q is proportional to x-1. We therefore assume

where c, d and m are constants. Substituting [Eqn 17] into [Eqn 16], we get
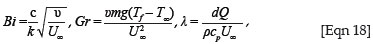
Bi, λ and Gr defined by [Eqn 18] are the Biot number, the internal heat generation parameter and the Grashof number, respectively. The solutions of [Eqn 12] to [Eqn 15] yield the similarity solutions. However, the solutions generated are the local similarity solutions whenever Bix, λx and Grx are defined as in [Eqn 13].
Results and discussion
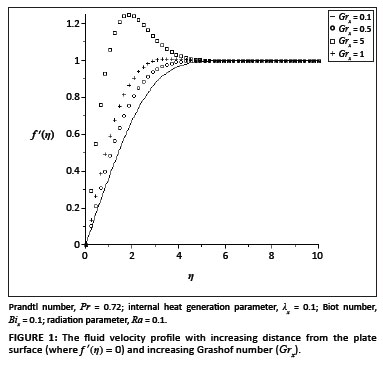
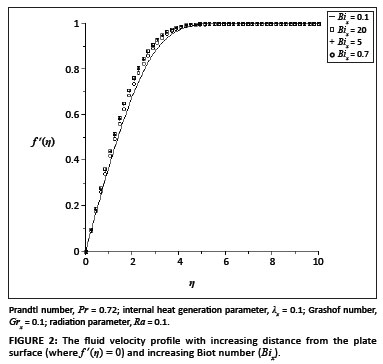
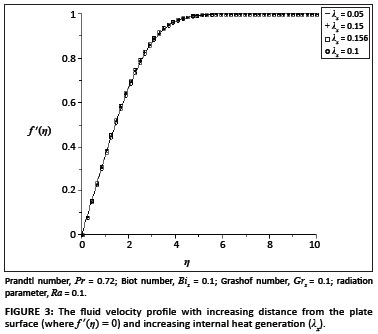
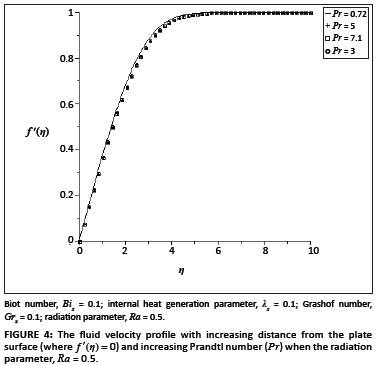
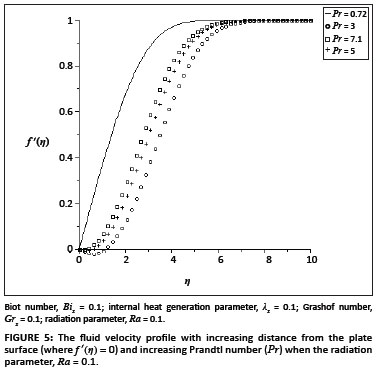
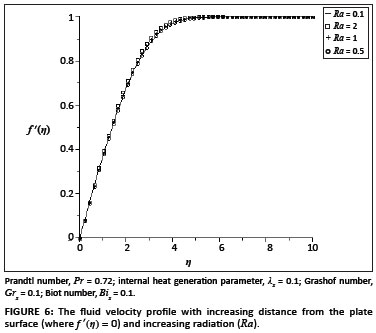
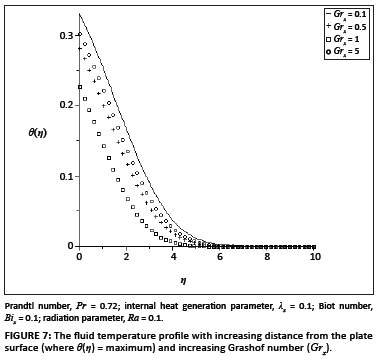
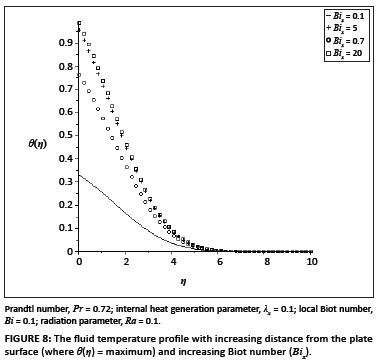
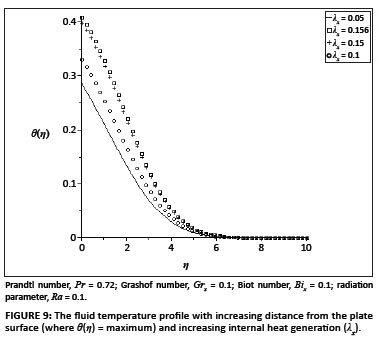
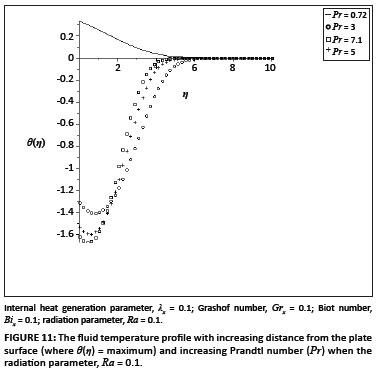
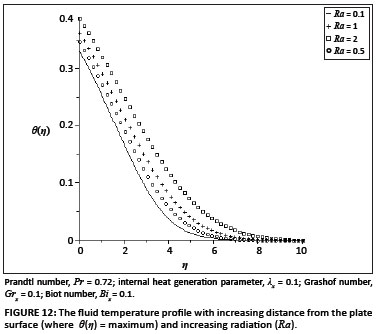
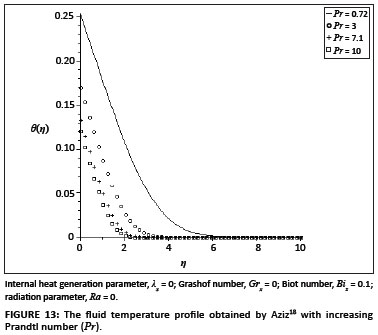
The ordinary differential equations ([Eqn 9] and [Eqn 10]) subject to the boundary conditions ([Eqn 11] and [Eqn 12]) were solved numerically using the symbolic algebra software Maple.22 Table 1 presents a comparison of the values of -θ' (0) and θ(0) with those reported by Aziz18, Ishak17 and Makinde and Olanrewaju20, which show an excellent agreement for Pr = 0.72. Table 2 shows the values of the skin-friction coefficient f ''(0) and the local Nusselt number -θ'(0), for various values of embedded parameters. From Table 2, it can be seen that the skin friction and the rate of heat transfer at the plate surface increased with an increase in the local Grashof number, the convective surface heat transfer parameter, the internal heat generation parameter and the radiation absorption parameter. However, an increase in the fluid Prandtl number decreased the skin friction but increased the rate of heat transfer at the plate surface. Figures 1-6 depict the fluid velocity profiles. Generally, the fluid velocity is zero at the plate surface and increases gradually away from the plate towards the free stream value satisfying the boundary conditions. It is clearly seen from Figure 1 that the Grashof number had profuse effects on the velocity boundary layer thickness. It is interesting to note that an increase in the intensity of the convective surface heat transfer (Bix) produced a slight increase inthe fluid velocity within the boundary layer (Figure 2). The local internal heat generation parameter, the Prandtl number and the local Biot number had little or no influence on the velocity profiles (Figures 3-4 and Figure 6), which could be justified by [Eqn 12], which had a small value for the Grashof number. When Ra = 0.1, the Prandtl number effected the velocity profile (Figure 5) and the negative part could have been caused by the value of the Grashof number used (see [Eqn 12]) and the value of the radiation parameter used (see [Eqn 13]). Figures 7-12 illustrate the fluid temperature profiles within the boundary layer. The fluid temperature was at a maximum at the plate surface and decreased exponentially to zero away from the plate, thus satisfying the boundary conditions. From these figures, it is noteworthy that the thermal boundary layer thickness increased with an increase in Bix,λx and Ra and decreased with increasing values of Grx and Pr. Hence, the convective surface heat transfer, the internal heat generation parameter and the radiation parameter enhanced thermal diffusion whilst an increase in the Prandtl number and the intensity of buoyancy force slowed down the rate of thermal diffusion within the boundary layer. Figure 13 shows the influence of Prandtl numbers on the thermal boundary layer, as obtained by Aziz18.

Conclusions
We analysed the effects of internal heat generation, thermal radiation and buoyancy force on the laminar boundary layer about a vertical plate in a uniform stream of fluid under a convective surface boundary. A similarity solution for the momentum and the thermal boundary layer equations is possible if the convective heat transfer of the fluid heating the plate on its left surface is proportional to x-½ and if the thermal expansion coefficient β and the heat released per unit per mass Q are proportional to x-1. Numerical solutions of the similarity equations were reported for the various parameters embedded in the problem. The combined effect of increasing the Prandtl number and the Grashof number tended to reduce the thermal boundary layer thickness along the plate whilst the effects of increasing the Biot number, the internal heat generation parameter and the radiation absorption parameter enhanced thermal diffusion.
Acknowledgement
O.P.O. wishes to thank Covenant University, Ogun State, Nigeria for its generous financial support. A.A.H., as a VP, appreciates the support of King Saud University, Saudi Arabia (KSU-VPP-117).
References
1. Sakiadis BC. Boundary-layer behavior on continuous solid surfaces. I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961;7:26-28. doi:10.1002/aic.690070108 [ Links ]
2. Crane IJ. Flow past a stretching plate. Z Angew Math Phys. 1970;21(56):1-37. [ Links ]
3. Gupta PS, Gupta AS. Heat and mass transfer on a stretching sheet with suction and blowing. Can J Chem Eng. 1977;55:744-746. doi:10.1002/cjce.5450550619 [ Links ]
4. Carragher P, Crane IJ. Heat transfer on a continuous stretching sheet. Z Angew Math Mech. 1982;62:564-565. doi:10.1002/zamm.19820621009 [ Links ]
5. Danberg JE, Fansler KS. A nonsimilar moving wall boundary-layer problem. Quart Appl Math. 1976;34:305-309. [ Links ]
6. Chakrabarti A, Gupta AS. Hydromagnetic flow and heat transfer over a stretching sheet. Quart Appl Math. 1979;37:73-78. [ Links ]
7. Vajravelu K. Hydromagnetic flow and heat transfer over a continuous moving porous, flat surface. Acta Mech. 1986;64:179-185. doi:10.1007/BF01450393 [ Links ]
8. Dutta BK. Heat transfer from a stretching sheet with uniform suction and blowing. Acta Mech. 1986;78:255-262. doi:10.1007/BF01179221 [ Links ]
9. Lee SL, Tsai JS. Cooling of a continuous moving sheet of finite thickness in the presence of natural convection. Int J Heat Mass Transfer. 1990;33:457-464. doi:10.1016/0017-9310(90)90181-S [ Links ]
10. Wanous KJ, Sparrow EM. Heat transfer for flow longitudinal to a cylinder with surface mass transfer. J Heat Transf ASME Ser C. 1965;87(1):317-319. [ Links ]
11. Catherall D, Stewartson K, Williams PG. Viscous flow past a flat plate with uniform injection. Proc R Soc A. 1965;284:370-396. doi:10.1098/rspa.1965.0069 [ Links ]
12. Sparrow EM, Quack H, Boerner CJ. Local non-similarity boundary layer solutions. J AIAA 1970;8(11):1936-1942. [ Links ]
13. Sparrow EM, Yu HS. Local non-similarity thermal boundary-layer solutions. J Heat Transf ASME. 1971;93:328-334. [ Links ]
14. Massoudi M. Local non-similarity solutions for the flow of a non-Newtonian fluid over a wedge. Int J Non-Linear Mech. 2001;36:961-976. doi:10.1016/S0020-7462(00)00061-5 [ Links ]
15. Raptis A, Perdikis C, Takhar HS. Effects of thermal radiation on MHD flow. Appl Math Comput. 2004;153:645-649. doi:10.1016/S0096-3003(03)00657-X [ Links ]
16. Hayat T, Abbas Z, Sajid M, Asghar S, The influence of thermal radiation on MHD flow of a second grade fluid. Int J Heat Mass Transfer. 2007;50:931-941. doi:10.1016/j.ijheatmasstransfer.2006.08.014 [ Links ]
17. Ishak A. Similarity solutions for flow and heat transfer over a permeable surface with convective boundary condition. Appl Math Comput. 2010;217:837-842. doi:10.1016/j.amc.2010.06.026 [ Links ]
18. Aziz A. A similarity solution for laminar thermal boundary layer over a flat plate with a convective surface boundary condition. Commun Nonlinear Sci Numer Simulat. 2009;14:1064-1068. [ Links ]
19. Aziz A. Hydrodynamic and thermal slip flow boundary layers over a flat plate with constant heat flux boundary condition. Commun Nonlinear Sci Numer Simulat. 2010;15:573-580. doi:10.1016/j.cnsns.2009.04.026 [ Links ]
20. Makinde OD, Olanrewaju PO. Buoyancy effects on thermal boundary layer over a vertical plate with a convective surface boundary condition. J Fluids Eng. 2010;132:044502-0044505. doi:10.1115/1.4001386 [ Links ]
21. Chamkha AJ. Hydromagnetic natural convection from an isothermal inclined surface adjacent to a thermally stratified porous medium. Int J Eng Sci. 1997;37:975-986. doi:10.1016/S0020-7225(96)00122-X [ Links ]
22. Heck A. Introduction to Maple. 3rd ed. New York: Springer-Verlag; 2003. [ Links ]
 Correspondence to:
Correspondence to:
Philip Olanrewaju
Postal address: Department of Mathematics, Covenant University, Ota
Ogun State
PMB 1023, Nigeria
Email: oladapo_anu@yahoo.ie
Received: 14 Oct. 2010
Accepted: 03 May 2011
Published: 07 Sept. 2011
© 2011. The Authors. Licensee: AOSIS OpenJournals. This work is licensed under the Creative Commons Attribution License.














